0 引　言

剖面浮标是海洋探测中应用最早的海洋观测平台之一，主要目标是观测与气候变化相关的海洋信息，包括海洋温度、盐度和海流等^[1]。目前国际上用于海洋水下移动观测的浮标主要是Argo浮标^[2]。一般浮标搭载的电池容量有限，能源问题是实现长时间观测的一个急需解决的问题。

浮标整个工作阶段耗能最大部分是周期运动中进行浮力调节所消耗的能量，因此需要重点研究浮力调节的控制策略，来实现能源的有效分配和合理利用。Agrawal^[3]和Sumantt^[4]等对应用变重力式浮力调节系统的UUV进行了运动过程模拟，具有一定的实际应用价值。对于应用变体积式浮力调节系统的水下载体这一类型也有大量的探索和研究。Emest Petzrick等^[5]在APEX-Deep浮标试验中验证了连续低速排油所消耗的能量少于常规的一次性排油所消耗的能量。陈鹿等^[6]通过设定上浮速度区间的方式实现特定条件下的排油，所采用的方法可以将能耗减少大约51.16%，但过程中对速度区间的设置仅为经验值，而且需要频繁启动电机和泵，对设备损耗较大。穆为磊等^[7]分析了当上浮速度为0时开启一次排油方法的能耗，此方法本质上是将速度区间中的最低速度设为0时的特殊情况，没有从实质上探究出速度区间对分段排油策略耗能的影响。针对浮力调节最佳策略的选择问题，本文对浮标运动特性以及耗能原因进行分析，研究浮标上浮过程中速度区间的设置对总体耗能的影响，得到能源消耗模型以及在设定某一速度区间的情况下总耗能与调节次数的关系曲线。

1 浮标运动过程中的耗能阶段

剖面浮标通过周期性上浮下潜运动完成目标海域海洋参数的测量。在一个完整的运动周期内，剖面浮标通过浮力调节系统进行回油和充油来改变浮标的排水体积，实现上浮和下潜运动^[8]。

浮标在一个周期内主要有“下潜-漂流-再次下潜-上浮”4个运动过程，剖面浮标下潜过程中，只需开启电磁阀，外油囊中的液压油在海水压力下自发被动回流。而上浮阶段中的排油过程通常是在深海高压环境下进行的，需要克服海水压力做功，是整个周期中的主要能量消耗阶段^[9]。因此，本文重点研究上浮阶段中浮力调节系统的低能耗控制策略。

通过采用分段排油策略，在海水压力大的深度下尽量少排油，随着浮标上浮，海水压力深度变小，此时再排油的功耗会小于高压环境下排等体积油所需要消耗的能量，因此分段排油策略可以有效减少能耗。

随着分段排油次数的增加，浮标完成一次上浮运动所需要的时间也会随之变得很大，从而使得浮标运动周期非常长，无法满足海洋科学数据的实际测量需求，因此在分段排油过程中所产生的浮力要能够使速度维持在数据测量所要求的速度区间。综上，需要同时考虑能耗和上浮时间这2个主要因素的影响。上浮时间的控制可以通过设置速度区间来实现，因此分段浮力调节策略的研究即是分别研究速度区间和调节次数与总功耗之间的关系。

2 模型建立与分析 2.1 运动分析

由于浮标外形尺寸一般较小，与水中运动尺度相比基本可忽略不计，因此在运动分析过程中，浮标可被视为质点。在本文的分段排油控制策略研究中，是把一次性排油分为 $n$ 次，在速度低于某一值时进行一次的排油，浮力调节系统工作时，每次的充油动作可以在很短的时间完成。因此，忽略排油动作这一短时间过程对于运动的影响，假设每段运动中排油已完成，浮力保持不变。

浮标上浮是一个变加速的运动过程，满足方程：

$m\frac{{{\rm d}u}}{{{\rm d}t}} = B - mg - {F_D}\text{。}$

(1)

式中： $m$ 为浮标在空气中的重量， $u$ 为沿深度方向的速度， $B$ 为浮力， ${F_D}$ 为水阻力。

某一时刻浮标的浮力

$B = \rho ({V_0} + \sum {\frac{V}{n})} g\text{。}$

(2)

式中， $\rho $ 为海水密度， $g$ 为重力加速度， ${V_0}$ 为浮标的固定排水体积， $\dfrac{V}{n}$ 为每次排油体积， $\sum {\dfrac{V}{n}} $ 为累积的排油量。

把水动力沿深度方向进行分解，得到作用在深度方向上等效阻力^[10]为：

${F_D} = \frac{1}{2}{C_D}\rho {A_w}{u^2}$

(3)

式中， ${C_D}$ 为阻力系数，可经过模型仿真得到^[11]， ${A_w}$ 为与运动垂直方向的横截面积。

可以得到上浮运动中的瞬时加速度

$\frac{{{\rm d}u}}{{{\rm d}t}} = \frac{{\rho g({V_0} + \sum {\frac{V}{n}} )}}{m} - g - \frac{1}{{2m}}{C_D}\rho {A_w}{u^2}\text{。}$

(4)

2.2 能耗分析

通过对浮力调节系统的分析，可以得到每次排油工作阶段电机的能耗。采用分阶段多次调节的策略，在速度低于某一值时进行一次排油，计算出每个阶段的能耗，最终得到整个上浮过程所需要的总能耗。

第 $i$ 次调节过程中，电机的功耗为：

$ \left\{ \begin{aligned} & {W_i} = {P_i}{t_i}\\ & {P_i} = Kp\\ & {t_i} = \frac{V}{{nQ}}\text{。} \end{aligned} \right. $

(5)

其中， ${P_i}$ 为第 $i$ 次调节时的电机功率， ${t_i}$ 为第 $i$ 次调节时间， $K$ 为系数，与电机和泵的性能参数有关，可通过计算得到， $p$ 为泵的输出压力， $Q$ 为泵的流量。

完成整个上浮过程所需要的总能耗为：

$W = \sum\limits_{i = 1}^n {{W_i}}\text{。} $

(6)

联立式（4）和式（5）得到求解上浮过程中第 $i$ 次排油需要的能耗所满足的方程组为：

$ \left\{ \begin{aligned} & \ddot z = \frac{{\rho g({V_0} + i\frac{V}{n})}}{m} - g - \frac{1}{{2m}}{C_D}\rho {A_w}{{\dot z}^2}\text{，}\\ & {W_i} = K\rho gh\frac{V}{{nQ}}\text{。} \end{aligned} \right. $

(7)

可以得到第 $i$ 次调节过程中，电机功耗

$ \begin{split} & {W_i} = (KV\rho g{\rm{(}}{h_0}{\rm{ + (2}}m\log {\rm{(tanh((}}\sqrt {2{A_W}{C_D}\rho g}\times \\ &\sqrt {V\rho i - mn{\rm{ + }}{V_0}\rho n} {\rm{t)/(2}}m \sqrt n {\rm{)) }}{\rm{ + 1))/(}}{A_W}{C_D}\rho ) -\\ & (\sqrt {{\rm{2}}g} \sqrt {V\rho i - mn{\rm{ + }}{V_0}\rho n} t)/\\ & (\sqrt {{A_W}{C_D}\rho n} {\rm{)))/(Q}}n{\rm{)}}\text{。} \end{split} $

(8)

3 主要因素的基本特性

本文所研究的浮标的基本参数如表1所示^[12]。通过仿真模拟，得到所选浮标的阻力系数 ${C_D}$ 为0.4。

3.1 海水密度变化

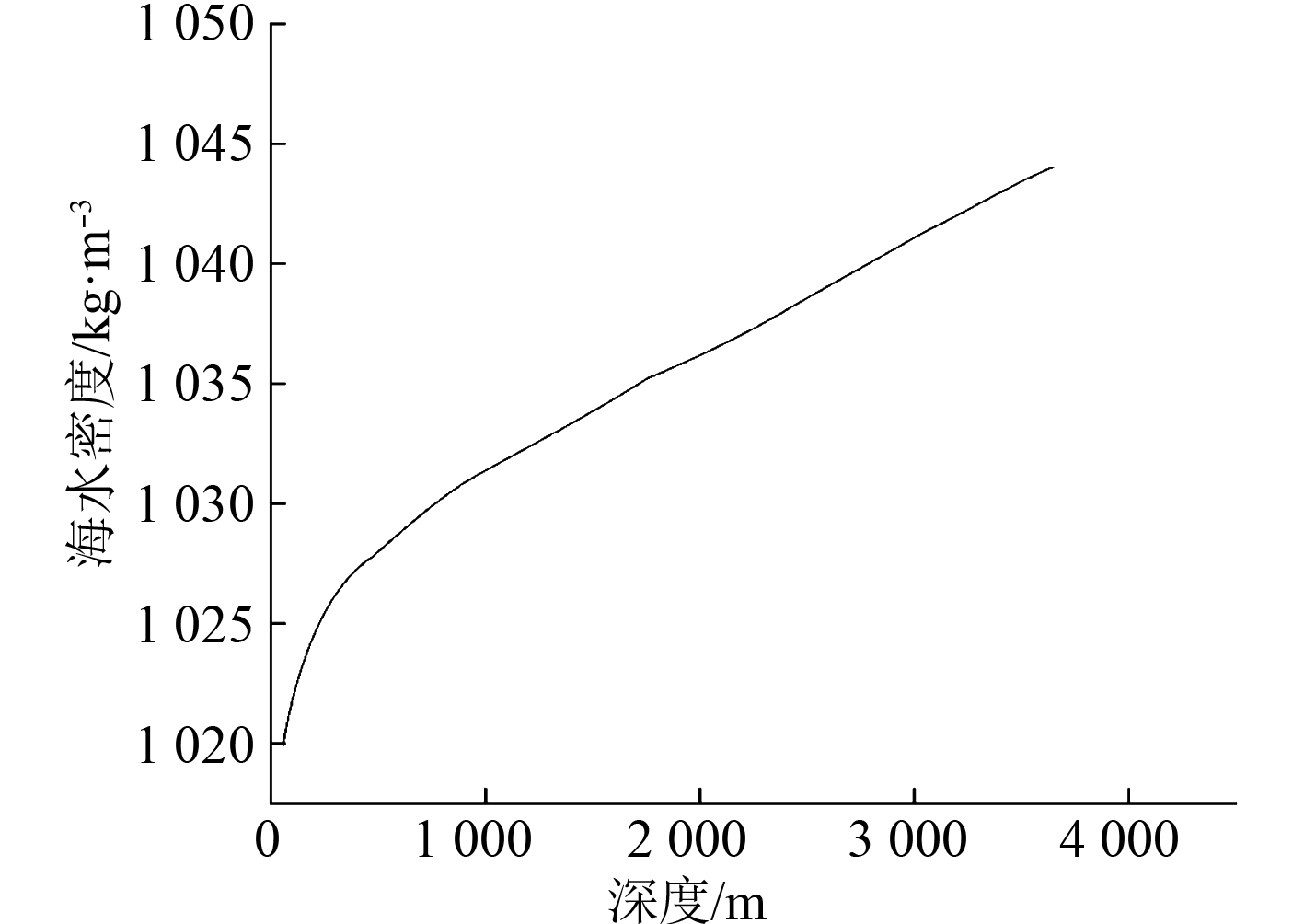
海水密度在深度方向逐渐增加，根据中国海洋信息网实测数据资料可以得到中国南海海水密度随深度变化的关系如图1所示。

经过拟合可知，深度超过500 m后海水密度变化与深度近似成线性关系：

$\rho = 0.0045h + 1026.2\text{。}$

(9)

3.2 液压泵和电机

本次所采用的浮标测量深度为0～2 000 m的海洋环境参数，所在的海洋压力环境范围为0～20 MPa。浮力调节系统中的液压泵采用法国某公司型号为PB33 HP的液压泵，该液压泵的主要参数如表2所示。

根据泵的特性进行简单的理论推导，可得到泵的输入功率为：

$ {P_{in}} = \frac{{{P_{out}}}}{{{\eta _v}{\eta _m}}} = \frac{{{\text{π}} nT}}{{30\;000}}\text{。} $

(10)

式中： ${P_{out}}$ 为泵的输出功率，kW， ${\eta _V}$ 为液压泵的容积效率； ${\eta _m}$ 为液压泵的机械效率； $n$ 为泵的转速，r/min； $T$ 为泵的输入扭矩，N·m。

液压泵所需要的输入扭矩与压强成正比，满足以下关系：

$ T = \frac{{vp}}{{2{\text{π}} }}\text{。} $

(11)

式中： $v$ 为液压泵的公称排量，该泵的公称排量为0.045 ml/r。

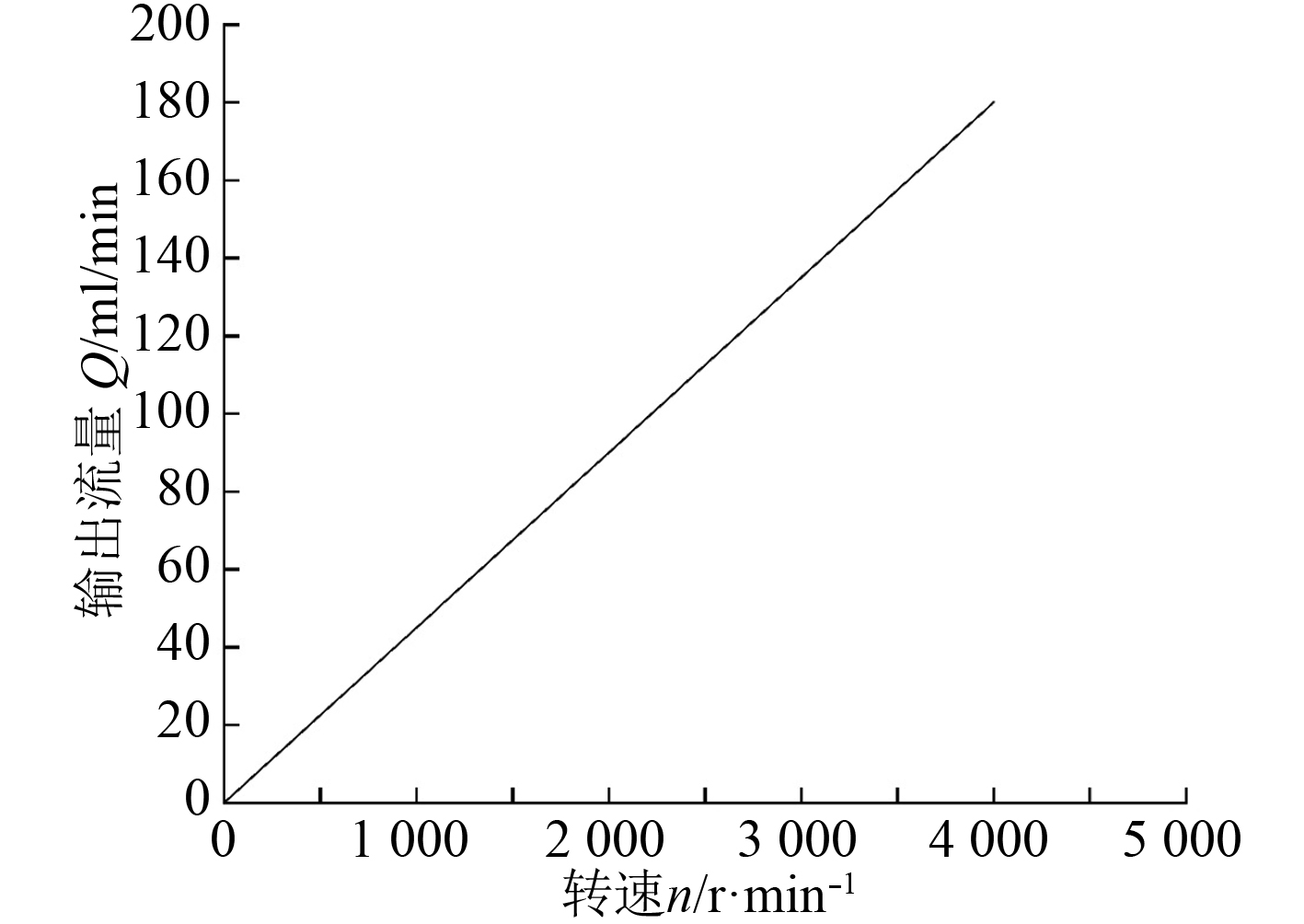
液压泵的输出流量 $Q$ 与转速 $n$ 满足线性关系，如图2所示。

根据所选择浮标的指标要求，该泵的最大工作压力为20 MPa，泵的输出流量 $Q$ 最小为0.1 L/min。通过指标要求可以得到，所需要的输入扭矩 $T$ 为0.143 N· m，转速 $n$ 取为2 500 r/min。通过图2可知，此时泵的输出流量 $Q$ 为0.112 5 L/min。将以上参数代入式（10），计算得到泵的输入功率

$ {P_{in}} = \frac{3}{{1\,600}}p$

(12)

浮力调节系统中的驱动电机采用瑞士某公司型号为RE-30 310005的减速电机，该减速电机的机械效率为0.87，则电机需要为泵提供的功率为：

${P_i} = \frac{{{P_{in}}}}{{0.87}} = \frac{3}{{1392}}p\text{。}$

(13)

4 数值求解及结果分析

将浮标的基本参数以及泵的性能参数代入式（7），可以得到

$ \left\{ \begin{aligned} & \ddot z = \frac{{\rho g({V_0} + i\frac{V}{n})}}{m} - g - \frac{1}{{2m}}{C_D}\rho {A_w}{{\dot z}^2}\text{，}\\ & h = {h_0} - z\text{，}\\ & \rho = 0.0045h + 1026.2\text{，}\\ & {W_i} = \frac{3}{{1392}}\rho gh\frac{V}{{nQ}}\text{。} \end{aligned} \right. $

(14)

考虑测量数据时对运动速度的要求，根据统计后的经验，一般上浮速度在0.1～0.5 m/s区间内，因此探究最低上浮速度分别为0.1 m/s，0.2 m/s，0.3 m/s时，分段排油次数 $n$ 与上浮过程耗能 $W$ 之间的关系，为不同速度设置最优的排油策略。

对式（14）中的运动方程采用四阶龙格库塔法来进行求解，4阶龙格库塔得计算公式为：

$ \left\{ \begin{aligned} & {y_{i + 1}} = {y_i} + \frac{h}{6}({K_1} + 2{K_2} + 2{K_3} + {K_4})\text{，}\\ & {K_1} = g({x_i},{y_i})\text{，}\\ & {K_2} = g({x_i} + \frac{h}{2},{y_i} + \frac{h}{2}{K_1})\text{，}\\ & {K_3} = g({x_i} + \frac{h}{2},{y_i} + \frac{h}{2}{K_2})\text{，}\\ & {K_4} = g({x_i} + h,{y_i} + h{K_3})\text{。} \end{aligned} \right. $

(15)

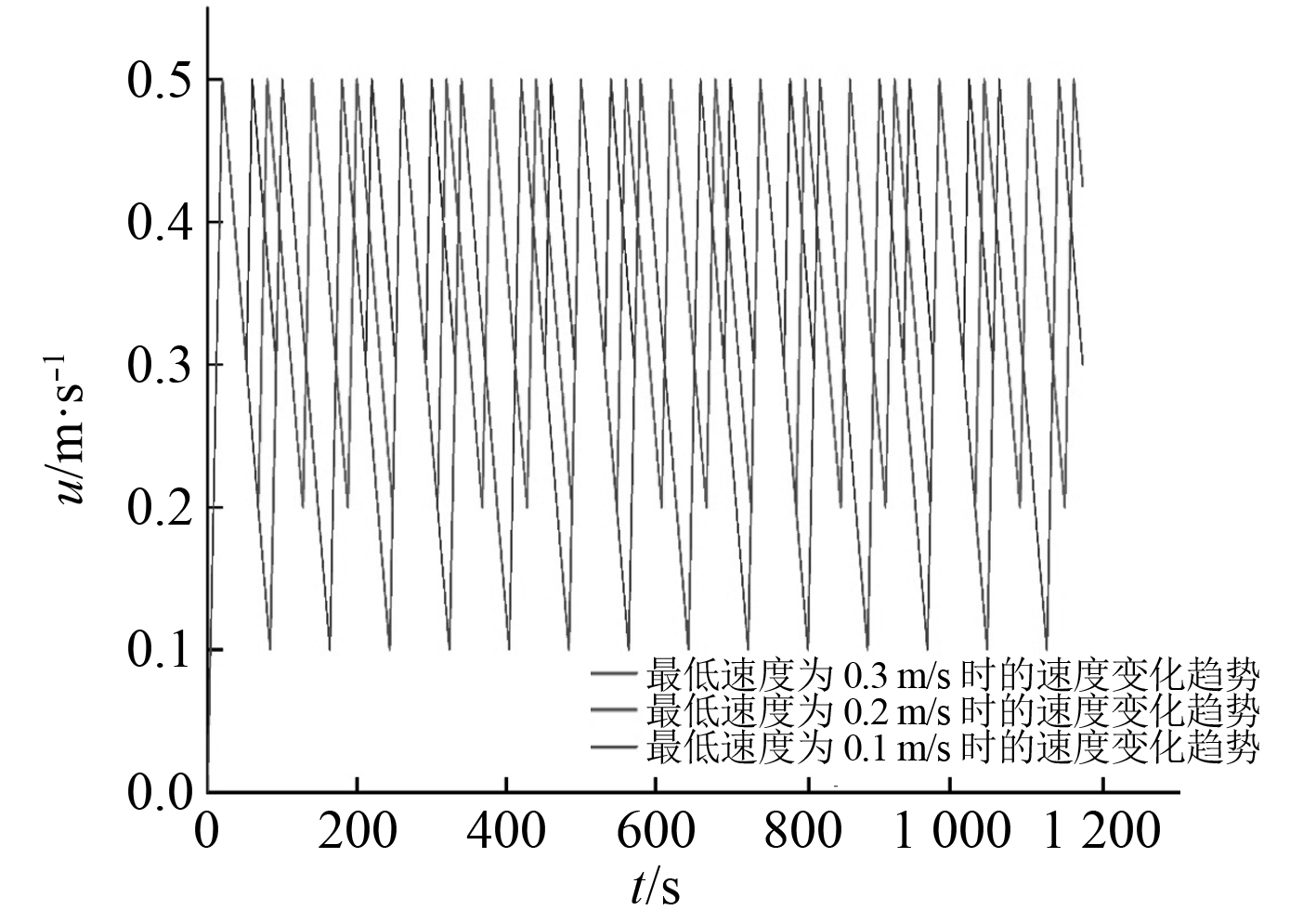
分别将速度区间设置为[0.1,0.5]，[0.2,0.5]，[0.3,0.5]，则可以得到分段排油控制下的速度变化趋势曲线，如图3所示。

通过对比分析不同最低速度条件下的速度变化趋势曲线可知，在每次排油体积固定的条件下，最低速度值越小，相邻2次排油的间隔时间相应的会较长，要完成整个排油过程所需要的时间也就越长。而速度区间越大，每次排油后浮标上浮距离也就越大，则在下一次排油时，浮标所处深度的海水压力也随之减小，克服海水压力做功所消耗的能量就会少，因此整个分段排油过程的能耗较少。因此，在满足数据测量所需的速度条件下，所设置的速度区间中最低速度越小，能耗越小。

基于以上分析，借助Matlab计算可以得到第 $i$ 次调节过程中所需要的功耗为：

$ \begin{split} & {W_i} = (0.111 \times (23.798 \times \log (\tanh ((1.295 \times {10^{ - 11}} \times\\ & (5.531 \times {10^{16}} \times i + 7.892 \times {10^{15}} \times n{)^{\frac{1}{2}}})/{n^{\frac{3}{2}}}) + 1) -\\ & (3.081 \times {10^{ - 10}} \times {\rm{(5}}{\rm{.531}} \times {\rm{1}}{{\rm{0}}^{16}} \times i{\rm{ }}+\\ & {\rm{ 7}}{\rm{.892}} \times {\rm{1}}{{\rm{0}}^{16}} \times n{{\rm{)}}^{\frac{1}{2}}}{\rm{)/}}{n^{\frac{3}{2}}}{\rm{ + 6937}}{\rm{.994)/n}}\text{。} \end{split} $

(16)

进一步即可得到总能耗

$W = \sum\limits_{i = 1}^n {{W_i}} \text{。}$

(17)

通过数值计算和仿真模拟，最终得到总能耗 $W$ 与调节次数 $n$ 之间的关系如图4所示。

从功耗与调节次数的关系图可以看出，理论上总能耗 $W$ 随着调节次数 $n$ 的增大而减小，最多可节约50%左右的能量。这是因为每次排油上升后，浮标所处深度的海水压力也随之减小，则在下一次排油时，克服海水压力做功所消耗的能量就会少，因此整个分段排油过程的能耗较少。从曲线的趋势可以看出，当调节次数 $n$ 小于20时，总能耗 $W$ 随调节次数 $n$ 变化曲线下降较为明显，当调节次数 $n$ 大于20之后，总能耗减少趋势变得较为平缓，减小幅度也比较小。考虑到充油时频繁启动电机和泵会对其工作寿命造成一定的影响，因此将调节次数 $n$ 维持在20附近时最佳，既可以取得较好的节能效果，又不会对电机和泵造成很大的损耗。

5 结　语

通过对剖面浮标上浮运动过程中耗能特性进行分析，建立运动模型和能耗模型，研究上浮过程中的分段排油策略对减少浮力调节系统的耗能影响，得到能量消耗与分段排油次数之间的关系式。通过设定不同的速度区间，从理论上研究上浮运动速度区间对能耗的影响。结果表明，当最低速度设定值较小时，具有一定的节能效果。在实例中验证所述能耗关系模型，得到能耗与分段排油次数的关系曲线，综合考虑节能和设备损耗两方面的因素，所述实例中调节次数保持在20次左右时可以达到较好的节能效果。