2. 中山大学海洋工程与技术学院,广东 珠海 519000
2. School of Marine Engineering and Technology, Sun Yat-sen University, Zhuhai 519000, China
近年来随着航运业的快速发展,船舶交通密度增大,两船对遇态势也增多,船舶间因水动力相互干扰产生船吸现象,特别在两船右舷对右舷相遇时,加上船舶避让措施不当,经常发生碰撞事故。因此,对两船对遇问题的研究引起了广大学者的关注。目前,对于两船会遇时水动力性能研究大都采用数值计算和模型试验方法。在基于模型试验研究中,国外学者所做的工作较多。例如,Remery等[1]开展了航行船舶诱导的系泊力的相关试验,讨论了两船之间的横向间距以及航行船舶的速度等有关因素对系泊船舶的水动力性能的影响。Dand等[2]开展了航行船与停泊船的模型试验,并在此基础上,推出船舶相互作用引起的力和力矩的经验公式。Simmons等[3]研究了在岸壁效应下两船船间相互作用力干扰试验。Duffy等[4-5]基于模型试验研究了航行船经过系泊船时,航道的不同因素对两船之间相互作用力的干扰。在基于数值计算研究中,关于两船会遇时非定常三维粘性流场的分析,更多学者采用势流理论进行了深入探究。Yeung等[6]基于细长体理论的匹配渐进展开法,对开阔水域以及深浅水中两船会遇时水动力以及耐波性的变化等做了有关研究。郑才土等[7]借助奇点叠加法相关理论,讨论了在浅窄航道中两船会遇时两船性能彼此受到干扰。Gourla等[8]采用势流理论,计算了两船会遇和追越态势下的两船发生横倾、纵倾等变化。
目前,随着CFD技术迅速发展与应用,研究两船会遇时水动力性能已经考虑粘性流的存在。李学东等[9]讨论了在狭窄水道内两船追越和对遇态势下船间水动力作用的问题。张晨曦等[10]基于数值模拟方法,深入讨论两船在浅水域中,追越船平行追越和会遇被追越船时的水动力性能变化规律。邹早建等[11]基于CFD流体软件,通过求解RANS方程,重点分析了浅水中两船会遇时水动力的相互作用问题。
综上所述,对于两船会遇问题研究,已引起众多学者的关注,并且开展了模型试验和数值模拟方法研究,取得了一些成果。本文为了精准研究船舶危险对遇时两船间水动力性能情况,采用动网格及滑动交界面等技术,并借助Star ccm+流体软件研究右舷对右舷危险对遇时的水动力情况。
1 控制方程和湍流模型 1.1 控制方程船舶危险对遇时的水动力的数值计算是通过求解三维粘性不可压RANS方程,具体的方程如下:
连续方程为
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0,\;(i=1, 2, 3){\text{;}} $ | (1) |
雷诺时均方程方程为
| $ \rho \frac{{\partial {u_i}}}{{\partial t}} + \rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \mu \frac{\partial }{{\partial {x_j}}}(\frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \overline {{u_i}'{u_j}'} ) {\text{。}} $ | (2) |
式中:
在数值计算中,湍流模型选择Realizable
| $\frac{{\partial (\rho k)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {(\mu + \frac{{{\mu _t}}}{{{\sigma _k}}})\frac{{{\partial _k}}}{{\partial {x_j}}}} \right] + {G_k} - \rho {\text{,}} $ | (3) |
| $ \begin{split} \frac{{\partial (\rho \varepsilon )}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} =\,& \frac{\partial }{{\partial {x_j}}}\left[ {(\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}})\frac{{{\partial _\varepsilon }}}{{\partial {x_j}}}} \right] + \rho {C_1}{E_\varepsilon } -\\ & \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {v\varepsilon } }} {\text{。}} \end{split} $ | (4) |
式中:
| $ {C_1}{{ = }}\max (0.43,\frac{\eta }{{\eta + 5}}) {\text{;}} $ |
| $ \eta {{ = }}{(2{E_{{{ij}}}}.{E_{{{ij}}}})^{0.5\frac{k}{\varepsilon }}}{\text{;}} $ |
| $ {E_{{{ij}}}}{{ = }}\frac{1}{2}\left(\frac{{\partial {u_i}}}{{\partial xj}} + \frac{{\partial uj}}{{\partial xi}}\right){\text{;}} $ |
| $ {{{u}}_t}{{ = }}\rho {C_u}\frac{{{\kappa ^2}}}{\varepsilon }{\text{;}} $ |
| $ {{{C}}_{{u}}}{{ = }}\frac{1}{{{A_0} + {A_S}U*K/\varepsilon }}{\text{;}} $ |
| $ \varepsilon {{ = }}\frac{{{u}}}{\rho }\overline {\left(\frac{{\partial u_i^{'}}}{{\partial {x_k}}}\right)\left(\frac{{\partial u_j^{'}}}{{\partial {x_k}}}\right)} {\text{;}} $ |
式中:
| $ W = \frac{{{E_{{{ij}}}}{E_{{{jk}}}}{E_{kj}}}}{{{{({E_{{{ij}}}}{E_{ij}})}^{1/3}}}};\;{{U* = }}\sqrt {{E_{ij}}{E_{{{ij}}}} + \overline {{\varOmega _{ij}}} \overline {{\varOmega _{ij}}} } {\text{;}} $ |
| $\overline {{\varOmega _{ij}}} {{ = }}{\varOmega _{{{ij}}}} - 2{\varepsilon _{ijk}}{\omega _k};{{ }}{\varOmega _{{{ij}}}} = {\varOmega _{{{ij}}}} - {\varepsilon _{ijk}}{\omega _k} {\text{。}} $ |
Realizable
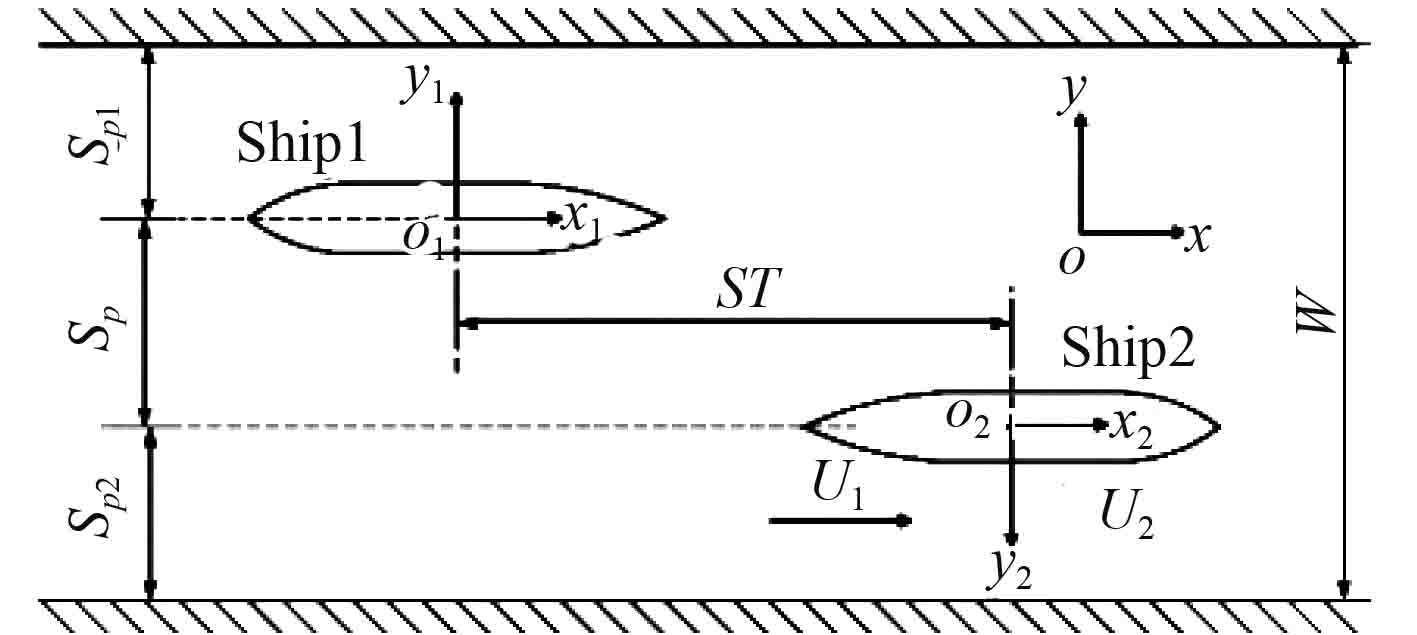
研究中为了简化计算模型,采用相对运动方法,设定一船相对静止,进行研究另一船右舷对右舷通过相对静止船时的水动力性能影响。如图1所示,SPth表示两船的横向距离,ST表示两船的纵向间距,船与两岸间距分别表示为Sp1和Sp2,航道宽度W=Sp1+Sp+Sp2,水深h。在船舶三维坐标中,采用空间固定右手坐标系统o-xyz,x轴指向航行船运动方向,y轴指向航行船左舷,z轴指向水面,空间固定坐标系原点位于静止船中心处。
|
图 1 计算坐标系统 Fig. 1 Calculates the coordinate system |
目前,在两船相遇问题研究中,Duffy等[4]为了研究在航道宽度、水深等多种因素存在时,静止船受到航行船经过时的受力影响情况,做了船模试验,分析了停泊船所受力以及力矩等无量纲值。本文研究中,以其中的一种试验工况为参考,停泊船相当于静止船,进行相关的数值模拟,Duffy等研究的试验中航道几何尺寸如图2所示。

|
图 2 航道的横切面几何 Fig. 2 Channel cross-section geometry |
试验中航行船与停泊船采用相同船型,皆为MarAd L系列散货船,船模参数见表1。航行船模速度为0.518 m/s,对应的Fr为0.074。本次计算中,由于缺乏试验船型资料,因此,选取了与试验船型相近的KVLCC2作为数值计算船型,船型参数见表2。
|
|
表 1 MarAd L系列散货船模型主尺度参数 Tab.1 Main scale parameters of MarAd L series bulk carrier model |
|
|
表 2 KVLCC2实船与船模的主尺度参数 Tab.2 Main scale parameters of KVLCC2 real ship and ship model |
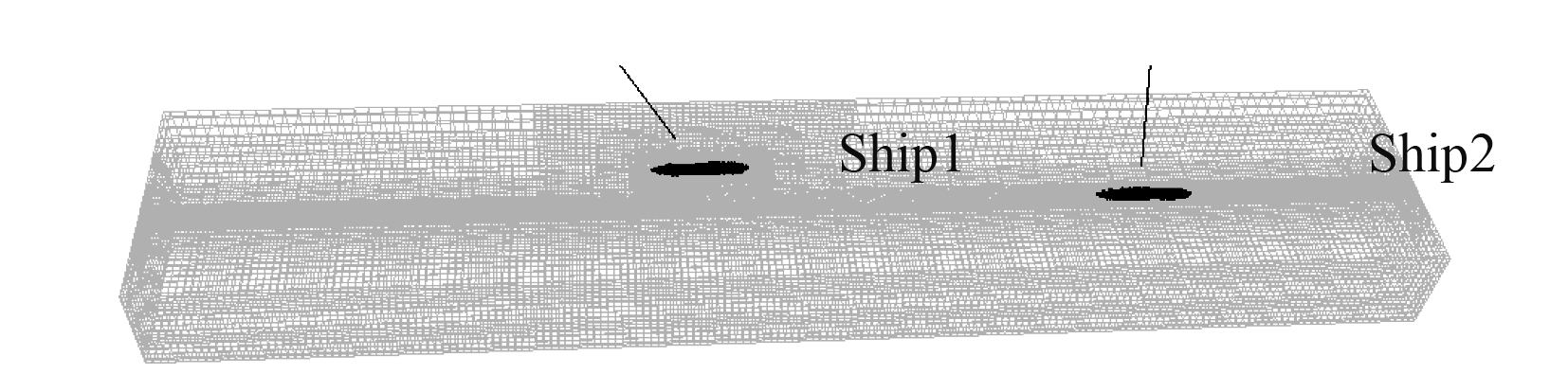
计算域应足够大,以避免岸壁对流场的影响,但是考虑到计算实际情况,本文将计算域设为长方体,船舶前后流域选取为8倍船长,岸壁与水底面方向以水底和无扰自由面为界,计算域如图3所示。网格单元为正六面体,在物面边界同时设置棱柱层网格,船艏和船尾处由于曲率变化较大,采用网格局部加密。船体网格如图4所示。
|
图 3 计算域示意图 Fig. 3 Schematic diagram of the calculation domain |

|
图 4 船体表面网格 Fig. 4 Hull surface grid |
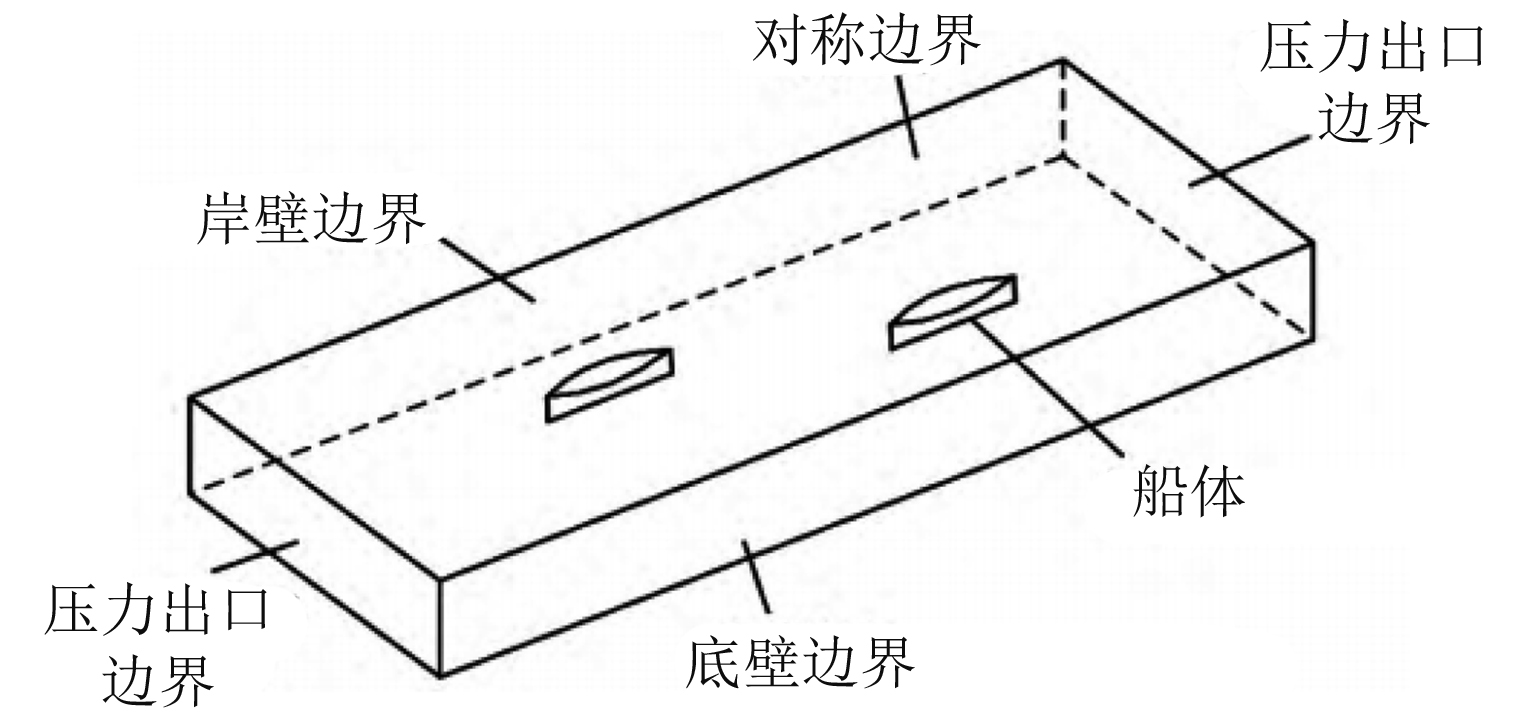
边界条件的示意图如5所示。对于流域入口与出口的边界均设定为压力边界条件,船体的表面、水底面以及岸壁设置统一定为无滑移壁面边界条件。在此数值模拟中,由于船舶的航行速度较低,可以忽略自由液面带来的影响,从而可使用刚性自由面假定,自由表面就设定为对称边界条件。
|
图 5 边界条件示意图 Fig. 5 Schematic diagram of boundary conditions |
基于计算流体软件Star ccm+中的动网格技术动态铺层法进行危险对遇时的两船网格的实时更新。动网格区域中的网格会随着船舶的航行而随之整体的移动,在船体的前后计算域边界处会进行相应的分割和合并,其他对应的区域就会作为静止网格区域,动网格与静止网格区域之间采用滑动网格交界面技术来实现流场信息的交换。
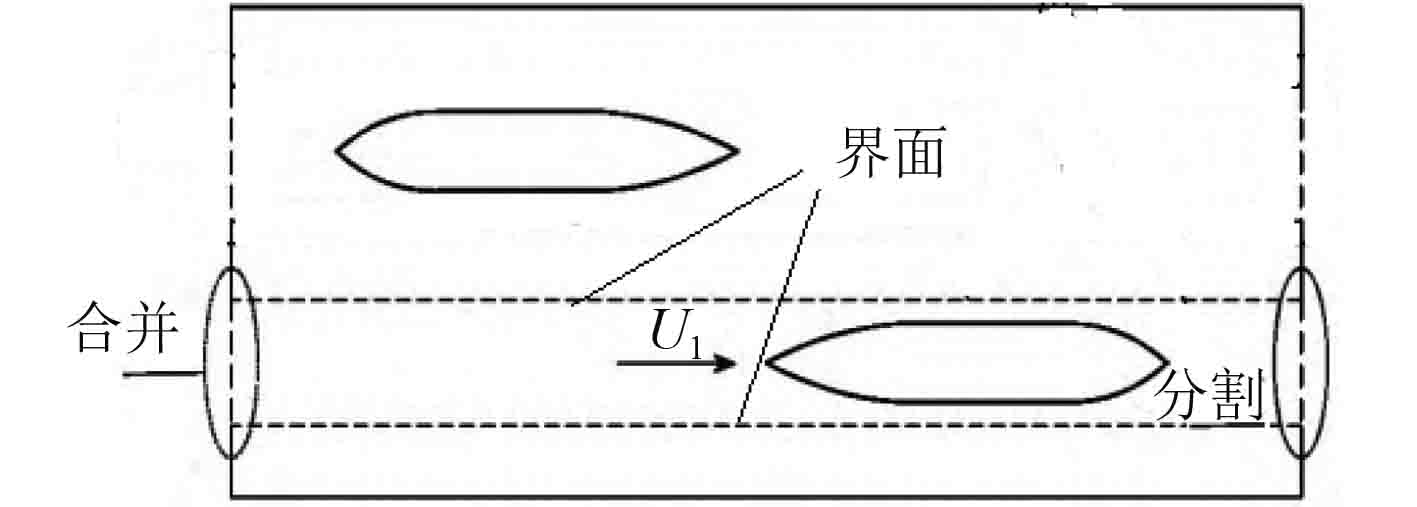
由于模型中的一船航行,一船静止,因此,只需设定航行船的动网格区域,具体示意图如图6所示。图6中虚线部分表示静止区域与运动区域之间的交界面,虚线区域内为航行船的动网格区域,两端椭圆部分为网格的合并或者分裂。需要定义此处边界为静止区域。
|
图 6 动网格示意图 Fig. 6 Schematic diagram of moving grid |
基于有限体积法对流体运动的控制方程和湍流方程展开离散,其中压力项离散采用标准格式,动量、湍流动能以及湍流耗散采用2阶迎风格式,速度、压力的耦合迭代选择Simplec算法,扩散项选择中心差分格式,湍流模型选择Realizable
为了便于比较分析,将计算结果进行无量纲化,以便与试验数据、理论曲线等进行对比,其中静止船的横向力系数
| $ C_F = \frac{F}{{0.5\rho {{{U}}^2}BD}},\;C_M = \frac{M}{{0.5\rho {U^2}L_{PP}BT}}\text{。} $ |
式中:F为静止船所受的横向力;M表示静止船偏航力矩。U为航行船速度,Lpp为静止船舶垂线间长,B为船舶型宽,T为船舶吃水。
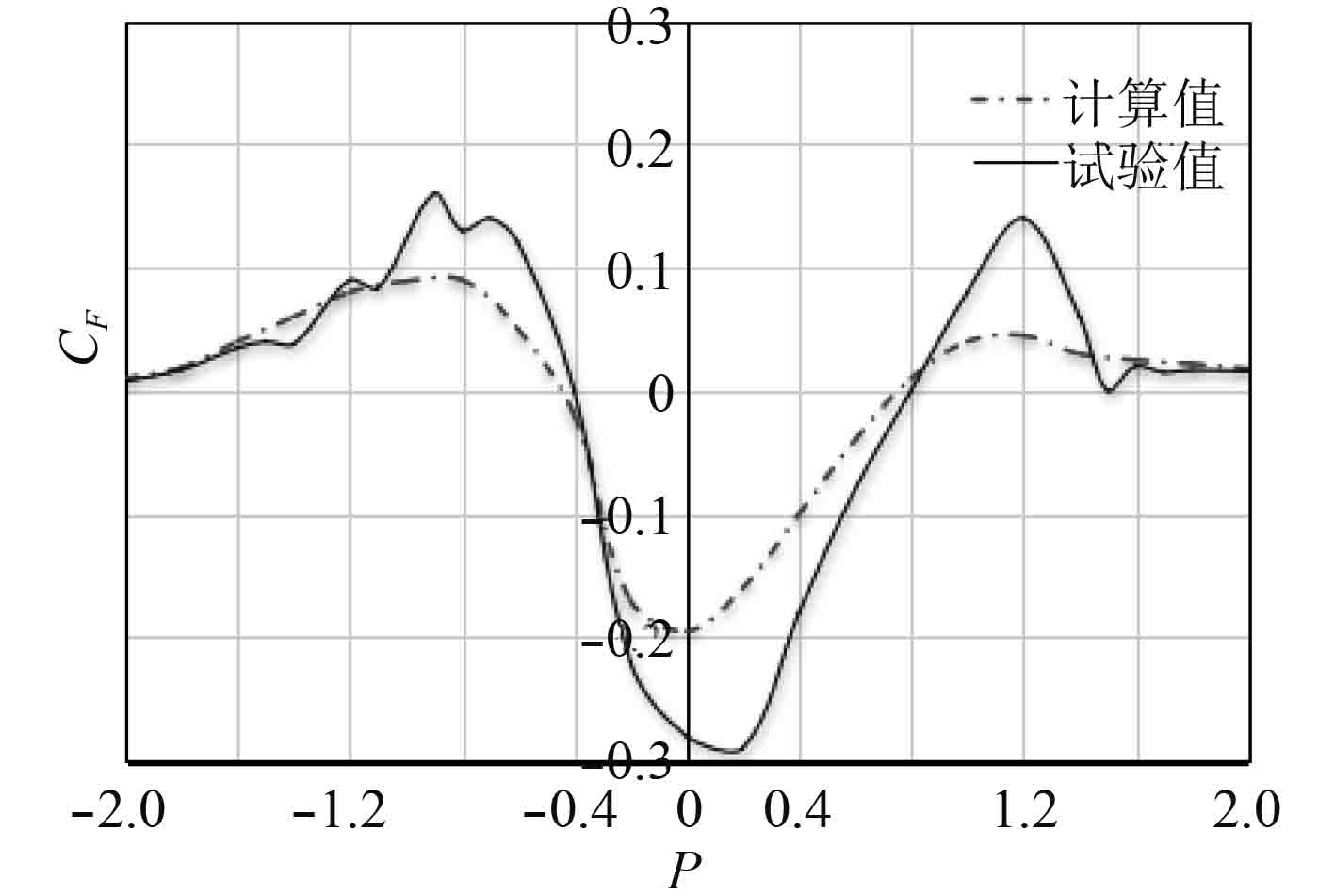
3.1 数值计算结果分析通过求解RANS方程,对航行船经过静止船时的三维非定常粘性流场进行数值模拟,主要计算静止船所受力和力矩,再将数据进行无量纲化,并转化为与相对位置P的函数关系,其中:定义P=SP/LC,SP(见图1)为两船中心纵向距离,Lc为特征船长,计算中静止船舶与航行船舶为相同船型条件下,因此,LC=LPP,LPP为船舶垂线间长。最后将计算结果与文献[10]中的试验结果进行对比,结果如图7和图8所示。
|
图 7 横向力计算值与试验值的比较 Fig. 7 Comparison of calculated values of transverse forces with experimental values |
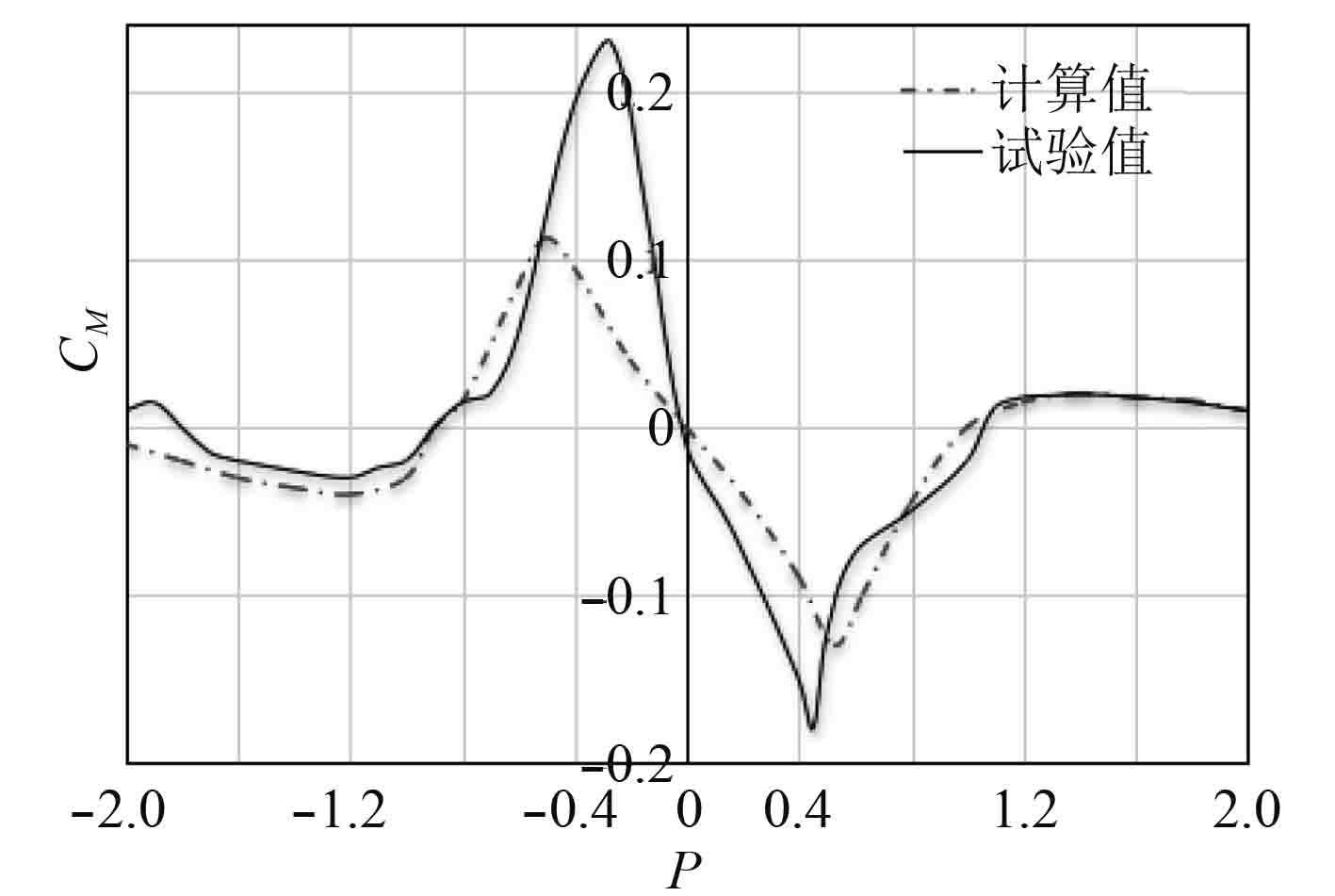
|
图 8 偏航力矩计算值与试验值的比较 Fig. 8 Comparison of calculated values of yaw moments with experimental values |
由图7和图8可知,总体上而言,计算值与试验值的曲线基本吻合,具有较好的一致性。图中横向力为正,代表排斥力,为负则表示吸引力;偏航力矩为正表示使船首向外,为负则表示使船首向内。
对横向力和偏航力矩的数值曲线进行综合分析可知,P=−1~1的范围是两船会遇过程中的危险区间。首先,在此范围前段P=−0.5处,船舶所受横向力和偏航力矩都出现一个极值点,此阶段最会出现船舶因稳性不够导致难以抵消干扰力而出现倾覆现象。之后在P=−0.5~0的过程中偏航力矩和横向力迅速下降,在0.5附近,两者均为负值,并且偏航力矩处于极值点,非常容易引起船舶的相互吸引而导致船首相碰撞。
由图6可知静止船舶所受横向力在P为−1,0,1时附近出现了3次峰值。在p=−2~−21区间,试验值与计算值表示船舶都受到正向横向力并逐渐递增至峰值。在p=−1~0区间,船舶所受横向力从正的峰值递减至负的峰值,在p=0.8附近,纵向力接近零,受力方向开始由负向变为正向。但总体看来,2条曲线的基本趋势一致。
从图7偏航力矩曲线变化来看,P=0~2区间偏航力矩曲线与P=−2~0区间相似,但方向相反。在P=−2~−1区间,船舶受到负的偏航力矩,且力矩值也随之增大。在p=−1~−0.5,3种曲线均逐步上升,力矩由负极值增至正极值。在P=0时,偏航力矩出现零值,此种现象与文献[11]的研究结论基本一致,均在此处出现零值。
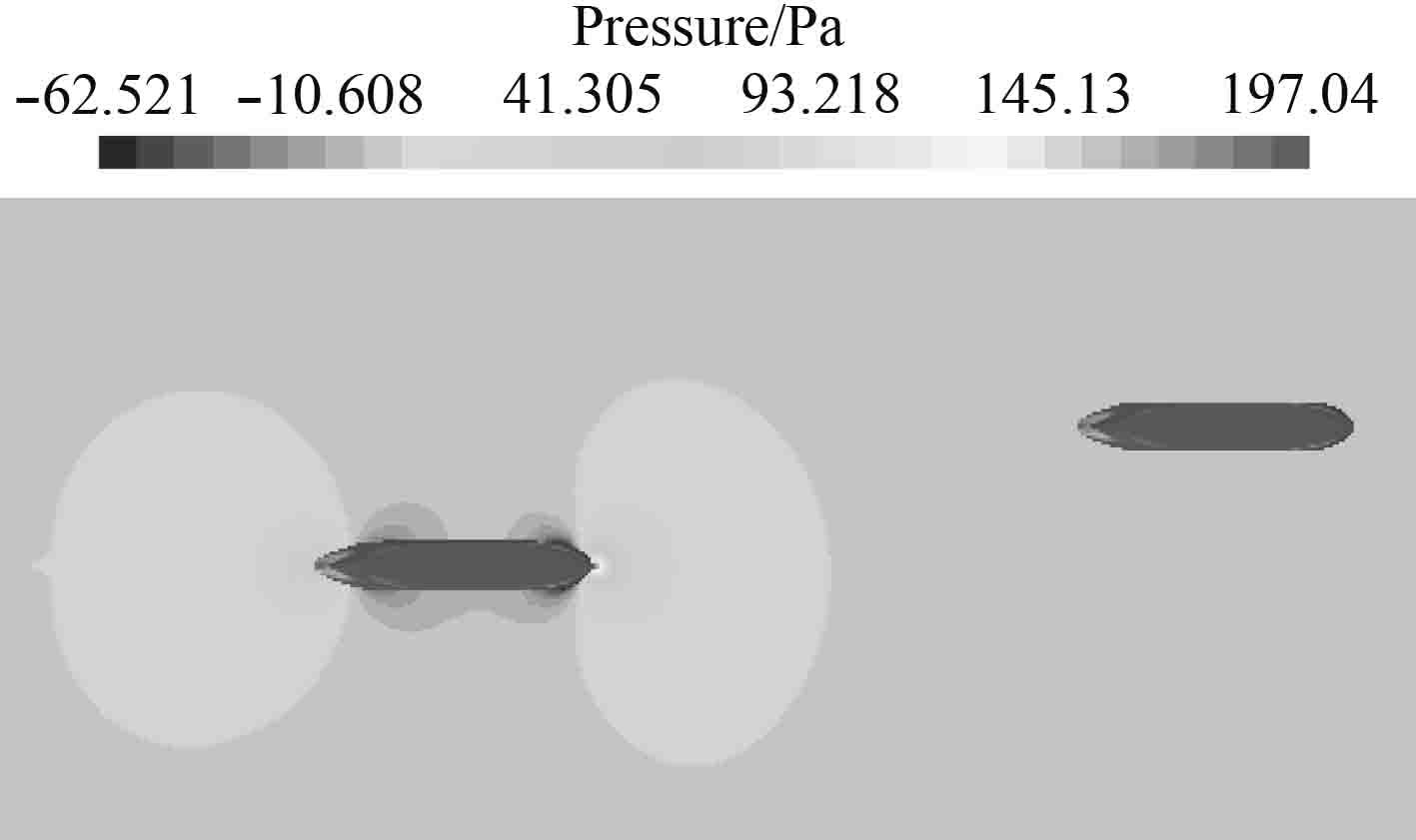
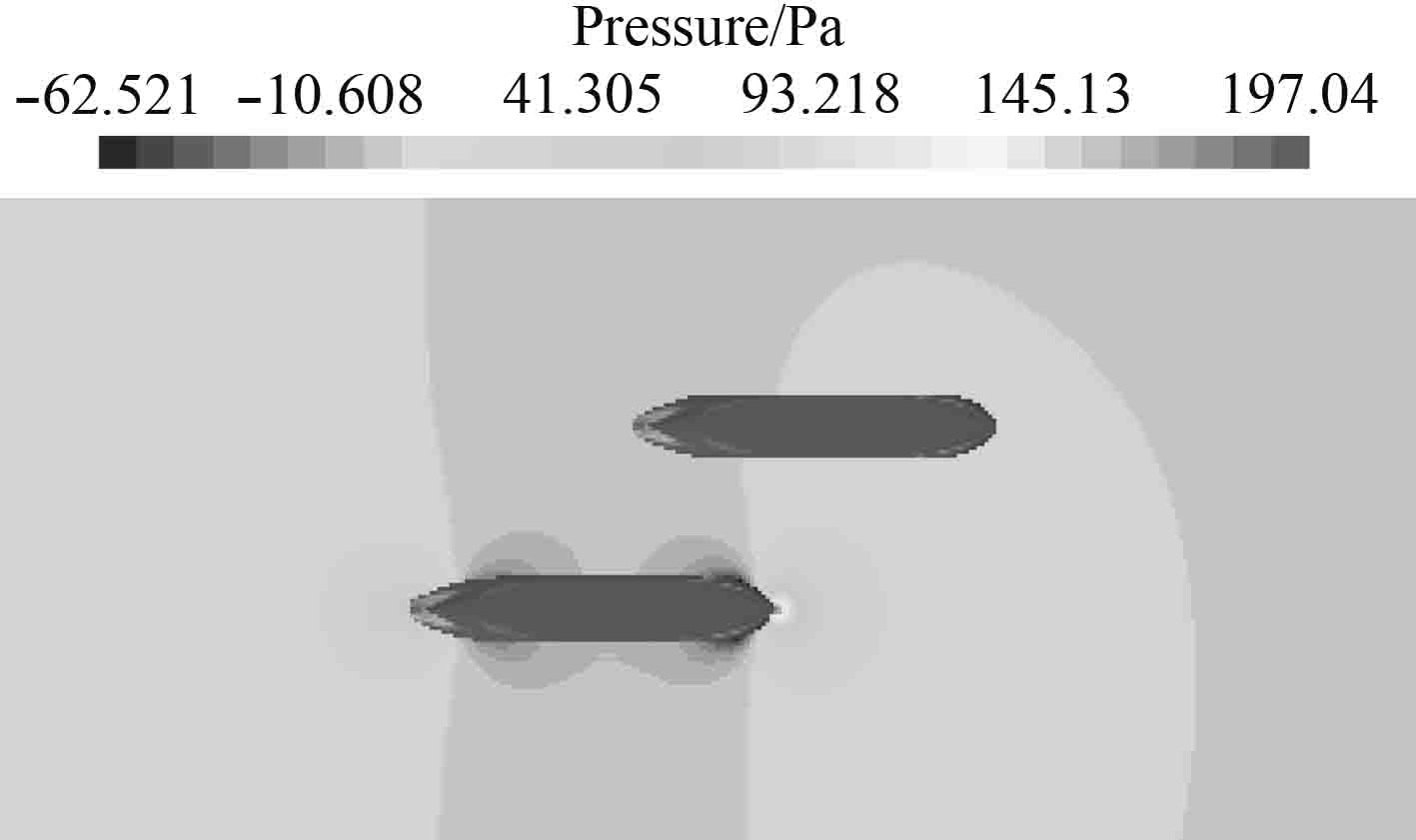
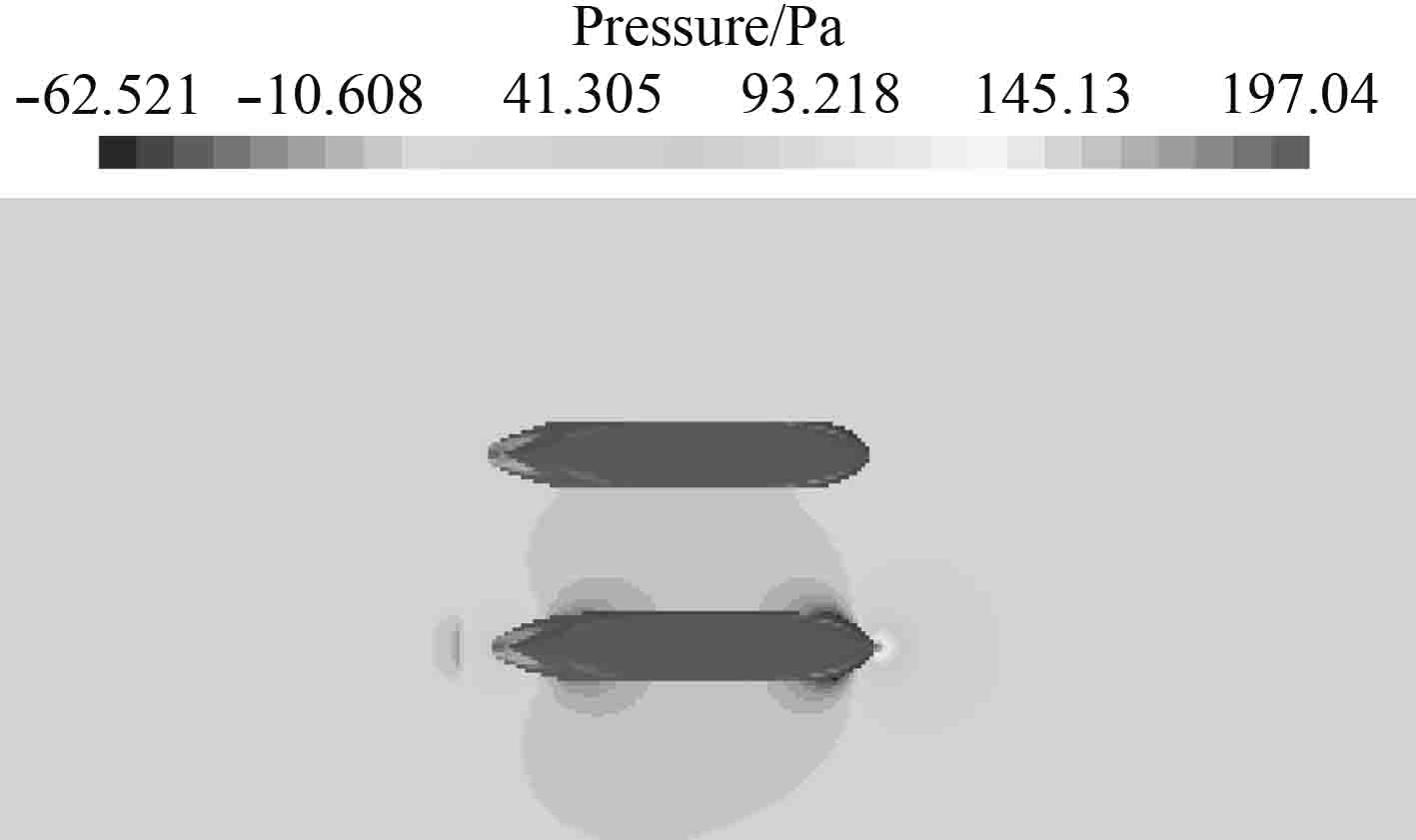
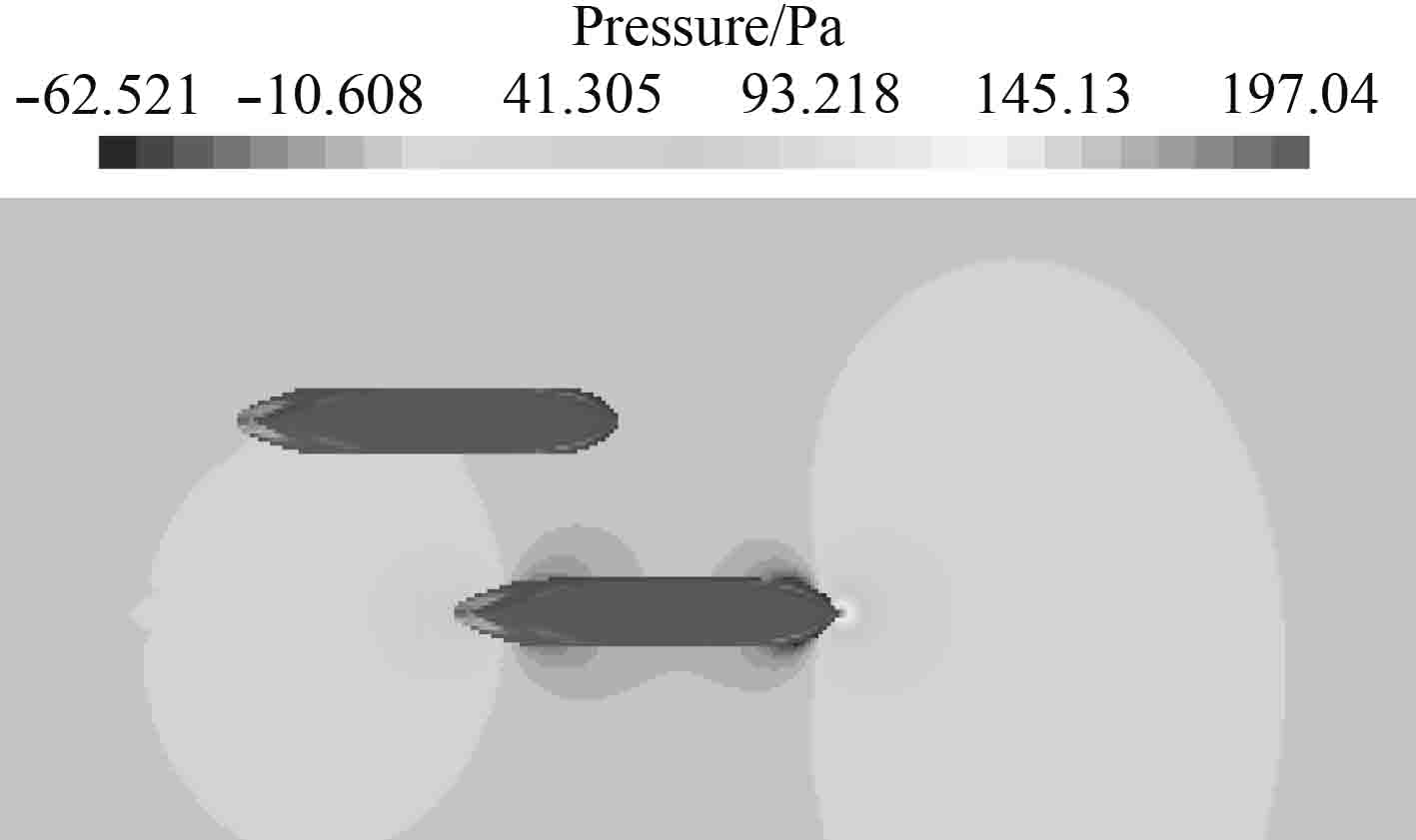
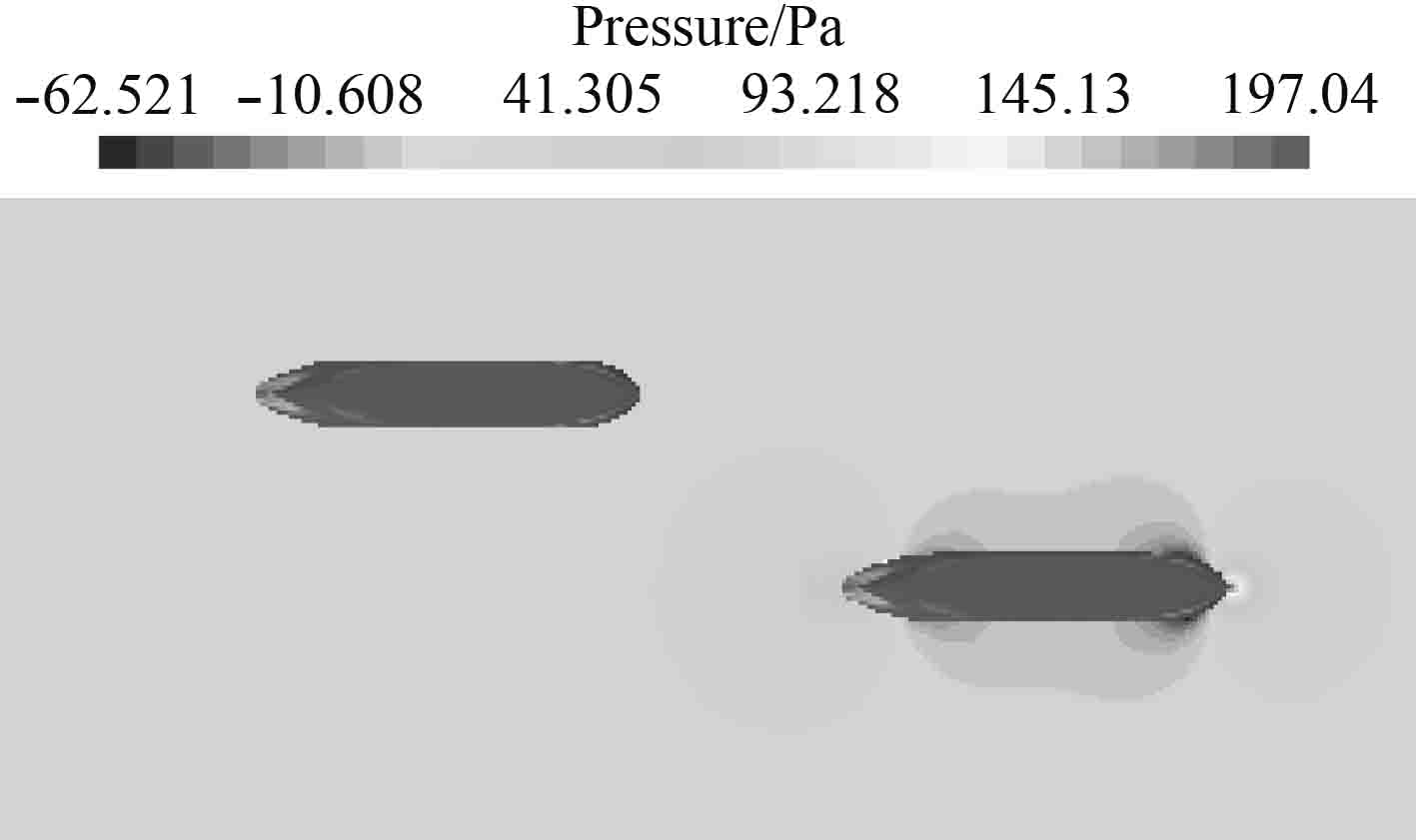
3.2 流场分析图9~图14给出了不同时刻自由面上的流场压力分布图。所有流场压力云图均在同一压力范围下进行对比。从图中可以看出,随着两船的接近,船体两侧的压力差也不断变化,干扰现象逐渐明显。图9中,航行船向静止船靠近,但因为纵间距较大,对静止船的影响较小。图10中两船中心纵向相距约1倍特征船长,此刻航行船的船首高压区对静止船造成影响,静止船受到排斥力。图11中两船相对位置p=−0.5,静止船左舷区域受航行船船首高压区和船中低压区的共同影响,此刻横向力很小。图12中p=0,沿船长方向上静止船舶压力平衡,横向处在航行船舶船中低压区,受到一个极大的指向航行船舶的横向力。图13中,p=0.5,静止船左舷侧受航行船船中低压区和船尾高压区共同影响,横向力接近零。图14航行船的船尾压力区对静止船产生的影响随着船舶间的纵向距离的加大逐渐变小。
|
图 9 P=−1.5流场压力分布 Fig. 9 P=−1.5 flow field pressure distribution |

|
图 10 P=−1流场压力分布 Fig. 10 P=−1 flow field pressure distribution |
|
图 11 P=−0.5流场压力分布 Fig. 11 P=−0.5 flow field pressure distribution |
|
图 12 P=0流场压力分布 Fig. 12 P=0 flow field pressure distribution |
|
图 13 P=0.5流场压力分布 Fig. 13 P=0.5 flow field pressure distribution |
|
图 14 P=−1流场压力分布 Fig. 14 P=−1 flow field pressure distribution |
本文研究采用CFD技术,基于Star ccm+计算流体软件,通过求解RANS方程,选取Realizable
1)本文计算值与已有试验值基本吻合,表明了本文数值方法能够用于两船危险对遇状态下水动力的数值模拟。
2)对两船对遇过程中横向力和偏航力矩变化情况的分析,可以看出P=−1~1为两船会遇过程中的难以操纵和发生碰撞的阶段,在航行中一定要谨慎驾驶,加强避让。
本文研究的成果能够为下一步复杂情景下的船间水动力干扰问题深入讨论奠定一定的研究基础,也为船舶相遇时的安全操纵提供一定的理论依据。
| [1] |
REMERY G F M. Mooring forces induced by passing ships[C]//Offshore Technology Conference. Houston, Texas, USA, May 6-8, 1974: 2066.
|
| [2] |
DAND I W. Some measurements of interaction between ship models passing on parallel courses[R]. National Maritime Institute, 1981, Report R108
|
| [3] |
SIMMONS T., ISAACS L.T., RENILSON M. Bank effects on vessel interaction forces[C]//Proceeding of the 11th(1992) Australasian Fluid Mechanics Conference. Hobart, Australia, 1992: 1217-1220.
|
| [4] |
DUFFY J.T, RENILSON M. R. The importance of the form of time domain forces and moments on berthed ship interaction[C]//Proceeding of 2nd(2011)International Conference on Ship Maneuvering in Shallow and Confined Water. Trondheim, Norway, 2011: 107-116.
|
| [5] |
DUFFY J T, DENEHY S E, RANMUTHUTHUGALA D. The effect of berthed blockage on berthed ship-passing ship interaction, Proceeding. of 3rd(2013) International Conference on Ship Maneuvering in Shallow and Confined Water. Ghent, Belgium, 2013: 237-247.
|
| [6] |
GOURLAY T. Sinkage and trim of two ships passing each other on parallel courses[J]. Ocean Engineering, 2009(36): 1119-1127. |
| [7] |
郑才土. 浅水中船舶相互作用的一种计算方法[J]. 船舶工程, 1994, 6(6): 8-14. ZHENG Caitu. Method for hydrodynamic interactions between ships in shallow water[J]. Ship Engineering, 1994, 6(6): 8-14. |
| [8] |
GOURLAY T. Sinkage and trim of two ships passing each other on parallel courses[J]. Ocean Engineering, 2009, 36: 1119-1127. DOI:10.1016/j.oceaneng.2009.06.003 |
| [9] |
李学东. 受限水域船间效应建模与仿真[D]. 大连: 大连海事大学, 2010. LI Xuedong. Modeling and simulation of interaction between ships in restricted water[D]. Dalian: Dalian Maritime University, 2010. |
| [10] |
张晨曦. 船-船非定常水动力相互作用数值研究[D]. 上海: 上海交通大学, 2011 ZHANG Chen-xi. Numerical study on unsteady hydrodynamic interaction between ships[D]. Shanghai: Shanghai Jiao Tong University, 2011 |
| [11] |
张晨曦, 邹早建, 杨勇. 浅水中会遇船舶水动力相互作用数值研究[J]. 船舶力学, 2012, 16(1-2): 8-14. ZHANG Chen-xi, ZOU Zao-jian, YANG Yong. Numerical study on hydrodynamic interaction between ships meeting in shallow water[J]. Journal of Ship Mechanics, 2012, 16(1-2): 8-14. |
 2020, Vol. 42
2020, Vol. 42
