2. 哈尔滨工程大学 船舶与海洋工程学院,黑龙江 哈尔滨 150001
2. Harbin Engineering University, Harbin 150001, China
随着计算机能力以及对图形、数字处理能力的提高,数值水槽模型成为国内外重点研究对象之一,与实验相比具有成本低,效率高的优势,且能避免缩比效应带来的影响。目前数值仿真软件的拓展模块越来越丰富,功能越来越全,进一步提高了计算能力。当波浪与结构物的相互作用时,波面会出现破碎、攀爬以及非线性响等现象,同时周围流场会发生变化,与大型船舶和海洋平台相比,其结果对小型结构物将产生更大的影响,所以流体的粘性一般不能忽视。由于浮标类结构物尺寸较小,主要受影响的波浪其波高波长较小,周期较短,并不需要建造较大的数值水槽进行数值模拟,所以如何保证小型数值水槽的波浪传递的稳定成为计算结果准确性的关键。
Brorsen M和Larsen J[1]根据源造波理论,通过在计算域内设置的造波源可分别向源区域两边同时生成2列方向相反的波;刘加海[2]通过设置边界造波版的运动来模拟物理造波板的运动过程,实现了二维规则波的数值模拟,并进一步分析了模拟波高随造波板运动周期、振幅和坐标的关系;Lal和Elangovan[3]通过设置不同的波浪周期等参数分析波高波长的影响因素,并研究了基于阻尼消波的沙滩斜坡方法的影响,结果表明当沙滩斜坡比例为1∶3时消波效果最佳;黄华和邓冰[4]通过建立二维数值水槽对2阶stokes波进行仿真模拟,运动摇板造波和增设消波区域保证了短时间内水槽内波浪的稳定性;Kim[5]通过调整消波区域的网格尺寸使得数值计算衰减来进行波浪反射的消除,通过改变网格尺寸的大小找到最佳的求解设置;Tian[6]等人为研究圆柱体与波浪的相互作用建造数值水槽,使用入口速度法进行数值造波,并通过尾部设置阻尼进行消波,得到了较为精确的规则波,并能保证一段时间内的稳定性;Fabio M和 Marques Machado[7]则对不同边界速度法和推板造波法进行了波浪模拟对比,结果表明边界速度法受波浪阻尼的影响更大,而推板造波法能造出更加准确地波浪。
本文使用STARCCM+软件,分别基于传统纯粘流以及势粘流结合的方法建立数值波浪水槽,使用边界流体函数直接输入的方式进行造波,通过对比波浪模拟结果,分析2种数值波浪水槽的特点,为数值波浪水槽的建立提供科学的参考依据。
1 数值方法 1.1 流体体积法在数值造波时需要跟踪气体和液体的界面,流体体积法(VOF)是由美国学者Hirt和Nichols等[8]提出的。在流场中的每个网格,这个函数定义为目标流体的体积与网格体积的比值,只要知道这个函数在每个网格上的值,就可以实现对运动界面的追踪。因此在这里选用VOF方法处理气体和液体的界面跟踪问题,该方法跟踪界面的连续性方程为:
| $ \frac{\partial {a}_{q}}{\partial t}+u\left(\frac{\partial {a}_{q}}{\partial x}\right)+\nu \left(\frac{\partial {a}_{q}}{\partial x}\right)+w\left(\frac{\partial {a}_{q}}{\partial x}\right)=0{\text{。}} $ | (1) |
式中:
在每个控制体积内,所有相的体积分数总和为1,所有变量及其属性在控制容积内各项共享,
目前雷诺平均方程(RANS)方法是计算流体力学中最常用的方法之一,从N-S方程出发对湍流进行直接的数值模拟(DNS)难以解决工程中遇到的复杂湍流问题,依靠实验取得经验数据,不仅耗资巨大,周期很长,而且对于某些实际工程问题,完全相似的实验室模拟不可能实现。在这种情况下,求解雷诺平均的N-S方程(RANS)方法成为解决工程问题比较有效和切实可行的手段,其中空间离散采用有限体积法,采用二阶时间差分方法保证计算的准确性。其连续性方程和动量方程为:
| $ \frac{\partial \rho }{\partial t}+\frac{\partial y}{\partial {x}_{i}}\left(\rho {u}_{i}\right)=0 {\text{,}}$ | (2) |
| $ \frac{\partial }{\partial t}\left(\rho {u}_{i}\right)+\frac{\partial }{\partial {x}_{j}}\left(\rho {u}_{j}{u}_{i}\right)=\frac{\partial P}{\partial {x}_{i}}+\frac{\partial {\sigma }_{ij}}{\partial {x}_{j}}+\frac{\partial }{\partial {x}_{j}}\left(-\rho {u}_{i}'{u}_{j}'\right){\text{。}} $ | (3) |
式中:
目前常见的数值造波方法主要可以分为两大类:源造波法和边界造波法。源造波法又分为质量源造波法和动量源造波法[9];边界造波法主要包括物理造波法和边界流体速度函数直接输入法;常用的消波方法包括常用的方法有辐射边界条件,主动消波器,阻尼消波区[10];波浪水槽边界条件的设置则要保证至少一个的速度入口和压力出口,前后边界选用对称平面,顶部距水面要足够高,以防止空气流动对波高的影响,底部设为壁面,水深设置为6 m。其他边界条件及具体设置如下:
1)模拟1
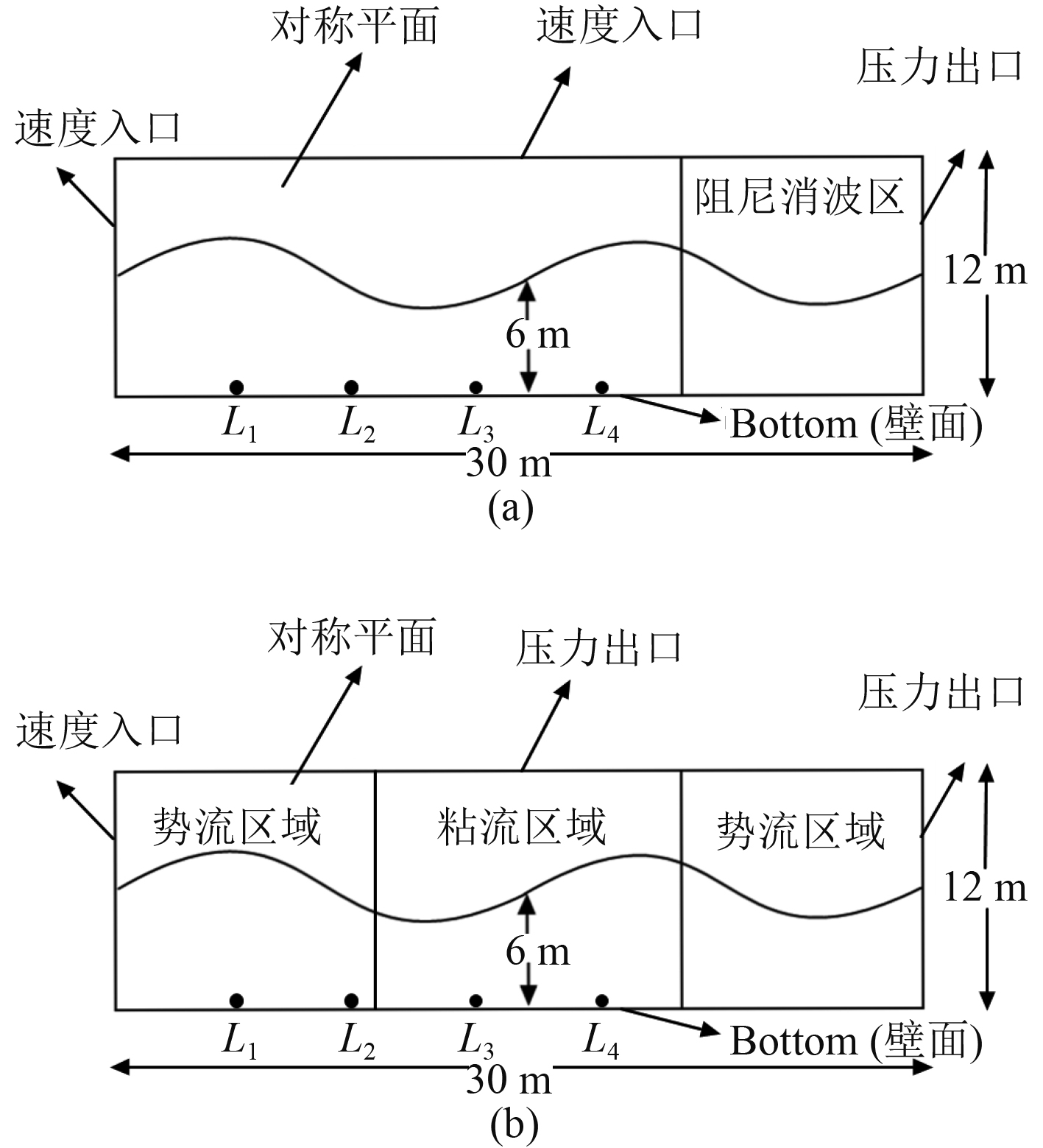
选用边界流体函数直接输入进行波浪的生成,在出口处增加阻尼区域进行消波,全流域为粘性流体;因为出口处设有阻尼区域,如果将出口边界定义为速度入口将定义出口区域的波高,这与消波意愿相违背,所以将出口边界设置为唯一压力出口,顶部设置为速度入口,实施开放边界允许空气双向流过边界。具体如图1(a)所示。
|
图 1 数值波浪水槽示意图 Fig. 1 Numerical wave tank schematic diagram |
2)模拟2
选用边界流体函数直接输入进行波浪的生成,在出入口两端设置一定长度的势流区域防止波的反射,整个流域中间为粘流区域,两边为势流区域;因为不需要考虑出口处反射波的影响,出口边界设置为速度入口定义出口区域波高,进而更加有利于保持中间粘流区域的波浪精度,顶部设置为唯一压力出口,保证压力的释放,具体如图1(b)所示。
文中模拟的波浪参数如表1所示。
|
|
表 1 波浪参数 Tab.1 Wave parameters |
通过切割体网格生成器生成六面体网格,为了更好地捕捉水线面,需要对水线面附近的网格进行多层加密以减少压力传递过程中的耗散,全域网格划分如图2(a)所示,水线面网格加密情况如图2(b)所示。

|
图 2 网格划分情况 Fig. 2 Meshing situation |
表2为Havn[11]提出的网格划分的具体标准,为了具体研究网格对波浪传递的影响,划分了3套质量不同的网格,其中第2和第3套符合Havn提出的网格划分要求,而第1套低于标准,具体网格质量见表3。
|
|
表 2 网格划分标准 Tab.2 Meshing standards |
|
|
表 3 网格参数 Tab.3 Mesh parameters |
在其他一些参数设置中,选取
在T=0 s时刻初始化定义全域波面,对不同时刻的全域波面以及各个监测位置波高进行监测。
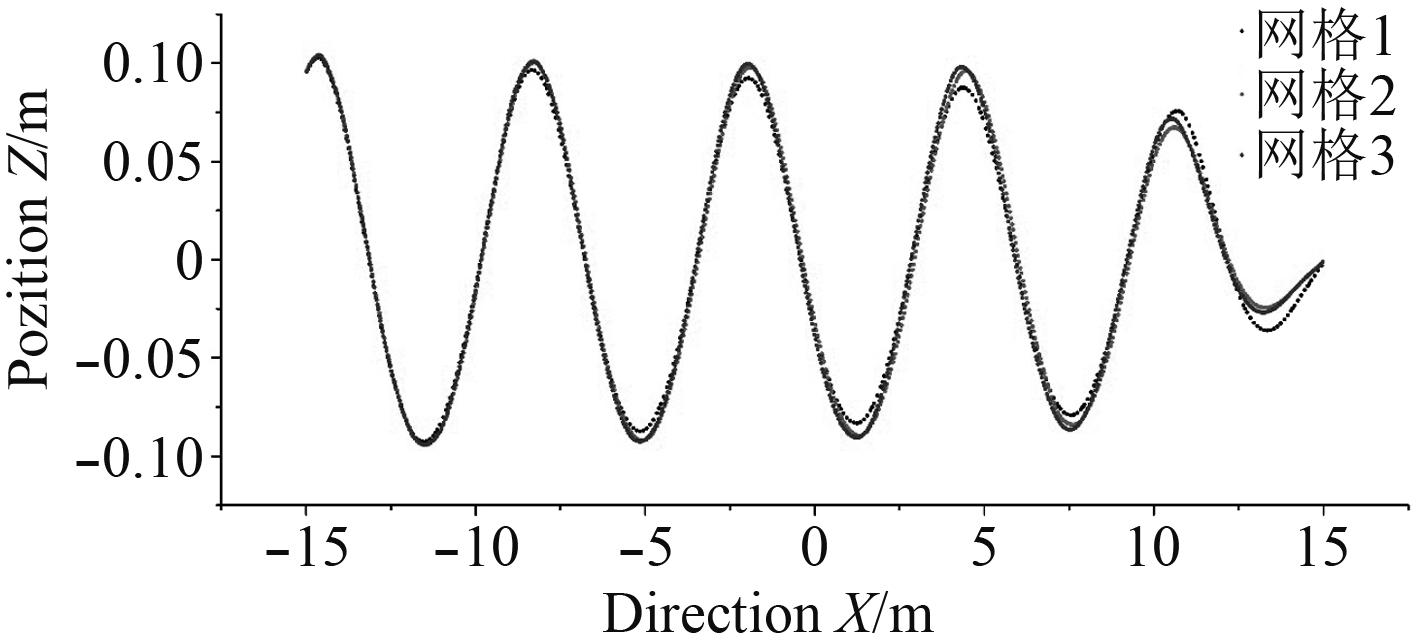
2.1 网格和时间步长的选取对于网格的选取,通过基于纯粘流数值水槽对不同质量的网格进行评价,3套网格的同一时刻波面高度情况如图3所示。
|
图 3 不同网格波面高度 Fig. 3 Wave front heights of different mesh |
通过对结果的分析表明,增加网格尺寸会加剧导致波浪的衰减,第1套网格相较于第2和第3套网格数值衰减更明显,且第2和第3套网格模拟下的波浪结果相差不大,综合考虑计算准确度与计算速度,认定网格2为最优网格划分方案,其基本划分尺寸符合Havn提出的网格划分标准。
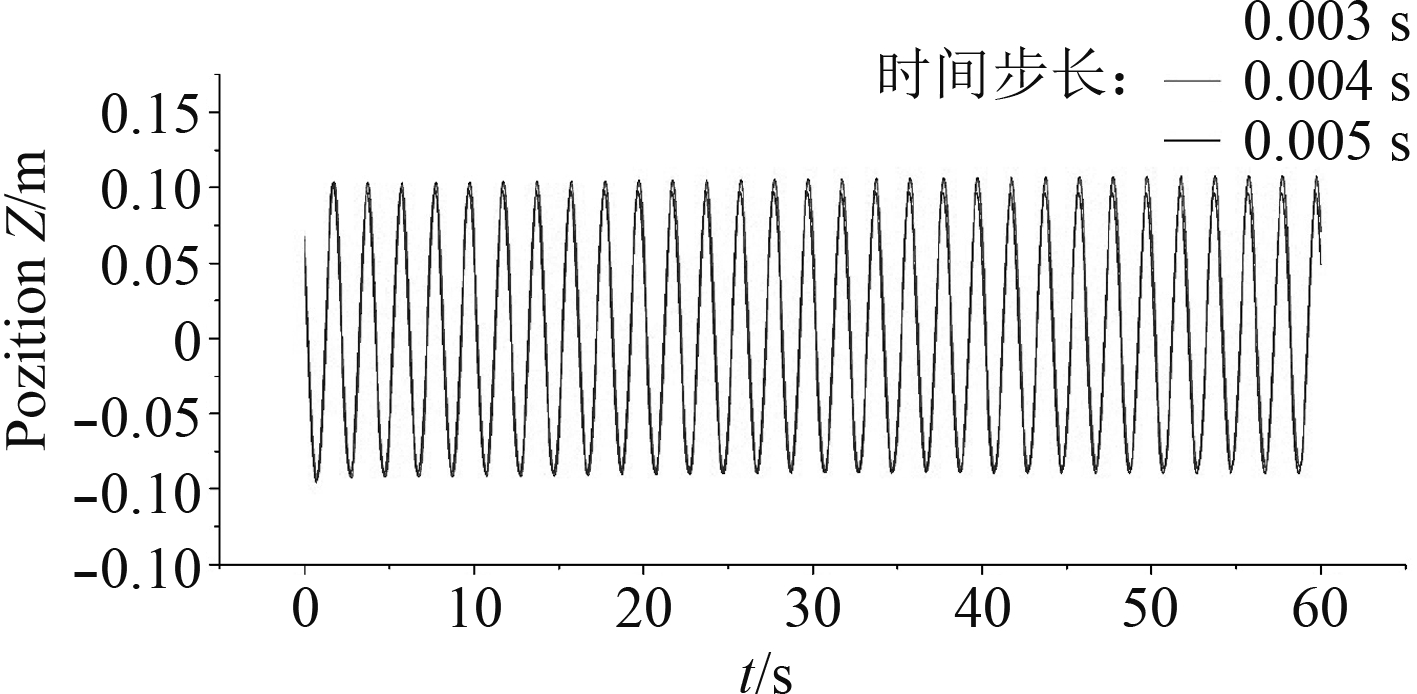
对于时间步长的选取,使用第2套网格并基于势粘流结合理论的数值水槽进行验证,选取L3监测点对不同时间步长下的波面高度结果进行对比,结果如图4所示。
|
图 4 不同时间步长L3位置对应波面高度 Fig. 4 Wave front height at L3 position at different time steps |
通过对结果的分析表明,时间步长为0.005 s(T/400)时计算结果与0.004 s(T/500)和0.003 s(T/650)有着很明显的误差,且0.004 s和0.003 s两种时间步长下的结果十分接近。图5所示计算过程中0.004 s时间步长下的库朗数稳定在0.19左右,而0.005 s时间步长下的库朗数稳定在0.28左右,而这2个时间步长都远远小于T/100,所以时间步长不能仅根据波浪周期的大小来选取,还要参考库朗数和网格质量来综合确定。

|
图 5 全域库朗数标量场景 Fig. 5 Scalar scene of global courant number |
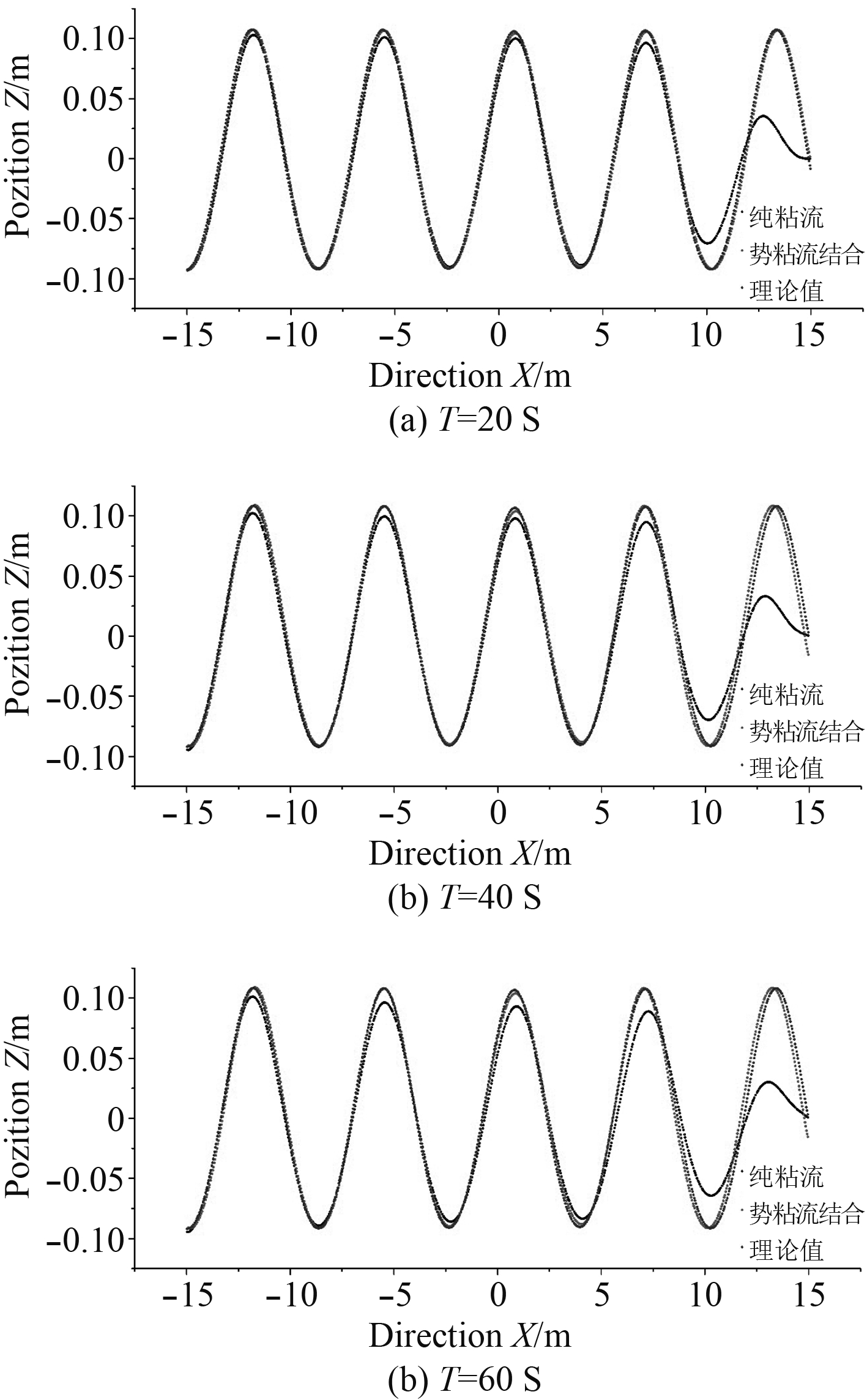
为了更直观地观察和对比2种数值水槽造波的结果,分别将第20 s,40 s,60 s的波面情况与理论值进行对比,如图6所示。
|
图 6 波面数值解与理论值比较 Fig. 6 Comparison of wave front numerical solutions and theoretical values |
|
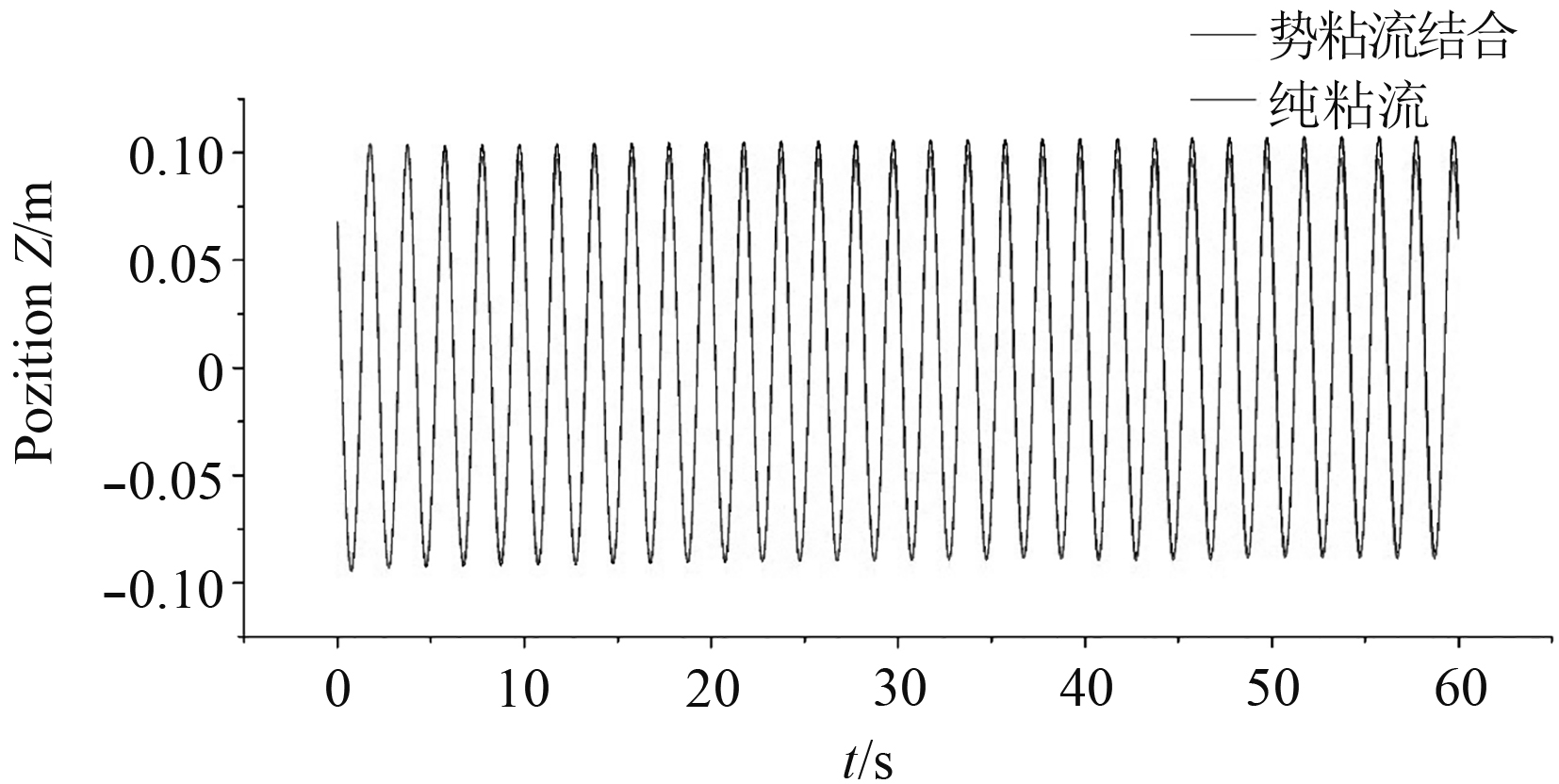
图 8 两种数值水槽L3位置波面随时间变化情况 Fig. 8 Wave front changes with time of two numerical wave tanks |
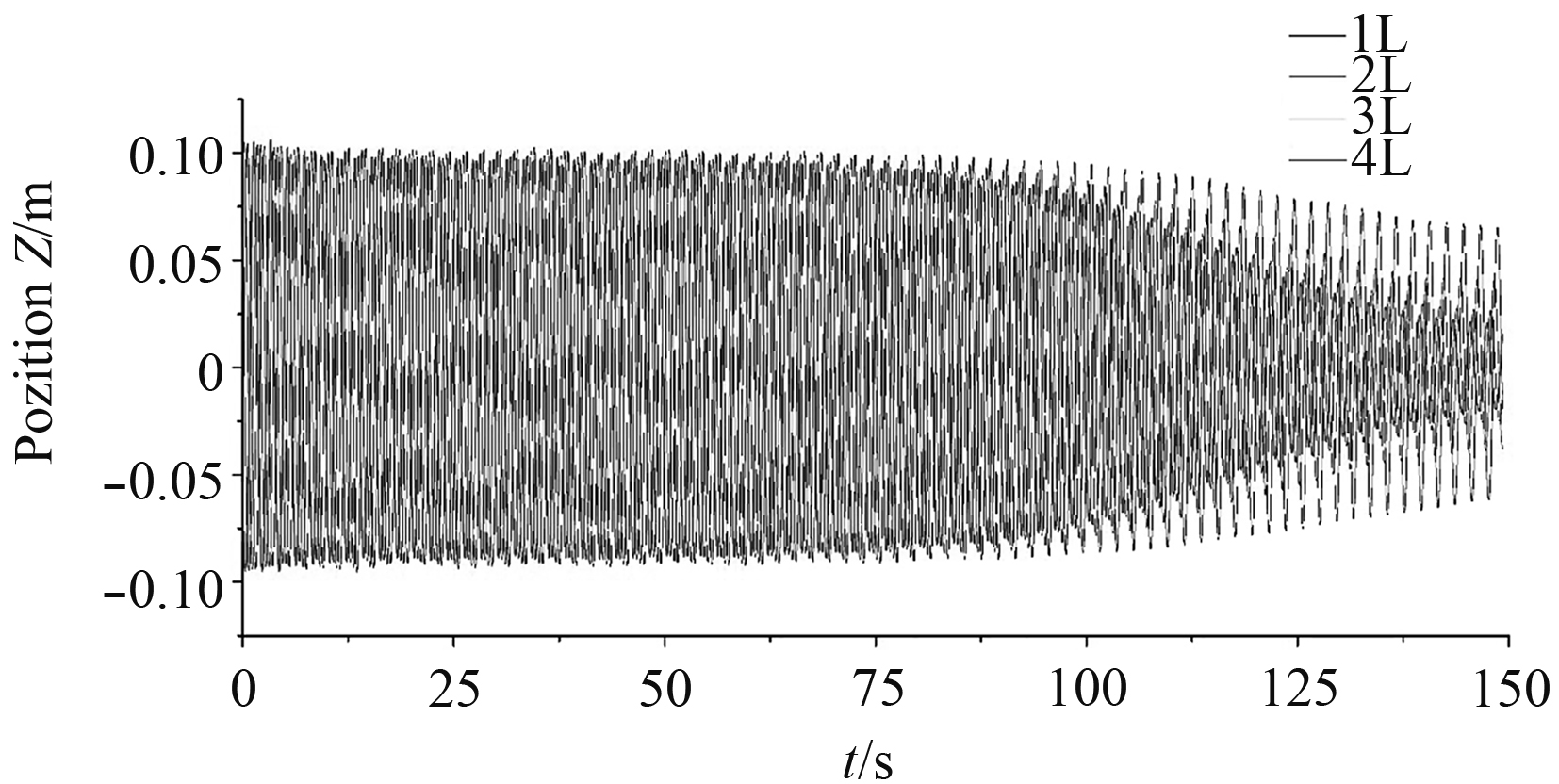
结果表明,基于纯粘流的水质波浪水槽,沿着波浪传递的方向波高逐渐减小,随着模拟时间的增加现象也越来越明显。这是因为波浪传递过程中由于流体存在粘性,部分动能转化为内能耗散,如图7所示。通过增加阻尼区域防止波浪在出口处的反射,但增设的阻尼对上游波浪的传递也会造成影响,且从第一波到达阻尼区域开始由近至远对波浪造成影响,离阻尼区域越近反射到来的越快,波面受其影响也会越大,且这种影响伴随着整个计算过程将越来越明显。增加计算域的长度可以一定程度减小阻尼区域对计算区域的影响,但由此导致网格的增加会大大增加模拟时间。也可以通过减少模拟的时间来确保一段时间波浪的稳定性,但是这只适合较短时间的数值模拟,对于较长时间的模拟并不可行。
|
图 7 基于纯粘流数值水槽不同位置波面高度随时间变化情况 Fig. 7 Viscous flow numerical water tank wave surface height changes with time |
基于势粘流结合建造的数值水槽的波浪与理论值相比更为接近,且波高不随着时间而衰减,因为波浪在非粘流区域传递并不会造成动能转化为内能的损耗,出口处的势流区域保证了波浪不受出口反射波的影响,波浪的精度只会因数值计算的耗散以及中间粘流区域将少量动能转化为内能而影响,相比较而言具有更高的精度。
3 结 语为了探究规则波在传递过程中的衰减问题,运用STARCCM+软件基于不同方式建立了2种数值波浪水槽,通过收敛性验证确定了最优的网格大小以及时间步长,结果显示造波网格可按照Havn提出的标准来划分,波高方向网格最小尺寸不小于H/25,波长方向网格最小尺寸不小于L/100;时间步长的选取应兼顾库朗数以及波浪周期,库朗数值应小于0.2,时间步长参考值不小于T/500。
基于纯粘流的数值水槽因为受流体粘性的影响,会造成波浪传递过程中部分动能的耗散,由于初始化定义了T=0 s的波面,模拟从第一时间就会受到消波阻尼反射的影响,并从下游逐渐影响至上游,且影响越来越大,导致不能进行长时间的计算模拟。为了保证计算区域波浪的精度,可以通过加长数值水槽使阻尼反射影响更晚到达计算区域,但这必然会增加网格数目进而导致计算速度的减慢。
对于基于势粘流结合的数值水槽,其中间计算区域流体为粘流,两侧流体为势流,使得上游波浪并不会受到出口处反射波的影响,且波浪在势流中的传递也不会造成动能的损失,保证了中间粘流区域波浪精度的同时进而提高了计算结果的准确性。
综合上述分析,传统的基于纯粘流的数值水槽适用于时间较短或者水槽长度较长的模拟,且波浪传递过程中衰减明显。基于势粘流结合的新型数值水槽传递过程中并无明显衰减,满足长时间计算模拟的要求。
| [1] |
BRORSEN M, LARSEN J. Source generation of nonlinear gravity waves with the boundary integral equation method[J]. Coastal Engineering, 1987, 11(2): 93-113. DOI:10.1016/0378-3839(87)90001-9 |
| [2] |
刘加海, 杨永全, 张洪雨, 等. 二维数值水槽波浪生成过程及波浪形态分析[J]. 四川大学学报(工程科学版), 2004, 36(6): 28-31. DOI:10.3969/j.issn.1009-3087.2004.06.006 |
| [3] |
LAL A, ELANGOVAN M. CFD simulation and validation of flap type wave-maker[J]. World Academy of Science, Engineering and Technology, 2018, 2(10): 708-714. |
| [4] |
黄华, 邓冰, 陈昱松, 等. 数值波浪水槽构建与二阶Stokes波仿真[J]. 系统仿真学报, 2012, 24(1): 227-231. |
| [5] |
KIM S Y, KIM K M, PARK J C, et al. Numerical simulation of wave and current interaction with a fixed offshore substructure[J]. International Journal of Naval Architecture and Ocean Engineering, 2016, 8(2): 188-197. DOI:10.1016/j.ijnaoe.2016.02.002 |
| [6] |
TIAN X, WANG Q, LIU G, et al. Numerical and experimental studies on a three-dimensional numerical wave tank[J]. IEEE Access, 2018, PP(99): 1-1. |
| [7] |
MARQUES MACHADO, FÁBIO M, GAMEIRO LOPES, ANTÓNIO M, FERREIRA A D. Numerical simulation of regular waves: Optimization of a numerical wave tank[J]. Ocean Engineering, 2018, 170: 89-99. DOI:10.1016/j.oceaneng.2018.10.002 |
| [8] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5 |
| [9] |
杨壮滔, 张涛, 段浩, 等. 基于数值波浪水槽的圆柱浮标运动仿真与分析[J]. 水下无人系统学报, 2018(3): 207-213. |
| [10] |
廉静静, 尹勇, 杨晓, 等. 基于粘性流船舶数值波浪水池造波和消波方法研究[J]. 船舶力学, 2013(1): 56-62. |
| [11] |
HAVN J. Wave loads on underwater protection covers[J]. Department of Marine Technology, 2012. |
 2020, Vol. 42
2020, Vol. 42
