0 引　言

寒区海域冬季气候寒冷，海气交换强烈，湿度很大，大部分时间相对湿度都在95%以上，表现为多雾、浓雾等极端气候，与其他海域相比，空气中的水汽凝结以及海浪拍击等极易在船舶结构表面上发生凝霜、冰釉等结冰现象^[1]，这些新增重量会降低船舶干舷高度，甚至引起船身倾斜，造成船舶倾覆^[2]。如1965年1月在白令海上10艘苏联船舶由于船体严重结冰造成结构失稳进而倾覆^[3]，图1为寒区船舶上的结冰现象。

寒区船舶上层建筑结冰多为大气结冰，目前关于大气结冰的研究多集中风力机结冰和飞机结冰。如李岩等^[5]在自行设计的冰风洞中以绕轴旋转圆柱为对象研究旋转模型的结冰问题，在该实验中分析了转速、结冰时间和圆柱直径对圆柱结冰形状的影响规律。陈维建^[6]提出一种适用于各种结冰气象条件下飞机机翼结冰过程的数值模拟方法，并以NACA0012翼型为模型进行霜冰、明冰的数值计算，将计算结果与试验数据进行对比，验证了该方法的有效性。顾声龙^[7]将NURLS-S809翼型作为研究对象，对在不同环境参数下，风力机叶片表面所结霜冰的形状和结冰量进行研究，结果显示结冰厚度和结冰量与来流风速的关系较大，随着风速的增大，结冰量也增加，两者之间基本呈线性关系。吴俊杰等^[8]为了确定机翼结冰过程中过冷水滴的运动轨迹，以NACA0012翼型为模型，分析在温度、时间步长和风速等因素不变的条件下，水滴直径和来流攻角对水滴轨迹的影响。结果表明，随着过冷水滴直径的增大，水滴在翼面的分布范围越广；来流攻角不同时，过冷水滴在翼面的撞击区域有很大不同。杜雁霞等^[9]基于液/固相变的基本理论，对飞机结冰过程中的液/固相变传热特性进行了研究，建立了水膜和冰层生长模型，将该模型的计算结果与冰风洞的实验结果进行对比，验证了模型的可靠性。之后采用该模型对风速、温度等各参数对冰层生长及速率的影响进行分析，结果显示冰层生长及速率不但与风速、温度等参数有关还与液、固相区的内部传热特性有关，但这些研究都是关于较高风速下结构表面的结冰。

由于寒区船舶上层建筑存在大量的杆件结构，本文采用Fluent和FENSAP-ICE相结合的方法对杆件结构结冰开展数值模拟，选取风速作为敏感参数，分析风速变化对结冰厚度和结冰量的影响。

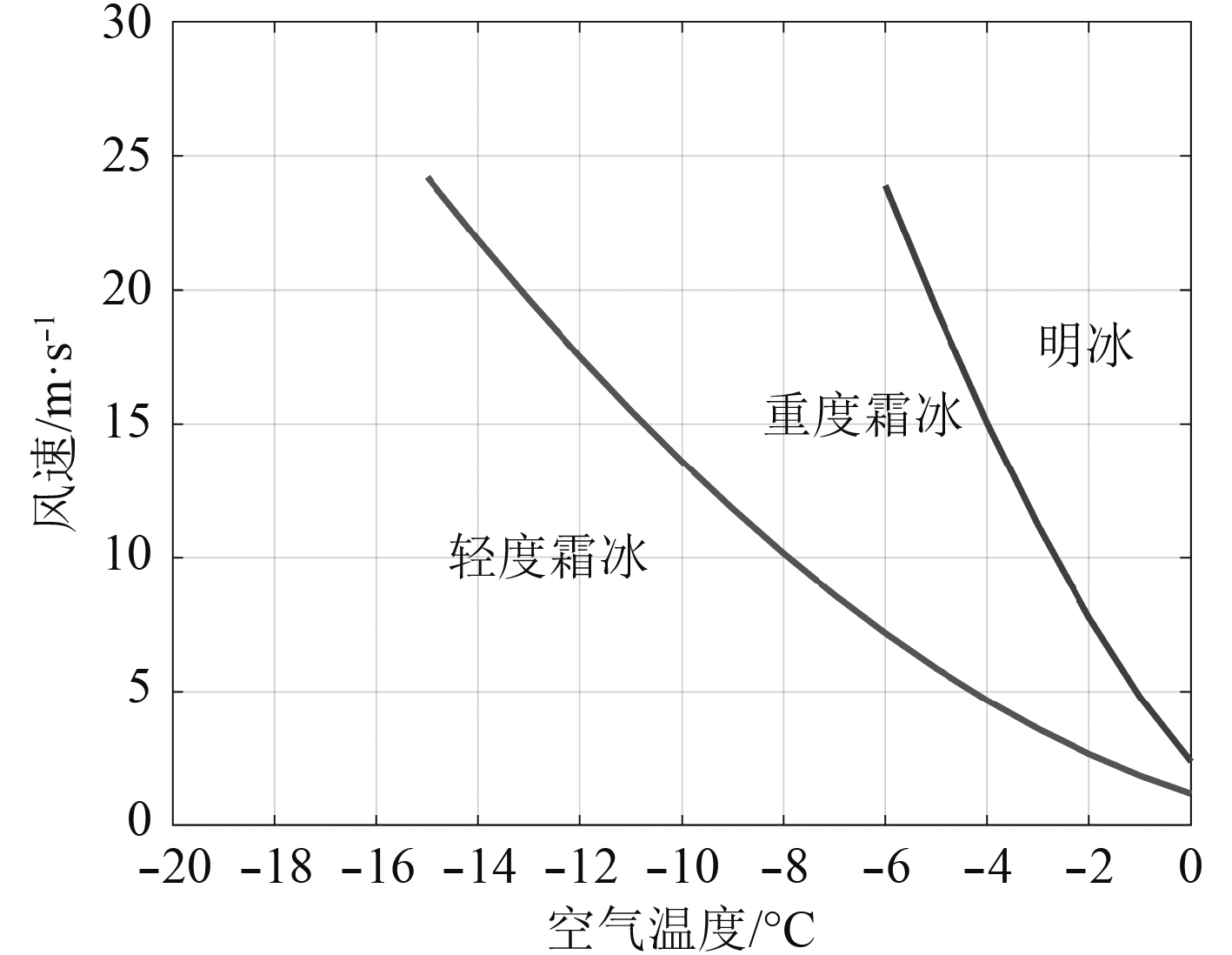
1 结冰气象条件与结冰机理 1.1 结冰气象条件

寒区结构结冰按冰的类型可分为霜冰、明冰、湿雪和混合冰^[10]，图2为霜冰、明冰与风速和温度的关系。Magne^[12]为了确定挪威西海岸Brosviksåta山的大气结冰条件，在山上4个位置处各放置一个探测当地风速、温度、液态水浓度等影响结冰参数的装置，通过该实验确定了该地区大气结冰的气象条件范围：1）气温在–15 ℃～0 ℃范围内，当气温高于0 ℃时不结冰，当气温低于–15 ℃时，空气中水滴会直接结晶从空气中掉落而不与结构接触；2）风速不超过4级（7.9 m/s）；3）空气中液态水浓度为0.05～0.25 g/m³。

1.2 结冰机理

图3为霜冰的形成过程简图。寒区空气中的冷水滴与结构表面接触后还未扩散就完全凝结形成的冰为霜冰^[13]。由于水滴几乎立刻凝结，霜冰的每个冰晶颗粒之间存在着一定量的空气并维持半球状，使其具有粗糙的外形和不透明的性质，而且密度和强度都比明冰较低^[14]。

2 方法验证

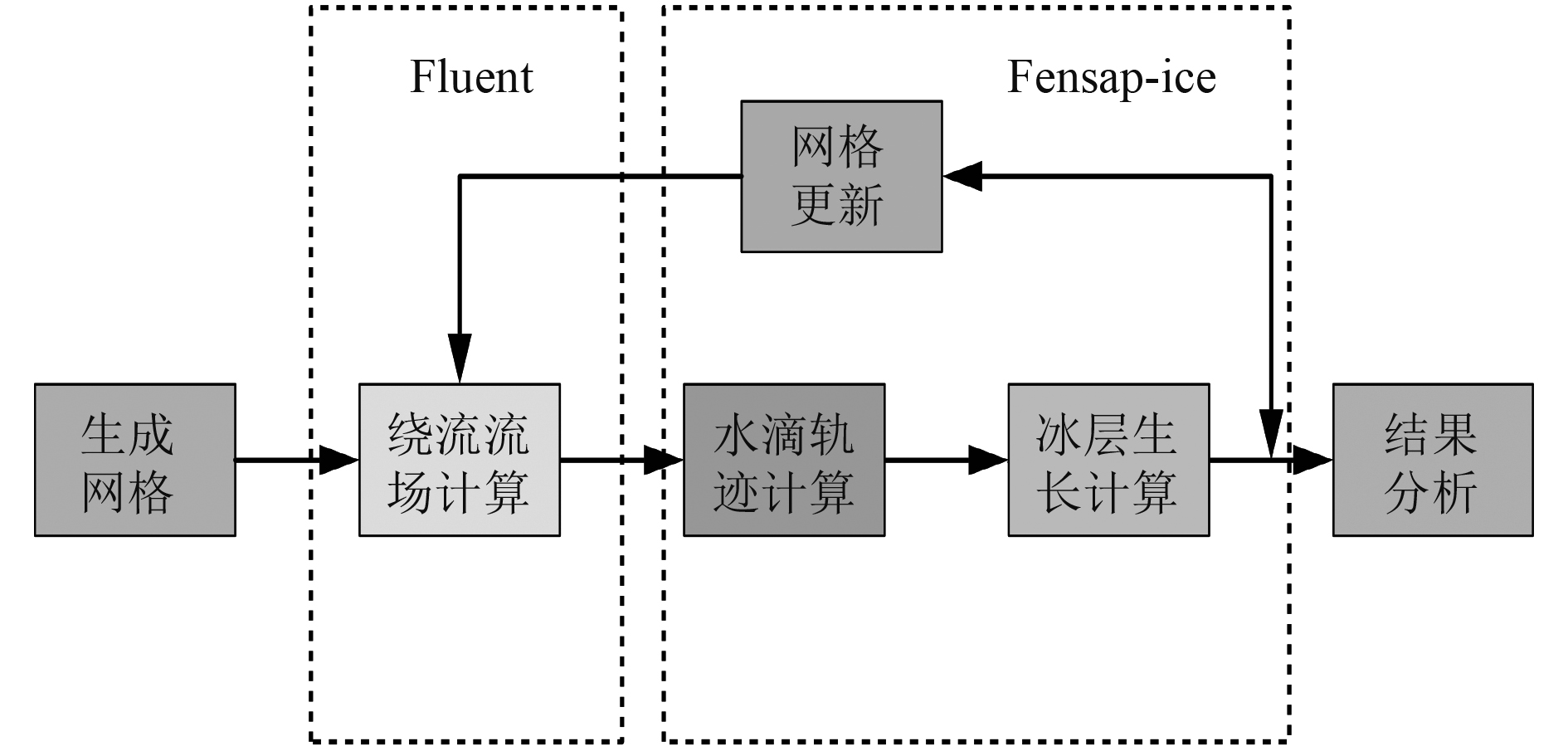
由于寒区船舶结构结冰的特殊性，通常对其的研究都是通过现场试验进行的，而受到我国地理位置的影响，现场试验是非常耗时且成本极高的^[15]。因此，本文结合Fluent和Fensap-ice软件进行杆件结构的结冰数值模拟研究，计算流程如图4所示。分为如下步骤：1）使用Fluent计算结构周围的流场分布，以得到结构周围空气流速 ${{{u}}_a}$ 等参数；2）使用式(1)和式(2)求解水滴的运动轨迹和流场中水滴容积系数的分布；3）使用公式 ${\dot m_{im}} = {\rho _d}\alpha {{{u}}_d} \cdot {{n}}$ 计算得到结构表面控制体内收集到的水滴质量；4）使用式(3)和式(4)计算各控制体内冻结冰的质量；5）使用式(5)得到各控制体内冰的厚度；6）将网格向前推进到霜冰的高度处，并重复上述过程直到给定的截止时间。

$ \nabla \cdot \left( {{\rho _d}\alpha {{{u}}_d}} \right) = 0 {\text{，}} $

(1)

$ \nabla \cdot \left( {{\rho _d}\alpha {{{u}}_d}{{{u}}_d}} \right) = {\rho _d}\alpha K\left( {{{{u}}_a} - {{{u}}_d}} \right) + {\rho _d}\alpha {{{G}}_d} {\text{。}} $

(2)

式中： $\alpha $ 为水滴容积系数， ${{{u}}_d}$ 为水滴的速度矢量， ${{{u}}_a}$ 为空气的速度矢量， ${{{G}}_d}$ 为水滴的重力， $K$ 为空气—水滴动量交换系数， ${\rho _d}$ 水滴密度。

${\dot m_{im}} = {\dot m_{evap}} + {\dot m_{ice}}{\text{；}}$

(3)

式中： ${\dot m_{ice}}$ 为冰质量， ${\dot m_{evap}}$ 为蒸发质量。

$ \begin{split} & \left[ {{c_f}\left( {T - {T_f}} \right) + \frac{{{{\left\| {{{{u}}_{\rm{d}}}} \right\|}^2}}}{2}} \right]{{\dot m}_{im}} + \left( {{L_{fusion}} - {c_s}T} \right){{\dot m}_{ice}}+\\ & \sigma \varepsilon ({T_\infty }^4 - {T_f}^4) =\\ & {L_{{\rm{evap}}}}{{\dot m}_{evap}}{\rm{ + }}{c_h}({T_f} - {T_{ice,rec}}) \text{。} \end{split} $

(4)

式中， ${c_f}$ 为空气比热， ${T_f}$ 为空气/冰交界面温度， ${L_{{\rm{evap}}}}$ 为蒸发潜热， ${T_{ice,rec}}$ 为冰面温度， $T$ 为远场空气温度。

$ \Delta H = \frac{{{{\dot m}_{ice}} \cdot \Delta t}}{{{\rho _{ice}}A}} \text{。} $

(5)

式中： $\Delta t$ 为时间步长， ${\rho _{ice}}$ 为冰密度， $A$ 为控制体底面积。

孟繁鑫等^[16]通过自建的引射式结冰风速研究了不同条件下静止圆柱表面的霜冰和明冰分布，本文选取该试验的一组霜冰结冰条件（见表1）进行数值模拟计算，并与试验结果对比分析。

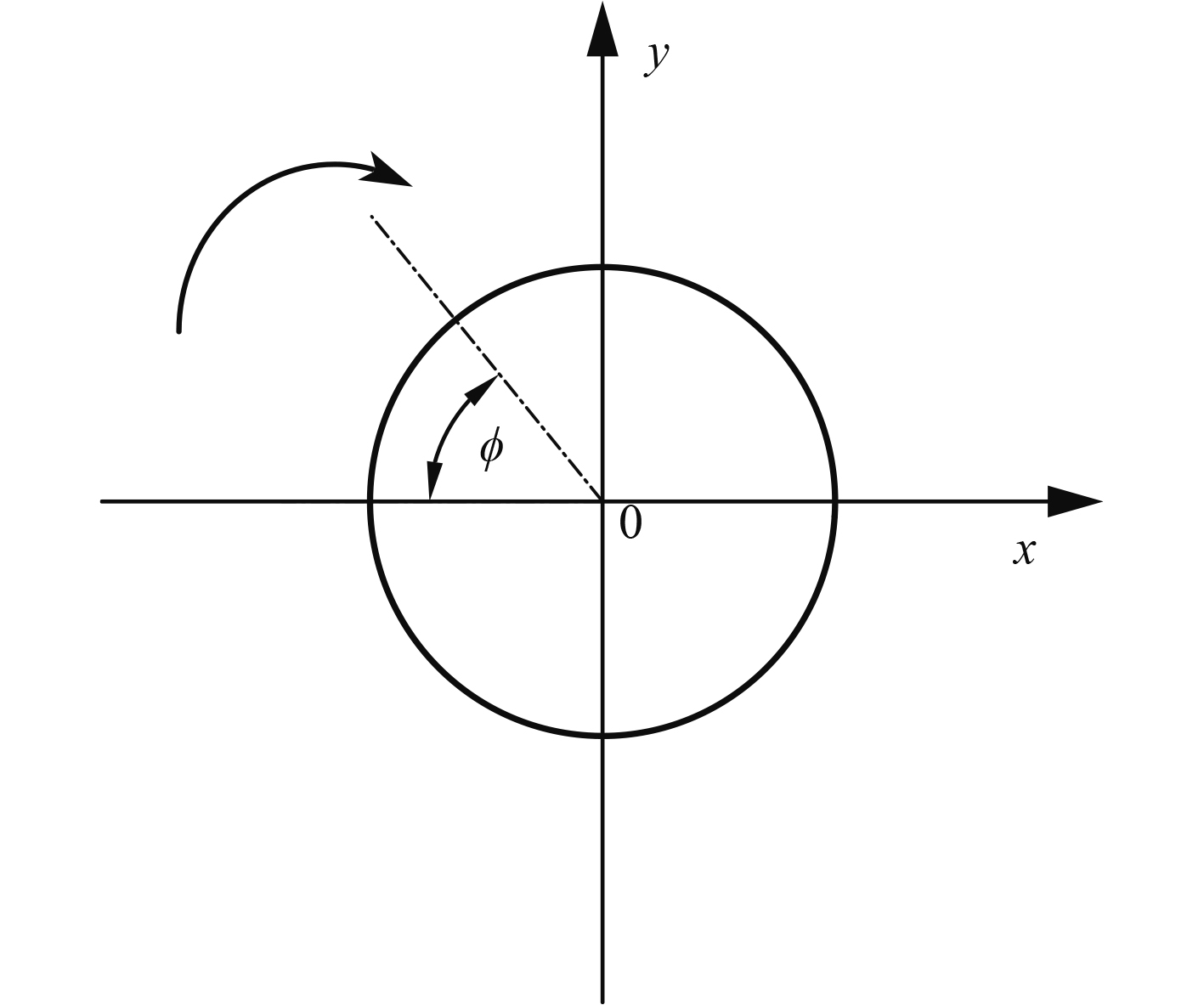
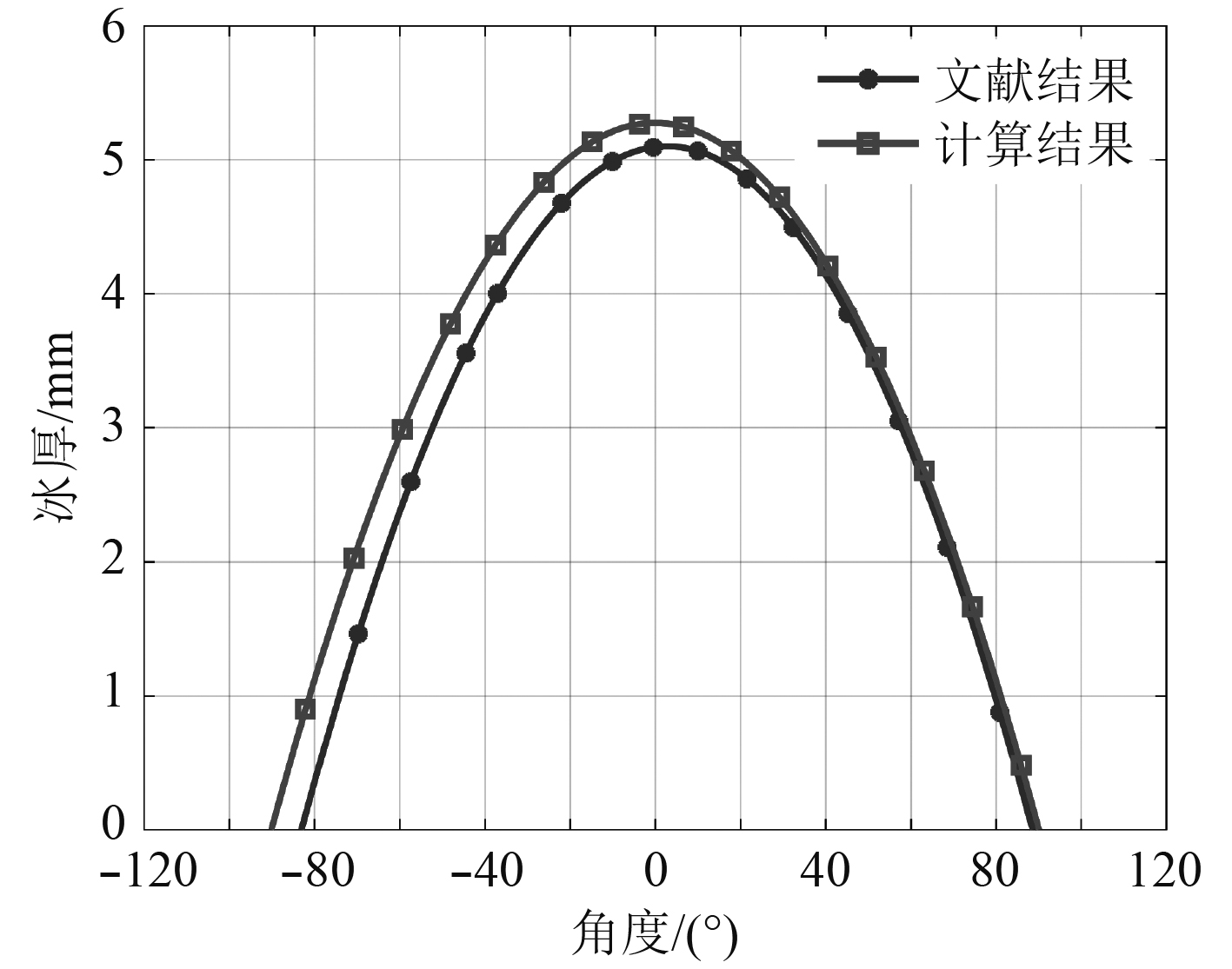
图5中的x轴坐标表示圆柱表面一点与X轴负半轴之间的夹角（如图5中φ），沿顺时针方向为正。图6中本文的冰形计算结果和文献中的试验结果变化趋势相同，数值也在同一个数量级，两者之间的偏差最大为3.5%，可证明本文采用的结冰数值模拟方法是可靠的。

3 风速对杆件结构结冰的影响

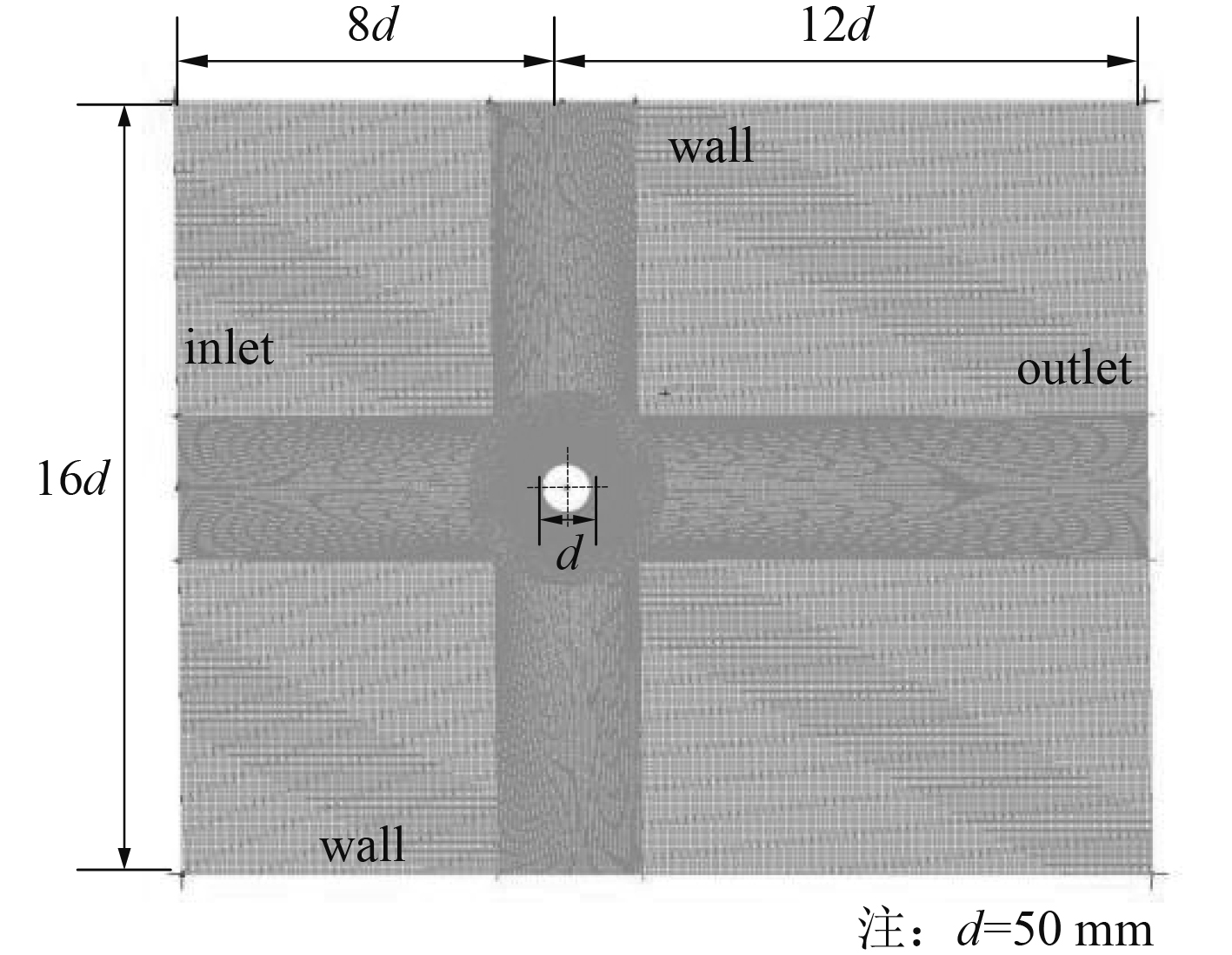
由于本文选取的风向与杆件结构轴向方向垂直，可简化为二维模型进行数值计算，如图7所示。图8为本文计算域模型，其中inlet为速度入口边界条件，outlet为压力出口边界条件，上下边界为壁面边界条件。结冰数值模拟条件由1.1节中的结冰气象条件确定（详细计算参数见表2），由图2可知本文的结冰类型应为霜冰，此外由于不同风速下所结霜冰的密度不同，本文参考Macklin^[17]根据冰风洞试验得到的霜冰密度经验公式（见公式9）确定霜冰密度。

$ {\rho _{{\rm{ice}}}} = 110{\left[ { - \frac{{{d_{50}} \cdot \left\| {{u_d}} \right\|}}{{2T}}} \right]^{0.76}}\left( {{{\rm kg} / {{\rm m^3}}}} \right)\text{，} $

(6)

上式的应用条件为：

$ 1 \leqslant - \frac{{{d_{50}} \cdot \left\| {{{{u}}_d}} \right\|}}{{2T}} \leqslant 17\text{，}\;\; {\rm{T}} \leqslant {\rm{ - }}5{\;^ \circ }{\rm{C}}\text{。} $

(7)

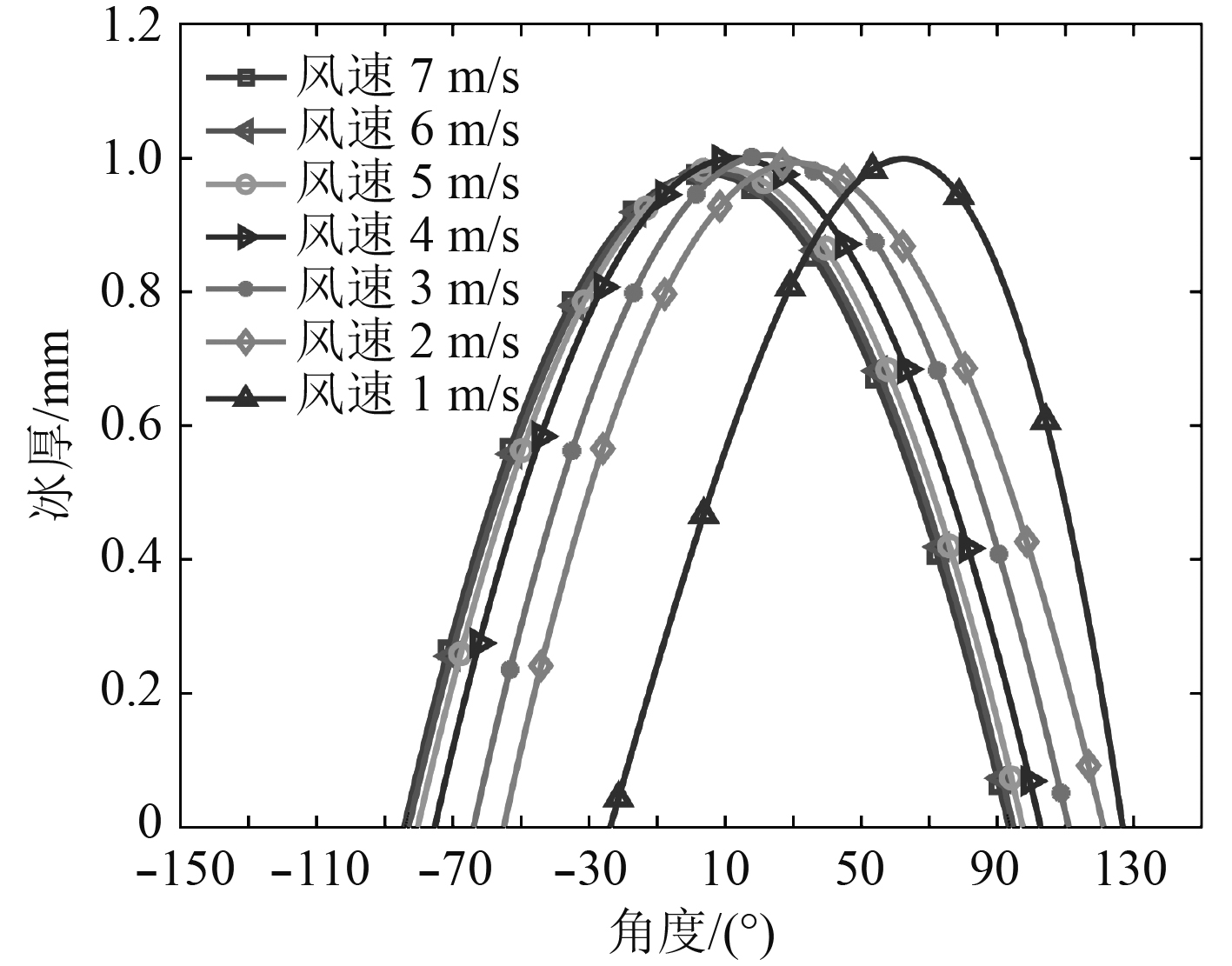
图9～图11分别为风速1.0 m/s，2.0 m/s，3.0 m/s，4.0 m/s，5.0 m/s和7.0 m/s时，杆件表面局部水收集系数、冰形和结冰量分布图。撞击到杆件表面的水滴，沿杆件表面的分布是不均匀的，使用式(8)可得到结构表面控制体内的局部水收集系数，进而可确定结构表面的水滴撞击范围，最终可确定结冰范围，如图9中1～7 m/s风速下杆件表面局部水收集系数的分布情况与图10中结冰的分布情况是一致的。此外，从图10可看出：1）随着风速从1 m/s增加到7 m/s，结构表面的冰厚逐渐增加，因为风速增大使单位时间内撞击到结构上的过冷水滴数量增多，同时风速增大也会带走更多结冰释放的潜热，使结冰更为迅速；2）随着风速从1 m/s增加到7 m/s，冰厚最大值的位置逐渐向左移动，因为水滴速度随来流速度的增加而增加，在相同时间内水滴更快的到达结构表面，水滴运动轨迹的偏转更小，更多的水滴撞击到0°位置处，冰厚最大值也随之向0°方向移动；3）风速为7 m/s时，杆件表面的冰厚最大值为16.59 mm仅比风速为1 m/s时增加了31.3%，因为1 m/s时霜冰的密度仅为7 m/s时的22.8%，当质量一定时，冰的密度越小体积就会越大，因此虽然1 m/s时结冰量仅为7 m/s的18.1%，但冰厚并未远小于7 m/s时的冰厚。从图11可看出，随着风速从1 m/s增加7 m/s，杆件表面的结冰量近似线性增长。

$\beta {\rm{ = }}\frac{{{W_\beta }}}{{{W_{\beta \max }}}}$

(8)

式中， ${W_\beta }$ 为微元表面实际水收集量， ${W_{\beta \max }}$ 为该微元表面上最大可能水收集量。

4 结　语

本文以寒区船舶杆件结构结冰为背景，采用Fluent和Fensap-ice相结合的方法对杆件结构结冰开展数值模拟，选取风速作为敏感参数，分析了风速变化对结冰厚度和结冰量的影响，得出如下结论：

1）随着风速从1 m/s增加到7 m/s，杆件表面冰厚最大值的位置逐渐向左移动，因为水滴速度随来流速度的增加而增加，在位移相同时水滴更快的到达结构表面，水滴运动轨迹的偏转更小，更多的水滴撞击到0°位置处，冰厚最大值也随之向0°方向移动。

2）风速为7 m/s时杆件表面的冰厚并未远大于1 m/s时的冰厚。因为风速为1 m/s时杆件表面所结霜冰的密度仅为7 m/s时的22.8%，当质量一定时，冰的密度越小体积就会越大，因此虽然1 m/s时结冰量仅为7 m/s的18.1%，但冰厚并未远小于7 m/s时的冰厚。

3）在风速为1～7 m/s区间内，随着风速的增加，杆件表面的结冰量近似的呈线性方式增加。