2. 上海交通大学海洋工程国家重点实验室,上海 200240;
3. 中国远洋海运集团有限公司,上海 200127;
4. 中远海运特种运输股份有限公司,广东 广州 510623
2. State key Laboratory of Ocean Engineering, Shanghai Jiaotong University, Shanghai 200240, China;
3. China COSCO Shipping Co.Ltd., Shanghai 200127, China;
4. COSCO Shipping Specialized Carriers Co., Ltd., Guangzhou 510623, China
北极航道是联系欧亚美三大洲最短航线,使用北极航道比绕行南部的苏伊士或巴拿马运河节省至少40%航程,缩短传统航道5千千米以上。极地蕴藏丰富的自然资源,是未来重要的能源资源基地。“海洋强国”、“一带一路”、“冰上丝绸之路”等提出,均表明北极航道的开发对我国具有重要的经济价值和战略意义[1-2]。2013年,中国商船“永盛轮”首航北极,圆满完成我国第1艘商船经由北极东北航道到达欧洲的首创[3],开启了我国商船的极地航行之旅。
与敞水航行不同,极地航行的商船将不可避免地遭遇冰载荷。冰载荷与水载荷不同,具有幅值大、强间断性和强非线性的特点,对极地航行商船的阻力计算、主机功率计算、操纵性计算以及结构安全性等均提出巨大挑战[4]。以主机功率的计算为例,以往的计算主要依赖船级社冰级规范的经验公式[5-6]。经验公式计算方法简便,但研究表明,经验公式计算得到的最小主机功率往往过于保守[7]。尤其对于常规商船配备中低速主机的船舶,此功率要求往往会大幅度高于日常使用所要求的经济值[7]。为此,正如芬兰-瑞典冰级规范[6]中所指出的,对于某些船型,需要采用更加精确的计算方法或者基于模型试验来确定船舶主机功率。
在计算船舶主机功率之前,需要确定船舶遭遇的冰阻力。目前对于冰阻力的计算方法主要有经验方法、试验方法和数值方法。经验公式法[8]通过对实船测量、模型试验以及数值计算的结果进行总结,归纳出经验公式以预报船舶在冰区航行的冰载荷,但是经验公式在预测冰载荷问题上经常局限于某种特定的船型或者结构形式。试验方法[9-10]是船舶冰阻力研究中比较直接有效的方法,但是试验需要比较苛刻的试验环境(如实测环境或者冰水池),同时需要比较昂贵的成本,使得试验方法具有很大的局限性。数值方法是通过数学建模,将海冰与船体的相互作用采用数值手段进行求解并积分获得冰阻力的方法。目前计算冰阻力主流的数值方法包含有限元法[11-12](FEM)和离散元法[13-14](DEM)。由于离散元法将海冰视为块体或颗粒体的思想更接近海冰真实的物理力学特性,近年来离散元法在计算海冰与船舶结构的碰撞和阻力方面的研究有了很大进展[15-16]。
针对目前极地航行商船主机功率预报中缺乏有效计算方法与模型的问题,本文借鉴中国商船“永盛轮”首航北极的实际航行经验,对航行东北航道至北欧地区的船舶进行技术调研,基于离散元方法和开敞水域船舶的主机功率计算理论,建立冰级船主机功率的计算模型和预报方法。将预报方法应用于中国远洋海运集团有限公司B1冰级的36 000 t冰级多用途船的主机功率预报中,计算结果与船级社规范方法进行对比,总结相关规律,旨在为我国极地航行商船设计制造提供技术支撑。
1 冰阻力数值模型 1.1 航道内冰况确定本文采用离散元方法计算船舶遭遇的冰阻力。在计算冰阻力之前,需要给出船舶在极地航道航行时遭遇的海冰状态,例如是平整冰、碎冰或冰脊甚至冰山等。根据“永盛轮”首航北极的实际航行经验,我国极地航行商船多航行于破冰船开拓的或者其他商船往复航行的碎冰航道内。碎冰航道内碎冰的尺度较小,形状更接近球形。在此基础上,本文将建立基于球形颗粒的海冰离散元模型。
1.2 碎冰离散元模型在采用离散单元模型计算碎冰间相互作用过程中,将碎冰看作为具有一定质量和大小的颗粒单元,考虑单元间相对速度和相对位置引起的非线性粘弹性作用力,并采用Mohr-Coulomb摩擦定律确定单元间的剪切力,其接触力模型[17]如图1所示。图1中MA和MB分别为圆球颗粒单元A,B的质量,Kn和Ks分别为法向和切向刚度系数,Cn和Cs分别为法向和切向阻尼系数,µ为滑动摩擦系数。
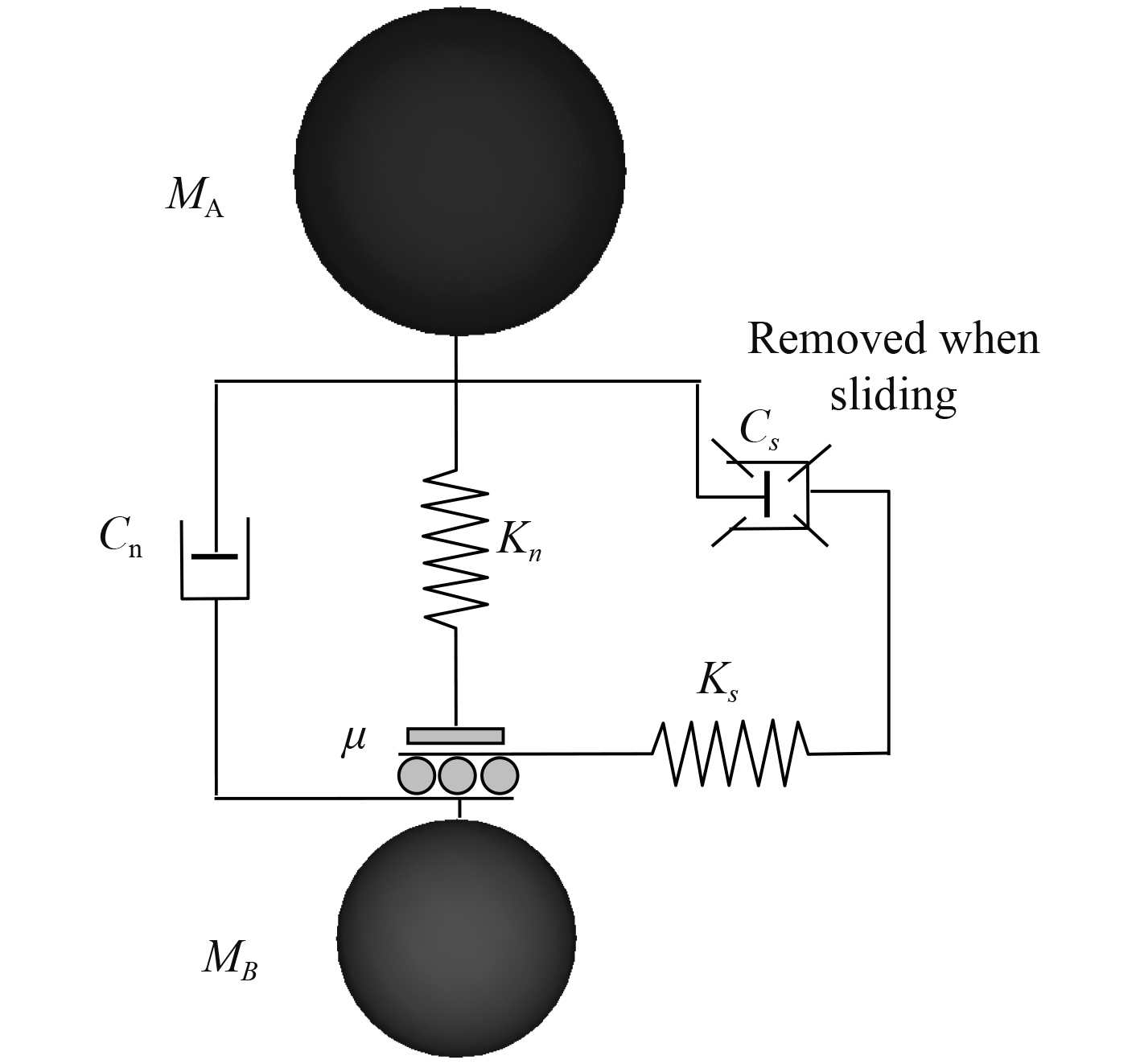
|
图 1 颗粒单元间的接触模型 Fig. 1 Contact model between elements |
在颗粒接触的法线方向,颗粒单元间的法向力包括Hertz非线性弹性力和非线性粘滞力。弹性力模拟颗粒间相互接触时的排斥力,而非线性粘滞力模拟颗粒接触过程中因相对速度导致的能量耗散,可表述为:
| ${F_{n}} = {K_{n}}{{x}}_{n}^{3/2}{{ + }}\frac{3}{2}A{K_{n}}{{x}}_{n}^{1/2}{{{\dot x}}_{n}}{\text{。}}$ | (1) |
式中:
在颗粒接触的切线方向,基于Mindlin理论和Mohr-Coulomb摩擦定律,并忽略切向粘滞力影响,则切向接触力为:
| $F_{{s}}^* = {K_{{s}}}{x_{{n}}}^{1/2}{x_{{s}}}{\text{,}}$ | (2) |
| $F_{{s}}^{} = \min (F_{{s}}^*,{{\rm{sign}}}(F_{{s}}^*)\mu F_{{n}}){\text{,}}$ | (3) |
| ${K_{{n}}} = \frac{4}{3}{E^ * }\sqrt {{R^ * }}{\text{,}} $ | (4) |
| $ {K_{{s}}} = 8{G^ * }\sqrt {{R^ * }}{\text{。}} $ | (5) |
式中:
非线性离散元模拟中,计算时间步长一般通过由颗粒表面瑞雷波的传播周期[18]来确定。首先定义临界时间步长为[18]:
| $ \Delta {t_{{{{\rm{crit}}}}}} = \frac{{{\text{π}} {R_{\min }}}}{{0.163v + 0.8766}}\sqrt {\frac{\rho }{G}} {\text{。}} $ | (6) |
式中,
在离散元计算时,实际时间步长要小于临界时间步长
| $ \Delta t = \frac{{\Delta {t_{{{{\rm{crit}}}}}}}}{K} {\text{。}} $ | (7) |
式中, K为经验系数,要求
采用网格划分前处理软件将船体离散化为一系列的三角形单元,如图2所示。建立三角形单元与球体海冰单元间的接触模型,由此计算海冰与船体之间的相互作用。这里主要介绍海冰与船体间的作用力模型,具体的接触判断算法详见文献[19]。

|
图 2 船体三角形离散单元模型 Fig. 2 Discrete triangle elements on ship surfaces |
通过接触模型可以确定海冰球状颗粒在船体三角形单元内的嵌入量
| $ \Delta L=\left|{{P}}_{C}{P}\right|-{R}_{\mathrm{b}\mathrm{a}\mathrm{l}\mathrm{l}}{\text{,}} $ | (8) |
式中,
| $ {{n}}_{{w}}=\frac{{{P}}_{{C}}{P}}{\left|{{P}}_{{C}}{P}\right|}{\text{,}} $ | (9) |
相对位移
| $ \Delta {x}=\left({{v}}_{{p}}-{{v}}_{{w}}\right)\Delta t{\text{。}}$ | (10) |
式中,
将相对位移沿接触面分解为法向分量
| $ \Delta {{x}}_{{n}}=\left({{n}}_{{w}}\Delta {x}\right){{n}}_{{w}}{\text{,}} $ | (11) |
| $ \Delta {{x}}_{{s}}=\Delta {x}-\Delta {{x}}_{{n}}{\text{。}}$ | (12) |
颗粒与边界单元之间的相互作用力采用线性接触模型计算,其中法向力可表示为:
| $ {{F}}_{{n}}={k}_{{w}}^{{n}}\Delta L{\text{。}} $ | (13) |
切向力的计算采用增量形式,并服从Mohr-Coulomb定律:
| $ {{F}}_{{s}}\leftarrow {{{F}}_{{s}}+k}_{{w}}^{{s}}\Delta {{x}}_{{s}}, {\rm{if}}\left|{{F}}_{{s}}\right|<\left|{\mu }_{{w}}{{F}}_{{n}}\right|{\text{,}}$ | (14) |
| $ {{F}}_{{s}}\leftarrow {{F}}_{{s}}\left({\mu }_{{w}}{{F}}_{{n}}/\left|{{F}}_{{s}}\right|\right), {\rm{if}}\left|{{F}}_{{s}}\right|\geqslant \left|{\mu }_{{w}}{{F}}_{{n}}\right| {\text{。}}$ | (15) |
式中:
| $ {R_i} = \iint\limits_{{S_i}} {({{{F}}_n} \cdot {{{n}}_x} + }{{{F}}_s} \cdot {{{n}}_x}){\rm{d}}s{\text{。}} $ | (16) |
式中,
由于B1冰级极地加强型船舶需要具有航行在碎冰区的能力,所以船体将遭受冰阻力和水阻力两大部分。首先忽略冰阻力和水阻力间的耦合作用,假设冰阻力和水阻力相互独立且满足线性叠加的关系。此外,考虑到海冰的存在将极大地消除自由液面的兴波,并改变船舶尾流的变化等,故在计算水阻力时,仅考虑水与船体间的摩擦阻力,忽略比重较小的兴波阻力和粘压阻力的作用。
对于实船的摩擦阻力,有较多的计算方法,较为通用的是1957ITTC公式[20]。根据ITTC(1995)经验公式摩擦水阻力
| ${R_w} = \left( {{C_f} + \Delta {C_f}} \right) \cdot \frac{1}{2}\rho {V^2}S{\text{。}}$ | (17) |
式中:
| ${C_f} = \frac{{0.075}}{{{{\left( {\lg \operatorname{Re} - 2} \right)}^2}}}{\text{,}}$ | (18) |
| $S = {L_{WL}}BT\left( {\frac{1}{T} + \frac{2}{B} + \frac{2}{{{L_{WL}}}}} \right) - 4.4{\left( {5\left( {\frac{1}{{{C_B}}} - 1} \right)} \right)^{\frac{2}{3}}}{\text{。}}$ | (19) |
式中:Re为雷诺数;
通过计算船舶阻力与航速的曲线,获得不同航速下的船体的有效功率为
| ${P_E} = R \cdot V \approx ({R_i} + {R_w}) \cdot V{\text{。}}$ | (20) |
式中:
| ${N_E} = {P_E}/P.C{\text{。}}$ | (21) |
推进系数P.C是多种效率相乘的综合名称,与轴系传送效率、相对旋转效率、螺旋桨的敞水效率和船身效率等多种因素有关,对于不同的螺旋桨和不同船体会有一定的变化。因为这里主要考虑冰区航行船舶的阻力问题,同时考虑到本船型螺旋桨以及桨机匹配情况,选取P.C为0.60进行计算,暂不考虑P.C的变化。根据船体总阻力-速度变化曲线,即可获得有效功率-速度变化曲线,再根据式(21)可获得主机功率曲线,从而根据最大航速可获得船舶所需的主机功率。
4 计算结果及分析 4.1 数值模拟结果根据上述数值模型和计算方法,本小节根据中国远洋海运集团有限公司B1冰级36 000 t冰级多用途船为对象,计算船舶冰阻力以及对应的主机功率等。在CUDA平台上基于GPU并行算法构建海冰及船-冰作用离散元模型。船体离散元模型如图2所示,由2 008块三角形边界单元拼接而成。碎冰块采用球体单元来模拟,主要计算参数如表1所示:
|
|
表 1 海冰离散元模型参数 Tab.1 Parameter of discrete elements of ice |
用离散元方法模拟的船舶在碎冰航道内以不同大小的恒定速度航行,船舶航行速率V分别设为1 m/s,3 m/s,5 m/s,7 m/s,冰厚H分别设定为0.8 m,0.5 m和0.3 m。这里选取以速率为5 m/s,冰厚0.8 m为例,船舶在碎冰航道内航行过程如图3所示。

|
图 3 离散元法模拟的船舶在碎冰航道中的航行过程(V=5 m/s,H=0.8 m) Fig. 3 Numerical simulation of ship moving in the brash ice channel based on DEM (V=5 m/s,H=0.8 m) |
由图3中可知,在船舶的作用下,碎冰航道将在船舶过后形成具有自由水面的水域,随着船舶继续向前运动,碎冰在流体的作用下逐渐闭合,再次形成碎冰与水的混合流域。现再次以冰厚0.8 m为例,获得不同航速下的船舶冰阻力时程曲线,如图4所示,其中横直线表示航行过程中的平均冰阻力。

|
图 4 不同航速时船舶冰阻力(H=0.8 m) Fig. 4 Ice resistance of ship at different speeds(H=0.8m) |
从图4可见,随着船舶的向前航行,碎冰将在船体上形成高频、非线性冰载荷作用,这与船舶不同部位与碎冰的不断接触、分离以及碎冰沿着船体的滑移等现象有关。此外,随着航速的增加,冰阻力均呈现非线性快速增加的趋势。
根据式(17)可计算不同航速下的摩擦水阻力,将摩擦水阻力和计算得到的冰阻力叠加可获得总阻力,采用式(20)可获得有效功率。本文将不同航速、不同冰厚下阻力值与有效功率计算值列于表2中。
|
|
表 2 船舶在不同航速下的阻力及主机有效功率 Tab.2 Resistance and effective power of main engine of ship at different speeds |
进一步地,可获得不同阻力值与航速变化以及有效功率与航速变化的曲线分别如图5和图6所示。
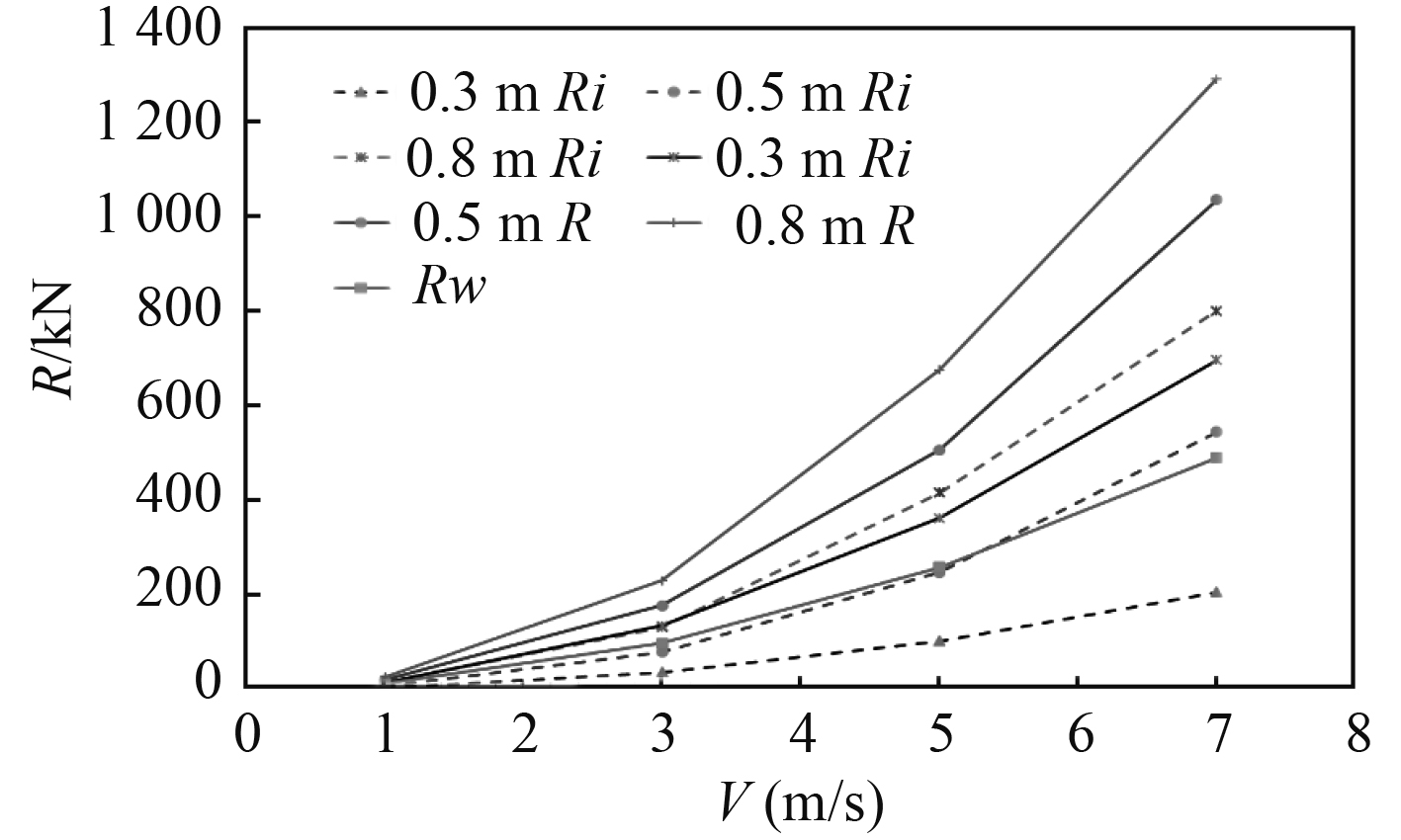
|
图 5 船舶在不同航速下的摩擦水阻力Rw,冰阻力Ri和总阻力R Fig. 5 Friction resistance of water Rw, ice resistance Ri and total resistance R of ship at different speeds |
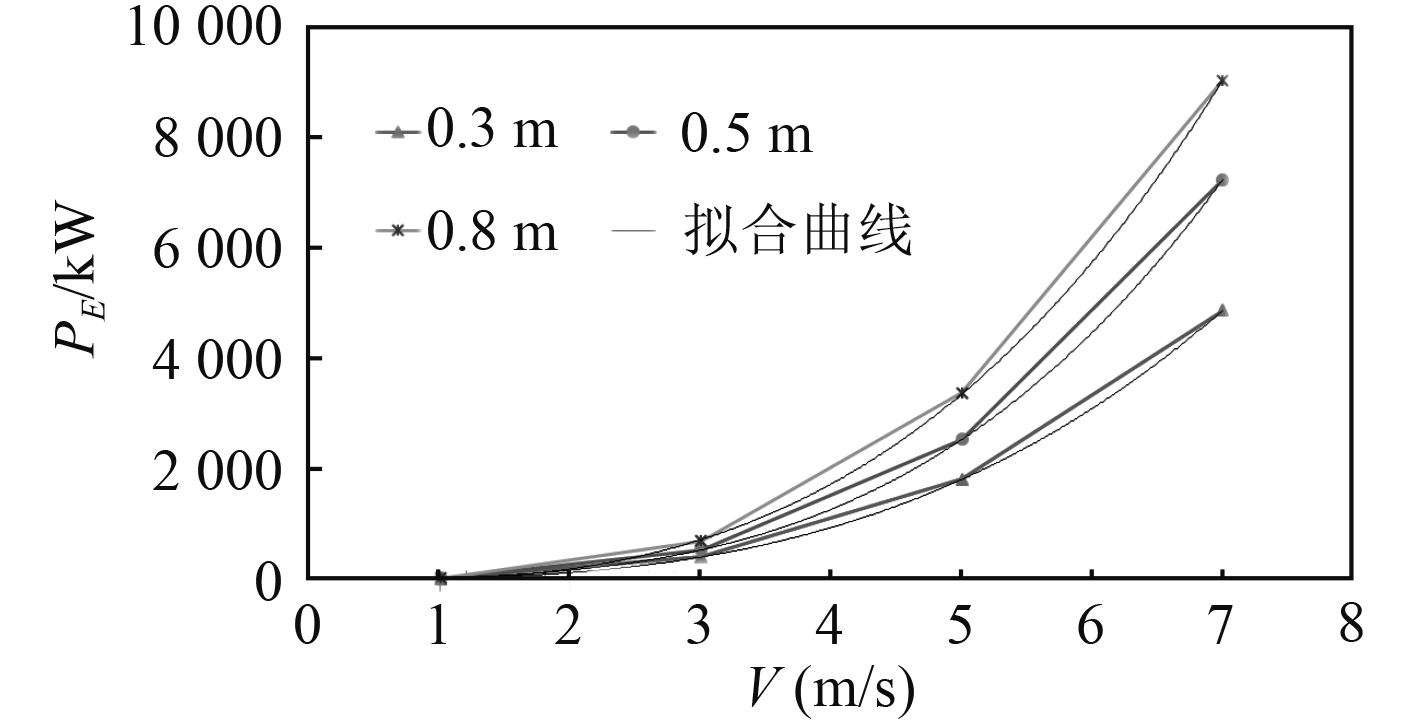
|
图 6 船舶在不同航速下的有效功率PE及其拟合曲线 Fig. 6 Effective power PE of ship at different speeds and its fitting curves |
为了判断有效功率随航速变化的特性,这里采用三次多项式对图6中有效功率与速度间的关系进行拟合,如下:
| $ \left\{ \begin{aligned} & {{P_{E\_}}_{0.3{{{\rm{m}}}}} = 13.40{V^3} + {{ }}6.75{V^2} - {{ }}4.96V}{\text{,}} \\ & {{P_{E\_}}_{0.5{{{\rm{m}}}}} = 24.02{V^3} - {{ }}24.60{V^2} + {{ }}32.53V} {\text{,}}\\ & {{P_{E\_}}_{0.8{{{\rm{m}}}}} = 23.58{V^3} + {{ }}27.62{V^2} - {{ }}53.42V} {\text{。}} \end{aligned} \right. $ | (22) |
借鉴中国商船“永盛轮”首航北极的实际航行经验,对航行东北航道至北欧地区的船舶进行技术调研可知,B1级冰区加强型船舶在最大0.8 m左右厚度的碎冰航道中航行的最大速度一般不超过8~10 kn。这里选取最厚冰厚0.8 m,最大航速10 kn计算,根据图6和式(22)计算可知此时的有效功率
如前所述,冰级船的主机功率通常是采用规范法的经验公式进行计算。这里为了对比和校核,选用芬兰-瑞典规范对上述船型的主机功率进行计算。根据芬兰-瑞典规范IA级(等同于B1级)冰级船的计算公式,主机输出功率应不小于下式所确定的值[6]:
| ${N_e} = {k_e}\frac{{{{\left( {{R_{CH}}/1\;000} \right)}^{3/2}}}}{{{D_P}}}{\text{。}}$ | (23) |
式中,
| $ \begin{split} {R_{CH}} =\,& {C_1} + {C_2} + {C_3}{C_\mu }{\left( {{H_F} + {H_M}} \right)^2}\left( {B + {C_\varphi }{H_F}} \right)+ \\ & {C_4}{L_{PAR}}H_F^2 + {C_5}{\left( {\frac{{LT}}{{{B^2}}}} \right)^3}\frac{{{A_{Wf}}}}{L}{\text{。}} \end{split} $ | (24) |
式中:
将实船的参数代入到式(24)和式(23)中,可计算得到阻力
通过将本文的数值计算结果(6 149.56 kW)与规范法的计算结果(6 785.87 kW)进行对比,可见本文模型计算获得的主机输出功率比经验公式小,说明经验公式计算值相对保守,且由于经验公式中没有考虑航速的变化,本文模型考虑了航速的影响,从理论上更具合理性。对于目前这艘B1级冰区加强型船舶而言,本文数值结果与规范法相差不大,但是对于其他船型,本文的计算结果明显小于经验公式计算结果[7]。
5 结 语极地强非线性冰载荷的存在对极地航行商船的阻力和主机功率计算均提出巨大挑战。本文借鉴中国商船“永盛轮”首航北极的实际航行经验,基于离散元的理论方法和数值模型,采用阻力-速度曲线法建立了冰区加强型商船主机功率计算方法,获得主要结论如下:
1)通过规范法可以粗估冰级航行船舶在碎冰航道内遭受的阻力以及所需的主机功率,规范法的公式简单,计算较为简便,但不同规范的计算略有不同,计算的阻力值以及主机功率与航速无关,计算结果相对保守。
2)基于离散元方法,建立了冰区加强型船舶在碎冰航道内直航的运动模型,能够预报不同冰情条件下的冰区加强型船舶的冰阻力,并与船舶摩擦水阻力叠加,获得冰区加强型船舶的总阻力,从而可以获得总阻力-航速曲线以及有效功率和主机功率-速度曲线。该方法考虑了航速和冰情对于主机功率的影响,理论上更具合理性。
3)根据“永盛轮”首航北极航道的冰情数据和航行经验,将冰情与航速等数据输入到本文数值模型中,可以应用该数值模型获得总阻力,从而获得相应的有效功率和主机功率,为冰区加强型船舶主机功率的选取提供创新性方法。计算结果表明,该方法计算获得的主机功率较规范法小;
4)应用此方法,对于已经选定了主机的冰区船舶,从主机实际能够持续输出最大功率的能力角度,还可以给出不同冰情下船舶最大航速的建议值,可为我国商船极地水域航行提供技术支撑。
| [1] |
中华人民共和国国务院新闻办公室. 中国的北极政策[R]. 2018年1月.
|
| [2] |
李振福, 王文雅, 刘翠莲. 北极丝绸之路战略构想与建设研究[J]. 产业经济评论, 2016(2): 113-124. DOI:10.3969/j.issn.2095-5073.2016.02.011 |
| [3] |
赵庆爱. “永盛”轮的北极破冰之旅[J]. 中国海事, 2014(9): 17-20. DOI:10.3969/j.issn.1673-2278.2014.09.008 |
| [4] |
薛彦卓, 倪宝玉. 极地船舶与浮体结构物力学问题研究综述[J]. 哈尔滨工程大学学报, 2016, 37(1): 36-40. |
| [5] |
中国船级社. 钢质海船入级与建造规范[S]. 2012.
|
| [6] |
Finnish Maritime Administration, Finnish-Swedish Ice Class Rules[S], 2002.
|
| [7] |
夏讨饭, 曹凯, 唐桂斌, 等. 极地航行船舶最小功率计算研究[J]. 船舶标准化工程师, 2017, 50(5): 38-42. |
| [8] |
LINDQVIST G A. Straightforward method for calculation of ice resistance of ships[J]. Performance, 1989. |
| [9] |
黄焱, 孙剑桥, 季少鹏, 等. 大型运输船极地平整冰区航行阻力的模型试验[J]. 中国造船, 2016, 57(3): 36-44. DOI:10.3969/j.issn.1000-4882.2016.03.005 |
| [10] |
DERRADJI-AOUAT A. Experimental uncertainty analysis for ship model testing in the ice tank[C]//25th Symposium on Naval Hydrodynamics, Canada, 2004.
|
| [11] |
IZUMIYAMA K, KITAGAWA H, KOYAMA K, et al. On the interaction between a conical structure and ice sheet[C].//Proceeding of 11th International Conference on Port and Ocean Engineering under Arctic Conditions. Newfoundland, Canada, 1991.
|
| [12] |
SU B, KAJ R, TORGEIR M. A numerical method for the prediction of ship performance in level ice[J]. Cold Regions Science and Technology, 2010, 60(3): 177-188. DOI:10.1016/j.coldregions.2009.11.006 |
| [13] |
HANSEN E H, LØSET S. Modelling floating offshore units moored in broken ice: model description[J]. Cold Regions Science and Technology, 1999, 29(2): 97-106. DOI:10.1016/S0165-232X(99)00023-3 |
| [14] |
LAU M, LAWRENCE K P, ROTHENBURG L. Discrete element analysis of ice loads on ships and structures[J]. Ships and Offshore Structures, 2011, 6(3): 211-221. DOI:10.1080/17445302.2010.544086 |
| [15] |
季顺迎, 李紫麟, 李春花, 等. 碎冰区海冰与船舶结构相互作用的离散元分析[J]. 应用力学学报, 2013(4): 520-526. DOI:10.11776/cjam.30.04.D032 |
| [16] |
蔡柯, 季顺迎. 平整冰与船舶结构相互作用的离散元分析[J]. 船舶与海洋工程, 2016, 32(5): 5-14. |
| [17] |
严颖, 李勇俊, 季顺迎. 自动卸煤车卸料时间的离散元分析[J]. 大连交通大学学报, 2016, 37(3): 73-78. DOI:10.11953/j.issn.1673-9590.2016.03.073 |
| [18] |
KREMMER M, FAVIER J F. A method for representing boundaries in discrete element modelling-part II- Kinematics[J]. International Journal for Numerical Methods in Engineering, 2001, 51: 1423-1436. DOI:10.1002/nme.185 |
| [19] |
狄少丞, 季顺迎, 薛彦卓. 船舶在平整冰区行进过程的离散元分析[J]. 海洋工程, 2017, 35(3): 59-69. |
| [20] |
ITTC committee. Proceeding of 8th International Towing Tank Conference (ITTC)[C]. Madrid, Spanish, 1957.
|
 2020, Vol. 42
2020, Vol. 42
