随着现代船舶性能标准的逐步提高,在航行性能、节能环保等方面的要求也越来越严格。吊舱推进器作为新型推进系统之一,由于其突出的特点和表现,在商用领域取得了巨大的成功。拖式单桨吊舱推进器是目前市场上比较常见的种类,如ABB公司的Azipod® XO系列、Azipod® CO系列、Rolls-Royce公司的Mermaid吊舱推进器、SIEMENS公司的SISHIP eSiPOD推进器等[1]。吊舱推进器的推进形式完全不同于传统的螺旋桨,由于吊舱的存在一定程度上改变了螺旋桨原本的尾流情况,尾流和吊舱之间的相互作用更是影响了推进器的整体性能。因此深入了解拖式吊舱推进器的水动力特性是设计和优化过程中至关重要的一环。
计算流体动力学(CFD)方法具有成本低,周期短的优点[8],因为考虑了流体黏性的影响,可以得到较为准确且详细的流场信息,被越来越多地应用于吊舱推进器的水动力性能预测[2-7]。本文借助流体计算软件FINE/Marine,采用滑移网格(Sliding Mesh)方法,对三维实尺度的裸桨及吊舱推进器进行了敞水情况下的数值模拟与分析,探讨了吊舱的存在对螺旋桨水动力性能的影响、吊舱在尾流中的侧向受力情况以及吊舱周围流体的运动情况。
1 数值方法 1.1 控制方程在本文中,水被认为是不可压缩流体,并且不考虑能量交换,所以只需考虑连续性方程和动量守恒方程:
| $ \frac{\partial }{\partial t}\int_{V}{\rho }dV+\int_{S}{\rho }\left( \vec{U}-{{{\vec{U}}}_{d}} \right)\cdot \vec{n}{\rm d}S=0\text{,} $ | (1) |
| $\begin{split} & {\frac{\partial }{{\partial t}}\displaystyle\int_V \rho {U_i}dV + \displaystyle\int_S \rho {U_i}\left( {\vec U - {{\vec U}_d}} \right) \cdot \vec n{\rm{d}}S} =\\ &{ \displaystyle\int_S {\left( {{\tau _{ij}}{I_j} - p{I_i}} \right)} \cdot \vec n{\rm d}S + \displaystyle\int_V \rho {g_i}{\rm d}V}\text{。} \end{split} $ | (2) |
式中:t为时间;ρ为密度;V为控制体体积;S为控制体面积;
CFD计算采用剪切压力传输k-ω(SST-Menter)模型,其湍动能K和湍流耗散率ω的输运方程为:
| ${\frac{{\partial \rho K}}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {\rho {U_j}K - \left( {\mu + {\sigma _k}{\mu _t}} \right)\frac{{\partial K}}{{\partial {x_j}}}} \right) = {\tau _{ij}}{S_{ij}} - {\beta ^*}\rho \omega K}\text{,} $ | (3) |
| $ \begin{split} &{ \frac{{\partial \rho \omega }}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left( {\rho {U_j}\omega - \left( {\mu + {\sigma _\omega }{\mu _t}} \right)\frac{{\partial \omega }}{{\partial {x_j}}}} \right)}=\\ &{ {P_\omega } - \beta \rho {\omega ^2} + 2(1 - {F_1})\frac{{\rho {\sigma _{\omega 2}}}}{\omega }\frac{{\partial K}}{{\partial {x_j}}}\frac{{\partial \omega }}{{\partial {x_j}}}}\text{。} \end{split} $ | (4) |
式中:Uj为xj坐标轴方向上的平均速度分量;μ为动力黏度;μt为湍流涡黏度;τij为雷诺应力张量;Sij为平均应变率张量;Pω为ω的导出项;F1为辅助混合函数;β,β*,σk和σω2均为湍流模型常数[9]。
1.3 滑移网格滑动网格技术将需要计算的网格模型分成若干区域,允许交界面网格之间的相对滑动。不要求交界面两侧上的网格节点彼此重叠,但必须计算交界面两侧的通量来传输数据。
在FINE/Marine中,在每一个时间步长内都要确定交界面两侧的相邻网格单元,通过搜索与交界面两侧最匹配的网格单元,作为相邻网格直接进行通量计算,不使用特定的插值方法。
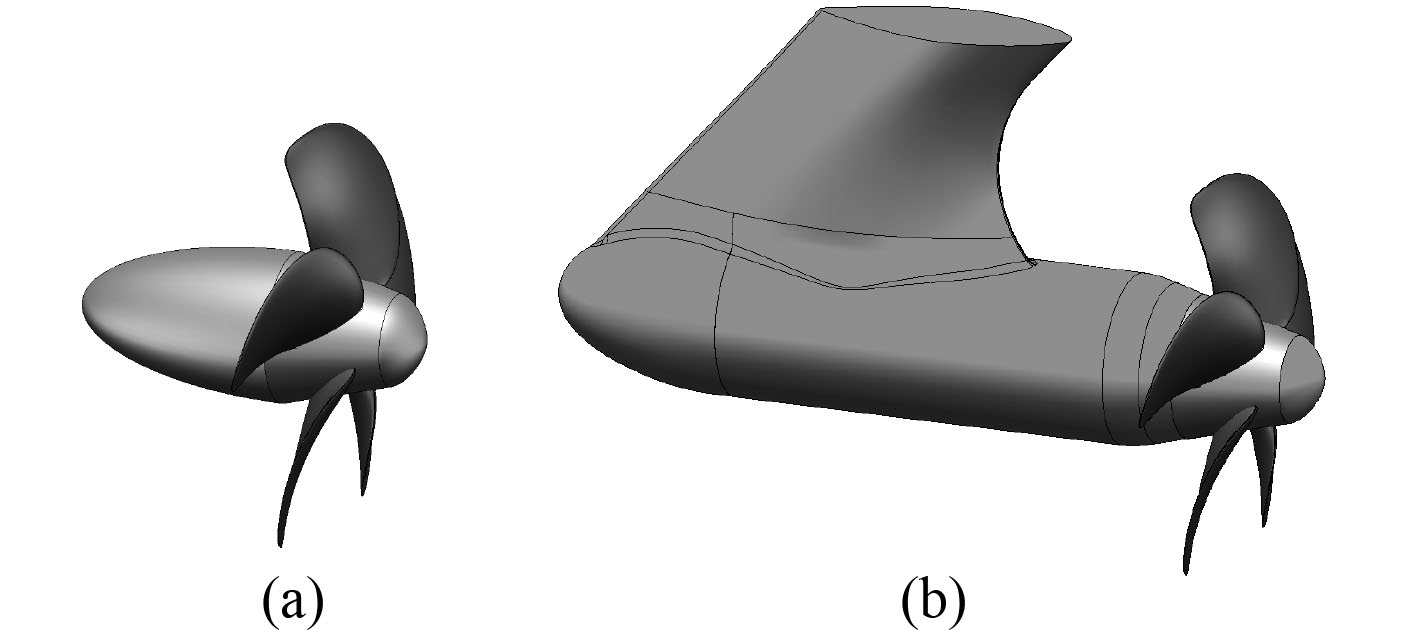
2 计算模型拖式吊舱推进器的主尺度参数,如表1所示。本文所使用的吊舱推进器可以分为螺旋桨,舱体与支架3部分。舱体为两端带有一定锥度的圆柱体,首部安装螺旋桨,尾部与支架相连,支架与舱体之间存在一定夹角。在桨毂锥度相同的条件下,建立了裸桨模型和吊舱推进器模型,如图1所示。
|
|
表 1 吊舱推进器主尺度参数 Tab.1 Main parameters of POD thruster |
|
图 1 螺旋桨和吊舱推进器的三维模型 Fig. 1 3D model of propeller and POD thruster |
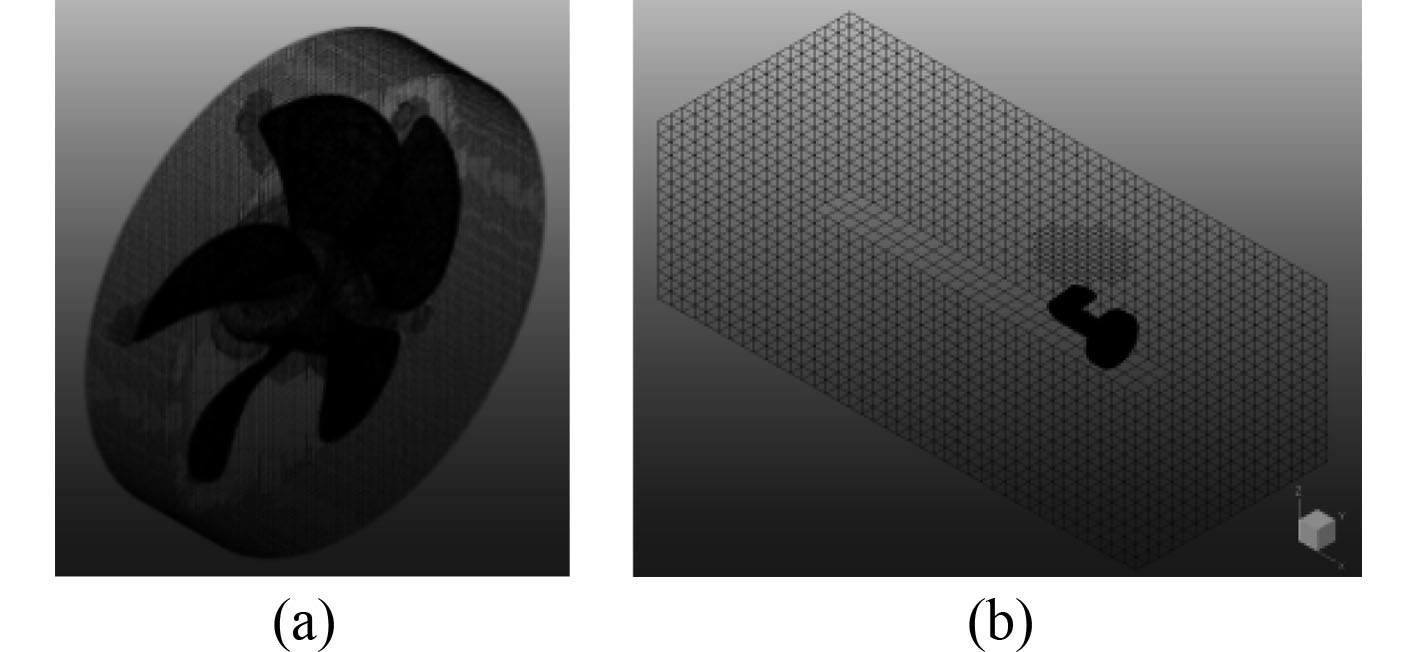
本文的所有计算均采用滑移网格方法来模拟螺旋桨的旋转,所以在划分计算网格时,需要建立2个计算域,一个为包含螺旋桨的旋转域,另一个为包含吊舱的固定域,如图2所示。2个域共用的面设置为交界面,以实现2个计算域之间压力、速度等流场参数的传递。
|
图 2 计算域网格划分 Fig. 2 Computing domain meshes |
选用伽利略坐标系来定义计算域中各个方向,推进器的前进方向为X轴正方向,吊舱左舷方向为Y轴正方向,重力的反方向为Z轴正方向,坐标原点位于桨盘面与桨轴中心线的交点处。
旋转域是一个与螺旋桨同轴的圆柱体,直径3.6 m(1.2D),长度0.75 m(0.25D),网格数量约382万;固定域为长方体,长40 m(13.33D),宽16 m(5.33D),高13 m(4.33D),前方入口边界距桨盘面10 m(3.33D),后方出口边界距桨盘面30 m(10D),左右边界距螺旋桨中心轴线8 m(2.67D),上下边界距螺旋桨中心轴线分别是5 m(1.67D)和8 m(2.67D),网格数量约132万。为了得到关键的流场信息,文中采用局部加密的方法,对桨叶的导边、随边及叶梢部分进行加密,同时对吊舱及支架区域也进行了加密,如图3所示。

|
图 3 局部网格加密 Fig. 3 Local mesh refinement |
完成2个域的网格划分后,同时导入旋转域和固定域的网格模型,用Non Matching Connections命令在交界面处建立连接。最后把合成的网格模型导入FINE/Marine中进行数值计算设置。
因为不考虑自由液面影响,选用单相流模型,非稳态计算;湍流模型为k-ω(SST-Menter);对于动量方程和湍流方程,均采用AVLSMART格式进行离散;螺旋桨和吊舱的固体边界条件设为带壁面函数的边界。计算域前后边界条件和左右侧边界条件设为速度远场条件,速度为0;顶部和底部边界条件设为指定压力条件,压力为0。
吊舱推进器的运动从静止开始,即吊舱的初始速度为零,螺旋桨相对吊舱无转动。吊舱推进器以0.01 s的时间步长,经过2 s时间,按1/4正弦曲线形式变化到给定的前进速度。螺旋桨和桨毂也以相同的时间步长、时间和运动方式变化到指定转速。此后,吊舱前进速度和螺旋桨转速固定不变,计算时间步长调整为0.001 s,即螺旋桨每转1.68°计算一次,直至计算稳定。
4 结果与分析 4.1 数值计算验证结果由于计算模型没有真实的实验模型和实验数据,为了保证数值计算的准确性,本文模拟了由纽芬兰纪念大学(MUN)的海洋工程研究中心(OERC)和加拿大国家海洋技术研究所(IOT)共同设计的吊舱推进器模型的敞水性能。将计算结果与实验值进行比较,验证本文所用数值计算方法的可行性。
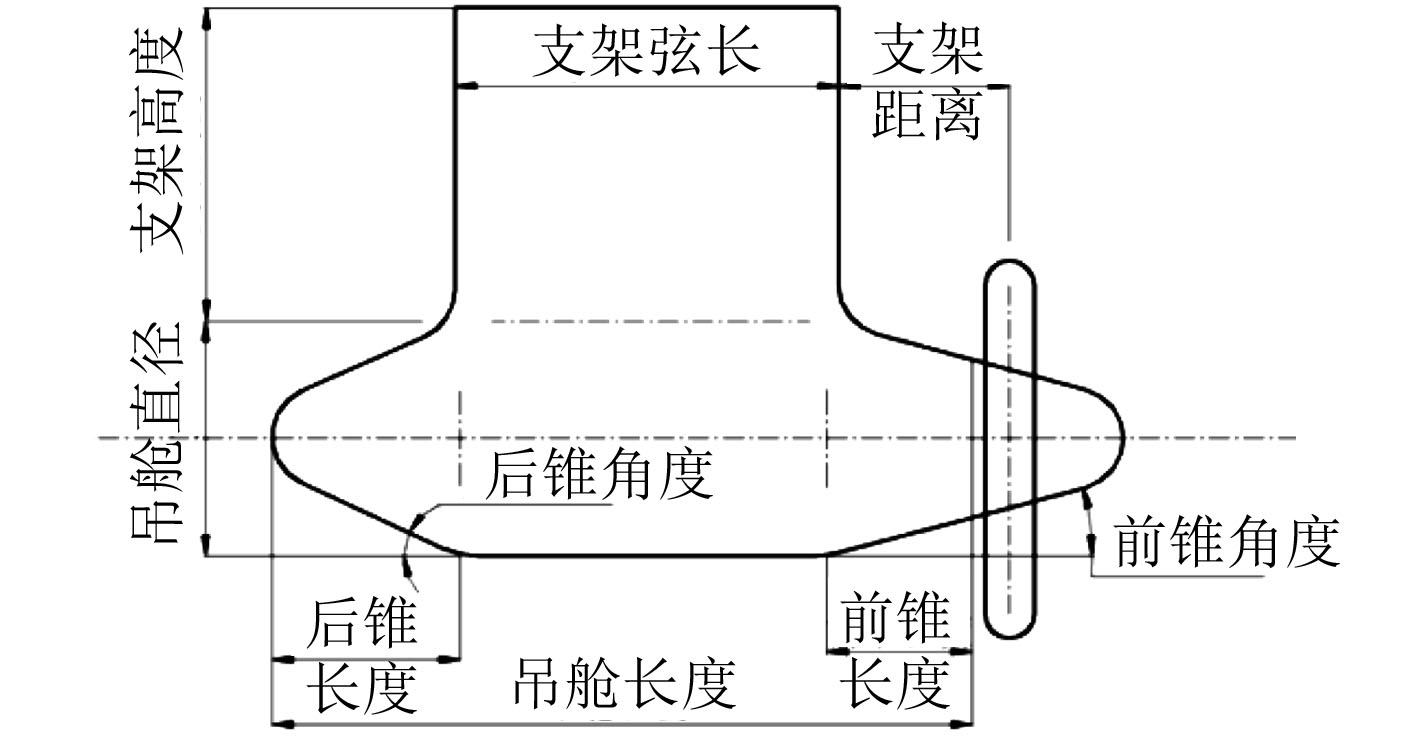
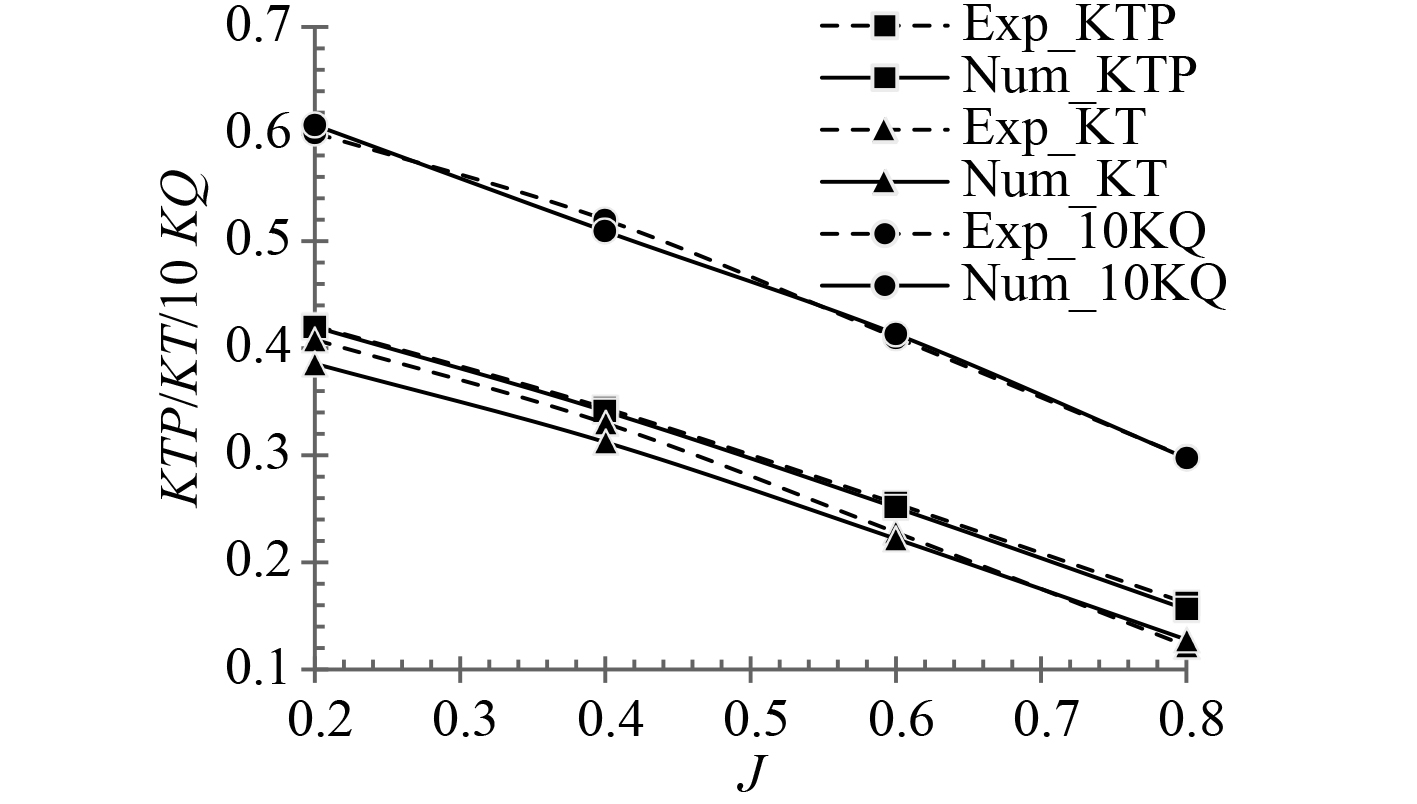
吊舱推进器的具体模型尺寸,如表2和表3所示[10-12],图4和图5为推进器各参数定义与模型三维示意图。选取进速系数为0.2,0.4,0.6,0.8四个工况,将计算结果与实验数据对比,如表4和图6所示。螺旋桨推力系数和扭矩系数的计算结果与实验值较为相近,最大误差仅为3.63%和2.06%,推进器整体推力系数误差也都小于5.5%。因此,本文的数值计算方法能较准确的模拟吊舱推进器的水动力性能,可以满足工程设计和分析的需要。
|
|
表 2 螺旋桨的主要参数 Tab.2 Main parameters of propeller |
|
|
表 3 吊舱的主要参数 Tab.3 Main parameters of POD |
|
图 4 推进器各参数定义 Fig. 4 Definitions of parameters for POD |
|
|
表 4 敞水性能数值计算结果 Tab.4 Numerical result of open water performance |

|
图 5 模型三维示意图 Fig. 5 3D model of POD thruster |
|
图 6 数值模拟与实验结果的比较 Fig. 6 Comparison between numerical results and experimental results |
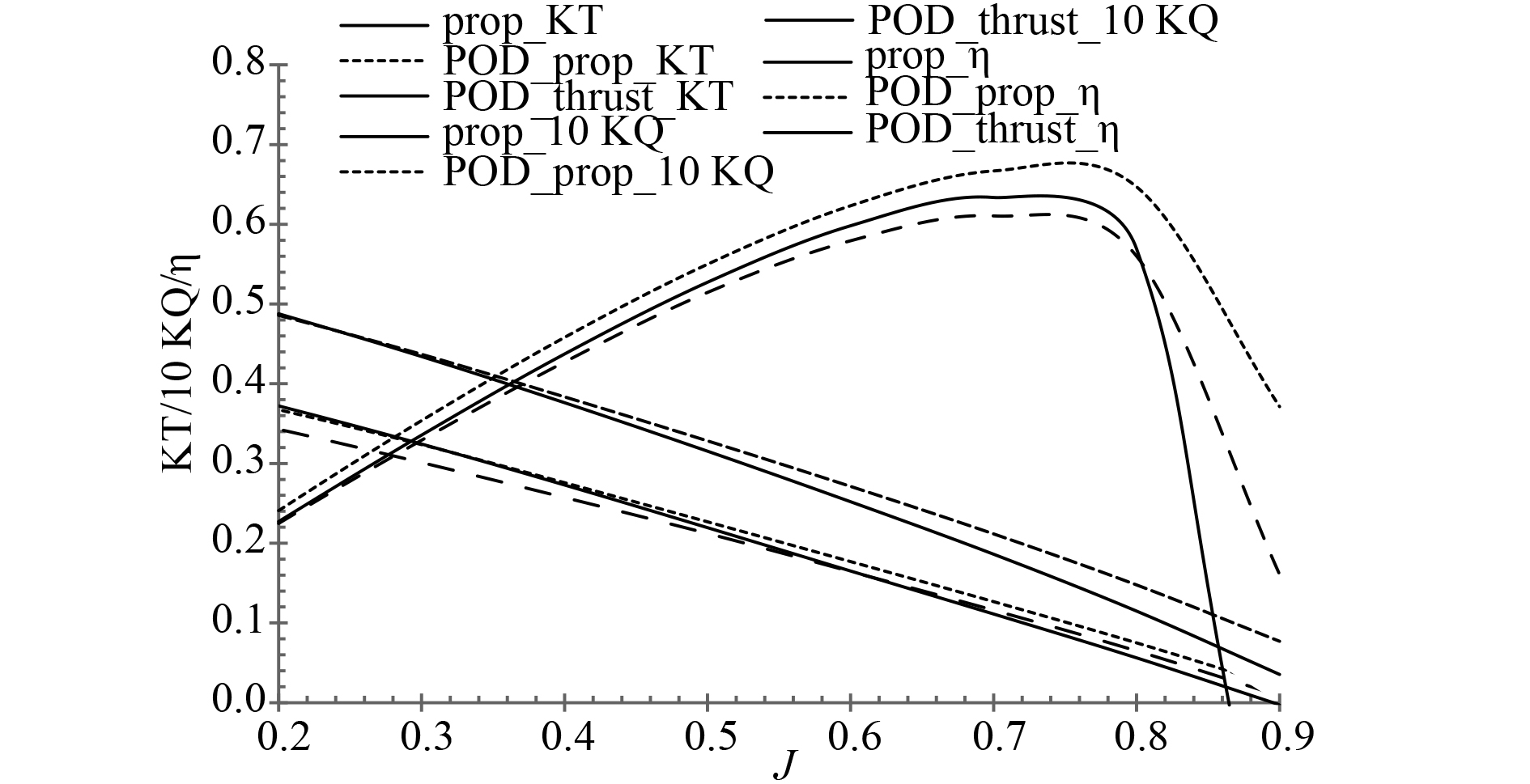
将计算得到的推力和扭矩做无因次变化后绘制裸桨和吊舱推进器的敞水性能曲线,如图7所示。其中,Prop,POD prop和POD thrust分别代表裸桨,吊舱推进器的螺旋桨和整个吊舱推进器。
|
图 7 敞水性能曲线 Fig. 7 The open water performance of POD thruster |
由于吊舱的存在,一定程度上阻挡了螺旋桨后方的流动,使叶面压力增大,从而增加了螺旋桨载荷并形成了有利干扰,因此吊舱推进器螺旋桨的推力要高于裸桨,随着进速系数的增加,影响更加明显,扭矩也有相同的趋势。虽然吊舱的存在会使螺旋桨的效率有一定程度的提高,但是由于吊舱本身还有阻力,吊舱推进器整体效率反而要低于裸桨的效率。
4.3 吊舱侧向力特性分析对于吊舱而言,因为它处于螺旋桨的尾流中,所以支架的部分区域始终处于有攻角的来流情况,从而使吊舱产生了额外的侧向力,即Y轴方向的力。
图8和图9分别为J=0.7时吊舱各部件的侧向力系数和吊舱总侧向力系数与推进器推力系数的比值。POD,Mainbody和Strut分别表示吊舱总侧向力、舱体侧向力和支架侧向力。

|
图 8 吊舱侧向力推力系数 Fig. 8 Transverse force coefficient of POD |
|
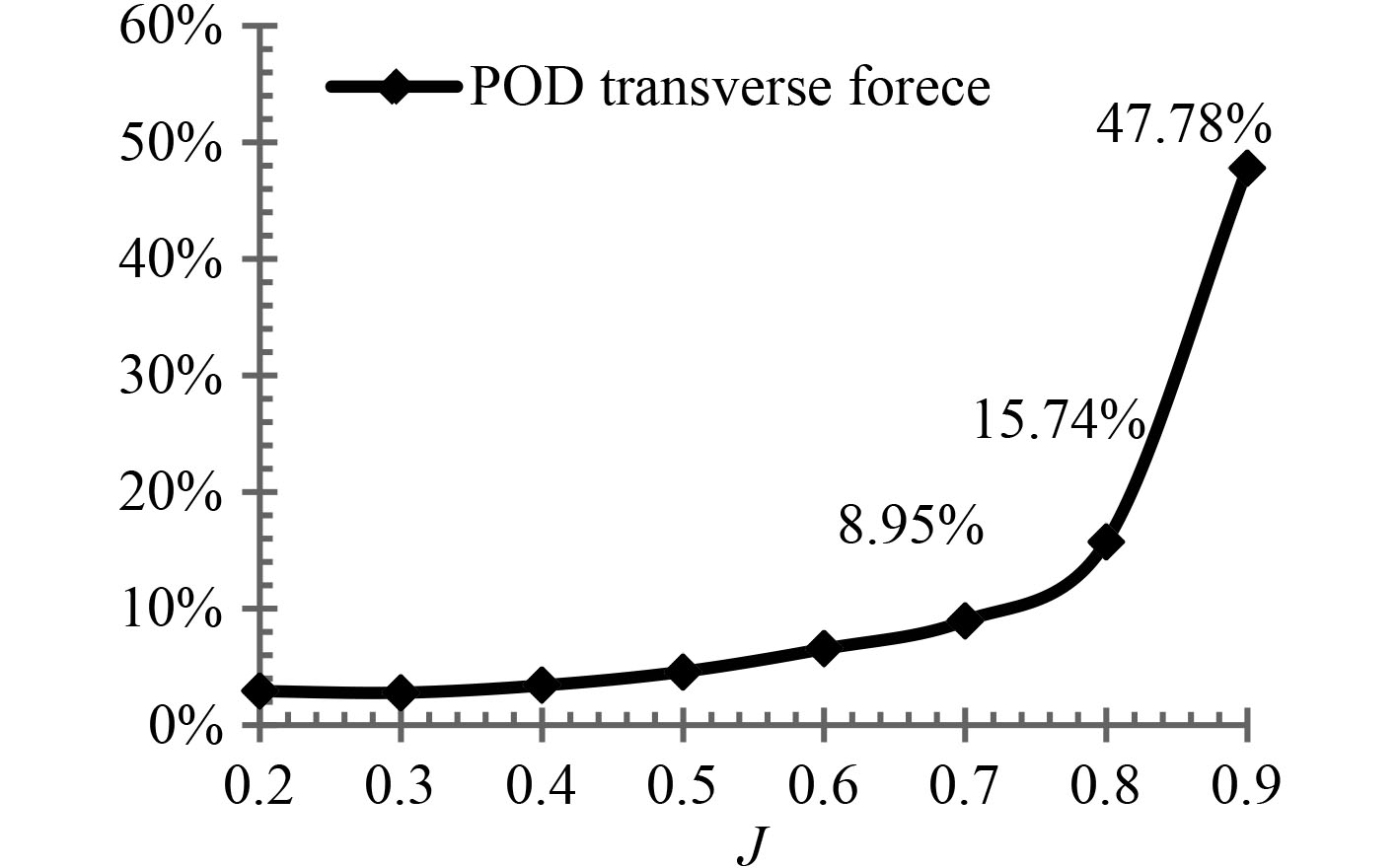
图 9 吊舱侧向力系数占推力系数的百分比 Fig. 9 Transverse force as a percentage of thrust of POD |
由图8可知,吊舱的侧向力主要由舱体(回转体)和支架提供。舱体的侧向力始终沿Y轴正方向,随着进速系数的增加而减小;而支架的侧向力,随着进速系数的增加,由Y轴负方向向Y轴正方向持续增大,在进速系数为0.4~0.5区间由负变正,在J=0.8时达到峰值。
由图9可知,吊舱总侧向力的大小相对于吊舱推进器推力而言,随着进速的增加,其比值明显提高。主要原因为推进器推力随着进速系数的增加而降低,但是吊舱的侧向力并没有明显的下降趋势,反而在J=0.3~0.7区间逐渐上升。结合图7和图9可知,在推进器处于最高效率点(J=0.7)时,吊舱侧向力大小占推进器推力的8.95%;在J=0.9时,吊舱侧向力大小占推进器推力的47.78%。
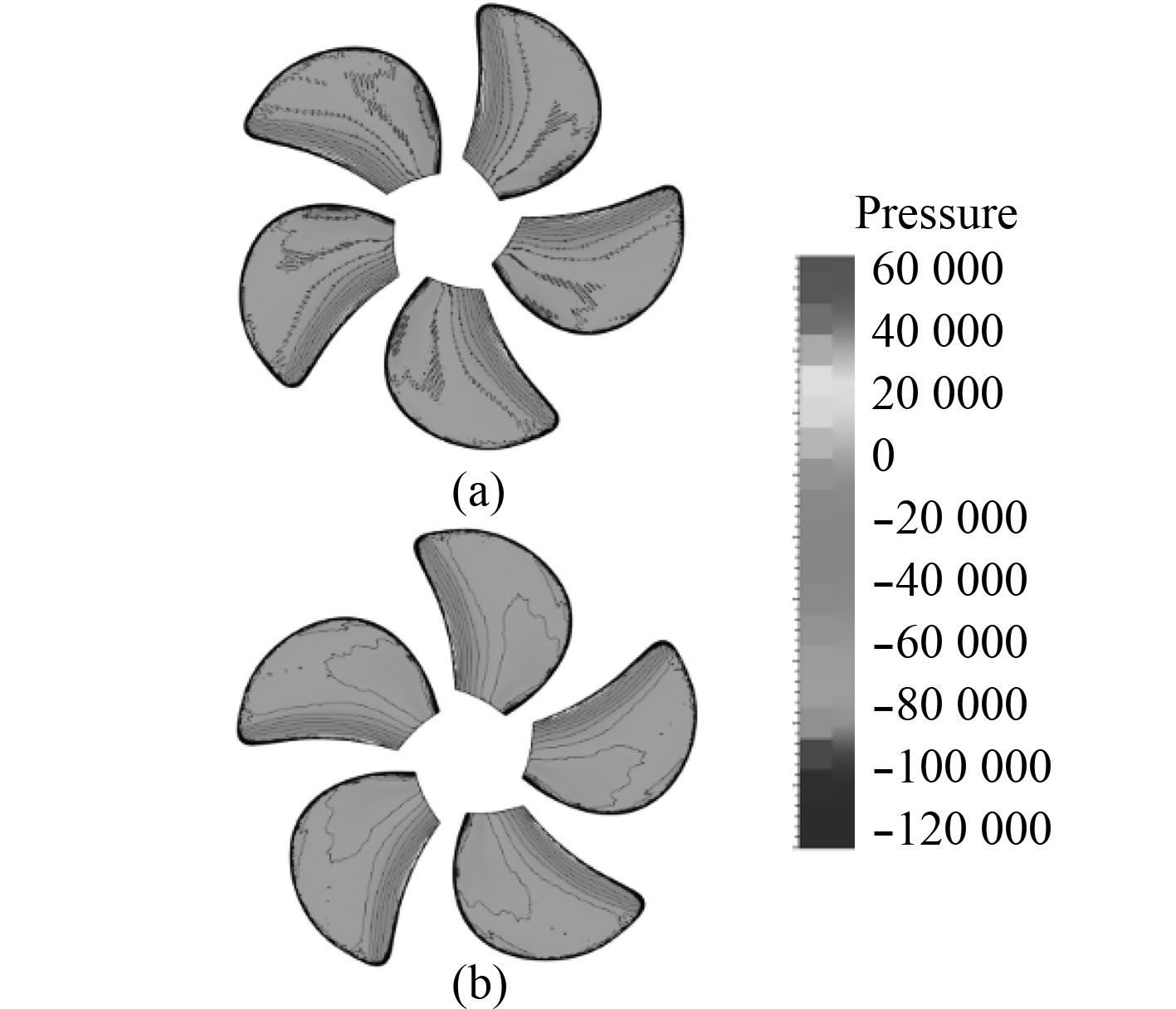
4.4 螺旋桨表面压力负荷特性分析图10和图11所示为J=0.7时螺旋桨叶表面压力分布图。其中,图10(a)和图10(b)分别代表吊舱推进器的螺旋桨和裸桨。
|
图 10 桨叶表面压力分布图(吸力面) Fig. 10 Pressure distribution of blade surface(suction surface) |
|
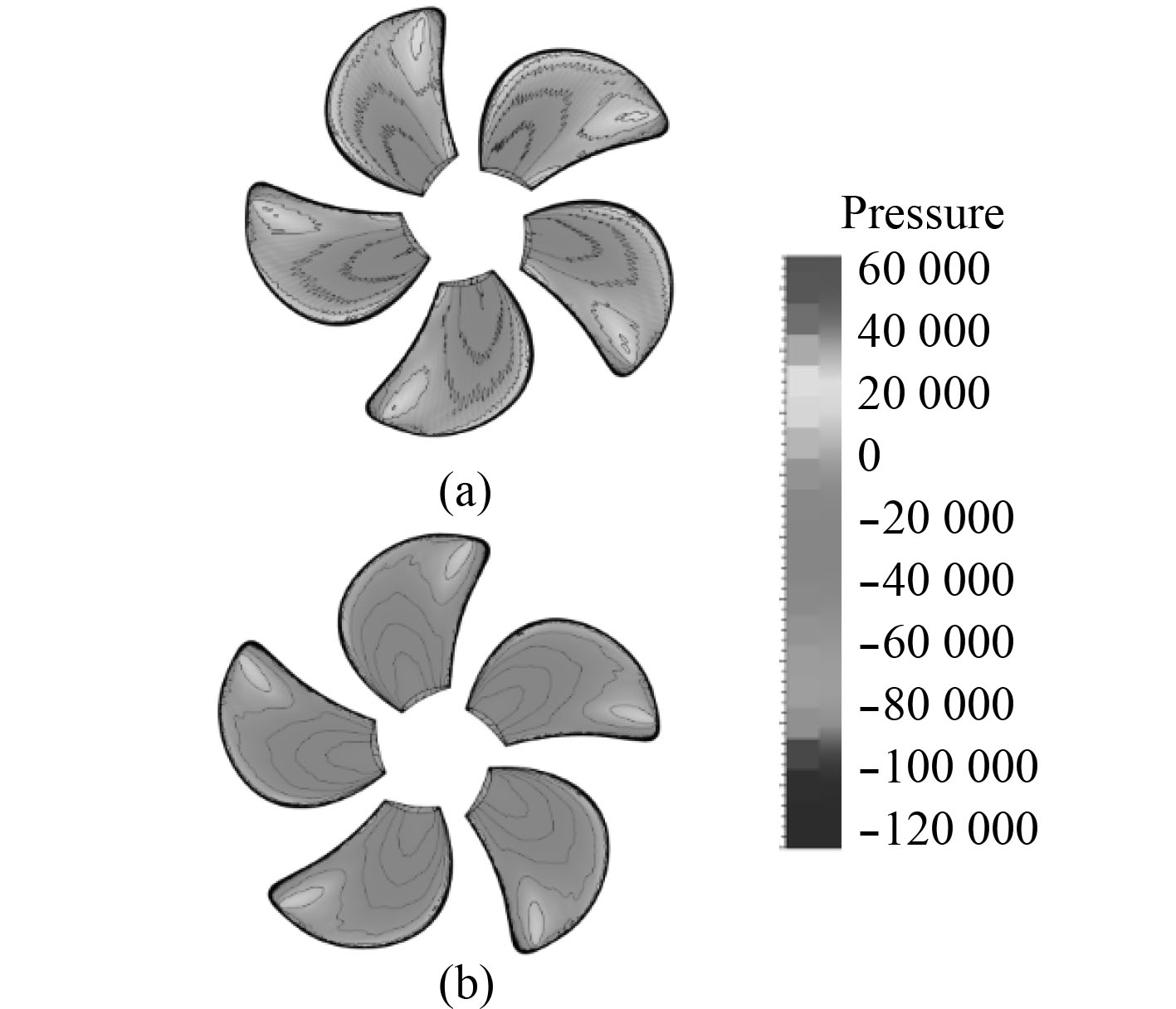
图 11 桨叶表面压力分布图(压力面) Fig. 11 Pressure distribution of blade surface(pressure surface) |
从吸力面上看,每个桨叶压力分布基本相同,压力自导边往随边逐渐升高。裸桨的最低压力出现在导边靠近叶根附近,但是由于吊舱的存在,吊舱推进器的螺旋桨最低压力沿径向向外偏移,出现在前部导边附近且压力更低,随边一侧压力更高,整体压力梯度变化更大。因此,由于吊舱的存在,桨叶空泡更有可能在叶背导边附近产生。
从压力面上看,裸桨的每个桨叶压力分布基本相同,导边处压力最高,整体压力梯度线呈发散状态,从叶根附近逐步向导边、随边和叶梢发散。但是由于吊舱的存在,吊舱推进器的螺旋桨叶面压力明显升高,同时旋转到支架前方的桨叶,其叶面的高压区面积大于其他桨叶,从而使螺旋桨的各个桨叶受力不均匀,产生推力的波动。
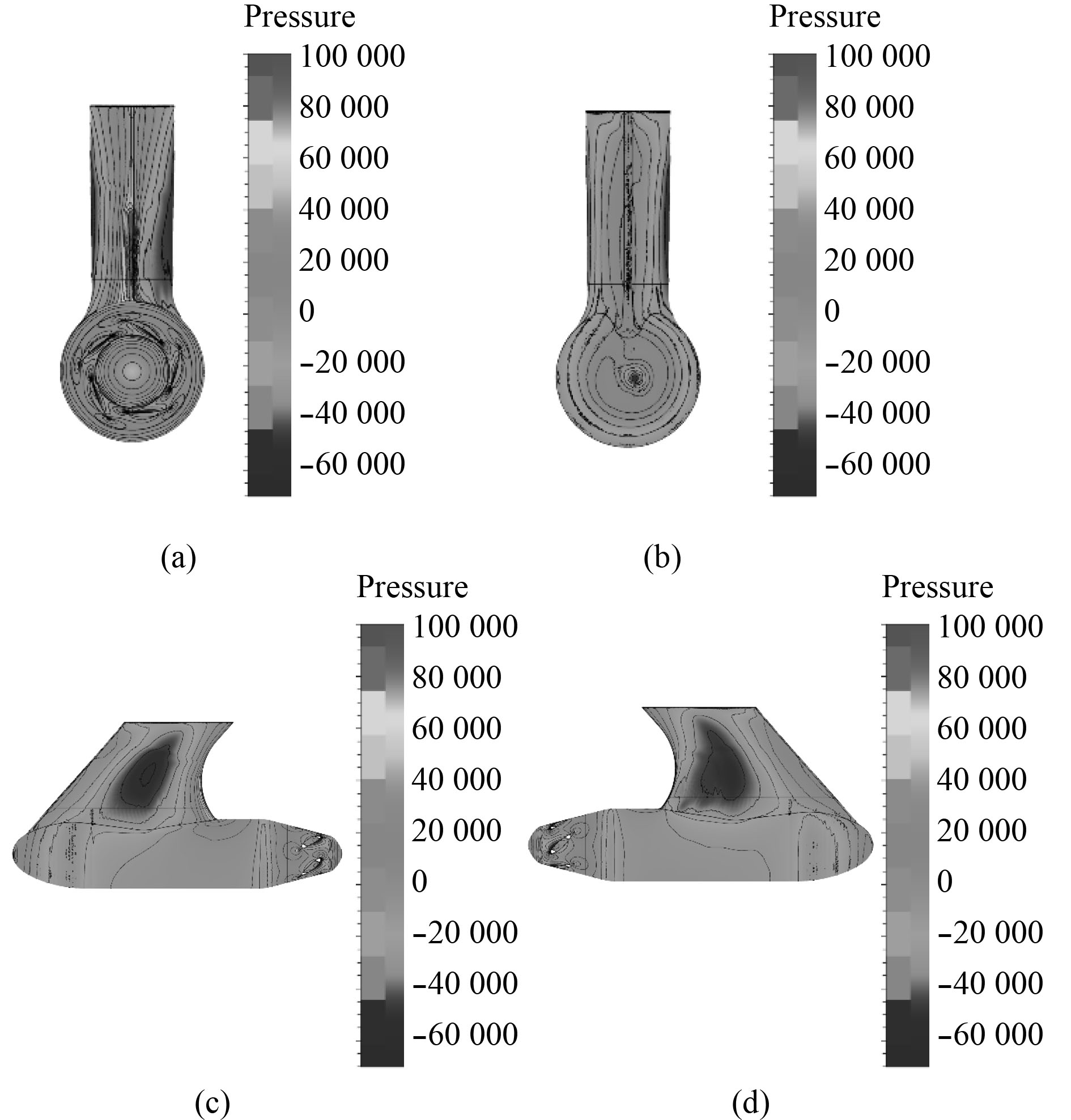
4.5 吊舱表面压力负荷特性分析图12为J=0.7时吊舱表面的压力分布图。由于螺旋桨的尾流影响,支架两侧的压力分布不对称,流动驻点出现在支架前缘的右侧表面,压力负荷较大。大量螺旋桨的旋转尾流从支架右侧导流至吊舱尾部,从而使支架左侧的流速大于右侧,由机翼理论可知支架两侧的流速差会导致压力差,压力差会产生Y轴方向的力,即吊舱的侧向力。较大的侧向力会直接影响船舶的直线稳定性,因此在设计吊舱推进器时应该尽量降低吊舱的侧向力,或在设计航速下将吊舱侧向力降至最低。舱体末端还有一个较为明显的低压区,这说明在尾部形成了尾涡,使吊舱阻力增加。
|
图 12 吊舱表面压力分布图 Fig. 12 Pressure distribution of pod surface |
拖式吊舱推进器的螺旋桨与吊舱之间互相干扰强烈,流场运动现象复杂,分析较为困难。本文主要从J=0.7时的吊舱周围流场的速度分布来分析其流场特性。
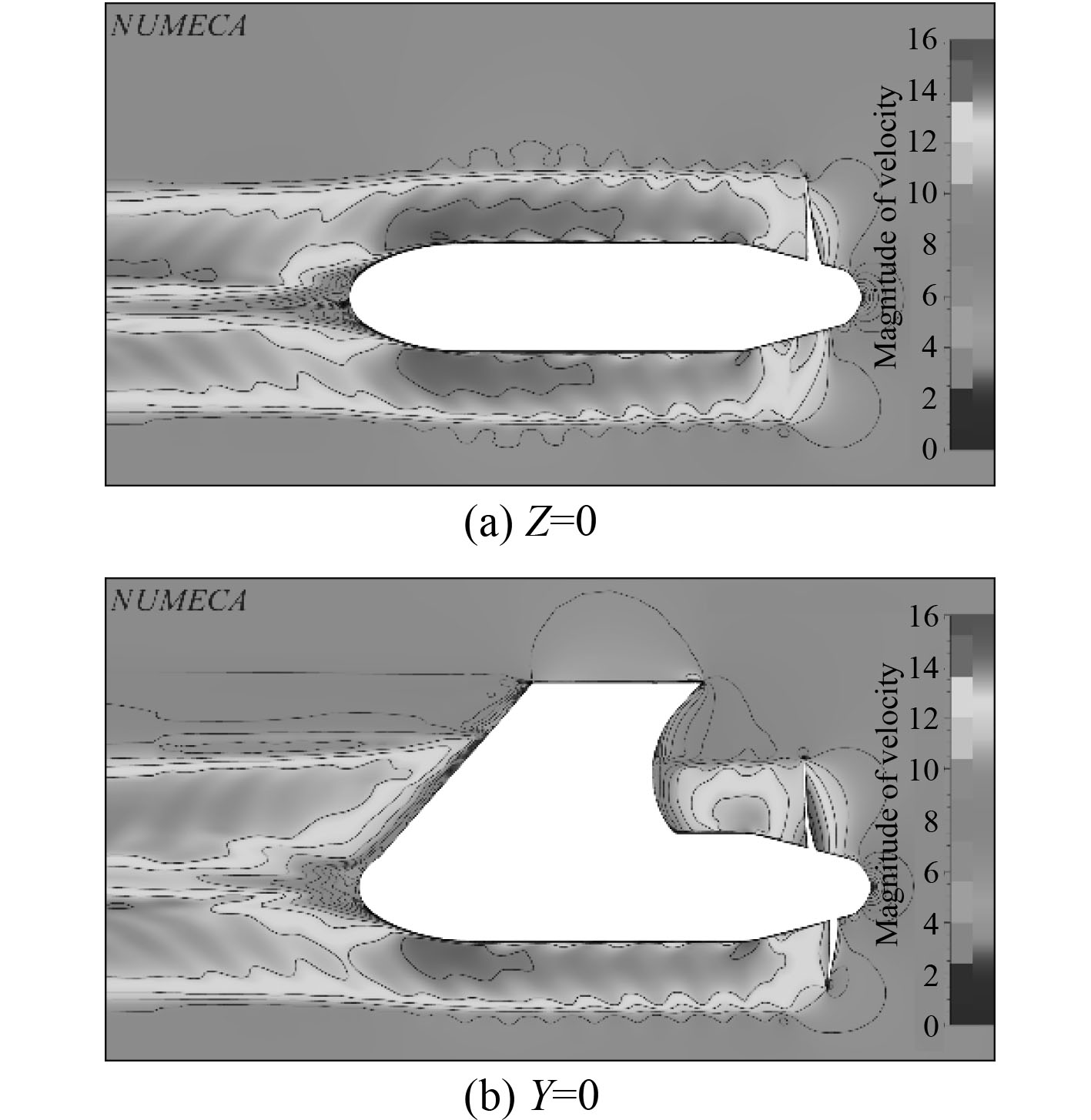
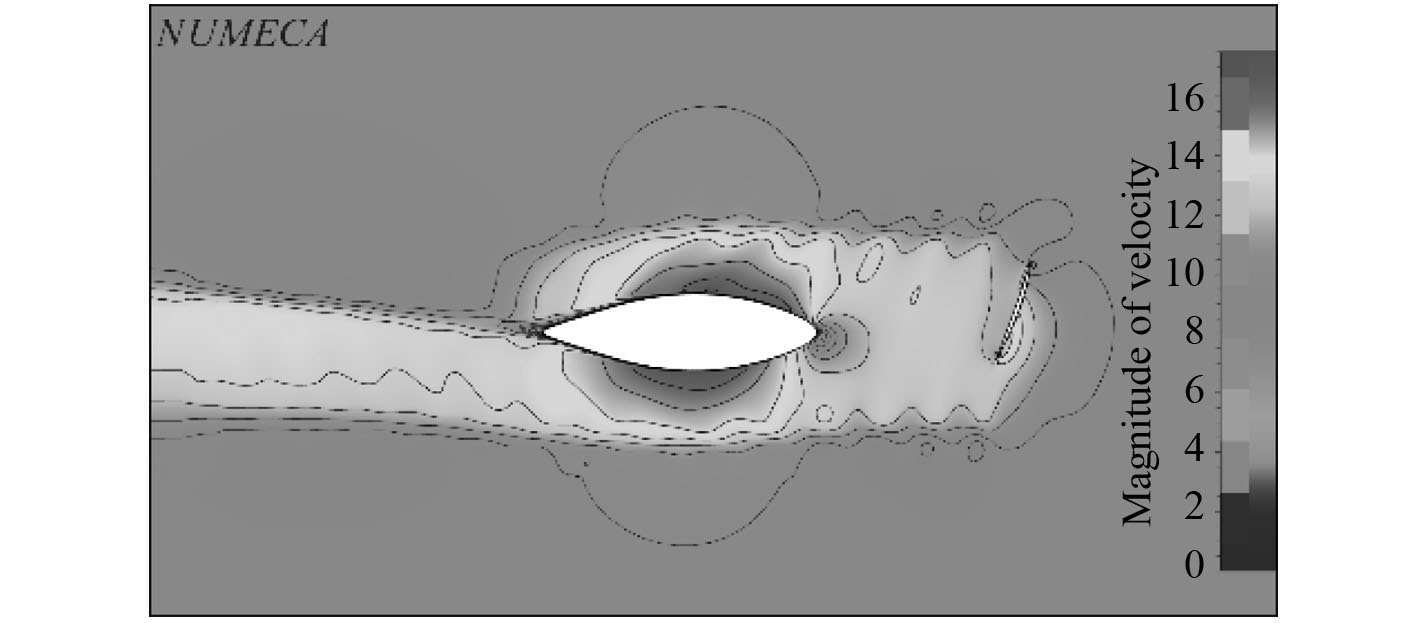
图13和图14为吊舱周围以及0.75倍螺旋桨半径处支架两侧的速度分布图。可知,舱体尾部收缩的位置流速较大,舱体末端流速骤降形成较大的尾涡区域。在尾流区域内支架两侧流速分布不对称,且远大于舱体周围速度。因此,在设计吊舱推进器时可在舱体尾部设置附体装置阻碍尾涡汇聚,改善舱体阻力性能。
|
图 13 吊舱推进器周围的速度分布 Fig. 13 Magnitude of velocity distribution around POD thruster |
|
图 14 支架两侧的速度分布(Z=0.75R) Fig. 14 Magnitude of velocity distribution around strut |
1)吊舱推进器螺旋桨的推力和扭矩较裸桨均有所提升,但是由于吊舱的存在及其自身的阻力,推进器的整体效率并没有明显改善,反而使螺旋桨推力波动增大。
2)吊舱会在螺旋桨尾流的影响下产生额外的侧向力,而且吊舱侧向力大小与推进器推力的比值会随着进速的增加而升高,在螺旋桨的最高效率点,侧向力大小可占整体推力的8.95%。
3)舱体尾部收缩位置以及支架两侧的流场流速较大;舱体末端流速骤降形成较大的尾涡区域。
4)设计吊舱时应尽可能地降低在设计工况下的侧向力;在舱体尾部可设置附体装置来改善舱体阻力性能。
本文对三维实尺度的裸桨及吊舱推进器的敞水性能进行了数值模拟,数值算法的可靠性和准确性通过与实验结果的对比进行了验证。主要分析了吊舱推进器的水动力特性及周围流场情况,可为后续拖式吊舱推进器的优化设计研究提供借鉴和参考。
| [1] |
高宜朋, 曾凡明, 张晓锋. 吊舱推进器在舰船推进系统中的发展现状及关键技术分析[J]. 中国舰船研究, 2011, 6(1): 90-6. DOI:10.3969/j.issn.1673-3185.2011.01.018 |
| [2] |
张志荣, 洪方文, 胡芳琳. 吊舱推进器水动力性能CFD预报及其验证[C]. 船舶水动力学学术会议暨中国船舶学术界进入ITTC30周年纪念会, 2008.
|
| [3] |
郭春雨, 杨晨俊, 马宁. RANS Simulation of Podded Propulsor Performances in Straight Forward Motion[J]. 中国海洋工程(英文版), 2008, 22(4): 663-74. |
| [4] |
沈兴荣, 蔡荣泉, 冯学梅. 粘性流场中吊舱推进器水动力性能数值研究[J]. 中国造船, 2010, 51(1): 17-26. DOI:10.3969/j.issn.1000-4882.2010.01.003 |
| [5] |
董小倩. 吊舱推进器水动力性能数值研究[D]. 上海: 上海交通大学, 2013.
|
| [6] |
吴琼, 冯学梅, 贾力平. 使用Numeca软件的吊舱推进器敞水性能计算[C]. 全国水动力学研讨会, 2014.
|
| [7] |
马骋, 陈科, 庄光宇. 基于粘流CFD方法的吊舱推进器水动力性能研究[C]. 船舶水动力学学术会议, 2013.
|
| [8] |
赵丙乾, 方昭昭, 肖曙明. 基于FINE/Marine的螺旋桨水动力性能研究[J]. 船舶工程, 2018, 40(4): 45-50. |
| [9] |
METHRIC E. Theoretical Manual of ISIS-CFD v7.2[ED/OL]. Ecole Centrale de Nantes, France: http://www.ec-nantes.fr. 2018.
|
| [10] |
P. LIU, The design of a podded propeller base model geometry and prediction of its hydrodynamics. No. TR-2006-16[R]. Canada: Institute for Ocean Technology, National Research Council, 2006.
|
| [11] |
ISLAM M. Performance study of podded propulsors with varied geometry and azimuthing conditions[J]. International Shipbuilding Progress 2009, (56): 135-57.
|
| [12] |
SHAMSI R, GHASSEMI H. Numerical investigation of yaw angle effects on propulsive characteristics of podded propulsors[J]. International Journal of Naval Architecture & Ocean Engineering, 2013, 5(2): 287-301. |
 2020, Vol. 42
2020, Vol. 42
