2. 哈尔滨工业大学(威海),山东 威海 264209;
3. 中国船舶科学研究中心 船舶振动噪声重点实验室,江苏 无锡 214082
2. Harbin Institute of Technology (Weihai), Weihai 264209, China;
3. China Ship Science Research Center, Wuxi 214082, China
船舶主机设备振动引起的机械噪声作为船舶振动噪声的主要来源,严重影响了船舶安静性和舒适性,同时会影响全船设备的正常使用,一直以来都是船舶振动噪声控制的研究重点,为此必须在船舶设计阶段对船舶结构振动性能进行预报,以便在结构设计方面采用合理方案和必要的措施。复合材料由于具有阻尼性能好、比强度大、比刚度高、材料可设计性强、耐腐蚀、成型方便等优点,在船体轻量化与减振降噪方面具有良好的应用前景。
在进行船舶振动噪声分析时,由于船体结构大而繁杂,难以用纯解析方法求解,相比而言,数值计算方法为解决工程减振降噪技术提供了可行方案。大型结构的复杂部件在材料、几何属性和声振特性等方面不同,因此在动力学分析过程中,往往根据结构不确定性对自身动态特性的影响将其分为中低频、高频两频段进行计算。
国内外众多学者分别使用有限元方法和统计能量法对船体或船体板的振动进行数值计算[1~7]。在低频段,结构中的波长大于结构的尺寸,结构的不确定性对结构动态响应的影响可以忽略不计,主要采用有限元法[2]、无限元法和边界元法对结构振动进行数值计算。在有限元计算中连续边界被离散、场变量由近似形函数来描述,因此为确保精确度,数值计算必须划分大量单元。离散误差随着频率的增加而增大,因此基于单元的方法通常局限于低频范围。在高频段,结构中的波长小于结构的尺寸,结构的不确定性对结构响应的影响很大,统计能量分析[3-4]是应用最广泛的方法。通过将复杂系统划分成多个弱耦合子系统,用能量描述各个动力学子系统的状态,使用功率流平衡方程描述祸合子系统间的相互关系。和有限元法相比,消耗的计算资源更少,而且由于复杂系统的内在复杂性,频率和空间平均量能较精确地从统计意义上预示整个子系统的响应级。但值得注意的是,统计能量分析只能用于高频段。
本文结合有限元方法和统计能量法,对复合材料船舶全频段振动噪声进行数值计算,通过改变基座周围船体板的板厚和复合材料铺层工艺,成功降低全船振动响应,对降低船舶振动噪声、提升船舶安静性和舒适性具有借鉴意义。
1 船舶振动噪声分析数值理论 1.1 结构有限元方法多自由度有阻尼振动的微分方程为:
| $ {{M}}\ddot x + {{C}}\dot x + {{K}}x = 0{\text{。}} $ | (1) |
其中:M为质量矩阵,C为阻尼矩阵,K为刚度矩阵。
设式(1)的解为
| $ \left( {{\omega ^2}{{M}} + \omega {{C}} + {{K}}} \right){{A}} = 0 {\text{,}} $ | (2) |
式中:M是对称正定矩阵。
假设刚度阵为半正定矩阵,不考虑系统阻尼的影响,则方程可转化为求无阻尼系统自由振动的微分方程:
| $ \left( { - {\omega ^2}M + K} \right)\phi = 0 {\text{。}} $ | (3) |
为使有限元的离散结构能更好地描述结构中的振动波传递,1个波长内至少应有5个节点,由此单元长度
由波动理论导出的单元细化标准,板的纵向波波速CL、板的弯曲波波速CB和波长λb分别为:
| $ {C_L} = \sqrt {{E/ {\rho \left( {1 - {\mu ^2}} \right)}}} {\text{,}} $ | (4) |
| $ {C_B} = \sqrt {2{\text{π}} fr{C_L}} {\text{,}} $ | (5) |
| $ {\lambda _B} = \sqrt {{{2{\text{π}} r{C_L}} / f}} {\text{。}} $ | (6) |
式中:r为板的惯性半径,
对于任意2个耦合的子系统i和j,在振动情况下,双耦合子系统之间能量平衡的基本关系式如下:
| $ {P_{oi}} = \omega {\eta _i}{E_i} + \omega {\eta _{ij}}{N_i}\left( {\frac{{{E_i}}}{{{N_i}}} - \frac{{{E_j}}}{{{N_j}}}} \right) = \omega \left( {{\eta _i} + {\eta _{ij}}} \right){E_i} - \omega {\eta _{ji}}{E_j} {\text{,}} $ | (7) |
| $ {P_{oj}} = \omega {\eta _j}{E_j} + \omega {\eta _{ji}}{N_j}\left( {\frac{{{E_j}}}{{{N_j}}} - \frac{{{E_i}}}{{{N_i}}}} \right) = \omega \left( {{\eta _j} + {\eta _{ji}}} \right){E_j} - \omega {\eta _{ij}}{E_i} {\text{。}} $ | (8) |
式中:Poi,Poj分别为外界输入子系统的功率;ω为计算频段中心频率;ηij,ηji为子系统之间的耦合损耗因子,ηij表示由第i个子系统至第j个子系统的能量耦合程度,ηji表示由第j个子系统至第i个子系统的能量耦合程度;ηi,ηj为子系统的内部损耗因子,即为阻尼参数;Ni,Nj表示子系统在频段Δω内的模态数;Emi,Emj表示子系统i和j在频段Δω内所具备的能量,Ei,Ej为各子系统的能量。
同理,对于由n个子系统组成的结构,子系统的平均模态能量与相连子系统发生功率交换满足下列方程:
| ${P_{oj}} = \omega \left( {{\eta _j}{\rm{ + }}\sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne i} \end{array}}^n {{\eta _{ij}}} } \right){E_i} - \omega\!\!\! \sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne i} \end{array}}^n {\left( {{\eta _{ij}}{E_j}} \right)} {\text{。}} $ | (9) |
联立一系列这种形式的方程就构成SEA的功率平衡(能量平衡)矩阵方程:
| $ \begin{split} & \scriptsize\left[ \begin{array}{l} {P_1} \\ {P_1} \\ \vdots \\ {P_n} \\ \end{array} \right] =\\ & \scriptsize\omega \left[ {\begin{array}{*{20}{c}} {\left( {{\eta _{11}} + \sum\limits_{i \ne 1}^n {{\eta _{1i}}} } \right){N_1}}&{\left( { - {\eta _{12}}{N_1}} \right)}& \cdots &{\left( { - {\eta _{1n}}{N_1}} \right)} \\ {\left( { - {\eta _{21}}{N_2}} \right)}&{\left( {{\eta _{11}} + \sum\limits_{i \ne 1}^n {{\eta _{1i}}} } \right){N_1}}& \cdots &{\left( { - {\eta _{2n}}{N_2}} \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {\left( { - {\eta _{n1}}{N_n}} \right)}&{\left( { - {\eta _{n2}}{N_n}} \right)}& \cdots &{\left( {{\eta _{nn}} + \sum\limits_{i \ne n}^n {{\eta _{nn}}} } \right){N_n}} \end{array}} \right] \left[ \begin{array}{l} \dfrac{{{E_1}}}{{{N_1}}} \\ \dfrac{{{E_{\rm{2}}}}}{{{N_{\rm{2}}}}} \\ \vdots \\ \dfrac{{{E_n}}}{{{N_n}}} \\ \end{array} \right] {\text{。}} \end{split} $ | (10) |
解此方程便可求出各子系统的能量Ei,对于每个结构或声学的子系统,具有一个与其时间平均和空间平均振动速度
以船体上测点的平均振级作为减振降噪评价指标。首先计算所选船体各测点在单位动态激励力作用下的壳体振动加速度响应:
| $ {a_i} = \frac{{a_f^i}}{{{F_1}}} {\text{。}} $ | (11) |
式中:ai为单位力下编号为i的测点的振动响应加速度;aif为激励力下编号为i的测点响应加速度;F1为激励点的动态力。
对于单位激励力作用下壳体上的n个测点,取加速度的均方根值:
| $ a = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {a_i^2} } {\text{。}} $ | (12) |
因此,壳体平均振动加速度级按下式计算:
| $ {L_a} = 20\lg (\frac{a}{{{a_0}}})(\rm dB){\text{。}} $ | (13) |
式中:a0为基准加速度,一般取1.0×10–6 m/s2,因此壳体平均振动加速度级可按下式计算:
| $ {L_a} = {\rm{120 + }}20\lg \left( {\sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {a_i^2} } } \right) {\text{。}} $ | (14) |
复合材料船舶建模时主要考虑了船体外板、舱壁、甲板和平台、主要支撑构件、上层建筑等主要结构部件。
有限元数值计算模型在非线性有限元程序Abaqus平台中建立,计算模型的X,Y,Z方向分别为沿船体纵向、横向、垂向。船底板、舷侧板、甲板板、舱壁板以及上层建筑板采用4节点S4R壳体单元模拟,加强筋采用B31梁单元模拟。根据式(4)~式(6),结构单元尺寸最大为89.9 mm,本文单元总体尺寸约为47 mm,局部过度区域如甲板与舷侧连接处采用精细化网格过渡,保证数值计算精确。模型一共划分75 864个节点,83 009个单元,总体有限元模型如 图1所示。
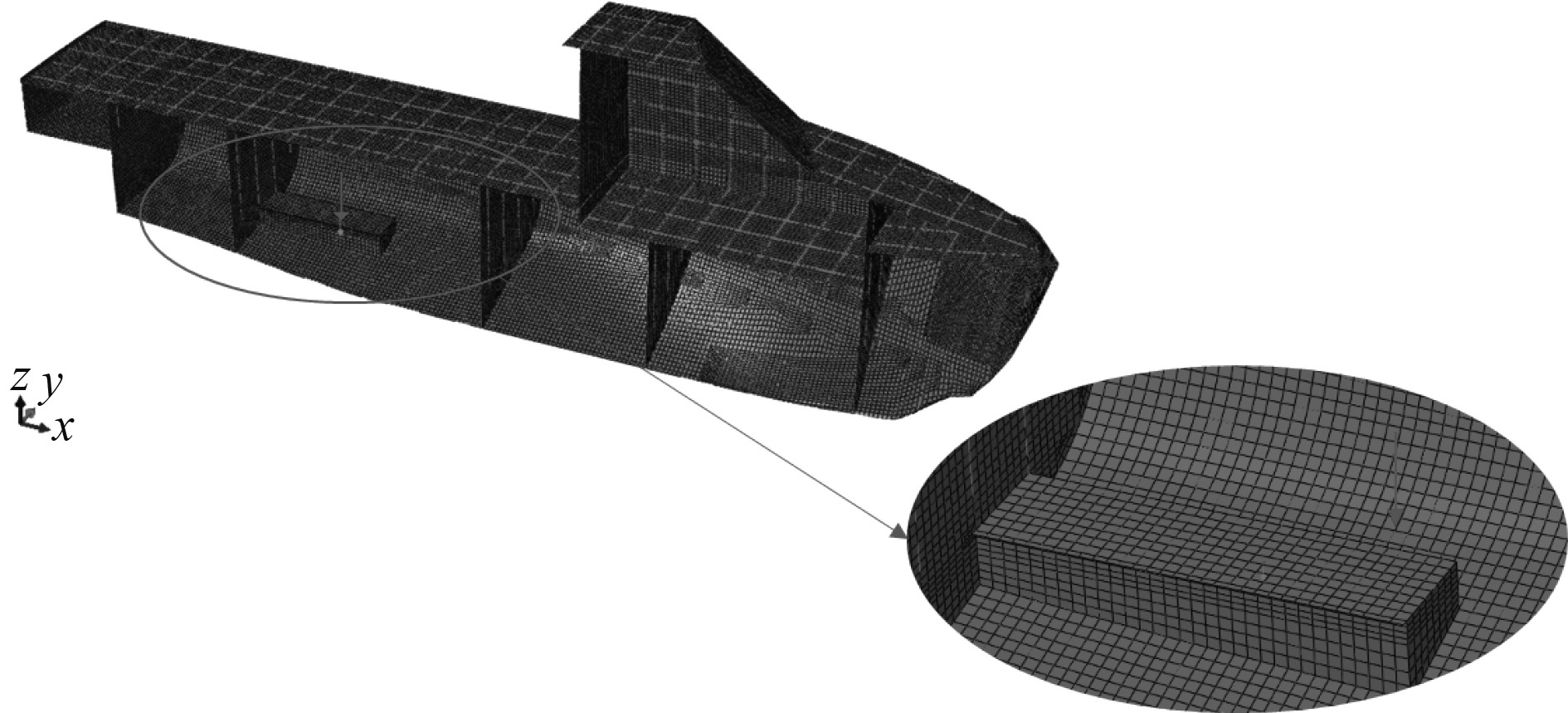
|
图 1 复合材料船有限元计算模型和振动激励位置 Fig. 1 Composite ship FEA model and vibrational excitation position |
高频振动模型在基于统计能量法的计算软件VA-One中建立,并进行单位激励力下的高频振动响应计算。统计能量模型中每个板都是一个统计能量单元,在各相邻的统计能量单元之间建立连接,允许单元之间的能量流动。某些带有正交加强筋的平面如甲板,其加强筋用软件中的加筋板功能设置,计算模型如 图2所示。
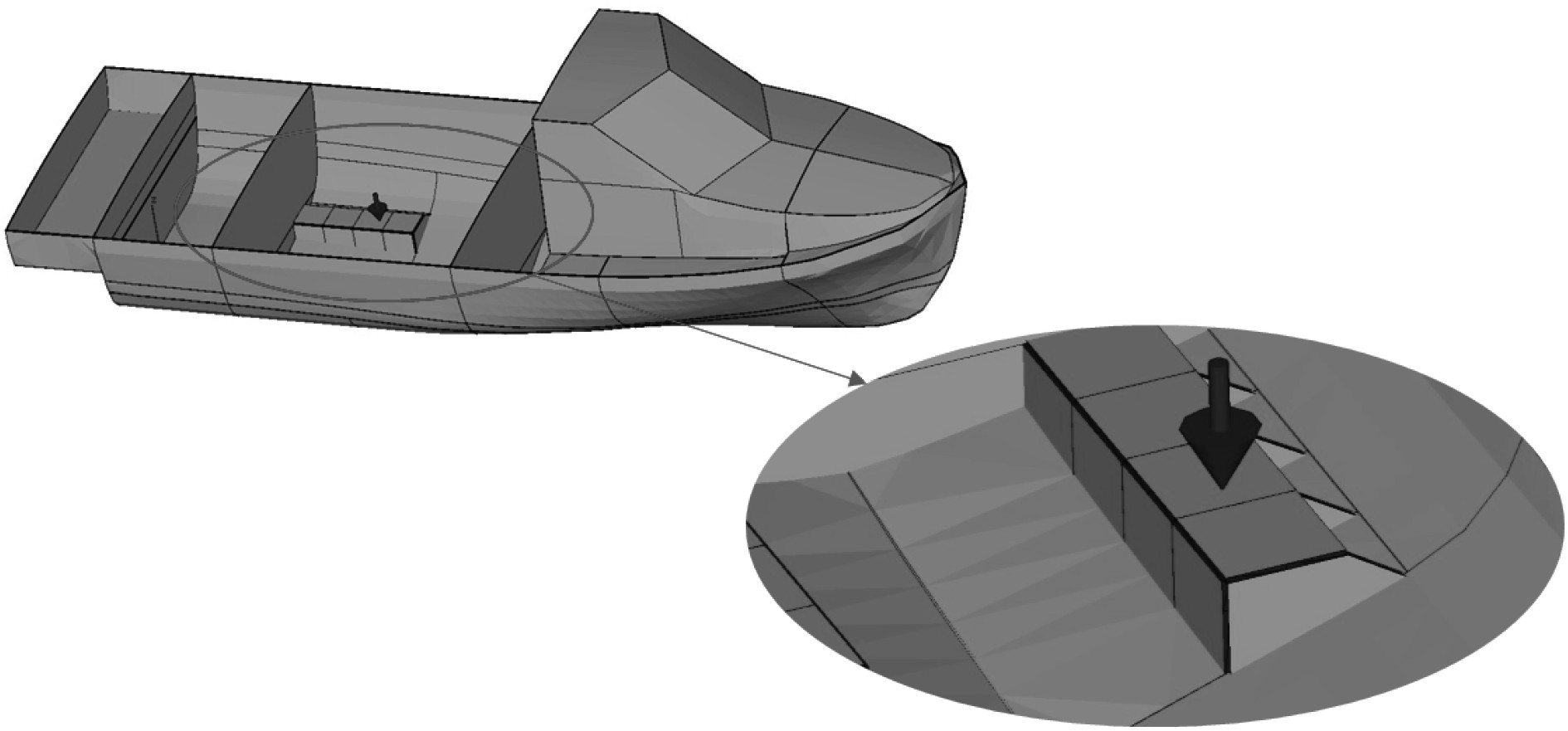
|
图 2 复合材料船统计能量计算模型和振动激励位置 Fig. 2 Composite ship SEA model and vibrational excitation position |
船体主要参数如表1所示。
|
|
表 1 复合材料船主要参数 Tab.1 Composite ship main parameters |
船舶低频振动有限元计算时,在复合材料船体基座上施加垂直于面板的单位激励力(见图1)。有限元计算采用直接法进行谐响应分析,计算频率范围为20~500 Hz,计算频率间隔为1 Hz。有限元计算结果包括基座输入点(激励点)和壳体输出点的振动加速度响应,经过数据处理得到振动加速度级。
船舶高频振动的统计能量计算时,在复合材料船体基座与低频有限元计算相同位置施加垂直于面板的单位激励力(见图2)。
为了确定噪声数据的特征点,本文先对船体不同测点计算结果进行对比。选取的测点分为两组,第1组主要分布在激励点的基座周围,共选取4圈,沿着船底、舷侧以及甲板均匀选取,每圈6个共24个测点;第2组沿全船分布,一共选取6圈,沿着船底、舷侧以及甲板均匀选取,每圈6个共36个测点,如图3所示。
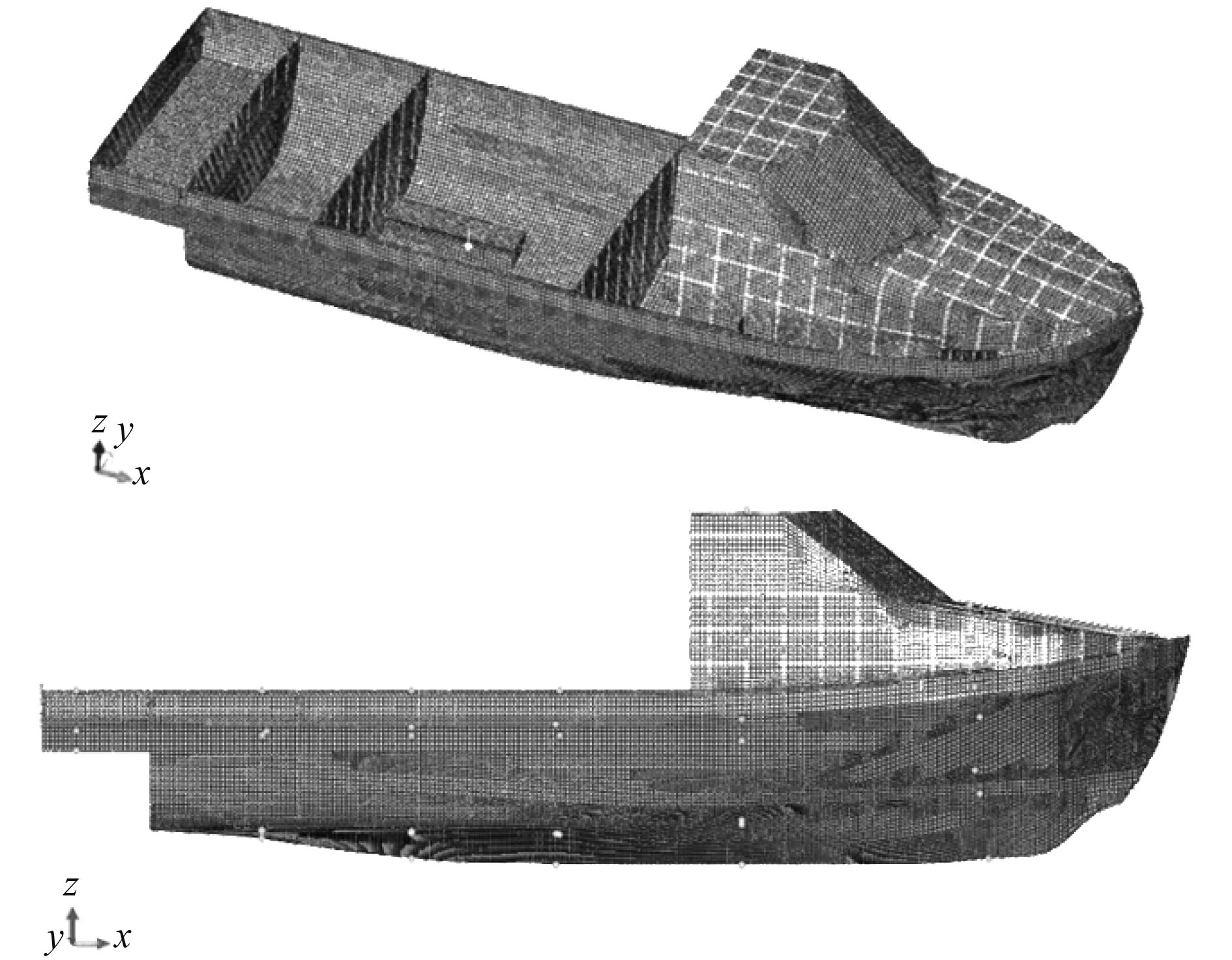
|
图 3 基座周围与全船监听测点选取示意图 Fig. 3 Monitor point around pedestal and entire ship |
在进行低频有限元计算和高频统计能量计算时,设置船体结构的材料属性如表2所示。
|
|
表 2 复合材料性能参数 Tab.2 Composite performance parameters |
复合材料船舶初步方案的各部位铺层及工艺如 表3所示。船体外板、甲板板、舱壁板及舱壁扶强材采用真空导流成型工艺,甲板横梁、甲板纵桁、甲板室强横梁及甲板室纵桁采用手糊成型工艺。
|
|
表 3 复合材料船初步铺层方式表 Tab.3 Initial composite lamination process |
图4为在单位激振力作用下,采用有限元计算得到的在20~500 Hz频段范围内,复合材料船激励点周围和全船分布的测点平均输出振动响应的对比。

|
图 4 初步方案两类测点平均低频振动响应(1/3 OCT,20~500 Hz) Fig. 4 Comparison between two types of monitor points on average low-frequency vibration(1/3 OCT,20~500 Hz) |
由图4可看出,激励点周围测点的平均振动响应在全频段均高于全船分布测点的平均振动响应,从二者1/3倍频程振动总级比较结果来看,基座激励点周围测点的平均总振级高于全船分布测点3.7 dB,说明振动能量主要集中传递到激励点周围的船壳结构上。随着离激励点的距离增加,振动响应逐渐减小。因此在计算过程中主要分析激励点周围测点的平均振动响应。
图5为采用统计能量法求得的在500~5 kHz频段范围内,复合材料船板架的高频振动响应结果。由 图5可以看出,基座激励点处船底板远高于甲板板、舷侧板和上层建筑处的平均总振级,由此说明在计算过程中取基座激励点处船底板处振动加速度为特征加速度进行计算结果的处理和对比。
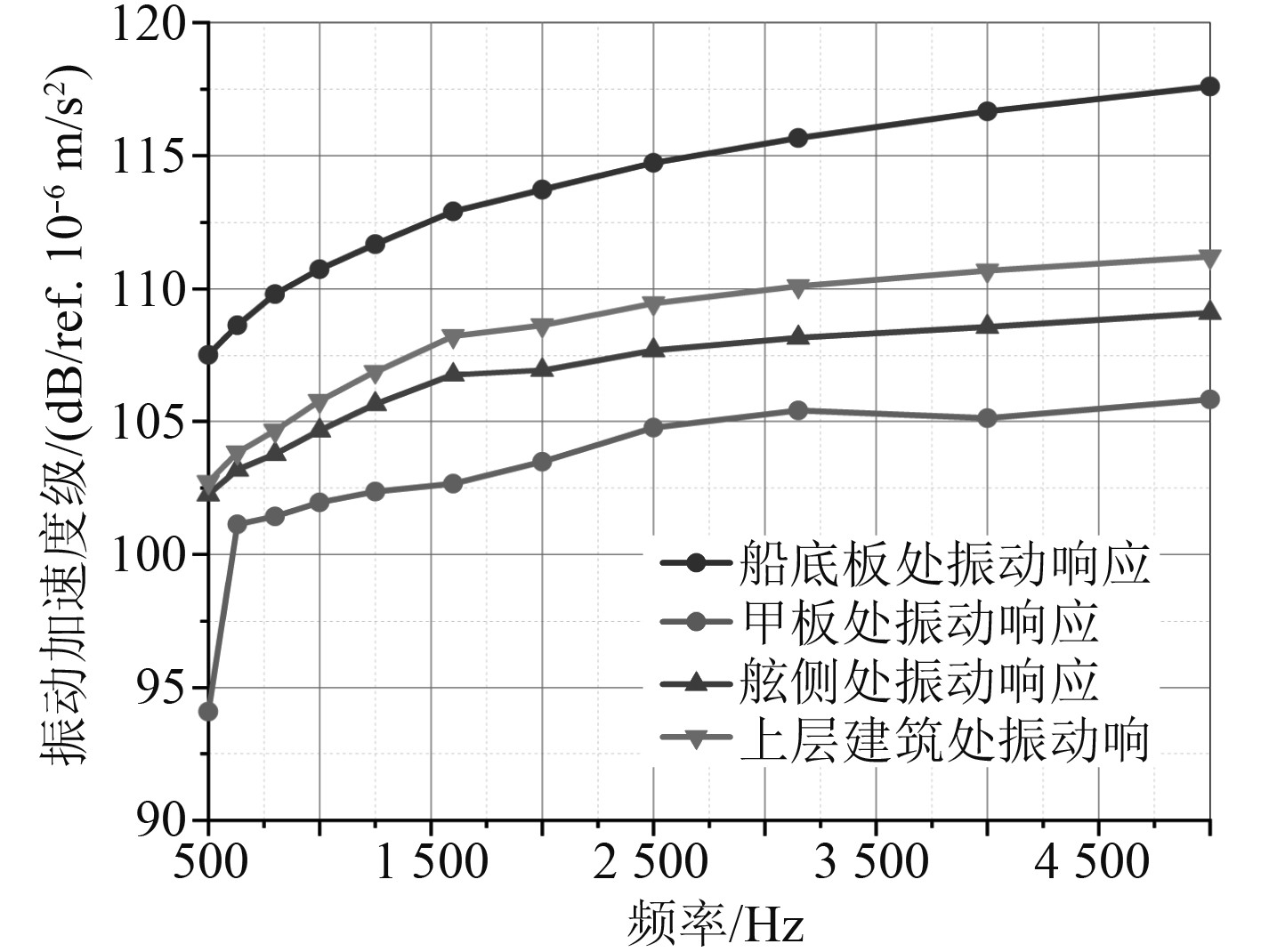
|
图 5 初步方案各船体结构平均高频振动响应(1/3 OCT,500~5 kHz) Fig. 5 Average high-frequency vibration response of ship structure(1/3 OCT,20~5 kHz) |
将有限元计算得到的中、低频段结果,与统计能量法求得的船体高频振动响应结果进行结合,获得复合材料船体全频段的振动响应计算结果。图6为激励点周围测点在20~5 kHz全频段1/3倍频程带级图。由 图6可知,在单位力激励下复合材料船体初步优化方案在20~5 kHz范围内平均振动总级为119.3 dB。
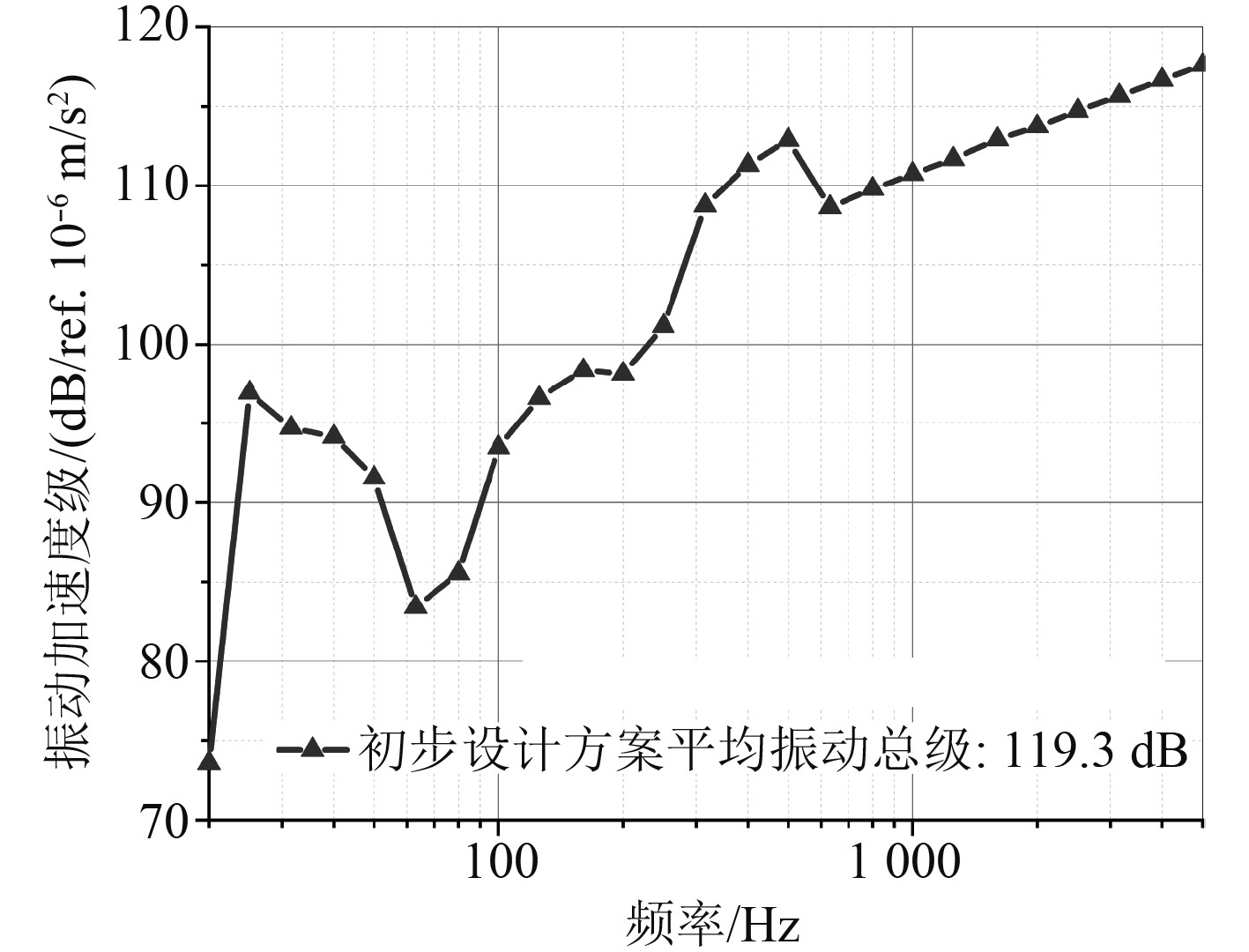
|
图 6 复合材料船初步方案平均振动响应(1/3 OCT,20~5 kHz) Fig. 6 Average vibration response of initial composite ship scheme(1/3 OCT,20~5 kHz) |
由图4研究结果可以看出,复合材料船舶基座周边为振动噪声敏感区域,因此对其周边船体结构进行加强将有助于提升船舶振动降噪性能。本文通过改变船体基座周围结构参数,对船体进行了2套方案优化计算分析。优化方案1将船底板与舷侧板的厚度分别调整为28 mm,22 mm,同时调整其复合材料铺层方案;优化方案2将船底板与舷侧板的厚度分别调整为32 mm,25 mm,其铺层参数如表4所示。图7为2种优化方案与初步方案的对比结果。
|
|
表 4 复合材料船体优化方案2铺层方式 Tab.4 Optimazation composite lamination process 2 |
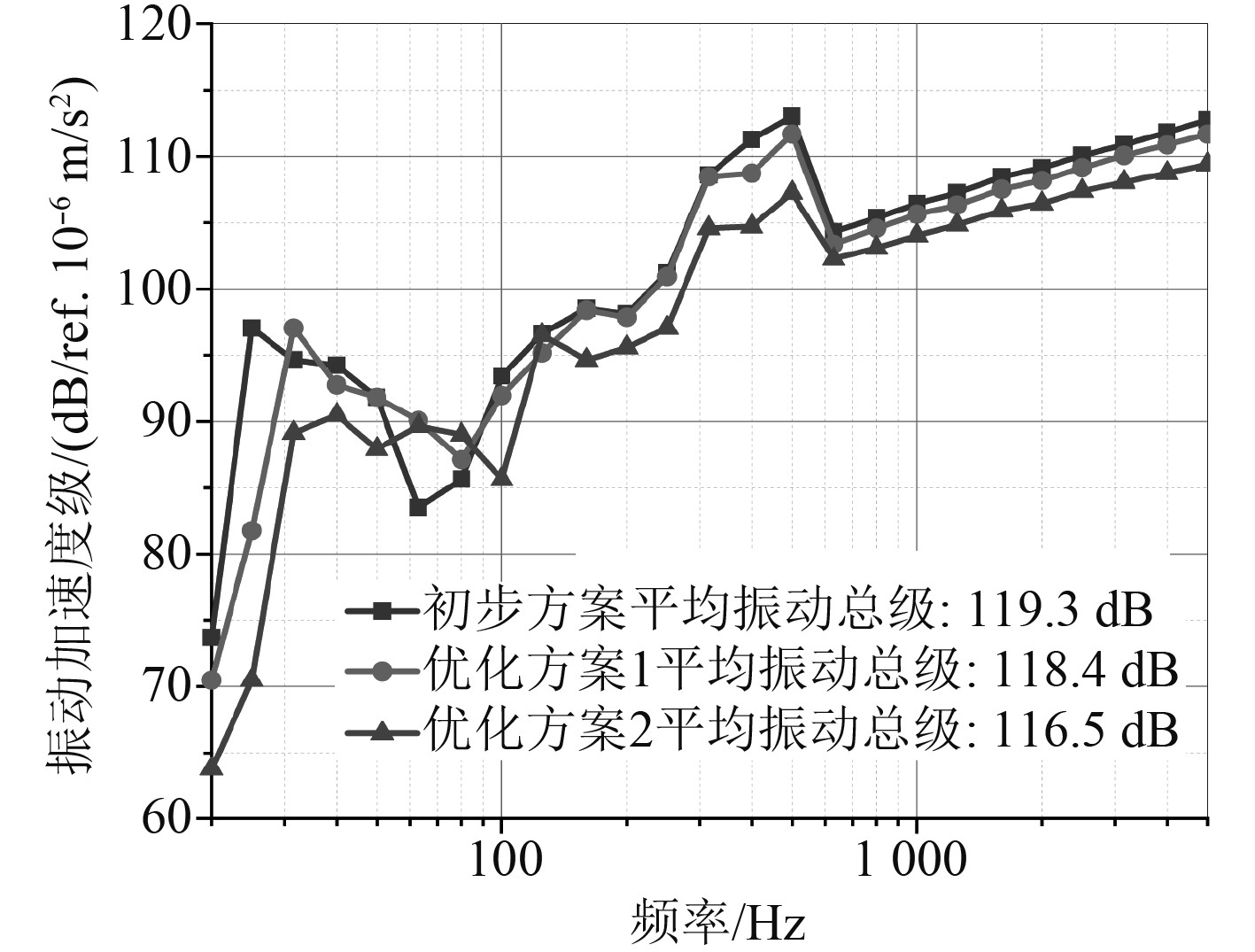
|
图 7 优化方案与初步方案平均振动响应对比(1/3 OCT,20~5 kHz) Fig. 7 Comparison between optimization and initial schemes on average vibration response(1/3 OCT,0~5 kHz) |
如图7所示,通过优化复合材料船体厚度同时改变复合材料的铺层工艺,复合材料船体振动响应得到了降低,其中优化方案2相对初步方案结构的振动响应明显降低。优化方案2在250~500 Hz之间的频段相对初步方案振动响应明显降低,20~5 kHz全频段结果相对初步方案平均振动总级降低约2.8 dB。
3.2.2 复合材料船减振降噪效果分析图8为复合材料船优化方案2的船体典型振动模态,优化方案2复合材料船1阶模态频率约在13.4 Hz,为上层建筑后端壁板的局部振动;1阶整体弯曲振动频率约在25 Hz。

|
图 8 复合材料船优化方案2典型振动模态 Fig. 8 Composite ship optimization scheme 2 typical vibration of membrane states |
图9为复合材料船优化方案2与相同船体结构参数的钢制船舶的全频段1/3倍频程带级噪声曲线对比。在使用复合材料进行船体建造后船体平均振动总级为116.5 dB,相对比钢结构船的平均振动总级121.6 dB,降低了5.1 dB,成功实现减振降噪目标。复合材料船优化方案2在20~80 Hz频段内,振动响应大于钢船,说明低频段时该设计方案的复合材料船舶振动降噪性能并不理想,但全频段降噪性能对于钢制船舶具有较为明显的优势。
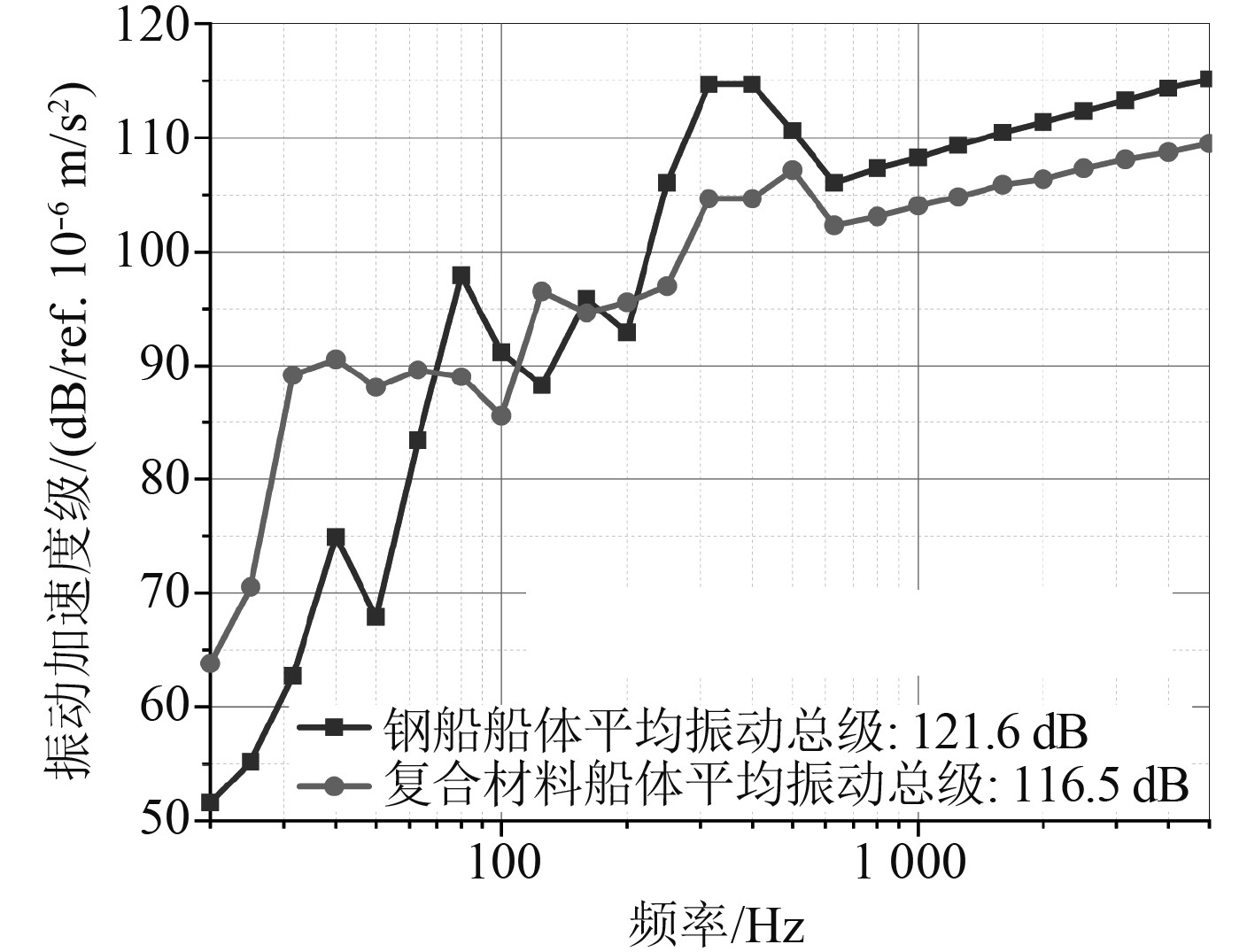
|
图 9 优化方案与钢船振动响应对比(1/3 OCT,20~5 kHz) Fig. 9 Comparison composite and steel ship on average viberation level(1/3 OCT,20~5 kHz) |
本文对复合材料船进行了减振降噪设计及计算分析,采用有限元法计算获得船体结构中、低频振动响应,采用统计能量法获得船体结构高频振动响应,从而获得20~5 kHz范围内船体振动响应谱,得出以下结论:
1)激励点周围测点的平均振动响应在全频段均高于全船分布测点的平均振动响应,其平均总振级高于全船分布测点3 dB以上,证明机舱周围结构形式对船舶减振降噪性能影响较大;
2)通过优化复合材料船体厚度以及铺层工艺,复合材料船体振动响应相对初步方案明显降低。在20~5 kHz频段范围内,优化方案2相对初步方案振动响应总级降低约2.8 dB;
3)优化后的复合材料船在20~5 kHz频段范围内,平均振动响应总级相对钢制船舶数值计算结果降低5.1 dB;
4)复合材料船在20~80 Hz的低频段的减振降噪性能劣于钢船,对于提高复合材料船在低频段的抵抗激励能量性能输入需要进一步研究。
| [1] |
BATHE, KLAUS‐JüRGEN. Finite Element Method[M]. Wiley Encyclopedia of Computer Science and Engineering. John Wiley & Sons, Inc. 2000.
|
| [2] |
LAFONT T, TOTARO N, BOT A L. Statistical energy analysis: from the understanding of its assumptions to the practical use[C]// Inter-noise & Noise-con Congress & Conference. 2017.
|
| [3] |
LYON R H. Statistical energy analysis of dynamical systems: theory and applications[J]. Annals of Probability An Official Journal of the Institute of Mathematical Statistics, 1977, 28(9): 430. |
| [4] |
YADAV D P S, SHARMA A K, SHIVHARE V. Free vibration analysis of isotropic plate with stiffeners using finite element method[J]. Engineering Solid Mechanics, 2015, 3(3): 167-176. DOI:10.5267/j.esm.2015.5.002 |
| [5] |
仇远旺, 王国治, 胡玉超. 基于振动传递分析的舰船辐射噪声特性研究[J]. 江苏科技大学学报(自然科学版), 2011, 25(2): 13-16. |
| [6] |
吴卫国, 魏杰证, 林永水, 等. 基于统计能量分析的船舶舱室阻尼降噪布置优化[J]. 中国舰船研究, 2017(4). DOI:10.3969/j.issn.1673-3185.2017.04.019 |
| [7] |
李广, 严斌, 刘朋, 等. 小水线面双体船振动传递特性研究[C]// 中国造船工程学会船舶力学学术委员会水下噪声学组成立三十周年第十五届船舶水下噪声学术讨论会.
|
| [8] |
李亚, 赵文峰. 多种方法计算水中薄板的固有振动频率[J]. 舰船科学技术, 2017(5). DOI:10.3404/j.issn.1672-7619.2017.05.001 |
| [9] |
王春雪. 基于有限元法的大型集装箱船振动分析[J]. 船舶工程, 2015(S2). |
| [10] |
张阳阳, 楼京俊, 朱石坚. 弹性板-圆柱壳水下声辐射特性及影响因素[J]. 舰船科学技术, 2016(11). |
| [11] |
郑荻. 船舶低频振动噪声的自主控制方法[J]. 舰船科学技术, 2018, 40(18): 32-34. |
 2020, Vol. 42
2020, Vol. 42
