0 引　言

缠绕工艺中不同缠绕层相互交织，使得纤维束具有特定的波动特征，从而可以充分发挥复合材料各向异性及可设计性的优势。近年来，缠绕复合材料因抗疲劳性好、可设计性强等优点被广泛应用于压力容器、火箭发动机壳体、鱼雷发射管等领域。探究纤维缠绕对结构刚度及承载特性的影响规律，对于缠绕容器的结构设计具有重要的意义。

目前，研究纤维起伏波动对缠绕复合材料结构刚度特性的影响尚不多见。Rosenow M W K^[1]采用经典层合板理论，分析了15°～85°的螺旋缠绕圆管的应力、应变分布，与试验结果吻合良好；Hahn H T^[2]介绍了采用纤维缠绕成型工艺制备水下航行器的流程，并分析了缠绕方式对轴压复合材料圆柱壳屈曲应力的影响；Xia M^[3]基于三维各向异性层合理论，推导了内压作用下纤维缠绕管道的应力应变理论解，为后续研究提供了理论基础，并分析了不同纤维缠绕方式对管道力学性能的影响；Mitao O^[4]提出了一套不依赖于几何缺陷形式的折减刚度理论，可用于求解外压作用下三明治夹芯圆柱壳的临界屈曲载荷，与经典Plantema理论解相比，其结果更偏安全；Hemandez -Moreno H^[5]研究了不同壁厚及缠绕方式的复合材料圆柱壳在外压作用下的失效模式及极限载荷，指出缠绕图形对结构的极限承载影响不大，数值预报与试验结果吻合良好；Morozov E V^[6]指出缠绕复合材料结构的应力应变与缠绕图形的大小及代表性晶胞的个数有关，采用均匀化建模方法低估了结构的应力水平；Gelebart^[7]建立代表性体积单元，分析了复合材料圆管的局部应力和应变；郭章新^[8]通过引入螺旋缠绕角和起伏层倾斜角对起伏区域纤维束的非正交性交织特性进行描述，选取三角函数描述起伏区域中纤维束中面的起伏形状，指出纤维束起伏、交织对拉扭及剪弯耦合刚度系数影响明显。

本文对缠绕复合材料夹层圆柱壳进行深水静压试验，选取层合区、环向起伏区、螺旋起伏区3种典型区域的32个典型测点，进行应变—载荷规律分析，并探究纤维交叉起伏对结构局部刚度的影响。

1 试验设计 1.1 纤维缠绕工艺特性

夹层复合材料圆柱壳模型采用湿法缠绕工艺制备，总长度610.5 mm（含上下法兰），两端的全复合材料段长60 mm，中部夹层段长430 mm。外径320.6 mm，内径290.5 mm，内蒙皮厚1.97 mm，外蒙皮厚2.28 mm，芯材厚10.8 mm。内外蒙皮均采用湿法缠绕工艺制备，材料体系为EM301树脂、HF10-12 K型T300碳纤维。中部为±55°螺旋缠绕，端部为环向与±55°的混合缠绕。纤维缠绕过程中出现周期性的交叉起伏，形成重复菱形区域，可划分为3种典型代表区域：层合区、环向起伏区、螺旋起伏区，如图1所示。

1.2 应变片布置

采用电阻式应变片测量应变，使用静态应变仪采集数据。缠绕复合材料夹层圆柱壳模型共设置32个应变测点，其中外蒙皮上17个测点，以大写字母编号，内蒙皮上15个测点，以对应小写字母编号。

以外蒙皮测点为例作说明，L，H₁，H₂，S₁，S₂分别为层合区、环向起伏区、螺旋起伏区的环向应变测点。A₁-A₆为外蒙皮轴向应变测点，沿圆柱壳长度方向，A₁，A₃，A₅与A₂，A₄，A₆呈对称分布。其中，A₁，A₂处于端部混合缠绕区，A₃处于环向起伏区，A₅处于螺旋起伏区，A₄，A₆对称处于层合区，这样布置便于对比层合区、环向起伏区、螺旋区交叉区的应变。同理，C₁-C₆号是与A₁-A₆测点相同位置的环向应变测点。内蒙皮的测点布置与外蒙皮基本相同，只有15个测点，省去测点h₂和s₂，测点详细布置如图2所示。

2 力学模型

因夹层圆柱壳的结构形式对称、载荷对称，沿周向取单位长度的壳带进行受力分析，如图3所示。作用于壳带上的力包括均匀静水外压力 $p$ 、轴向压力 ${T_1}$ 及横向力 ${T_2}$ ，且由平衡条件可知 ${T_1} = - \dfrac{{\rm{1}}}{{\rm{2}}}pR$ 。

本文为分析外蒙皮上测点的应变规律，将芯层视为外蒙皮的弹性基础，芯层的弹性基础刚度为 $k{\rm{ = }}\displaystyle\frac{{{E_{\rm{c}}}}}{{{t_{\rm{c}}}}}$ ，则问题转化为单位宽度弹性基础梁的复杂弯曲问题，既受到横向均匀载荷作用同时还受到单侧轴向载荷作用，在受力分析时应同时考虑两方面的作用。

3 应变—载荷规律分析

为探究缠绕形成的纤维交叉起伏对结构局部刚度及应变分布的影响，现研究0～1 MPa静水外压载荷作用下，复合材料夹层圆柱壳各测点应变值随压力变化规律。

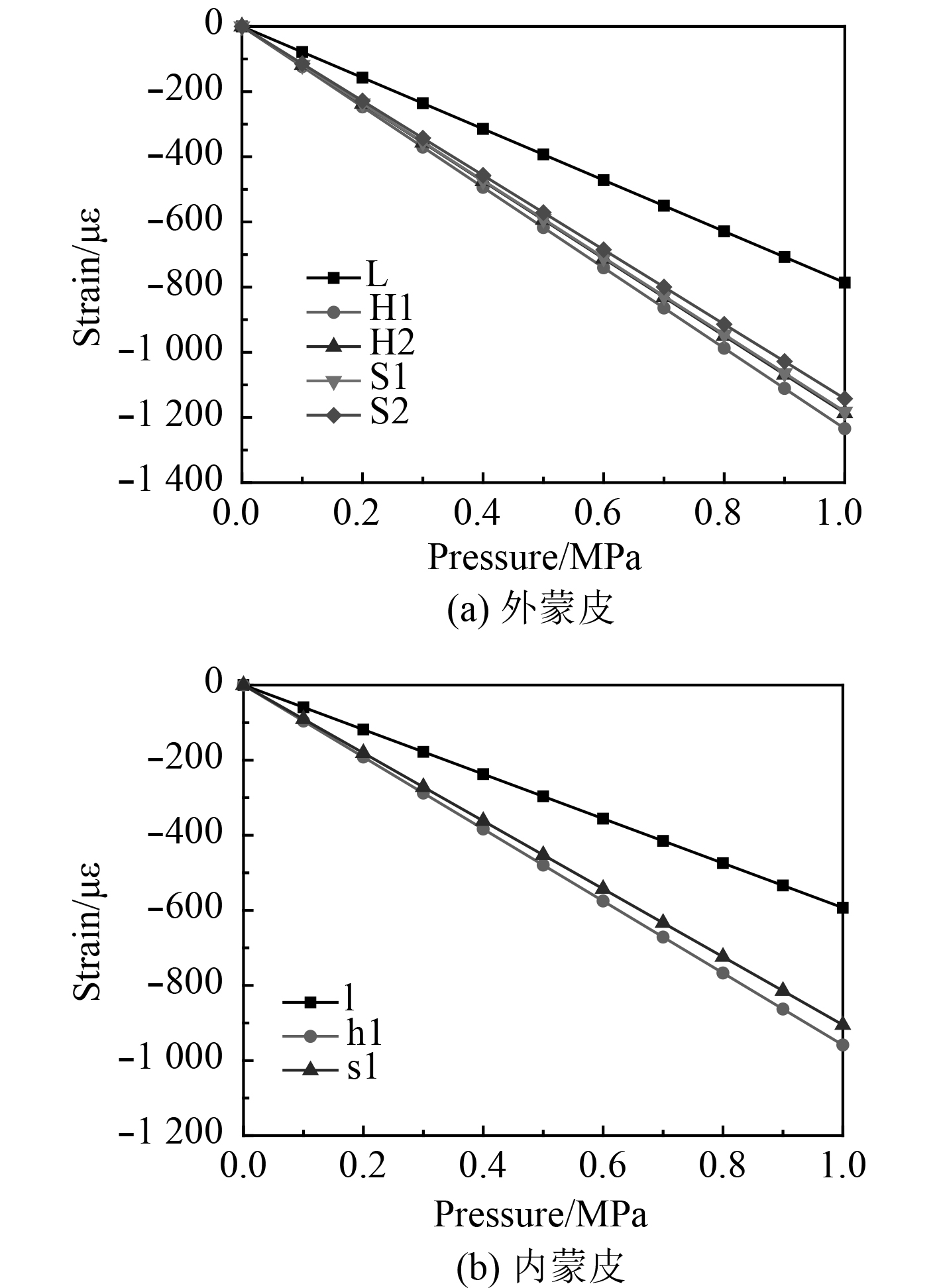
3.1 典型代表区域刚度规律分析

认为轴向压缩载荷对环向应变的影响可忽略，取3种典型区域的环向应变进行分析，以探究缠绕造成的纤维起伏对结构局部刚度的影响。由图4可知，3种典型区域的环向应变均为负，随载荷增加呈线性增长，应变绝对值满足L<S₁<H₁，内蒙皮测点也满足同样规律l<s₁<h₁，即层合区<螺旋起伏区应变<环向起伏区应变。

这是因为采用湿法缠绕工艺制备时，纤维出现周期性弯曲交叠，层合区的纤维走向都相同，而交叉区的纤维存在交叠起伏，从而产生环向起伏区和螺旋起伏区。且纤维弯曲起伏导致孔隙率升高、刚度降低、抗剪能力减弱，使得环向起伏区与螺旋起伏区的刚度低于层合区。

由载荷-应变曲线斜率可知三典型区域的刚度关系为：环向起伏区<螺旋起伏区<层合区。即同样载荷条件下，环向起伏区域的应变值最大，层合区域的应变值最小。纤维的弯曲起伏导致结构的应变分布是非均匀的。由应变—载荷曲线的斜率，可预估纤维的交叉起伏导致局部刚度下降约33.4%。

3.2 轴向应变–载荷规律分析

由图5可知，外蒙皮的A₁-A₆轴向测点在静水压力载荷作用下均为负应变，随载荷增大线性增加。相同载荷作用下，各测点应变绝对值满足：A₁<A₂<A₅<A₆<A₃<A₄，A₁测点应变绝对值最小，A₆测点应变略小于A₃，A₄测点应变绝对值最大。内蒙皮上的a₁至a₆应变也呈线性关系，规律与外蒙皮测点相似，a₁测点应变绝对值最小，a₄测点应变绝对值最大。

首先分析轴压载荷 $T$ 的作用，在线弹性阶段，结构在 $T$ 作用下出现均匀的轴向压缩变形，对各测点贡献几乎相同；其次，分析横向静水外压载荷 $p$ 作用。在均布载荷 $p$ 作用下，结构出现典型弯曲变形，其轴向应力应变的分布规律，与壳带的径向挠度密切相关。由各测点的几何位置，可近似认为测点A₁和A₂属于边界区，A₃和A₄属于过渡区，A₅和A₆属于均匀沉降区。由经典弹性基础板的变形规律知，均匀外压载荷 $p$ 作用下，A₅和A₆的径向位移近似为 ${p / k}$ ，A₃和A₄的最大径向位移为 ${\rm{1}}{\rm{.043}}{p / k}$ ，略大于均匀沉降区变形，而靠近法兰的A₁和A₂测点径向位移最小。从而导致各测点应变值大小关系为：A₁<A₆<A₄。

进而分析纤维交叉起伏影响，由前文分析知，纤维交叉起伏造成局部刚度降低，且环向起伏区<螺旋起伏区<层合区。由于A₃处于环向起伏区，A₅处于螺旋起伏区，A₄，A₆处于相应对称位置的层合区，因而满足：A₁<A₂<A₅<A₆<A₃<A₄。

内蒙皮上轴向测点的分布规律与外蒙皮相似，但数值小于外蒙皮应变值。基于夹层结构界面粘接良好、应变连续性假设，可认为芯层的径向挠度与外蒙皮相同，即在静水外压载荷 $p$ 作用下，芯层产生了体积压缩变形，故而外力功转化为压缩应变能积蓄在芯层中，使得内蒙皮的径向变形减小，相应的应变也小于外蒙皮。

3.3 环向应变-载荷规律分析

由图6可知：在静水压力载荷作用下，内外蒙皮上的环向测点均为负应变，随载荷增大线性增加。相同载荷作用下，各测点应变绝对值满足C₁<C₂<C₅<C₆<C₃<C₄，C₄测点应变绝对值最大，C₁测点应变绝对值最小，中部区域的各测点应变值接近，边界区域测点受刚性法兰影响，应变值较小。内蒙皮也呈现上述规律。

首先分析轴压载荷 ${T_1}$ 作用，轴向载荷对各测点的环向应变的影响主要是由于泊松效应引起，贡献较小。其次，分析横向均布静水压力载荷 $p$ 作用，壳带受静水外压作用时会产生径向的均匀压缩，从而在相邻两壳带之间会产生挤压，即出现作用于壳带纵向边界上的侧向力。该力的合力方向与外压载荷 $p$ 方向一致，其大小与壳带的径向挠度 $w$ 有关，且壳带中面沿环向的线应变 $\varepsilon $ = $\displaystyle\frac{{{\rm{2}}{\text π} \left( {R - w} \right){\rm{ - 2}}{\text π} R}}{{{\rm{2}}{\text π} R}}$ = $ - \displaystyle\frac{w}{R}$ ，故可知各测点的环向应变规律与壳带的径向挠度直接相关。由前文对静水压力载荷作用下，外蒙皮的变形规律可知，各测点应变绝对值关系依旧满足边界区<中心区<过渡区，即C₁<C₂<C₅<C₆<C₃<C₄。内蒙皮上分布规律类似于外蒙皮环向测点，但总体上内蒙皮上环向测点比对应位置处的外蒙皮环向测点绝对值小，分析原因相同外压载荷作用下，对应测点位置的外蒙皮半径大于内蒙皮，因而内蒙皮上的环向变形量小于外蒙皮。

4 结　语

通过开展缠绕复合材料夹层圆柱壳的深水静压试验，得到圆柱壳内外蒙皮的3种典型代表区域层合区、环向缠绕区、螺旋缠绕区的应变—载荷规律曲线。分析规律可知，湿法缠绕工艺中纤维的周期性交叉起伏导致结构局部刚度下降，应变分布不均匀。三典型区域的刚度关系为环向起伏区<螺旋起伏区<层合区，且环向起伏区的刚度比层合区降低约33.4%。