2. 哈尔滨工程大学,黑龙江 哈尔滨 150001;
3. 中国船舶集团公司第七一四研究所,北京 100101;
4. 海军装备部,北京 100071
2. Harbin Engineering University, Harbin 150001, China;
3. The 714 Research Institute of CSSS, Beijing 100101, China;
4. Navy Equipment Department, Beijing 100071, China
舱室噪声是评价船舶舒适性的重要指标,国际海事组织(IMO)在第MSC.337(91)号决议[1]中对船舶各类舱室的噪声等级提出了更为严格的要求,未满足噪声指标要求的船舶将无法按期交付,造成巨额的经济损失,因此在船舶设计阶段中,如何准确地进行噪声预报并提出有效的防护措施是目前亟待解决的问题。
目前,已有大量学者对舱室噪声预报方法及噪声防护措施做出了相关研究[2-5]。付佳[6]重点讨论舱室噪声预报过程中声学模型的建立与噪声源的设置,并将所得预报结果与实测值进行对比,研究成果具有一定的工程应用价值。任毅[7]在计算船舶舱室噪声过程中,考虑主机排气口所产生的噪声,并建立船体外包络声腔作为排气口噪声的传递路径。研究表明,考虑主机排气孔噪声时,所得仿真值与实测值更加为接近。欧礼坚[8]对游艇的舱室噪声进行预报分析,重点谈论舱室噪声预报过程中的激励源特性,给出了螺旋桨、主机等主要设备对舱室噪声的影响规律。许浩、闫森森等[9-11]针对不同类型船舶,利用统计能量法预报并找出噪声超标舱室,给出相应的控制措施。研究表明,通过附加阻尼等措施可有效的降低舱室内的噪声水平。
众多学者虽开展了船舶舱室噪声预报方法及噪声控制措施的相关研究工作,并且对舱室噪声预报过程中基础参数进行了相应的研究,但有关实船测试损耗因子对船舶舱室噪声的研究相对较少。为此,本文以多舱段船舶典型结构为例,探究损耗因子对舱室噪声的影响,并开展某船的舱室噪声预报。通过与实测值对比,验证基于实船损耗因子获取的船舶舱室噪声预报方法的准确性。在此基础上,给出全船舱室噪声分布及设备对附近舱室的影响规律,旨在为船舶舱室噪声控制防护提供参考。
1 船舶舱室噪声统计能量分析预报方法 1.1 统计能量分析原理统计能量法将系统整体划分为多个离散的子系统,并通过能量的空间时间平均值、简正方式的数目和损耗因数等参数来描述每个子系统的状态,子系统间通过边界进行能量交互。由此可建立整体的能量平衡方程,通过求解便可以得到各个子系统的最终状态,再通过换算就可以得出所需的物理量。在进行船舶舱室噪声计算时,相邻的子间系统的功率流方程如下:
| $ {P_{i{n_i}}} = {P_{dis{s_i}}} + {P_{ij}}{\text{。}} $ | (1) |
式中:
将所有子系统的功率流方程联立,则可得到如下方程组:
| $ \begin{split} &\scriptsize\omega \left[ {\begin{array}{*{20}{c}} {({\eta _1} + \sum\limits_{i = 1,i \ne j}^N {{\eta _{1i}}} ){n_1}}&{ - {\eta _{12}}{n_1}}& \cdots &{ - {\eta _{1N}}{n_1}} \\ { - {\eta _{21}}{n_2}}&{({\eta _2} + \sum\limits_{i = 1,i \ne j}^N {{\eta _{2i}}} ){n_2}}& \cdots &{ - {\eta _{2N}}{n_2}} \\ \vdots & \vdots & \ddots & \vdots \\ { - {\eta _{N1}}{n_N}}&{ - {\eta _{N2}}{n_N}}& \cdots &{({\eta _N} + \sum\limits_{i = 1,i \ne j}^N {{\eta _{Ni}}} ){n_N}} \end{array}} \right]\times\\ & \left[ {\begin{array}{*{20}{c}} {\frac{{{{\bar E}_1}}}{{{n_1}}}} \\ {\frac{{{{\bar E}_2}}}{{{n_2}}}} \\ \vdots \\ {\frac{{{{\bar E}_N}}}{{{n_N}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\bar P}_{i{n_1}}}} \\ {{{\bar P}_{i{n_2}}}} \\ \vdots \\ {{{\bar P}_{i{n_N}}}} \end{array}} \right]{\text{。}}\\[-40pt] \end{split} $ | (2) |
式中,
对于板子系统而言:
| $ {E_i}={m_i}{v_i}^2{\text{。}} $ | (3) |
式中:
对于声腔子系统而言:
| $ {E_i}=\frac{{{p_i}^2}}{{\rho {c^2}}}{V_i}{\text{。}} $ | (4) |
式中:
通过解上述方程便可以得到各个子系统在平衡状态下的声场响应或振动响应。
1.2 船舶舱室噪声统计能量分析方法船舶舱室噪声统计能量分析方法主要步骤如下:
1)建立整船的统计能量模型
整船结构较为复杂,首先需要对其进行合理的子系统划分,用板子系统来模拟船体结构,用声腔子系统模拟舱室,同时需保证子系统在计算中心频率下的模态数大于5[13]。
2)施加载荷
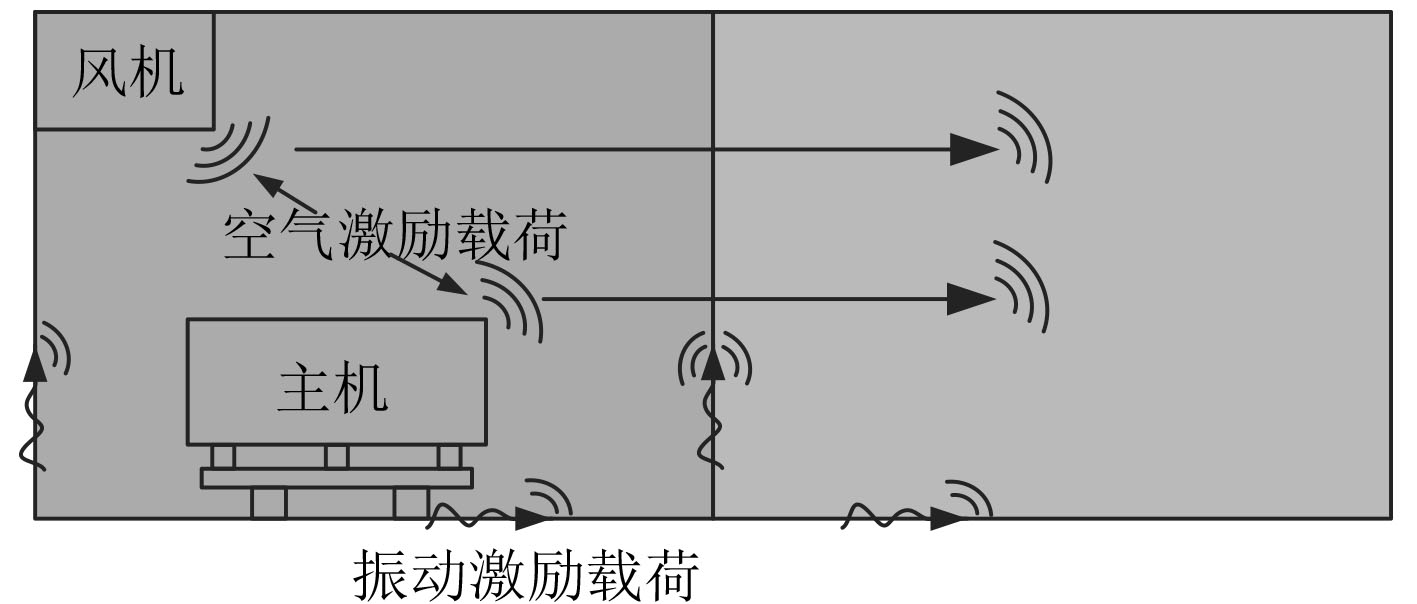
船体激励载荷共包含2种:一种是空气激励载荷,设备工作时的直发声,直接向外辐射;另一种是振动激励载荷,通过结构的振动发声向舱室内辐射。2种载荷的能量传递路径如图1所示。
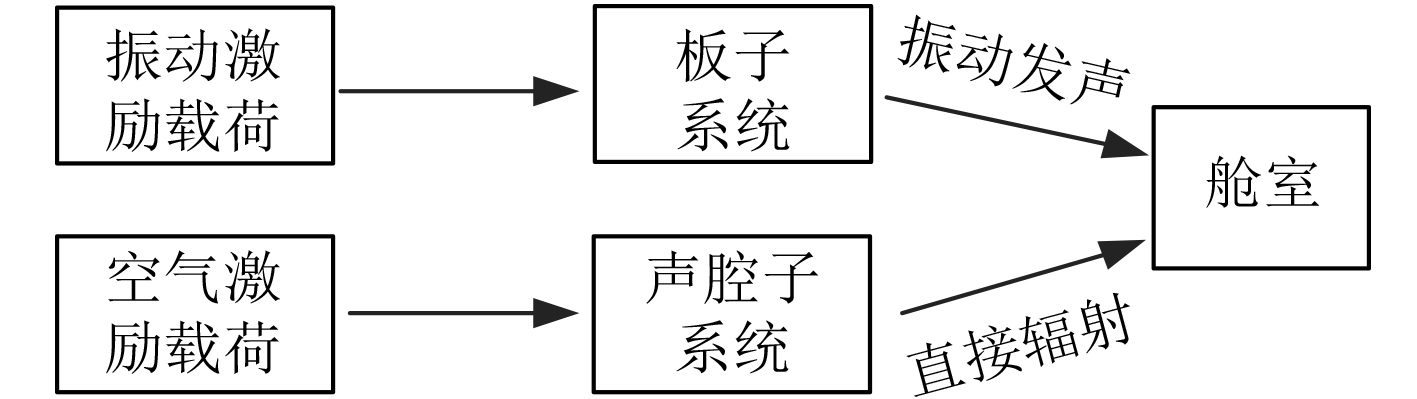
|
图 1 子系统能量传递图 Fig. 1 Subsystem energy transfer diagram |
3)边界条件
利用半无限域模块,建立船体外板的无反射边界条件,即当能量传递至船体结构边缘时,会继续向外扩散,用以模拟流场对船体的影响。
4)舾装材料
舾装材料对舱室噪声影响较大,需根据舾装布置图,在对应舱壁、甲板和天花板位置设置相应的舾装材料,输入舾装材料的吸隔声系数。
5)求解及结果分析
1.3 损耗因子对舱室噪声计算结果的影响 1.3.1 船体结构损耗因子的取值结构损耗因子是衡量系统对振动能量耗散能力的物理量,是舱室噪声预报的关键参数之一,结构损耗因子包含耦合损耗因子及内损耗因子,其中耦合损耗因子表征子系统间功率传递的大小,在进行舱室噪声计算时,其值直接由软件计算给出;内损耗因子是指在单位时间内,子系统每振动一次损耗的能量与平均储存能量的比值,一般通过经验公式、船级社规范以及实验测试获取,其中各方法中的取值大小存在一定差异。图2给出了63 Hz~8 kHz频域范围不同的内损耗因子取值,包括经验公式值[14]、CCS(中国船级社)建议值[15]和实船测试值,其中实船测试采用瞬态衰减法测得。
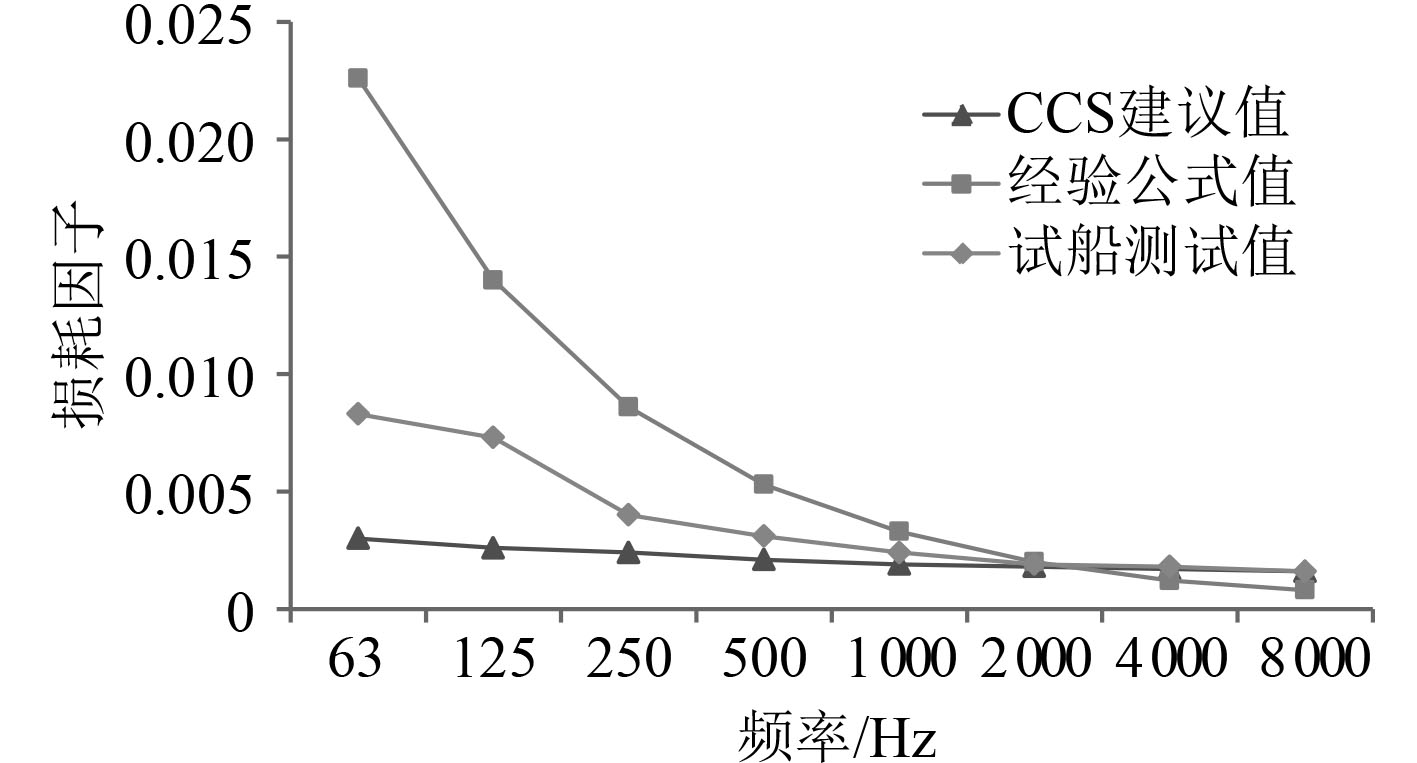
|
图 2 内损耗因子取值 Fig. 2 Internal loss factor |
为探究结构内损耗因子对舱室噪声计算的影响,建立多舱段典型船舶结构模型如图3和图4所示。由于在船舶舱室噪声预报过程中涉及的载荷类型包含振动加速度载荷和空气噪声载荷,所以设置2种载荷施加工况:1)在Ⅴ舱下底板位置施加单位振动加速度载荷;2)在Ⅴ舱内部施加单位声功率载荷。在每种工况下依次改变整个模型板子系统的损耗因子设置,计算不同损耗因子工况下各舱的噪声水平。
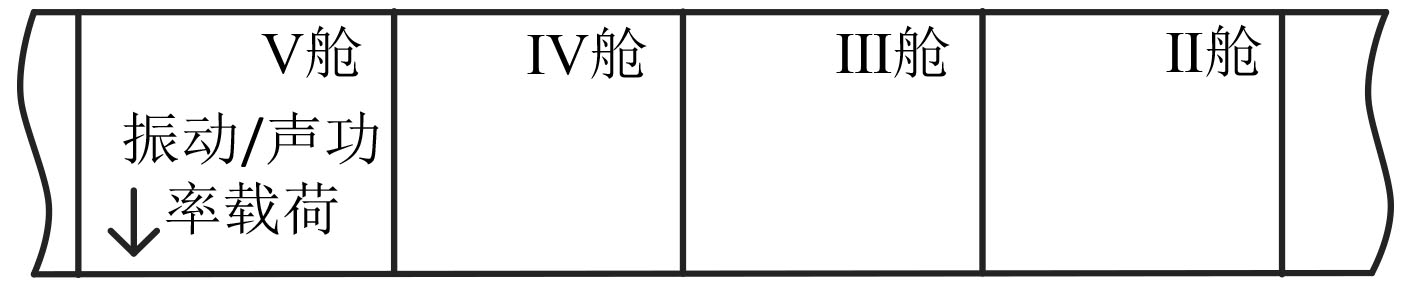
|
图 3 多舱段典型船舶结构示意图 Fig. 3 Schematic diagram of typical ship structure with multiple compartments |

|
图 4 多舱段典型船舶结构 Fig. 4 Multi-class section typical ship structure |
各舱室噪声总级计算结果如表1所示,Ⅱ舱和Ⅴ舱的舱室频带噪声曲线如图5所示。
|
|
表 1 不同损耗因子工况下各舱室噪声计算结果 Tab.1 Calculation results of cabin noise under different loss factors |
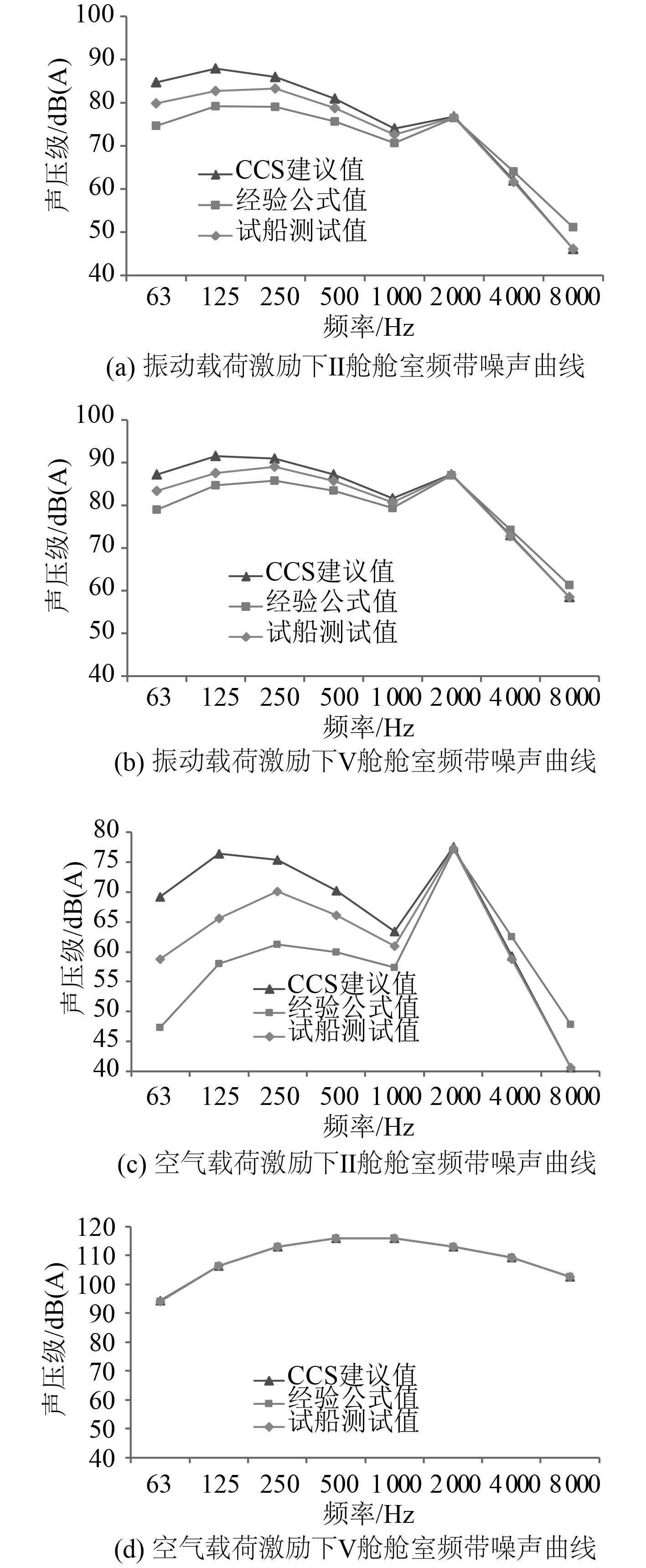
|
图 5 舱室频带噪声曲线 Fig. 5 Cabin band noise curve |
1)振动激励载荷下的结果分析
从振动激励载荷作用下各舱室噪声预报总级结果可以看出,不同的损耗因子对舱室噪声总级影响较大,舱室噪声计算结果对多相差7.2 dB(Ⅱ舱CCS规范值和经验公式值),最少相差2.2 dB(Ⅴ舱实测值和经验公式值)。除此之外,3种工况下,均呈现Ⅴ舱噪声仿真计算值相差最少,Ⅱ舱噪声仿真计算值相差最多的趋势,说明损耗因子对距离激励源越远的区域,影响越大。从Ⅱ舱和Ⅴ舱的舱室频带噪声曲线可以看出,不同损耗因子对舱室中低频噪声影响较大,对高频影响较小,同时中低频噪声占舱室噪声的主导地位,对舱室噪声总级影响较大。
2)空气噪声激励下的结果分析
从空气激励载荷作用下各舱室噪声预报总级结果可以看出,不同的损耗因子对舱室噪声总级影响较大,舱室噪声计算结果对多相差4.5 dB(Ⅱ舱CCS规范值和经验公式值),而Ⅴ舱内舱室噪声值基本不受结构内损耗因子影响,其原因是空气激励载荷位于舱室内部,直接影响舱室内的噪声水平。与振动激励影响相似,在空气激励载荷作用下,不同损耗因子对距离激励源越远的舱室影响越大,对舱室噪声中低频噪声影响较大。
综上,可以看出,无论在那种激励载荷作用下,损耗因子对舱室噪声预报结果影响较大,其中CCS规范建议值偏于安全,所得舱室噪声计算值较高。在进行船舶舱室噪声预报时,应针对具体船舶,开展结构损耗因子试验测试,以期得到准确的舱室噪声预报结果。
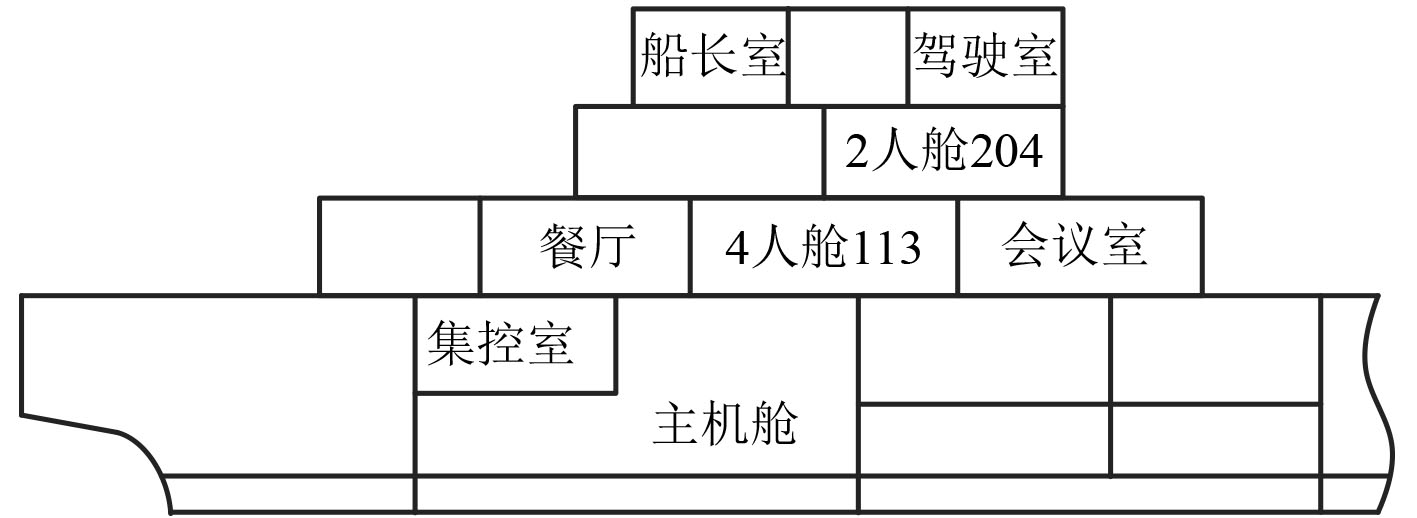
2 船舶舱室噪声预报 2.1 船舶舱室噪声模型 2.1.1 统计能量模型统计能量模型建立涉及模型的简化以及考核舱室的细化。其中模型简化是指在建模过程中不考虑对预报结果影响较小的因素,例如骨材、桅杆等结构;考核舱室细化是指在某个考核舱室内由于舱室功能不同,人耳所处高度不同,并且舱室内不同高度位置的声压大小也不同,因此在进行舱室噪声预报之前,按照0.5 m高度对舱室内声腔分层(见图6),从而得到舱室内不同高度的声压大小。
|
图 6 Deck 1考核舱室细化后离散图 Fig. 6 Discrete map after refinement of Deck 1 assessment cabin |
本文建立的统计能量中共包含板子系统共1 248个,声腔子系统306个,其中水线以下的船体外板建立半无限域,用以模拟水线以下部分的无反射边界条件。舱室分布示意图如图7所示,最终建立的统计能量模型如图8所示。
|
图 7 舱室分布示意图 Fig. 7 Schematic diagram of cabin distribution |

|
图 8 某船舶统计能量模型 Fig. 8 Statistical energy model of ship |
引起船舶舱室噪声的激励源类型可分为2种:一种是空气激励载荷,设备工作时的直发声,以空气为传播介质,加载时以声功率的形式加载在对应设备的声腔子系统上;另一种是振动激励载荷,以船体结构为船舶介质,通过结构的振动发声向舱室内辐射,仿真计算时以振动加速度级的形式加载在设备基座位置。对于船舶主机、柴发机组等大功率、高噪声设备,既要考虑其振动激励载荷,又要考虑空气激励载荷;对于风机等小型设备,则只考虑其空气激励载荷即可。
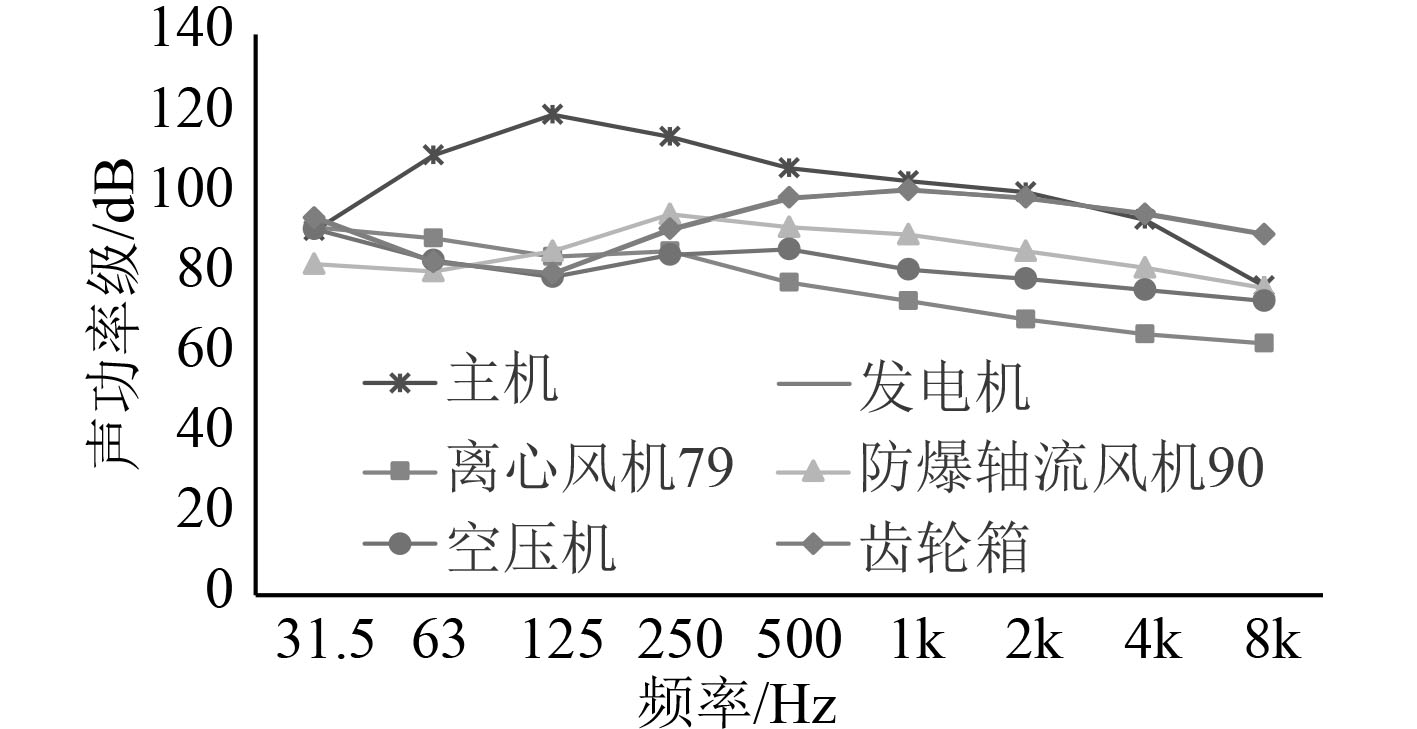
本次舱室噪声预报分析中,绝大部分设备载荷大小为实船测试结果,部分未能测试设备,其载荷大小则根据相关规范依进行指标分解。图10和图11分别给出了部分设备在额定工况下声功率级频谱及振动加速度级频谱。
|
图 9 设备激励载荷类型 Fig. 9 Equipment excitation load types |
|
图 10 设备声功率级曲线 Fig. 10 Equipment's sound power level curve |

|
图 11 设备振动加速度级曲线 Fig. 11 Equipment's vibration acceleration level curve |
考虑到实船测试工况,本次仿真预报工况共设有2种,分别为全速航行工况和锚泊工况,其中相对于全速航行工况,锚泊工况关闭了主机、柴发机组、供油泵等设备。
2.2 船舶舱室噪声分析 2.2.1 预报值与实测值对比分析在全速及锚泊2种工况下,对比全船各考核舱室的噪声预报值和实测值,部分舱室噪声值对比如表2所示。从对比结果可以看出,全船绝大部分舱室预报值与实测值小于3 dB,说明基于实船损耗因子获取的舱室噪声预报方法准确可靠,其预报结果具有较高的工程应用价值。
|
|
表 2 典型舱室噪声预报及测试结果对比 Tab.2 Comparison of typical cabin noise prediction and test results |
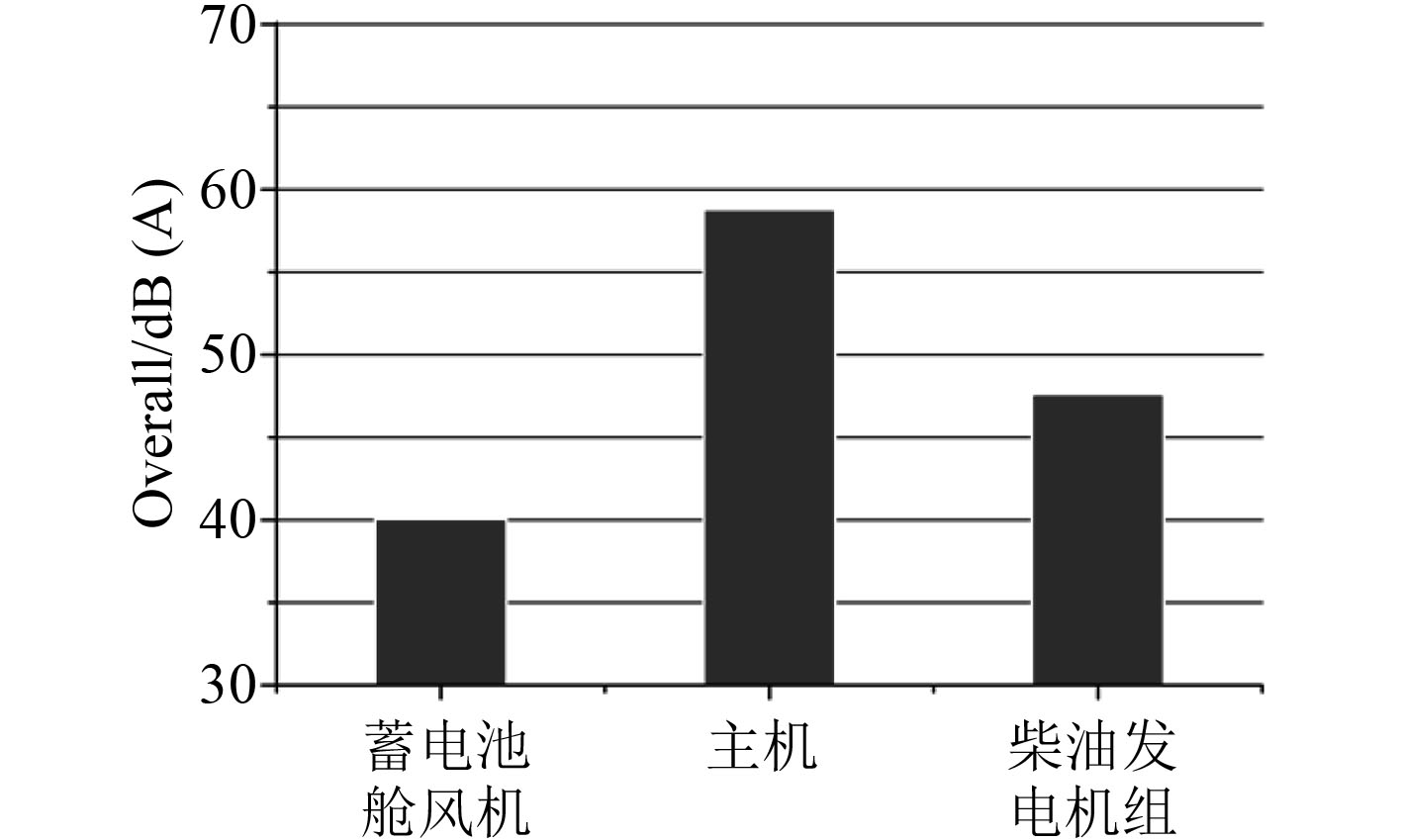
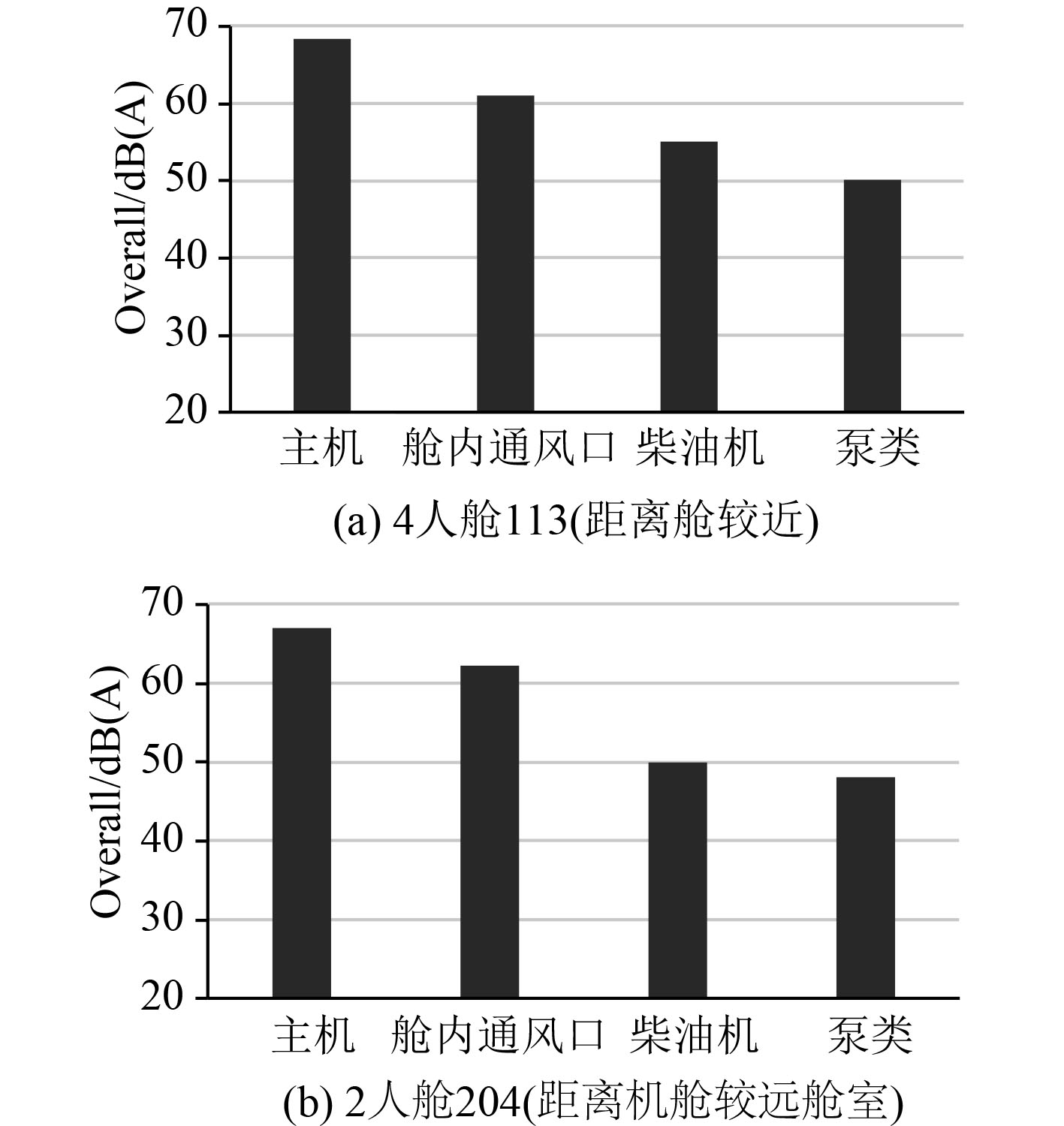
在全速工况下,距离机舱较近的舱室,如一甲板餐厅、会议室等,其预报误差较小,小于1 dB,而远离机舱的舱室,如驾驶室、船长室,其误差相对较大,约在2 dB左右;在锚泊工况下,各舱室噪声误差约在1 dB左右。上述现象原因是,全速航行工况下,全船噪声主要集中在机舱附近(见图12),且远离机舱区域的驾驶室和船长室,其噪声主导分量均为机舱内主机(见图13),说明统计能量法对靠近主要激励源舱室的噪声水平预报更为准确。对于距离主要激励源较远舱室,预报误差相对较大。

|
图 12 舱室噪声分布云图 Fig. 12 Cloud diagram of cabin noise distribution |
|
图 13 驾驶室噪声主导致分量 Fig. 13 Main caused components of cab noise |
全速航行工况下,全船舱室噪声声压分布云图如图14所示。可以看出在全速航行工况下,全船舱室噪声主要集中在机舱位置附近,并且在低频范围内,主机影响范围更大。从机舱附近舱室的噪声主导分量分析中可以看出,在该工况下,此类舱室噪声主导分量均已机舱内设备(包括主机、柴油机、泵类等)为主,而远离机舱的舱室,其噪声主导分量,虽然以主机为主,但舱室内风机对其噪声水平有一定影响。
|
图 14 舱室噪声分布云图 Fig. 14 Cloud diagram of cabin noise distribution |
|
图 15 舱室噪声主导致分量(全速) Fig. 15 Main component of cabin noise(full speed) |
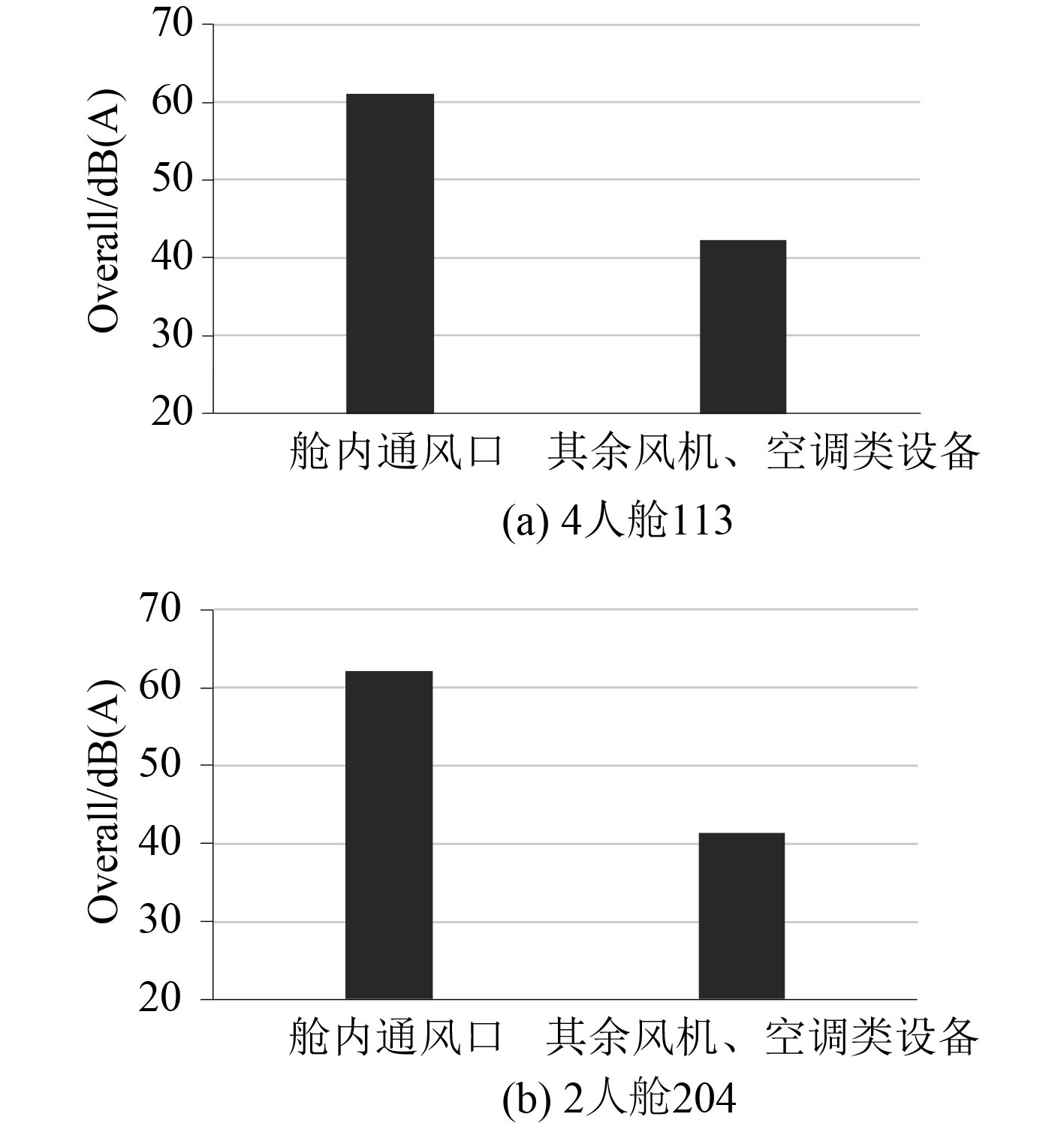
单独开启风机、空调类设备时,所得部分频点下全船舱室噪声声压的分布云图如图16所示。可以看出,风机、空调类设备所在舱室较相邻舱室的噪声水平差异较大,说明此类设备产生的噪声仅对所在舱室影响较大,对附近舱室影响较小。同时,从舱室噪声主导分量分析图也可以看出,除舱内通风口以外,其余风机类设备对该舱室的贡献量可忽略不计。
|
图 16 舱室噪声分布云图 Fig. 16 Cloud diagram of cabin noise distribution |
|
图 17 舱室噪声主导致分量 Fig. 17 Main component of cabin noise |
基于上述舱室噪声分布规律,在进行船舶舱室噪声防护工作时,对于机舱附近舱室,应主要针对舱室内主机噪声分量进行防护,可采用在靠近主机一侧舱壁附加隔声、吸声材料等方法;对于远离主机区域的舱室而言,除考虑主机噪声对其影响之外,还应从降低舱室内激励源噪声水平着手,比如更换低噪声通风口、低噪声空调机等。
3 结 语本文建立了多舱段船舶典型结构,探究了损耗因子对舱室噪声计算结果的影响,然后基于损耗因子实测值,开展某船舶舱室噪声预报,并与实船测试值进行比对,最后根据全船舱室噪声分布云图以及部分舱室噪声主导分量计算结果,探究了舱室噪声分布规律,并根据舱室位置不同给出了初步的噪声防护建议。主要结论如下:
1)单位振动激励载荷作用下,对于距离激励源超过15 m的舱室,不同损耗因子取值对其舱室噪声声压产生的3~7 dB的影响,且距离激励源越远,影响越大。
2)单位空气噪声激励载荷作用下,对于距离激励源超过15 m的舱室,不同损耗因子取值对其舱室噪声声压产生的2~5 dB的影响,对激励源所在舱室影响较小。因此开展实船舱室噪声预报时,建议使用实船损耗因子测试值作为参数输入。
3)基于实测损耗因子的舱室噪声预报方法准确可靠,与主机舱间隔封闭舱数量小于或等于2的舱室,噪声预报值与实测值误差小于1 dB,距离主要噪声源较远舱室,预报误差稍大,但全船舱室噪声误差小于3 dB。
4)主机柴油机等大功率设备,作为全船主要噪声源,影响舱室多、范围广;风机、空调机等小型设备,仅对所处舱室内的噪声水平影响较大,影响范围小。
| [1] |
International Marine Organization. Code on noise levels on board ships (IMO MSC. 337(91)). 2012.
|
| [2] |
李婷婷. 船舶舱室内部噪声精细化预报研究[D]. 大连: 大连理工大学, 2019.
|
| [3] |
黄志平, 朱敬燕, 杨春. 船舶舱室噪声控制设计措施[J]. 中国水运(下半月), 2016, 16(9): 10-11+14. |
| [4] |
肖蕾, 李小灵, 陈浩. 基于统计能量法的船舶舱室噪声预报方法研究[J]. 船舶与海洋工程, 2016, 32(04): 46-53+65. |
| [5] |
苏楠, 高处, 刘文夫, 等. 基于传递路径分析法的船舶舱室噪声预报研究[J]. 噪声与振动控制, 2020, 40(1): 30-35+85. |
| [6] |
付佳, 王铭, 张伟. 超大型集装箱船的舱室噪声预报与测试[J]. 舰船科学技术, 2019, 41(11): 62-65. |
| [7] |
任毅, 王博涵, 单衍贺, 等. 主机排放噪声对船舶舱室噪声的影响研究[J]. 舰船科学技术, 2019, 41(13): 35-39. |
| [8] |
欧礼坚. 游艇主要噪声声源对舱室噪声影响研究与分析[J]. 广东造船, 2019, 38(02): 39-42. DOI:10.3969/j.issn.2095-6622.2019.02.011 |
| [9] |
许浩, 李邦华. 舱室通风系统设计中的噪声控制[J]. 船海工程, 2018, 47(4): 98-101. DOI:10.3963/j.issn.1671-7953.2018.04.023 |
| [10] |
闫森森. 基于统计能量法的船舶舱室噪声控制研究[C]. 2018中国西部声学学术交流会, 中国兰州, 2018.
|
| [11] |
冯博, 桂洪斌, 杨群. 船舶尾部舱室噪声预报及控制分析[J]. 舰船科学技术, 2017, 39(15): 22-27. |
| [12] |
PLUNT J. Methods for predicting noise levels in ships: Experiences from empirical and sea calculation methods[M]. Noise level prediction methods for ships, based on empirical and data, 1980.
|
| [13] |
冯涛, 王晶. 统计能量法的原理及其在声学工程上的应用[J]. 北京工商大学学报(自然科学版), 2002, 4: 25-27. |
| [14] |
中国船级社. 船舶及产品噪声控制与检测指南[S]. 2013.
|
| [15] |
程广利, 朱石坚, 伍先俊. 统计能量分析法及其损耗因子确定方法综述[J]. 船舶工程, 2004, 4: 10-15. DOI:10.3969/j.issn.1000-6982.2004.02.004 |
| [16] |
吴晓佳, 温华兵, 吴俊杰, 李军, 李晓亮. 基于统计能量法的邮轮舱室噪声预报与控制[J]. 噪声与振动控制, 2019, 39(1): 89-93+191. DOI:10.3969/j.issn.1006-1355.2019.01.017 |
| [17] |
Jee-Hun SONG, Suk-Yoon HONG, Won-Ho JOO. Analysis of structure-borne noise in ship cabins using a floating floor with an inserted viscoelastic layer[J]. Journal of Marine Science and Technology, 2009, 14(1): 127-135. DOI:10.1007/s00773-008-0039-9 |
 2020, Vol. 42
2020, Vol. 42
