2. 海军工程大学 舰船与海洋学院,湖北 武汉 430033
2. College of Ship and Ocean, Naval University of Engineering, Wuhan 430033, China
加肋圆柱壳是水下结构的主要结构形式,也是水下结构向流体辐射噪声的主要结构。由于结构内部设备布置形式各异,内部机械激励会从不同位置作用于壳体结构产生辐射噪声,因此,研究激励位置对加肋圆柱壳结构的振声特性,有助于优化基座与壳体的连接形式,从而降低水下航行器的辐射噪声,具有重要的理论价值和实际意义。
针对水下加肋圆柱壳结构,可以采用近似的薄壳理论,根据模态叠加法得到结构振动、辐射声压、辐射声功率、辐射效率等的解析表达式。Lynch[1]研究了各类薄壳结构的振动响应和声辐射。Filippov[2]将薄壳振动方程中的厚度进行无量纲化,得到无量纲厚度与加肋圆柱壳结构特征频率的关系。陈美霞[3]基于flugge壳体理论,采用波动法对带框架肋骨加筋圆柱壳的自由振动特性和频响特性进行研究。张波[4]采用多种有限元计算方法,计算了加肋圆柱壳肋骨对各频段总辐射声功率的影响。孙瑶[5]通过建立圆柱壳的解析辐射阻抗矩阵来分析厚度和边界条件对圆柱壳声辐射的影响。张一麟[6]提出了一种重建圆柱壳结构表面速度的插值方法。Alzahabi[7]从波动方程出发,对圆柱壳的辐射噪声进行分析,揭示圆柱壳模态频率随其几何形状的变化趋势。这些研究揭示了圆柱壳体结构基本的振动和声辐射特性,为加肋圆柱壳的设计提供重要帮助,但是较少考虑结构内部激励的问题,因此对结构内部的激励位置变化对结构振动和声辐射的影响研究是有必要的。
本文基于薄壳理论,将肋骨的作用近似为只有径向力,采用模态展开法导出了有限长加肋圆柱壳结构的近似解析解。然后改变内部激励力的作用位置,对比分析得到激励位置对结构振动和声辐射的影响规律。
1 基本理论 1.1 加肋圆柱壳体的基本解建立柱坐标系
| $ \left\{ \begin{array}{l} u(\theta ,z) = \sum\limits_{m,n} {{U_{mn}}\cos n\theta \cos {k_m}z} \text{,} \\ v(\theta ,z) = \sum\limits_{m,n} {{V_{mn}}\sin n\theta \cos {k_m}z}\text{,} \\ w(\theta ,z) = \sum\limits_{m,n} {{W_{mn}}\cos n\theta \sin {k_m}z} \text{。} \end{array} \right. $ | (1) |
其中:m,n都取
假设肋只对壳体产生法向压力
| $ \left\{ \begin{array}{l} f\left( {\theta ,z} \right) = \sum\limits_{m,n} {{f_{mn}}\cos n\theta \cos {k_m}z} \text{,}\\ p\left( {\theta ,z} \right) = \sum\limits_{m,n} {{p_{mn}}\cos n\theta \cos {k_m}z} \text{,}\\ g\left( {\theta ,z} \right) = \sum\limits_{m,n} {{g_{mn}}\cos n\theta \cos {k_m}z} \text{。} \end{array} \right. $ | (2) |
其中各展开系数为:
| $ \left\{ \begin{aligned} & {f_{mn}} = \frac{{{\varepsilon _n}}}{{2 {\text π} L}}\int_{ - {\text π} }^{\text π} {\int_{ - L}^L {f\left( {\theta ,z} \right)\cos n\theta \cos {k_m}z{\rm d}\phi {\rm d}z} } \text{,}\\ & {p_{mn}} = \frac{{{\varepsilon _n}}}{{2 {\text π} L}}\int_{ - {\text π} }^{\text π} {\int_{ - L}^L {p\left( {\theta ,z} \right)\cos n\theta \cos {k_m}z{\rm d}\phi {\rm d}z} } \text{,}\\ & {g_{mn}} = \frac{{{\varepsilon _n}}}{{2 {\text π} L}}\int_{ - {\text π} }^{\text π} {\int_{ - L}^L {g\left( {\theta ,z} \right)\cos n\theta \cos {k_m}z{\rm d}\phi {\rm d}z} } \text{。} \end{aligned} \right. $ | (3) |
其中:当
将式(1)和式(2)代入控制方程可得加肋圆柱壳在外法线方向的耦合振动方程为:
| $ {\dot U_{mn}}Z_{mn}^M = {f_{mn}} - {p_{mn}} - {g_{mn}} \text{。} $ | (4) |
式中
声辐射引起的表面声压为:
| $ {p_{mn}} = \sum\limits_q {{{\dot U}_{qn}}Z_{qmn}^a} \text{。} $ | (5) |
其中:
| $ \begin{aligned} & Z_{qmn}^a = \frac{4}{{{\text{π}} L}}\int_0^\infty {\frac{{{k_q}{k_m}{{\left( { - 1} \right)}^{q + m}}{{\cos }^2}KL}}{{\left( {k_q^2 - {K^2}} \right)\left( {k_m^2 - {K^2}} \right)}}Z_n^a\left( K \right){\rm d}K}\text{,}\\ & Z_n^a\left( K \right) = \frac{{i{\rho _0}\omega H_n^{(1)}\left( {\sqrt {k_0^2 - {K^2}} a} \right)}}{{\left( {k_0^2 - {K^2}} \right)H_n^{(1)'}\left( {\sqrt {k_0^2 - {K^2}} a} \right)}}\text{。} \end{aligned} $ |
由于环肋是间隔布置,因此环肋的作用是不连续的,假设圆柱壳内共有T根环肋,第j根环肋的z坐标为
| $ g_n^j = Z_n^r\dot U_n^{rj}{\text{。}} $ |
其中:
| $ \begin{aligned} Z_n^r = & \frac{i}{{\omega a}}\left( {\frac{{2{\rho _r}{A_r}c_{pr}^2}}{{2a + {h_r}}}} \right) \times\\ & \left[ {\frac{{h_r^2}}{{12{a^2}}}{{\left( {{n^2} - 1} \right)}^2} - {{\left( {\frac{{\omega a}}{{{c_{pr}}}}} \right)}^2} + \frac{{{{\left( {\omega a} \right)}^2}}}{{{{\left( {\omega a} \right)}^2} - {{\left( {n{c_{pr}}} \right)}^2}}}} \right] \text{。} \end{aligned} $ |
则环肋的总作用力为:
| $ g\left( {\theta ,z} \right) = \sum\limits_{m,n}^\infty {\sum\limits_{j = 1}^T {Z_n^r{{\dot U}_{mn}}\cos n\theta \cos {k_m}{z_j}\delta \left( {z - {z_j}} \right)} } \text{,} $ |
其展开系数为:
| $ {g_{mn}} = \frac{{Z_n^r}}{L}\sum\limits_{q = 0}^\infty {\sum\limits_{j = 1}^T {{{\dot U}_{qn}}\cos {k_q}{z_j}\cos {k_m}{z_j}} } = \sum\limits_{q = 0}^\infty {{{\dot U}_{qn}}Z_{qmn}^r} \text{。} $ | (6) |
将式(5)和式(6)代入式(4),得
| $ {\dot U_{mn}}Z_{mn}^M + \sum\limits_q {{{\dot U}_{qn}}\left( {Z_{qmn}^a + Z_{qmn}^r} \right)} = {f_{mn}}\text{。} $ |
由上式求解出模态振动速度后即可得到有关的声学量,壳体的辐射声功率为:
| $ \begin{split} P\left( \omega \right) =\,& \frac{1}{2}\int_S {{\rm{Re}} \left\{ {p\left( {\theta ,z} \right){{\dot u}^ * }\left( {\theta ,z} \right)} \right\}{\rm d}S}= \\ & \dfrac{S}{4}{{Re}} \left\{ {\sum\limits_{qmn} {\frac{1}{{{\varepsilon _n}}}{{\dot U}_{qn}}Z_{qmn}^a\dot U_{mn}^ * } } \right\} \text{。} \end{split} $ |
壳体表面的平均的振速为:
| $ \begin{split} & \left\langle {\dot u\left( {\theta ,z} \right){{\dot u}^ * }\left( {\theta ,z} \right)} \right\rangle = \frac{1}{{2S}}\int_S {\left\{ {\dot u\left( {\theta ,z} \right){{\dot u}^ * }\left( {\theta ,z} \right)} \right\}{\rm d}S} = \\ & \quad \quad \frac{1}{4}\sum\limits_{mn} {\frac{1}{{{\varepsilon _n}}}{{\dot U}_{qn}}\dot U_{mn}^ * } \text{。} \end{split} $ |
当壳体受单点激励时,假设激励力位于壳体上
| $\left\{ \begin{aligned} & f\left( {\theta ,z} \right) = {F_0}\frac{1}{a}\delta \left( {{z_0}} \right)\delta \left( {{\theta _0}} \right)\text{,}\\ & {f_{mn}} = \frac{{{\varepsilon _n}}}{{2{\text{π}} La}}{F_0}\cos \left( {n{\theta _0}} \right)\cos \left( {{k_m}{z_0}} \right)\text{。} \end{aligned}\right. $ |
当壳体受对称的双点激励时,假设激励力分别位于壳体上
| $\left\{ \begin{aligned} & {f_1}\left( {\theta ,z} \right) = \frac{{{F_0}\delta \left( {{z_0}} \right)\delta \left( {{\theta _0}} \right)}}{{2a\cos {\theta _0}}}\text{,}\\ & {f_2}\left( {\theta ,z} \right) = \frac{{{F_0}\delta \left( {{z_0}} \right)\delta \left( { - {\theta _0}} \right)}}{{2a\cos {\theta _0}}}\text{,} \end{aligned}\right. $ |
| $\left\{ \begin{aligned} & {f_{1mn}} = \frac{{{\varepsilon _n}}}{{4 {\text π} La\cos {\theta _0}}}{F_0}\cos \left( {n{\theta _0}} \right)\cos \left( {{k_m}{z_0}} \right)\text{,}\\ & {f_{2mn}} = \frac{{{\varepsilon _n}}}{{4 {\text π} La\cos {\theta _0}}}{F_0}\cos \left( { - n{\theta _0}} \right)\cos \left( {{k_m}{z_0}} \right)\text{。} \end{aligned}\right. $ |
多源激励下壳体结构响应和辐射声场可近似为单源激励下的非相干叠加[10],因此:
| $ {f_{mn}} = {f_{1mn}} + {f_{2mn}} \text{,} $ |
当壳体受线激励作用时,假设线激励沿轴线方向分布,作用于
| $\left\{ \begin{aligned} & f\left( {\theta ,z} \right) = \frac{{{F_0}\delta \left( {{\theta _0}} \right)}}{{a({z_2} - {z_1})}},({z_1} \leqslant z \leqslant {z_2})\text{,}\\ & {f_{mn}} = \frac{{{\varepsilon _n}{F_0}[\sin \left( {{k_m}{z_2}} \right) - \sin \left( {{k_m}{z_1}} \right)]}}{{2 {\text π} La{k_m}\left( {{z_2} - {z_1}} \right)}}\cos \left( {n{\theta _0}} \right)\text{。} \end{aligned}\right. $ |
同理,当激励为双边线激励,假设位于
| $\left\{ \begin{aligned} & {f_1}\left( {\theta ,z} \right) = \frac{{{F_0}\delta \left( {{\theta _0}} \right)}}{{2a({z_2} - {z_1})\cos {\theta _0}}},({z_1} \leqslant z \leqslant {z_2})\text{,}\\ & {f_2}\left( {\theta ,z} \right) = \frac{{{F_0}\delta \left( { - {\theta _0}} \right)}}{{2a({z_2} - {z_1})\cos {\theta _0}}},({z_1} \leqslant z \leqslant {z_2})\text{,} \end{aligned}\right. $ |
| $\left\{ \begin{aligned} & {f_{1mn}} = \frac{{{\varepsilon _n}{F_0}[\sin \left( {{k_m}{z_2}} \right) - \sin \left( {{k_m}{z_1}} \right)]}}{{4{\text{π}} La{k_m}\left( {{z_2} - {z_1}} \right)\cos {\theta _0}}}\cos \left( {n{\theta _0}} \right)\text{,}\\ & {f_{2mn}} = \frac{{{\varepsilon _n}{F_0}[\sin \left( {{k_m}{z_2}} \right) - \sin \left( {{k_m}{z_1}} \right)]}}{{4{\text{π}} La{k_m}\left( {{z_2} - {z_1}} \right)\cos {\theta _0}}}\cos \left( { - n{\theta _0}} \right)\text{,} \end{aligned}\right. $ |
| $ {f_{mn}} = {f_{1mn}} + {f_{2mn}}{\text{。}} $ |
取圆柱壳结构参数为:a = 2 m,L = 6 m,h = 0.006 m,ρ = 7 800 kg/m3,η = 0.01,E = 2.1×1011 Pa,υ = 0.3;流体材料参数为:ρ0= 1 000 kg/m3,c0= 1 500 m/s;壳内均匀分布有10根环肋,肋的高度为hr= 0.3 m,宽度为dr= 0.02 m,材料参数与壳体一致。计算圆柱壳低频5~400 Hz的振声特性。取
辐射声功率级和均方速度级由下式给出:
| $ {L_P} = 10\lg \left( {{P / {{P_0}}}} \right),\;{L_u} = 10\lg \left( {{{\left\langle {\dot u{{\dot u}^ * }} \right\rangle } / {\dot u_0^2}}} \right)\text{。} $ |
其中:参考声压
单点激励力的幅值保持为
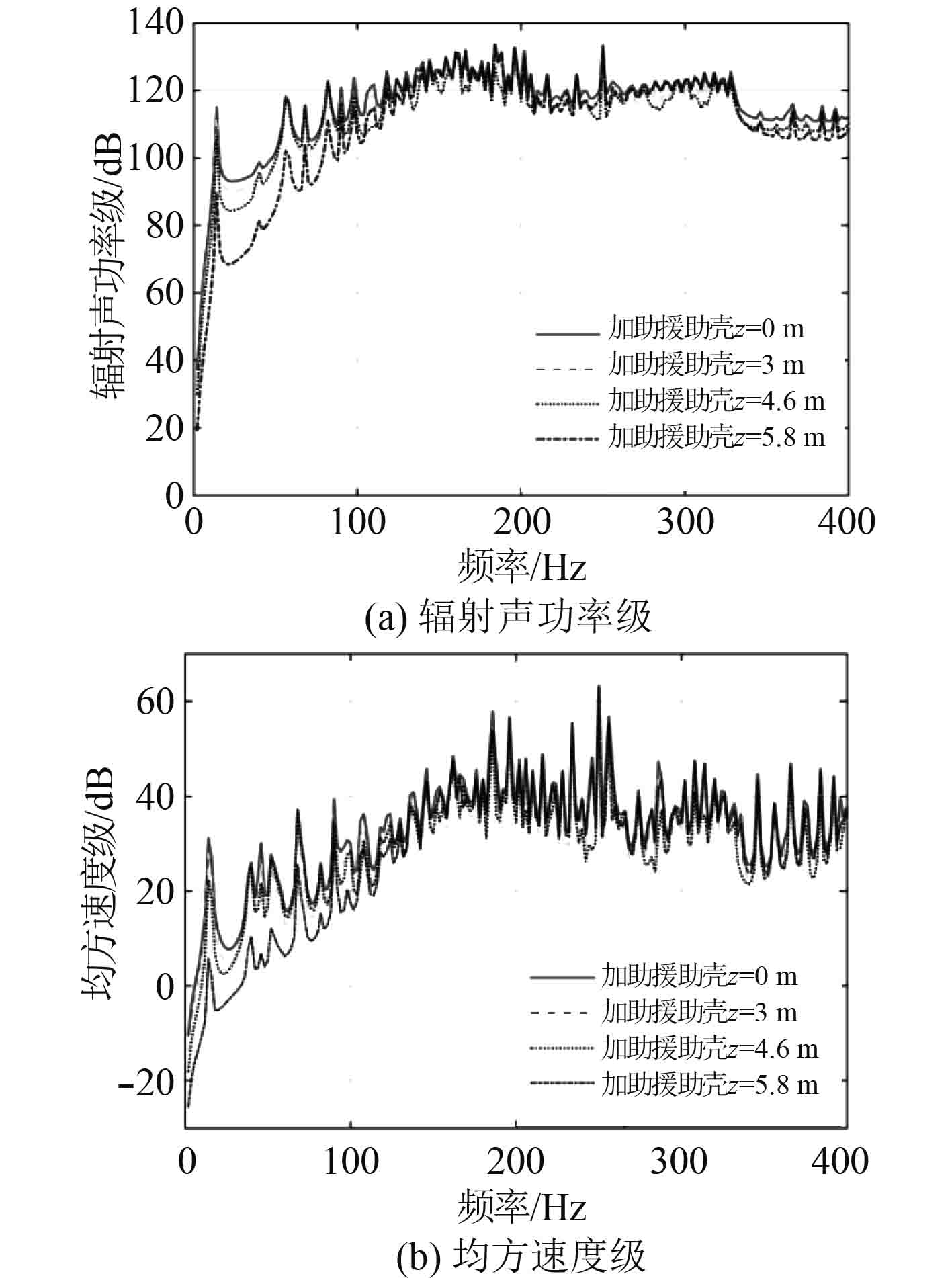
|
图 1 单点激励下加肋圆柱壳的振声特性 Fig. 1 The vibro-acoustic characteristics of stiffened cylindrical shells under single point force |
可以看出,单点激励位置的变化对5~150 Hz频段结构的辐射声功率和均方速度影响较大,激励力向边界靠近,结构的辐射声功率和均方速度都显著降低,而且越靠近界,降低的幅度越。在150~400 Hz频段,激励力位置的变化对其影响不大。
2.2 双点激励双点激励的幅值也保持为
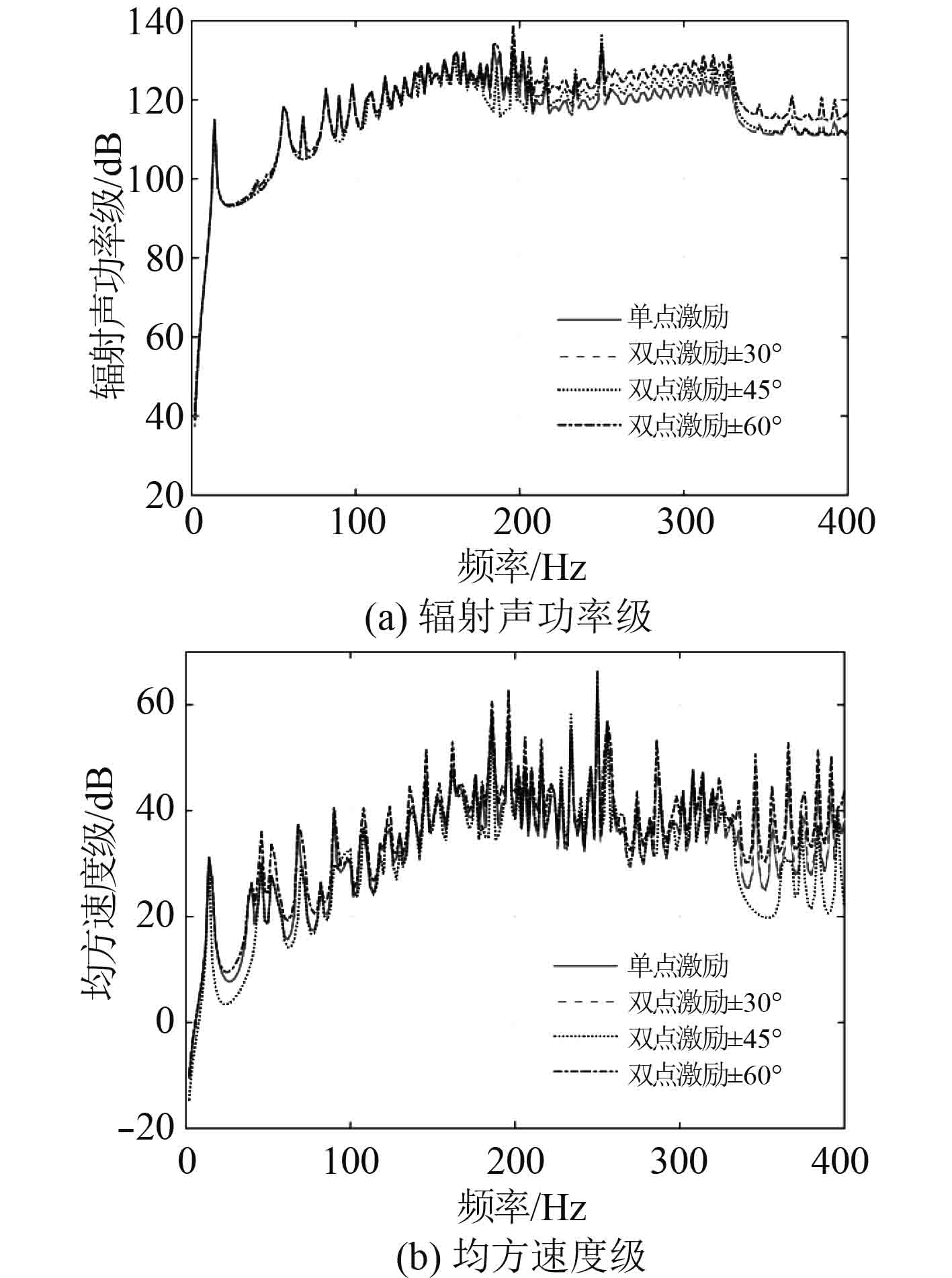
|
图 2 双点激励下加肋圆柱壳的振声特性 Fig. 2 The vibro-acoustic characteristics of stiffened cylindrical shells under double point force |
可以看出,与单点激励相比,双点激励在周向分开的角度不大时,辐射声功率变化不大,均方法向速度会明显降低,其中在
取线激励的幅值也保持
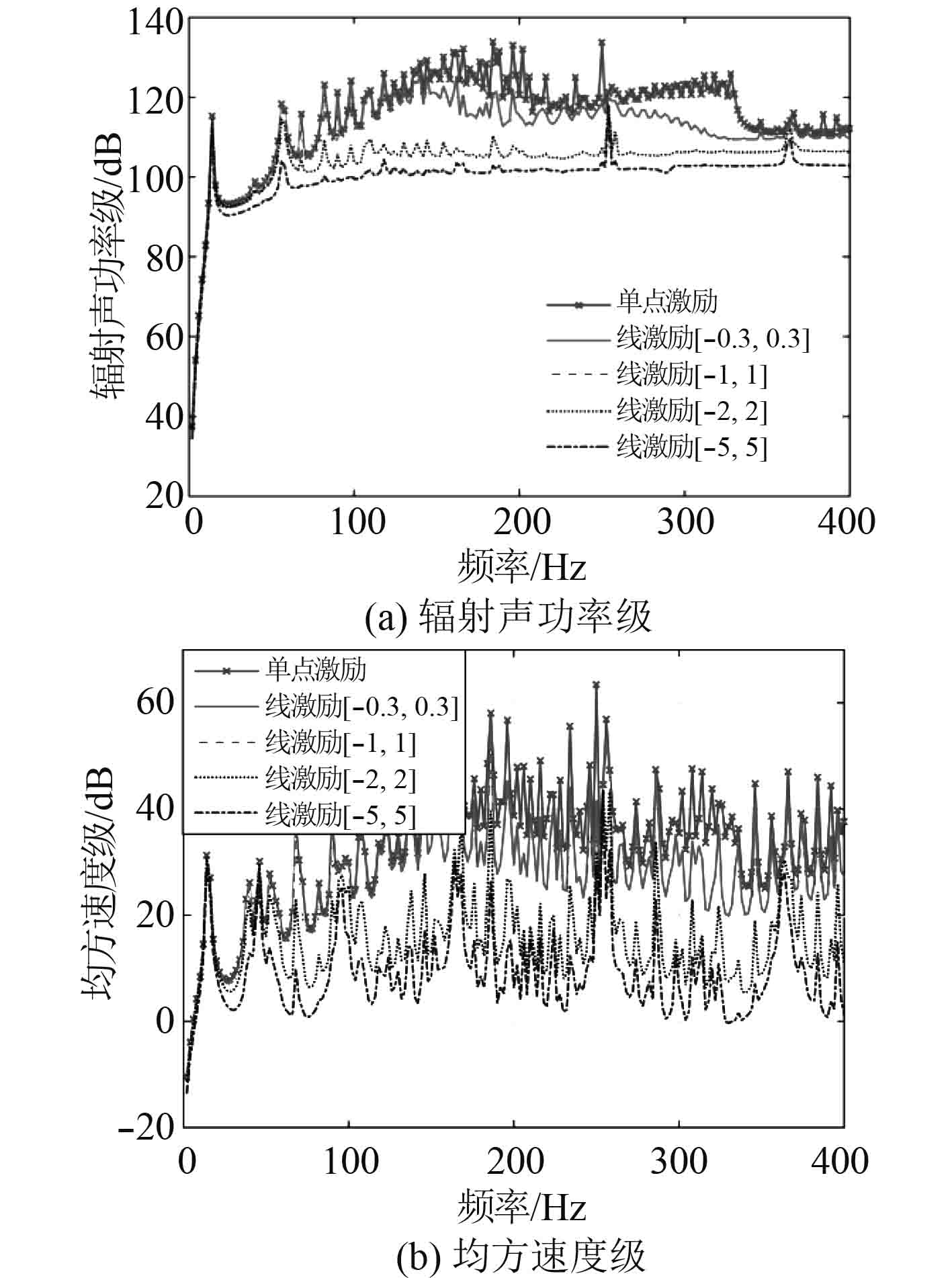
|
图 3 线激励下加肋圆柱壳的振声特性 Fig. 3 The vibro-acoustic characteristics of stiffened cylindrical shells under single line force |
可以看出,与点激励相比,在同等大小力作用下,线激励可以明显降低圆柱壳结构辐射声功率和均方法向速度,而且线激励的作用范围越长,其减振降噪的效果越好,但是随着作用范围的增加,辐射声功率和均方法向速度降低的幅度变缓。
2.4 双线激励从2.3节的计算可知,线激励的作用范围在[−2 m, 2 m]时已经有较好的效果,而且再增加其作用范围,对降低圆柱壳的振动和声辐射效果也不是很明显,因此双线激励在z向的作用范围保持在[−2 m, 2 m]范围内,在轴向关于
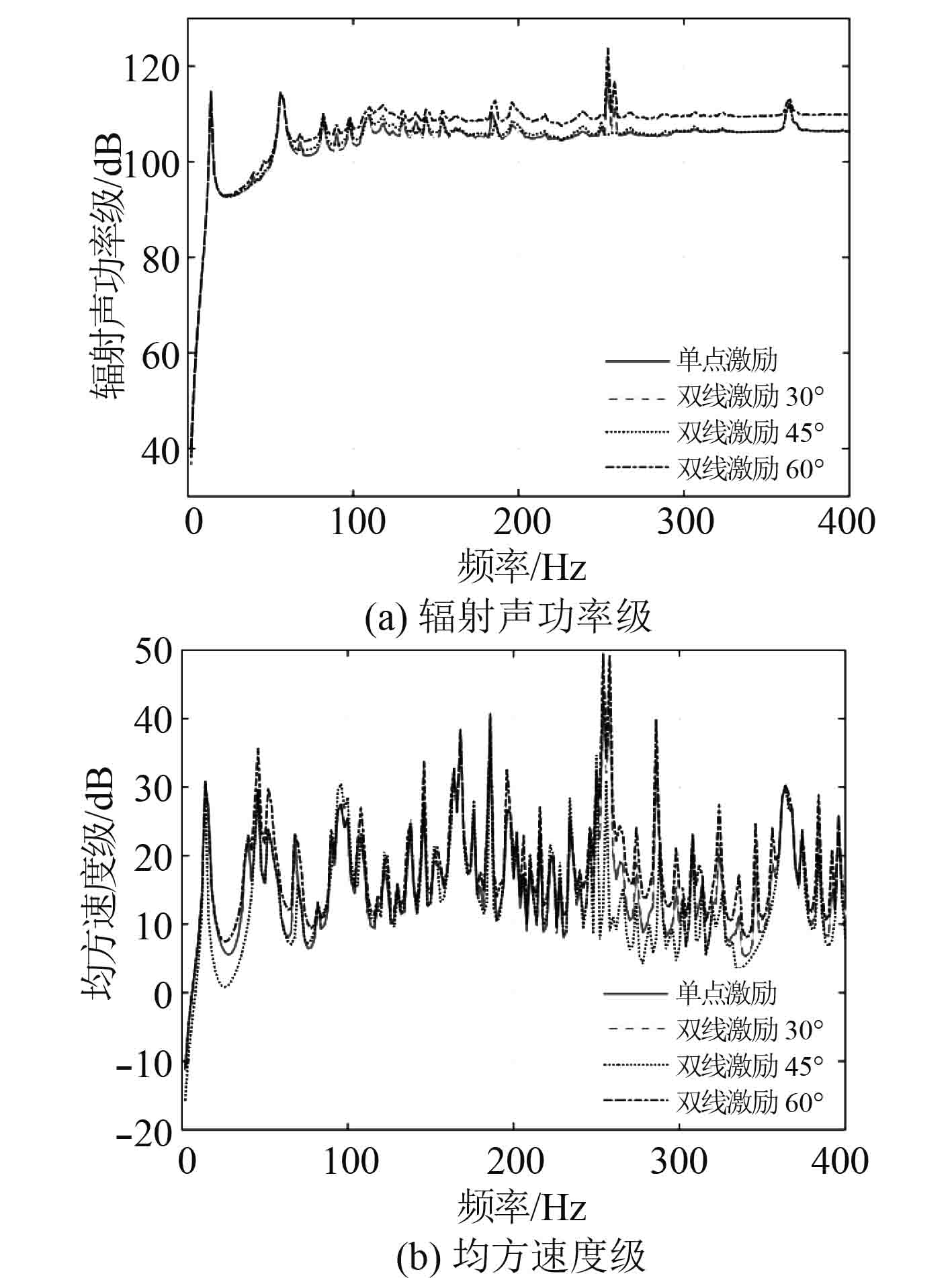
|
图 4 双线激励下加肋圆柱壳的振声特性 Fig. 4 The vibro-acoustic characteristics of stiffened cylindrical shells under double line force |
可以看出,当双线激励在周向分开的角度不大时,辐射声功率变化不大,均方速度会明显降低,其中
本文基于薄壳理论,采用模态展开法导出有限长加肋圆柱壳结构的近似解析解,并以圆柱壳结构的辐射声功率和均方法向速度为研究目标,研究单点激励在圆柱壳上不同位置、双点激励在圆柱壳上不同角度、线激励在圆柱壳上的作用范围、双线激励在在圆柱壳上不同角度等情况下对圆柱壳结构的振声特性的影响。主要结论如下:
1)单点激励对中高频的振声特性影响不大;在低频段,单点激励力向圆柱壳的边界靠近时,结构的辐射声功率和均方速度都会显著降低,并且越靠近界,降低的幅度变快。
2)在合力幅值相等的情况下,对称力(双点力、双线力)作用在适当的角度时可以有效的降低结构的均方法向速度;而当两力分开的角度过大时,反而会增大结构的辐射噪声和均方速度。
3)与点激励相比,在同等大小的力作用下,线激励可以明显降低圆柱壳结构辐射声功率和均方法向速度,而且线激励的作用范围越长,其减振降噪的效果越好,但是随着作用范围的增加,辐射声功率和均方法向速度降低的幅度变缓。
| [1] |
C M LYNCH,J WOODHOUSE,R S LANGLEY. Sound radiation from point-driven shell structures[J]. Journal of sound and Vibration, 2013, 332(26): 7089-7098. DOI:10.1016/j.jsv.2013.08.044 |
| [2] |
FILIPPOV S B. Asymptotic and numerical analysis of free low-frequency ring-stiffened shells vibrations[J]. Procedia Engineering, 2017, 199: 342-347. DOI:10.1016/j.proeng.2017.09.027 |
| [3] |
陈美霞, 谢坤, 魏建辉. 带框架肋骨圆柱壳振动特性分析[J]. 华中科技大学学报(自然科学版), 2014, 42(3): 127-132. CHEN Meixia, XIE Kun,WEI Jianhui. Vibration characteristics analysis of cylinder shell with frame rib[J]. J. Huazhong Univ. of Sci. & Tech. (Natural Science Edition), 2014, 42(3): 127-132. |
| [4] |
张波, 向阳, 李飞. 加筋圆柱壳声辐射特性研究及声学优化设计[J]. 噪声与振动控制, 2017, 37(3): 31-36. ZHANG Bo,XIANG Yang,LI Fei. Research of Sound Radiation Characteristics of A Stiffened Cylindrical Shell and Its Acoustic Optimal Design[J]. Noise and Vibration Control, 2017, 37(3): 31-36. DOI:10.3969/j.issn.1006-1355.2017.03.006 |
| [5] |
SUN Yao, YANG Tiejun, CHEN Yuehua. Sound radiation modes of cylindrical surfaces and their application to vibro-acoustics analysis of cylindrical shells[J]. Journal of Sound and Vibration, 2018, 424: 64-77. DOI:10.1016/j.jsv.2018.03.004 |
| [6] |
ZHANG Yilin,WU haijun,JIANG Weikang. Prediction of sound radiation from submerged cylindrical shell structure with an interpolation method for the measured surface velocity[J]. Advances in Acoustics and Vibration, 2017, 5: 35-41. |
| [7] |
ALZAHABI B, ALMIC E. Sound radiation of cylindrical shells[J]. International Journal of Multiphysics, 2016, 5(2). |
| [8] |
JUNGER M C, FEIT D. Sound stucture and their interaction[M].The MIT Press, 1986.
|
| [9] |
汤渭霖, 何兵蓉. 水中有限长加肋圆柱壳体结构振动和声辐射近似解析解[J]. 声学学报, 2001, 26(1): 1-5. TANG Weilin,HE Bingrong. Approximate Analytic Solution of Vibration and Sound Radiation from Stiffened Finite Cylindrical Shell in Water[J]. Acta Acustica, 2001, 26(1): 1-5. DOI:10.3321/j.issn:0371-0025.2001.01.001 |
| [10] |
陈明, 王斌, 曹为午. 水下复杂壳体结构在多源激励下的振动及声辐射特性研究[J]. 声学学报, 2009, 34(6): 498-505. CHEN Ming,WANG Bin,CAO Weiwu. Research on vibration and acoustic radiation of the submerged complicated shell structure with multiple excitations[J]. Acta Acustica, 2009, 34(6): 498-505. DOI:10.3321/j.issn:0371-0025.2009.06.003 |
 2020, Vol. 42
2020, Vol. 42
