2. 华中科技大学 船舶与海洋工程学院,湖北 武汉 430074
2. School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
潜艇操纵性是潜艇重要的综合航行性能之一,对于潜艇迅速占据有利阵地发动攻击,以及攻击后能快速机动撤离战场具有重要的意义,直接体现了潜艇的机动能力和作战能力。因此,如何从设计上保证潜艇自身具有良好的操纵性,并能对其性能进行准确的预报与评估显得尤为重要。第25届ITTC操纵性委员会的会议报告[1]将迄今为止的操纵性预报方法大致分为3类:非模拟法、基于系统的操纵性模拟、基于CFD的操纵性模拟。目前所有的预报方法都可归为这3类或者它们的结合。
关于潜艇操纵性的研究也发展迅速,尤其是基于CFD的操纵性预报受到了国内外研究机构的关注,研究的重点从基于水动力导数的数学模型逐渐转移到基于粘流理论的直接数值模拟,深入到复杂操纵下潜艇的六自由度运动规律和精细流场特性。目前基于CFD的操纵性预报主要有2种方式:一是基于CFD的间接预报,即运用势流或粘性流方法数值模拟约束模型试验从而计算得到潜艇运动方程中的水动力导数;二是基于CFD的直接预报,即通过CFD数值模拟联立求解潜艇操纵运动方程和流体控制方程,从而实现对实艇或自由自航模型在各种机动方式下操纵性能的直接预报。相比传统预报方式,基于CFD的操纵性预报具有以下无可比拟的优势:首先,CFD方法无需加工实体模型只需在计算机上建立数值模型,方便多方案的艇型优化设计,且省时省力;其次,CFD技术可以对模型试验难以实现的流体环境进行模拟,且可借助可视化技术方便地获取流场的细节信息;最后,随着计算技术和硬件的发展,为避免“尺度效应”的影响,将CFD方法直接应用于实艇的操纵性能预报已成为可能。
1 基于CFD的间接预报CFD技术在潜艇操纵性预报方面,首先在相对简单的约束模型试验的数值模拟上得到大量应用[2-4]。潜艇的操纵运动会形成诸如翼梢涡、马蹄涡等复杂的三维流动现象,流场特征包括沿凸面的停滞和边界层分离。潜艇运动产生的自由涡片卷起形成一对流向体涡,随着流体入射角的增加,体涡对的轨迹和强度导致升力的非线性增加。因此,要准确预测运动潜艇周围的流场及由此产生的流体动力对于CFD而言依然是一项具有挑战的工作。
1.1 静态约束模试验模拟通过斜航试验等静态约束模试验的数值模拟获得水动力导数已经被广泛认可,大量的工作被投入到如何获得更真实流场的研究中,通常认为湍流模型的选择至关重要:常用的RANS(Reynolds-Averaged-Navier-Stokes)模型,特别是两方程混合k–ε/k–ω模型的阻力预测结果已经能够达到一般的工程精度要求,然而它们不能准确预测平均涡和湍流结构,各向异性的LES(large eddy simulation)模型或者混合了RANS和LES的DES(detached-Eddy-Simulation)模型在预测这些特征方面比线性模型有所改进[5],但同时也意味着更高的网格和求解时间要求。
Watt G.D等[6]评估了商业软件Ansys CFX对裸艇体在偏航18°时的流场预报能力,并对比了不同RANS模型的适用性;Sung-Eun Kim等[7]开展了DARPA Suboff模型处于有漂角回转过程剪切流的高精度RANS仿真研究,文中对2种不同的k–ω湍流模型进行了分析,指出Wilcox′ k–ω模型能更好的再现如横流分离、流向涡及作用于物体上的合力和力矩等流动显著特征。Toxopeus S.L[8]介绍了潜艇水动力工作组对裸艇体Suboff模型展开的一次联合CFD研究工作,在研究中使用了不同的商业软件如Fluent,CFX和定制流求解器OpenFOAM,ReFRESCO,结合不同的湍流模型和网格拓扑结构对Suboff模型处于定常回转状态时的流场、力及力矩进行了模拟计算。Phillips A.B等[9]强调了网格收敛和湍流闭合模型对DOR潜艇模型在入射角15°时所经历的横流诱发体涡的强度和轨迹的重要性。文中讨论了5种不同湍流闭合模型的影响,指出SSG Reynolds应力模型在预测旋涡运动轨迹和强度具有潜力。柏铁朝等[10]则针对Suboff模型在不同漂角(攻角)情况下的流动进行了数值模拟,通过与试验结果的比对,讨论了6种不同湍流模型的计算精度与适用范围。
Toxopeus S.L[11]从网格划分、不确定度分析、敏感度分析等方面对Suboff潜艇模型直航及偏航时的流场计算进行了详细讨论,Vaz. G等[12]分别采用MARIN开发的有限体积求解器ReFRESCO和有限元商用求解器AcuSolve对裸艇体及全附体Suboff模型在不同漂角时的流场进行了数值计算,并与试验结果进行了验证。文中还研究了不同湍流模型的影响,并将用RANS方法得到的结果与理论上更真实的DDES结果进行了比较。C.Fureby等[13]利用RANS和LES方法对全附体DSTO通用潜艇模型在直航条件下和偏航10°时的流场进行了数值模拟,其中,LES计算使用OpenFOAM开发的不可压缩LES流求解器和利用基于贴片的方法生成的非结构四面体网格来执行,以提高近壁的分辨率和对附体尾迹的任意细化,模型尺度的网格划分多达3.4亿个单元。计算结果与低速风洞的实验结果进行了比较。
Boger D等[14]采用RANS方法结合重叠网格技术对Suboff模型及外形更复杂的ONR Body-1潜艇模型直航及偏航情况进行了预报,并与实验结果吻合良好。S. Zaghi等[15]则利用动态重叠网格技术解决了全附体潜艇在偏转不同舵角时准确描述附体边界层内流动的问题,并给出了计算舵角导数的示例。孙铭泽等[16]讨论了潜艇操纵性水动力系数数值计算中尺度效应问题,采用虚流体粘度和基于网格变形的动网格技术方法计算了不同量级雷诺数下潜艇的水动力系数,分析了潜艇操纵性水动力计算中雷诺数的影响。J.T. Zhang等[17]利用RANS方法结合一种新的混合网格方案,通过网格细化来精确求解近场粘性流动特征。针对DRDC STR,Suboff和Series 58潜艇模型在相对回转半径1~10、漂角1°~17°时的稳定回转运动进行了计算,并通过已有的试验结果进行了验证。A.G.L. Holloway等[18]则着重讨论了上述3种细长回转体潜艇模型在稳定转弯时的流动分离问题。通过不同雷诺数条件的仿真,利用推导的沿中体和尾部分离发展的尺度规律,建立预测任意轮廓旋转体分离线的分析模型。
1.2 动态约束模试验模拟PMM试验能测得操纵性预报所需的大量水动力系数,在潜艇模型试验中占有重要地位。对纯横荡、纯首摇、纯俯仰等试验的模拟要求预报出整个动态操纵运动过程中的潜艇水动力变化,只能以动态的方式进行,因此对数值计算提出了更高的要求。国际上针对此类约束模试验有大量的标模试验数据,为CFD数值模拟预报方法的验证和应用提供了依据。
Mustafa Can[19]对DARPA Suboff及Autosub AUV两种水下模型开展了全面的水池拖曳试验、悬臂水池试验及PMM试验,并以此对商业软件Fluent数值仿真算法的精度进行了验证。B.J.Racine等[20]为解决潜艇方案设计阶段操纵性预报的问题首先对潜艇六自由度运动方程中水动力系数的敏感性进行了分析,并利用RANS方法对主要的水动力系数开展了数值仿真。随后对通过理论和经验公式得到的水动力系数与通过CFD计算得到的水动力系数分别代入潜艇运动方程对NNEMO潜艇模型进行了操纵性预报对比。文中指出,该方法虽然目前尚未得到验证,但不失为一种评估NNEMO等新概念潜艇稳定性和机动特性的可行方法。潘雨村等[21]利用RANS方法对Suboff模型的斜航拖曳试验及PMM试验(纯横荡、纯垂荡、纯首摇、纯俯仰)进行了数值仿真,并与试验结果进行了对比;在对悬臂水池试验的数值模拟中还开展了验证与确认(verification and validation,V&V)研究[22]。肖昌润等[23]通过Mesh Motion方法和基于源项法旋臂试验对全附体Suboff模型进行了回转运动仿真,通过与试验结果的对比,分析了RNG k-ε与SST k-ω两种湍流模型的计算精度和时间。曹留帅等[24]也对相同的问题进行了研究,并且基于相同的网格拓扑对偏航和定常回转进行了仿真[25]。
总的来讲,对于潜艇操纵性运动方程中的水动力系数的CFD数值仿真计算逐渐趋于成熟,某些系数与实验数据的比对已经达到了工程可接受的范围。对于大偏(攻)角及强机动产生的非线性水动力流场的计算精度还有待进一步提高,重点可在湍流模型的选择及CFD的不确定度分析上深入研究,形成一套适用于工程的标准计算流程。
2 基于CFD的直接预报 2.1 操纵运动实现基于粘性流的操纵性数值模拟通常使用RANS方法结合刚体六自由度运动方程实现艇体运动仿真。但在潜艇的实际操纵运动中难以避免地存在艇、桨、舵的分级运动,因此使用CFD方法进行直接模拟时必须解决各个部件之间的耦合运动问题。在当前研究中,动网格、滑移网格、重叠网格等技术都能在不同程度上实现网格的相对运动,其中动网格方法中一般的网格光顺变形只适用局部小幅运动,而网格重构对运动后的网格进行重新划分,理论上可以解决所有网格运动问题,但计算代价高昂,且易产生负体积,在操纵性模拟中应用较少。
滑移网格方法将求解域划分为几个相对运动的区域,区域与区域之间通过交界面进行信息传递,在螺旋桨网格运动求解中应用广泛,但这种方法只适用于区域运动,在直接操纵运动模拟中一般仅用于实现螺旋桨、舵等的旋转运动。G. Venkatesan等[26]用STAR-CCM+对ONR Body 1潜艇模型的定深回转及水平面的超越机动进行了模拟仿真,计算与实验结果吻合较好。其采用的方法也是URANS方法结合六自由度运动,螺旋桨和控制面的运动则通过集成到求解过程的滑移网格进行计算。M M Amiri等[27]则利用STAR-CCM+对SUBOFF潜艇在不同水深、不同航速下直航运动时自由面对潜艇阻力、升力及力矩的影响进行了分析,文中指出自由面对近水面航行潜艇的力学特性影响显著。Bettle M[28]在其博士论文中运用URANS结合六自由度方程的方法对潜艇应急上浮、潜艇与水面通过油轮之间相互作用等问题进行了数值模拟。潜艇运动通过一种鲁棒的预测器-校正器方法隐式积分得到,该方法使用半经验和基于系数的模型来加速每个时间步的收敛。滑移界面和网格变形的组合被用来计算油轮和潜艇之间的相对运动。模拟结果再现了应急上浮潜艇所观测到的横摇不稳定性,并提供了大型油轮越过柴-电潜艇时所产生的扰动力及潜艇运动的大小。
重叠网格通过对物体的各个部件单独划分网格,然后将各个部件网格嵌入到背景网格中,经过挖洞等预处理将计算域之外的网格(如艇体内部的网格)排除在计算之外,然后对剩余重叠区域的网格建立插值关系,以达到对整个计算域的求解。动态重叠网格方法在每一步计算中重新检测重叠区域并进行插值计算,因其更灵活的网格生成方式、更大的运动实现范围、更高的网格质量保证、利于并行计算的分区特性,在自航操纵运动数值模拟研究中得到了最广泛的应用。借助重叠网格技术,基于粘性流RANS方法结合刚体六自由度运动方程对潜艇的操纵运动进行直接数值预报已经涌现了不少的成果。J. E. Poremba[29]在其硕士论文中利用宾夕法尼亚州应用研究实验室自主开发的程序REL-TCURS对带X舵NNEMO1潜艇模型(见图1)的水动力和运动进行了数值模拟。该程序也是采用URANS结合六自由度运动的方法,附体网格与主艇体网格之间的重叠使用商业软件SUGGAR完成。文中分别对X舵偏转10°,20°和30°时(首舵为0)的回转工况进行CFD模拟分析,并与模型湖试结果进行了比对。虽然由于初始条件和潜艇质量特性的不确定性导致刚体动力学的某些细节与实验模型存在差异,但REL-TCURS求解器模拟了模型实验中所见的横滚不稳定性,并指出这种不稳定性是由于围壳与操纵面之间的相互作用产生的。

|
图 1 NNEMO1潜艇模型 Fig. 1 NNEMO1 submarine model |
Esmaeilpour M等[30]提出了一种预测舰船近场密度分层流的方法。该方法对自由表面采用单相水平集方法,采用动态重叠技术来处理运动和控制器以实现自航和机动,密度采用耦合动量和质量守恒的高阶传输方程求解,同时采用基于k−ε/k-ω的DDES方法实现湍流。文中采用该方法对自由自航水面船和潜艇的分层流动进行了研究。结果表明,与表面波的情况一样,内波的产生需要的能量导致阻力增加。此外,与固体/液自由表面流动一样,密度交界面的存在导致船体边界层加厚。
王支林等[31]、江伟健等[32]利用基于粘性流自主开发的程序求解URANS方程,采用动态重叠网格技术结合六自由度运动方程对Suboff潜艇分别在遭遇海流和规则横浪情况下的应急上浮运动进行了数值仿真研究。冯大奎等[33]采用同样的求解器数值方法对带十字舵和X舵2种不同尾操纵面Suboff潜艇的操纵性能进行了数值仿真研究,结果表明,相同航速及舵角情况下,定常回转直径X舵比十字舵减少了20%。
2.2 推进模拟方法如何实现潜艇的自航推进是潜艇操纵运动数值模拟的一大难题,从现有的研究来看,对螺旋桨的模拟大致可以分为体积力法和实桨建模法两大类。
体积力法不对螺旋桨进行离散化,而是在螺旋桨占据空间内,在动量中附加一体积力源项,显著减小了网格量,降低了时间步长要求,应用广泛。Howan Kim等[34]利用CFD商业软件STAR-CCM+对Joubert BB2潜艇模型(见图2)进行了直航和20°及30°舵角下定常转弯机动的模拟,与实验数据吻合较好,其中螺旋桨的推力是用拟合了真实螺旋桨特性的体积力代替。J. E. Poremba[35]在对带X舵NNEMO1潜艇模型的水动力和运动模拟中对控制面及推进器均采用体积力模型代替,代码的有效性经过了相关实验的验证。

|
图 2 Joubert BB2潜艇模型 Fig. 2 Joubert BB2 submarine model |
实桨建模法依据螺旋桨几何模型划分网格,其网格运动通常使用滑移网格或重叠网格实现,但螺旋桨的运动计算通常需要较高的空间和时间分辨率,其与艇体的总网格量很容易达到上千万,将其应用于物理时间尺度较大的操纵运动模拟中时需要非常长的求解时间。尽管如此,由于直接建模法更精确和真实的流场描述,仍有大量关于实桨建模法的研究。M. Liefvendahl等[36]为了捕捉大尺度非定常相干结构的流动,使用LES模型和动网格技术对全附体Suboff潜艇带E1619标准螺旋桨自航时的水动力及载荷波动进行了仿真分析,并将计算结果分别与艇体(不带桨)及敞水桨的结果进行了比较。Nathan Chase[37-38]利用CFDShip-Iowa V4.5流体求解器对全附体Suboff潜艇带E1619标准螺旋桨自航的数值仿真问题进行了研究,采用2套网格计算得到螺旋桨高和中低载荷进速系数下的敞水曲线,并与现有的实验数据进行了比较,尾流速度在J=0.74时与实验数据吻合良好;对进速系数J=0.71时采用4套不同的网格及3个不同时间步长的仿真验证表明,网格细化对推力和扭矩影响很小,但对尾流影响很大;通过采用RANS,DES,DDES以及无湍流模型4种情况对螺旋桨在J=0.4时仿真计算研究了湍流模型对尾流的影响,结果表明,RANS方法中尾流过快消失,而无湍流模型时桨叶梢涡很快变得不稳定。
Martin J. E等[39]介绍了2种方法对无线电控制潜艇模型ONR Body 1在2个相近速度下的水平面超越机动及高速下的垂直面超越机动和回转机动的数值模拟问题。在直接模拟方法中,舵、尾平面和螺旋桨被网格化,并使用动态重叠技术作为移动对象;第2种方法将CFD求解器与势流螺旋桨程序耦合,2个程序在螺旋桨平面和尾迹处交换速度、艇体受力和螺旋桨力和力矩。结果表明:
1)2种CFD方法都可以重现所有参数的实验结果,且误差通常在10%以内;
2)2种方法对螺旋桨敞水性能的仿真表明耦合方法能够很好地匹配;
3)由于允许比直接模拟方法大一个数量级的时间步长,耦合方法运行时间大约快5倍,且推进系数的范围与设计点相差不大,使得耦合方法成为标准机动仿真的有效选择。同时指出,由于螺旋桨直接模拟可以解决桨叶涡结构,因此耦合方法的缺点是尾流中分辨率会部分损失。
2.3 潜艇操纵运动数值仿真验证目前,基于CFD的直接预报方面正在进行着大量的数值模拟结果可靠性和准确性的验证,验证内容包括局部流场特性、操纵运动指标与自航模或实船试验结果的比对等。较多验证通过对回转运动的模拟进行,大部分计算结果在宏观指标上与实验数据显示出较好的一致性。
Carrica P.M等[40]介绍了Joubert BB2通用潜艇模型在自由自航条件下的数值仿真和实验工作。在荷兰MARINE水池开展的自航模实验包括:近自由面及深水中的自航、回转,水平面及垂直面的ZigZag机动,以及应急上浮。实验中采用自动舵来控制垂直面的俯仰和深度以及水平面的偏航和横荡。文中使用2个不同的代码(非结构化的ReFRESCO程序,结构化重叠的REX程序)对实验工况进行了数值模拟计算,结果表明,CFD对自航因子预报误差在5%以内,对潜艇模型在自由自航条件下的运动和速度均能较好的预测,但实验中自动舵的控制指令难以复制。同时,潜艇在近水面的自航及应急上浮的数值计算与实验结果吻合良好,显示了使用CFD对潜艇在潜望镜深度的操作进行模拟的能力。
R. Broglia等[41]分析了承压水对潜艇操纵能力的影响。采用基于RANS的数值模拟方法分析了潜艇在零和非零偏航/俯仰角、开阔水域、靠近底部和靠近自由水面条件下,在直线上以恒定速度运动的情况。其中,对不可压缩湍流自由表面流动的数值模拟采用INSEAN开发的2阶有限体积求解器进行。从速度场和压力场的角度描述了潜艇绕流的特征,给出了计算得到的力和力矩系数,并与INSEAN的实验数据进行了比较。该项工作是WEAO支持的欧洲研究项目的一部分,其目标是提高潜艇在受限水域操纵的数值预报方法,提供在承压水中潜艇操纵的实验数据库,验证接近边界的物体上的力和力矩的CFD预报。
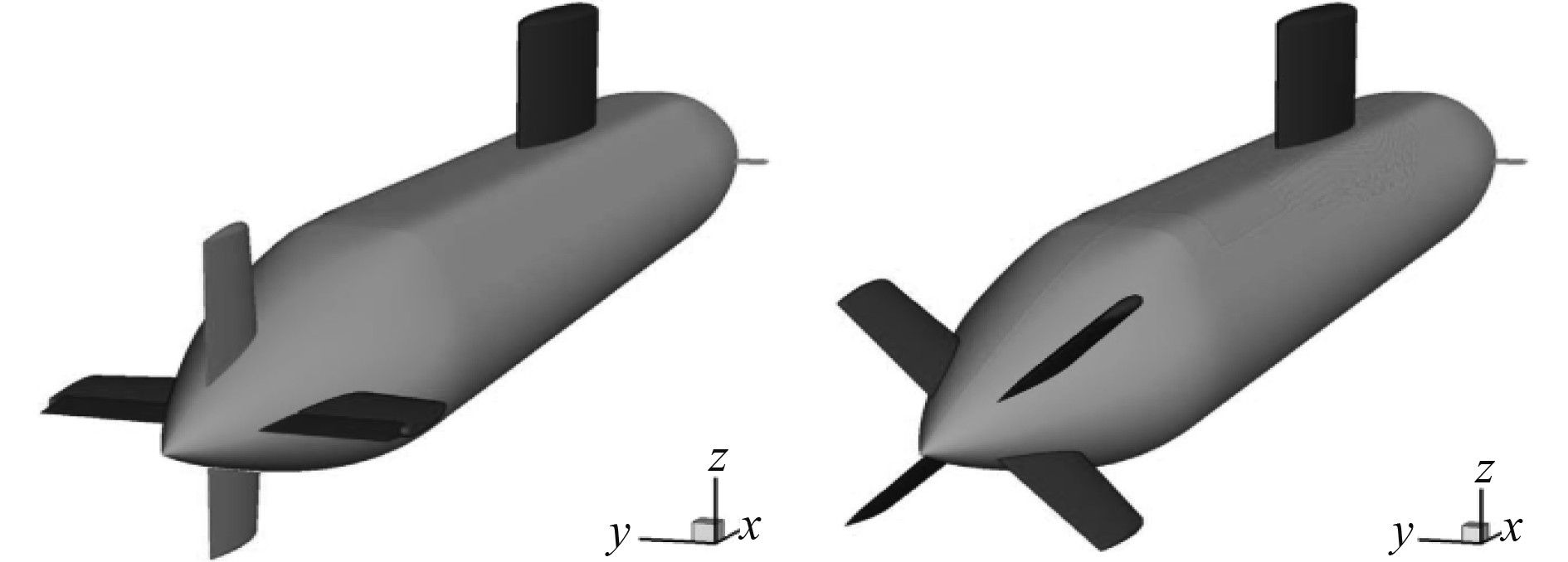
G. Dubbioso等[42]利用自主开发的软件对带十字舵和X舵的CNR-INSEAN 2475两种潜艇模型(见图3)在无限水深及靠近自由面情况下的三自由度水平面转舵回转运动进行了数值仿真研究。计算结果部分为十字舵潜艇的实验数据所验证。结果表明,X舵相对十字舵而言具有更优越的回转性能。文中还重点研究了网格细化对机动载荷和模型动态响应的影响。分析表明,至少对于论文所研究的对象和实验工况而言,较少的网格(几百万个网格点的数量级)也能对潜艇运动轨迹和运动参数进行可靠的预测,但水动力载荷估计则不够准确。
|
图 3 CNR-INSEAN 2475潜艇模型 Fig. 3 CNR-INSEAN 2475 submarine model |
总体来讲,由于潜艇操纵性研究中越来越高的精度要求,以及CFD方法具有的低成本、短周期、高信息量等独特优势,采用CFD结合潜艇六自由度运动方程的方法对潜艇的操纵运动直接进行数值仿真研究的工作已成为该领域目前研究的热点,采用CFD技术对潜艇操纵性能直接进行数值预报在现有的条件下已成为可能。从国内外操纵性研究动态和实际需求分析,系统的数值模拟结果验证与确认仍将是很长一段时间内潜艇操纵性直接预报研究的重点,而随着CFD直接预报技术的逐渐成熟,以下方向可能成为未来的研究热点:
1)实尺度模型的操纵性预报方法与尺度效应分析;
2)实桨推进的操纵性预报与适用于大幅机动的体积力模型;
3)基于LES,DES等非RANS方法的更精确的操纵性预报;
4)下一代高性能并行计算集群的利用与更快速的操纵性预报数值方法;
5)非常规艇型与近水面等特殊环境中的潜艇操纵性预报。
可以预见,随着计算机能力的不断增强及CFD技术的不断发展,基于CFD的直接预报方法将会逐渐替代其他方法成为潜艇设计优化及操纵性能预报的主流。
| [1] |
The Manoeuvring Committee Final Report and Recommendations: 25th International Towing Tank Conference (ITTC) [C]// 2008.
|
| [2] |
MARTIN Renilson. Submarine Hydrodynamics[M]. Springer International Publishing, 2015.
|
| [3] |
MARSHALLSAY P.G., ERIKSSON A.M. Use of computational fluid dynamics as a tool to assess the hydrodynamic performance of a submarine[C]// 18th Australasion Fluid Mechanics Conference, Launceston, Australia, 2012.
|
| [4] |
潘子英, 吴宝山, 沈泓萃. CFD在潜艇操纵性水动力工程预报中的应用研究[J]. 船舶力学, 2004, 8(5): 42-51. DOI:10.3969/j.issn.1007-7294.2004.05.006 |
| [5] |
STERN F, YANG Jianming, et al. Computational ship hydrodynamics: Nowadays and way forward[J]. International Shipbuilding Progress, 2013, 60: 3-105. |
| [6] |
WATT G.D, BAKER C.R, GERBER A.G. ANSYS CFX-10 RANS normal force predictions for the Series 58 Model 4621 unappended axisymmetric submarine hull in translation[R]. DRDC Atlantic TM 2006-037, Canada, 2006.
|
| [7] |
SUNG-EUN Kim, BONG Jae Rhee, RONALD W. Miller. Anatomy of turbulent flow around DARPA SUBOFF body in a turning maneuver using high-fidelity RANS computations[J]. International Shipbuilding Progress, 2013, 60: 207-231. |
| [8] |
TOXOPEUS S.L., ATSAVAPRANEE P., et al. Collaborative CFD exercise for a submarine in a steady turn[C]// Proceedings of the ASME 31st International Conference on Ocean, Offshore and Arctic Engineering, Rio de Janeiro, Brazil, 2012.
|
| [9] |
PHILLIPS A B, TURNOCK S R, FURLONG M. Influence of turbulence closure models on the vortical flow field around a submarine body undergoing steady drift[J]. Journal of Marine Science and Technology, 2010, 15(3): 201-217. DOI:10.1007/s00773-010-0090-1 |
| [10] |
柏铁朝, 梁中刚, 周轶美, 等. 潜艇操纵性水动力数值计算中湍流模式的比较与运用[J]. 中国舰船研究, 2010, 2: 22-28. DOI:10.3969/j.issn.1673-3185.2010.05.005 |
| [11] |
TOXOPEUS, S.L. Viscous-flow calculations for bare hull DARPA SUBOFF submarine at incidence[J]. International Shipbuilding Progress, 2008, 55(3): 227-251. |
| [12] |
VAZ. G., TOXOPEUS S.L., HOLMES, S. Calculation of manoeuvring forces on submarines using two viscous-flow solvers[C]// 29th International Conference on Ocean, Offshore and Arctic Engineering, Shanghai, China, 2010, 621-633.
|
| [13] |
FUREBY C, ANDERSON B, CLARKE D, et al. Experimental and numerical study of a generic conventional submarine at 10° yaw[J]. Ocean Engineering, 2016, 116: 1-20. DOI:10.1016/j.oceaneng.2016.01.001 |
| [14] |
BOGER D, DREYER J. Prediction of hydrodynamic forces and moments for underwater vehicles using overset grids[C]. Proc 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nevada, USA, 2006: 9-12.
|
| [15] |
ZAGHI S, Di MASCIO A, BROGLIA R, et al. Application of dynamic overlapping grids to the simulation of the flow around a fully-appended submarine[J]. Mathematics and Computers in Simulation, 2015, 116: 75-88. DOI:10.1016/j.matcom.2014.11.003 |
| [16] |
孙铭泽, 王永生, 杨琼方. 潜艇操纵性数值模拟中雷诺数的影响分析[J]. 哈尔滨工程大学学报, 2012, 11: 1334-1340. |
| [17] |
ZHANG J.T., MAXWELL J A, et al. Simulation of the flow over axisymmetric submarine hulls in steady turning[J]. Ocean Engineering, 2013, 57: 180-196. DOI:10.1016/j.oceaneng.2012.09.016 |
| [18] |
HOLLOWAY A.G.L., JEANS T.L., WATT G.D.. Flow separation from submarine shaped bodies of revolution in steady turning[J]. Ocean Engineering, 2015, 108: 426-438. DOI:10.1016/j.oceaneng.2015.07.052 |
| [19] |
MUSTAFA C. Numerical simulation of hydrodynamic planar motion mechanism test for underwater vehicles numerical[M]. Middle East Technical University, Turkey, 2014.
|
| [20] |
RACINE, B.J. PATERSON E.G.. CFD-based method for simulation of marine vehicle maneuvering[C]// 35th AIAA Fluid Dynamics Conference and Exhibit, Toronto, Ontario, Canada, 2005.
|
| [21] |
PAN Yucun, ZHANG Huaixin, ZHOU Qidou. Numerical prediction of submarine hydrodynamic coefficients using CFD simulation[J]. Journal of Hydrodynamics, 2012, 24(6): 840-847. DOI:10.1016/S1001-6058(11)60311-9 |
| [22] |
Yucun PAN, Qidou ZHOU, Huaixin ZHANG. Numerical simulation of rotating arm test for prediction of submarine rotary derivatives[J]. Journal of Hydrodynamics, 2015, 27(1): 68-75. DOI:10.1016/S1001-6058(15)60457-7 |
| [23] |
肖昌润, 刘瑞杰, 许可, 等. 潜艇旋臂回转试验数值模拟[J]. 江苏科技大学学报(自然科学版), 2014, 4: 313-316. |
| [24] | |
| [25] |
CAO Liushuai, ZHU Jun, ZENG Guanghui. Viscous-flow calculations of submarine maneuvering hydrodynamic coefficients and flow field based on same grid topology[J]. Journal of Applied Fluid Mechanics, 2016, 9(2): 817-826. DOI:10.18869/acadpub.jafm.68.225.24570 |
| [26] |
VENKATESAN G., CLARK W. . Submarine maneuvering simulations of ONR Body 1[C]// In Proceedings of the International Conference on Offshore Mechanics and Arctic Engineering OMAE, San Diego, California, USA, 2007.
|
| [27] |
AMIRI M. M., ESPERANCA P. T., VITOLA M. A., et al. How does the free surface affect the hydrodynamics of a shallowly submerged submarine?[J]. Applied Ocean Research, 2018, 76: 34-50. DOI:10.1016/j.apor.2018.04.008 |
| [28] |
BETTLE, M. Unsteady computational fluid dynamics simulations of six degrees of freedom submarine manoeuvres[D]. University of New Brunswick, Canada, 2013.
|
| [29] |
POREMBA J. E.. Hydrodynamics and maneuvering simulations of a non-body-of-revolution submarine[M]. The Pennsylvania State University, 2009.
|
| [30] |
ESMAEILPOUR M, MARTIN J. E, CARRICA P.M.. Near-field flow of submarines and ships advancing in a stable stratified fluid[J]. Ocean Engineering, 2016, 123: 75-95. DOI:10.1016/j.oceaneng.2016.06.038 |
| [31] |
WANG Zhilin, DONG Zhenwei, HE Ran, et al. Numerical simulation of submarine surfacing with 6 DOF model in the ocean current effect[C]// 26th International Ocean and Polar Engineering Conference, Gold Coast, Australia, 2016.
|
| [32] |
JIANG Weijian, WANG Zhilin, HE Ran, et al, Dakui FENG. Numerical simulation of submarine surfacing with six degrees of freedom in regular waves[C]// Proceedings of the ASME.35th International Conference on Ocean Offshore and Arctic Engineering, Busan, South Korea, 2016.
|
| [33] |
FENG Dakui, CHEN Xuanshu, LIU Hao, et al. Comparisons of turning abilities of submarine with different rudder configurations[C]// Proceedings of the ASME 2018 37th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, 2018.
|
| [34] |
HOWAN Kim, DEV Ranmuthugala, et al. Six-DOF simulations of an underwater vehicle undergoing straight line and steady turning manoeuvres[J]. Ocean Engineering, 2018, 150: 102-112. DOI:10.1016/j.oceaneng.2017.12.048 |
| [35] |
POREMBA J. E.. Hydrodynamics and Maneuvering Simulations of a Non-Body-of-Revolution Submarine[M]. The Pennsylvania State University, 2009.
|
| [36] |
LIEFVENDAHL M., TROËNG C.. Simulation based analysis of the hydrodynamics and load fluctuations of a submarine propeller behind a fully appended submarine hull[C]// 29th Symposium on Naval Hydrodynamics, Gothenburg, Sweden, 2012.
|
| [37] |
NATHAN C.. Simulations of the DARPA Suboff submarine including self-propulsion with the E1619 propeller[R]. University of Iowa, USA, 2012.
|
| [38] |
NATHAN C., CARRICA P. M.. Submarine propeller computations and application to self-propulsion of DARPA suboff[J]. Ocean Engineering, 2013, 60: 68-80. DOI:10.1016/j.oceaneng.2012.12.029 |
| [39] |
MARTIN J. E, MICHAEL T, CARRICA P M. Submarine maneuvers using direct overset simulation of appendages and propeller and coupled CFD/potential flow propeller solver[J]. Journal of Ship Research, 2015, 59(1): 31-48. DOI:10.5957/JOSR.59.1.140053 |
| [40] |
CARRICA P.M., KERKVLIET M., et al. CFD simulations and experiments of a maneuvering generic submarine and prognosis for simulation of near surface operation[C]// 31st Symposium on Naval Hydrodynamics, Monterey, CA, 2016.
|
| [41] |
BROGLIA R., Di MASCIO A., MUSCARI R.. Numerical study of confined water effects on a self-propelled submarine in steady manoeuvres[J]. International Journal of Offshore and Polar Engineering, 2007, 17(2): 89-96. |
| [42] |
DUBBIOSO G., BROGLIA R., ZAGHI S.. CFD analysis of turning abilities of a submarine model[J]. Ocean Engineering, 2017, 129: 459-479. DOI:10.1016/j.oceaneng.2016.10.046 |
 2020, Vol. 42
2020, Vol. 42
