2. 潍柴动力股份有限公司 发动机研究院,山东 潍坊 261001;
3. 中国船级社秦皇岛分社,河北 秦皇岛 066002
2. Weichai Power Co., Ltd., Weifang 261001, China;
3. Qinhuangdao of China Classification Society, Qinhuangdao 066002, China
在无人驾驶船舶发展热潮下,智能船舶成为各大船舶科研院所研究的重点。其中,如何实现船舶动力装置的智能运行和智能维护保养是实现智能船舶的重要基础和前提。2015年中国船级社(CCS)颁布《智能船舶规范》中明确了“智能机舱(M)”为“智能船舶(iShip)”六大模块之一,随之颁布的《船舶智能机舱检验指南》客观上要求智能机舱系统能够实现对船舶动力装置的健康状态评估及状态预测,为轮机管理人员对机舱的维护保养工作提供参考,最终实现船舶机舱的视情维修。
对于远洋商船而言,实现对若干个船舶动力设备的健康状态评估是实现对完整船舶动力系统或动力装置状态评估的基础和前提。对具有重要特征参数和性能指标的船舶动力设备而言,目前实船应用性较强的状态评估方法是通过衡量实时参数与基线间的偏离程度获得评估值。所谓基线就是设备在规定条件下,完成规定功能时参数的理想值。但是船舶动力设备通常会受自身性能退化影响,参数会发生趋势性变化,但是若使用静止的、单一不变的基线作为设备性能退化后的评估基准,会导致评估值较低甚至误报警情况。然而在相当一段时间内,设备依然会完成规定功能,对系统的正常运行也不产生影响,因此需根据设备的性能退化程度制定相应的状态评估基准,即动态基线。
本研究以目标设备按性能退化时间序列采集的特征参数为研究对象,建立滑动概率神经网络,以滑动窗口为单位获取特征参数条件概率密度分布,进而获得连续窗口的概率密度曲线,设定基线限值,以超出限值的概率分布函数值作为设备性能退化各个阶段的性能可靠度,建立性能可靠度与基线值间的函数关系,实现性能可靠度向基线值的转换。在基线值变化趋势确定前提下,建立ARMA模型,对特征参数进行预测,结合退化基线计算方法实现对基线变化时间节点的预测,为实现船舶动力设备的状态预测具有重要意义。
1 退化基线计算方法 1.1 退化基线计算方法体系的建立基线理论的应用范围较为广泛,并且在某些领域中表示特定的术语[1-2]。在针对基线的方法研究与应用中,文献[3]提出运用序列设计质量检测方法建立了性能参考基线,实时监测磁共振成像设备的性能;文献[4]利用非线性最小二乘法和质量控制原则确定某系统CPU使用率的分布基线,以及时发现系统的潜在风险;文献[5]建立基线分析系统,可快速实现对统计报告中数据的趋势分析以及故障发现和故障预警,提高管理人员的运维水平;文献[6]提出基于支持向量机的改进时间序列预测方法获取关键绩效指标的实时性能监测基线;文献[7]建立合理的基线有限元模型来监测大跨度斜拉桥的结构性能以实现对大跨度斜拉桥的长期健康监测和状态评估。基线理论在轮机工程领域的应用较少,且大多集中在能效分析和氮氧化物的排放测试分析中[8-10]。本文利用基线的概念表示船舶动力设备性能退化过程中特征参数或性能指标的理想值,并称之为退化基线,它是评判设备性能状态变化程度的重要依据,科学合理的基线是实现船舶动力设备状态评估并获得健康评估值的基础。退化基线计算方法基本流程如图1所示。

|
图 1 退化基线计算方法流程图 Fig. 1 Degradation baseline calculate method |
基本步骤为:
步骤1 确定具有重要特征参数或性能指标的船舶动力设备作为目标对象。
步骤2 按性能退化时间序列采集目标对象的参数或指标并作为研究对象。
步骤3 建立滑动概率神经网络,并确定参数。
步骤4 将研究对象输入至滑动概率神经网络,获取目标对象随性能退化时间序列的性能可靠度。
步骤5 建立性能可靠度与基线值间的转换函数,获取目标对象随性能退化时间序列的动态退化基线。
1.2 滑动概率神经网络原理滑动概率神经网络[11]由滑动窗口与概率神经网络(PNN Probabilistic Neural Network)两部分组成。其中概率神经网络在1989年首先由D.F.Specht提出[12],该网络基于贝叶斯最优分类决策理论,并且能够实现概率密度函数的非参数估计,具有结构简单,收敛速度快,算法设计和训练容易,实时处理速度快,目前广泛应用于模式分类和早期故障诊断[13-15]。
滑动概率神经网络包含抽样层、样本层和求和层3层网络结构,如图2所示。其中抽样层由待分析数据区间的等间隔抽样点组成,按顺序排列,固定不变。样本层为测量数据序列,按顺序滑动进入网络。为了消除窗口内对数据分布模型的依赖性问题,可采用Parzen窗[16]进行非参数密度估计,也称核密度估计方法。此方法从样本序列自身出发,不需规定样本序列的概率分布,以加权平均中心点在样本值中的局部函数对未知密度进行估计,对任何形式的密度函数渐进逼近,可根据外界影响因素变化动态调整概率模型。求和层(输出层)是抽样集合在当前测量数据条件下的概率密度。
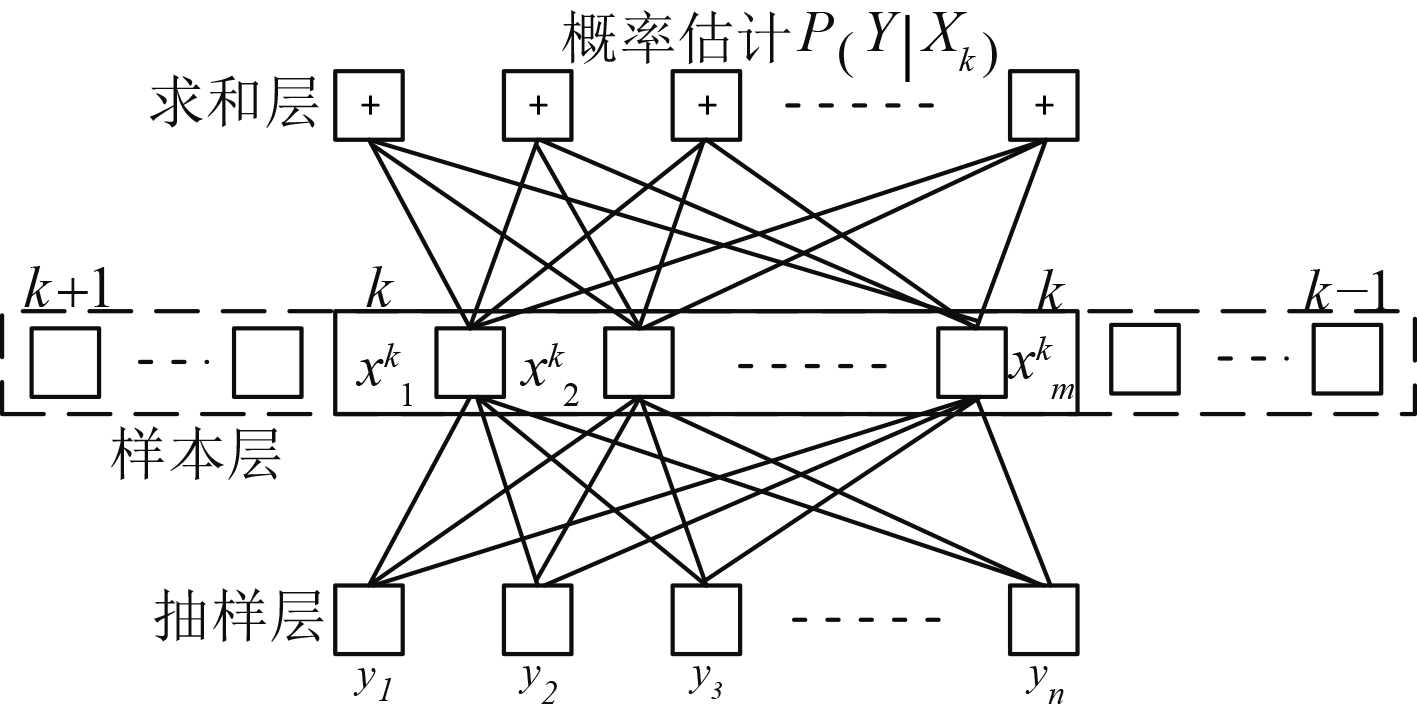
|
图 2 滑动概率神经网络拓扑图 Fig. 2 Diagram of sliding probabilistic neural network |
根据文献[17]在研究设备的可靠性问题时,将特征参数作为分析对象,在任意t时刻,确定固定的失效阈值为VL,认为超过VL的分布函数
步骤1 按目标设备性能退化时间序列采集特征参数,记为X。
步骤2 确定滑动概率神经网络窗口长度为s、滑动步长为d、平滑因子为
步骤3 当特征参数序列按顺序进入网络后,以s截取时间序列并将其作为统计样本。
步骤4 在进行第k次运算时,样本层滑动窗口内数据为
| $ K\left( {x_j^k,{y_i}} \right) = \frac{1}{{{{\left( {2s} \right)}^{1/2}}}}{e^{ - {{\left( {x_j^k - {y_i}} \right)}^2}/2{\varsigma ^2}}}\text{,} $ | (1) |
| $ P\left( {{y_i}\left| {{X_k}} \right.} \right) = \frac{1}{{s\varsigma }}\sum\limits_{j = 1}^m {K\left( {x_j^k,{y_i}} \right),i = 1,2, \cdots ,n} \text{。} $ | (2) |
式中:
| $ F\left( Y \right) = P\left( {{y_i} \leqslant Y} \right) = \sum\limits_{\left\{ {i:{y_i} \leqslant Y} \right\}} {P\left( {{y_i}\left| {{X_k}} \right.} \right)} \text{。} $ | (3) |
步骤5 利用式(3),假设目标设备基线限值为VZ,对tk时刻的超限概率分布及性能可靠度进行计算,超限概率分布式为:
| $ F\left( {{t_k},{V_Z}} \right) = P\left( {{y_i} \leqslant {V_Z}} \right) = \sum\limits_{\left\{ {i:{y_i} \leqslant {V_Z}} \right\}} {P\left( {{y_i}\left| {{V_k}} \right.} \right)} \text{,} $ | (4) |
则性能可靠度为:
| $ R\left( {{t_k},{V_Z}} \right) = 1 - F\left( {{t_k},{V_Z}} \right) \text{。} $ | (5) |
步骤6 当进行第k+1次运算时,保留第k次运算时窗口内的s-d个特征参数,并新增d个特征参数,重复步骤4及步骤5,可以获得tk+1时刻的概率密度分布,经过滑动时间窗口的不断滑动,可以连续获得各窗口处特征参数的概率密度分布和性能退化量,进而获得性能可靠度值,如图3和图4所示。
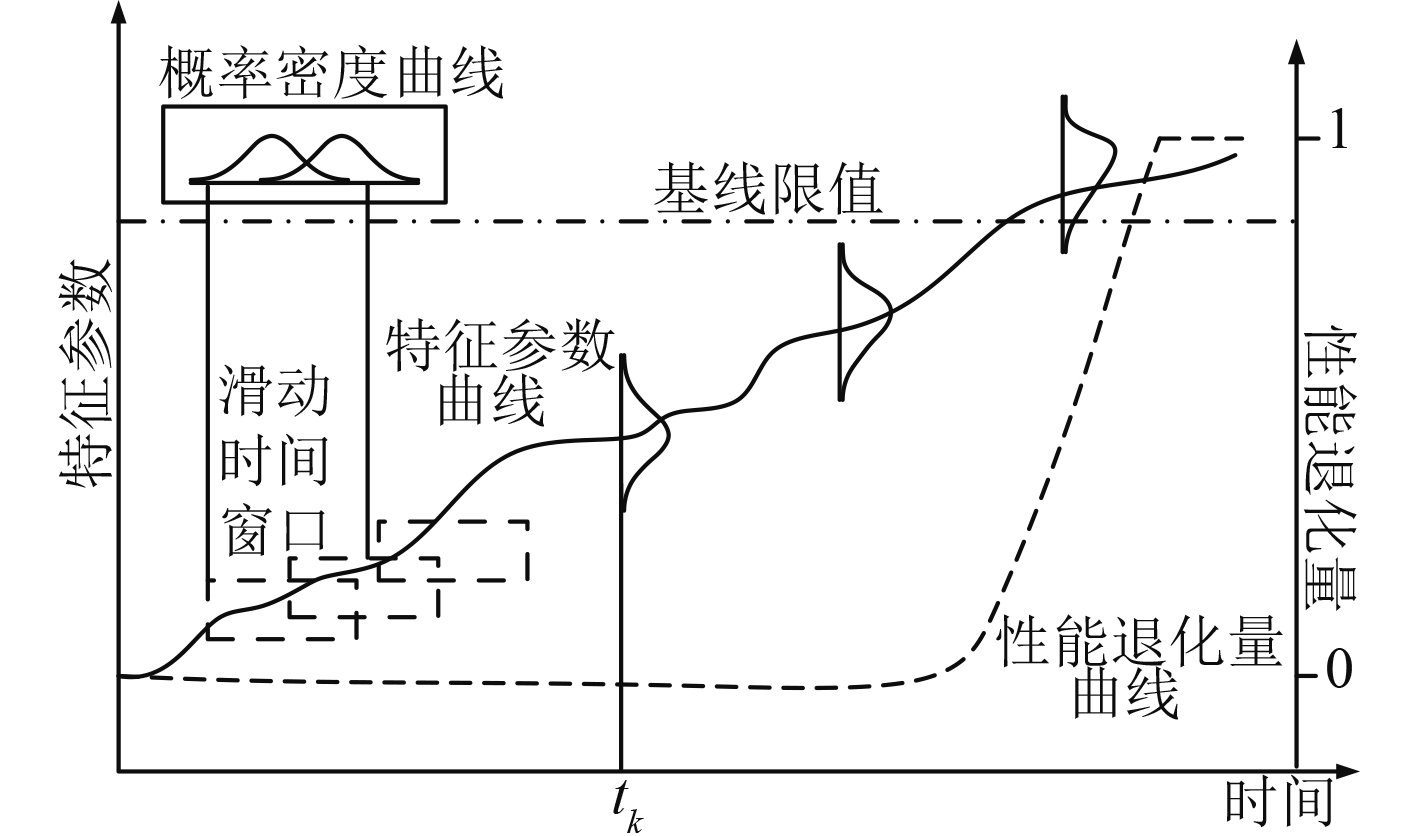
|
图 3 性能退化量跟踪曲线示意图 Fig. 3 Tracking curve of performance degradation measures |
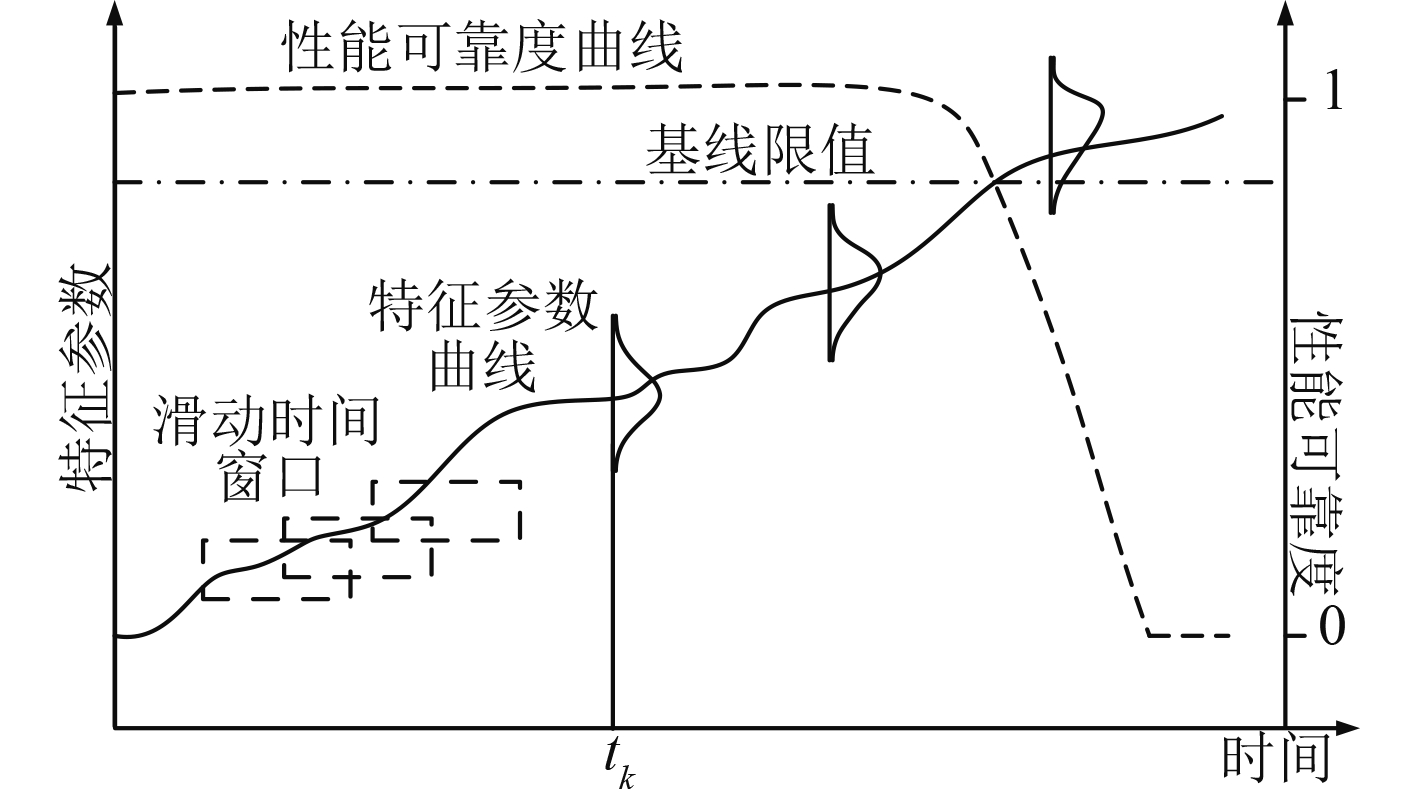
|
图 4 性能可靠度跟踪曲线示意图 Fig. 4 Tracking curve of performance reliability |
步骤7 假设目标设备完好无损正常状态下的基线值为VH,根据式(6)获得随性能可靠度变化的动态基线值
| $ \begin{array}{l} {Y_Z}\left( {{t_k}} \right) = {V_H} - \left| {{V_H} - {V_Z}} \right| \times \left( {1 - R\left( {{t_k},{V_Z}} \right)} \right),{V_H} > {V_Z} \text{,}\\ {Y_Z}\left( {{t_k}} \right) = {V_H} + \left| {{V_H} - {V_Z}} \right| \times \left( {1 - R\left( {{t_k},{V_Z}} \right)} \right),{V_H} < {V_Z}\text{。} \end{array} $ | (6) |
式中,性能可靠度
上述退化基线计算方法是以目标设备的特征参数为研究对象,因此对于退化基线预测方的重点就是按性能退化时间序列对目标设备未来一段时间的特征参数进行预测。对于数据预测方法的研究,主要集中在股票等经济领域,近几年随着机舱智能化、无人化的发展,参数预测方法在轮机工程领域有了更多的研究与应用。文献[18]建立神经网络预测模型对船舶柴油机排烟温度的变化趋势进行预测;文献[19]利用支持向量机对短期内船舶电力负荷进行预测;文献[20]建立ARMA时间序列模型对海水冷却系统状态参数进行预测且预测效果较好。由于本文研究对象为按时间序列采集的特征参数,应用ARMA模型在预测时间序列数据优点对目标设备未来一段时间的特征参数进行预测。
根据式(6)可知,退化基线计算方法最终获得呈梯度型变化的动态基线,即设备性能退化过程中下一性能阶段的基线值是可以确定的,因此对退化基线的预测的实质是对基线值的变化时间节点进行预测,基本流程如图5所示。

|
图 5 退化基线预测方法流程图 Fig. 5 Degradation baseline prediction method |
基本步骤为:
步骤1 确定具有重要特征参数或性能指标的船舶动力设备作为目标对象。
步骤2 按性能退化时间序列采集目标对象的参数或指标并作为研究对象。
步骤3 建立ARMA预测模型,调节模型精度,确定模型参数,获得特征参数预测数据。
步骤4 将预测数据与历史数据混合,利用退化基线计算方法,对动态基线的变化时间节点进行预测。
2.2 ARMA预测模型原理自回归滑动平均模型(Auto Regression Moving Average Model)简记为ARMA(p, q)模型,由自回归模型(AR)和移动平均模型(MA)混合构成,其基本原理为:由于完成时间序列变化发展具有一定的规律性,按照其规律性,通过序列中的原始数据来预测未来序列的单值[20]。
1)自回归模型AR(p)
若时间序列xt满足以下公式:
| $ {x_t}{\rm{ = }}\sum\limits_{i = 1}^p {{\phi _t}{x_{t - i}} + {\varepsilon _t}} \text{,} $ | (7) |
称时间序列xt为服从p阶的自回归模型。式中:
2)移动平均模型MA(q)
若时间序列xt满足下式子:
| $ {x_t}{\rm{ = }}{\varepsilon _t}{\rm{ - }}\sum\limits_{i = 1}^q {{\theta _t}{\varepsilon _{t - i}}} \text{,} $ | (8) |
称时间序列xt为服从q阶的移动平均模型。式中:
3)自回归移动平均模型ARMA(p, q)
若时间序列xt满足下式:
| $ \begin{split} {x_t} =& {\phi _1}{x_{t - 1}} + {\phi _2}{x_{t - 2}} + \ldots + {\phi _p}{x_{t - p}} + {\varepsilon _t} - {\theta _1}{\varepsilon _{t - 1}} - \\ &{\theta _2}{\varepsilon _{t - 2}} - \ldots - {\theta _q}{\varepsilon _{t - q}}\text{,} \end{split} $ | (9) |
称时间序列xt为服从(p, q)阶自回归移动平均模型。
将ARMA(p, q)引进延迟算子B,k步线性延迟算子用Bk表示,使得:
| $ B{x_t} = {x_{t - 1}} \text{,} $ | (10) |
| $ {B^k}{x_t} = {x_{t - k}} \text{,} $ | (11) |
则式(9)可简记为:
| $ \varPhi \left( B \right){x_t} = \Theta \left( B \right){\varepsilon _t}\text{。} $ | (12) |
式中:
ARMA 模型是根据平稳时间序列建立的,在模型建立之前需要检验时间序列的平稳性。假如时间序列是非平稳的,则需要进行相关平稳化处理,直到满足平稳性要求,之后建立ARMA 模型。ARMA 模型的建模步骤如下[20]:
步骤1 对时间序列特征参数集进行预处理,若数据在一定范围内呈现一定的周期性和规律性,则说明参数集平稳性差,利用式(13)对数据进行不定次差分处理,直至数据在一定范围内随机波动,没有明显的规律性。
| $ {\hat X_j} = \frac{{{X_i} - {X_{\min }}}}{{{X_{\max }} - {X_{\min }}}}i = 1,2, \cdots ,N \text{。} $ | (13) |
式中:Xi表示训练数据集中特征参数;Xmin表示训练数据集中的最小值;Xmax表示训练数据集中的最大值;
步骤2 模型的识别和定阶。建立ARMA模型时,自相关函数和偏自相关函数的收敛速度决定p,q值,AR(p)模型的自相关函数具有拖尾性,而偏自相关函数具有p步截尾性;MA(q)模型的自相关函数具有q步截尾性,而偏自相关函数具有拖尾性;ARMA(p、q)模型的自相关函数和偏自相关函数都具有拖尾性。自相关函数
| $ {\gamma _k} = \frac{{{\rm{cov}} ({Y_t},{Y_{t - k}})}}{{\sqrt {D{Y_t},D{Y_{t - k}}} }}\text{,} $ | (14) |
| $ {\varphi _{kk}} = \left\{ \begin{aligned} & {\gamma _1}\\ & \frac{{{\gamma _k} - \sum\limits_{j = 1}^{k - 1} {{\varphi _{k - 1,j}}.{\gamma _{k - j}}} }}{{1 - \sum\limits_{j = 1}^{k - 1} {{\varphi _{k - 1,j}}.{\gamma _j}} }} \end{aligned} \right.\text{,}k = 2,3 \ldots \ldots \text{。} $ | (15) |
式中:
之后根据模型选取不同的p, q值及参数,采用AIC方法给模型定阶,定阶准则如下式:
| $ {\rm{AIC}} = \ln \hat \sigma _a^2 + \frac{{2(p + q)}}{N} {\text{。}} $ | (16) |
当AIC值最小即残差方差
步骤3 模型参数估计。选取适当的时间序列模型参数估计方法,最小二乘估计法在对线性模型的估计中具有良好的统计性且计算量少等优势,因此被应用的最为广泛。
步骤4 模型检验。对估计得到的模型进行检验,当模型的某些参数显著为0时要对模型进行优化处理,必要时要重新建模,使模型达到最优。
3 实例验证在船舶中央冷却水系统中,为了使海水、低温淡水和高温淡水具备足够的机械能以供换热需求,会在系统中配置多台离心泵,并将出口压力作为离心泵性能状态的特征参数。由于海水泵直接与舷外海水接触容易导致零部件磨损,并且海水冷却系统作为独立的运行单元受柴油机负荷影响较小,因此可选取海水离心泵作为目标设备。在海水泵长时间运行过程中出现零部件磨损情况是不可避免的,并且会伴随着海水泵出口压力下降,若使用定基线进行状态评估,会出现评估值连续较低现象,甚至出现故障报警,但很长一段时间之内,零部件的磨损不会影响设备和系统的正常运行,为了解决评估值较低甚至误报警情况,需建立动态的退化基线作为海水泵性能退化过程中每一性能阶段的状态评估基准。
3.1 特征参数选取选取某轮2号海水泵出口压力作为验证数据集,该轮海水冷却系统配备3台主海水离心泵,并在离心泵进口和出口处均安装压力传感器,以10 s为采集间隔记录一次数据并保存至数据库中。经查看轮机日志发现,在2017年9月6日中央冷却器换热效果差且2号主海水泵出口压力低,轮机管理人员对2号泵进行检修,启用3号主海水泵后换热恢复正常,将2号泵拆卸检查发现密封环(口环)出现严重磨损情况,查询数据库中海水泵出口压力数据,选取2号泵出口压力明显变化前后10 000 h的出口压力数据,10 000 h是将船舶维护安排或传感器故障等原因导致的数据缺失而造成长时间数据间隔情况消除后的累计时长,由于数据量过于庞大,以累计时长1 h等间隔采集,共确定10 000条数据进行分析称为特征参数集A,如图6所示。由于密封环的磨损过程属于性能逐渐退化过程,使用滑动概率神经网络对其性能退化过程进行研究。
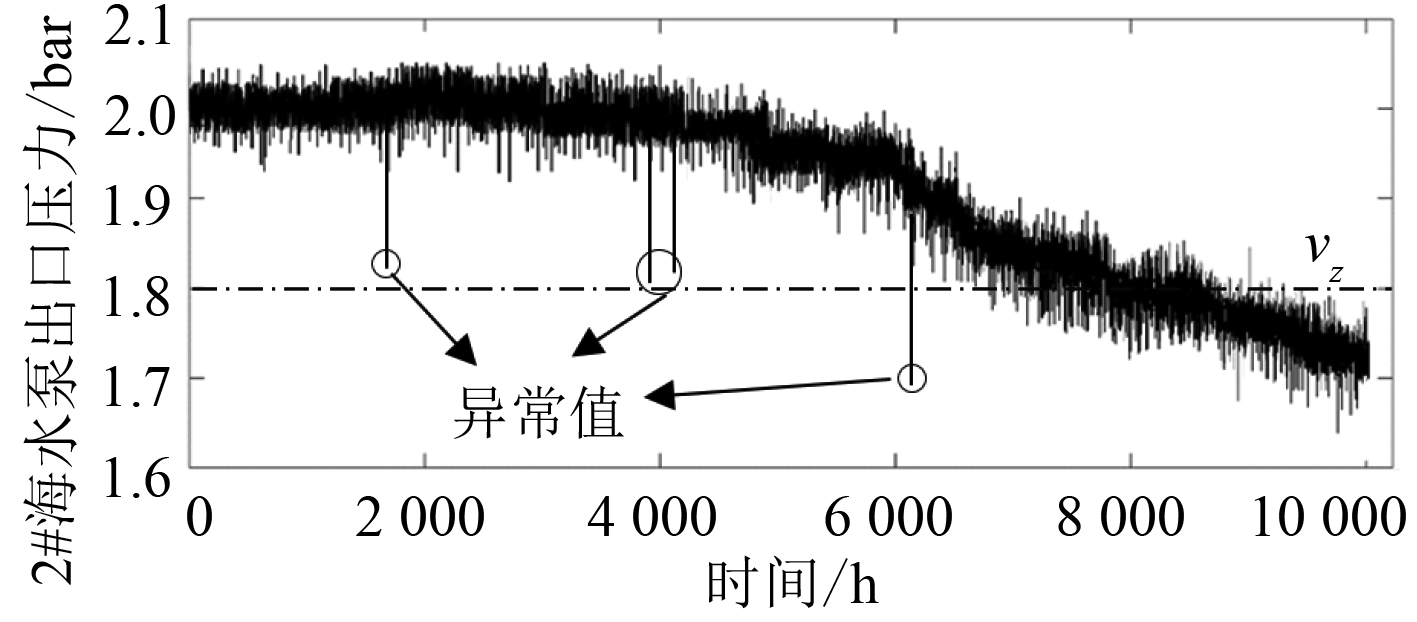
|
图 6 特征参数集A时序图 Fig. 6 Sequence diagram of characteristic parameter set A |
确定目标对象并选取特征参数集后建立滑动概率神经网络模型,根据数据集A的数据量以及序列趋势变化,确定滑动概率神经网络参数窗口长度s=130,滑动步长d=20,平滑因子
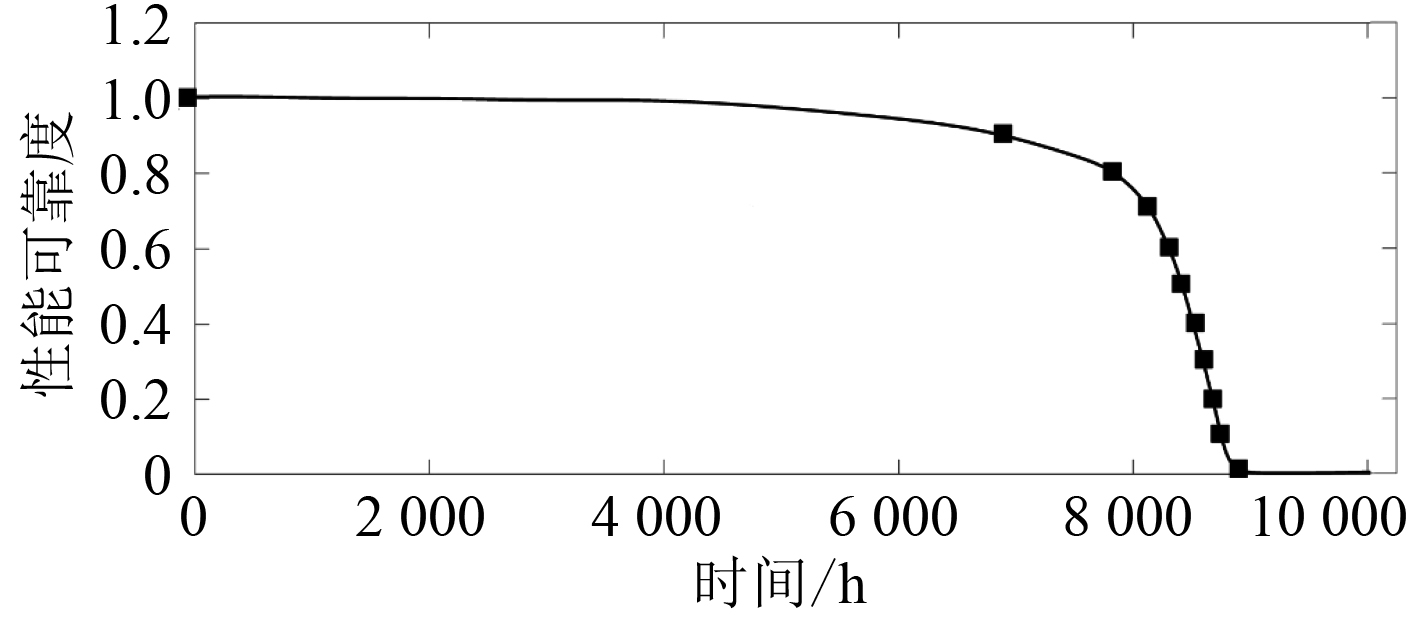
|
图 7 性能可靠度曲线 Fig. 7 Performance reliability curve |
确定该海水泵在完好无损稳定状态的基线值
|
|
表 1 海水泵退化基线变化区间 Tab.1 Sea water pump degradation baseline change interval |
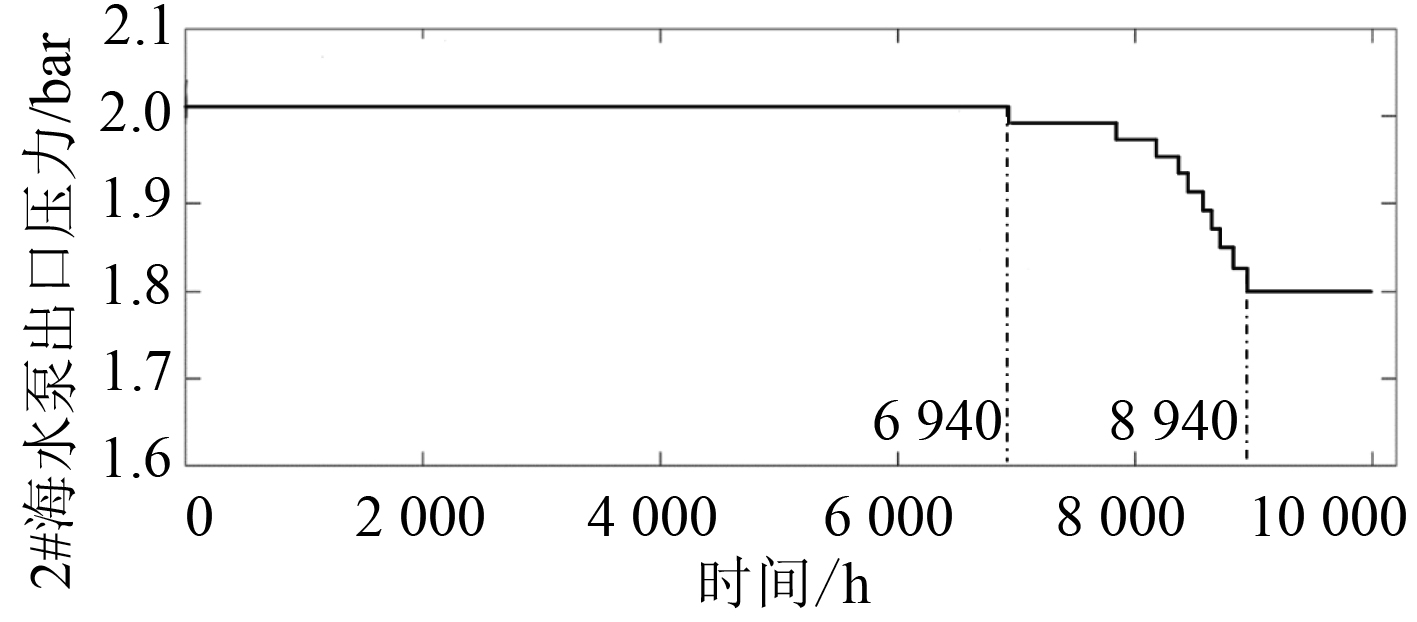
|
图 8 海水泵退化基线 Fig. 8 Sea water pump degradation baseline |
由图7及表1可以发现,退化基线计算方法能够以海水泵性能退化过程中的性能可靠度为依据获取基线值;动态基线作为目标设备性能退化过程中不同性能阶段的评估基准,为解决定基准造成的评估分值较低甚至误报警情况提供参考。
3.3 特征参数预测选取特征参数集A中数据趋势平稳阶段1 901–2 400 h、数据趋势呈下降阶段7 921–8 420h 2个时间区间各500组特征参数作为训练数据集B1,B2,分别对2 401–2 450 h,8 421–8 470这 2个时间区间内50组特征参数进行预测,对本文建立的ARMA预测模型的预测效果进行验证。利用平均绝对百分比误差法(MAPE Mean Absolute Percentage Error)作为模型预测结果的评价指标,公式如下:
| $ {\rm{MAPE}} = \frac{1}{N}\sum\limits_{i = 1}^n {\left| {\frac{{{x_{fi}} - {x_{ai}}}}{{{x_{ai}}}}} \right|} \times 100\% \text{。} $ | (17) |
式中:N表示预测个数;
1)训练数据集B1
首先对训练数据集B1进行平稳性检验发现平稳性较差,利用式(13)进行归一化处理获得训练数据集C1;然后将C1输入至ARMA模型,利用式(16)AIC准则对ARMA预测模型定阶;之后通过检验确定ARMA(4,5)为最佳模型,对未来50个数据进行预测,预测结果如图9所示。最后,通过式(17)获得MAPE值为0.91%。
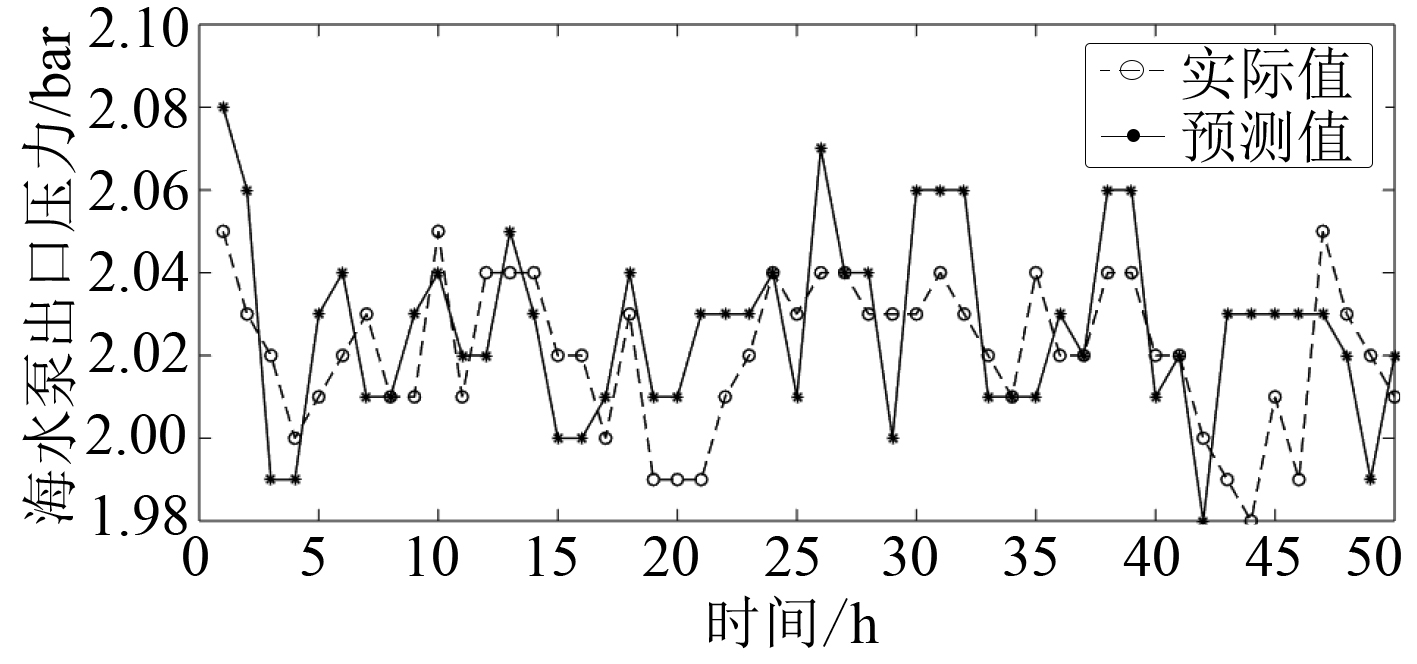
|
图 9 2 401–2 450 h预测数据对比 Fig. 9 Comparison of 2 401-2 450 hour prediction data |
2)训练数据集B2
首先对训练数据集B2进行平稳性检验发现平稳性较差,利用式(13)进行归一化处理获得训练数据集C2;然后将C2输入至ARMA模型,利用式(16)AIC准则对ARMA预测模型定阶;之后通过检验确定ARMA(6,4)为最佳模型,对未来50个数据进行预测,预测结果如图10所示。最后,通过式(17)获得MAPE值为1.45%,MAPE值明显高于前一时间段,分析原因是该时间段海水泵性能退化,数据波动幅度较大,且训练数据处于整体下降趋势,会对预测模型的准确性造成一定影响。
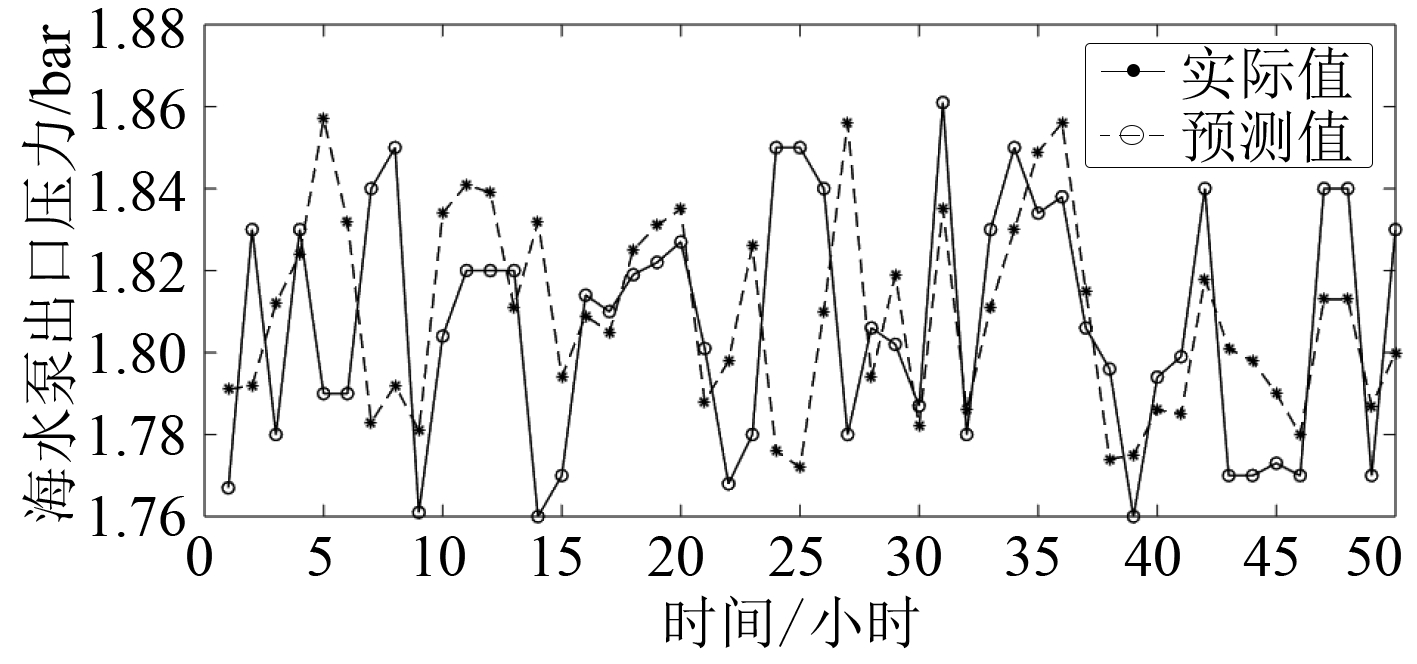
|
图 10 8 421–8 470 h预测数据对比 Fig. 10 Comparison of 8 421-8 470 hour prediction data |
通过图8和图9可以发现,预测值与实际值的变化趋势吻合度高,且获得的2个时间段预测数据的MAPE值较小,表明建立的ARMA预测模型具有良好的预测精度,能够对性能退化时间序列特征参数起到良好的预测功能。
3.4 退化基线变化时间节点预测将8 421–8 470 h的预测数据与7 861–8 420 h内的特征参数混合,根据建立的退化基线预测方法,对退化基线变化时间节点进行预测。预测结果如图11所示。与表1进行对比发现,含有预测数据的预测基线变更时间点与实际数据计算得到的动态基线变更时间点一致。
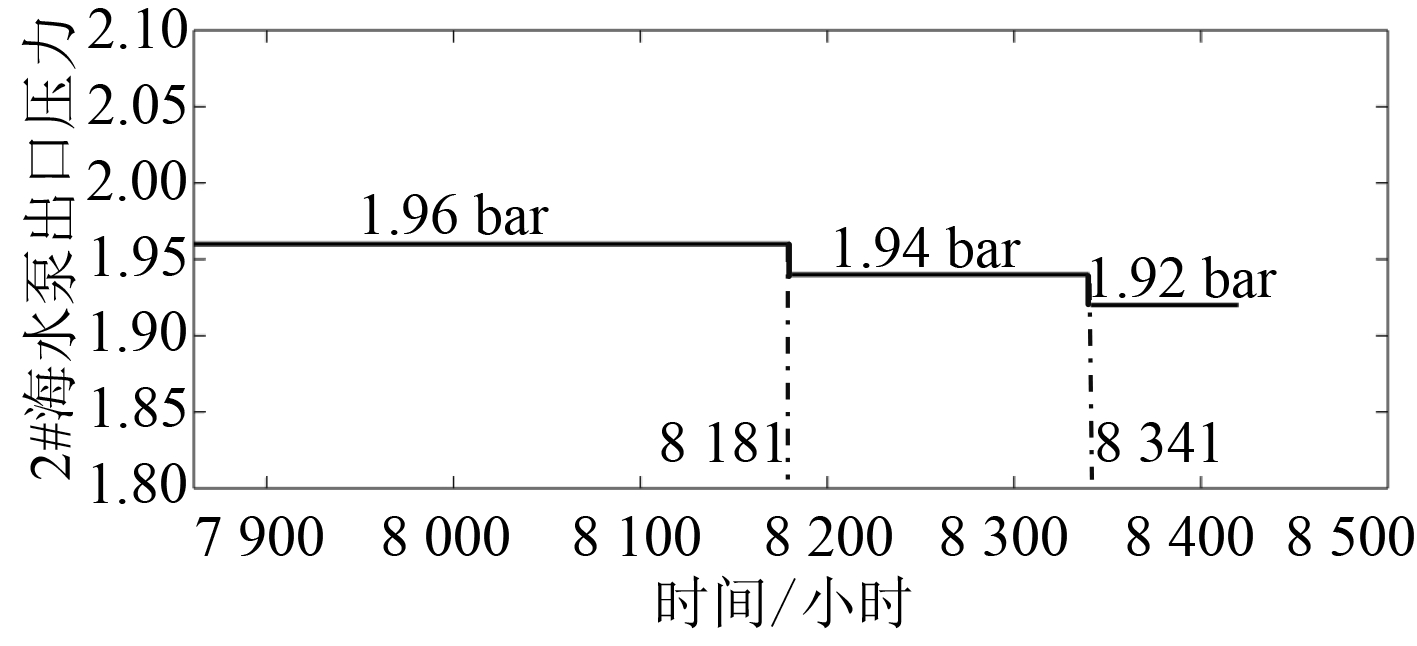
|
图 11 预测基线 Fig. 11 Prediction baseline |
分析原因如下:
使用滑动概率神经网络获得性能可靠度的核心是动态获得滑动时间窗内数据的概率分布,对低于设定基线限值的数据辨识度较高,而对预测数据的精度要求不高。通过图9可以发现低于设定的基线下限值1.8 bar的数据数量相似,并且滑动时间窗口的长度和滑动步长为定值,即基线变更时间点会是某滑动时间窗口的起点。综上原因,可以解释预测基线与实际基线变更时间的一致性。
其变更时间的一致性也可以表明本文建立的退化基线预测方法能够对未来基线变更时间进行良好预测,在能够确定变更基线值前提下,结合预测数据,运用适当的状态评估方法可实现对目标对象未来一段时间的状态预测,为系统和设备的剩余寿命预测以及实现“事后维修”向“视情维修”转变奠定基础。
4 结 语基线的科学性和合理性是实现船舶动力装置健康状态评估并提高评估值精确度的关键。本文以船舶动力设备自身性能退化为主要影响因素,对该影响因素下船舶动力设备退化基线的计算及预测方法进行研究。文章首先利用滑动概率神经网络以性能退化时间序列特征参数为研究对象,实现特征参数向性能可靠度转换,之后建立性能可靠度与基线值间函数关系确定随性能可靠度动态更新的退化基线,然后建立ARMA预测模型对特征参数进行预测,并与退化基线计算方法结合实现对退化基线的变化时间节点进行预测,最后利用海水泵对本文建立的方法可行性进行验证。结果表明:
1)本文建立的退化基线计算方法能够以目标设备性能可靠度为依据实现退化基线的动态更新,为解决定基线问题提供一种参考,有利于提高船舶动力装置健康状态评估值的科学性和合理性。
2)ARMA预测模型能够有效的对特征参数进行预测,建立的退化基线预测方法能够准确的对退化基线的变化时间节点进行预测,退化基线计算及预测方法可为实现船舶动力装置的状态预测提供一种思路,在实船应用上能够帮助轮机人员尽早判断设备状态变化趋势,为设备的零部件置换策略和维修策略提供相应的依据,提高船舶运行的安全性,是实现智能机舱、无人驾驶船舶的重要环节。
| [1] |
姜文, 刘立康. 软件配置管理中的基线问题研究[J]. 计算机技术与发展, 2016, 26(6). |
| [2] |
王昕, 吕世龙, 李岩, 等. 基于基线漂移模型的气体光谱自动基线校正[J]. 光谱学与光谱分析, 2018, 38(12): 3946-3951. |
| [3] |
史刚, 杨明, 倪萍. 脑功能磁共振设备性能参考基线建立方法初探[J]. 中国医疗设备, 2013(8): 26-29. DOI:10.3969/j.issn.1674-1633.2013.08.009 |
| [4] |
管文琦. 数据中心基线研究[J]. 中国金融电脑, 2014(2): 65-69. DOI:10.3969/j.issn.1001-0734.2014.02.014 |
| [5] |
梁军科. 基线分析方法在系统性能优化中的应用[J]. 数字技术与应用, 2016(5): 110. |
| [6] |
YAN-HUA Y U, PAN Y F, SONG J D. An improved baseline acquisition approach for real-time performance monitoring based on support vector machines[J]. The Journal of China Universities of Posts and Telecommunications, 2008, 15(supp-S): 59-63. |
| [7] |
ZHANG J, AU F T K. Effect of baseline calibration on assessment of long-term performance of cable-stayed bridges[J]. Engineering Failure Analysis, 2013, 35(Complete): 234-246. |
| [8] |
朱强. 船舶废气排放与能效水平在线监测[D]. 武汉: 武汉理工大学, 2017.
|
| [9] |
于巧婵, 纪永波, 骆义. 我国沿海船舶CO2排放限值与EEDI比对分析
[J]. 中国航海, 2016, 39(3): 99-103. DOI:10.3969/j.issn.1000-4653.2016.03.022 |
| [10] |
颜林. 国内船舶能效指数与CO2排放基线实船研究[D]. 武汉: 武汉理工大学, 2011.
|
| [11] |
华成, 张庆, 徐光华, 谢俊, 李淑智. 动态概率模型跟踪性能退化的实时可靠性评估方法[J]. 西安交通大学学报, 2010, 44(01): 46-50. DOI:10.3969/j.issn.1008-245X.2010.01.007 |
| [12] |
郑亚莉, 王康. 基于概率神经网络的垃圾邮件分类[J]. 计算机与现代化, 2008, 2008(1): 8-10. DOI:10.3969/j.issn.1006-2475.2008.01.003 |
| [13] |
李强, 刘晓峰. 基于PNN的音乐情感分类[J]. 计算机工程与设计, 2019, 40(2): 528-532. |
| [14] |
张习习, 顾幸生. 基于集成学习概率神经网络的电机轴承故障诊断[J/OL]. 华东理工大学学报(自然科学版): 1-11[2019-03-25]. https://doi.org/10.14135/j.cnki.1006-3080.20181206001.
|
| [15] |
宋娟, 蒙晔. 基于神经网络的柴油发动机的故障诊断[J]. 工业控制计算机, 2018, 31(11): 72-73+76. |
| [16] |
应文豪. 基于Parzen Window估计的分类与聚类方法及应用研究[D]. 无锡: 江南大学, 2013.
|
| [17] |
LU H, KOLARIK W J, LU S S. Real-time performance reliability prediction[J]. IEEE Transactions on Reliability, 2001, 50(4): 353-357. DOI:10.1109/24.983393 |
| [18] |
王新全, 孙培廷, 邹永久, 等. 基于GA-BP模型的船舶柴油机排气温度趋势预测[J]. 大连海事大学学报, 2015, 41(3): 73-76. DOI:10.3969/j.issn.1671-7031.2015.03.014 |
| [19] |
侯文君, 汪英英, 姚艺新, 等. 支持向量机的船舶短期电力负荷预测方法[J]. 舰船科学技术, 2018, 40(18): 79-81. |
| [20] |
孙晓磊, 丁亚委, 郭克余, 等. 基于ARMA模型的船舶海水冷却系统参数预测[J]. 计算机测量与控制, 2017, 25(7): 285-289. |
 2020, Vol. 42
2020, Vol. 42
