2. 海洋工程国家重点实验室,上海 200240;
3. 高新船舶与深海开发装备协同创新中心,上海 200240
2. State Key Laboratory of Ocean Engineering, Shanghai 200240, China;
3. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
近海风机结构所处的海洋环境十分复杂恶劣,承受着多种随时间和空间变化的随机载荷,如风、浪、海流、海冰等作用。因此,准确分析近海风机结构在风浪等随机载荷作用下的动力响应,对于保证其安全性具有实际意义[1]。
目前,在近海风机的仿真分析中,对于波浪的模拟仅限于线性不规则波,然而,这并不能准确地表示近海风机所在位置(浅水区域)的波浪。一般而言,波浪在本质上是非线性的,而非线性在浅水区域变得更为明显[2]。事实上,在近海区域,随着水深的减小,非线性变得越来越相关,海洋表面波高程变化明显偏离线性高斯假设。在这些条件下,由于各余弦波之间的相互作用,波形变得不对称,波峰越来越高且越来越陡,波谷越来越浅且越来越平[3]。因此,本文引入浅水斯托克斯波(2阶非线性不规则波)模型对近海风机进行仿真分析。
通常,海洋状态是由于各种波浪系统的共存而形成的,并不是所有的海洋状态都具有单峰波浪谱和狭窄(或有限)的频谱带宽。特别地,局部风浪往往是在有一定背景的低频涌浪的情况下发展而来,这些低频涌浪来自遥远的风暴,由此产生的混合海况将是双峰波浪谱[3]。在风机仿真软件FAST中,它提供了JONSWAP谱。然而,JONSWAP谱仅用来描述风浪,而不包括涌浪。本文使用Ochi-Hubble六参数波浪谱,它涵盖了与风暴的生长和衰减有关的包括涌浪在内的各种波浪谱的形状[4]。在本文实际研究中,为了使近海风机处于混合海况下,选择Ochi-Hubble六参数波浪谱族中的双峰波浪谱。
使用的风机模型是美国国家可再生能源实验室开发的5MW_Baseline Monopile近海风机,应用美国国家风能中心研发的风机仿真软件FAST对其进行随机时域仿真分析。
首先,给出线性与2阶非线性不规则波模型的理论公式。其次,介绍Ochi-Hubble六参数波浪谱以及NREL 5MW_Baseline Monopile近海风机的基本参数和使用FAST软件的分析过程中的主要设置。然后,在一定的环境状态下,比较线性和2阶非线性不规则波对风机响应,主要是对自由表面波高程,塔筒底部首尾向剪力和弯矩2个量的影响,并利用短期载荷极值,给出了塔筒底部首尾向剪力和弯矩在线性和2阶非线性不规则波作用下的超越概率曲线对比图。结果表明,非线性波作用下,近海风机承受的载荷增大,塔体动力学也受到一定的影响。最后,建议在未来的近海风机工程设计与实践中,非线性混合海况下的随机时域仿真分析应该成为常态。
1 浅水斯托克斯波非线性的自由表面波高程
| $ \eta (x,t) = {\eta ^{(1)}}(x,t) + {\eta ^{(2)}}(x,t) + \ldots \text{,} $ | (1) |
对于一个以特定波浪谱
| $ {\eta ^{(1)}}(x,t) = {\rm{Re}} \sum\limits_{n = 0}^N {{c_n}\exp (i({\omega _n}t - {k_n}x + {\varepsilon _n})} \text{,} $ | (2) |
式中,N趋于无穷。Re表示复数的实部,
| $ {\omega _n}^2 = g{k_n}\tanh ({k_n}d)\text{。} $ | (3) |
式中,g和d分别表示重力加速度和水深。
由于底层效应,浅水波数据通常不遵循线性高斯海洋模型。线性高斯海洋模型可以通过包含2阶项来修正,2阶项
| $ {\eta ^{(2)}}(x,t) = {\rm{Re}} \sum\limits_{m = 0}^N {\sum\limits_{n = 0}^N {{c_m}{c_n}\left[\!\!\! \begin{array}{l} {r_{mn}}\exp (i({\omega _m}t - {k_m}x + {\varepsilon _m} + {\omega _n}t -\\ {k_n}x + {\varepsilon _n})) + {q_{mn}}\exp (i({\omega _m}t -\\ {k_m}x + {\varepsilon _m} - {\omega _n}t + {k_n}x - {\varepsilon _n})) \end{array} \!\!\!\right]} } \text{。} $ | (4) |
式中,
| $\scriptsize \begin{split} &{r_{mn}} = - \left( {\frac{1}{g}} \right)\\ &\left( {\frac{{\left( {\frac{1}{{4{\omega _m}{\omega _n}}}} \right)2\left( {{\omega _m} + {\omega _n}} \right)\left( {\omega _n^2\omega _m^2 - {k_n}{k_m}{g^2}} \right) + {\omega _n}\left( {{\omega _m}^4 - {g^2}k_m^2} \right) + {\omega _m}\left( {{\omega _n}^4 - {g^2}{k_n}^2} \right)}}{{{{\left( {{\omega _m} + {\omega _n}} \right)}^2}\cosh \left( {\left( {{k_m} + {k_n}} \right)d} \right) - g\left( {{k_m} + {k_n}} \right)\sinh \left( {\left( {{k_m} + {k_n}} \right)d} \right)}}} \right)\times \\ & \left( {{\omega _m} + {\omega _n}} \right)\cosh \left( {\left( {{k_m} + {k_n}} \right)d} \right) - \left( {\frac{1}{{4g{\omega _m}{\omega _n}}}} \right)\left( {{k_m}{k_n}{g^2} - {\omega _n}^2{\omega _m}^2} \right) + \left( {\frac{1}{{4g}}} \right)\left( {{\omega _m}^2 + {\omega _n}^2} \right)\text{,} \end{split} $ | (5) |
| $\scriptsize \begin{array}{l} {q_{mn}} = - \left( {\frac{1}{g}} \right)\left( {\frac{{\left( {\frac{1}{{4{\omega _m}{\omega _n}}}} \right)2\left( {{\omega _m} - {\omega _n}} \right)\left( {\omega _n^2\omega _m^2 + {k_n}{k_m}{g^2}} \right) - {\omega _n}\left( {{\omega _m}^4 - {g^2}k_m^2} \right) + {\omega _m}\left( {{\omega _n}^4 - {g^2}{k_n}^2} \right)}}{{{{\left( {{\omega _n} - {\omega _m}} \right)}^2}\cosh \left( {\left| {{k_m} - {k_n}} \right|d} \right) - g\left| {{k_n} - {k_m}} \right|\sinh \left( {\left| {{k_n} - {k_m}} \right|d} \right)}}} \right) \times \\ \left( {{\omega _m} - {\omega _n}} \right)\cosh \left( {\left| {{k_n} - {k_m}} \right|d} \right) - \left( {\frac{1}{{4g{\omega _m}{\omega _n}}}} \right)\left( {{k_m}{k_n}{g^2} + {\omega _n}^2{\omega _m}^2} \right) + \left( {\frac{1}{{4g}}} \right)\left( {{\omega _m}^2 + {\omega _n}^2} \right)\text{。} \end{array} $ | (6) |
式中,
最后,将1阶项和2阶项相加,即得到浅水斯托克斯波(2阶非线性不规则波)的波高程
| $ \begin{split} &\eta \left( {x,t} \right) = {\eta ^{(1)}}\left( {x,t} \right) + {\eta ^{(2)}}\left( {x,t} \right) = {\rm{Re}} \sum\limits_{n = 0}^N {{c_n}\exp ({\rm i}({\omega _n}t - {k_n}x + {\varepsilon _n})} +\\ & {\rm{Re}} \sum\limits_{m = 0}^N {\sum\limits_{n = 0}^N {{c_m}{c_n}\left[\!\! \begin{array}{l} {r_{mn}}\exp ({\rm i}({\omega _m}t - {k_m}x + {\varepsilon _m} + {\omega _n}t - {k_n}x + \\ {\varepsilon _n})) + {q_{mn}}\exp (i({\omega _m}t - {k_m}x + {\varepsilon _m} -\\ {\omega _n}t + {k_n}x - {\varepsilon _n})) \end{array} \!\!\right]} } \text{,} \end{split} $ | (7) |
在特定的参考位置
| $ \begin{array}{l} \eta \left( {0,t} \right) = \eta \left( t \right) = {\eta ^{(1)}}\left( t \right) + {\eta ^{(2)}}\left( t \right) = {\rm{Re}} \sum\limits_{n = 0}^N {{c_n}\exp ({\rm i}({\omega _n}t + {\varepsilon _n})}+ \\ {\rm{Re}} \sum\limits_{m = 0}^N {\sum\limits_{n = 0}^N {{c_m}{c_n}\left[ \begin{array}{l} {r_{mn}}\exp ({\rm i}({\omega _m}t + {\varepsilon _m} + {\omega _n}t + {\varepsilon _n})) + \\ {q_{mn}}\exp ({\rm i}({\omega _m}t + {\varepsilon _m} - {\omega _n}t - {\varepsilon _n})) \\ \end{array} \right]} } \text{。}\\[-15pt] \end{array} $ | (8) |
Michel K. Ochi和E. Nadine Hubble提出一种新的包含6个参数的波浪谱即Ochi-Hubble六参数波浪谱。在此波浪谱的发展过程中,将其分解为两部分,每一部分用包含3个参数的数学公式表示,总谱由2组三参数谱的组合表示[6]。
本文的研究正是基于Ochi-Hubble六参数波浪谱,其表达式如下:
| $ \begin{split} & S\left( \omega \right){\rm{ = }}\frac{1}{4}\sum\limits_{{\rm{j}} = 1}^2 {\frac{{{{\left( {\left( {\left( {4{\lambda _j} + 1} \right)/4} \right){\omega _{mj}}^4} \right)}^{{\lambda _j}}}}}{{\Gamma \left( {{\lambda _j}} \right)}}} \frac{{{H_{sj}}^2}}{{{\omega ^{4{\lambda _j} + 1}}}} \times \\ & \exp \left[ { - \left( {\frac{{4{\lambda _j} + 1}}{4}} \right){{\left( {\frac{{{\omega _{mj}}}}{\omega }} \right)}^4}} \right]\text{。} \end{split} $ | (9) |
式中:
式中的6个参数均可以转化为用有义波高Hs(m)来表示,因此就得到了由11个波浪谱组成的六参数波浪谱族[6],如表1所示。
|
|
表 1 六个参数的值 Tab.1 Values of six parameters |
在这11个波浪谱中,1号波浪谱参数被认为是代表特定海洋的“最可能的波谱”,剩下的2~11号波浪谱参数被认为是代表特定海洋“95%可信的”。
在本文的研究中,波浪的有义波高Hs=7.5 m,将其代入到上述11个波浪谱中,观察到3号波浪谱具有明显的双峰,如图1所示。即该波浪谱既有低频的涌浪,又有高频的风浪,符合混合海况的要求。

|
图 1 3号波浪谱 Fig. 1 Wave spectrum No. 3 |
本文的研究对象为NREL 5MW_Baseline Monopile近海风机。这种近海风机是将风机安装在弹性基础的单桩(monopile)上,水深为20 m。目的是应用实际岩土性能和标准设计流程,以得到对系统动态响应有显著影响的设计,从而促进对不同代码风机基础模型的校核[7]。
近海风机的运行环境是正常稳态风和正常海况,风速v = 5 m/s,有义波高Hs=7.5 m,谱峰周期Tp = 12.3 s。该风机的仿真模型图和基本参数分别见图2与表2。

|
图 2 NREL 5MW_Baseline Monopile近海风机 Fig. 2 NREL 5MW_Baseline Monopile offshore wind turbine |
|
|
表 2 NREL 5MW_Baseline Monopile近海风机基本参数 Tab.2 Basic parameters of NREL 5MW_baseline monopile offshore wind turbine |
应用美国国家风能中心(NWTC)研发的风机仿真软件FAST对NREL 5MW_Baseline Monopile近海风机进行仿真。FAST可仿真垂直轴陆上、离岸的3叶片及2叶片风机,提供时域仿真分析。对于环境载荷,采用FAST已有的入流稳态风文件作为风载荷,应用FAST中的HydroDyn模块进行波浪的仿真。
在波浪的仿真中,首先,用Fortran语言对前述的3号波浪谱编制程序,并将此程序嵌入到FAST的HydroDyn模块下的波浪源文件中以便调用。其次,在NRELOffshrBsline5MW_OC3Monopile_HydroDyn.dat输入文件中,设置仿真时长,时间步长,有义波高以及谱峰周期等参数。然后,生成20组波浪随机数用于对风机的随机仿真。生成的波浪随机数见表3。最后,对每一次仿真都进行线性和非线性的计算。因此,每一次仿真都得到2个结果文件用于完成考虑非线性的情况与仅考虑线性情况的对比。
|
|
表 3 波浪随机数 Tab.3 Random seed of waves |
选择仿真结果中的波高程、塔筒底部首尾向剪力和弯矩3个变量,阐述在线性与2阶非线性不规则波作用下的风机响应。对仿真计算得到的塔筒底部首尾向剪力和弯矩的短期载荷,采用分块最大值法提取极值,再基于20次仿真所得的极值做概率统计分析,给出在线性与2阶非线性不规则波作用下,10 min仿真的短期载荷极大值的经验(短期)概率分布。
4.1 风机响应对1次10 min的仿真分析结果的时间历程曲线截取300 s(200~500 s)的片段,如图3~图5所示。对于波高程曲线图、塔筒底部首尾向剪力曲线图和弯矩曲线图,可以明显地看出,考虑非线性的结果高于仅考虑线性的结果。进一步对比,还能看出,塔筒底部首尾向剪力和弯矩最大值出现的时刻几乎与波浪高程最大值出现的时刻吻合,这说明了塔筒底部载荷最大值的确与波浪作用息息相关。
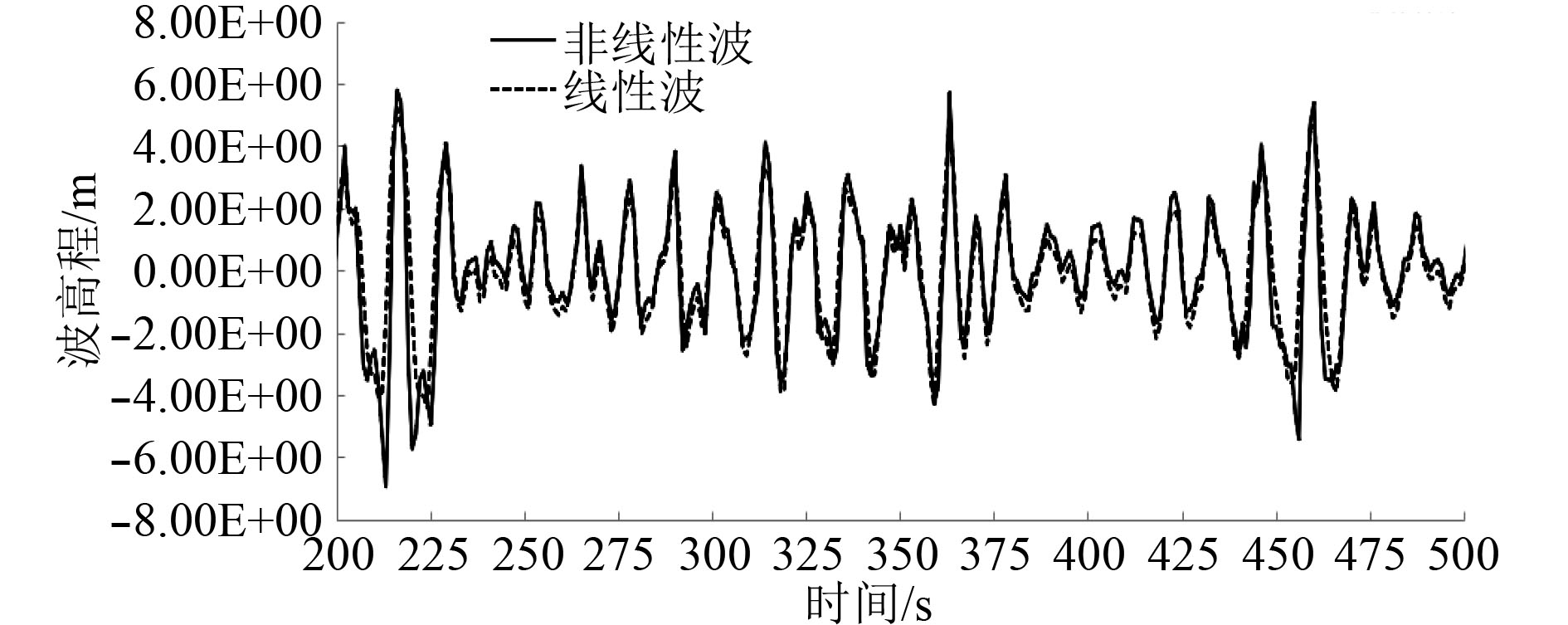
|
图 3 波高程 Fig. 3 Wave Elevation |
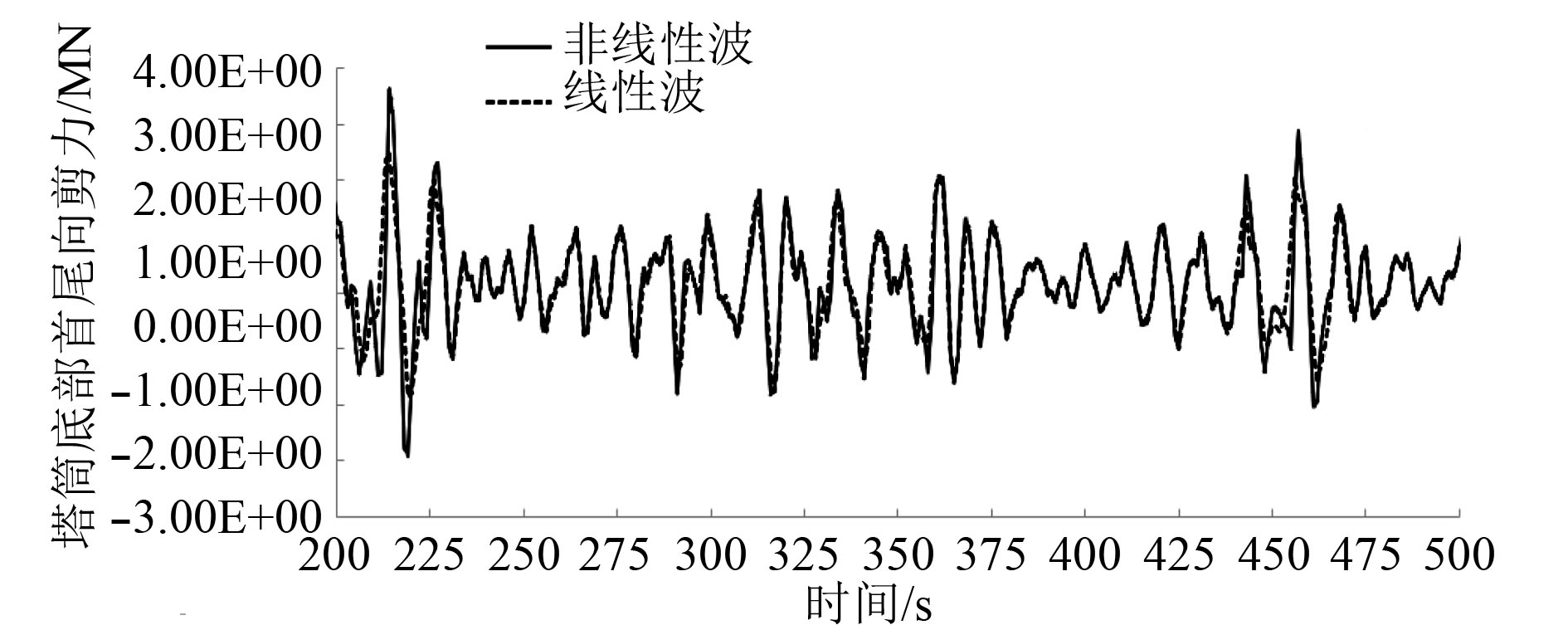
|
图 4 塔筒底部首尾向剪力 Fig. 4 Fore-aft Tower Base Shear at the baseline |
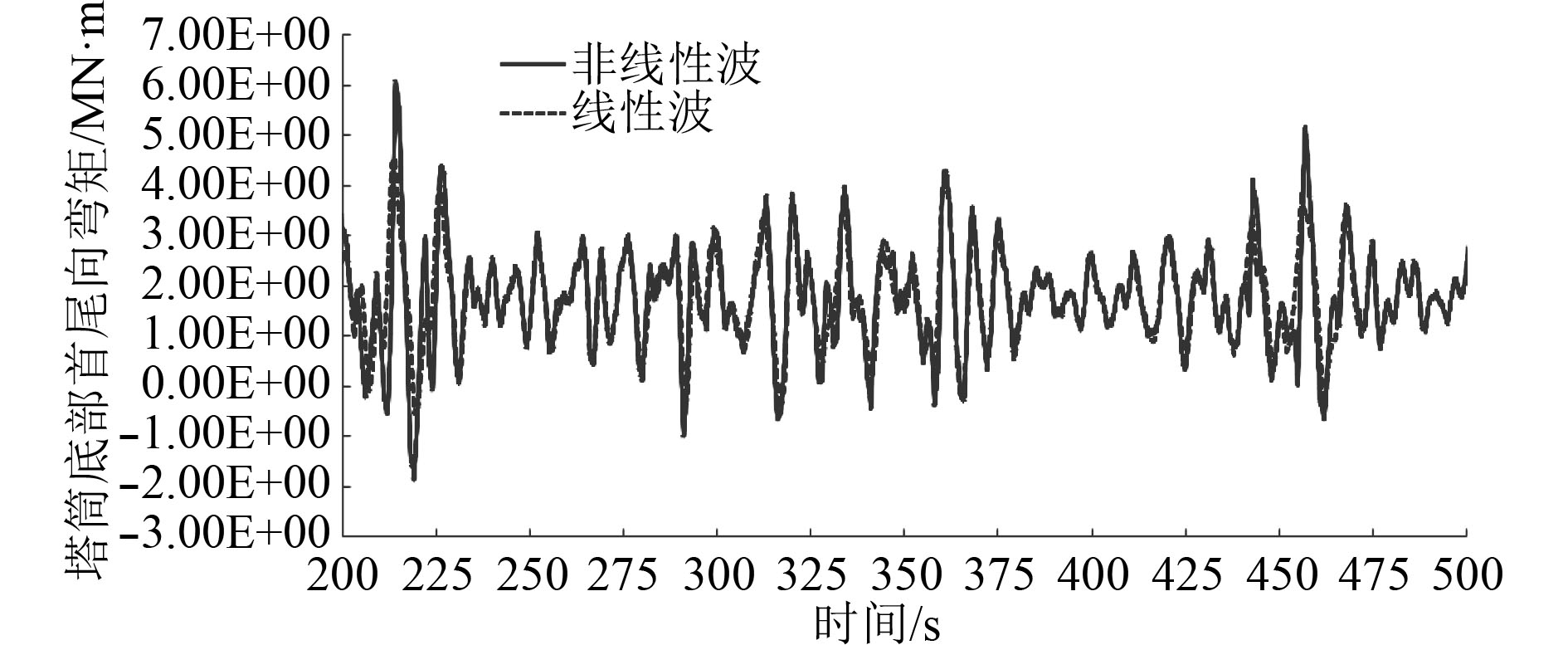
|
图 5 塔筒底部首尾向弯矩 Fig. 5 Fore-aft Tower Bending Moment at the baseline |
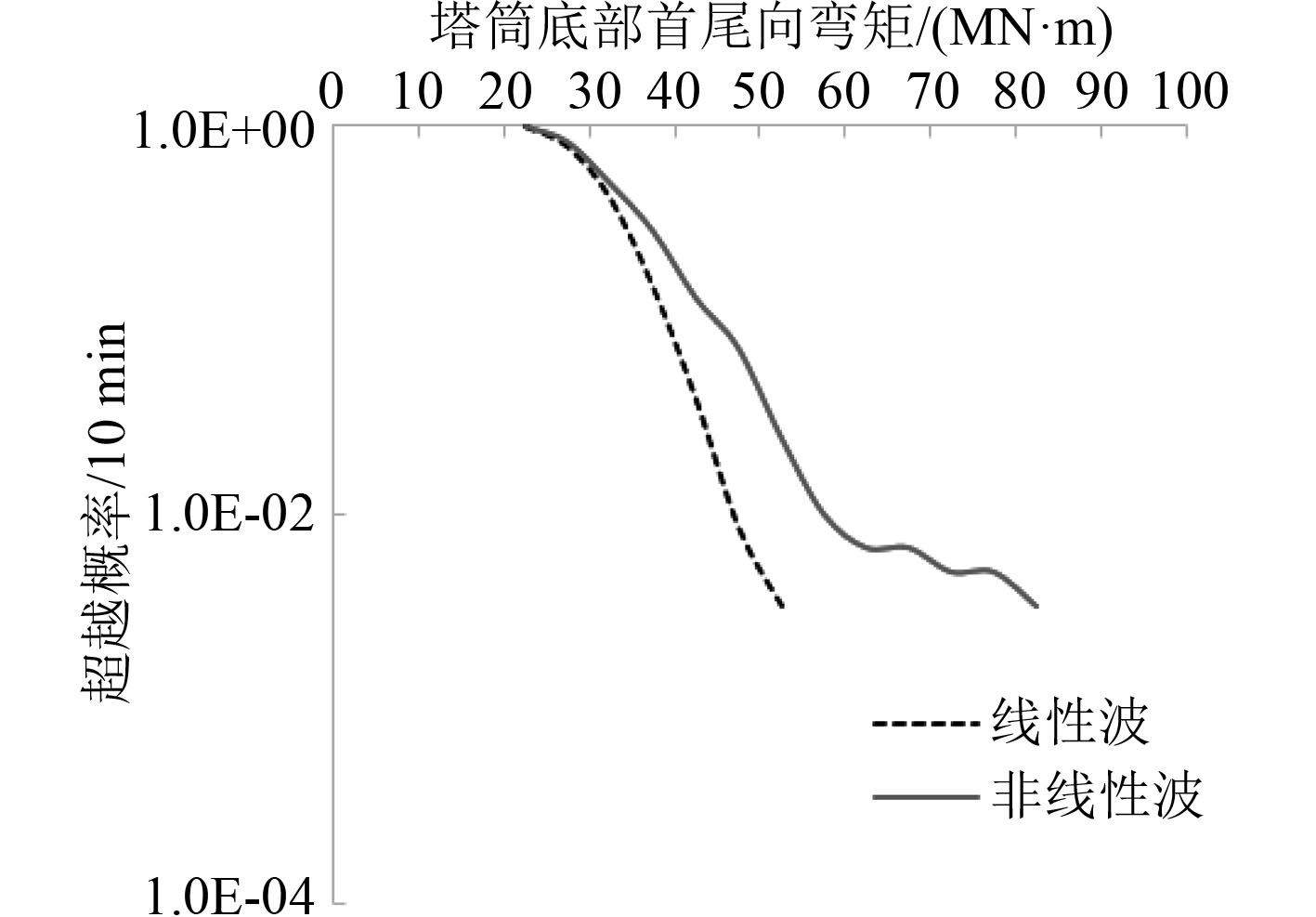
采用分块最大值法提取短期载荷极值,是把每次仿真计算所得的短期载荷时间序列以固定的时间间隔将其分为若干小块,再从每一个小块中提取该块时间序列内的极值[8]。以波高程时间序列说明上述方法,本文每次仿真时长为10 min,相当于600 s,设定的输出步长为0.05 s,那么一次仿真将输出12 000个值。以20 s的时间间隔把600 s的短期载荷时间序列分为30块,每块的容量为400个值,再从每一块中提取块极大值。因此,一次仿真即可得到30个短期载荷极值。本文共仿真了20次,提取600个短期载荷极值,并基于这些极值给出了塔筒底部首尾向剪力和弯矩的经验(短期)概率分布,如图6和图7所示。
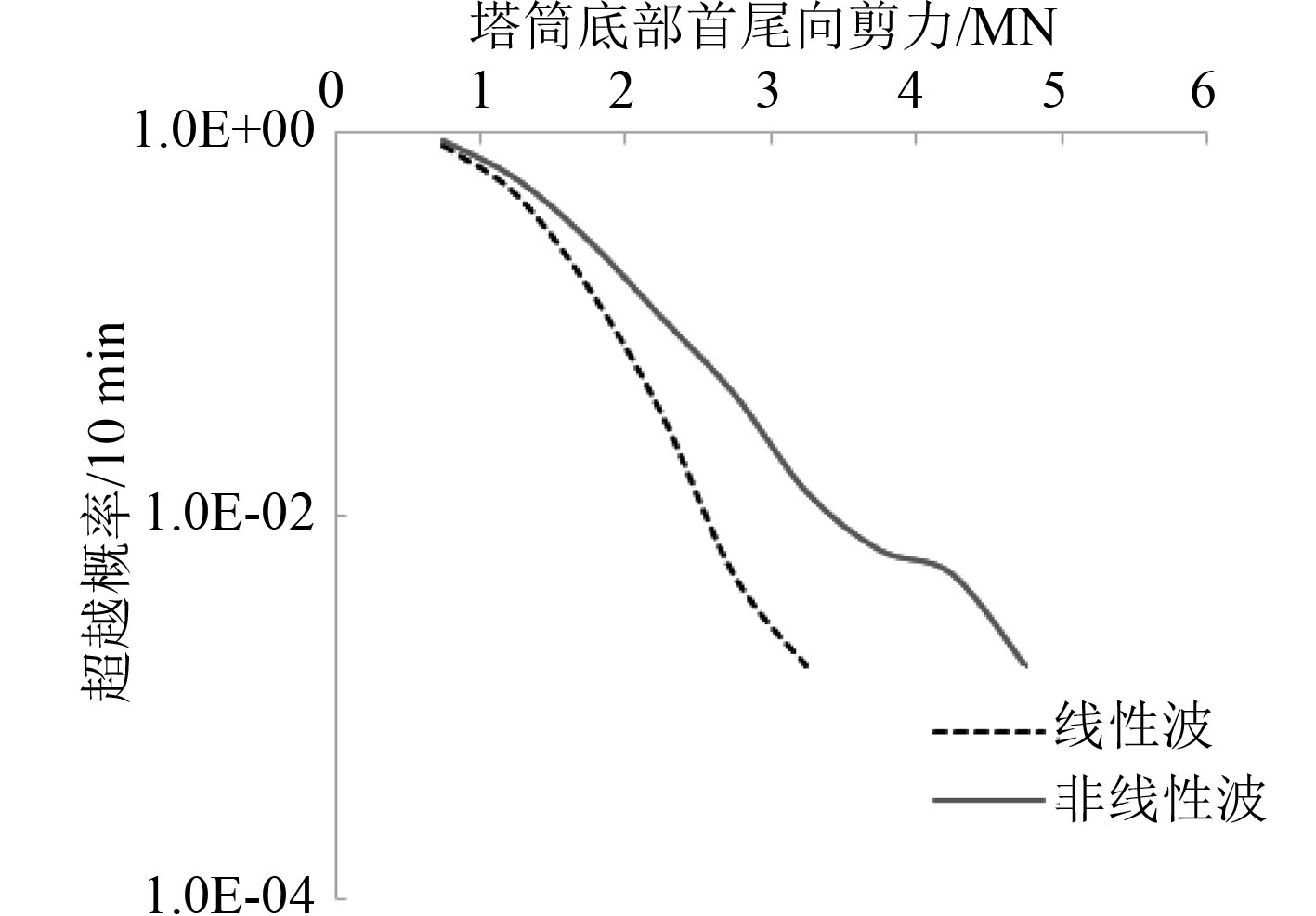
|
图 6 基于20次10 min仿真的塔筒底部首尾向剪力极大值的经验概率分布 Fig. 6 Empirical probability distribution of 10 min maximum of the fore-aft tower base shear at the baseline based on 20 10 min simulations |
|
图 7 基于20次10 min仿真的塔筒底部首尾向弯矩极大值的经验概率分布 Fig. 7 Empirical probability distribution of 10 min maximum of the fore-aft tower bending moment at the baseline based on 20 10 min simulations |
从图6和图7中可以看出,对于塔筒底部首尾向剪力和弯矩,当近海风机遭遇相同载荷时,非线性情况下的超越概率是大于仅线性情况下的。这就说明了在一段时期内,相同海况下近海风机受到的载荷是高于线性不规则波计算出的值,这对于近海风机的使用是不利的。因此,非常必要采用非线性不规则波对近海风机进行仿真计算。
5 结 语本文研究关注的是在混合海况(即风浪和涌浪组合海况)下,引入线性与2阶非线性不规则波模型应用风机仿真软件FAST对NREL 5MW_Baseline Monopile近海风机进行仿真分析,得出以下结论:
1)波高程、塔筒底部首尾向剪力和弯矩3个变量在非线性不规则波浪作用下的结果高于在线性不规则波浪作用下的结果。
2)用分块最大值法对10 min仿真的短期载荷提取极大值,在相同的环境状况时,塔筒底部在非线性不规则波浪作用下将会承受更大载荷作用。
3)在未来的近海风机工程设计与实践中,非线性混合海况下的仿真分析应该成为常态的工作。
| [1] |
李昕雪, 王迎光. 不同外推方法求解近海风机的极限载荷[J]. 上海交通大学学报, 2016, 50(6): 844-848. LI Xin-xue, WANG Ying-guang. Comparison of different statistic extrapolation methods in calculation of extreme load of offshore wind turbines[J]. Journal of Shanghai Jiao Tong University, 2016, 50(6): 844-848. |
| [2] |
PUNEET AGARWAL, LANCE MANUEL. Incorporating irregular nonlinear waves in coupled simulation and reliability studies of offshore wind turbines[J]. Applied Ocean Research, 2011, 33(3). |
| [3] |
WANG Y G, XIA Y Q. Simulating mixed sea state waves for marine design[J]. Applied Ocean Research, 2012, 37. |
| [4] |
ABS. Guidance notes on selecting design wave by long term stochastic method[S]. American Bureau of Shipping, 2016.
|
| [5] |
WANG Y G. Nonlinear crest distribution for shallow water stokes waves[J]. Applied Ocean Research, 2016, 57. |
| [6] |
MICHEL K. OCHI, E. NADINE HUBBLE. Six-Parameter wave spectra[C]. 15th International Conference on Coastal Engineering, July 11-17, 1976, Honolulu, Hawaii, United States.
|
| [7] |
夏一青. 近海风机极限载荷与疲劳载荷研究[D]. 上海: 上海交通大学, 2014.
|
| [8] |
周帅, 王迎光, 李昕雪. 应用经典极值理论对风机极端载荷的预报[J]. 舰船科学技术, 2018, 40(19): 93-98. ZHOU Shuai, WANG Ying-guang, LI Xin-xue. Application of classical extreme value theory to the prediction of extreme load of wind turbines[J]. Ship Science and Technology, 2018, 40(19): 93-98. |
 2020, Vol. 42
2020, Vol. 42
