0 引　言

多水下无人航行器（UUV）协同作业系统能够承担诸多复杂困难任务，具有高效率、高可靠性等优点，应用前景广阔^[1-3]。基于水声距离观测的UUV协同定位在UUV协同作业系统中具有重要作用，但因水下情况复杂多变，导致其收到的水声距离观测信息经常被异常噪声干扰。如何有效解决水声距离异常噪声影响条件下高精度水下协同定位，是水下协同定位所面临的一个重要问题，对实现UUV高精度协同定位具有重要意义^[4]。

在水下声学定位技术的发展历程中，声学异常噪声处理一直是一项重要研究内容。S. Misra 等^[5-6]针对长基线系统中的声学异常量测问题进行了研究，通过设置一固定异常量测判定调节参数，并基于马氏距离判定方法对声学异常量测进行判定。但是该方法需要保证航位推算信息的一致性，且具有相对准确的推算不确定度，否则便会造成对异常噪声的不敏感性。K. H. Kim等^[7]采用谱图像分割技术对长基线系统中的水声异常量测问题进行了研究，通过比较多次量测信息间相对一致性的大小来进行异常噪声判定，虽然离线试验数据处理取得比较理想的效果，但是由于该方法是基于长基线系统固定信标条件下的，对于动态条件下的航行器协同定位系统来说则具有局限性。针对新近发展的UUV协同定位问题，C. B. Medeiros等^[8]通过在每次数据融合过程中对先前一系列距离观测信息的综合处理，有效实现了对由于异常量测造成的估计误差的及时校正，但还是无法避免异常量测时刻对状态误差的严重影响。

为寻求更为及时、有效的异常噪声处理方法，本文将极大似然估计理论（Maximum Likehood Estimation，M估计）^[9]应用于扩展卡尔曼滤波算法（Extended Kalman Filter，EKF），提出一种基于M估计多UUV协同定位算法。该算法可以有效解决UUV协同定位过程中水声距离异常条件下的状态估计问题，进一步改善异常噪声情况下协同定位系统的状态估计性能。

1 UUV协同定位系统运动学模型

为简化问题分析，本文中参与协同的低精度UUV以航位推算方式进行自主定位^[10]。因UUV定位时在水面上运动，进一步简化为二维空间下的协同定位问题。若已知UUV在起始时刻的东北向位置坐标为 ${{x}} = {[\begin{array}{*{20}{c}} {{x_1}}&{{x_2}} \end{array}]^{\rm T}}$ ，则根据自身传感器测得的速度及方位信息实时推算得到的 $k$ 时刻位置状态为：

$ \left\{ \begin{aligned} & x_1^k = x_1^{k - 1} + \Delta t \cdot \left( {v_y^k \cdot \cos {\theta ^k} - v_x^k\sin {\theta ^k}} \right)\text{，} \\ & x_2^k = x_2^{k - 1} + \Delta t \cdot \left( {v_y^k \cdot \sin {\theta ^k} + v_x^k\cos {\theta ^k}} \right) \text{。} \end{aligned} \right. $

(1)

式中： ${{{x}}^{k - 1}}$ ， ${{{v}}^{k - 1}} = {\left[\begin{array}{*{20}{c}} {v_x^{k - 1}} & {v_y^{k - 1}} \end{array}\right]^{\rm T}}$ ， ${\theta ^{k - 1}}$ 分别为 $k - 1$ 时刻UUV东北向位置、沿载体系的横向和纵向速度测量信息、载体航向信息； $\Delta t$ 为采样时间间隔。

根据式（1）可以得到相应离散系统状态方程：

$ {{{x}}^k} = {{{F}}^k}{{{x}}^{k - 1}} + {\bf{\varGamma }}\left( {{u^k} + {w^k}} \right)\text{，} $

(2)

式中： ${{{F}}^k}$ 为状态转移矩阵； ${{\varGamma }}({u^k} + {w^k})$ 为非线性项， ${{{u}}^k} = {[\begin{array}{*{20}{c}} {{v^k}}&{{\theta ^k}} \end{array}]^{\rm T}}$ 表示控制输入量， ${{{w}}^k} = {[\begin{array}{*{20}{c}} {w_v^k}&{w_\theta ^k} \end{array}]^{\rm T}}$ 为系统过程噪声，包括速度噪声和方位噪声，协方差矩阵为:

$ {{{Q}}^k} = E\left[ {{w^k}{{\left( {{w^k}} \right)}^{\rm T}}} \right] = \left[ {\begin{array}{*{20}{c}} {\sigma _{{v^k}}^2}&0 \\ 0&{\sigma _{{\theta ^k}}^2} \end{array}} \right]\text{。} $

(3)

为抑制航位推算误差的不断积累，ASV间可以通过相对距离观测进行导航误差的协同校正。根据 $k$ 时刻接收到的主艇参考位置信息 ${{x}}_m^k = [\begin{array}{*{20}{c}} {x_{1m}^k} & {x_{2m}^k} \end{array}]^{\rm T}$ ，以及从艇自身位置状态 ${{{x}}^k} = {[\begin{array}{*{20}{c}} {x_1^k} & {x_2^k} \end{array}]^{\rm T}}$ 可以得到相应的距离量测方程：

$ {z^k} = h({x^k}) + {e^k} = \sqrt {{{(x_{1m}^k - {x^k})}^2} + {{(x_{2m}^k - {x^k})}^2}} + {e^k} {\text{。}} $

(4)

式中： ${e^k}$ 为水声距离量测噪声，协方差矩阵为：

$ {{{R}}^k} = E\left[ {{e^k}{{\left( {{e^k}} \right)}^{\rm T}}} \right] = \sigma _{{e^k}}^2\text{。} $

(5)

2 基于M估计多UUV协同定位算法

将统计理论中的M估计算法与EKF算法进行融合，提出M估计多UUV协同定位算法。

对式（2）和式（4）进行改写，得到EKF框架下的数学模型：

$ \left\{ \begin{array}{l} {{{x}}_k} = {{{F}}_k}{{{x}}_{k - 1}} + {{{B}}_k}{{{u}}_k} + {{\bf{w}}_k} \text{，} \\ {{{z}}_k} = {{{H}}_k}{{{x}}_k} + {{{e}}_k}\text{。} \\ \end{array} \right. $

(6)

其中： ${{{B}}_k}$ ， ${{{H}}_k}$ 分别为对应项的雅克比矩阵； ${{{e}}_k}$ 为重尾噪声。

对于M估计多UUV协同定位算法，增加如下状态方程：

$ {{{\hat x}}_{k|k - 1}} = {{{F}}_k}{{\bf{\hat x}}_{k - 1|k - 1}} + {{{B}}_k}{{{u}}_k} + {{{w}}_k} \text{，} $

(7)

$ {{{\hat x}}_{k|k - 1}} = {{{x}}_k} + {{\bf{\delta }}_{k|k - 1}}\text{。} $

(8)

其中： ${{{\hat x}}_{k - 1|k - 1}}$ 和 ${{{\hat x}}_{k|k - 1}}$ 分别为 $k - 1$ 时刻对 ${{{x}}_{k - 1}}$ 和 ${{{x}}_k}$ 的最优估计； ${{\bf{\delta }}_{k|k - 1}}$ 为 ${{\bf{\hat x}}_{k|k - 1}}$ 与真实值 ${{{x}}_k}$ 的估计误差。

根据式（6）和式（8）得到以量测噪声和状态误差最小为评价指标的M估计数学模型：

$ \left[ \begin{array}{l} {{\hat {{x}}}_{k|k - 1}} \\ {{{Z}}_k} \\ \end{array} \right] = \left[ \begin{array}{l} {{I}} \\ {{{H}}_k} \\ \end{array} \right]{{\bf{x}}_k} + \left[ \begin{array}{l} {{\bf{\delta }}_{k|K - 1}} \\ {{{e}}_k} \\ \end{array} \right]\text{，} $

(9)

将上式简写为

$ {{\tilde{{Z}}}_k} = {{\tilde{{H}}}_k}{{{x}}_k} + {{\tilde{{e}}}_k} \text{，} $

(10)

其中， ${{\tilde{\bf{Z}}}_k} = \left[ \begin{array}{l} {{\hat {{x}}}_{k|k - 1}} \\ {{{z}}_k} \\ \end{array} \right]$ ， ${{\tilde{{H}}}_k} = \left[ \begin{array}{l} {{I}} \\ {{{H}}_k} \\ \end{array} \right]$ ， ${{\tilde{{e}}}_k} = \left[ \begin{array}{l} {{\bf{\delta }}_{k|k - 1}} \\ {{{e}}_k} \\ \end{array} \right]$ 。

对上式改写

$ f\left( {{{\tilde e}_k}} \right) = \tilde { Z}_{_k} - \tilde { H}_{_k}{x_k}{\text{。}} $

(11)

对式（11）进行计算，欲令 ${\tilde e_k}$ 取最小，根据M估计的思想，利用函数 $J({x_k}) = - \sum\limits_{i = 1}^{m = 2} {{\rho _i}({{\tilde e}_k})} $ 求导并令导数为0，有

$ \frac{{\partial J({x_k})}}{{\partial {x_k}}} = \sum\limits_{i = 1}^{m = 2} {\frac{{\partial {\rho _i}(\tilde e_k^i)}}{{\partial (\tilde e_k^i)}}} \cdot \frac{{\partial \tilde e_k^i}}{{\partial {x_k}}} = 0 \text{，} $

(12)

$ \frac{{\partial J({x_k})}}{{\partial {x_k}}}= \sum\limits_{i = 1}^{m = 2} {{h_i} \cdot \frac{{\partial {\rho _i}(\tilde e_k^i)}}{{\partial (\tilde e_k^i)}}} = 0 \text{，} $

(13)

$ \frac{{\partial J({x_k})}}{{\partial {x_k}}}= \sum\limits_{i = 1}^{m = 2} {{h_i} \cdot \frac{{\tilde e_k^i}}{{\tilde e_k^i}}\frac{{\partial {\rho _i}(\tilde e_k^i)}}{{\partial (\tilde e_k^i)}}} = 0\text{，} $

(14)

$ \frac{{\partial J({x_k})}}{{\partial {x_k}}}= \sum\limits_{i = 1}^{m = 2} {{h_i} \cdot (\tilde Z_k^i - {h_i}{x_k})\frac{1}{{\tilde e_k^i}} \cdot \frac{{\partial {\rho _i}(\tilde e_k^i)}}{{\partial (\tilde e_k^i)}}} = 0\text{。} $

(15)

其中， ${{\tilde{{H}}}_k} = \left[ \begin{array}{l} {h_1} \\ {h_2} \\ \end{array} \right]$ ， $\rho \left( {{{\tilde e}_k}} \right) = \left[ \begin{array}{l} {\rho _1}\left( {{{\tilde e}_k}} \right) \\ {\rho _2}\left( {{{\tilde e}_k}} \right) \\ \end{array} \right]$ ， ${{\tilde{\bf{e}}}_k} = \left[ \begin{array}{l} e_k^1 \\ e_k^2 \\ \end{array} \right]$ ， ${{\tilde{{Z}}}_k} = \left[ \begin{array}{l} \tilde Z_k^1 \\ \tilde Z_k^2 \\ \end{array} \right]$ ， ${\rho _i}({\tilde e_k})$ 称为极值函数，设 ${\psi _i}(\tilde e_k^i) = \frac{{\partial \rho (\tilde e_k^i)}}{{\partial (\tilde e_k^i)}}$ ，称 $\psi ({\tilde e_k})$ 为得分函数。

将式（15）改写为

$ \sum\limits_{j = 1}^{m = 2} {{h_i} \cdot {q_i}(e_k^i) \cdot (\tilde Z_k^i - {h_i}{x_k})} = 0\text{，} $

(16)

将式（16）写成矩阵形式

$ {{\tilde{{H}}}^{\rm T}}{{Q}}({\tilde{{Z}}} - {\tilde{{Hx}}}) = {{0}}\text{，} $

(17)

其中， ${{Q}} = {\rm diag}\{ q({\tilde e_k})\} $

利用Newton法解上式方程，得

$ {{\hat x}}_{k|k}^{j + 1} = {({{\tilde{{H}}}^{\rm T}}{{{Q}}^j}{\tilde{{H}}})^{ - 1}}{{\tilde{{H}}}^{\rm T}}{{{Q}}^j}{{\tilde{{Z}}}_k}\text{，} $

(18)

其中，j为迭代次数。

利用式（18）进行迭代即可得到 $\hat x_{k|k}$ 的最优值，此时，协方差阵为：

$ {{P}}_{k|k} = {({{\tilde{{H}}}^{\rm T}}{{Q}}{\tilde{{H}}} )^{ - 1}}\text{。} $

(19)

对极值函数进行分析。可以看出，当极值函数 $\rho $ 取不同的函数形式时，最后获得的最优估计 $\hat x_{k|k}$ 也会不同。如当 $\rho ({\tilde e_k}) = \dfrac{{{{\tilde e}_k}^2}}{2}$ 时，M估计就可以转化成最小二乘估计，此时 ${\tilde e_k}$ 应服从正态分布，但对于本文中所提量测噪声 ${\tilde e_k}$ 是重尾噪声，即非正态分布，因此，对极值函数 $\rho $ 进行调整，使其能对重尾噪声进行处理就是本算法的根本任务。

对于极值函数 $\rho $ 的设定，在M估计理论中有很多方法^[11-13]，如Huber法，Hample法和IGG法等，本算法选取IGG法，其极值函数如下式：

$ \left\{ \begin{aligned} & \rho (t) = \frac{{{t^2}}}{2},\left| t \right| < 1.5\sigma \text{，} \\ & \rho (t) = c\left| t \right|,1.5\sigma \leqslant \left| t \right| < 3\sigma\text{，} \\ & \rho (t) = d,3\sigma \leqslant \left| t \right| \text{。} \end{aligned} \right. $

(20)

可以发现，IGG法将权值函数分成了3段，可依次视为可信段、怀疑段和异常噪声段，然后分别采用保留、降权和舍去的方法进行处理，显然这种处理方式很适合处理重尾噪声。

本文所提算法如图1所示。可以看出，相较于经典EKF算法，所提算法的优点是通过函数 $\rho (\tilde e)$ 在 ${l_1}$ 范数和 ${l_2}$ 范数之间不断转换来实现 ${l_1}$ 范数与 ${l_2}$ 范数混合滤波。当 $t \to 0$ 时， $\rho (\tilde e)$ 接近于 ${l_1}$ 范数下的 $J(x)$ 最小，鲁棒性好；当 $t \to \infty $ 时， $\rho (\tilde e)$ 越近于 ${l_2}$ 范数下的 $J(x)$ 最小，即 $\psi \to I$ ，与传统EKF算法等价，从而来抑制重尾噪声的影响。

3 实验验证

采用湖上实验数据进行半实物仿真，验证所提算法有效性。实验具体情况说明如下：

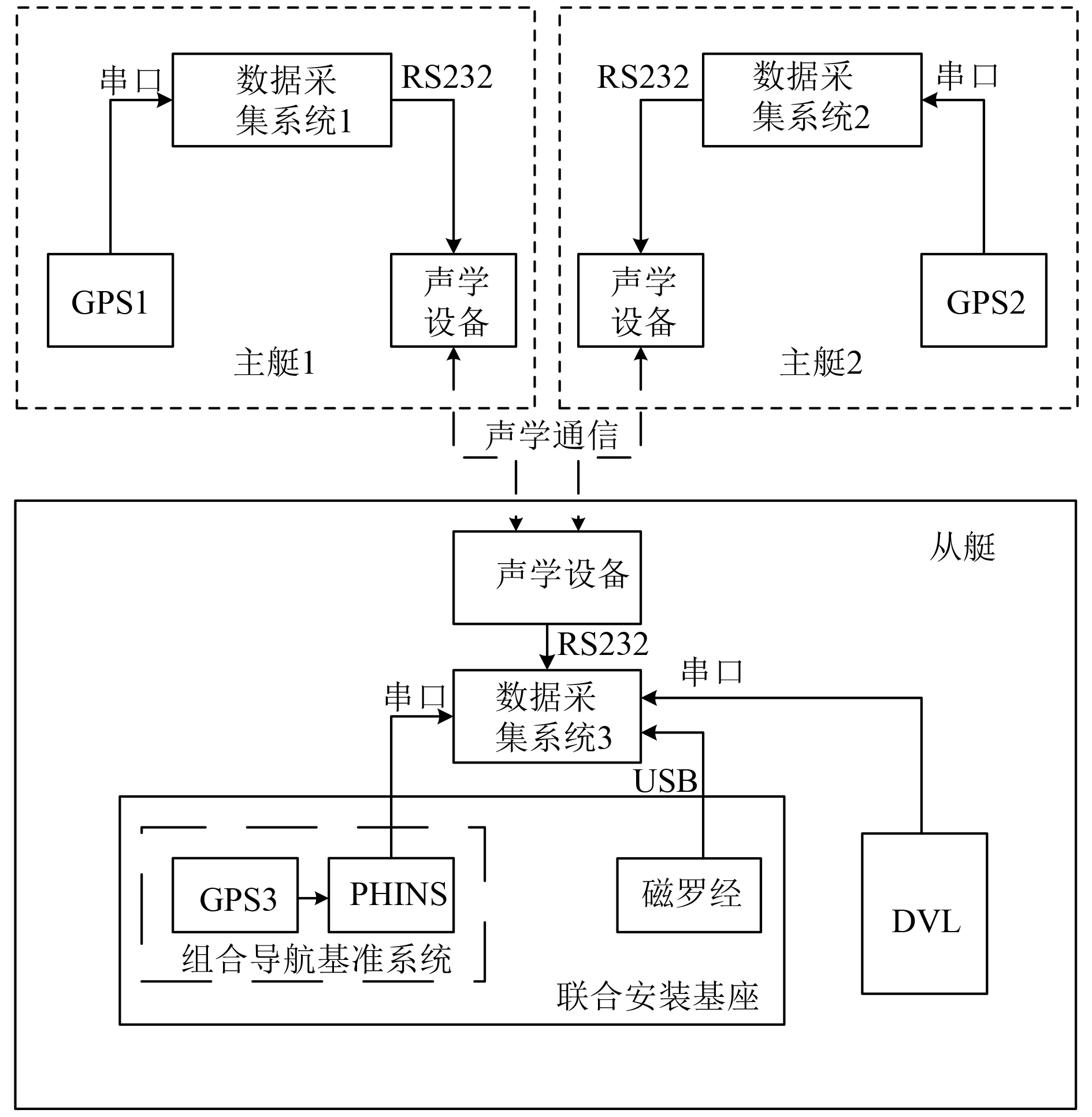
湖上实验采用图2所示水面艇模拟UUV进行，实验方案如图3所示。实验共配置2艘主艇、1艘从艇，实验过程中2条主艇采用高精度的实时GPS位置信息作为基准参考，利用水声通信设备实现主从艇间参考信息的传输及相对距离信息的观测，从而实现对从艇航位推算误差的协同校正。从艇航位推算中的位置信息是采用DVL提供的绝对速度信息以及磁罗经提供的航向信息经推算得到的。为进行比对，从艇上还安装有GPS/PHINS组合导航系统，用来提供从艇相对精确的位置、速度和航向信息。水声通信设备采用图4所示的德国Evologics公司S2CR 7/17型水声通信设备构建水声通信网络，实现主从艇间相对距离的测量以及信息的传递。为便于操作，实验时2艘主艇各自以固定通信周期向从艇发送自身带标识符的GPS位置信息以及二者相对距离量测信息，辅助从艇进行导航误差的协同校正；从艇无论接收到哪个主艇的观测信息，都利用该信息进行协同导航。实验用声学设备采用RSS原理进行测距，当从艇成功接收到主艇参考信息后，向主艇返回一个应答脉冲信号，主艇接收到该应答信号后，利用该信号进行基于RSS原理的信号传播距离的解算，即在协同导航过程中，主艇每次通过水声通信传递给从艇的参考信息为自身GPS位置信息+前一时刻的水声距离量测信息。实验过程中采用的相关传感器指标如表1所示。

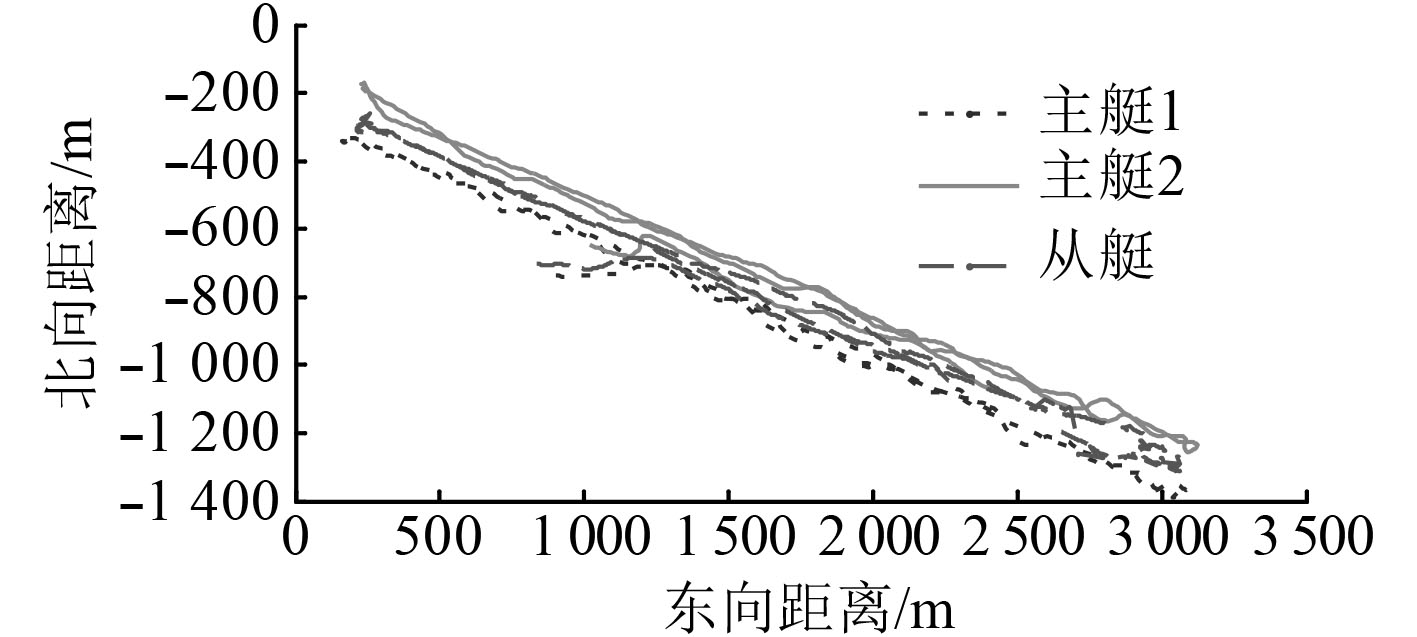
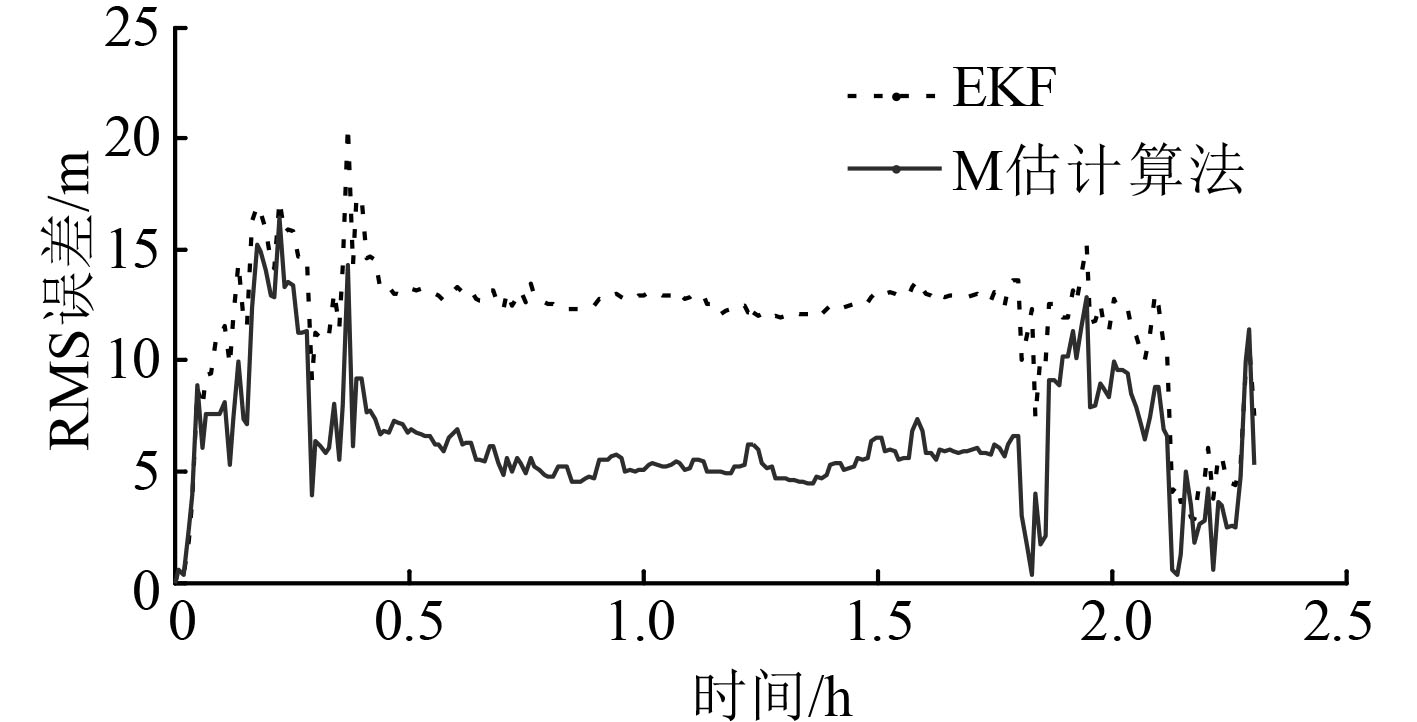
主从艇按5 s周期进行通信，实验时间超过2.3 h。主从艇运行轨迹如图5所示。分别采用EKF算法和本文所提算法对从艇位置信息进行解算，实验结果如图6所示。可知，2种算法定位误差均收敛，即都可以用于协同导航；M估计多UUV协同定位算法的定位误差在10 m以下，且在0.5–1.75 h时，误差稳定在5 m左右，相较于传统EKF算法，其定位效果得到提升约30%，说明了所提算法在处理水下异常噪声方面的优越性。

4 结　语

　　本文针对多UUV协同导航技术中存在的异常量测噪声进行处理，通过实际实验数据分析，对异常量测噪声采用重尾噪声模型进行重新建模，并针对重尾噪声特点，提出M估计多UUV协同定位算法，有效克服了水声距离异常量测噪声对于UUV协同定位系统的影响。实验结果表明，采用本文所提算法，多UUV协同定位精度一般可达5 m左右，相较于传统EKF算法，协同定位精度可提升30%左右，工程应用价值巨大。