船舶注水系统在舷外海水背压作用下向浮力调整水舱自流注水,动态均衡船舶因海水密度和舱内载荷改变引起的浮力变化。系统管路结构与管内流体相互作用,结构在流体力的激励下会产生弹性变形,结构耦合振动产生的噪声沿通海系统向海洋环境辐射。大压差工况下,由于注水系统流量调节阀的节流作用,管路结构在流体激励作用下振动剧烈,舷外辐射噪声问题突出。因此,开展注水系统管路流固耦合作用下的振动和噪声研究对于船舶系统的减振降噪具有重要意义。
针对管路系统振动噪声问题,学者开展了大量研究。刘翠伟[1]针对输气管道阀门的流噪声进行了研究,分析了管路流噪声产生的机理和传播规律;冯志鹏[2]对直管的动态特性和流致振动进行数值模拟研究,指出了流体力与结构位移间的相位关系;徐存东[3]采用附连水质量法建立压力管道数值模型,基于流固耦合理论对泵站压力管道的模态和振动位移进行了分析,提出了针对压力管道的具体减振措施。目前诸文献的研究成果主要集中在管路流噪声和流固耦合作用下的结构振动上,对于流体激励管道结构振动产生的辐射噪声相关研究却鲜见报道。
本文基于流固耦合理论对船舶自流注水系统管内流体激励结构产生的振动和噪声进行分析,探究注水系统流激振动噪声产生、传播和衰减规律,为注水系统振动和噪声治理提供理论依据。
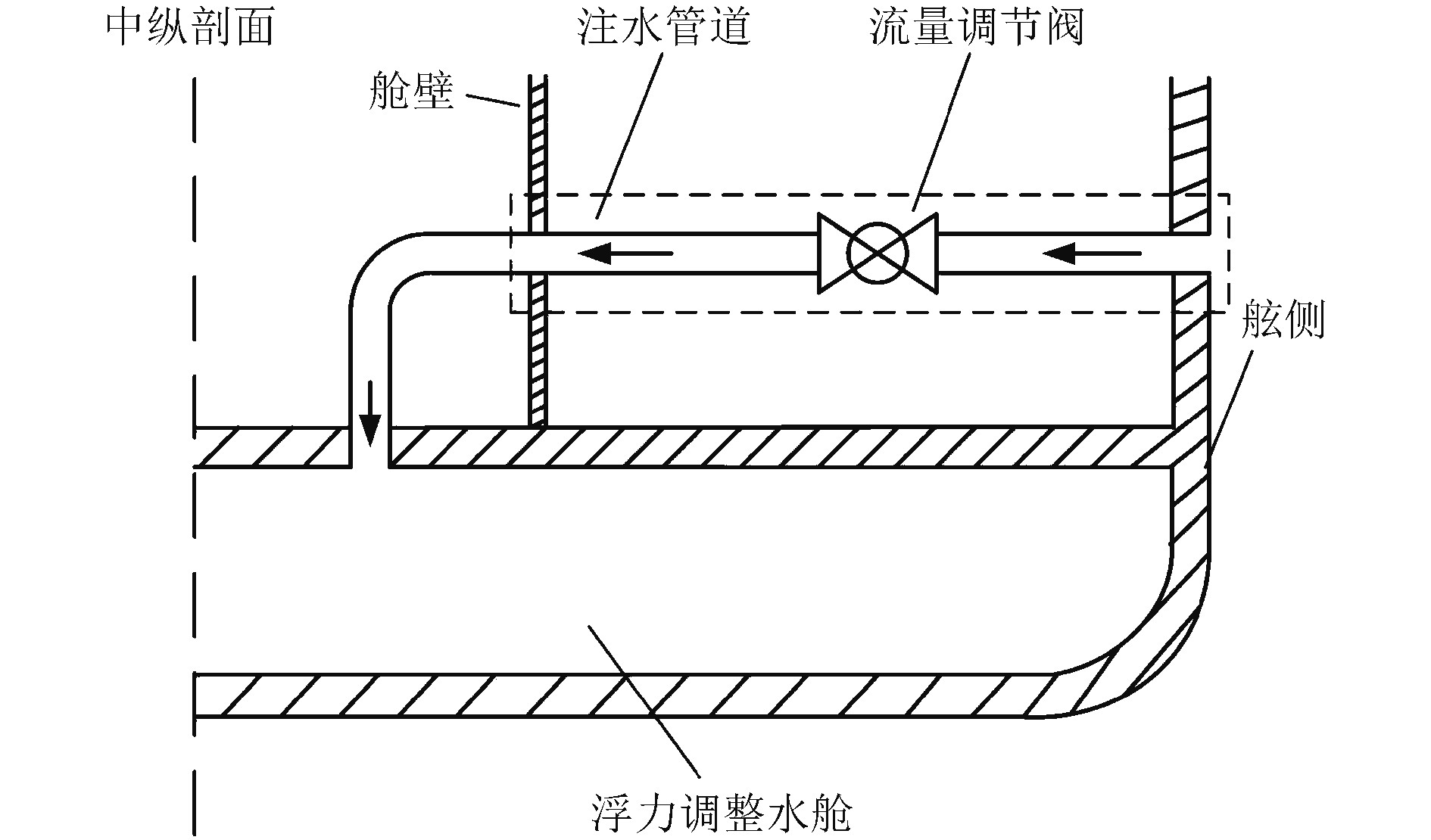
1 研究模型 1.1 注水系统管路几何模型注水系统管路布置如图1所示,系统管路主要由管道、流量调节阀以及浮力调整水舱等组成,管路穿过船体外壳、舱内金属围壁后与位于舱底的浮力调整水舱相通。在舷外海水压力的作用下,海水通过管道由舷外进入浮力调整水舱调整船舶的浮态。
|
图 1 注水管路平面布置 Fig. 1 Water injection pipeline layout |
自流注水系统注水流量由流量调节阀调节,流量调节阀的内部结构形式类似于球阀,阀芯通径为80 mm,布置在船体外壳与舱内金属围壁中间;与流量调节阀连接的是内径为100 mm、壁厚为7 mm的铁白铜管,流量调节阀进出口的管道长度均为1 000 mm,分别与船体外壳和舱内金属围壁通过焊接的形式刚性连接。
本文选取位于船体外壳与舱内金属围壁间的压力管道及阀门等作为研究对象,如图2所示。法兰、阀杆以及阀门执行机构等对结构的模态和振动影响可忽略不计,因此三维建模时对部分附件结构作简化处理。

|
图 2 管路结构三维模型 Fig. 2 3D- model of pipeline structure |
流固耦合的基本原理是建立在流体力学和固体力学的基本理论之上,对流固耦合作用下的结构振动进行分析需要从流体力学和固体力学出发。流体在固体管道内运动的过程中,流体运动在固体管道表面产生流体力的作用,反之,固体管道在流体力激励作用下产生结构振动又以力的形式反作用于流体,改变流体在固体管道内的运动状态[4-9]。流体和固体耦合交界面上,二者具有相同的力和速度,固体管道可视作弹性体,其动力学离散方程可表示为:
| $ { M}\{ \ddot \delta \} + { C}\{ \dot \delta \} + { K}\{ \delta \} = F(t) + {R_f}(t){\text{。}} $ | (1) |
式中:
管内流体激励管道结构振动的计算采用分离解法[10],即流场计算和结构计算分开进行,二者通过交界面进行载荷数据传递。管道结构的振动对压力管道内流体流场的影响较小,可忽略不计,因此只考虑流体力对结构的单向传递,即进行单向流固耦合分析。采用Fluent软件进行流场分析,再将流场数据导入Virtual. Lab软件通过交界面传递给结构。
1)结构离散
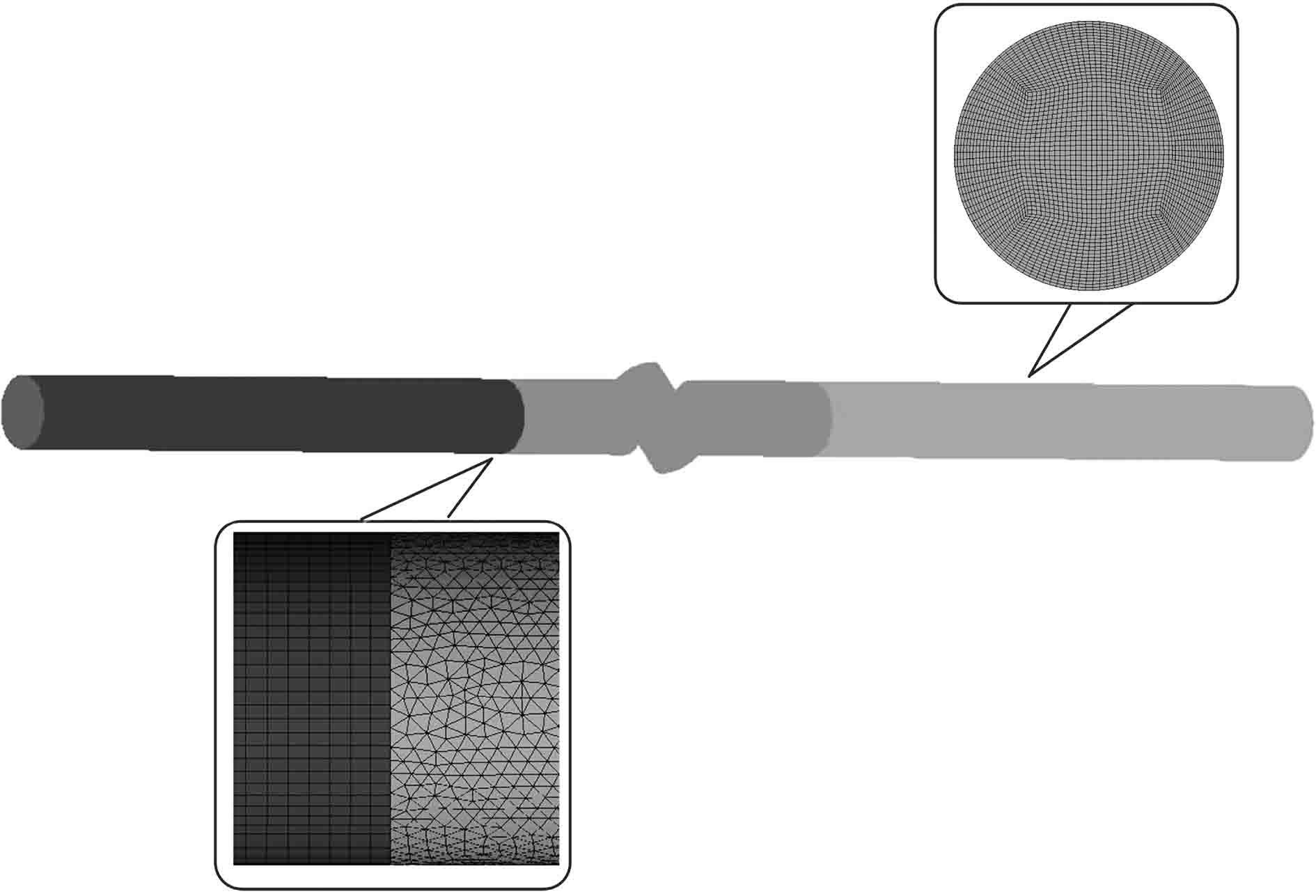
采用混合网格划分方案,阀门附近流场采用非结构化网格且网格适当细化,管道采用结构化网格,网格总数为236万,满足网格无关性要求。流场网格模型如图3所示。
|
图 3 流场网格模型 Fig. 3 Flow field mesh model |
2)参数设置
参考压力为一个标准大气压,结合注水系统典型运行工况的特点,模型进口压力设为1.8 MPa,水舱背压为一个标准大气压,因此模型出口压力设为0。湍流模型选择大涡模拟,求解器采用耦合式求解器,时间步长设为
注水系统压力和速度分布云图4所示。在进出口大压差和阀门节流的联合作用下,阀内海水介质流速最大值达到55.71 m/s,通过阀门后流速迅速降低。同样,阀门前后压力变化剧烈,压力和流速剧降伴随着水力能量损失,压力能和动能向声能和振能转化,因此流场的迅速变化是阀门及管道结构振动的根源。

|
图 4 注水系统压力和速度分布云图 Fig. 4 Distribution of pressure and velocity of water injection system |
本文对船体外壳与舱内金属围壁间管路结构进行模态分析,考虑海水介质对结构模态计算的影响,即应该基于“湿模态”计算管道结构在壁面压力脉动激励作用下的耦合振动。在对结构进行模态计算时,管道内海水介质作为附加质量处理。管材为铁白铜,考虑附加水质量后的等效密度为10 524 kg/m3,弹性模量取2.1 × 1011 N/m2,泊松比为0.32。
经过简化后的结构有限元模型如图5所示,管道网格适当细化,阀门处网格适当加粗,网格单元总数为29万,满足计算精度要求。注水系统管道与舷侧外壳、船内舱壁通过焊接固定,因此有限元模型两端可以看作固定端,即在模型管端截面单元节点上施加全约束。

|
图 5 管道及阀门结构有限元网格 Fig. 5 Finite element mesh of pipe and valve structure |
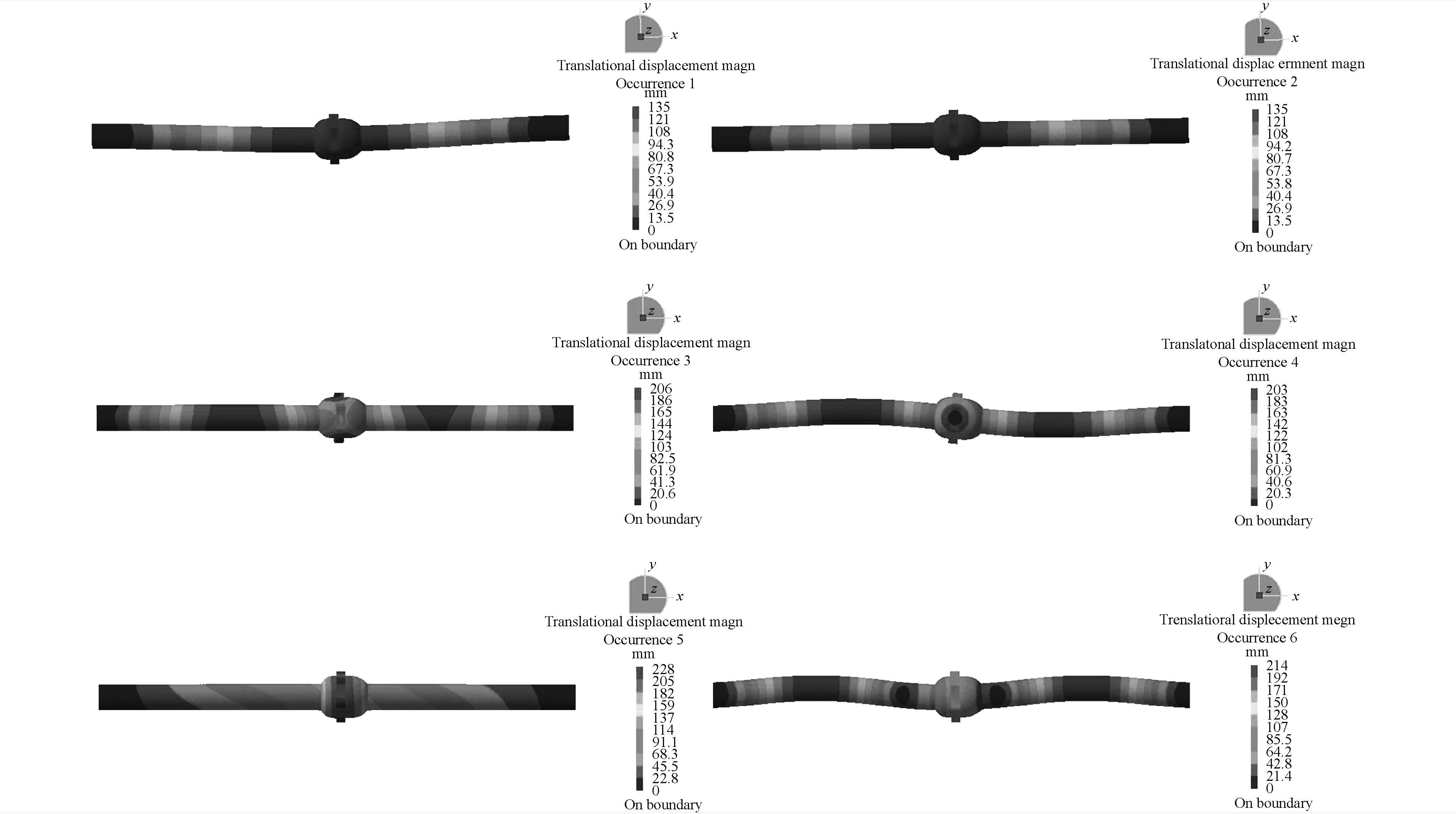
前6阶模态固有频率和最大振幅如表1所示。管道及阀门结构的前6阶模态分别为84.71 Hz,84.82 Hz,323.69 Hz,324.11 Hz,340.14 Hz,571.25 Hz。管道及阀门前6阶模态振型如图6所示。根据注水系统管路振型图分析可知,结构的薄弱部位是阀门和阀门两侧管道的中间部位。阀门以及阀门两侧管道的中间部位需要进行加固处理以减小振动,可采取分别在两侧管道的中间部位增设弹性连接的支吊架、马脚等措施。
|
|
表 1 前6阶模态固有频率和最大振幅 Tab.1 Natural frequency and amplitudes of the first 6 modes |
|
图 6 结构前6阶模态振型 Fig. 6 The first 8 modal shapes of the structure |
声学计算采用有限元法,有限元法计算内场噪声具有较大的优势[11]。声学有限元模型如图7所示,为使计算结果准确,要求1个波长内有6个单元。根据流场瞬态计算参数设置可知,声学有限元网格最大尺寸为:

|
图 7 声学有限元网格 Fig. 7 Acoustics finite element mesh |
基于注水系统管内流场和结构“湿模态”的计算结果,在Virtual. Lab软件中对流固耦合作用下的结构振动及流激振动辐射噪声进行计算,结构振动的激励源是管内壁面的压力脉动,流场数据通过交界面向结构单向传递。结构振动产生的噪声向管内海水中辐射,并沿管路向舷外传播。为对管道内流激振动噪声沿管道传播、衰减特性进行研究,沿模型管道进口至出口布置监测点:A(0,0.0),B(500,0,0),C(900,0,0),D(1055,0,0),E(1211,0,0),F(1612,0,0),G(2112,0,0)。
沿管道进口至出口的7个监测点声压级频域分布曲线如图8所示。各监测点10 000 Hz内声压级波动范围、中间幅值、平均幅值如表2所示。由图8和表2可以看出:

|
图 8 监测点声压级频域分布曲线 Fig. 8 The frequency distribution curve of sound pressure level on monitoring points |
|
|
表 2 各监测点声压级 Tab.2 Sound pressure level of monitoring points |
1)注水系统各监测点流激振动噪声频带较宽,各监测点峰值频率均为80 Hz,290 Hz,510 Hz,660 Hz,1 490 Hz,2 050 Hz,2 230 Hz,2 540 Hz,2 910 Hz,4 390 Hz,4 810 Hz,其中主频为80 Hz,峰值频率主要集中在低频。由此可知,流激振动噪声低频部分能量相对较大,高频部分能量相对较小。
2)沿注水管路进口至出口分布的各监测点总声压级大小基本相同,可见流激振动噪声由管内向舷侧传播无衰减。
3)注水系统流固耦合作用下的管内各监测点流激振动噪声整体幅值均较大,且噪声频域分布规律相近,即流体激励结构振动产生的辐射噪声在各监测点具有相同的特性。原因是各监测点具有相同的振动噪声,且注水管路振动产生的辐射噪声沿管道传播基本无衰减。
5 结 语通过对船舶注水系统典型运行工况下管路振动及流激振动噪声数值模拟分析,可以得到以下结论:
1)注水系统舷侧外壳与船内舱壁间注水管路整体振动较剧烈,沿管路进口至出口管内振动辐射噪声总声压级在219 dB以上,注水系统的流激振动噪声问题不可忽视。
2)注水系统容易激振的部位集中在阀门及阀门两侧管道的中间部位,需在此部位进行加固处理,可采取的措施包括增设弹性连接的吊支架、马脚等。
3)注水系统的流激振动噪声频带较宽,主频为80 Hz,噪声由管内向舷外传播基本无衰减,水下辐射效率较高,将对总体辐射噪声造成影响。
| [1] |
刘翠伟, 等. 输气管道气体流经阀门气动噪声产生机理分析[J]. 振动与冲击, 2014, 33(2): 152-157. DOI:10.3969/j.issn.1000-3835.2014.02.029 |
| [2] |
冯志鹏, 等. 三维横向流体诱发直管振动的数值模拟[J]. 应用数学与力学, 2013, 34(12): 1311-1320. |
| [3] |
徐存东, 等. 附加水体质量模型的压力管道流激振动分析[J]. 南水北调与水利科技, 2014, 12(1): 138-144. |
| [4] |
陈贵清, 郝婷玥, 戚振宕. 物理参数对压力管道振动固有频率的影响[J]. 唐山学院学报, 2005, 18(4): 96-99. CHEN Gui-qing, HAO Ting-yue, QI Zhen-dang. Physical parameters of the natural frequency of the pressure pipe vibration effects[J]. Tangshan College, 2005, 18(4): 96-99. DOI:10.3969/j.issn.1672-349X.2005.04.028 |
| [5] |
王其正. 结构耦合动力学[M]. 北京: 宇航出版社, 1999: 226-234.
|
| [6] |
BUNGARTZ F H J. Fluid-Structure Interaction-modeling, Simulation, Optimization[M]. Springer, Berlin, Heidelberg, 2006.
|
| [7] |
OZDEMIRA Z, SOULIB M, FAHJANC Y M. Application of nonlinear fluid-structure interaction methods to seismic analysis of anchored and unanchored tanks[J]. Engineering Structure, 2010, 32(2): 409-423. DOI:10.1016/j.engstruct.2009.10.004 |
| [8] |
刘忠族, 黄玉盈, 钟伟芳. 无限长圆柱壳附连水质量与波数的关系[J]. 中国造船, 1998(1): 52-56. LIU Zhong-zu, HUANG Yu-ying, ZHONG Wei-fang. Relationship between added mass and wave numbers of an infinitely long cylindrical shell submerged in water[J]. Shipbuilding of China, 1998(1): 52-56. |
| [9] |
刘祖军. 拱式渡槽力学性能三维有限元分析及研究[D]. 郑州: 华北水利水电学院, 2006. LIU Zu-jun. Analysis on stressed performance of structure for arched aqueduct with 3-D FEM[D]. Zhengzhou: North China Institute of Water Conservancy and Hydropower, 2006. |
| [10] |
宋学官, 蔡林, 张华. Ansys流固耦合分析与工程实例[M]. 北京: 中国水利水电出版社, 2012.
|
| [11] |
詹福良, 徐俊伟.Virtual. Lab Acoustics 声学仿真计算从入门到精通[M]. 西安: 西北工业大学出版社, 2013.
|
 2020, Vol. 42
2020, Vol. 42
