十字型尾舵潜体虽然能够有效控制潜体运动,但对潜体高速旋回时出现的严重横倾难以通过操舵加以控制和改善,从而限制了潜体回转机动的速度和安全性[1]。针对传统十字舵的缺点,多国新型潜体已经正式确定采用分离式舵,其尾升降舵的左右2个舵板可独立转动,当2个舵板操不同舵角时,便可产生差动舵角,在控制潜体潜伏的同时产生横倾力矩,从而对潜体横倾进行主动控制[2]。分离式尾舵能够有效控制潜体运动姿态,并能有效控制、消除横倾,对于潜体的作战使用十分有利。
本文通过分析潜体差动舵角在空间机动时的舵力和舵力矩,建立潜体差动舵操纵运动数学模型,并针对高速旋回情况下潜体运动姿态控制进行仿真研究。
1 差动舵角横倾受力分析 1.1 单独操纵控制能力分析单独操纵分离式舵的某一舵板,即产生差动舵角,差动舵角既能改变潜体的深度和纵倾,又能使潜体产生一定的横倾。尾升降舵单操某一舵共有4种情况,下面分别对分离式尾升降舵单舵操纵进行定性分析。
操纵左尾升降舵下潜舵,操舵产生的垂向力和纵倾力矩使潜体首倾下潜,产生的横倾力矩
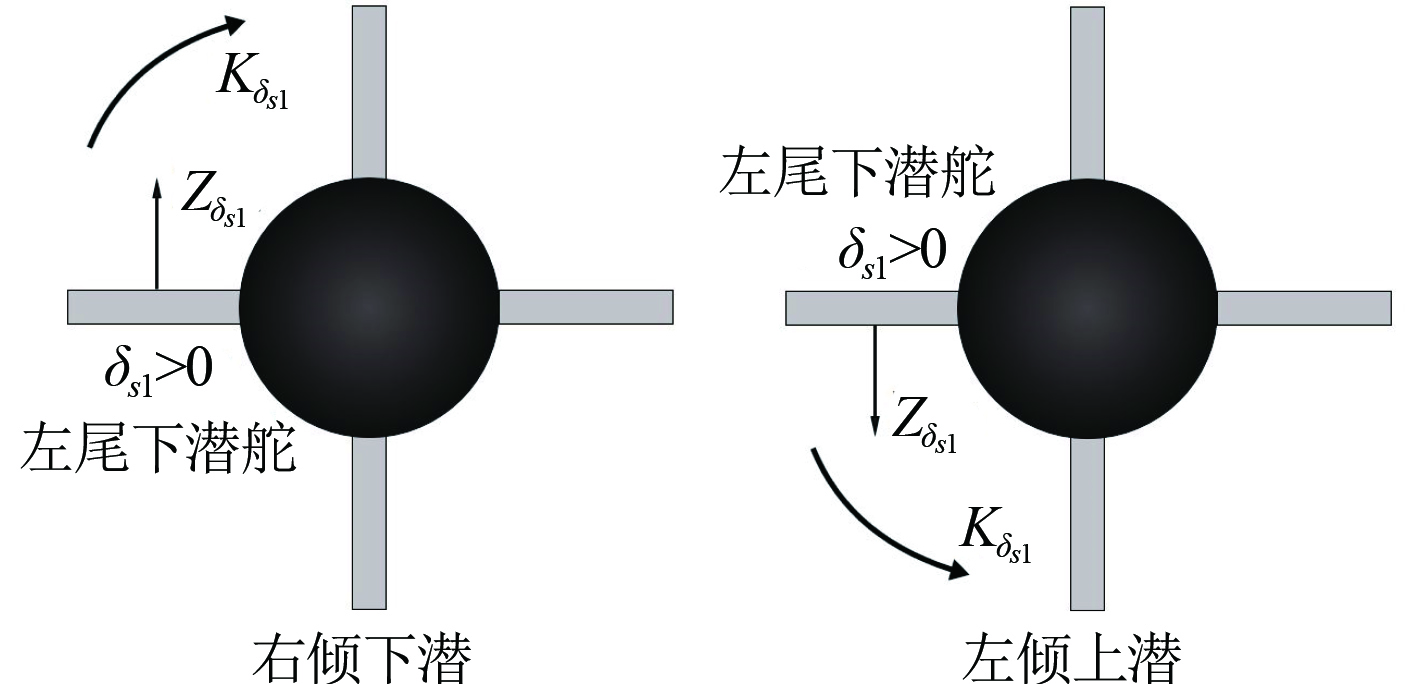
|
图 1 单独操纵左艉升降舵下潜舵、上浮舵 Fig. 1 Left stern plane in diving and surfacing |
操纵右尾升降舵下潜舵,这时操舵产生的垂向力和纵倾力矩使潜体首倾下潜,同时产生的横倾力矩
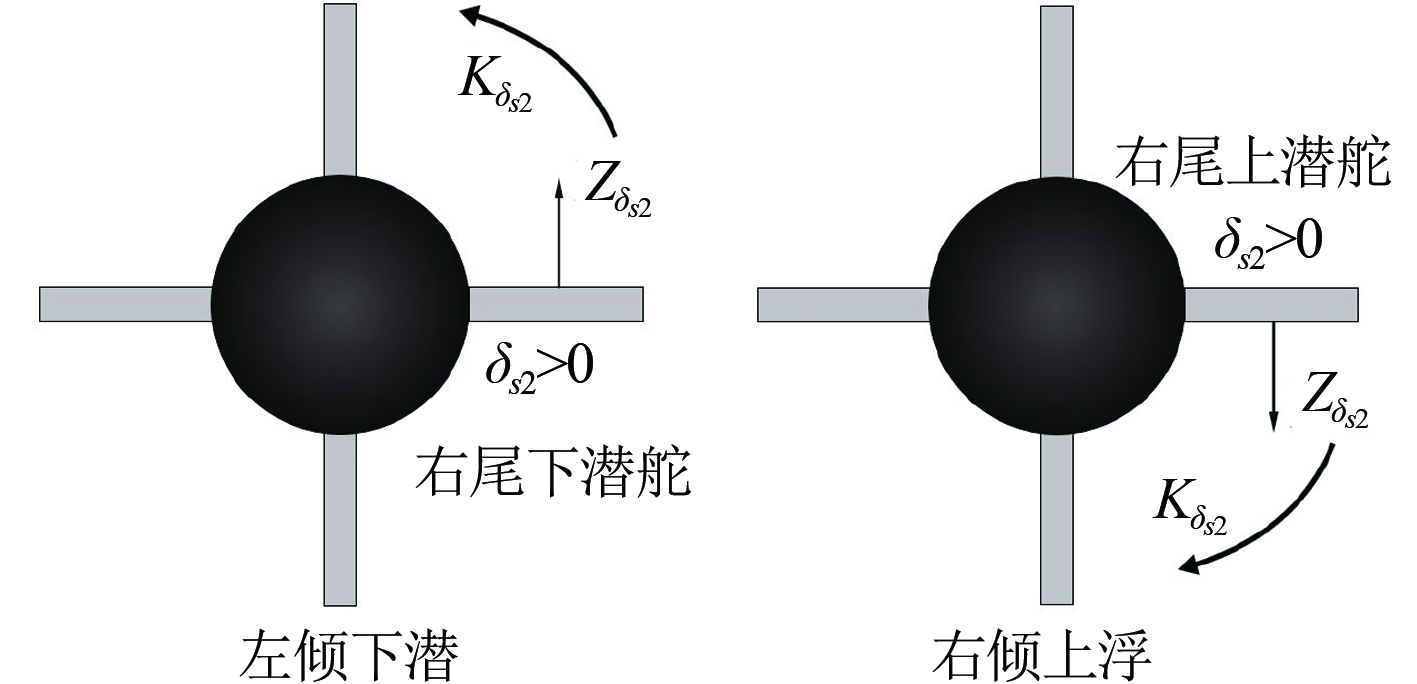
|
图 2 单独操纵右尾升降舵下潜舵、上浮舵 Fig. 2 Controlling right stern plane in diving and surfacing |
绝大多数情况下差动舵应采用双舵操纵控制,左右尾升降舵同时操纵时,共有12种组合,下面选取3种情况对双舵操纵进行分析。
1)当左右尾升降舵均操下潜舵且

|
图 3
同操左右艉升降舵下潜、上浮舵且
|
当左尾升降舵操上浮舵,右尾升降舵操下潜舵,且
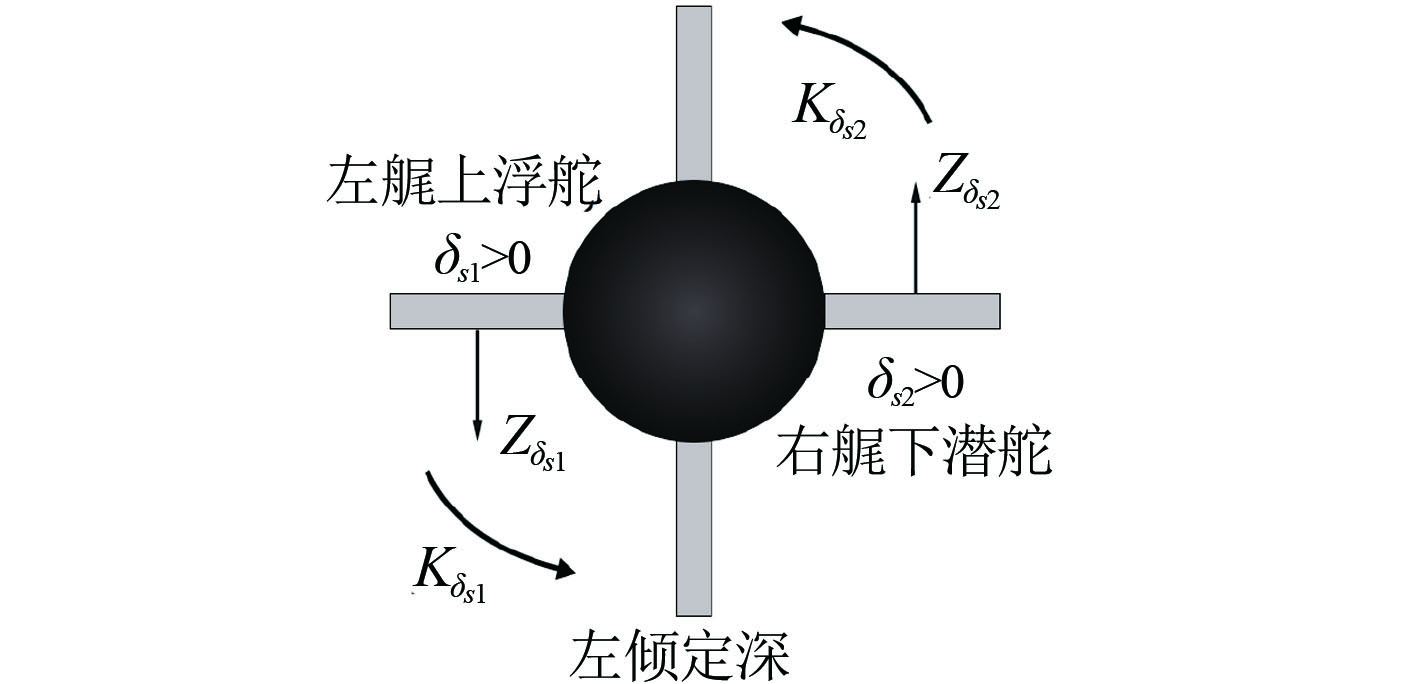
|
图 4
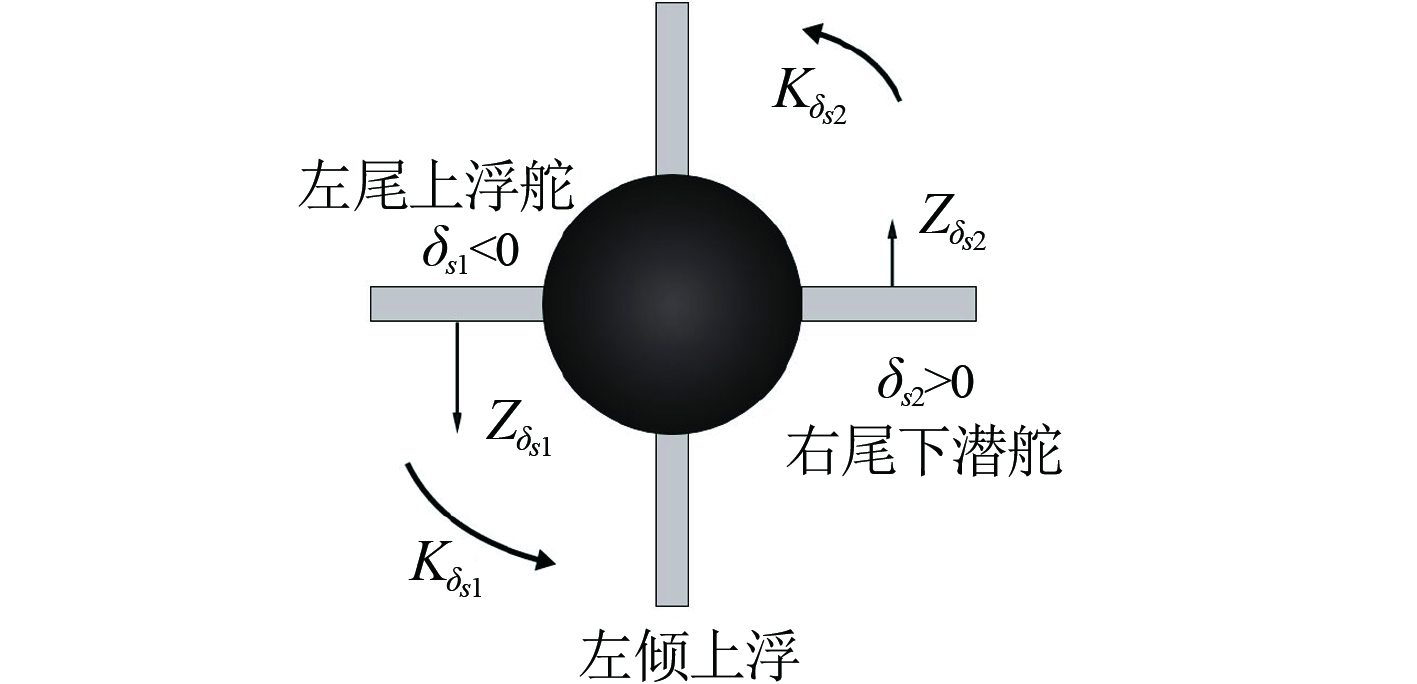
左尾舵操上浮舵,右尾舵操下潜舵且
|
3)当左尾升降舵操上浮舵,右尾升降舵操下潜舵,且
潜体高速定深旋回是最重要的运动方式之一,旋回性能是水平面运动的重要指标。本文潜体在高速旋回过程中的响应方程采用2阶转首响应方程[3],其可写成:
| $ \ddot r + \left(\frac{1}{{{T_1}}} + \frac{1}{{{T_2}}}\right)\dot r + \frac{1}{{{T_1}{T_2}}}r = \frac{K}{{{T_1}{T_2}}}{\delta _r} + \frac{{K{T_3}}}{{{T_1}{T_2}}}{\dot \delta _r}\text{,} $ | (1) |
对于阶跃操舵方程可简略为:
| $ \ddot r + \left(\frac{1}{{{T_1}}} + \frac{1}{{{T_2}}}\right)\dot r + \frac{1}{{{T_1}{T_2}}}r = \frac{K}{{{T_1}{T_2}}}{\delta _0} \text{,} $ | (2) |
其全解为:
| $ r(t) = {C_1}{e^{ - \frac{t}{{{T_1}}}}} + {C_2}{e^{ - \frac{t}{{T2}}}} + K{\delta _0} \text{。} $ | (3) |
式中:
将
则全解可进一步写成:
| $ r(t) = K{\delta _0}\left(1 - \frac{{{T_1}}}{{{T_1} - {T_2}}}{e^{ - \frac{t}{{{T_1}}}}} - \frac{{{T_2}}}{{{T_1} - {T_2}}}{e^{ - \frac{t}{{{T_2}}}}}\right)\text{。} $ | (4) |
对式(4)进行求导和积分,便可求得转首角加速度和首向角:
| $ \dot r(t) = \frac{{K{\delta _0}}}{{{T_1} - {T_2}}}({e^{ - \frac{t}{{{T_1}}}}} - {C_2}{e^{ - \frac{t}{{T2}}}})\text{,} $ | (5) |
| $ \psi (t) = K{\delta _0}\left[t - ({T_1} + {T_2}) + \frac{{{T^2}_1}}{{{T_1} - {T_2}}}{e^{ - \frac{t}{{{T_1}}}}} - \frac{{{T_2}^2}}{{{T_1} - {T_2}}}{e^{ - \frac{t}{{{T_2}}}}}\right] \text{。} $ | (6) |
差动舵潜体数学模型以DTNSRDC空间运动方程为基础[4],加入了分离式尾升降舵对横倾的控制力(力矩),省略了螺旋桨负荷的影响,同时设动坐标系的原点和艇的重心重合[5-6]。
空间运动时差动尾升降舵舵力及力矩为:
| $ \left\{ \begin{aligned} & X(\delta ) = \sum\limits_{i = 1}^2 {{X_{{\delta _{si}}{\delta _{si}}}}{\delta _{si}}^2}\text{,} \\ & Y(\delta ) = 0\text{,}\\ & Z(\delta ) = \sum\limits_{i = 1}^2 {({Z_{{\delta _{si}}}}{\delta _{si}} + {Z_{|q|{\delta _{si}}}}|q|{\delta _{si}})} \text{,} \end{aligned} \right.\left( {i{\rm{ = }}1,2} \right)\text{,} $ | (7) |
| $ \left\{ \begin{aligned} & K(\delta ) = \sum\limits_{i = 1}^2 {{K_{{\delta _{si}}}}{\delta _{si}}} \text{,}\\ & M(\delta ) = \sum\limits_{i = 1}^2 {({M_{{\delta _{si}}}}{\delta _{si}} + {M_{|q|{\delta _{si}}}}|q|{\delta _{si}})}\text{,} \\ &N(\delta ) = 0\text{。} \end{aligned} \right.\left( {i{\rm{ = }}1,2} \right)\text{,} $ | (8) |
将分离式尾升降舵力(矩)的表达形式无因次化后代入潜体六自由度运动方程,就得到适用于分离式尾升降舵潜体的运动模型,如下式[7-8]:
| $ \begin{split} &m(\dot v - wp + ur)=\\ & \frac{1}{2}\rho {L^4}\left[ {{{Y'}_{\dot r}}\dot r + {{Y'}_{\dot p}}\dot p + {{Y'}_{p\left| p \right|}}p\left| p \right| + {{Y'}_{pq}}pq + {{Y'}_{qr}}qr} \right]+\\ & \frac{1}{2}\rho {L^3}\left[ {{{Y'}_{\dot v}}\dot v + {{Y'}_{vq}}vq + {{Y'}_{wp}}wp + {{Y'}_{wr}}wr} \right]+\\ & \frac{1}{2}\rho {L^3}\left[ {{Y'}_r}ur + {{Y'}_p}up + \sum\limits_{i = 5}^6 {{Y'}_{|r|{\delta _i}}}u|r|{\delta _i} +\right. \\ & \left.{{Y'}_{v|r|}}\frac{v}{{|v|}}\left| {{{({v^2} + {w^2})}^{\frac{1}{2}}}} \right|\left| r \right| \right]+\\ & \frac{1}{2}\rho {L^2}\left[ {{{Y'}_{vw}}vw + {{Y'}_{{\delta _r}}}{u^2}{\delta _r}} \right] + (P - B)\cos \theta \sin \varphi \text{,} \end{split} $ | (9) |
| $ \begin{split} & m(\dot w - uq + vp)=\\ & \frac{1}{2}\rho {L^4}\left[ {{{Z'}_{\dot q}}\dot q + {{Z'}_{pp}}{p^2} + {{Z'}_{rr}}{r^2} + {{Z'}_{rp}}rp} \right]+\\ & \frac{1}{2}\rho {L^3}\left[ {{{Z'}_{\dot w}}\dot w + {{Z'}_{vr}}vr + {{Z'}_{vp}}vp} \right]+\\ & \frac{1}{2}\rho {L^3}\left[ {{{Z'}_q}uq + \sum\limits_{i = 3}^4 {{{Z'}_{|q|{\delta _i}}}u|q|{\delta _i} + {{Z'}_{w|q|}}\frac{w}{{|w|}}\left| {{{({v^2} + {w^2})}^{\frac{1}{2}}}} \right|\left| q \right|} } \right]+\\ & \frac{1}{2}\rho {L^2}\left[ {{{Z'}_{\left| w \right|}}u\left| w \right| + {{Z'}_{ww}}\left| {w{{({v^2} + {w^2})}^{\frac{1}{2}}}} \right|} \right]+ \\ & \frac{1}{2}\rho {L^3}\left[ {{{Z'}_{vv}}{v^2}{\rm{ + }}{{Z'}_{{\delta _b}}}{u^2}{\delta _b}{\rm{ + }}\sum\limits_{i = 1}^2 {{{Z'}_{{\delta _{si}}}}{u^2}{\delta _{si}}} } \right]+\\ & (P - B)\cos \theta \cos \varphi \text{,} \\[-10pt] \end{split} $ | (10) |
| $ \begin{split} & {I_{xx}}\dot p + ({I_{zz}} - {I_{yy}})qr=\\ & \frac{1}{2}\rho {L^5}\left[ {{{K'}_{\dot p}}\dot p + {{K'}_{\dot r}}\dot r + {{K'}_{qr}}qr + {{K'}_{pq}}pq + {{K'}_{p\left| p \right|}}p\left| p \right|} \right]+\\ & \frac{1}{2}\rho {L^4}\left[ {{{K'}_p}up + {{K'}_r}ur + {{K'}_{\dot v}}\dot v} \right]+\\ & \frac{1}{2}\rho {L^3}\left[ {{{K'}_0}{u^2} + {{K'}_v}uv + {{K'}_{v\left| v \right|}}v\left| {{{({v^2} + {w^2})}^{\frac{1}{2}}}} \right|} \right]+\\ & \frac{1}{2}\rho {L^3}\left[ {{{K'}_{vw}}vw + \sum\limits_{i = 1}^2 {{{K'}_{{\delta _{si}}}}{u^2}{\delta _{si}}} } \right]-\\ & Ph\cos \theta \sin \varphi \text{。} \end{split} $ | (11) |
式中:
在高速变向变深的过程中,潜体各运动要素显著变化。其中,横倾角变化最为剧烈,其对潜体运动安全的影响也最大。以下仿真在分析潜体各要素运动的同时,着重分析横倾对潜体航行安全造成的影响。
4.1 潜体定深时仿真分析仿真初始条件:航速16 kn,潜体操方向舵右满舵,围壳舵控制潜体深度,使潜体保持定深航行为初始状态为:深度20 m,升降舵角都为0°,纵倾角0°。图5~图9为差动舵角分别操0°,–10°,–20°,–30°时,潜体纵倾角
|
图 5
左尾舵操上浮舵,右艉舵操下潜舵,且
|
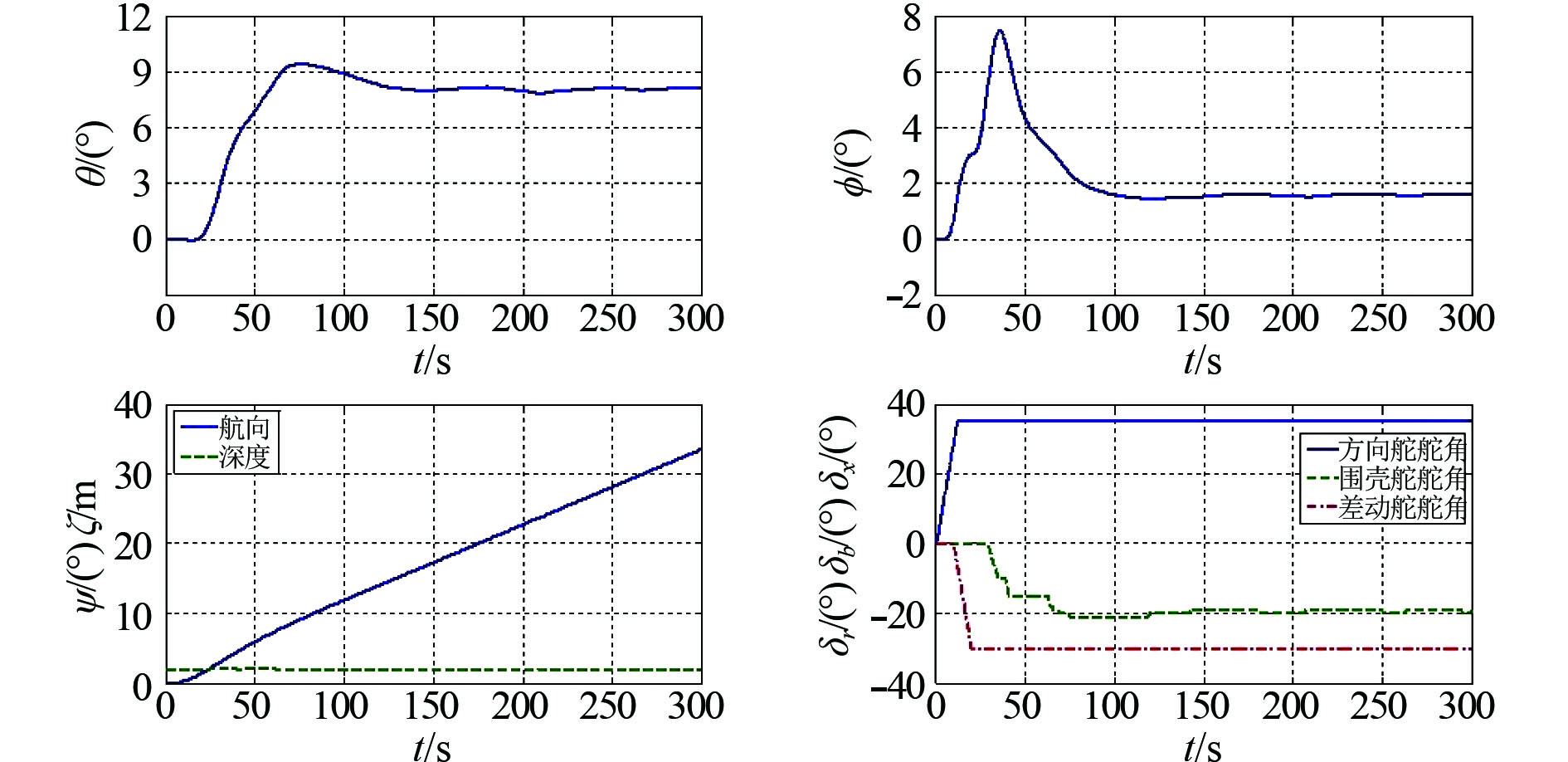
|
图 9 差动舵角–30°时潜体定深旋回仿真曲线 Fig. 9 Cycle curve with plane angle –30°in certain depth |

|
图 7 差动舵角-10°时潜体定深旋回曲线 Fig. 7 Cycle curve with plane angle -10°in certain depth |
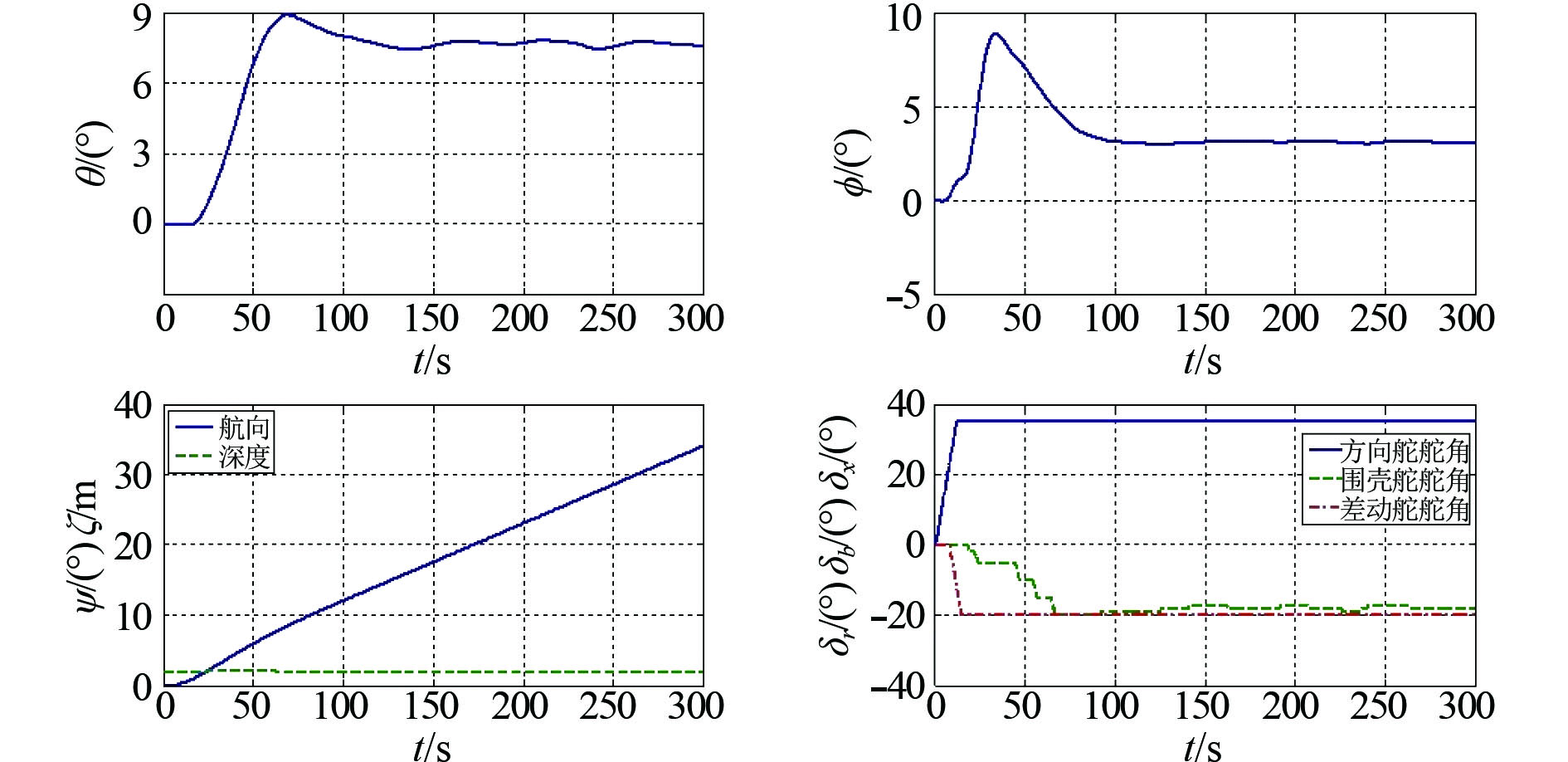
|
图 8 差动舵角–20°时潜体定深旋回曲线 Fig. 8 Cycle curve with plane angle –20°in certain depth |
潜体高速定深时产生的横倾角,传统的尾升降舵难以对其进行控制,较大的横倾降低了潜体水下旋回的安全性。分离式尾升降舵通过操纵左右分舵产生差动舵角,可以有效控制潜体横倾,使潜体在旋回过程中横倾保持在一个安全的范围内,仿真横倾角值如表1所示。
|
|
表 1 差动舵角对定深潜体突倾角和稳定横倾角影响 Tab.1 Influence of detach plane to heel in certain depth |
仿真结果表明,在潜体水下定深旋回的过程中,通过操纵分离式艉升降舵,可以有效控制潜体运动姿态。图10给出了不同差动舵角对潜体横倾的抑制效果,从图中可以看出,潜体在旋回初期中会产生较大突倾角,在差动舵角作用下该值逐渐减小至平稳。从表1可以看出,潜体在定深旋回过程中产生的横倾角,随着差动舵角的增大,该横倾角逐渐减小。

|
图 6 差动舵角0°时潜体定深旋回曲线 Fig. 6 Cycle curve with plane angle 0°in certain depth |
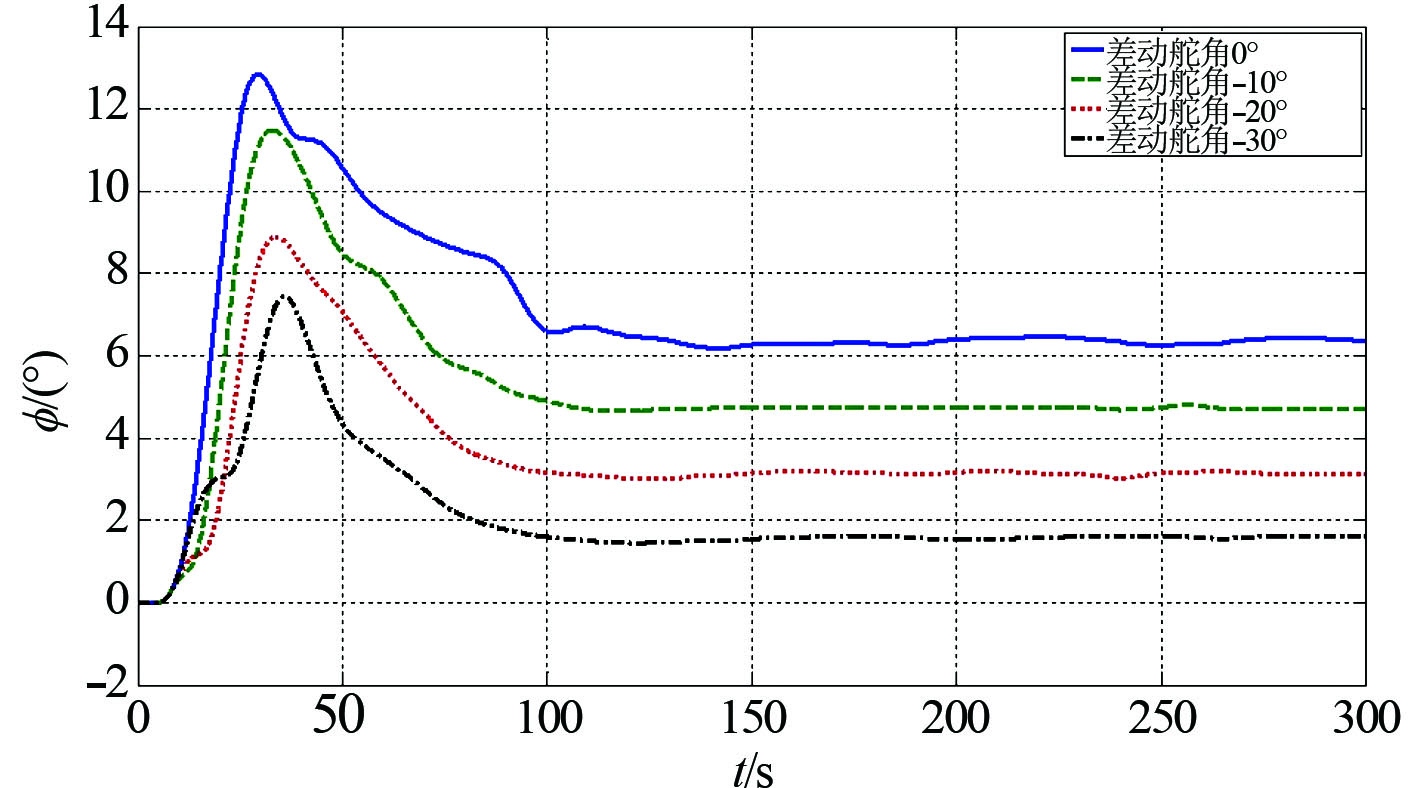
|
图 10 不同差动舵角时潜体定深旋回横摇影响 Fig. 10 Influence of detach plane to heel in certain depth |
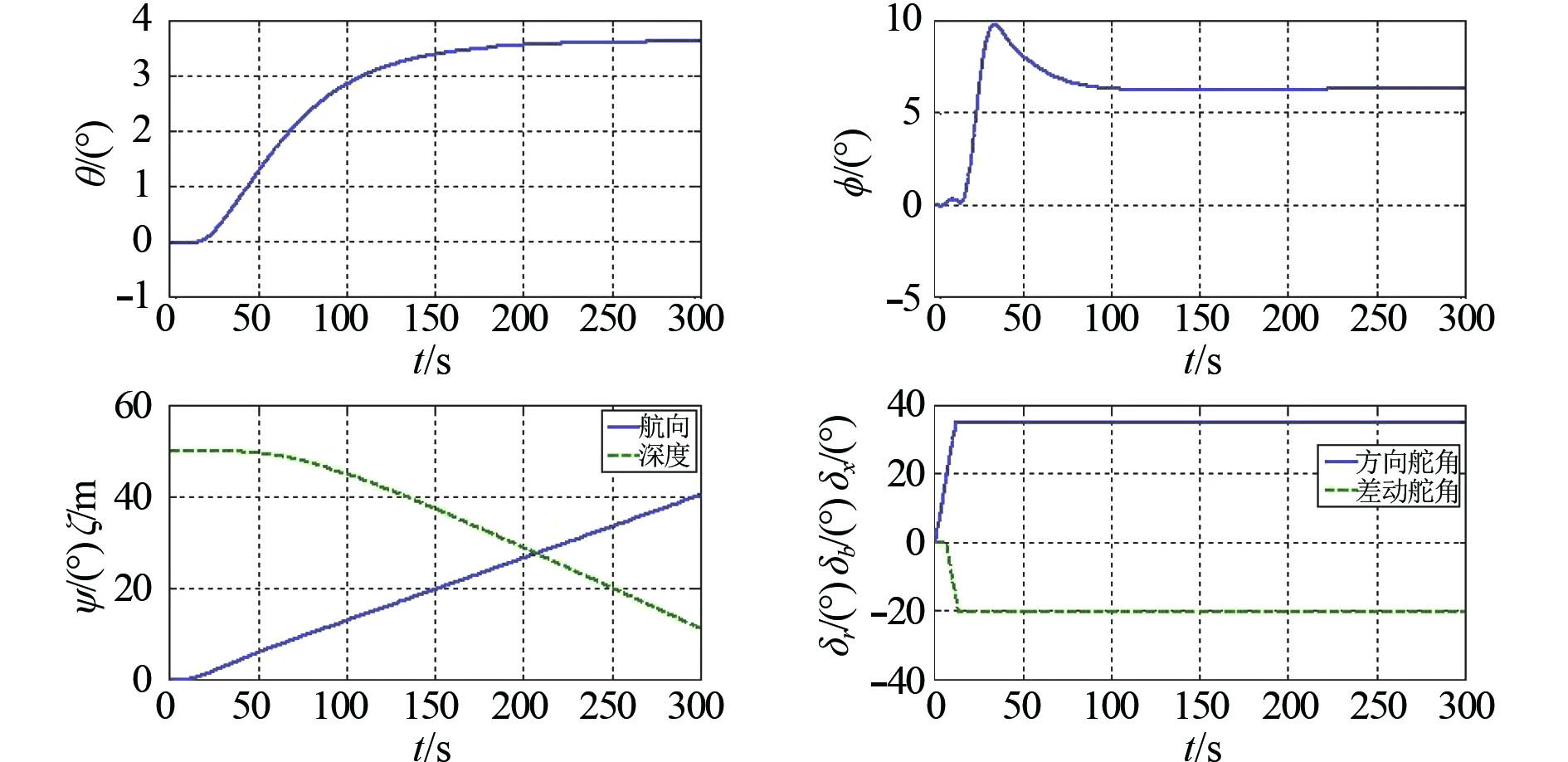
图11~图14给出了航速16 kn,潜体操方向舵右满舵,潜体同时变向变深,机动过程中差动舵角分别操–10°,–20°,–30°,潜体纵倾角

|
图 11 差动舵角–10°时潜体变向变深曲线 Fig. 11 Cycle curve with plane angle –10°in changing depth |
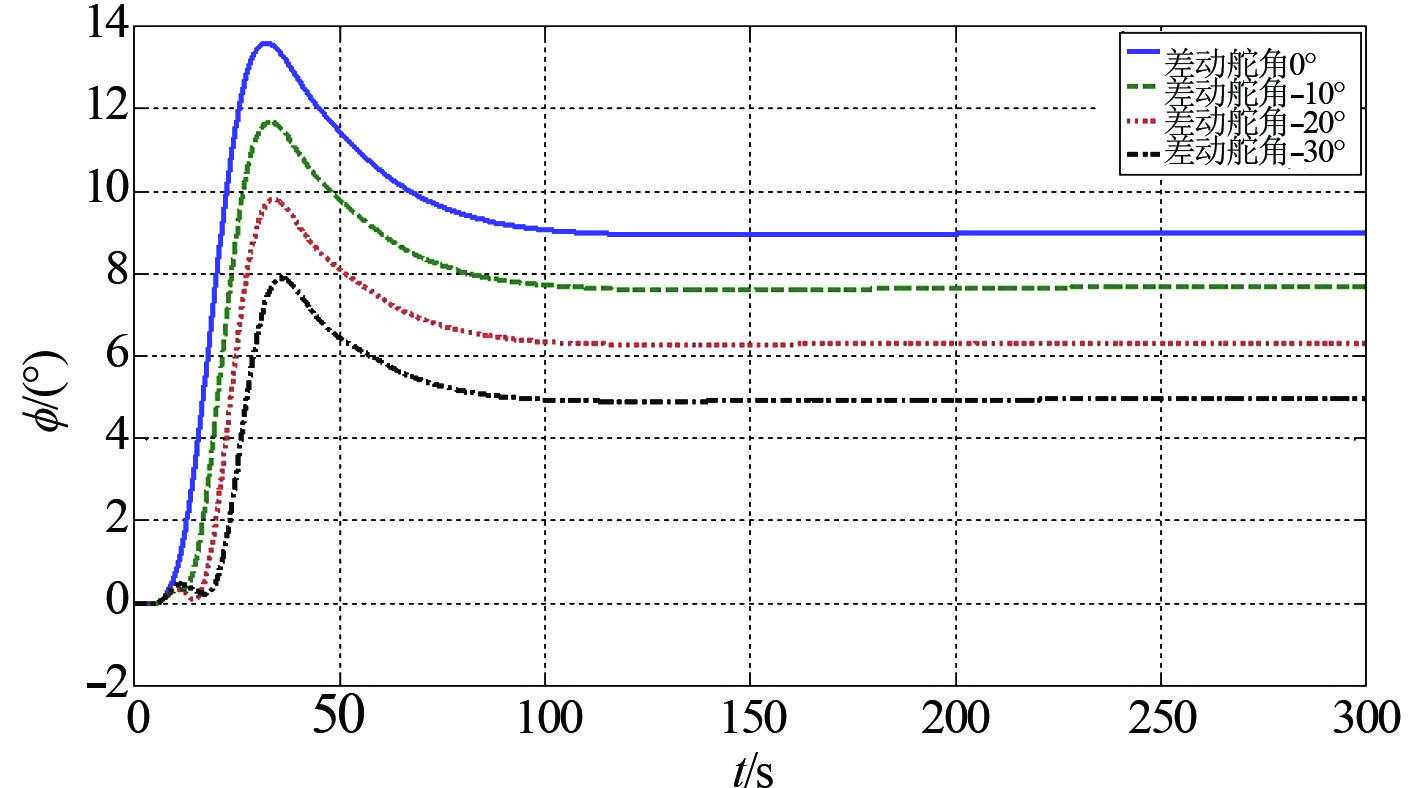
|
图 14 不同差动舵角时潜体变向变深旋回横摇影响 Fig. 14 Influence of detach plane to heel in changing depth |
|
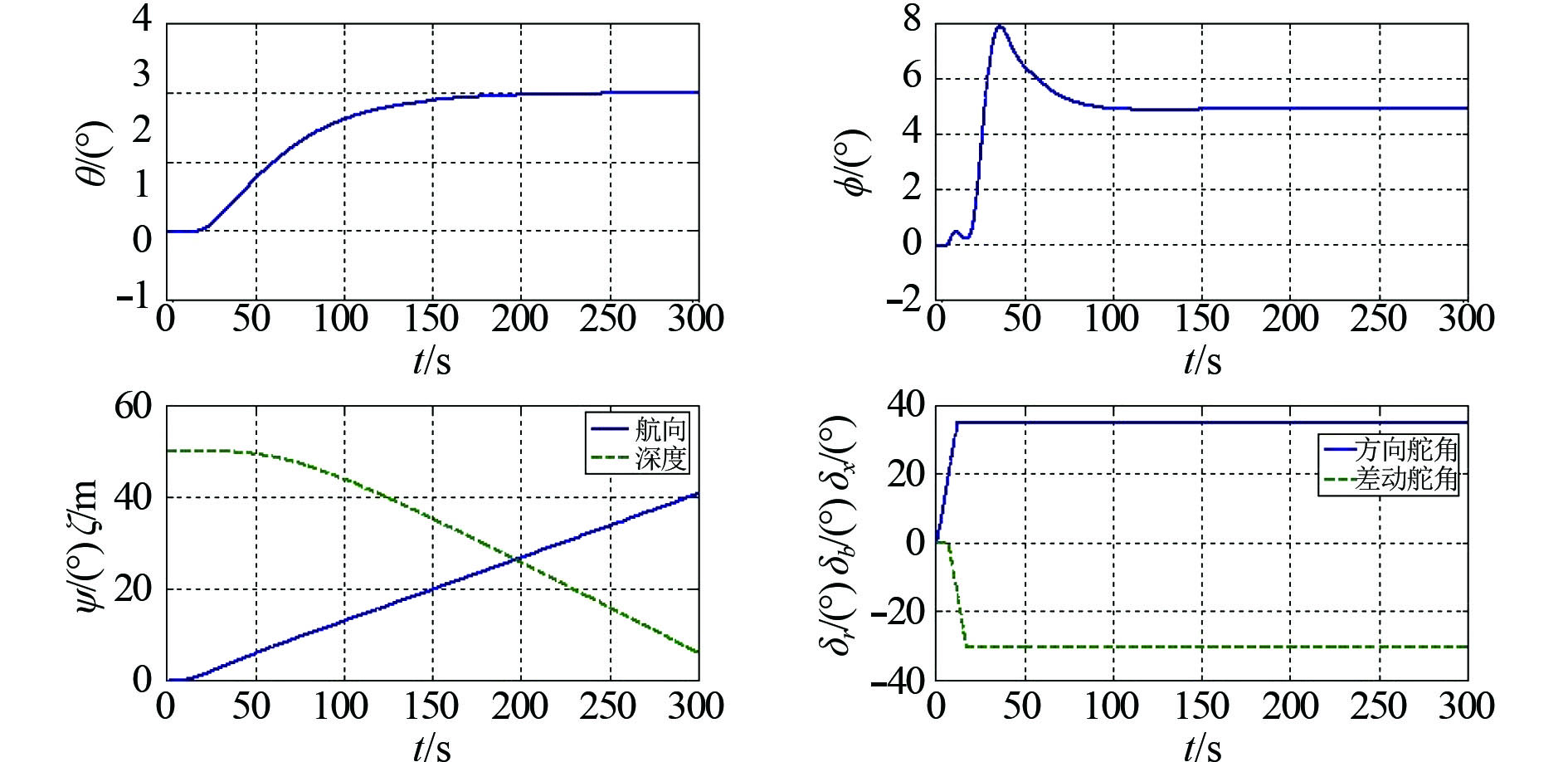
图 12 差动舵角–20°时潜体变向变深曲线 Fig. 12 Cycle curve with plane angle –20° in changing depth |
|
图 13 差动舵角–30°时潜体变向变深曲线 Fig. 13 Cycle curve with plane angle –30° in changing depth |
潜体高速变向变深时产生的横倾角如表2所示。
|
|
表 2 差动舵角对变深潜体突倾角和稳定横倾角影响 Tab.2 Influence of detach plane to heel in changing depth |
仿真结果表明,在潜体水下同时变向变深的过程中,与定深旋回类似,通过操纵分离式尾升降舵产生的差动舵角,可以有效减小潜体在同时变向变深过程中产生的横倾角,且随着差动舵角的不断增大,该横倾角逐渐减小。
5 结 语本文对潜体水下高速定深旋回和变深旋回的运动过程进行数值仿真,研究了差动舵角对潜体运动姿态、特别是潜体横倾的运动响应影响。仿真结果表明,潜体水下高速旋回时差动舵角能有效控制潜体运动姿态,旋回过程中产生的较大突倾角,差动舵角可有效对其进行抑制、控制。差动舵角对潜体水下高速旋回横倾控制能力与差动舵角的大小成正比,差动舵角越大,对横倾的控制能力越强。
| [1] |
陈俊峰, 田巍, 车梦虎. 潜艇定深旋回控制仿真与分析[J]. 舰船科学技术, 2007, 29(2): 116-118. CEHN Jun-feng, TIAN Wei, CHE Meng-hu. Modeling and analysis on the control of submarine’s certain depth and gyration motion[J]. Ship Science and Technology, 2007, 29(2): 116-118. |
| [2] |
王京齐, 施生达. 现代潜艇尾操纵面的发展现状[J]. 舰船科学技术, 2007, 29(1): 33-36. WANG Jin-qi, SHI Sheng-da. The developing situation of modern submarine’s tail control planes[J]. Ship Science and Technology, 2007, 29(1): 33-36. |
| [3] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995:71–74.
|
| [4] |
徐亦凡. 潜艇操纵原理与方法[M].北京:兵器工业出版社,2002:136-145.
|
| [5] |
何晋秋, 佘莹莹. 基于鲁棒滑模控制的水下航行器运动控制仿真研究[J]. 舰船科学技术, 2016, 38(6): 92-96. HE Jin-qiu, SHE Ying-ying. Non-linear robust slide-model control for underwater vehicle[J]. Ship Science and Technology, 2016, 38(6): 92-96. DOI:10.3404/j.issn.1672-7619.2016.06.018 |
| [6] |
胡坤, 武志东, 张建华. 潜艇水下旋回操纵运动特性仿真研究[J]. 舰船科学技术, 2015, 37(12): 18-22. HU Kun, WU Zhi-dong, ZHANG Jian-hua. Simulation research on gyratory maneuVerability of submarine underwater[J]. Ship Science and Technology, 2015, 37(12): 18-22. DOI:10.3404/j.issn.1672-7649.2015.12.004 |
| [7] |
FELDMAN J.DTNSRDC Revised standard submarine equations of motion[M]. DTNSRDC Report SPD-0393-09, 1979.
|
| [8] |
Motton Gertier, Grant R. Hagen. Standard equations of motion for submarine simulation[M]. SNAME: AD-652861, 1967.
|
 2020, Vol. 42
2020, Vol. 42
