充液管路是舰船机械系统中的重要组成部件,被广泛应用于舰船冷却、疏水等系统。复合材料管构件具有比强度大、比刚度大,耐腐蚀和抗疲劳,并且具有较好的材料可设计性能和减振性能等优点[1]。因此,复合材料管路力学性能也成为了船舶工程与学术研究的热点。谭安全等[1-2]采基于Love壳体理论,讨论了简支、固支和自由边界条件、轴向模态和铺层角对圆柱壳振动特性的影响。白宇杰等[3]基于1阶壳理论建立复合材料圆柱壳的振动方程,运用波动法进行求解并建立圆柱壳结构阻尼分析模型。李剑[4]对轴向运动分层复合材料薄壁圆柱壳的非线性特性进行了研究。蔡德咏等[5]基于有限元方法,建立混杂纤维增强复合材料圆柱壳的数值模型,研究了混杂比、边界条件、缠绕角度与复合材料圆柱壳基频之间的关系。肖汉林等[6]对复合材料圆柱壳在自由悬挂的边界下进行了振动模态试验,讨论了不同铺层角度,不同脱层对复合材料结构固有频率、振型的影响。郭明涛[7]采用稳态正弦的实验方法,获得了复合材料圆柱壳弹性模量与激振频率的关系曲线,通过该曲线可以用半功率法得到圆柱壳固有频率对应的模态阻尼比。针对普通钢材料充液管路振动特性的研究[8-9]已经很成熟,但对于复合材料充液管路振动特性的研究则比较少,而对于复合材料管与钢管振动特性对比的研究则更少。
本文从试验的角度对复合材料管和同尺寸的钢管进行了传递函数与模态测试的研究,从传递函数、传递损失、模态阻尼3个方向对2种材料的振动特性进行了对比分析,研究结果可为复合材料管路在船舶振动噪声控制中的应用提供基础。
1 试验对象与过程 1.1 试验对象试验对象为2根长度为1 m,直径为80 mm,壁厚为5 mm的直管。其中一根为树脂-玻璃钢复合材料直管(重量为8 kg),另一根为普通的钢管(重量为16 kg)。复合材料管路由环氧树脂(Epoxy coating)、增强层(Wall)和高粘度树脂(Resin rich liner)2层组成。以高粘度树脂作为基体,以玻璃纤维作为增强层进行缠绕,最外层为环氧树脂,如图1所示。
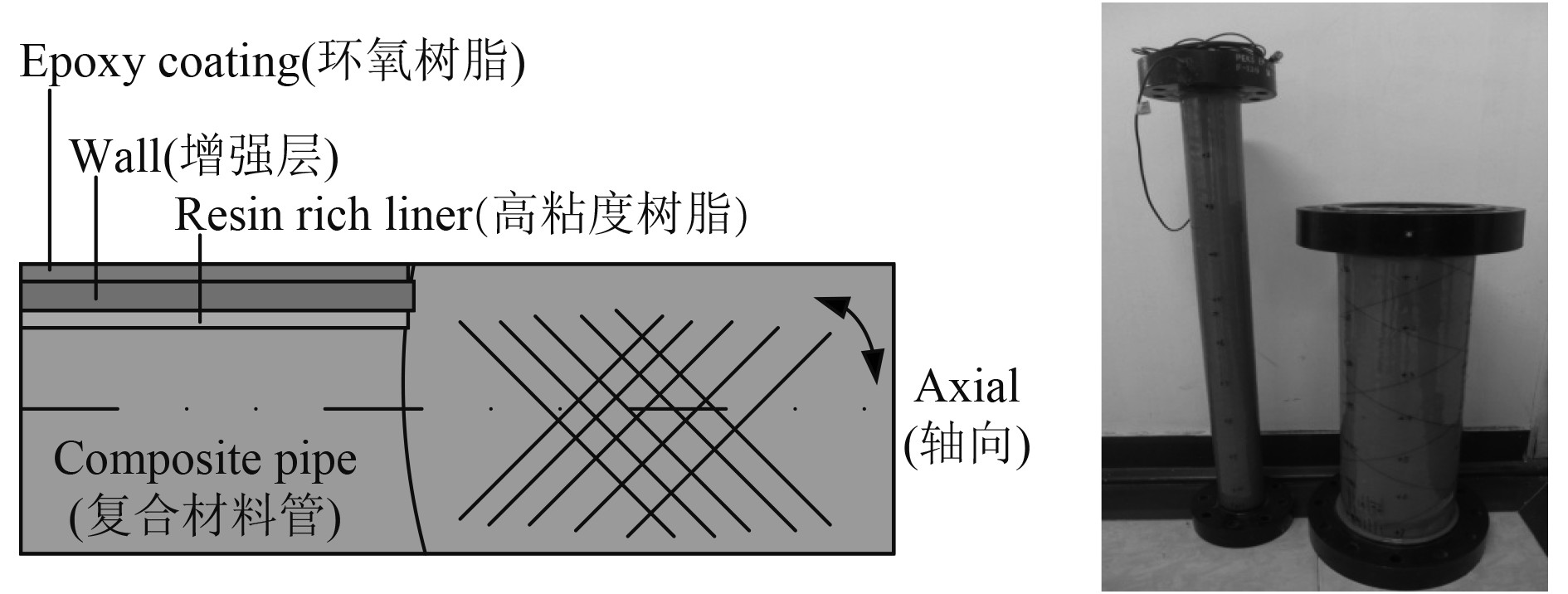
|
图 1 复合材料管路图 Fig. 1 Composite pipe |
振动传递试验采用一端固支,一端自由的边界条件。2根直管下端通过转接方板、螺栓连接固定在阻抗平台上。由于阻抗平台的质量远大于管路,因此可以认为管路的边界条件为固定约束。试验过程中可以在直管内充水与不充水,研究管内流体作为附加质量分别对2种材料直管的振动传递特性的影响。
1.2 测点布置为了获得直管的原点阻抗与传递阻抗,在直管的上端、中部、下端3个位置布置加速度传感器。激励力信号采用力传感器,布置在直管的上端。加速度传感器采用PCB356A16型号,力传感器信号采用PCB288D01型号。激振器采用弹性绳吊挂,分为横向与垂向两个方向对直管进行激励。

|
图 2 测点示意图 Fig. 2 Schematic diagram of measuring points |
振动传递试验中由信号发生器、功率放大器、滤波器、激振器、采集系统、测试电脑组成。模态测试试验中由力锤、BK采集卡、测试电脑组成。试验过程中原始记录如表1所示。
|
|
表 1 测点编号 Tab.1 Number of measurement point |
为了验证试验测试结果的精确与有效性,对钢管采用Abaqus有限元建模,对比分析有限元计算结果与试验测试结果。其中管壁采用Shell单元,两端法兰采用Solid实体单元。网格尺寸为5 mm,符合计算频率上限的需求,整个有限元模型共划分为30 864个单元,37 482个节点,有限元模型质量为16.22 kg,与实际模型质量误差为1.375%,因此认为该有限元模型计算结果能真实反映实际结果。以钢管横向激励,上端测点为对比分析点,两者的对比结果如图3所示,可见在1 000 Hz以内,试验结果与有限元计算比较吻合,证明了本次试验的测试与数据处理的正确性。
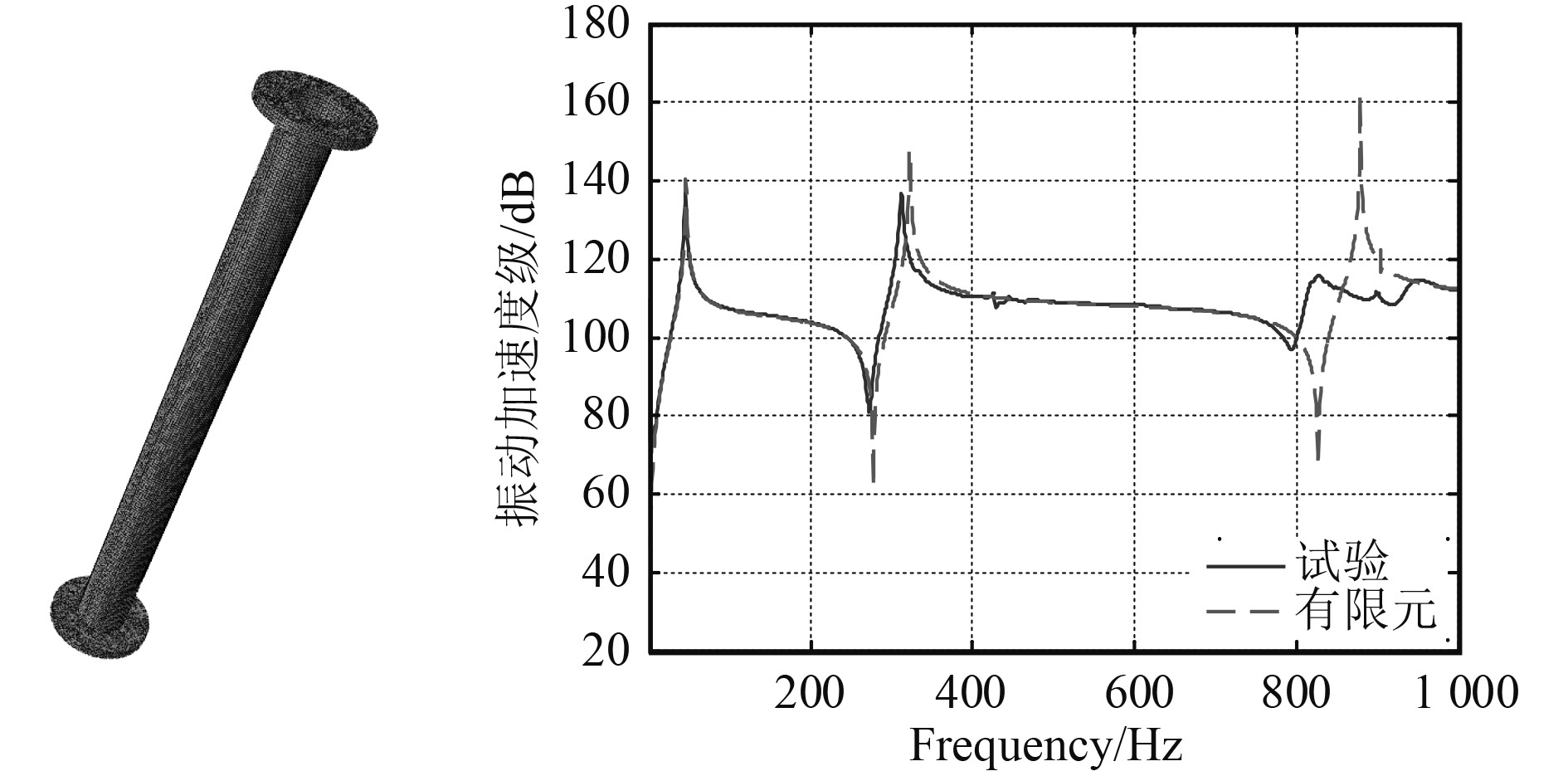
|
图 3 钢管横向激励有限元与试验对比 Fig. 3 Comparison FEM results with experiment |
将钢管与复合材料管横向充水、横向不充水、垂向充水、垂向不充水44种工况下,直管上中下3个测点的传递函数对比如下图4所示。因直管横向振动峰值频率较为丰富,轴向固有频率较高,因此横向激励测试频率为1~1 600 Hz,轴向激励测试频率为1~3 200 Hz。从图5可以看出,由于复合材料直管的质量与密度要低于钢管,因此复合材料管传递函数中的峰值都向左端偏移。在轴向方向,复合材料管的振动传递函数幅值要大于直管,特别是在500 Hz以内,存在一个主要的峰值,且对比分析管内是否充水,发现直管内的水的附加质量对轴向的传递函数几乎没有影响。而钢管的轴向传递函数则存在很多的峰值。
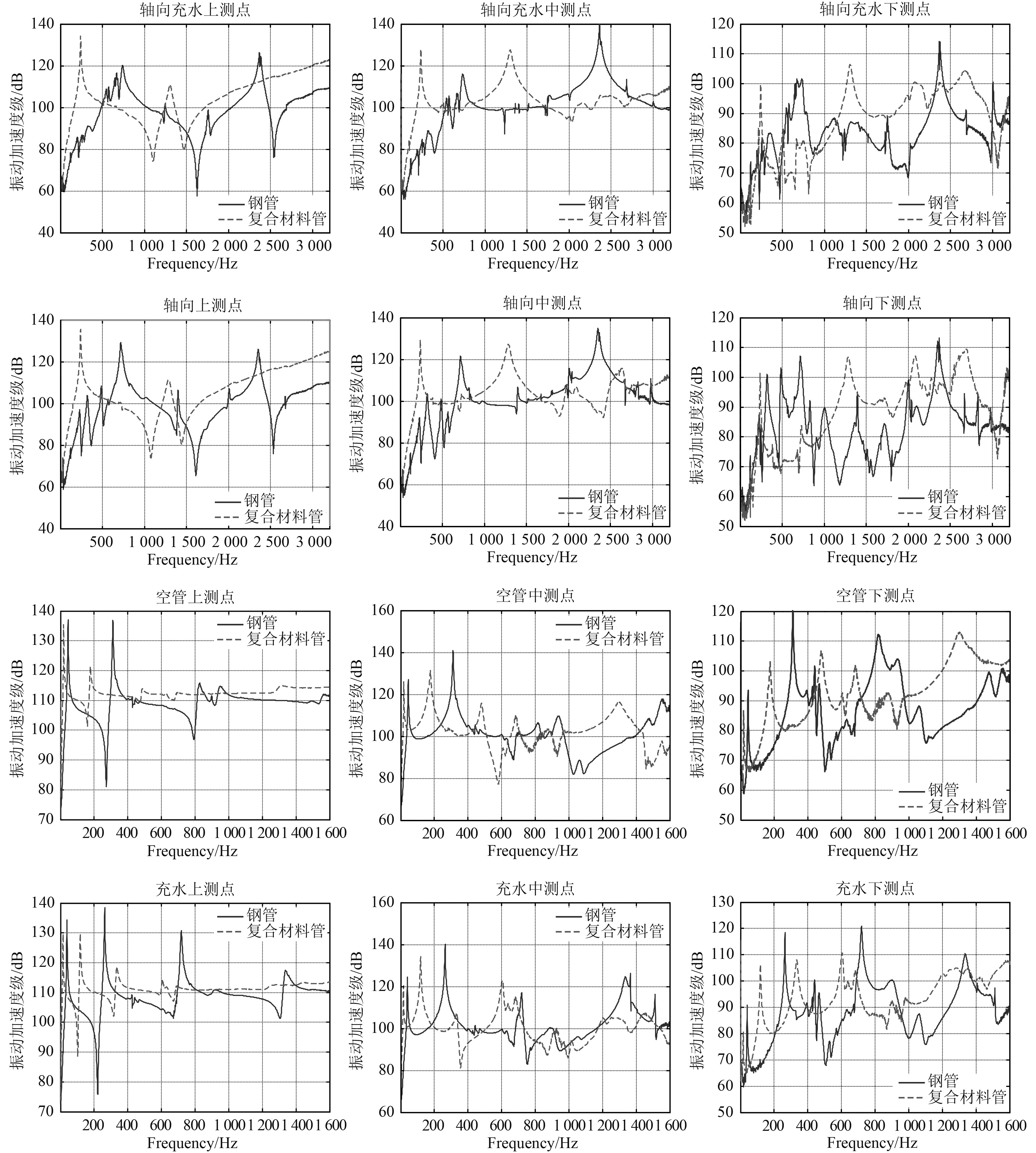
|
图 4 两种材料直管传递函数对比 Fig. 4 Comparison of transfer function between two materials in straight pipe |
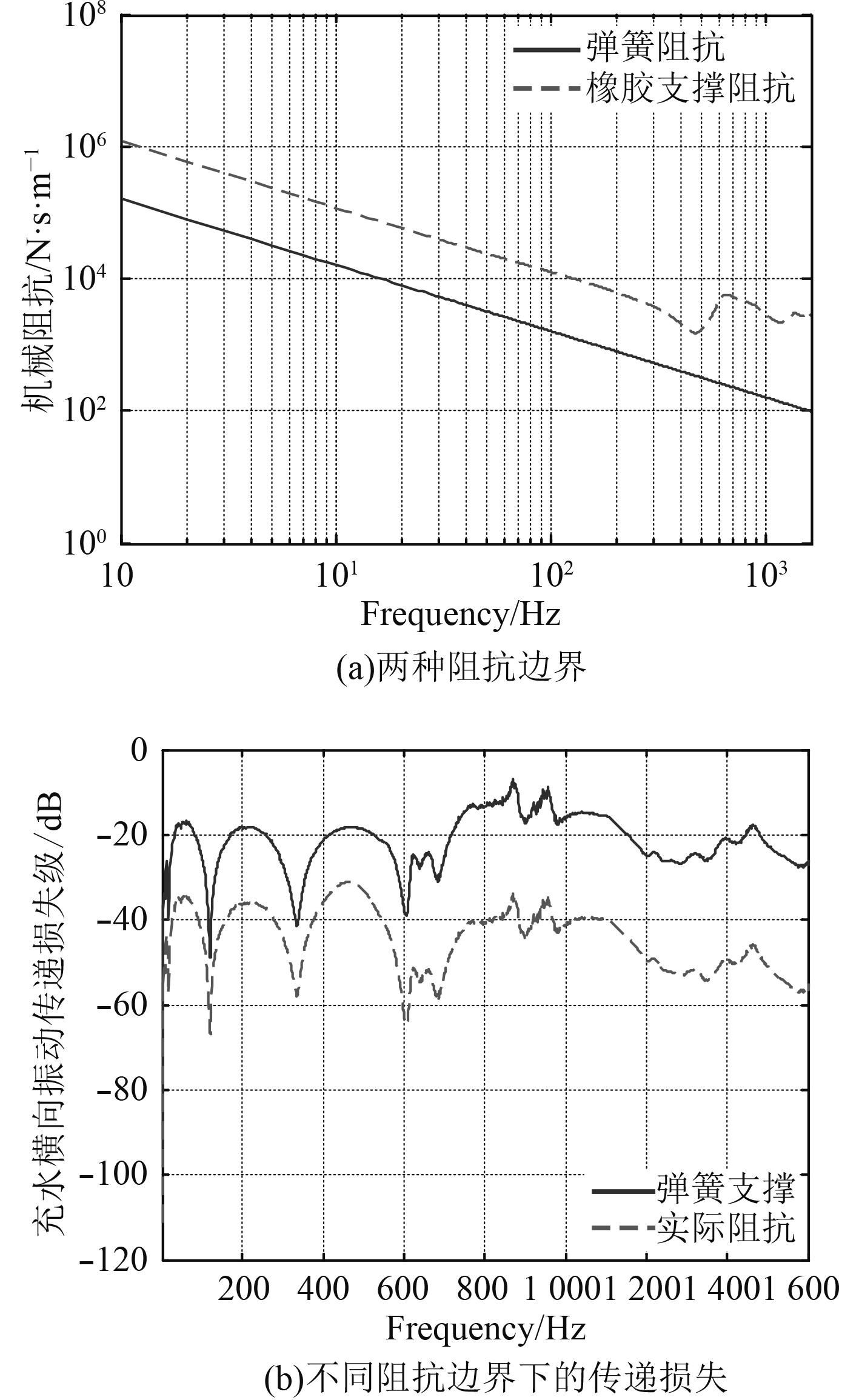
|
图 5 弹簧与橡胶支撑机械阻抗 Fig. 5 Mechanical impedance of Spring and rubber support |
在横向方向,复合材料管的传递函数幅值明显的小于钢管,受直管本身质量与管内水的质量的影响,复合材料直管峰值频率发生了明显的偏移,以上端测点为例,复合材料管的振动峰值全部在400 Hz以内,而400 Hz以后的传递函数几乎是一条直线。因此复合材料直管的振动共振峰值低于钢管。
2.2 传递损失对比分析实际中的船舶管路系统都不是单独的一根管,而是复杂的空间管系,振动从管路的一端传递到另一端。本节从传递损失的角度对钢管和复合材料管进行对比分析。对于单向振动,管路元件两端的动态力与振动速度间的关系可用下面方程描述:
| $\left\{ {\begin{array}{*{20}{c}} {{F_1}} \\ {{F_2}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {{Z_{11}}}&{{Z_{12}}} \\ {{Z_{21}}}&{{Z_{22}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{{\dot q}_1}} \\ {{{\dot q}_2}} \end{array}} \right\}\text{。}$ | (1) |
式中:
试验通常采用加速度计测量结构振动,因此
| $ \begin{split} & {Z_{11}} = {\left. {\frac{{j\omega {F_1}}}{{{{\ddot q}_1}}}} \right|_{{{\ddot q}_2} = 0}},\;{Z_{12}} = {\left. {\frac{{j\omega {F_1}}}{{{{\ddot q}_2}}}} \right|_{{{\ddot q}_1} = 0}},\\ &{Z_{21}} = {\left. {\frac{{j\omega {F_2}}}{{{{\ddot q}_1}}}} \right|_{{{\ddot q}_2} = 0}},\; {Z_{22}} = {\left. {\frac{{j\omega {F_2}}}{{{{\ddot q}_2}}}} \right|_{{{\ddot q}_1} = 0}}\text{。} \end{split} $ |
式中:
| $ \begin{split} & \left\{ {\begin{array}{*{20}{c}} {{F_1}} \\ {{{\dot q}_1}} \end{array}} \right\} = \left[ {\begin{array}{*{20}{c}} {\dfrac{{{Z_{11}}}}{{{Z_{21}}}}}&{{Z_{12}} - \dfrac{{{Z_{11}} \cdot {Z_{22}}}}{{{Z_{21}}}}} \\ {\dfrac{1}{{{Z_{21}}}}}&{ - \dfrac{{{Z_{22}}}}{{{Z_{21}}}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{F_2}} \\ {{{\dot q}_2}} \end{array}} \right\}= \\ & \left[ {\begin{array}{*{20}{c}} {{\alpha _{11}}}&{{\alpha _{12}}} \\ {{\alpha _{21}}}&{{\alpha _{22}}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {{F_2}} \\ {{{\dot q}_2}} \end{array}} \right\} = \left[ \alpha \right]\left\{ {\begin{array}{*{20}{c}} {{F_2}} \\ {{{\dot q}_2}} \end{array}} \right\}\text{。} \end{split} $ | (2) |
因此传递损失可以写成:
| $ TL = 20{\log _{10}}\left| {\frac{{{V_4}}}{{{V_1}}}} \right| = 20{\log _{10}}\left| {\frac{1}{{{T_{21}} * {Z_B} + {T_{22}}}}} \right| \text{。} $ | (3) |
从上式可以看出,直管本身的振动传递损失与直管后端连接的部件阻抗
图5(b)为复合材料直管在后端连接弹簧与橡胶两种支撑时的传递损失。可以看出,支撑阻抗的大小对直管的传递损失的幅值起着重要的影响,对传递损失曲线峰值的频率没有影响,橡胶支撑的隔振效果要优于弹簧支撑。
图6为2种材料管路在充水与不充水时轴向、横向振动传递损失。可以看出,在1 000 Hz以内,复合材料管路的轴向振动传递损失要劣于钢管,而在高频段,复合材料管的轴向传递损失又优于钢管。并且钢管在轴向的振动传递损失的峰值较为突出,频率成分也比较多。空管时,横向传递损失的峰值不多,钢管与复合材料管的传递损失峰值也是交替出现,在1 000 Hz以后,复合材料管的传递损失要大于钢管。当管内充水时,复合材料管路横向传递损失要优于钢管,2种直管都在800 Hz以内具有较好的传递损失,2 500 Hz以后2种直管的传递损失基本重合。

|
图 6 两种材料直管传递损失对比 Fig. 6 Comparison of transmission losses of the two materials |
当管路系统内充水时,因质量效应、泊松耦合、连接耦合效应等影响,管路系统的振动特性会发生改变。图7为钢管横向、轴向激励时,管内充水对其振动传递损失的影响。由于复合材料管路本身的质量比较轻,因此管内的充水在低频段对复合材料管路的振动传递损失影响较大,在1 000 Hz以后管内充水影响不大。而钢管则在整个频段内的因充水发生的变化几乎没有。

|
图 7 充水对传递损失的影响 Fig. 7 Effect of water on transmission loss |
由于直管的质量比较小,为了避免过多的加速度传感器引起的测试误差。模态试验采用单点测试-多点锤击法,即采用单个加速度计测量振动响应,力锤在管壁上不同的点移动敲击的方法。测试程序采用BK公司paulse采集模块中的modal test功能,试验对象为前文中描述的复合材料直管和钢直管。2种材料的直管段均采用弹性绳悬挂。由于直管段比较细长,模态主要呈现为梁状振型,因此沿直管轴向布置了11个力锤敲击点。
为了验证模态测试结果的正确与否,本文采用Abaqus建立了钢直管的有限元模型(见图3)并进行了模态计算。固有频率计算结果与试验测试结果基本一致,1阶误差为4.2%,2阶误差为1.77%,3阶误差为0.14%。根据模态振型的正交性,2种材料直管的模态正交数据如表2和表3所示。由上面的对比分析和正交性可知,本次试验测试的模态数据较为真实可靠。
|
|
表 2 测试阻尼比 Tab.2 Test damping ratio |
|
|
表 3 模态频率正则化 Tab.3 Modal frequency regularization |
在1 500 Hz之前,2种材料的管路各有3阶频率,由于玻璃钢的密度要低于钢管,因而复合材料管的频率低于钢管。而复合材料管的阻尼比要大于钢管,1阶中复合材料管阻尼比为钢管的7.49倍,2阶为17.56倍,3阶为11.3倍,振动能量在复合材料管中更容易衰减损耗。
4 结 语本试验研究包括复合材料直管和钢直管充水与不充水时,在横向和轴向激振器激励下的振动响应试验和空管时两种材料直管自由悬挂状态下的模态试验。对试验数据进行分析,得到以下结论:
1)管内流体对钢管的横向振动传递损失没有影响,对复合材料直管在低频段的传递损失有影响,高频段没有影响;
2)复合材料直管在横向激励下,横向振动传递损失要优于钢管(2 500 Hz以后);
3)复合材料直管在轴向激励下,低频段(1 500 Hz以内)的传递损失劣于钢管,在高频段要优于钢管;
4)相同几何尺寸下的复合材料管路固有频率要低于钢管,且模态阻尼系数要远大于钢管,有利于振动能量的消耗衰减。
| [1] |
谭安全. 复合材料层合圆柱壳的波传播和功率流特性研究[D]. 武汉: 华中科技大学, 2012.
|
| [2] |
谭安全, 刘敬喜, 李天匀, 等. 复合材料层合圆柱壳的振动特性[J]. 船舶力学, 2017(8): 109-114. |
| [3] |
白宇杰, 张小章. 基于波动法的复合材料圆柱壳阻尼特性分析[J]. 振动与冲击, 2014, 33(9): 111-115. |
| [4] |
李健, 郭星辉, 杨坤. 轴向运动复合材料圆柱壳的非线性振动研究[J]. 固体力学学报, 2011, 32(2): 176-185. |
| [5] |
蔡德咏, 马大为, 朱忠领. 混杂复合材料圆柱壳振动特性仿真研究[J]. 兵器材料科学与工程, 2011, 34(2). DOI:10.3969/j.issn.1004-244X.2011.02.027 |
| [6] |
肖汉林, 周心桃. 含脱层复合材料圆柱壳的振动模态试验分析[J]. 船海工程, 2010, 39(4): 11-13. DOI:10.3963/j.issn.1671-7953.2010.04.004 |
| [7] |
郭明涛. 复合材料薄壁圆柱壳振动实验研究[D]. 沈阳: 东北大学, 2008.
|
| [8] |
吴江海, 孙凌寒, 孙玉东,等. 舰船管路安装参数对其振动传递特性影响试验研究[J]. 舰船科学技术, 2018, 40(19): 60-66. |
| [9] |
尹志勇, 吴江海, 孙凌寒. 管路阻尼敷层减振效果评估研究[J]. 船舶力学, 2018, v. 22; No. 178(8): 127-134. |
 2020, Vol. 42
2020, Vol. 42
