2. 厦门船舶重工股份有限公司,福建 厦门 361026
2. Xiamen Shipbuilding Industry Co., Ltd., Xiamen 361026, China
船舶因受到风浪等外力扰动,航行过程中产生横摇、纵摇、首摇、横荡、纵荡、垂荡(或升沉)等各种摇摆运动。而对于科研平台、科考船等船型,受限于工作条件的限制,常需工作在零航速工况中。受零航速下横摇阻尼较小影响,其横摇幅值远高于高航速航行状态,剧烈的横摇可使舱内物品移动,引起船舶、平台发生倾斜,影响人员工作和生活[1]。
目前国内外常用的减摇装置主要有舭龙骨、减摇水舱、减摇鳍、减摇陀螺等[1]。其中,舭龙骨是从增大船宽的角度出发,沿船长方向、在船中两舷舭部外侧安装与舭部外板垂直的长条型板材(即舭龙骨)的方法进行减摇。其减摇原理为将横摇运动中船体的动能通过涡流的粘性效应转化为流体阻力动能,缺点是减摇效率较低,不适用于大横摇角时减摇,减摇水舱的原理是通过水的重力抵消波浪对船体的扰动力,从而产生减摇效果。减摇水舱适用于全航速航行条件下的船舶减摇,具有成本低、免维修、操作简单等优点;缺点是占用船内空间,故较适用于有较大空间的船舶。减摇鳍是安装在船舶水下两侧的鳍型装置,按鳍面布置方式分为固定式、收放式及伸缩式,按适航条件分为传统型和零航速(全航速)型[2];二者的对比如图1所示。按照不同升力机制,零航速横摇减摇鳍主要分为3种类型:

|
图 1 传统减摇鳍与零航速减摇鳍的分类对比 Fig. 1 Classification and comparison of traditional fin and zero speed fin |
1)低展弦比纵向拍动式零航速减摇鳍(见图1(b) );
2)Weis-Fogh机构式双翼零航速减摇鳍(见图1(c) );
3)高展弦比扑翼式零航速减摇鳍(见图1(d))。
低展弦比纵拍式零航速减摇鳍是世界首套零航速减摇鳍系统,与传统减摇鳍兼容性强,零航速时采用类似“划桨”的动作进行减摇;中高航速下采用传统减摇鳍的控制方式进行减摇,拓展了传统减摇鳍的工作条件,缺点在于所需功率较大、鳍轴易磨损、噪音较大。受英国生物科学家Weis-Fogh观察黄蜂的扑翼飞翔运动所提出的“挥翅拍击和挥摆急动”机构启发,一些学者[2-3]进行了Weis-Fogh机构减摇鳍方面的研究,证明了Weis-Fogh减摇鳍能产生较大升力、启动性良好,具有实际应用前途,难点是该类型鳍涉及两个鳍面,机械结构复杂,与普通减摇鳍不兼容,工作模式切换困难,成本高,可靠性差。借鉴扑翼飞行器的原理,出现了高展弦比扑翼式零航速减摇鳍[4],该鳍在减摇过程中鳍角较小,鳍根部距离鳍轴较短,可有效减少升力损失,但该鳍型的建模和测试研究还不够成熟。
针对现有减摇系统的灵活性、快响应、高效率、强环境适应性的要求,本文受螺旋桨式推进器[5]启发,提出一种基于矢量螺旋推进器的新型零航速船舶减摇系统,力争满足全航速范围内的减摇需求,提高减摇装置的响应效率。
1 矢量螺旋推进式船舶减摇系统概述 1.1 系统机构设计本设计是基于一种二维矢量螺旋推进器的船舶减摇装置。该减摇装置主要由摆臂电机、螺旋桨自旋电机、锥齿轮摆动链(传动机构)、螺旋桨轴、螺旋桨等部分组成[6]。
其三维模型图如图2所示。该装置主要基于左右对称的模块化二元矢量螺旋桨推进器组合而成,每个二元矢量螺旋桨既可以自旋又可以进行偏摆运动,如沿桨轴自转及桨轴沿船长方向前后摆动。沿桨轴自转时,螺旋桨产生推力,进而产生抵抗海浪扰动的减摇力矩。此外,桨轴亦可沿船长方向前后摆动,摆动幅度可根据船舶航速适当调整,用以减少航行时的阻力。具体而言,桨轴的摆向可由船体两侧的摇摆电机控制,配合螺旋桨的转动,不同摆动方向可以实现船舶的加速或刹车以及起到动力定位的作用。当桨轴垂直于水面时,力臂最大,此时产生最大横摇减摇效果;当桨轴向船首方向摆动时,可在减摇的同时用于船舶快速制动;当桨轴向船尾方向摆动时,则兼具减摇及推进效果。
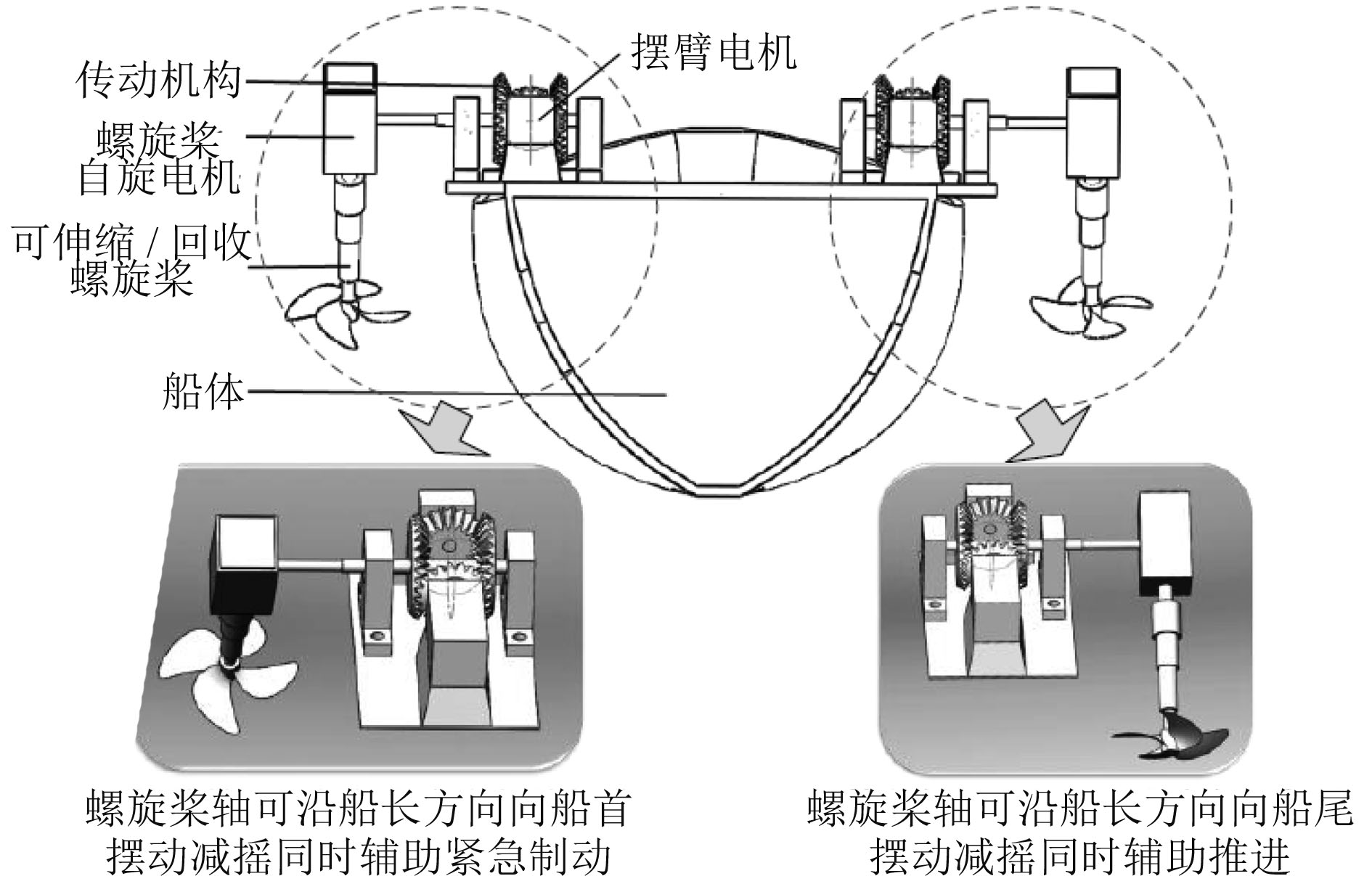
|
图 2 整体模型边线及减摇模块部分三维实体图 Fig. 2 The whole model boundary line and the three-dimensional solid diagram of the anti-rolling module |
如图3所示,将船舶和减摇装置视为一个系统,其运动可以用船舶横摇角
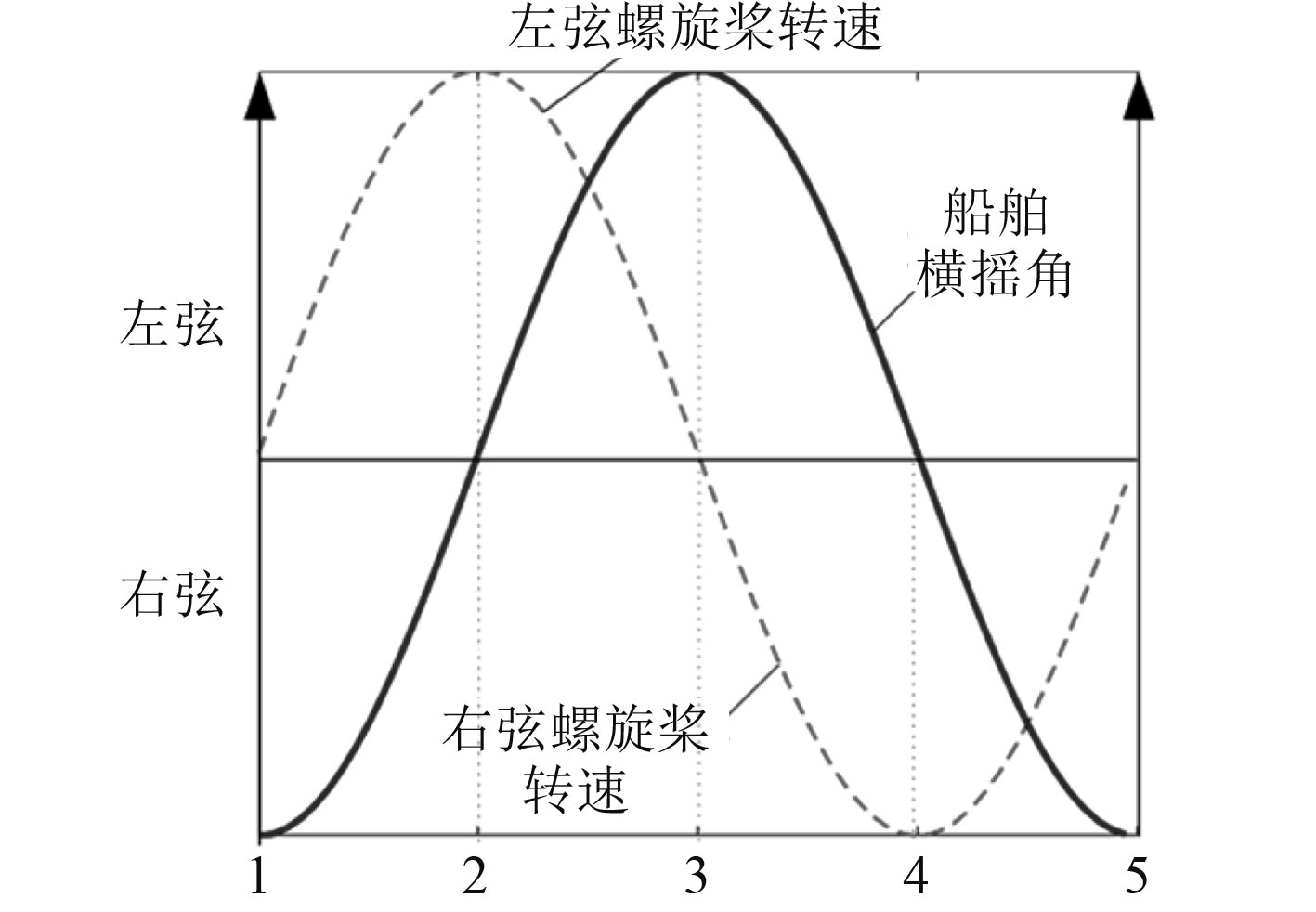
|
图 3 矢量螺旋推进式减摇系统工作原理 Fig. 3 Working principle of the vector anti-rolling system |
| $ ({J_\phi } + \Delta {J_\phi })\ddot \phi + 2N\dot \phi + D \cdot GM \cdot \phi = D \cdot GM \cdot {\alpha _m} + {M_s}\text{。} $ | (1) |
其中:
| $ {M_s} = \frac{{ - B\cos \theta kv\dot \phi }}{2} \text{。} $ | (2) |
其中:B为船体型宽,
| $ \begin{split} &({J_\phi } + \Delta {J_\phi })\ddot \phi + \left( {2N + \frac{{B\cos \theta kv}}{2}} \right)\dot \phi + D \cdot GM \cdot \phi =\\ &D \cdot GM \cdot {\alpha _m}\text{。} \end{split} $ | (3) |
为提高减摇效果,采用CFD方法,分析螺旋桨推力与转速的关系。依据计算船舶横摇运动的分析数据,获得零航速时螺旋桨推力与转速的关系,如图4所示。通过计算,航速为0 kn时,采用曲线拟合方法,得出推力与转速的关系为:

|
图 4 推力转速关系图 Fig. 4 Relationship between the force and the rotate speed |
| $ F = 5.7 \times {10^{ - 8}}{v^3} + 3.9 \times {10^{ - 5}}{v^2} + 0.012v + 0.1 \text{。} $ | (4) |
其中:F为推力;v为转速,r·min–1。由图4(b)可知,推力与转速近似抛物线关系,在螺旋桨转速为833 r/min时,推力可达到69 N。
在减摇系统工作原理及螺旋桨推力与转速关系分析的基础上,进一步确定螺旋桨转速的控制方法,以获得最佳减摇效果。由于螺旋桨自转电机的转速和供电电压呈一定关系,可以得出一个近似的2阶振荡环节的转速相对于电压的传递函数:
| $ G(s) = \frac{{V(s)}}{{U(s)}} = \frac{{40}}{{{s^2} + 60s + 40}} \text{。} $ | (5) |
进而可以根据所需推力对螺旋桨电机的电压进行调节控制,以获得相应的稳定力矩,提高减摇效果。
2 船舶耐波性分析通过Ansys-Aqwa软件的计算分析,获得规则波和非规则波条件下,船舶在零航速时的横摇周期以及横摇规律。通过船舶模型的耐波性理论仿真分析,得出船模耐波性初始数据,为船模减摇实验奠定理论基础。为研究矢量减摇装置的减摇效果,设计用U型船模与实船对比参数如表1所示。
|
|
表 1 实船与船模对比参数表(比例1∶30) |
考虑可能的航区,本文采用ITTC two parameter pectrum波谱[7],其海浪谱密度公式为:
| $ {S_{ITTC}}(\omega ) = \frac{A}{{{\omega ^5}}}\exp (\frac{{ - B}}{{{\omega ^4}}}) \text{。} $ | (6) |
式中:
建立图5所示计算水域:设计水池深100 m,长500 m,宽400 m,海平面设置为0 m。
|
图 5 计算水域 Fig. 5 Calculation water domains |
数据主要监测点如图6所示。其中,CG为重心、starboard为右舷、stern为船尾,baseline为基线、CB为浮心、CF为漂心、FP/AP为首尾垂线[7]。根据AQWA计算得到船体耐波性分析波形,如图7所示。在3级海况、有义波高1.25 m、航向角90°、遭遇频率0.265 Hz时,舷侧处最大波高为5.869 8 m,船舶横摇角度约为11°,接近谐横摇状态。
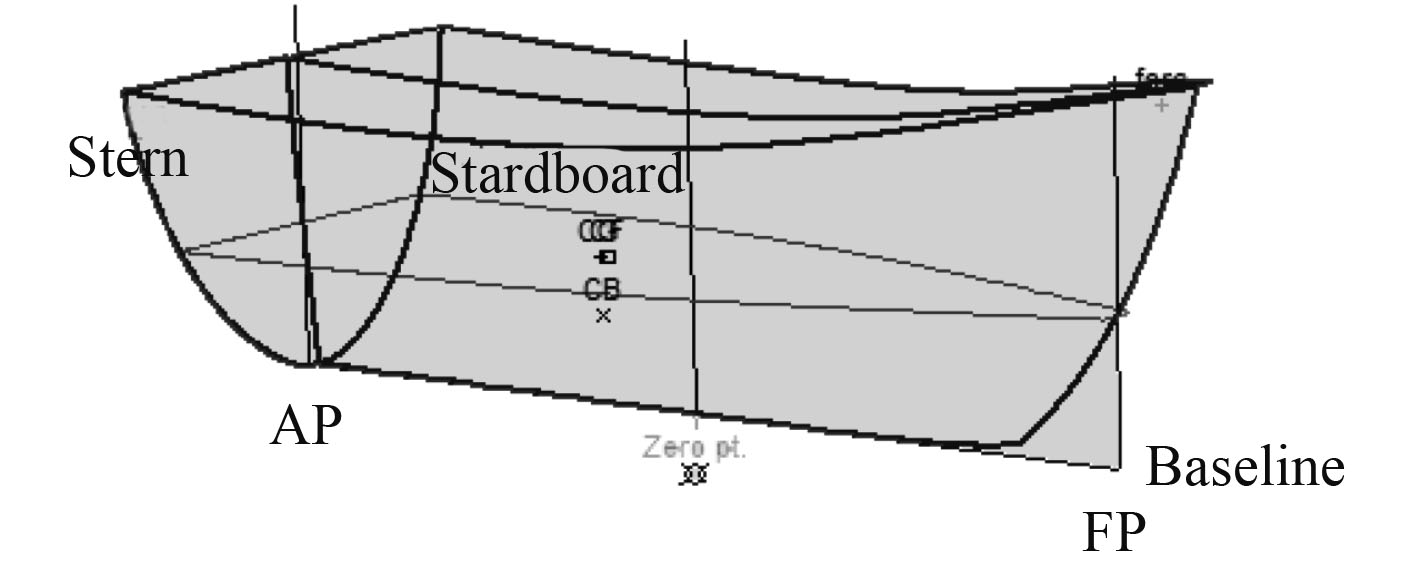
|
图 6 主要监测点 Fig. 6 Major monitoring points |

|
图 7 90°横摇遭遇频率0.265 Hz的波形图 Fig. 7 The waveform with the rolling angle of 90° and the encountered frequency of 0.265 Hz |
依据理论计算得出主要监测点的加速度等主要分析数据如表2所示。
|
|
表 2 零航速下90°横浪状态船体的主要耐波性分析数据 |
由表2可知,在海况3级、有义波高1.25 m情况下,零航速时船中横摇最大加速度为0.378 mm/s2,船舶横摇角范围为3°~12°,横摇周期范围为1~8 s。
3 规则波下零航速矢量减摇系统实验为实现实验室条件下的系统减摇模拟测试,首先构建试验平台,用以模拟规则波使船模产生横摇,进而对零航速条件下该系统的减摇效果进行验证。
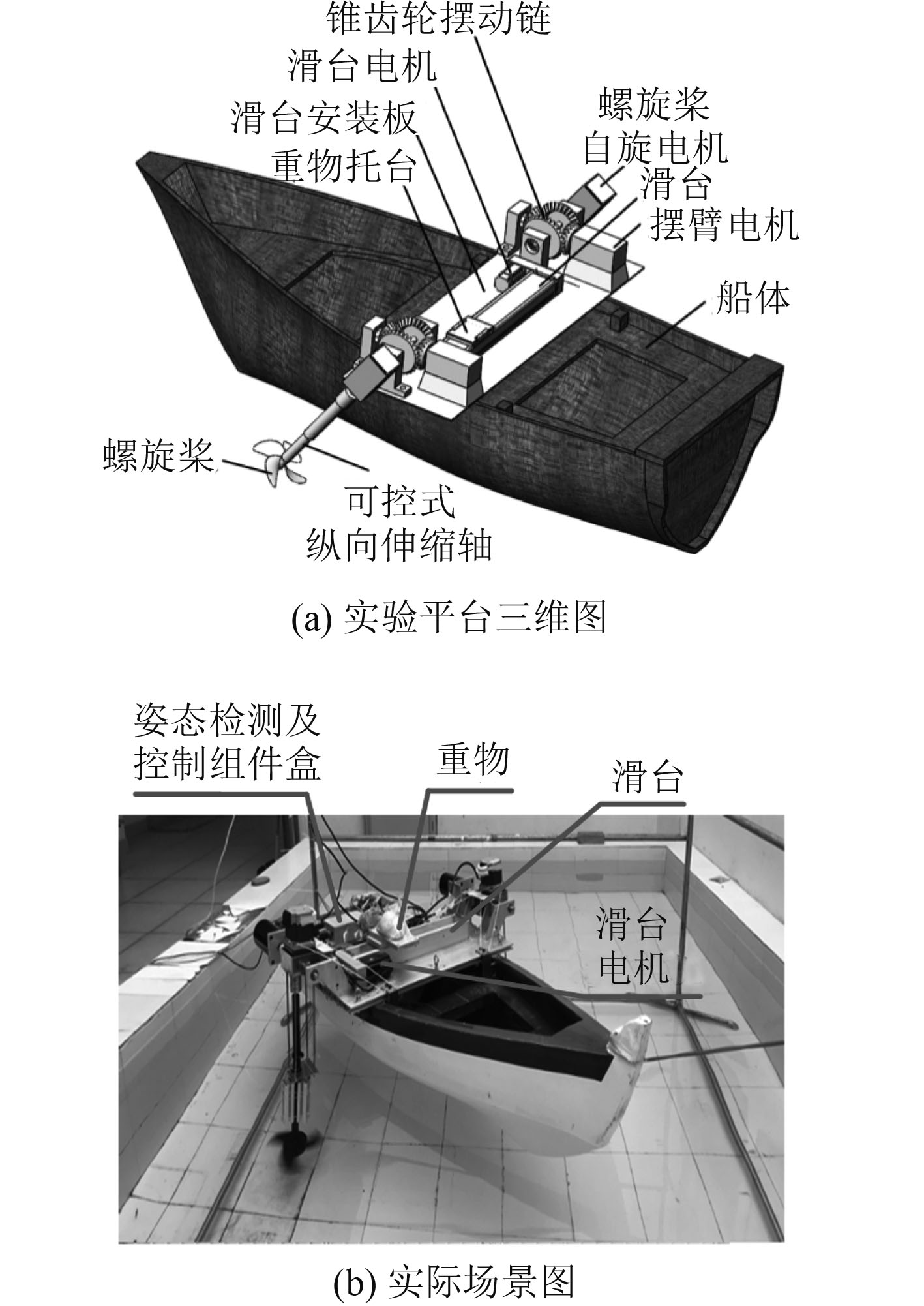
3.1 零航速实验平台搭建如图8所示,搭建静水实验平台。图8(a)为实验平台的三维模型图。滑台部分主要由滑台安装板、滑台电机、滑台导轨、重物托台等部分组成。图8(b)为实际实验场景图。沿中线面系泊船体,利用滑台搭载重物的往复移动来模拟产生规则波下横摇效果,通过对比矢量推进螺旋桨开启前/后船舶横摇的2种不同情况,验证基于矢量螺旋推进舵的船舶零航速下的减摇效果。通过改变重物质量以及横摇周期,进行多组实验条件下的模拟减摇实验。
|
图 8 矢量减摇系统零航速实验平台示意图 Fig. 8 Schematic diagram of zero speed experimental platform of the vector anti-rolling system |
实验用水池长5.46 m、宽3.12 m、深0.75 m,容积9.849 m3,采用重物滑块模拟船舶规则横摇。实验时,依据理论分析,调整滑块移动速度和控制螺旋桨的转速,模拟实验船模横摇运动及验证矢量减摇效果。实验中采用周期为4.0 s,4.8 s,8.0 s的1 kg滑块往复运动,模拟船舶规则波下横摇,3种周期下的减摇效果分别如图9~图11所示。

|
图 9 横摇周期为4 s时的减摇效果 Fig. 9 Anti-rolling effect at the period of 4 s |

|
图 11 横摇周期为8 s时的减摇效果 Fig. 11 Anti-rolling effect at the period of 8 s |

|
图 10 横摇周期为4.8 s时的减摇效果 Fig. 10 Anti-rolling effect at the period of 4.8 s |
可以看到,因在静水中采用滑块重物往复移动的方式模拟产生船舶横摇,往复运动周期越短,横摇惯性力越大,因此减摇前船舶横摇角随运动周期减小而增大;而由减摇后船首和船尾姿态图可看出,3种运动周期情况下的减摇效果都非常明显。为定量分析,列出减摇前后具体横摇幅值对比图如图12所示。

|
图 12 减摇前后具体横摇幅值对比图 Fig. 12 Comparison of specific rolling amplitude before and after anti-rolling |
由图12可知,横摇周期为4 s,最大横摇角为15.9759°,横摇峰值的均方根为14.4023°,开启矢量减摇系统后,最大横摇角为3.0065°,横摇峰值的均方根为2.0188°,减摇效果为81.2%;船舶横摇周期为4.8 s,最大横摇角11.2346°,横摇峰值的均方根为10.7501°,开启矢量减摇系统后,最大横摇角1.4911°,横摇峰值的均方根为1.0292°,减摇效果为86.7%;横摇周期为8 s时,最大横摇角为5.6656°,横摇峰值的均方根为5.0584°,采用矢量减摇后横摇角为1.2481°,横摇峰值的均方根为0.5894°,减摇效果为78.0%.
服务航速0 kn时模拟船舶横摇,减摇后平均剩余横摇角
上述实验研究以及仿真分析结果表明,该零航速矢量减摇装置具有以下优点:
1)减摇装置结构简单,模块化设计方法方便船舶进行安装,可移植性强;
2)采用主动式减摇方法,改善了被动式减摇装置的不足,在零航速时具备较好的减摇效果。
此外,该减摇装置可应用于海上科研平台姿态稳定的场合中,以更好保障海洋科研平台工作的进展。未来拟进行无规则海浪条件下的实船实验研究,并针对不同类型船舶开展减摇装置具体参数的匹配与优化研究。
| [1] |
中国船舶工业集团公司. 船舶设计实用手册(总体分册)[M]. 国防工业出版社. 2013.
|
| [2] |
王帆. 零航速减摇鳍仿生机理及控制关键技术[D]. 哈尔滨: 哈尔滨工程大学, 2010.
|
| [3] |
李梦玉, 刘超, 章社生. WEIS-FOGH机构水动力学研究与进展[C]// 全国水动力学研讨会并周培源诞辰110周年纪念大会, 2012.
|
| [4] |
DALLINGA R P, RAPUC S. Merits of flapping roll stabilizer fins[R]. HISWA Symposium, 2014.
|
| [5] |
GONZALEZ L A. Design, modeling and control of an autonomous underwater vehicle[J]. Be Thesis, 2004. |
| [6] |
王凌云, 肖晶晶, 孙道恒, 等. 一种用于船舶减横摇的摇摆伸缩臂减摇装置[P]. 中国专利: CN201810833904.0, 2018-12-28.
|
| [7] |
李积德. 船舶耐波性[M]. 哈尔滨: 哈尔滨船舶工程学院出版社, 1992.
|
 2020, Vol. 42
2020, Vol. 42
