导弹命中舰船后,战斗部爆炸产生高温高压气体及高强度的冲击波,在舰船舱室内迅速传播。这对舰船舱室设备、舰员生命安全造成严重危害,作用在弹药库中弹药上的冲击波甚至可能引发爆炸。在舱室中喷洒细水雾形成水幕,遭遇到冲击波后,液滴颗粒被击碎成更细小的水滴,增大了与空气的接触面积,水滴吸热蒸发,消耗冲击波能量。
开展水幕衰减冲击波强度的研究,提高冲击波防护技术,对军事装备技术发展具有重要意义。早在20世纪末期,美国海军工程实验室[1]就对被水包围炸药爆炸时的现象进行了试验研究。实验证明水能够明显减弱炸药爆炸对周围的物体冲击作用。2013年,李士军等[2]在国内首次提出了主动式水爆抑制系统,对液滴抑爆原理及该系统的组成、安装进行了分析说明。之后,李钰阳[3]对受限通道内水幕帘减弱冲击波的问题进行了数值研究,分析水幕帘与冲击波相互作用的主要机理,比较了不同了爆炸压力、不同喷嘴流量、不同水幕位置工况下的冲击波减弱情况。陈攀等[4]对舰船舱室内冲击波载荷特性进行分析,冲击波在舱室内部进行多次反射,舱室板架承受多次冲击波反射载荷。王超等[5]通过实验方法和CFD模拟得到了液滴在激波作用下的雾化破碎过程。刘贵兵等[6, 7]利用有限元软件Ls-dyna对爆炸冲击波与液滴相互作用特性进行仿真分析,得出液滴可衰减冲击波超压峰值,且水滴直径越小对冲击波衰减效果越好的结论。
本文以密闭舰船舱室为模型,舱室中心发生爆炸产生冲击波,在爆炸中心右侧喷洒细水雾形成水幕,爆炸中心左侧冲击波在空气中自由传播,通过对比两侧的温度压力变化情况,分析水幕对冲击波的衰减作用。
1 数值方法 1.1 连续相控制方程通过Eulerian方法描述冲击波在连续介质中的传播,满足以下非定常可压缩流体控制方程:
连续性方程:
| $\frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho {u}} \right) = 0\text{,} $ | (1) |
动量方程:
| $ \frac{{\partial \left( {\rho {u}} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho {uu}} \right) + \nabla P = \rho {g} + \nabla \cdot {\tau } \text{,} $ | (2) |
能量方程:
| $ \frac{\partial }{{\partial t}}\left( {\rho h} \right) + \nabla \cdot \left( {\rho h{u}} \right) = \frac{{{\rm D}P}}{{{\rm D}t}} + {\dot q^m} - \nabla \cdot {q_r} + \phi \text{,} $ | (3) |
理想气体状态方程:
| $ P = \frac{{\rho RT}}{M} = \rho RT\sum\limits_i^{} {\left( {\frac{{{Y_i}}}{{{M_i}}}} \right)} \text{。} $ | (4) |
通过Lagrangian方法描述分散液滴颗粒的位置变化
| $ {\dot m_{pn}} = \frac{{{\rm d}{m_{pn}}}}{{{\rm d}t}} \text{。} $ | (5) |
式中:
液滴运动轨迹满足:
| $ {u_{pn}} = \frac{{{\rm d}{r_{pn}}}}{{{\rm d}t}}\text{,} $ | (6) |
液滴的力平衡方程:
| $ \frac{{{\rm d}{u_{pn}}}}{{{\rm d}t}} = \frac{{3{\mu _m}{C_{Dn}}{{\operatorname{Re} }_{pn}}}}{{4{\rho _p}d_{pn}^2}}(u - {u_{pn}})\text{,} $ | (7) |
液滴的能量平衡方程:
| $ {m_{pn}}{C_{pd}}\frac{{{\rm d}{T_{pn}}}}{{{\rm d}t}} = {\text{π}} {h_{pn}}d_{pn}^2(T - {T_{pn}}) + {h_{fg}}{\dot m_{pn}}\text{。} $ | (8) |
式中:
计算选取TAB破碎模型,TAB模型是Taylor根据液滴的变形和振荡与弹性质量系统的相似性提出的,液滴表面张力类比恢复力,液滴阻力类比外力,液滴粘性力类比阻尼力。球形液滴控制方程:
| $ \begin{gathered} y(t) = W{e_C} + {e^{ - (t/{t_d})}}\biggl[({y_0} - W{e_C})\cos (\omega t) + \\ \frac{1}{\omega }\left(\frac{{{\rm d}{y_0}}}{{{\rm d}t}} + \frac{{{y_0} - W{e_C}}}{{{t_d}}}\right)\sin (\omega t)\biggl]\text{,} \end{gathered} $ | (9) |
We为液滴韦伯数。
子液滴直径为:
| $ d_{pn}^ * = \frac{{{d_{pn}}}}{{1 + \dfrac{4}{3}{y^2} + \dfrac{{{\rho _p}d_{pn}^3{{({\rm d}y/{\rm d}t)}^2}}}{{8\sigma }}}}\text{。} $ | (10) |
由于液滴的蒸发,液滴与气相之间进行了质量交换:
| $ {S_m} = \sum\limits_{n = 1}^{{N_p}} {\frac{{{\rm d}{m_{pn}}}}{{{\rm d}t}}} \text{,} $ | (11) |
液滴在气相中运动所受阻力:
| $ {F_d} = \sum\limits_{n = 1}^{{N_p}} {{m_{pn}}} \left[\frac{{3{\mu _m}{C_{Dn}}{{\operatorname{Re} }_{pn}}({u_{pn}} - u)}}{{4{\rho _p}d_{pn}^2}}\right]\text{。} $ | (12) |
式中:
液滴蒸发所产生的能量损失为:
| $ {S_h} = \sum\limits_{n = 1}^{{N_p}} {\left[\frac{{\text{π}} }{6}d_{pn}^3{\rho _p}{C_{pd}}\frac{{{\rm d}{T_{pn}}}}{{{\rm dt}}} + \left( - {h_{fg}} + \int\nolimits_{{T_{ref}}}^{{T_{pn}}} {{C_{p,{H_2}0}}dT} \right)\frac{{{\rm d}{m_{pn}}}}{{{\rm d}t}}\right]} \text{。} $ | (13) |
式中:
建立
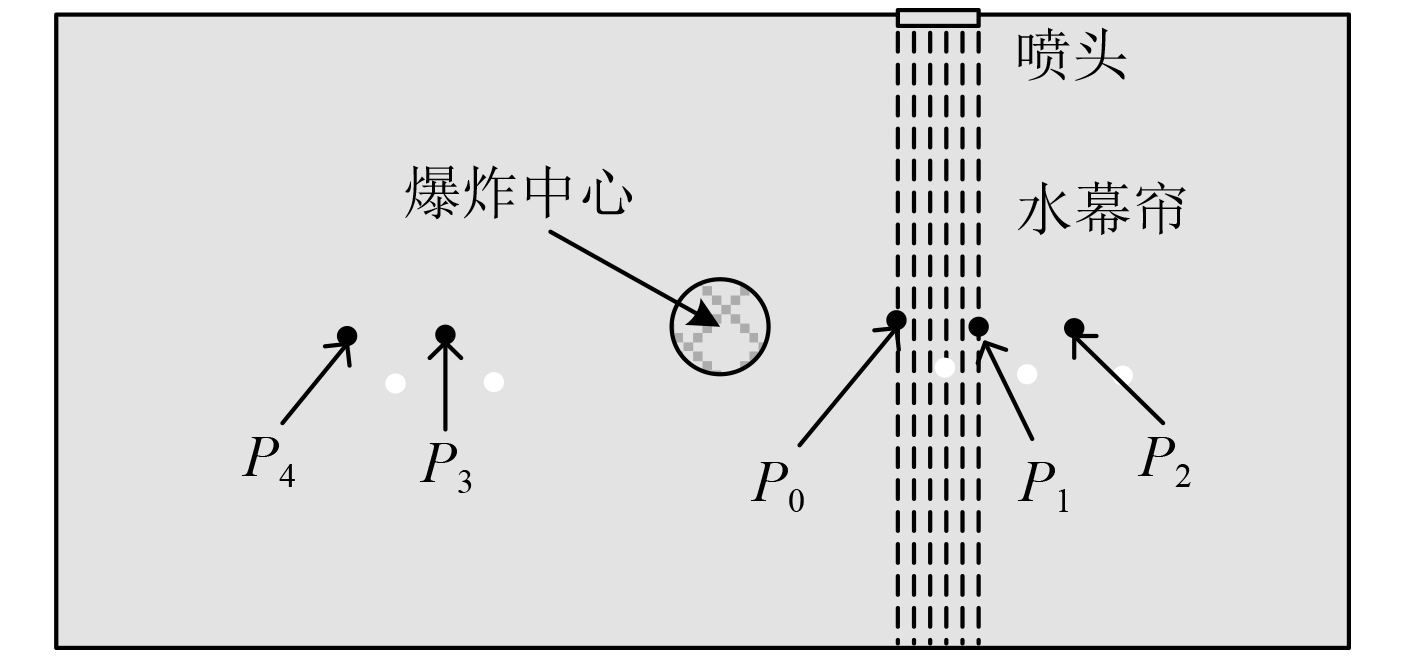
|
图 1 计算模型 Fig. 1 Calculation model |
| $ {\rm {C_3}{H_6}{N_6}{O_6}} = {\rm 3H{}_2O + 3CO + 3{N_2}} + 335.4{\rm Kcal}\text{。} $ | (14) |
| $ {\rm 3CO + 1.5{O_2} = 3C{O_2} }+ 256.1{\rm Kcal}\text{。} $ | (15) |
舱室中心位置定义为坐标原点,右上方顶部布置一个喷头,喷出直径200 μm,速度50 m/s,质量流量为0.084 kg/s的水雾,形成水幕。在水幕两侧布置5个监测点(P0(0, 0.15),P1(0, 0.2)、P2(0, 0.25)、P3(0, –0.2)、P4(0, –0.25)),实时监测这5处的压力、温度变化。
计算选用密度基隐式求解器,湍流模型使用
从物理上看,冲击波可以看作空间中一个很薄的间断面,其两侧流体的宏观状态参量是不连续的。冲击波穿过水幕时,将水滴击碎为更细小的液滴颗粒,并给予液滴一定的速度使其顺着冲击波传播方向运动,这个过程消耗了冲击波的动量,降低了冲击波速度;破碎的液滴增大了与空气的接触面积,加快了吸热蒸发速率,这个过程吸收大量能量,冲击波压力、温度随之降低。
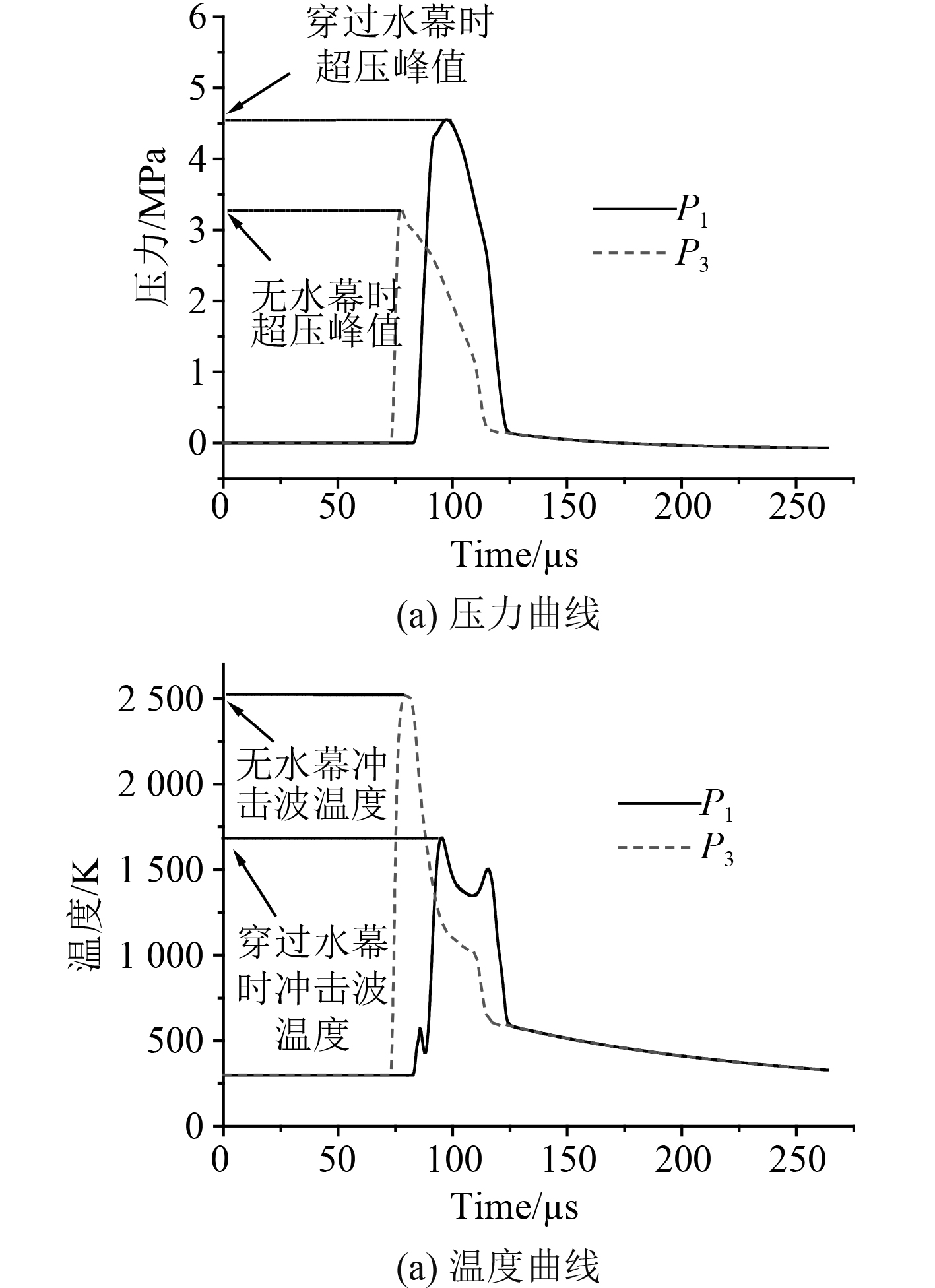
图2与图3为4个监测点的压力和温度随时间变化曲线。监测点P1在水幕正后方,其对称位置为监测点P3。图2(a)中显示P1位置的超压峰值明显高于P3位置,原因是冲击波穿过水幕过程中,细小的水滴对冲击波有反射作用,多个反射波与冲击波强度叠加。图2(b)反映出水幕对高温爆炸波的降温作用,温度峰值由2 519 K下降到1 687 K。另外,从表1可以看出,穿过水幕的冲击波呈现明显的滞后性,冲击波穿过P1的时间较P3滞后11.4 μs,穿过P2的时间较P4滞后15.4 μs,即穿过水幕的冲击波速度明显降低;可计算出冲击波从P0到P1位置,无水幕时速度为5.63 Ma,而在水幕中仅为3.90 Ma,水幕中冲击波速度衰减达到31%。
|
|
表 1 冲击波经过各个监测点的时间 Tab.1 Time of shock wave passing through monitoring points |
|
图 2 监测点1和监测点3参数变化曲线 Fig. 2 Pressure and Temperature curves of P1 and P3 |
|
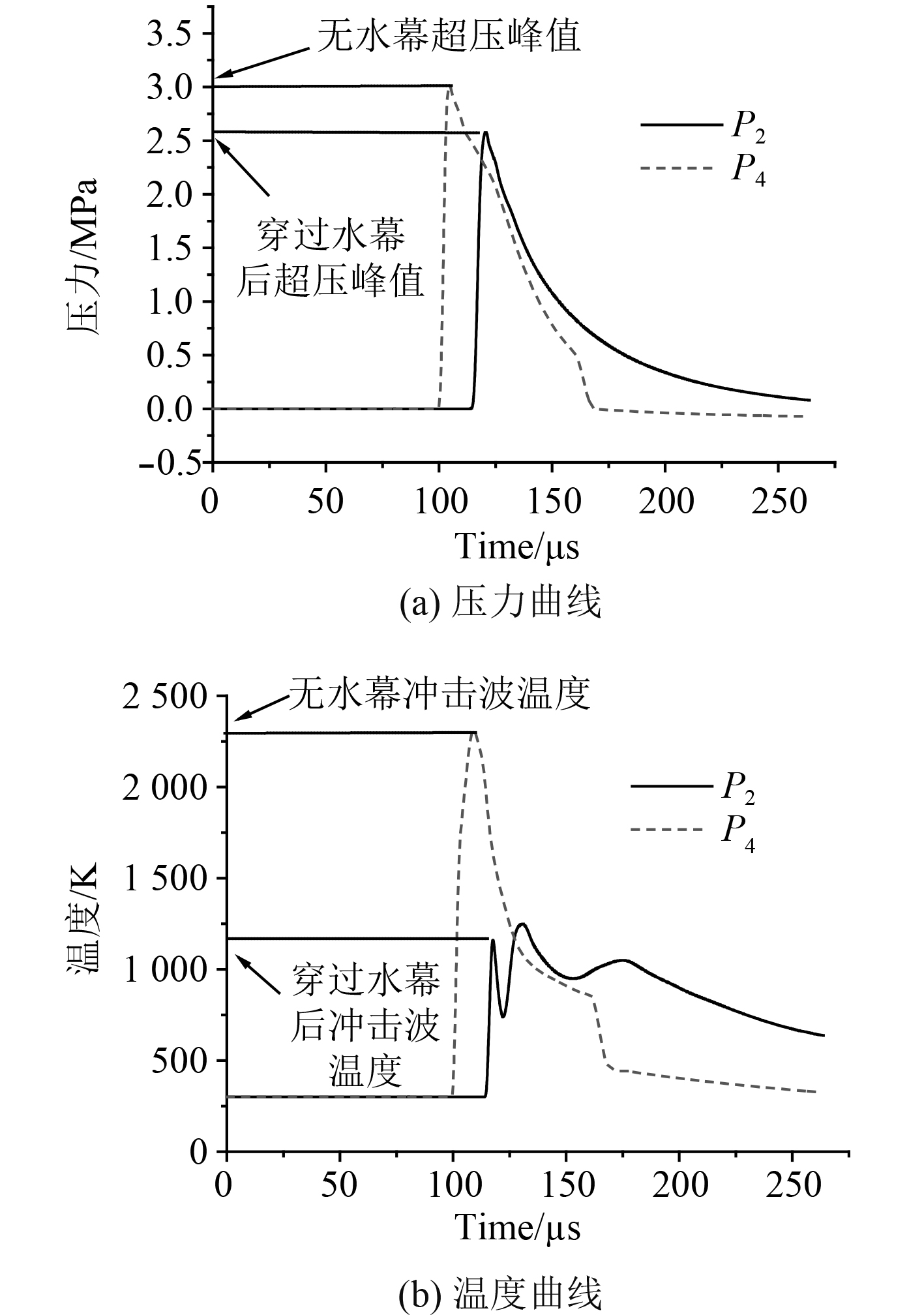
图 3 监测点2和监测点4参数变化曲线 Fig. 3 Pressure and Temperature curves of P2 and P4 |
监测点P2在水幕正后方0.05 m处,图3(a)中P2处的超压峰值明显低于P4位置,约为P4处超压峰值的85%,可以看出穿过水雾区的冲击波强度降低,超压峰值衰减了15%,这是由于波阵面穿过水雾区后,无反射波叠加,监测压力即为冲击波的真实压力。图3(b)显示冲击波穿过P4处时温度为2 310 K,而P2处仅为1 160 K,冲击波温度降低了一半,但由于高温水蒸气的存在,波后气体温度下降速率会慢于空气中传播的冲击波。
为了更直观显示冲击波通过水幕过程中状态参数的变化,图4为50 μs,80 μs,120 μs时波阵面的压力与温度云图。50 μs时,冲击波传播至水幕帘左侧,云图显示爆炸中心及波阵面上压力、温度较高;80 μs冲击波处于水幕中,图中显示水幕中的冲击波前缘压力高于其他区域,这与前面分析的反射波与冲击波强度叠加导致超压峰值增大吻合。另外,水幕的降温效果也十分明显。120 μs时,冲击波局部已经穿过水幕区,而水幕正下方液滴与冲击波相遇的局部区域压力仍然高于冲击波压力,冲击波传播到舱室顶部和底部,形成局部高温高压,对舱室结构极为不利。

|
图 4 不同时刻压力、温度云图 Fig. 4 Pressure and Temperature field at different times |
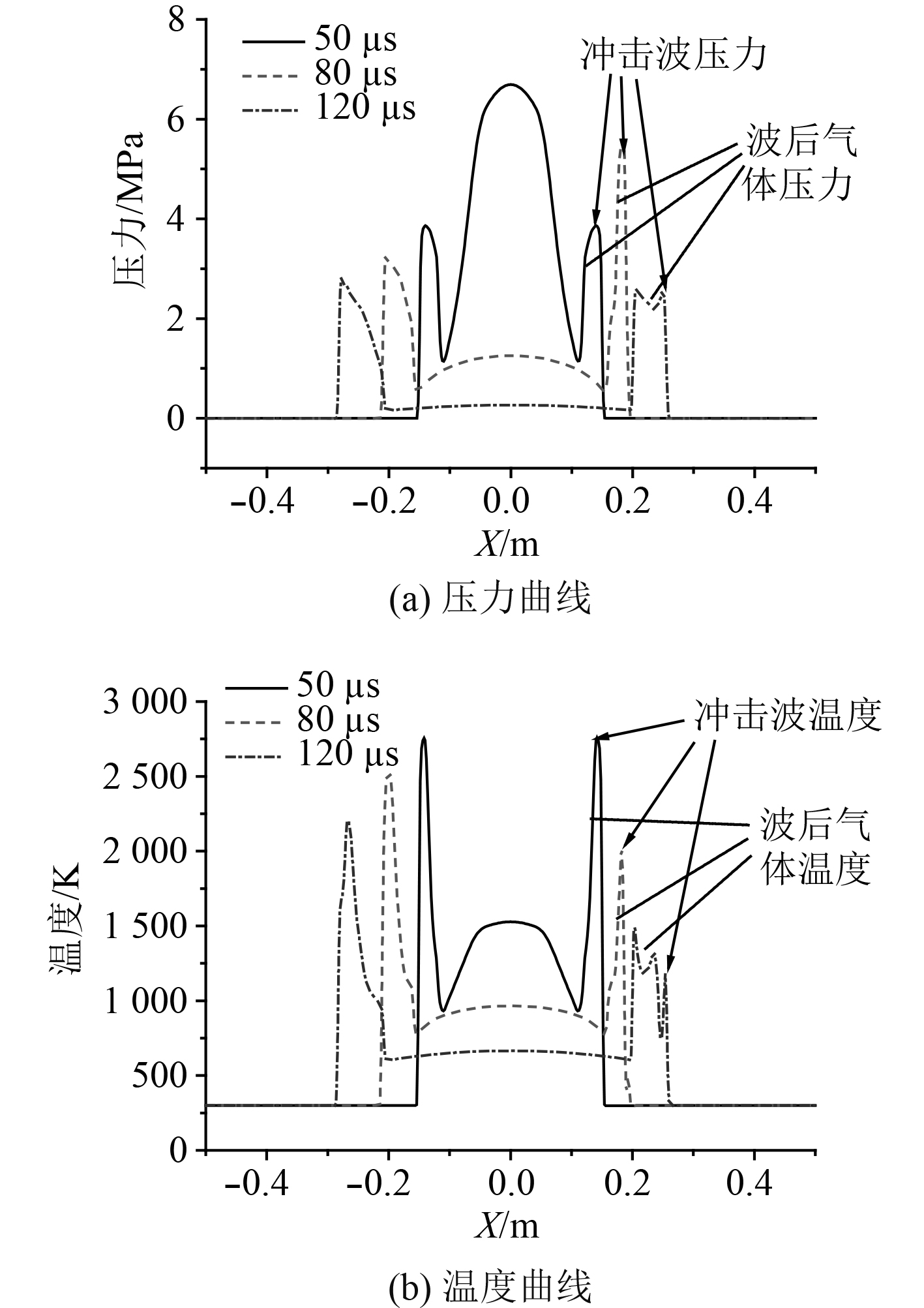
图5(a)和图5(b)分别给出了3个时刻舱室中心线(Y=0)上压力、温度分布曲线。
|
图 5
舱室中心线Y=0上压力、温度分布
Fig. 5
Distribution of pressure and temperature on Y |
可以看出:
50 μs时,冲击波刚刚到达水幕帘左侧,此前,冲击波在空气中传播,波阵面及爆炸中心位置处温度与压力较高,且两侧温度与压力关于爆炸中心对称;
80 μs时,冲击波在水幕中传播,冲击波波阵面附件存在大量液滴并同时驱使水雾颗粒向右运动,液滴对冲击波有反射作用,产生的反射波与冲击波叠加导致冲击波超压峰值高达5.42 MPa,而无水幕一侧的超压峰值仅为3.25 MPa,与此同时,冲击波的温度由2 517 K下降到2 010 K;
120 μs时,冲击波已离开水雾区,无反射波强度叠加,监测的压力即为冲击波真实压力。从图5(a)中可以看出,有水幕一侧超压峰值为2.57 MPa,较另一侧的2.83 MPa 下降了9.2%,表明水幕可有效衰减冲击波强度,但图中显示波后气体压力却并不像舱室左侧一样以较稳定的梯度下降,而是大小维持在冲击波峰值附近。此时,图5(b)中显示水幕对冲击波降温效果显著,但波后气体温度甚至会高于冲击波温度。
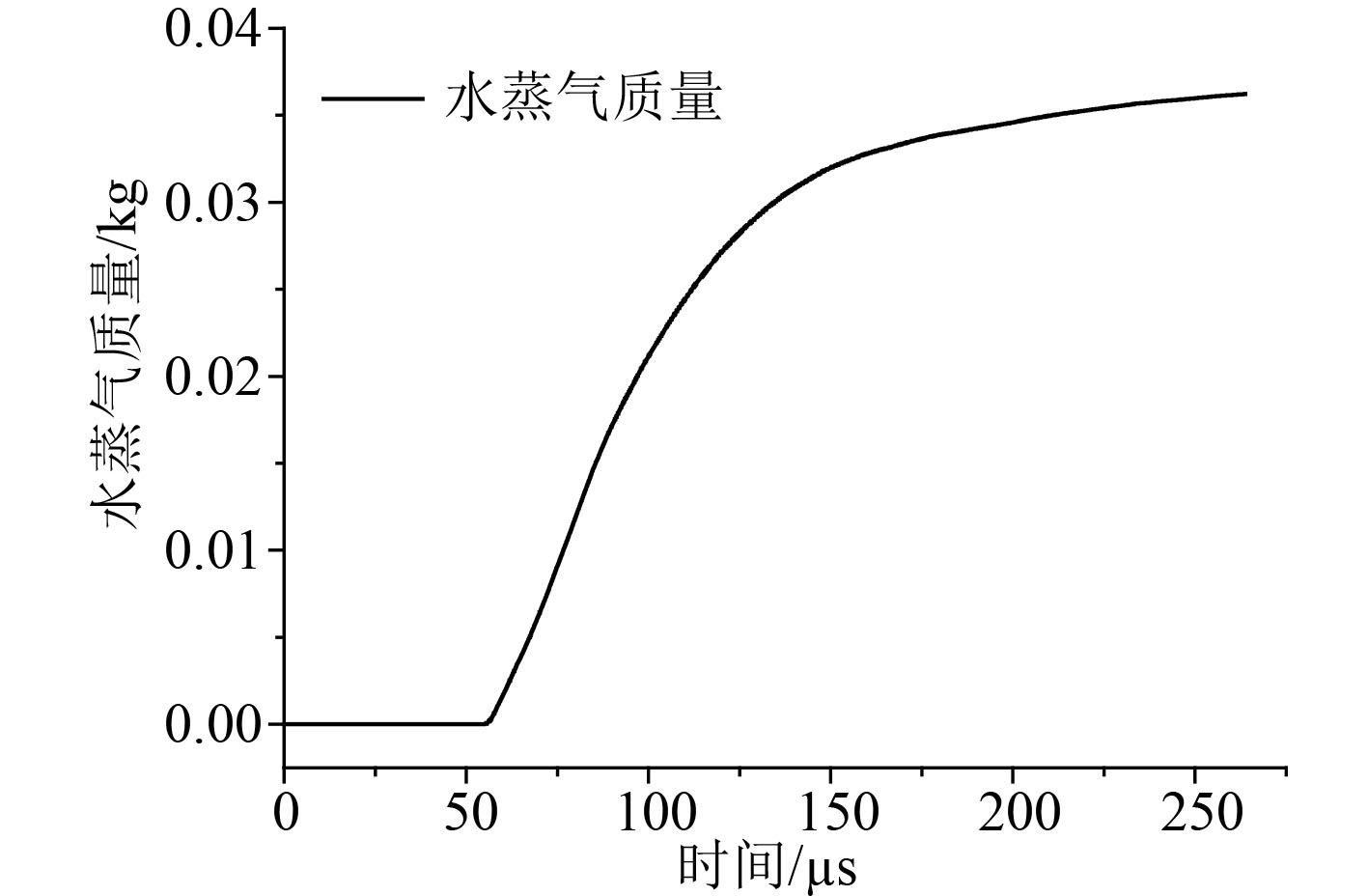
爆炸前,已在冲击波后方布置有一道水幕,冲击波抵达后,液滴快速蒸发,随着冲击波穿过水幕区,剩余液滴数量大大减少,蒸发速率下降,水蒸气质量增长速率变慢,如图6所示。冲击波穿过水幕区后,波后气体聚集了大量高温水蒸气,由于喷淋速度远小于冲击波速度,冲击波扫过后只有少量常温液滴喷出,无法对波后高温水蒸气进行有效降温,造成波后方温度下降缓慢,这与图3(b)中P2位置温度变化及图5(b)中120 μs时波后气体温度分布的计算结果一致。增大喷淋速度可一定程度上加快波后气体降温。
|
图 6 水蒸气质量变化 Fig. 6 Vapor mass changes |
为了提高战时舰船生命力,增强国内的冲击波防护技术,本文通过对水幕衰减爆炸冲击波的定量计算分析,证实了水幕抑爆的可行性。文中工况下的计算结果表明:
1)在充满细水雾的水幕中,冲击波传播速度大大降低,可达30%左右;
2)冲击波穿过水幕时,遇到液滴颗粒会产生反射波,反射波与冲击波叠加,造成超压峰值大大增加;
3)冲击波穿过水幕后,冲击波超压峰值与温度下降明显,水幕对冲击波强度衰减效果显著;
4)冲击波穿过水幕后,波后聚集了大量高温水蒸气,波后气体压力与温度下降速率变慢。
| [1] |
KEENAN W A, WAGER P C. Mitigation of confined explosion effects by placing water in proximity of explosions, 25th DoD Explosives Safety Seminar[R]. Anaheim Hilton Hotel, Anaheim, California, 1992.
|
| [2] |
李士军, 赖孝军. 主动式水爆抑制系统的研究状况[J]. 船海工程, 2013. LI Shi-jun, NAI Xiao-jun. Research development of the active water explosion suppression system[J]. Ship & Ocean Engineering, 2013. DOI:10.3963/j.issn.1671-7953.2013.06.034 |
| [3] |
李钰阳. 通道内水幕帘减弱冲击波强度问题的数值研究[D]. 哈尔滨: 哈尔滨工程大学, 2014. LI Yu-yang. Numerical study of water curtain decreasing the intensity of shock wave in a channel[D]. Harbin: Harbin Engineering University, 2014. |
| [4] |
陈攀, 刘志忠. 舱室内爆炸冲击波载荷特性及影响因素分析[J]. 舰船科学技术, 2016. CHEN Pan, LIU Zhi-zhong. Research on loading of explosive and influencing factors inside closed cabin[J]. Ship Science and Technology, 2016. DOI:10.3404/j.issn.1672-7649.2016.1.022 |
| [5] |
王超, 吴宇, 施红辉, 等. 液滴在激波冲击下的破裂过程[J]. 爆炸与冲击, 2016, 36(1): 129-134. WANG Chao, WU Yu, SHI Hong-hui, et al. Breakup process of a droplet under the impact of a shock wave[J]. Explosion and Shock Waves, 2016, 36(1): 129-134. DOI:10.11883/1001-1455(2016)01-0129-06 |
| [6] |
刘贵兵, 候海量, 朱锡. 液滴对爆炸冲击波的衰减作用[J]. 爆炸与冲击, 2017. LIU Gui-bing, HOU Hai-liang, ZHU Xi. Attenuation of shock wave passing through liquid droplet[J]. Explosion and Shock Waves, 2017. DOI:10.11883/1001-1455(2017)06-0893-08 |
| [7] |
刘贵兵, 候海量, 朱锡. 等体积比水雾对冲击波衰减规律研究[J]. 舰船科学技术, 2017. LIU Gui-bing, HOU Hai-liang, ZHU Xi. Attenuation of a shock wave interacting with same volume ratio of water droplets[J]. Ship Science and Technology, 2017. DOI:10.3404/j.issn.1672-7619.2017.01.001 |
| [8] |
RAMAGOPAL A, HEATHER H D. Willauer effects of fine water mist on a confined blast[J]. Fire Technology, 2012. |
 2020, Vol. 42
2020, Vol. 42
