2. 华中科技大学船舶与海洋工程学院,湖北 武汉 430074
2. Institute of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
襟翼舵全舵由主舵和子舵组成,主舵后面可以转动的部分即为襟翼,称子舵。当进行转舵的时候,2个一起转动,但是主舵的转动方向相同但角度比子舵的小。由于襟翼的存在,转动舵角时相当于增加了舵剖面的拱度,可使舵力增大至普通舵的1.6~1.8倍,因而它具有高舵效,尤其是小舵角时舵效更高。装设襟翼舵的推船操纵性明显改善,致使其运输能力得以充分发挥。1960年襟翼舵第一次被作为船用舵使用,以其特有的结构简单,高舵效的优势被看重,因此在近些年里,襟翼舵的发展非常快。目前实船上采用襟翼舵已见到显著的经济效益,表明它是一种有效、可靠、简单、易于推广的优良舵型。
前人对襟翼舵的研究,主要是从剖面形状,主副舵的面积比,展弦比等方面展开,对主副舵之间的缝隙大影响以及襟翼舵尺度效应的研究很少。本文以NACA0020为基本剖面的襟翼舵为研究对象,改变襟翼舵模型缝的大小以及缩尺比,采用RANS方法计算不同间隙大小以及不同缩尺比下的襟翼舵升力和阻力,分别比较各自对升力阻力的影响规律,分析主副舵缝隙流动对整体的影响,并且与许汉珍风洞实验所得图谱进行了比较验证。
1 数学模型 1.1 控制方程本文采用无量纲化雷诺平均方程对襟翼舵在敞水域中流场进行模拟计算,不可压缩牛顿流体连续性方程与RANS方程为:
| $ \frac{{\partial \overline {{u_i}} }}{{\partial {x_i}}} = 0 \text{,} $ | (1) |
| $ \rho \frac{{\partial \overline {{u_i}} }}{{\partial t}} + \rho \overline {{u_j}} \frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} = \rho \overline {{F_i}} - \frac{{\partial \overline p }}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left(\mu \frac{{\partial \overline {{u_i}} }}{{\partial {x_j}}} - \rho \overline {{{u'}_i}{{u'}_j}} \right)\text{。} $ | (2) |
其中:
标准k-ε湍流模型,湍动耗散率ε的定义如下:
| $ \varepsilon = \frac{\mu }{\rho }\overline {\left(\frac{{\partial u_i'}}{{\partial {x_k}}}\right)\left(\frac{{\partial u_i'}}{{\partial {x_k}}}\right)} \text{。} $ | (3) |
湍动粘度
| $ {\mu _t} = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon } \text{。} $ | (4) |
在标准k-ε模型中,k和ε是2个基本未知量,相对应的变换方程为:
| $ \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial \mathop x\nolimits_j }}\left( {\rho \mathop u\nolimits_j k} \right) = \rho P - \rho \varepsilon + \frac{\partial }{{\partial \mathop x\nolimits_j }}\left[ {\left( {\mu + \frac{{\mathop \mu \nolimits_t }}{{\mathop \sigma \nolimits_x }}} \right)\frac{{\partial k}}{{\partial \mathop x\nolimits_j }}} \right]\text{,} $ | (5) |
| $ \begin{split} \frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial \mathop x\nolimits_j }}\left( {\rho \mathop u\nolimits_j \varepsilon } \right) =\,& {C_{{\varepsilon _1}}}{f_1}\frac{{\rho P\varepsilon }}{k} - {C_{{\varepsilon _2}}}{f_2}\frac{{\rho {\varepsilon ^2}}}{k} +\\ &\frac{\partial }{{\partial \mathop x\nolimits_j }}\left[ {\left( {\mu + \frac{{\mathop \mu \nolimits_t }}{{\mathop \sigma \nolimits_\varepsilon }}} \right)\frac{{\partial \varepsilon }}{{\partial \mathop x\nolimits_j }}} \right]\text{。} \end{split} $ | (6) |
根据Launder等的推荐值以及后来的实验验证,模型中的一些参数取值如下:
| $ {C_{_\mu }} = 0.09\;\;{C_{{\varepsilon _1}}} = 1.44\;\;{C_{{\varepsilon _2}}} = 1.92\;\;{\sigma _k} = 1.0\;\;{\sigma _\varepsilon } = 1.3\text{。} $ |
本文采用NACA0020作为基本翼型剖面,通过改变主副舵之间的间隙以及计算的缩尺比得到不同的计算模型。原始模型为许汉珍风洞实验模型,主舵高h为242.6 mm,全舵宽C为197.1 mm,子舵宽Cz为60 mm,展弦比A为1.225,主舵与子舵间隙为1.69 mm,通过改变缝大小分别得到缝宽1,5,10,15,20,25,30,35,40 mm的襟翼舵模型,如图1所示。
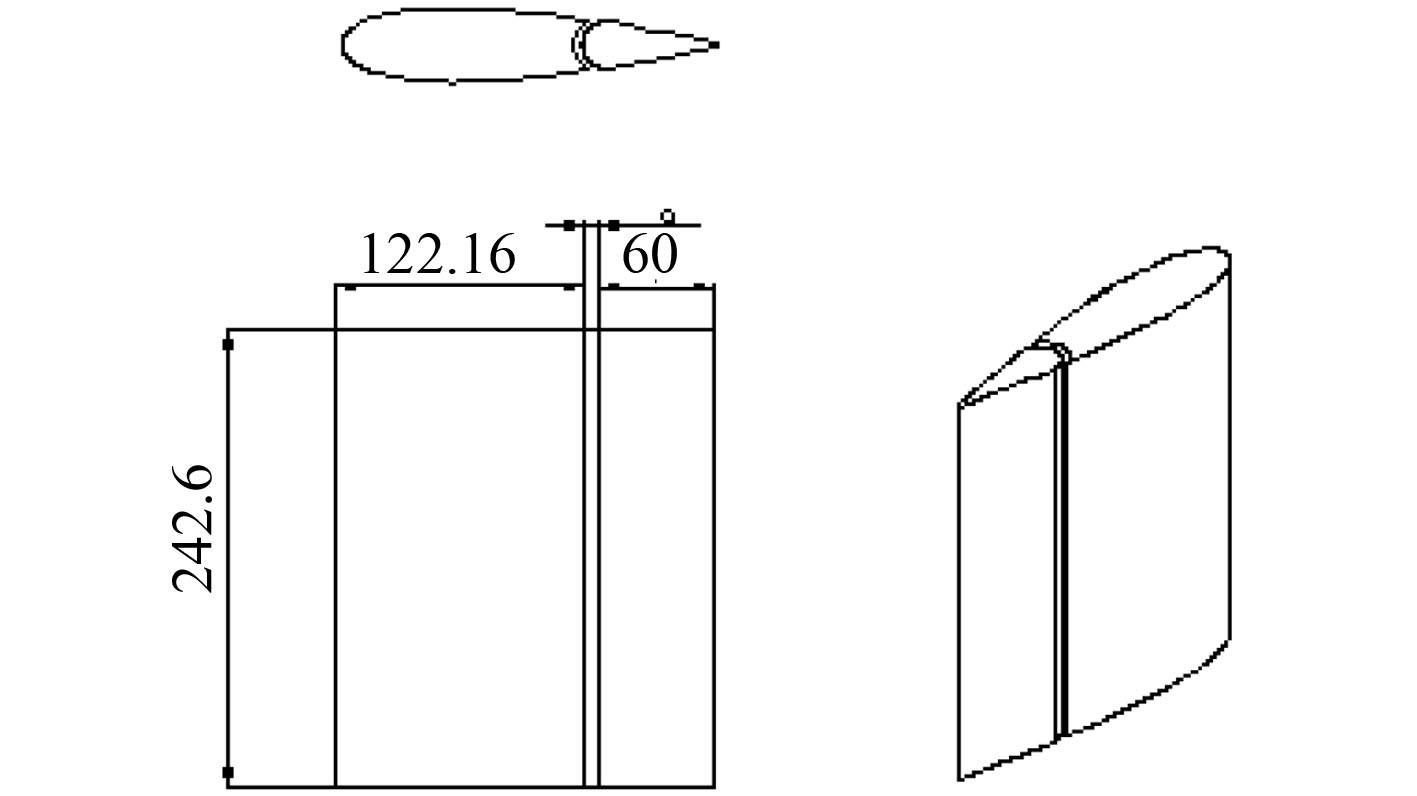
|
图 1 仿真模型 Fig. 1 Simulation model |
计算速度为v=10 kn=5.144 m/s,Re=0.123×107,此时流动已经充分发展,从文献[7]可知RNG k-ε湍流模型适用于襟翼舵阻力计算以及其他水动力计算。
1.3 计算域及边界条件单舵计算域如图2所示,计算域为长7b,宽3b,高10b的包围舵的长方体,轴线与单舵模型(wall)对称轴重合。进流边界面为长方体体前端面,为速度入口(velocity inlet),距离模型首部为2b;出流边界面为长方体后端面,为压力出口(pressure outlet),距离模型尾部距离为5b;外边界为长方体侧面,为外场速度入口(velocity inlet)。
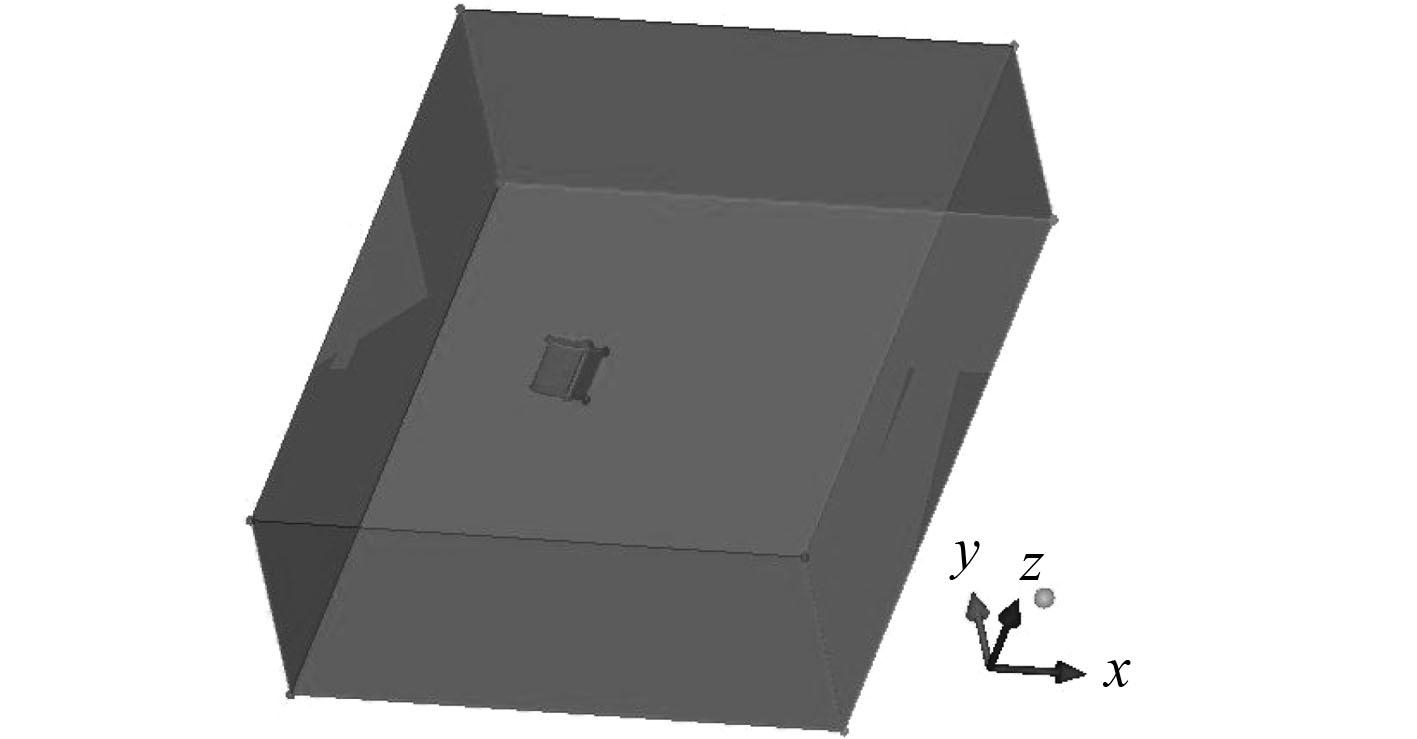
|
图 2 计算域 Fig. 2 Simulation model |
本文包括下列边界(b为襟翼舵模型总长):
1)速度入口(velocity inlet)。襟翼舵首部向前2b,设定来流速度的大小与方向
2)压力出口(pressure outlet):襟翼舵艉部向后5b,认为流动在该处已经充分发展,故边界条件使用压力出口。
3)壁面(wall)。舵外表面,设定无滑移条件,u=v=w=0。
4)外场。因为流域外表面距离襟翼舵足够远,故可以认为在该面上没有法向速度,因此可以取边界条件为速度入口(velocity inlet)。
坐标系:坐标原点在舵中部,x轴沿来流向布置,z轴指向水面,坐标系符合右手定则。
模型计算采用SIMPLEC算法结合RNG k-ε湍流模式计算雷诺平均纳维-斯托克斯方(RANS),来流速度(试验工况)为10 kn(5.144 m/s)。对于压力方程采用标准的离散格式进行离散,对于动量方程、湍流方程、雷诺应力方程,均采用2阶迎风格式进行离散。
2 数值模拟计算采用结构化网格,取得了很好的计算精度。为了有效模拟近壁面处的流动,在边界层区域内合理布置网格和选择适合的网格尺度。为提高计算精度,边界层以及出入流段都进行了过度处理。计算时主舵偏转角为10°,主舵相对主舵偏转角为6°,单舵网格总数为3 000 000。根据前期的试验研究结果,计算速度为10 kn(5.144 m/s),y+取在30~300之间以充分捕捉近壁面的流动信息。
先对网格进行无关性验证,在这里对NACA0020翼型进行网格独立性的验证,对主舵子舵全部零舵角情况下的NACA0020翼型网格数分别为60万、100万、150万、230万和300万进行阻力对比分析,如表1所示。可以看出在网格量为230万和300万计算得到的计算值相差不到1%,在计算误差范围之内,验证了网格无关性。
|
|
表 1 网格无关性验证结果 Tab.1 Grid Independent Validation |
为了说明计算方法的可靠性,对本实验模型进行了计算分析,并与已有文献[8]中的实验值进行对比如表2所示,可以看到误差均在5%以内,验证了计算方法的可靠性(表中实验值是由许汉珍《襟翼舵的实验与分析》的图谱中所读得)
|
|
表 2 阻力系数Cd对比结果 Tab.2 Comparison of Cd between experimental simulation data |
|
|
表 3 升力系数CL对比结果 Tab.3 Comparison of CL between experimental simulation data |
计算得到的襟翼舵整体和主舵子舵的阻力(压差阻力和摩擦阻力)和升力以及力矩(对主舵前缘点)对比结果如图3~图13所示。

|
图 3 襟翼舵整体升力系数CL Fig. 3 The lift coefficient of flap rudder CL |
|
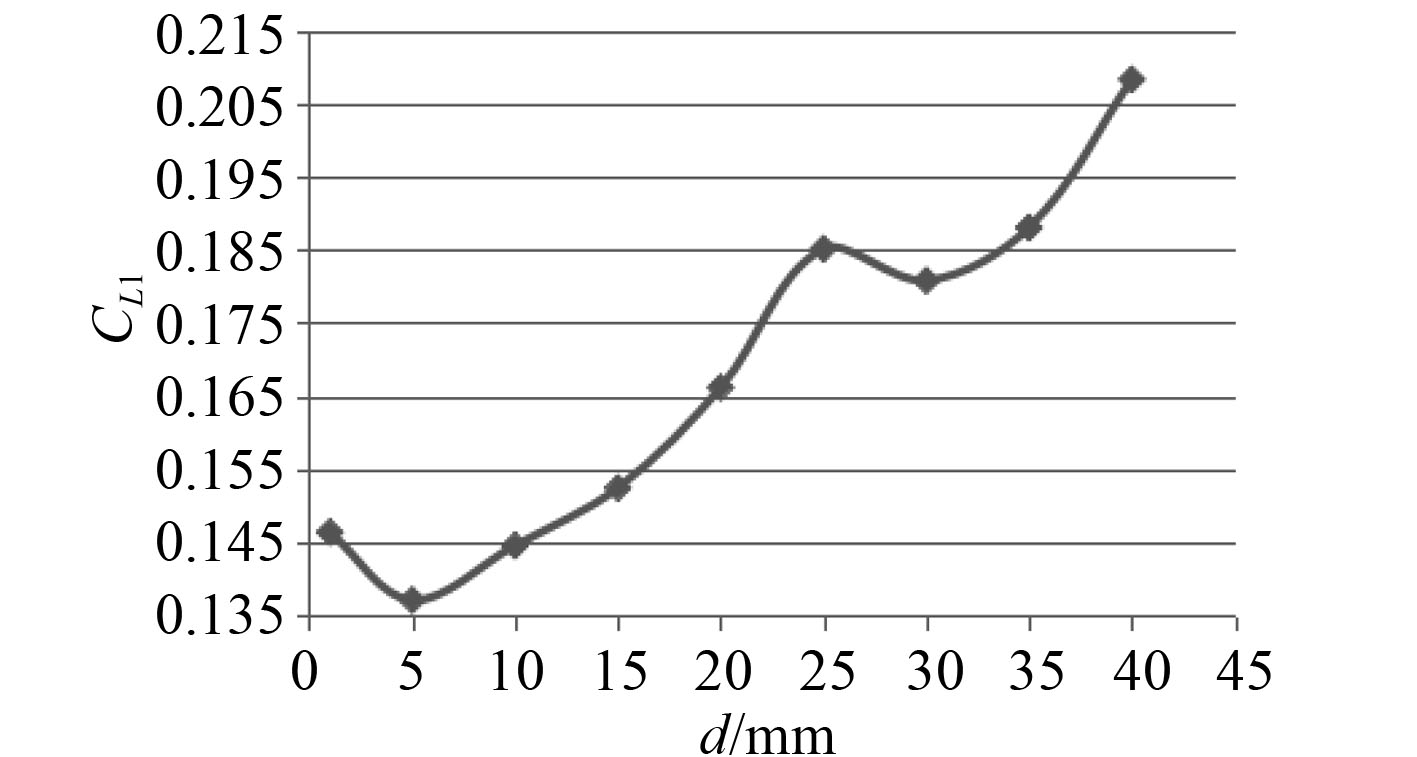
图 4 襟翼舵子舵升力系数CL1 Fig. 4 The lift coefficient of flap CL1 |
|
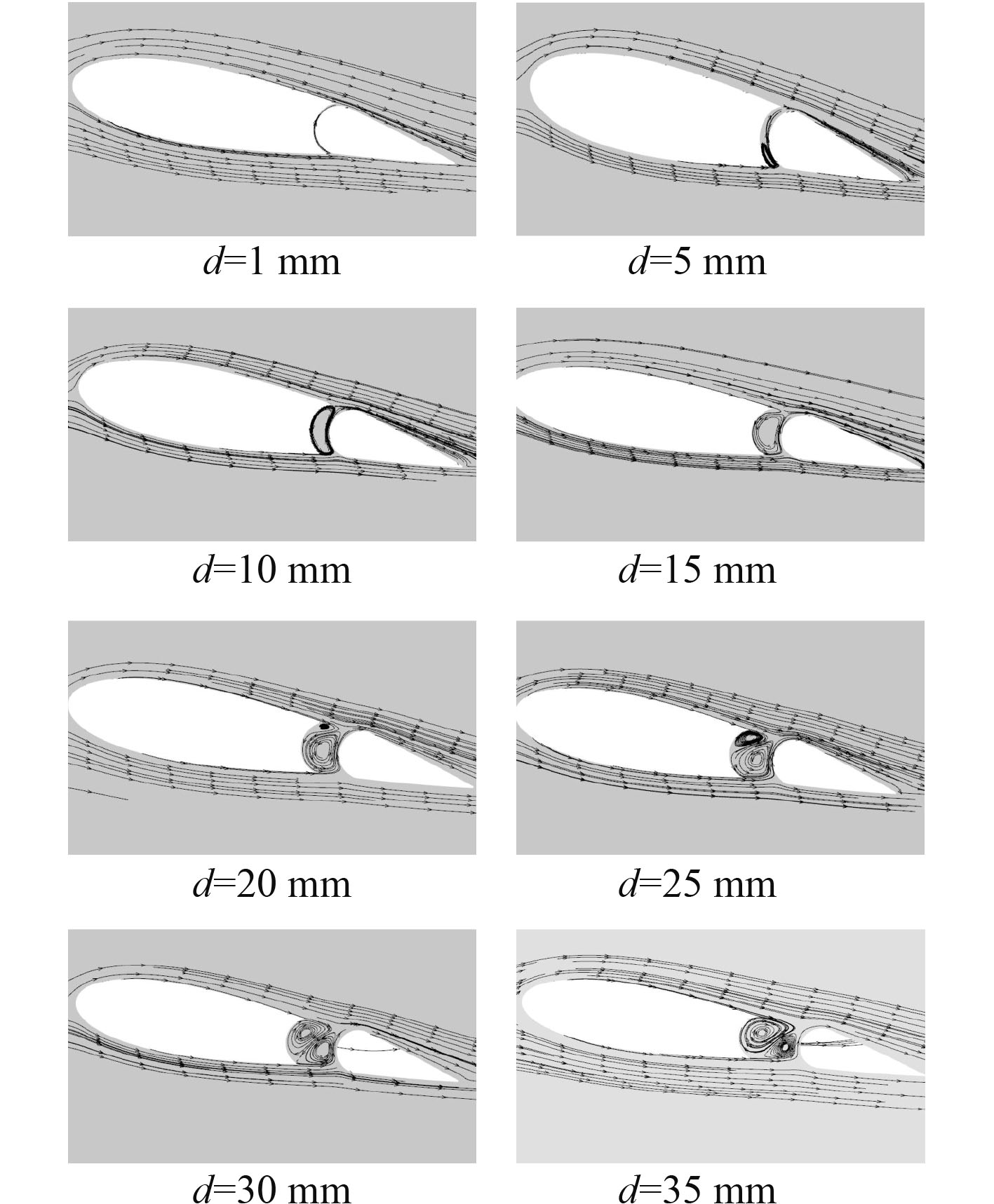
图 13 不同缝隙大小下Z=0.12处的流线图 Fig. 13 Flow chart of different gap size |
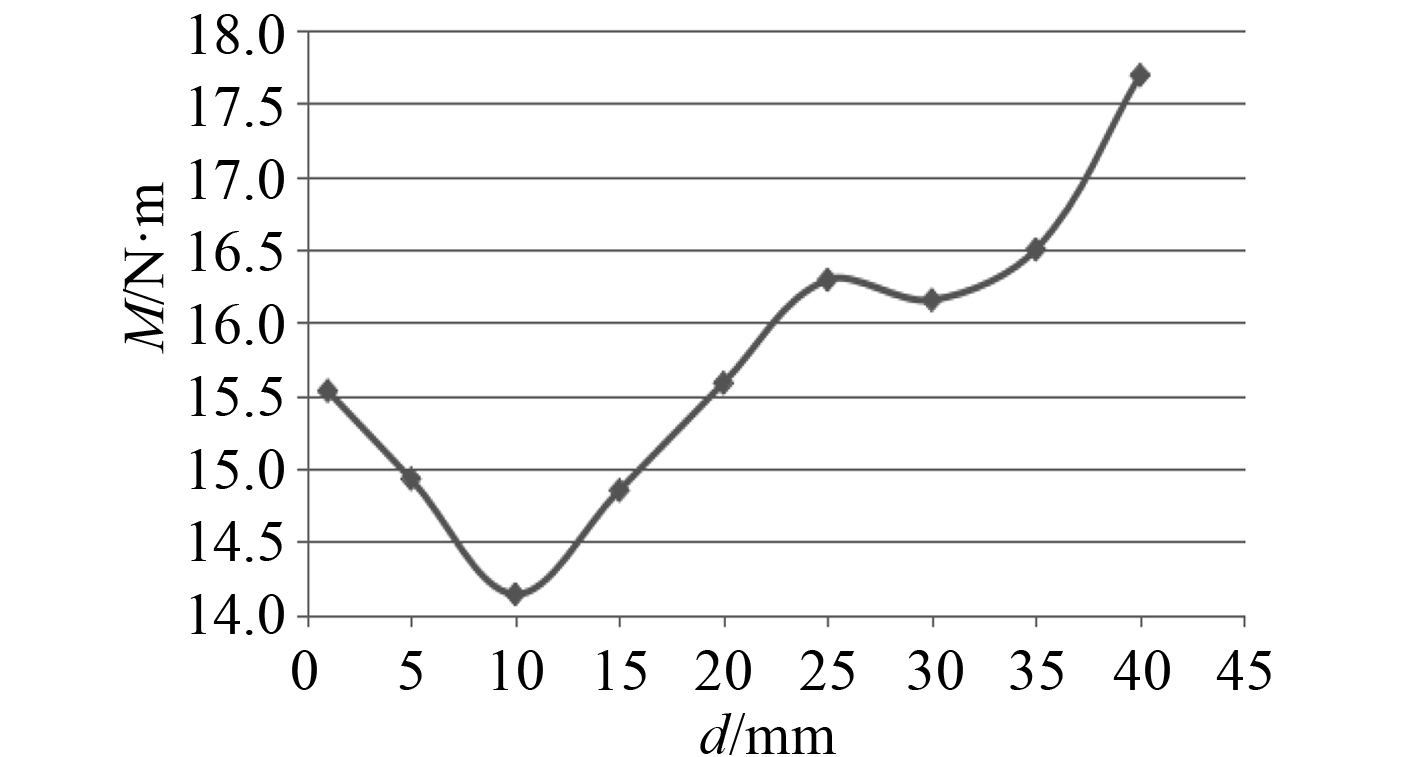
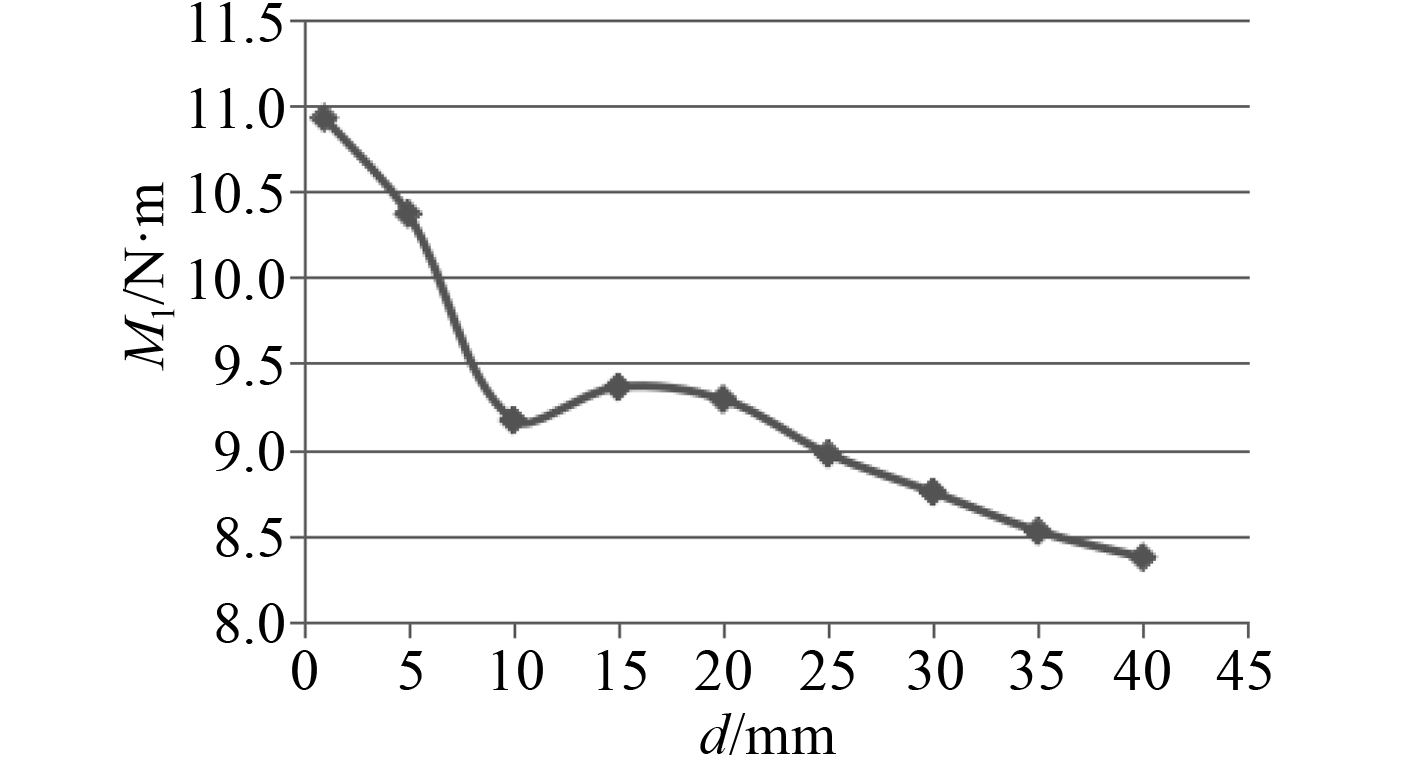
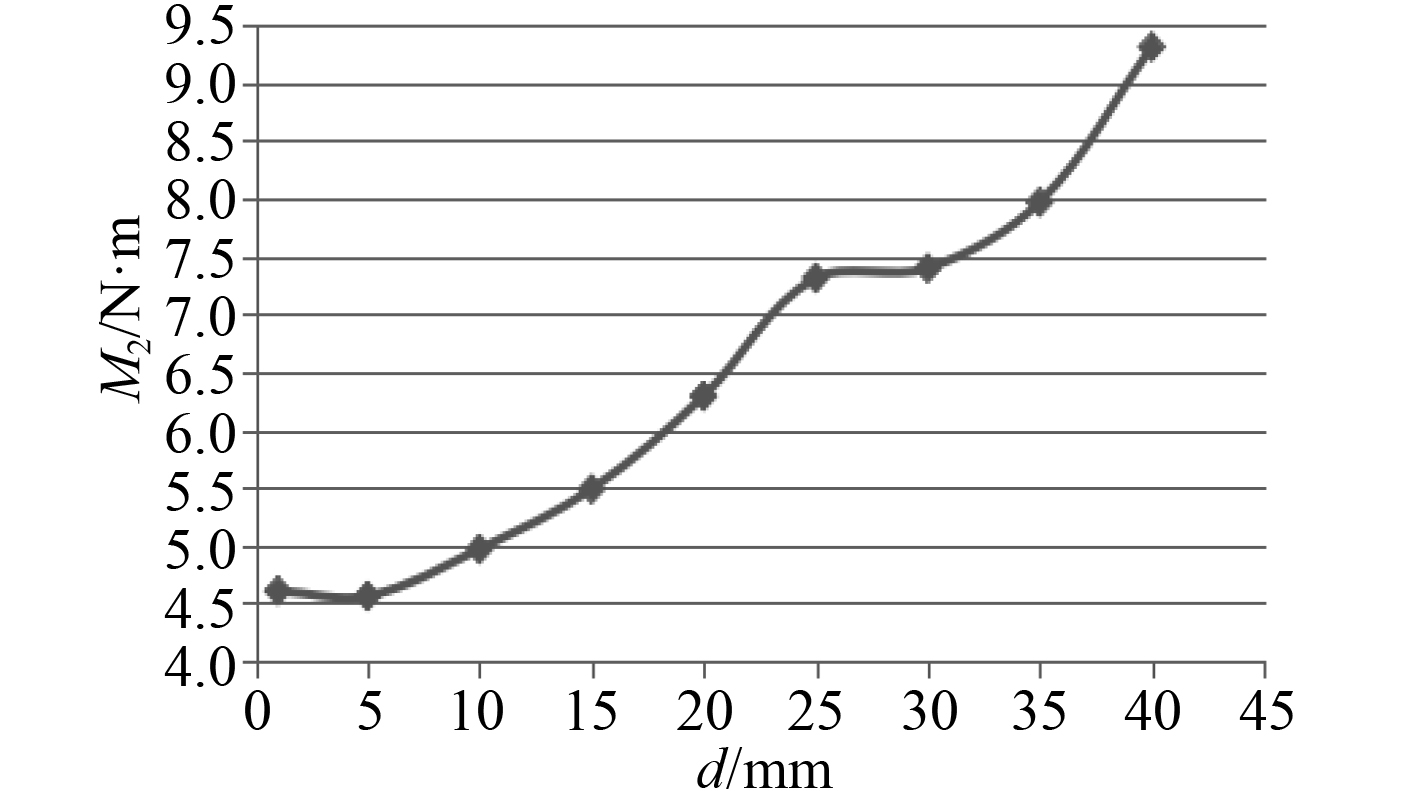
可以发现,随着缝隙的增大,升力系数在1~10 mm时快速减小(最大变化值超过7%),随着缝隙继续增大至25 mm,升力系数一直在缓慢增大,超过25 mm后,升力系数开始减小。同时子舵的升力系数同样也先减小,随后便保持增大的趋势不断增大。整舵的力矩(对主舵的前缘点)变化规律与升力变化相似,同样在10 mm前不断减小,随后开始增大,超过25 mm又开始减小。其中整舵力矩为主舵和子舵所产生的力矩和,从计算发现,主舵力矩在不断减小,最大减少值达到20%,相反子舵力矩在不断的增大,增大幅度超过62%。
|
图 5 襟翼舵整体力矩M Fig. 5 The moment of flap rudder M |
|
图 6 主舵产生的力矩M1 Fig. 6 The moment of main part of rudder M1 |
|
图 7 子舵产生的力矩M2 Fig. 7 The moment of the flap M2 |

|
图 8 襟翼舵整体阻力系数Cdt Fig. 8 The drag coefficient of flap rudder Cdt |
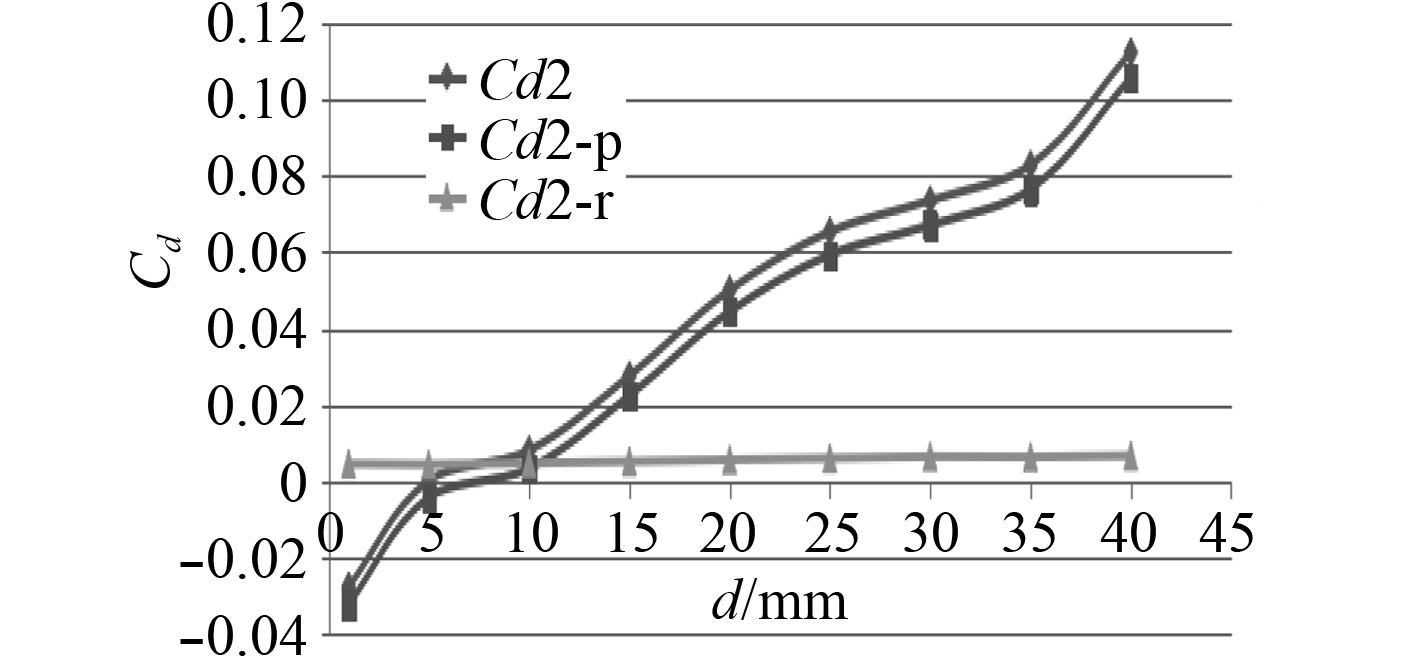
随着缝隙的增大,襟翼舵整体的阻力系数在不断增大,子舵的阻力系数与整体保持一致,在缝隙较小时,子舵的阻力位负值,即子舵将产生向前的推力,减小了整体阻力;主舵的阻力保持减小的趋势,当缝隙到达一定大小时,主舵阻力系数将保持不变。
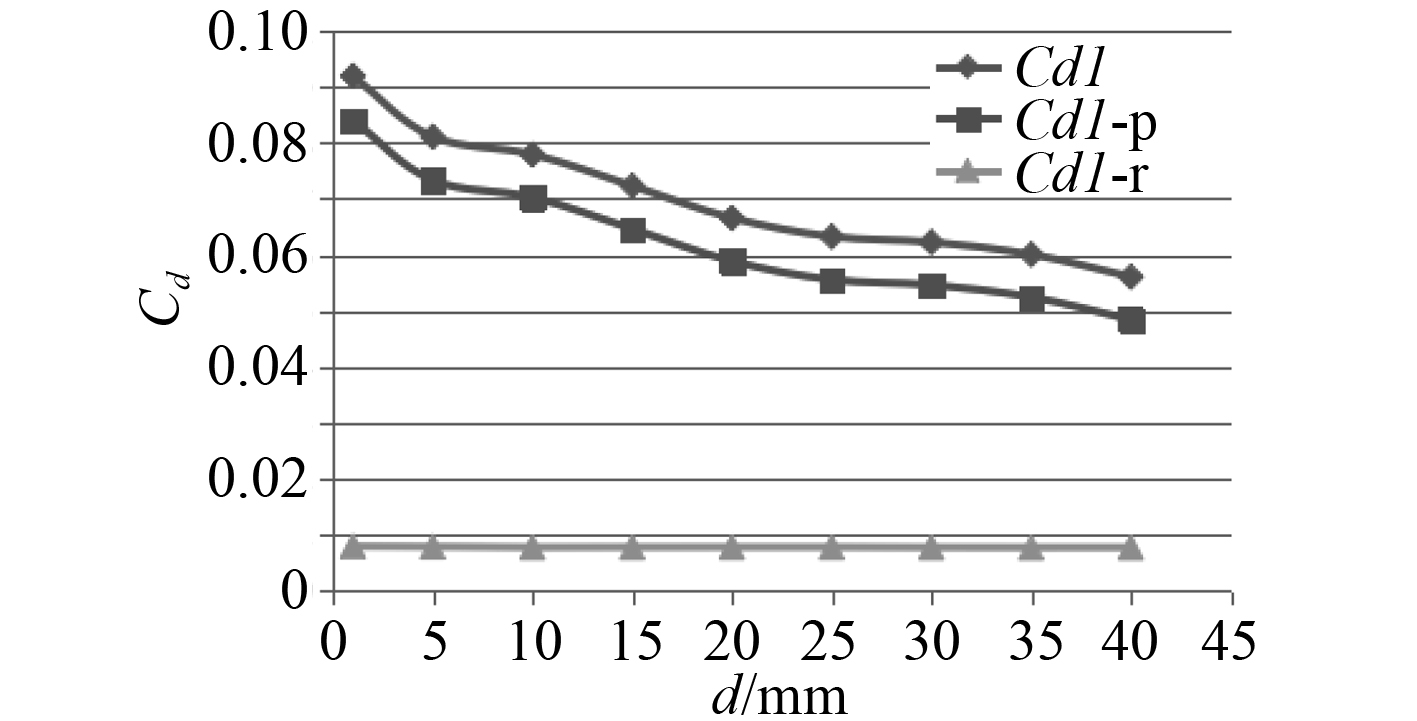
|
图 9 襟翼舵主舵阻力系数Cd1 Fig. 9 The drag coefficient of main part of rudder Cd1 |
|
图 10 襟翼舵子舵阻力系数Cd2 Fig. 10 The drag coefficient of the flap Cd2 |
|
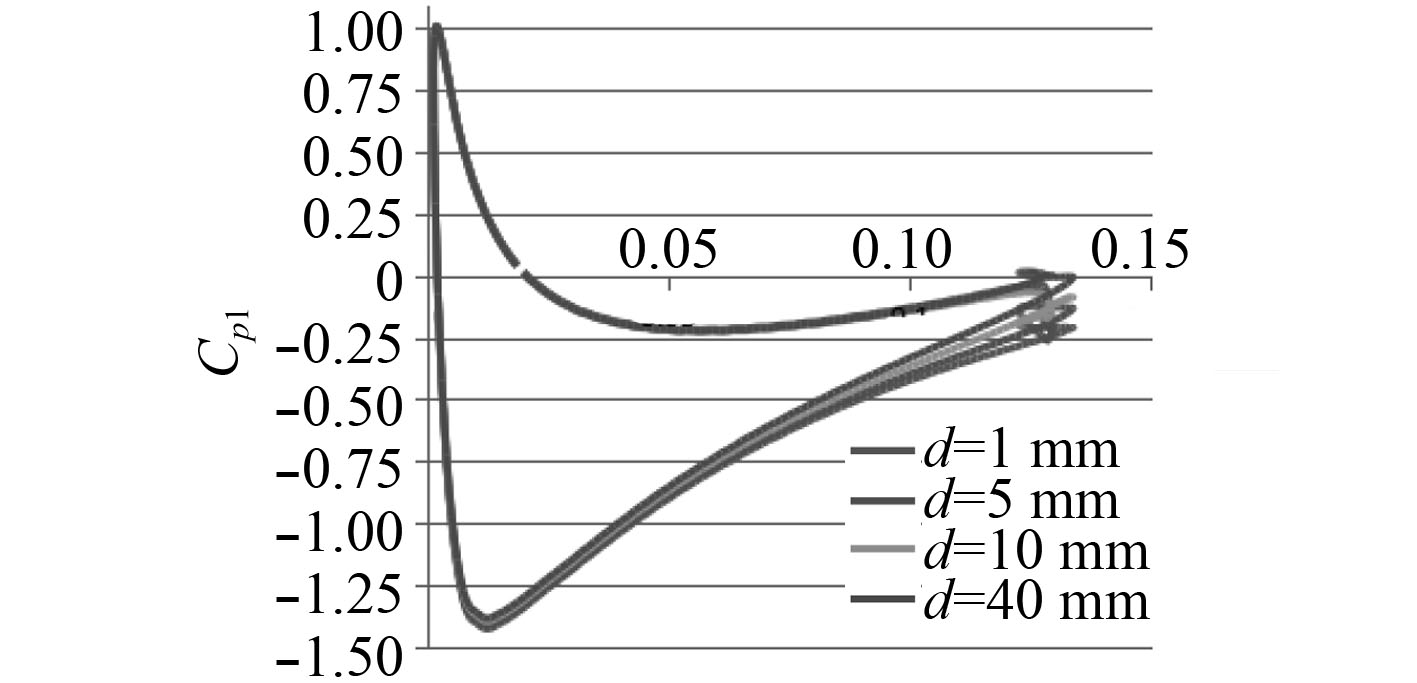
图 11 襟翼舵主舵压力系数Cp1 Fig. 11 The pressure coefficient of main part of rudderCp1 |

|
图 12 襟翼舵子舵压力系数Cp2 Fig. 12 The pressure coefficient of the flap Cp2 |
通过压力分布曲线可以发现,随着缝隙的增大,由于主舵后缘的压力随之增大,前后压力差减小使压差阻力不断减小,同时摩擦阻力几乎保持不变,因此主舵产生的阻力不断减小;由于子舵前缘的压力也不断增大,前后压力差也随之变大,增大了压差阻力,从而使子舵产生的阻力不断增大,整舵的阻力系数先减小后保持增大的趋势,最大差距达到10%。子舵单独产生的升力系数在不断的增大,同时升力系数也在增大。在缝隙小于5 mm时,子舵产生的阻力为负值,表明在小缝隙的时候子舵将产生向前的推力。由于缝隙的存在,在主舵后面形成了一个低压区,因此子舵后面的压力大于前面的低压,形成了一个向前的推力(图中d表示缝宽)。
同时,在襟翼舵中间高度(Z=0.12)的截面处,发现,随着缝隙的增大,缝隙间会慢慢形成一个涡;当缝隙进一步增大时,涡也随之变大直到充满整个缝隙;当缝隙大小到达一定值时,之前的涡开始变小,同时伴随着另外一个涡的产生,2个涡方向相反,并且后来生成的涡在不断挤压原先的涡结构,自身也在不断的变大。涡的形成改变了周围的压力分布,随着缝隙的增大,缝隙内的流速变大,同时子舵吸力面的负压区也在不断变大,增大了子舵两面的压力差,因此子舵产生的升力在不断增大。
4 结 语对计算结果的分析和对比,可以得到缝隙大小对阻力系数以及升力系数都有一定影响,对子舵的影响尤为明显,同时在一定程度上降低了主舵的总体效率。综上可得以下结论:
1)缝隙的增大使缝隙内流场的压力变大,减小了主舵压差阻力,同时增大了子舵的阻力,襟翼舵整体的阻力系数会随着缝隙的增大而增大,最大将会有10%左右的增加;
2)缝隙的增大改变了主舵尾端和子舵首端的压力分布,虽然子舵的升力会增大,但是主舵的升力减小的更快,因此襟翼舵的升力系数随着缝隙的增大有减小的趋势;
3)襟翼舵主副舵缝隙的增大将会使襟翼舵产生的力矩有一个增大的趋势,对子舵力矩影响最为明显,有近60%的增加。
| [1] |
许汉珍, 周谟蟾. 船用襟翼舵流体动力系数的计算[J]. 华中科技大学学报: 自然科学版, 1983, 4. |
| [2] |
丁玲玲, 刘胜, 邓志红, 等. 舰船主舵/襟翼舵广义预测联合控制规律研究[J]. 哈尔滨工程大学学报, 2000. DOI:10.3969/j.issn.1006-7043.2000.01.018 |
| [3] |
孙长龙. 襟翼舵的设计计算[J]. 武汉水运工程学院学报, 1979, 4. |
| [4] |
韦云生. 襟翼舵的设计探讨[J]. 船舶工程, 1978, 1. |
| [5] |
沈国光, 张泽盛. 襟翼舵水槽敞水试验[J]. 船海工程, 1981. |
| [6] |
李亚臣, 王晋军. NACA0012翼型Gurney襟翼增升特性及其机理实验研究[C]// 全国低跨声速空气动力学会议2003.
|
| [7] |
张攀峰, 陈迎春, 左林玄, 等. 超临界翼型Gurney襟翼增升技术实验研究[J]. 实验流体力学, 2010. DOI:10.3969/j.issn.1672-9897.2010.06.016 |
| [8] |
谢俊超. 襟翼舵设计计算及水动力性能仿真研究 [D]. 武汉: 武汉理工大学, 2011.
|
| [9] |
丁玲玲, 刘胜. 舰船主舵/襟翼舵广义预测联合控制规律研究[J]. 哈尔滨工程大学学报, 2000, 21(3): 1-6. DOI:10.3969/j.issn.1006-7043.2000.03.001 |
| [10] |
崇谦. 船用襟翼舵[M]. 北京: 国防工业出版社, 1989.
|
| [11] |
杨建民. 襟翼舵水动力性能研究[J]. 上海交通大学学报, 1997, 31(11): 133-136. |
| [12] |
黄胜, 虞海军. 贝克型襟翼舵性能理论计算及图谱[J]. 哈尔滨工程大学学报, 1995, 16(3): 1-10. |
| [13] |
周执平. 渔船襟翼舵的设计[J]. 中外船舶科技, 2005(2): 10-15. |
| [14] |
KERWIN J E, MANDEL P, LEWIS S D. An experimental study of a series of flapped rudders[R]. Massachusetts Inst of Tech Cambridge Dept of Ocean Engineering, 1971.
|
| [15] |
AHN H S, KIM H C. An application of coanda effect to a flapped rudder[J]. J. of Ship and Ocean Technology, 1999, 3(4): 23-24. |
| [16] |
HAE-SEONG A. Experimental study on the effects of water jetting on a flapped rudder[J]. Journal of the Society of Naval Architects of Korea, 1999, 36(1): 22-29. |
| [17] |
MOLLAND A F, TURNOCK S R. Marine rudders and control surfaces: principles, data, design and applications[M]. utterworth-Heinemann, 2011.
|
| [18] |
SHENG H, HAIJUN Y, YUNLING N, et al. Theoretical calculation and chart for the performance of becker flap-rudder[J]. Journal of Harbin Engineering University, 1995, 3. |
| [19] |
YUE-WEN B I. Design and installation of 4000 DWT multi-purpose carrier flapped rudder[J]. Ship Engineering, 2009, 3: 002. |
 2020, Vol. 42
2020, Vol. 42
