2. 华中科技大学 船舶与海洋工程学院,湖北 武汉,430074
2. School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
I型夹层板是一种由上、下面板和中间芯层组成的新型轻质结构,具有重量轻,比强度和比刚度高,抗振、隔热、隔声等优越性能[1-2],在船舶与海洋工程领域具有很好的应用前景。有研究表明,在舰船上用金属夹层板代替传统加筋板,可为舰船最大减重50%,最大空间节省50%,受非接触冲击时,如海浪,可吸收高达50%的冲击能量[3-7],是一种可以应用于飞行甲板的新型结构形式。
但由于夹层板结构力学性能复杂,用单纯的理论解法难以获得满意的结果,所以通过试验研究,可以获得直观的数据结果,对于理论分析以及有限元数值仿真研究有很大的指导意义。Norris[8-9]通过试验与理论研究相结合的方法,研究了横向均布载荷下点焊波纹型和帽型芯材金属夹层板的结构响应。Tan等[10]进行了长6 m,宽2.1 m的波纹夹层板模型的试验,并与有限元和理论方法对比,二者误差不超过10%。Valdevit和Wei[11]通过三点弯曲试验研究波纹型夹层板在受面外载荷作用时候的结构响应问题。Siwowski[12]对夹层板进行了轮印载荷下的弹性试验和极限承载能力试验,指出该种夹层板在刚度、强度和极限承载能力方面都能满足桥梁设计的要求。
作为具有良好工程运用前景的I型夹层结构,其在被用于板架结构时,经常会受到局部轮印载荷的作用。为了进一步掌握其在轮印载荷下的静强度力学性能,本文设计并制备了一个I型夹层板架结构模型,通过开展试验,研究其在轮印载荷下的静强度力学特性。
1 试验布置 1.1 试验模型本文的试验模型根据某船舶飞行甲板的实际尺寸形式,采用几何相似方法对其尺寸进行缩比设计,并使用激光焊接技术制备模型。
试验模型的长度方向包含2根横梁及横梁外侧延伸300 mm范围,即模型总长L=1382 mm;考虑到轮印载荷及其载荷效应具有局部特性,模型宽度方向包括11个胞元,胞元间距

|
图 1 I型夹层板架结构试验模型 Fig. 1 Test model of I-core sandwich grillage structure |
I型夹层板架结构模型的基体材料为304不锈钢,其主要力学性能参数如下:材料密度ρ=7 900 kg/m3,弹性模量E=210 GPa,泊松比μ=0.3。
为了表述方便,现将试验模型的坐标系做如下定义:x轴为沿板架模型的长度方向,称为船长方向;y轴为沿板架模型的宽度方向,称为船宽方向;z轴为沿板架模型的芯层高度方向,称为垂向或高度方向。
1.2 贴片方案及测试系统本文研究的主要是I型夹层板架结构在典型位置轮印载荷下的静强度力学特性。为了考察轮印载荷下,受载区域上下面板的弯曲特性,故在模型上下表面的板格中心及焊缝处布置双向应变片,用来监测面板上各特征点的弯曲应力,上下面板的贴片位置局部放大图如图2所示。
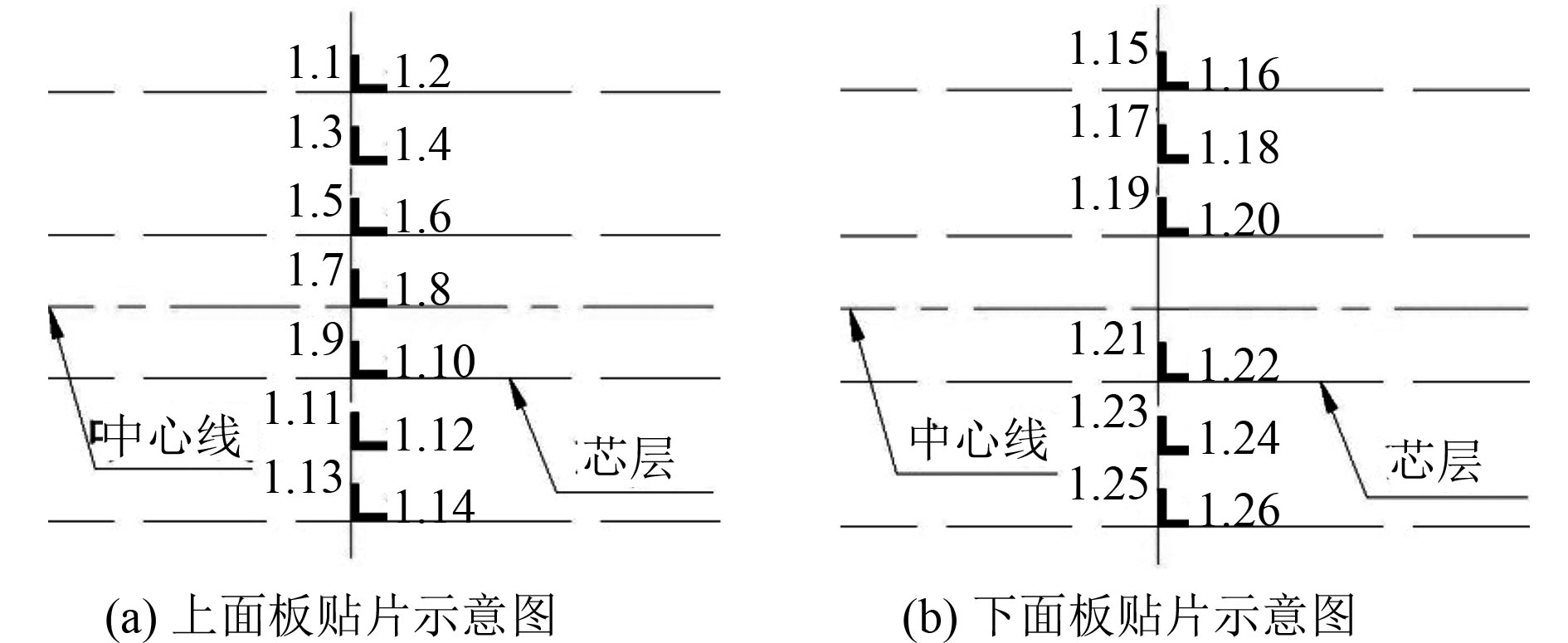
|
图 2 面板贴片位置示意图(13个双向片) Fig. 2 Sketch of coating place for panel (13 bi-directional strain gauges) |
本试验采用的主要测量设备包括EX1629动态应变仪、力传感器等。所有应变数据由EX1629动态应变仪采集,并传输至计算机进行实时处理并存储。应变测点分配如表1所示,测试系统的名称、型号、参数等情况如表2所示。
|
|
表 1 应变测点分配表 Tab.1 Strain gauge measuring point distribution |
|
|
表 2 试验测试仪器仪表 Tab.2 Parameters of test instrument |
为了分析I型夹层板架的板格在不同典型位置轮印载荷下的力学性能,故在夹层板架中部区域设置不同的加载工况,包括以下4种:
1)在模型2根横梁间距中部板格范围施压轮印均布载荷,载荷中心线与芯材中心线重合,轮印长边与芯材方向平行。
2)在模型2根横梁间距中部板格范围施压轮印均布载荷,载荷中心线与芯材中心线重合,轮印长边与芯材方向垂直。
3)在模型2根横梁间距中部板格范围施加轮印均布载荷,载荷中心线与板格中心线重合,轮印长边与芯材方向平行。
4)在模型2根横梁间距中部板格范围施加轮印均布载荷,载荷中心线与板格中心线重合,轮印长边与芯材方向垂直。
本试验的加载范围尺寸为230 mm×140 mm,但由于试验中上面板最中部的对称轴上贴有应变片,导致试验过程中在中间宽30 mm的范围不能布置橡胶块,以免损坏应变片。因此,加载区域由2个大小为230 mm×55 mm的矩形区域和3个大小为140 mm×100 mm的矩形区域组成。本试验的加载工况示意图如图3所示。
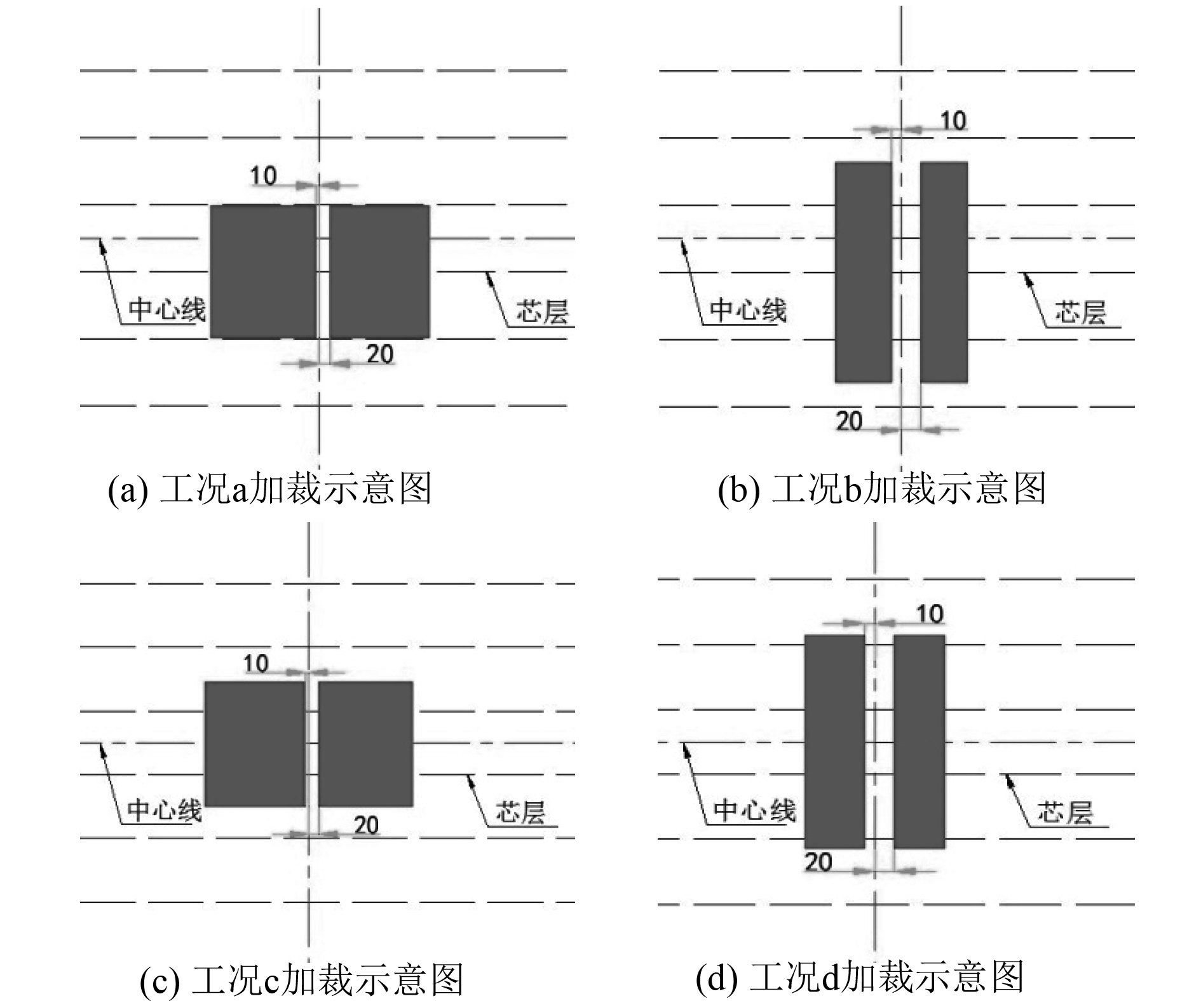
|
图 3 工况a~工况d加载示意图 Fig. 3 Sketch of case a-d |
轮印载荷大小为25.0 kN,利用橡胶块模拟轮印。使用液压油缸进行加载,其间隔为5 kN,为了更准确掌握最终载荷下的板格及芯层的力学性能,至20 kN后加载间隔为2.5 kN。加载程序如下:0→5→10→…20→22.5→25.0→22.5→20→…10→5→0。
在加载过程中,每个阶段稳压30 s后进行应变测量,并记录和保存数据。在加载至25.0 kN后按照加载程序逐步卸力,重复3次试验,取平均值作为最终值。
3 试验结果分析 3.1 应变结果分析试验开始后,按照加载程序记录各应变片在各档载荷下的应变值,但由于应变仪通道数目的限制以及应变片的完好情况,导致了某些工况中的应变片的应变数据无效(工况a和工况c中的应变片1.20,工况d中的应变片1.8、1.23及1.25)。
根据测点在各档载荷下的应变值,绘制出了各工况的载荷-应变曲线。本文给出工况a中编号1.1-1.8的载荷-应变曲线,如图4所示。
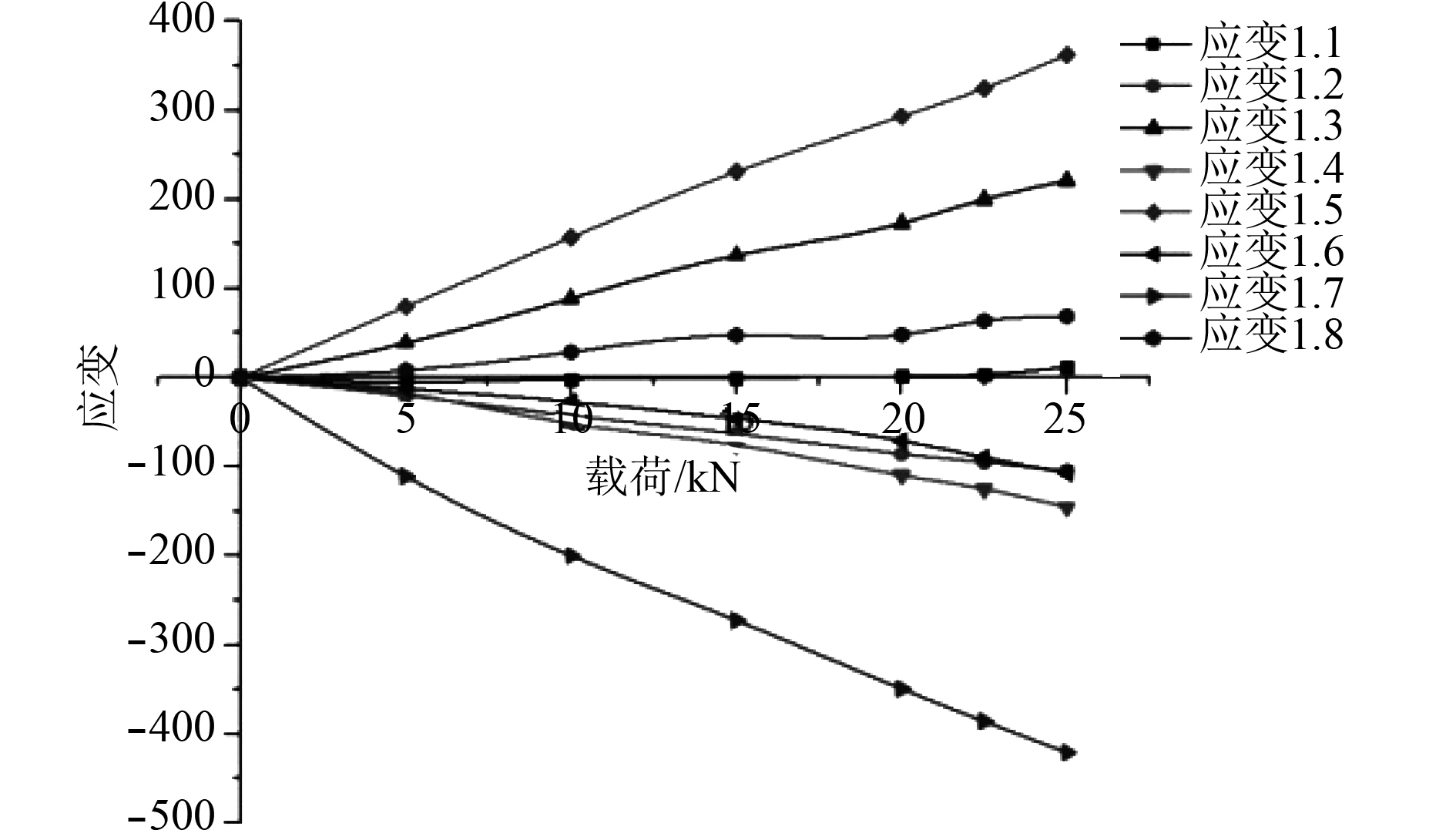
|
图 4 工况a中1.1-1.8号应变片的载荷-应变曲线 Fig. 4 Load-Strain curve of 1.1-1.8 in case a |
可以看出,除了少部分测点,其载荷-应变曲线的线性程度不好之外,大部分测点载荷-应变曲线呈现出较好的线性关系。此外,当测得的应变数据较大时,对应的应变片编号的载荷-应变曲线呈现较好的线性关系;而当测得的应变数据较小时,对应的应变片编号的载荷-应变曲线呈现的线性关系则比较差。这是由于试验采用应变数据采集仪是动态数据采集,应变数据会随时间有一定的波动,因此当应变数据较小时,数据的相对误差比较大。
其余3种工况以及工况a剩下的应变数据情况与1.1-1.8号应变片相似,故其数据均只给出各测点在最终载荷下的应力值,应变数据不再阐述。
从应变数据中可以得出,在4种典型位置的轮印载荷作用下,结构上面板主要承受局部板格弯曲作用,同时上面板板格长边跨度比短边跨度大,故其各特征点沿船宽方向的应变值大于沿船长方向的应变值;结构下面板主要承受整体板架弯曲作用,板架沿船长方向无约束,从而导致模型下面板各特征点沿船长方向的应变值大于沿船宽方向的应变值。
3.2 应力结果分析将试验过程中捕捉测点的应变数据,根据广义胡克定律(式(1)和式(2)),计算出各工况测点在最终25.0 kN载荷下的应力值。本文对于上面板只给出表沿船宽方向弯曲应力的应力数据,对于下面板只给出表沿船长方向弯曲应力的应力数据,其数据如表3所示。
|
|
表 3 最终载荷下工况a-d各测点应力值 Tab.3 The stress value of each measuring point in case a to d under the final load |
| $ {\sigma _x} = \frac{E}{{1 - {\mu ^2}}} \cdot ({\varepsilon _x} + \mu \cdot {\varepsilon _y}) \text{,} $ | (1) |
| $ {\sigma _y} = \frac{E}{{1 - {\mu ^2}}} \cdot ({\varepsilon _y} + \mu \cdot {\varepsilon _x}) \text{。} $ | (2) |
根据表3的试验应力数据可得到如下结论:
1)因为轮印载荷及其载荷效应具有局部特性,故I型夹层板架结构在轮印载荷作用范围内的测点应力水平较大,远离载荷作用范围测点的应力水平较低。
2)对于I型夹层板架结构上面板的上表面,在轮印载荷作用下,主要承受局部板格弯曲作用,板格中心点的应力状态表现为压应力,板格长边(芯层焊缝处)的应力状态则表现为拉应力。试验所得结果也与这一结论一致。
3)对于I型夹层板架结构下面板的下表面,在4种典型位置的轮载荷作用下,主要承受整体板架弯曲作用,各测点的应力状态均表现为拉应力,故试验所得结果均为正值;同时其最大弯曲应力出现在模型中线两侧的芯层焊缝处。这是因为下面板开孔边缘处会产生应力集中,故在此处弯曲应力最大。
4)对于轮印长边与芯材方向平行的工况(工况a,工况c)模型上面板的最大弯曲应力出现在最中部的板格的中心处。
5)对于轮印长边与芯材方向垂直的工况(工况b,工况d),当载荷中心线与芯材中心线重合(工况b)时,模型上面板最大弯曲应力出现在载荷中心线旁的芯层焊缝处;当载荷中心线与板格中心线重合(工况d)时,模型上面板最大弯曲应力出现在载荷中心线旁的板格中心处。
3.3 试验与理论对比分析针对I型夹层板架结构的上面板,本文采用2对边刚固(芯层焊缝边)、2对边简支的边界条件下承受均布载荷的绝对刚性板理论来计算板格中心点(式(3))和长边中点(式(4))沿船宽方向的弯矩。
| $ {M_1} = - {k_1}p{b^2} \text{,} $ | (3) |
| $ {M_1}' = {k_2}p{b^2} \text{。} $ | (4) |
式中:
理论计算时,根据4种轮印载荷的加载位置,取一个板格内的轮印加载区域作为理论计算模型,即工况a和工况c计算时取b=70 mm,A=230 mm,工况b和工况d计算时取b=70 mm,A=140 mm。理论计算的边界条件如图5所示。
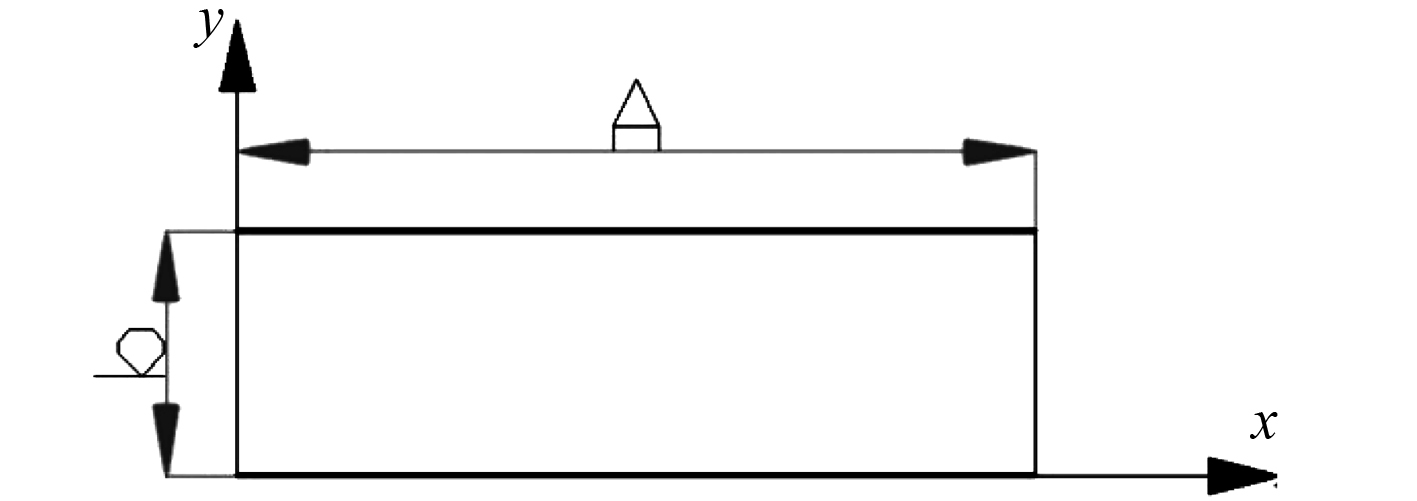
|
图 5 理论计算的边界条件 Fig. 5 Boundary conditions of theoretical calculation |
在计算得到板格中心点和长边中点沿船宽方向的弯矩后,根据公式6计算各特征点的弯曲应力。
| $ \sigma = \frac{{6M}}{{{t^2}}} \text{,} $ | (5) |
式中:
考虑到动态应变仪的采集波动对于试验数据的影响,故在分析试验数据与理论解的关系时,对于轮印长边与芯材方向平行的工况试验结果取模型最中部板格的最大应力数据;对于轮印长边与芯材方向垂直的工况试验结果取模型最中部旁板格的最大应力数据。理论计算结果与试验的对比情况如表4所示。
|
|
表 4 理论计算与试验数据对比表 Tab.4 Comparison between theoretical calculation and experiment |
由表4可知,在4种载荷工况下,理论计算值均比试验值大,其中板格中心的弯曲应力误差较小,而板格长边中点的弯曲应力误差较大;轮印载荷作用下,理论计算的板格中点及长边中点的受力情况与试验测得的相同;对于工况a、工况c和工况d的试验数据,板格中心的弯曲应力大于板格长边中点的弯曲应力,与理论计算结果相反。造成这些的主要原因如下:
1)在试验中,因为轮印加载区域的中部需要布置应变片,故在测点上实际未施加轮印载荷,导致试验所测得的数据实际为测点两旁橡胶块联合作用下产生的弯曲应力。
2)在实际试验中因为模型有初始缺陷,所以在轮印载荷作用下,板格中心点的变形最大,且接触力最小,从而导致接触力不均匀,而理论计算时认为在加载区域载荷为均匀分布的,这两者并不完全相同。
3)对于板格中心沿船宽方向的弯曲应力,在试验中因计算板格的相邻板格也会承受一定的载荷,这时会产生一个附加的边界弯矩,使板格中心沿船宽方向的弯矩减小。
4)在轮印载荷作用下,结构发生局部弯曲,在局部变形范围内,应力梯度较大,贴片位置的偏差也会导致比较大的误差。
4 结 语本文通过对I型夹层板架结构进行典型位置轮印载荷下的静强度试验,并将试验数据与理论解相比较,掌握其在轮印载荷下的静强度力学性能,得到了如下主要结论:
1)因为轮印载荷及其载荷效应具有局部特性,故I型夹层板架结构在轮印载荷作用范围内的测点应力水平较大,远离载荷作用范围测点的应力水平较低。
2)I型夹层板架结构在轮印载荷作用下,上面板沿船宽方向的弯曲应力较大;下面板沿船长方向的弯曲应力较大。
3)轮印载荷下,理论计算与试验所得结果有一定的差异。这主要是因为在试验中,模型中部需要布置应变片,故在测点上实际未施加轮印载荷,导致试验所测得的数据实际为测点两旁橡胶块联合作用下产生的弯曲应力。
| [1] |
邓钫印. 建筑工程装饰材料手册[M]. 河南科学技术出版社, 2000.
|
| [2] |
姜继圣, 罗玉萍, 兰翔, 等. 新型建筑绝热、吸声材料[M]. 化学工业出版社, 2002.
|
| [3] |
DENNEY P. Corrugated core LASCOR structures in shipbuilding and other applications: proceedings of the Presentation Lightweight Sandwich Seminar[C]. Helsinki, Finland, 1998.
|
| [4] |
PANTSAR H, JANSSON A, SALMINEN A, et al. Manufacturing procedure and costs analysis of laser welded all steel sandwich panels[C]. Proceedings of the 20 th International Congress on ICALEO 2001: applications of lasers & electro-Optics, 2001.
|
| [5] |
PANTSAR H, SALMINEN A, JANSSON A, et al. Quality and costs analysis of laser welded all steel sandwich panels[J]. Journal of Laser Applications, 2004, 16(2): 66-72. DOI:10.2351/1.1710881 |
| [6] |
SÄYNÄJÄKANGAS J, TAULAVUORI T. A review in design and manufacturing of stainless steel sandwich panels[J]. Stainless steel world, 2004, 55-59. |
| [7] |
KUJALA P, KLANAC A. Steel sandwich panels in marine applications[J]. Brodogradnja, 2005, 56(4): 305-314. |
| [8] |
NORRIS C. Spot welded corrugated-core steel sandwich panels subjected to lateral loading[D]. University of Manchester, 1987.
|
| [9] |
NORRIS C, MONTAGUE P, TAN K H. All-steel structural panels to carry lateral load: experimental and theoretical behaviour[J]. Structural Engineer, 1989, 67: 167-76. |
| [10] |
TAN K H, MONTAGUE P, NORRIS C. Steel sandwich panels: finite element, closed solution, and experimental comparisons, on a 6 mx 2.1 m panel[J]. Structural Engineer, 1989, 67: 159-66. |
| [11] |
VALDEVIT L., WEI Z., MERCER C., ZOK F. W.. Structural performance of near-optimalsandwich panels with corrugated cores[J]. International Journal of Solids andStructures, 2006, 43(16): 4888-4905. DOI:10.1016/j.ijsolstr.2005.06.073 |
| [12] |
SIWOWSKI T W. Structural behaviour of aluminium bridge deck panels[J]. Engineering Structures, 2009, 31(7): 1349-1353. DOI:10.1016/j.engstruct.2009.02.002 |
| [13] |
船舶设计实用手册[Z]. 中国船舶工业集团公司、中国船舶重工集团公司和中国造船协会. 2013.
|
 2020, Vol. 42
2020, Vol. 42
