2. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China
当今舰船的大型化及轻量化发展趋势对船体结构设计提出更高要求,经常需要在船体横梁、纵桁等构件的高腹板上开孔,这将严重破坏支撑构件的连续性。当构件受到均布或集中载荷时,开孔周边应力一般远大于其他位置,容易引起局部破坏。此外,开孔严重削弱腹板截面尺寸,构件抗剪性能远小于实腹梁,剪力次弯矩的影响不能忽略,在船舶结构设计时应充分重视[1]。各大船级社规范均对开孔的位置和大小做出了规定和要求,但由于船舶主要构件受力情况复杂,并且开孔后截面发生变形,所以很难得到精确的理论解析公式。Allftlish等[2]把蜂窝梁比拟为费氏空腹桁架,提供了研究空腹梁强度的概念模型和理论方法,并已成为许多国家制定其相应规范的重要参考。Liu和Chung等[3-7]采用空腹桁架理论分析了开孔桁材的屈服性能。苏益声等[8-10]提出蜂窝梁的强度简化计算方法。蒋赘[11]分析了受集中载荷作用的圆孔空腹梁强度问题;蒋彩霞[12]将腰圆形开孔附近应力的理论结果与有限元结果进行了对比分析。
本文分析开孔纵向位置、开孔长度和高度等参数对孔周强度的影响,并且在费氏空腹桁架理论的基础上,借助有限元分析及数值拟合方法对该理论作适当修正,解决该理论应用于船体构件高腹板开孔强度计算中误差偏大的问题,使计算过程快速简便,理论结果更加准确,具有实际工程应用价值。
1 费氏桁架理论费氏空腹桁架理论通常用于蜂窝梁内力计算,已被多国规范使用。蜂窝梁受力后,其内力分布较实腹梁更为复杂,费氏空腹桁架理论对其进行适当简化,提出4个假设:
1)截面受力变形符合平截面假设;
2)在剪力作用下,空腹截面处的剪力按刚度分配到上、下2个T形截面;
3)剪力引起的次弯矩反弯点位于梁桥中点和墩腰处;
4)纯弯矩作用下,弯曲正应力均匀分布在空腹截面上。
1.1 孔周正应力计算方法外载荷作用下,开孔周边正应力
| $ \begin{split} & \sigma = {\sigma _{M\varphi }} + {\sigma _{V\varphi }}\text{,}\\ & {\sigma _{M\varphi }} = \frac{{{M_x}}}{{{h_c}{A_T}}},{\rm{ }}{\sigma _{V\varphi }} = \frac{{jk{V_x}}}{{{W_{T\min }}}}\text{。} \end{split} $ | (1) |
式中:
图1为理论计算示意图。
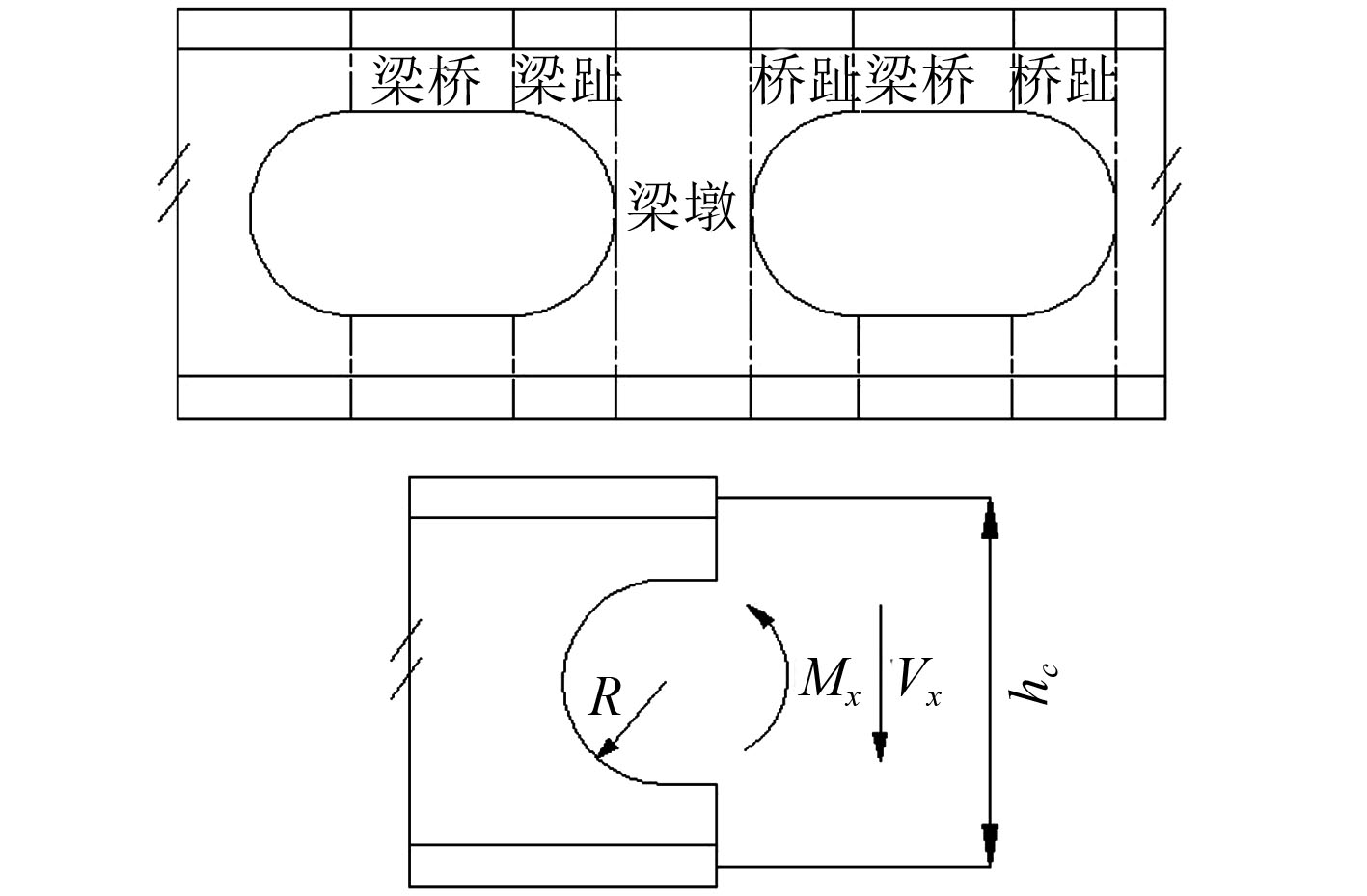
|
图 1 梁腹板开孔理论计算示意图 Fig. 1 Schematic diagram of theoretical calculation of beam web with openings |
截面处剪应力计算如下式:
| $ \tau = \frac{{j{V_x}{S_T}}}{{{t_w}{I_T}}} \text{。} $ | (2) |
式中:
选取某尺寸为T500×8/200×10纵桁作为分析对象,跨距为6 200 mm,带板宽度取纵骨间距841 mm,厚度取为10 mm,纵桁尺寸参数及含义如图2所示。开孔垂向中心与腹板垂向中心对齐,形状为腰圆孔(长轴平行于纵桁跨距方向),开孔参数共3个,x为孔的纵向位置,即开孔中心距梁端部的距离,a,b分别为孔的长度和宽度的一半。由x,a,b可以组合成一系列开孔方案,利用有限元方法对此进行逐一分析。

|
图 2 纵桁腹板开孔参数含义 Fig. 2 The meaning of the parameters of the longitudinal web opening |
针对孔边区域进行局部细化,网格尺寸控制在10 mm左右,远离孔边区域控制在20 mm左右。通过比较不同单元模拟方式的有限元计算结果可以得到,带板和面板均采用梁单元模拟,腹板采用板单元模拟得到的应力最大,故基于安全性考虑,本文采用此种单元模拟方式。材料的弹性模量

|
图 3 纵桁腹板开孔有限元模型 Fig. 3 Finite element model of longitudinal web opening |
本文选用无量纲参数分析开孔纵向位置和开孔大小对孔边强度的影响以排除不同尺寸型材的影响。孔的纵向位置对应无量纲参数为

|
图 4 开孔纵向位置示意图 Fig. 4 Longitudinal position diagram of openings |
图5为纵桁腹板孔周

|
图 5 a/b=2,2b/H=0.5工况下mises应力云图 Fig. 5 Mises stress contour with a/b=2,2b/H=0.5 |
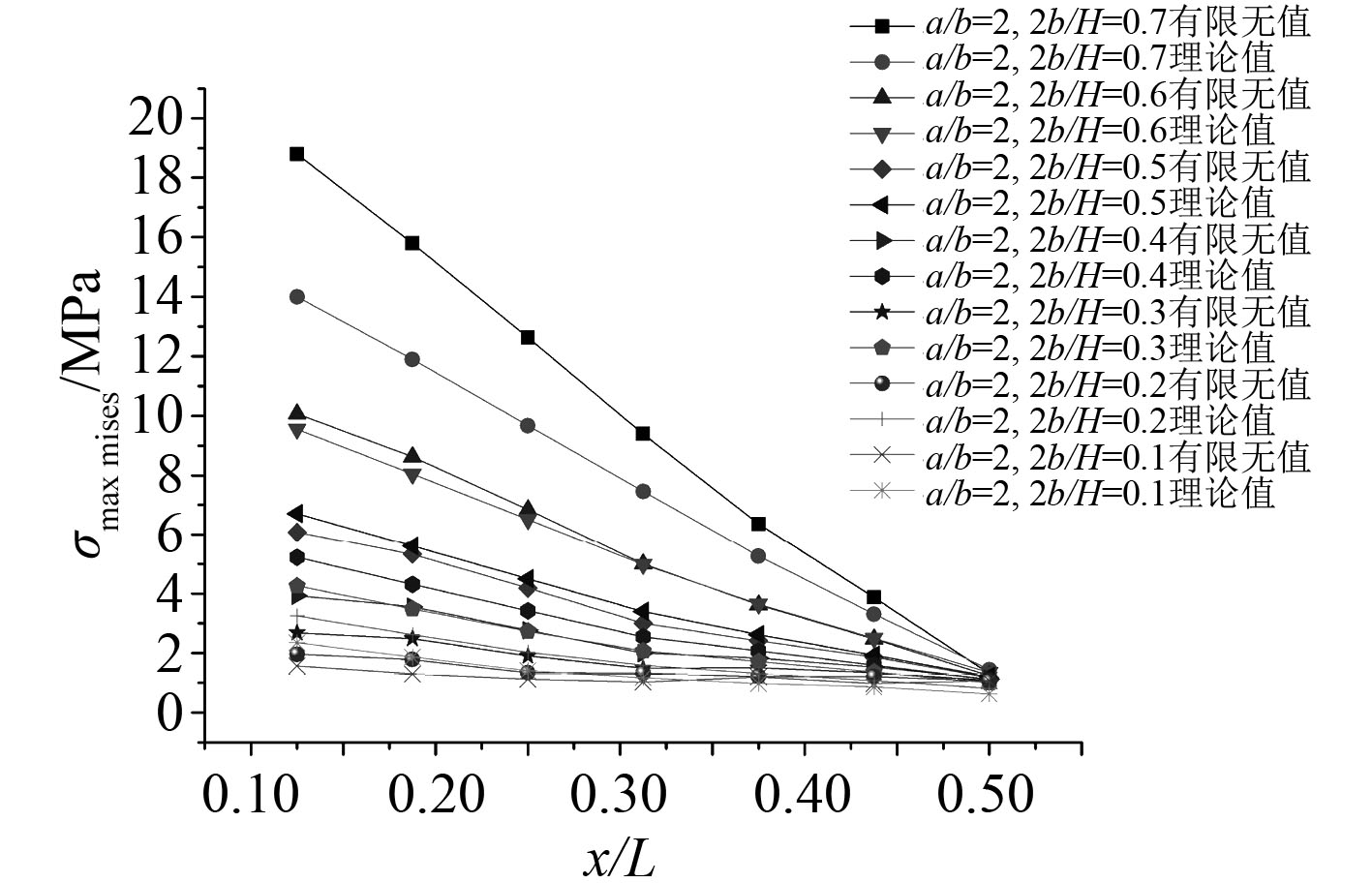
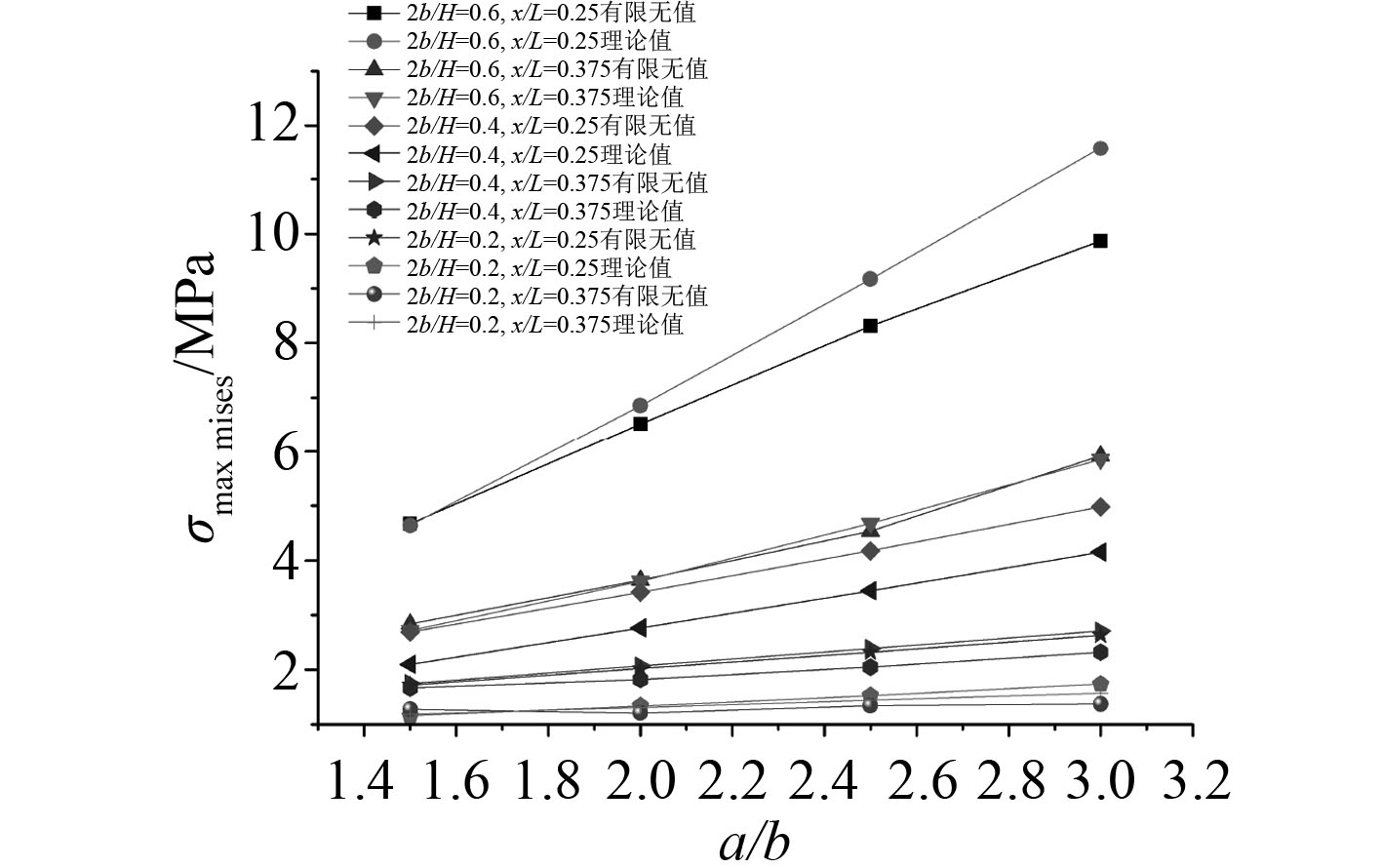
图6~图8为各开孔参数对孔周最大
|
图 6 x/L对孔周最大mises应力的影响 Fig. 6 Effects of x/L on mises stress |
|
图 8 a/b对孔周最大mises应力的影响 Fig. 8 Effects of a/b on mises stress |

|
图 7 2b/H对孔周最大mises应力的影响 Fig. 7 Effects of 2b/H on mises stress |
1)孔周最大
2)开孔的纵向位置越靠近梁端部,孔周最大mises应力值越大。这是由于固支梁两端剪力作用较大,使得剪力次弯矩引起的正应力显著增大从而导致mises应力显著增大。
3)开孔的高度越大,孔周最大mises应力值越大。这是由于开孔严重削弱腹板截面,使得剪应力增大导致mises应力随之增大。
4)开孔的长宽比越大,孔周最大mises应力越大。主要由于剪力次弯矩与开孔长度近似呈线性关系,当开孔长度增大时,剪力次弯矩相应增加,导致孔周正应力增加。
通过对比理论结果与有限元结果可知,两者趋势相符,但数值偏差较大,尤其对于开孔在跨中位置及大开孔情况下,误差可能达到81.31%。这也意味着不便于将费氏空腹桁架理论直接应用于船体结构腹板开孔强度的计算,需要对其进行合理修正。
4 费氏空腹桁架理论修正费氏空腹桁架理论公式的特点在于:1)需要分别计算孔边的正应力和剪应力,并假定正应力由弯矩和剪力引起的两种成分组成;2)需要计算出开孔全周(即360°方向)的应力,然后对比得到最大应力。
针对上述特点,结合有限元分析结果,对费氏空腹桁架理论公式进行简化和修正,使其更适用于本文分析对象。
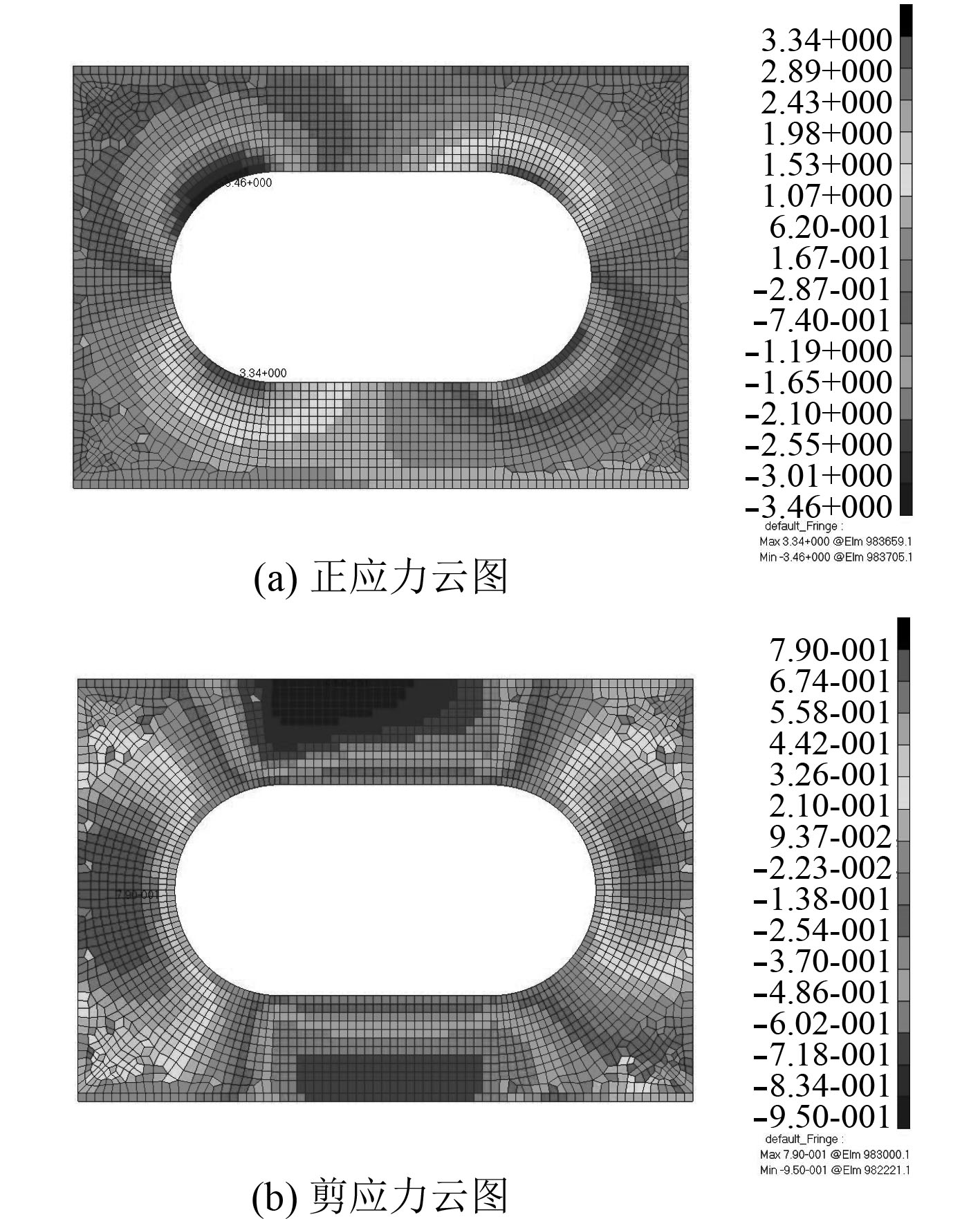
4.1 孔周最大应力分析观察有限元分析结果可以发现,孔周最大mises应力出现位置与最大正应力位置相同。以
|
图 9 a/b=2,2b/H=0.5,x/L=0.312 5工况下应力云图 Fig. 9 Stress contour with a/b=2,2b/H=0.5,x/L=0.312 5 |
采用最大正应力位置所处象限和与空腹梁正截面的夹角
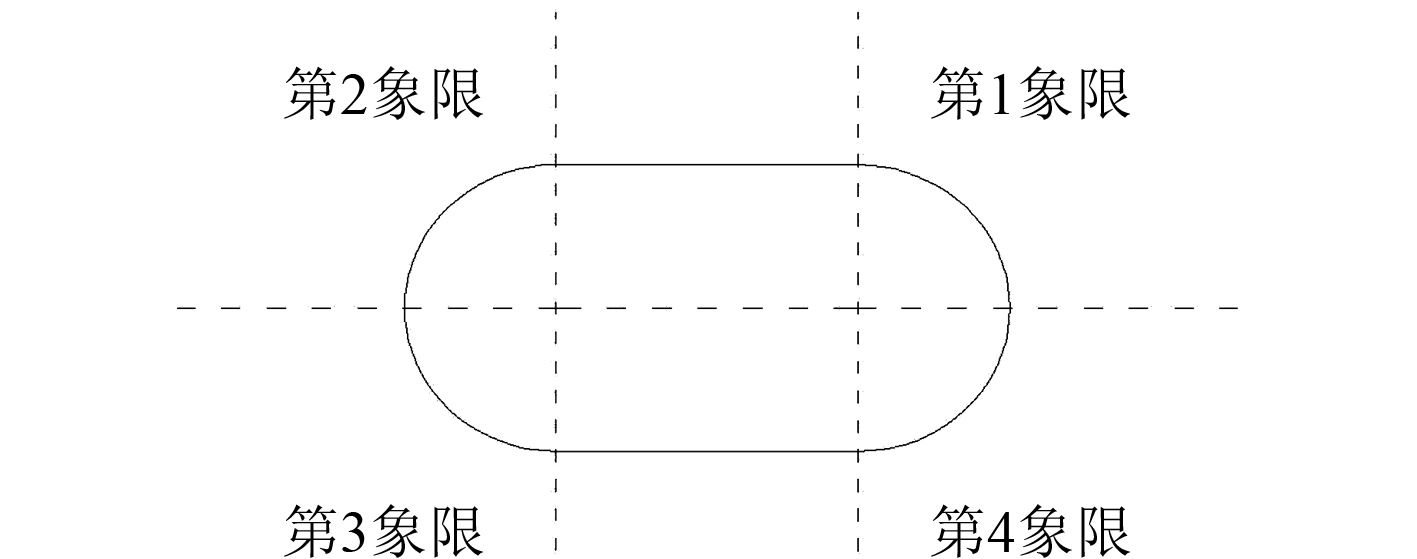
|
图 10 孔周象限位置说明 Fig. 10 Opening quadrant position description |
图11为

|
图 11
a/b=2孔周最大正应力对应的
|
可以发现有限元分析得到的
本文主要针对大开孔(
1)
2)
3)
费氏桁架理论假定正应力分别由弯矩和剪力引起,本文同样采用对
| $ RMSE = \frac{{{{({{x'}_1} - {x_1})}^2} + {{({{x'}_2} - {x_2})}^2} + \cdots + {{({{x'}_n} - {x_n})}^2}}}{{{x_1} + {x_2} + \cdots + {x_n}}}\text{。} $ | (3) |
式中:
拟合得到正应力理论修正公式如下:
| $ \begin{split} &{\sigma _{\text{修正理论值}}} = \left({\rm{101}}{\rm{.91}}\eta - \frac{{{\rm{0}}{\rm{.89}}}}{\gamma }\right){\sigma _{M\varphi }}+\\ &{\rm{( - 20}}{\rm{.06}}{\eta ^{\rm{2}}}{\rm{ - 12}}{\rm{.24}}\eta \gamma {\rm{ + 16}}{\rm{.26}}\eta ){\sigma _{V\varphi }}\text{;} \end{split} $ | (4) |
| $ \begin{split} & {\sigma _{\text{修正理论值}}}{\rm{ = (621}}{\rm{.96}}{\eta ^{\rm{2}}}{\rm{ - 36}}{\rm{.7}}\eta \gamma {\rm{ - 192}}{\rm{.55}}\eta ){\sigma _{M\varphi }}+\\ & {\rm{ (13}}{\rm{.02}}{\eta ^{\rm{2}}}{\rm{ + 6}}{\rm{.8}}\eta \gamma {\rm{ - 10}}{\rm{.96}}\eta ){\sigma _{V\varphi }}\text{;} \end{split} $ | (5) |
| $ \begin{split} & {\sigma _{\text{修正理论值}}}{\rm{ = ( - 8}}{\rm{.52}}{\eta ^{\rm{2}}}{\rm{ + 2}}{\rm{.49}}\eta \gamma {\rm{ + 5}}{\rm{.24}}\eta ){\sigma _{M\varphi }}+\\ & {\rm{ ( - 7}}{\rm{.65}}{\eta ^{\rm{2}}}{\rm{ - 4}}{\rm{.27}}\eta \gamma {\rm{ + 7}}{\rm{.96}}\eta ){\sigma _{V\varphi }}\text{。} \end{split} $ | (6) |
式中,
表1为修正公式(5)~式(7)的拟合及修正效果。
|
|
表 1 正应力修正公式拟合及修正效果 Tab.1 Normal stress correction formula fitting and correction effect |
由表可知,各分段的
为验证本文得到的修正公式能够适用于不同尺寸的高腹板开孔结构,本节选取某LNG船纵桁作为计算对象,进行算例验证。
5.1 验证工况该桁材尺寸为T450×9/180×10,跨距为5 000 mm,带板宽度为800 mm,厚度为10 mm。纵桁两端设置固支边界条件,受横向均布载荷,大小为
选取2种开孔长宽比(
|
|
表 2 验证工况对应的开孔参数表 Tab.2 Opening parameters table of verification condition |
表3为孔周最大正应力修正前后的理论值与有限元值对比结果。
|
|
表 3 验证模型孔周最大正应力理论值与有限元值对比表 Tab.3 Comparison table of theoretical and finite element values of maximum normal stress in verification condition |
由表可知,修正后的理论值与有限元值的误差基本在5%以内,较修正前误差明显减小。本文提出的修正公式具有一定的普适性。
6 结 语本文结合费氏空腹桁架理论和MSC PATRAN /NASTRAN有限元软件,开展船体结构腹板开孔强度简化分析方法研究。研究表明,本文提出的理论修正公式能够快速简便地计算出孔边最大正应力,并且大幅度提高理论公式的精确度,修正公式计算误差基本在5%左右,可用于船舶工程中对船体结构腹板开孔强度进行分析研究。
| [1] |
张隽华, 张世联, 王红旭, 等. 超规范要求的主要构件腹板开孔设计研究[J]. 中国海洋平台, 2013. ZHANG Yuhua, ZHANG Shilian, WANG Hongxu, et al. Study on the design of web openings for main components required by super-standards[J]. China Ocean Platform, 2013. DOI:10.3969/j.issn.1001-4500.2013.01.011 |
| [2] |
周朝阳, 周云峰. 蜂窝梁等效抗弯刚度的确定方法[J]. 建筑科学与工程学报, 2008(1): 102-106. ZHOU Chaoyang, ZHOU Yunfeng. Determination of equivalent bending stiffness of honeycomb beams[J]. Journal of Architecture and Civil Engineering, 2008(1): 102-106. DOI:10.3321/j.issn:1673-2049.2008.01.017 |
| [3] |
K F CHUNG, T C H LIU, A C H KO. Investigation on Vierendeel mechanism in steel beams with circular web openings[J]. Journal of Constructional Steel Research, 2001(57): 467-490. |
| [4] |
K F CHUNG, LAWSON R M. Simplified design of composite beams with large web openings to Eurocode 4[J]. Journal of Constructional Steel Research, 2001(57): 135-163. |
| [5] |
K.F.CHUNG, T.C.H.LIU, A.C.H.KO.. Investigation on vieredeel mechanism in steel beams with circle web openings[J]. Journal of Constructional Steel Research, 2001(57): 467-490. |
| [6] |
T.C.H.LIU, K.F.CHUNG. Steel beams with large web openings of various shapes and sizes: finite element investigation[J]. Journal of Constructional Steel Research, 2003(59): 1159-1176. |
| [7] |
K.F.CHUNG, C.H.LIU, A.C.H.KO.. Steel beams with large web openings of various shapes and sizes: an empirical design method using a generalized moment-shear interaction curve[J]. Journal of Constructional Steel Research, 2003(59): 1177-1200. |
| [8] |
苏益声. 圆孔蜂窝梁验算截面的确定及梁桥高度取值分析[J]. 红水河, 1994. SU Yisheng. Determination of checking section of round hole honeycomb beam and analysis of height of beam bridge[J]. Hongshui River, 1994. |
| [9] |
苏益声, 王良才. 圆孔蜂窝梁及其强度计算[J]. 广西大学学报(自然科学版), 1993(3): 63-69. SU Yisheng, WANG Liangcai. Circular honeycomb beam and its strength calculation[J]. Journal of Guangxi University(Natural Science Edition), 1993(3): 63-69. |
| [10] |
李鹏飞, 许宏伟, 李义强. 蜂窝梁应力的简化计算[J]. 四川建筑, 2008. LI Pengfei, XU Hongwei, LI Yiqiang. Simplified calculation of honeycomb beam stress[J]. Sichuan Architecture, 2008. |
| [11] |
蒋赘. 腹板大尺度圆形开孔梁的受力性能分析[D]. 长沙. 湖南大学 JIANG Wei. Analysis of the mechanical behavior of large-scale circular apertured beams with webs[D]. Changsha: Hunan University |
| [12] |
蒋彩霞, 祁恩荣, 竺一峰. 梁腹板开孔简化计算方法及有限元优化[C]// 中国钢结构协会海洋钢结构分会论文集, 2010. JIANG Caixia, QI Enrong, YAN Yifeng. Simplified calculation method and finite element optimization of beam web opening[C]// Proceedings of Ocean Steel Structure Branch of China Steel Structure Association, 2010. |
 2020, Vol. 42
2020, Vol. 42
