2. 海军驻上海江南(造船)集团有限责任公司军事代表室,上海 201913
2. Naval Military Representative Office in Jiangnan Shipyard (Group) Co., Ltd., Shanghai 201913, China
对于船舶、海洋平台等海上结构物,除了会遭受风浪的作用外,有时还会受到爆炸载荷的威胁,尤其是对于作战舰艇,承受空中核爆、武器命中、水下非接触爆炸等是典型的战斗工况。在这些工况中,水下非接触爆炸是较为复杂的工况。随着波浪载荷研究的不断成熟和固化,学者们逐渐把研究重点转移到水下非接触爆炸的描述和在水下非接触爆炸载荷下结构的响应上来[1-4]。
对于水下非接触爆炸载荷的描述,用经验公式的方法比较普遍,而对于水下非接触爆炸载荷下的结构响应,由于结构的几何非线性和材料非线性,用解析或经验公式的方法是难以解决的,模型试验存在尺度效应,实船试验不仅会消耗巨大的人力、物力、财力,还有可能是破坏性试验。所以,在水下非接触爆炸分析领域,数值法已占主导地位[5]。
水下非接触爆炸一般可分为近场爆炸、中场爆炸和远场爆炸。吴广明等[6]提出一种基于梁模型的船体水下非接触爆炸弯矩简化计算方法,运用Abaqus有限元软件,建立船体详细有限元模型和船体梁简化模型,并分别进行水下非接触爆炸工况下危险剖面的爆炸弯矩计算。吴敌等[7]以舱段模型为基础,分别修改外底板板厚、增加强肋骨和龙骨数量得到了3种新的舱段结构模型。使用Abaqus软件对各舱段水下非接触爆炸冲击下的动态响应进行仿真计算,对外板塑性变形、内底及各层甲板应力和加速度峰值进行分析和对比。
在近场计算方面,Autodyn软件在水下爆炸模拟方面的功能最为全面,其次是Ls-dyna和Dytran。由于爆炸载荷采用半解析的方法,Abaqus计算速度最快,计算稳定性也非常好,在很大的范围内,有时甚至是近场,Abaqus的计算结果也非常好[8]。Abaqus采用其内嵌的声结构耦合法来处理水下爆炸问题。所谓声结构耦合法,就是在处理流固耦合问题时将流体当作声学介质来处理。利用声结构耦合法计算水下爆炸问题可以采用2种公式:“总波”公式和“散波”公式。在“总波”公式中声学单元中的基本变量为流体总压力,包括静压力和动压力;流体是非线性的,可以考虑其空化作用。如果使用“散波”公式,则流体被认为是线性的,声学单元中的基本变量只有流体动压力。此外,Abaqus在计算水下爆炸载荷时,是通过经验公式首先计算出非常接近结构表面一点处流体的压力时程曲线,然后再自动计算流场中其余各点的压力分布。这是AbaquS计算水下爆炸的最大优点,避免了冲击波在流体域中传播造成的能量损失[9]。所以,本文将使用Abaqus,以一环肋圆柱壳为例,对其水下非接触爆炸下的响应进行数值模拟,分析结构变形随肋骨间距、壳板厚度和外载荷的变化关系,从而为环肋圆柱壳抗爆设计提供参考。
1 爆炸载荷的描述文献[10]表明水中冲击波除了在爆点附近之外,几乎是以声波的速度传播的。因此,当不考虑近场和接触爆炸时,可以假设冲击波以声速传播。这样,冲击波可以用声波方程描述。本文使用Abaqus求解器求解,其内嵌的水下爆炸分析法(AUA)以水下爆炸载荷计算方法和声-结构耦合方法为关键技术,对中远场非接触爆炸可给出令人满意的结果。
为了完整描述爆炸压力的整个过程,Geers和Hunter[11]将爆炸载荷分成5个阶段:
1)指数衰减阶段
该阶段水中任意一点的压力为:
| $ P(t) = {P_m} \cdot {e^{ - t/\theta }},0 \leqslant t < \theta \text{。} $ | (1) |
其中:
2)倒数衰减阶段
该阶段压力随时间变化公式为:
| $ \begin{array}{l} P(t) = 0.368{P_m} \cdot \frac{\theta }{t}\left[ {1 - {{\left( {\frac{t}{{{t_p}}}} \right)}^{1.5}}} \right], \\ \theta \leqslant t \leqslant {t_1}\text{。} \end{array} $ | (2) |
其中
| ${t_p} = \frac{{{R_0}}}{c}\left[ \begin{array}{l} 850{\left( {\frac{{{P_0}}}{P}} \right)^{0.81}} - 20{\left( {\frac{{{P_0}}}{P}} \right)^{\frac{1}{3}}} + 11.4 \\ - 1.06{\left( {\frac{{{R_0}}}{R}} \right)^{0.13}} + 1.51{\left( {\frac{{{R_0}}}{R}} \right)^{1.26}} \\ \end{array} \right]\text{,}$ | (3) |
其中
3)倒数衰减后段
该阶段压力为:
| $ P(t) = {P^*}\left[ {1 - {{\left( {\frac{t}{{{t_p}}}} \right)}^{1.5}}} \right] - \Delta P,{t_1} \leqslant t \leqslant {t_p} \text{。} $ | (4) |
4)气泡膨胀收缩段
该阶段压力为:
| $ \begin{split} & P(t) = \frac{{{R_0}}}{R}\left[ \frac{{0.686}}{\xi }{{\left( {\frac{{{P_0}}}{{{P_{atm}}}}} \right)}^{0.96}} + \frac{{5.978\left( {1 - {\xi ^2}} \right)}}{{{\xi ^{0.92}}}}{{\left( {\frac{{{P_0}}}{{{P_{atm}}}}} \right)}^{0.62}}-\right. \\ & \left. 30.1{{\left( {\frac{{{P_0}}}{{{P_{atm}}}}} \right)}^{0.65}}{\xi ^{0.36}} \right]\times {10^5} - \\ & 1.73\left( {1 - {\xi ^2}} \right){\xi ^{0.1}}{\left( {\frac{{{R_0}}}{R}} \right)^4}{\left( {\frac{{{P_0}}}{{{P_{atm}}}}} \right)^{0.43}} \times {10^{10}},\\ &{t_p} \leqslant t \leqslant T - {t_2}\text{。}\\[-10pt] \end{split} $ | (5) |
其中T为气泡脉动周期。
5)脉动压力段
该阶段压力为:
| $ \begin{split} & P(t) = {P_{m1}} \cdot \exp \left[ { - {{\left( {t - T} \right)}^2}/\theta _1^2} \right], \\ & T - {t_2} \leqslant t \leqslant T + {t_2} \text{。} \end{split} $ | (6) |
本文环肋圆柱壳受到60磅炸药爆炸载荷的作用。根据上述公式,可以计算出作用到圆柱壳上的压力脉冲波时间–幅值表如表1所示。
|
|
表 1 时间–幅值表 Tab.1 Amplitude-time table |
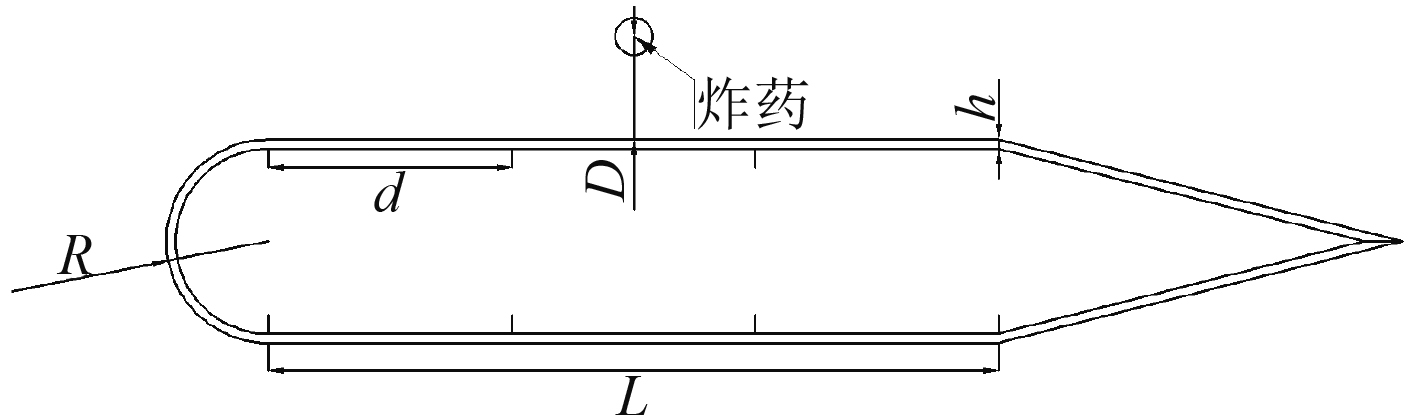
设一环肋圆柱壳,其柱状部分长度为L,柱壳厚度为h,肋骨间距为d,圆柱壳球艏半径为R,炸药距圆柱壳的垂直距离为D=50R,如图1所示。
|
图 1 环肋圆柱壳几何参数 Fig. 1 Geometrical parameters of the stiffened cylindrical shell |
用Abaqus自带前处理器建立环肋圆柱壳有限元模型,如图2所示。其中,环肋圆柱壳的材料为合金钢,其弹性模量为

|
图 2 环肋圆柱壳有限元模型 Fig. 2 FEM model of the stiffened cylindrical shell |
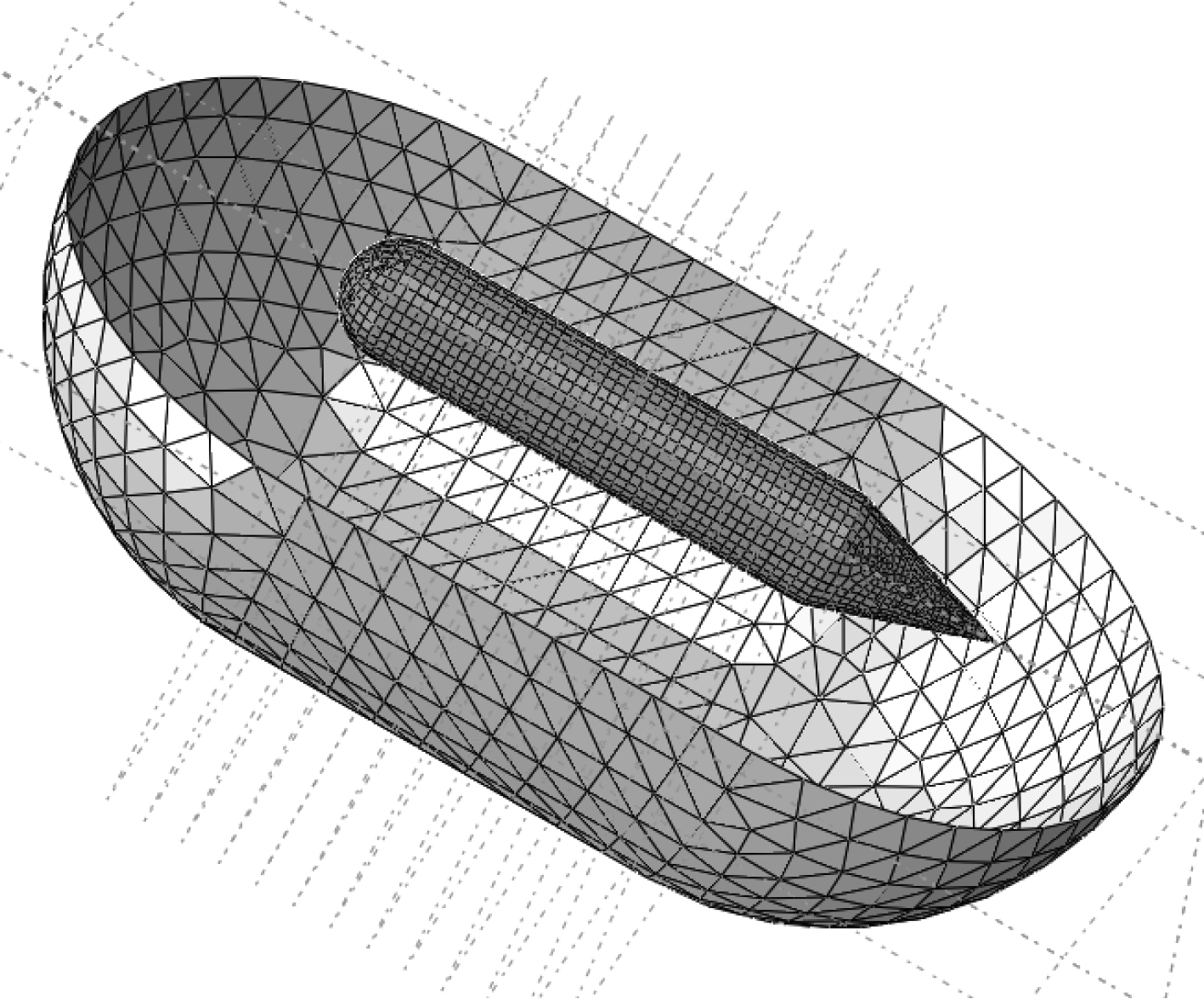
环肋圆柱壳的网格为S4R(4节点双曲线薄/厚壳缩减积分各向同性有限薄膜应变单元),水的网格为AC3D4(4节点线性声四面体单元),如图3所示。
|
图 3 网格的划分 Fig. 3 Mesh of the model |
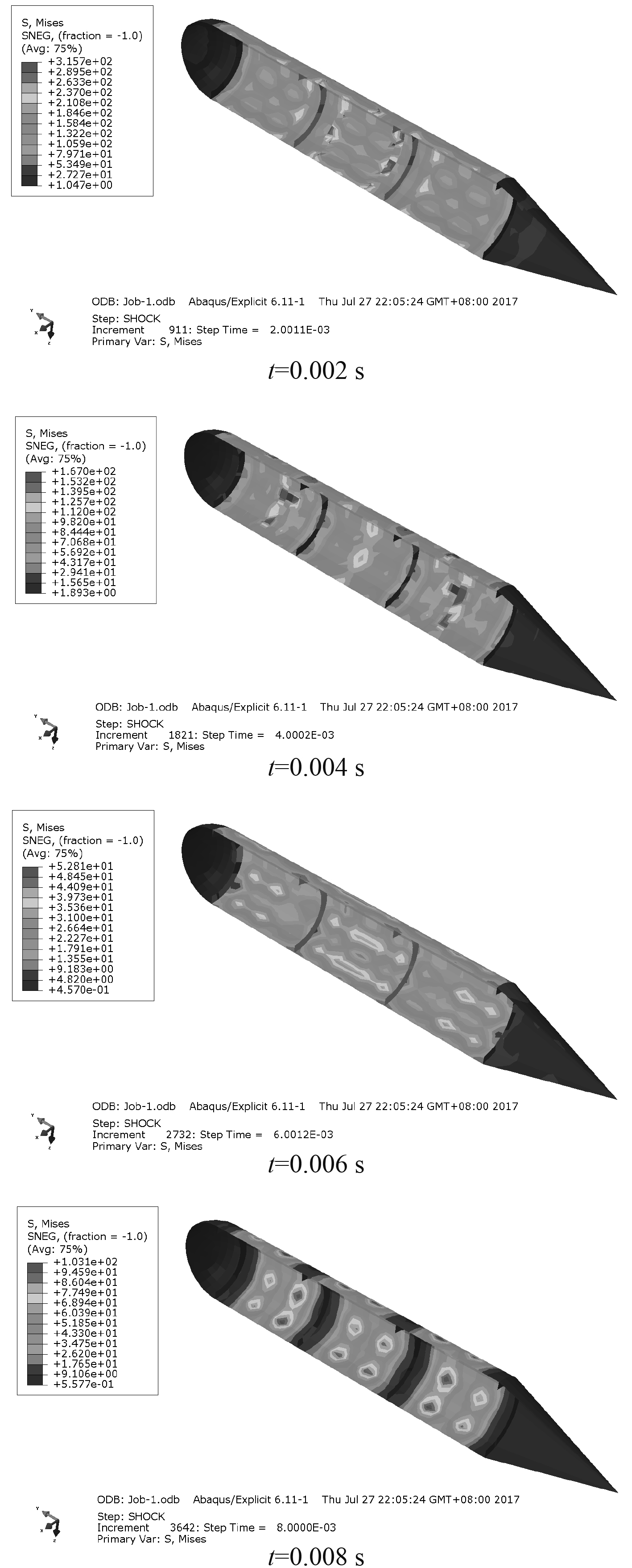
提交作业分析,得到环肋圆柱壳在不同时刻下的应力云图如图4所示。
|
图 4 环肋圆柱壳应力云图 Fig. 4 Stress nephogram of the stiffened cylindrical shell |
可以看出,随着冲击波的入射,环肋圆柱壳中心开始发生变形,当t=0.002 s时,圆柱壳中心最大应力为315.7 MPa。随着时间的推移,应力波开始由中心向两端扩散,到第0.004 s时最大应力出现在圆柱壳两端,最大应力值为167 MPa。到第0.006 s时,由于圆柱壳的弹性作用,变形开始恢复,圆柱壳两端和中心的最大应力几乎一致,其值为52.81 MPa。到第0.008 s时,在爆炸载荷的持续作用下,环肋圆柱壳的变形再次反弹,最大应力均匀分布在除肋骨附近的整个圆柱壳上,最大应力值为103.1 MPa。
3 肋骨间距的影响设计

|
图 5 5个测点沿x方向位移随时间的变化 Fig. 5 x-direction displacements of the five gauging points against time |
可知,当
当d=0.25L时,随着冲击波的入射,测点A,E发生较为明显的变形,其最大变形发生在t=0.001 s时,最大变形量为–4E-9m,而此时B,C,D点几乎无变形,直到t=0.002 s时才发生微小的变形,最大变形不超过1E-9m。这是因为当d=0.25L时,测点B,C,D恰好位于肋骨处,说明肋骨对圆柱壳有了明显的加强作用。当
设计
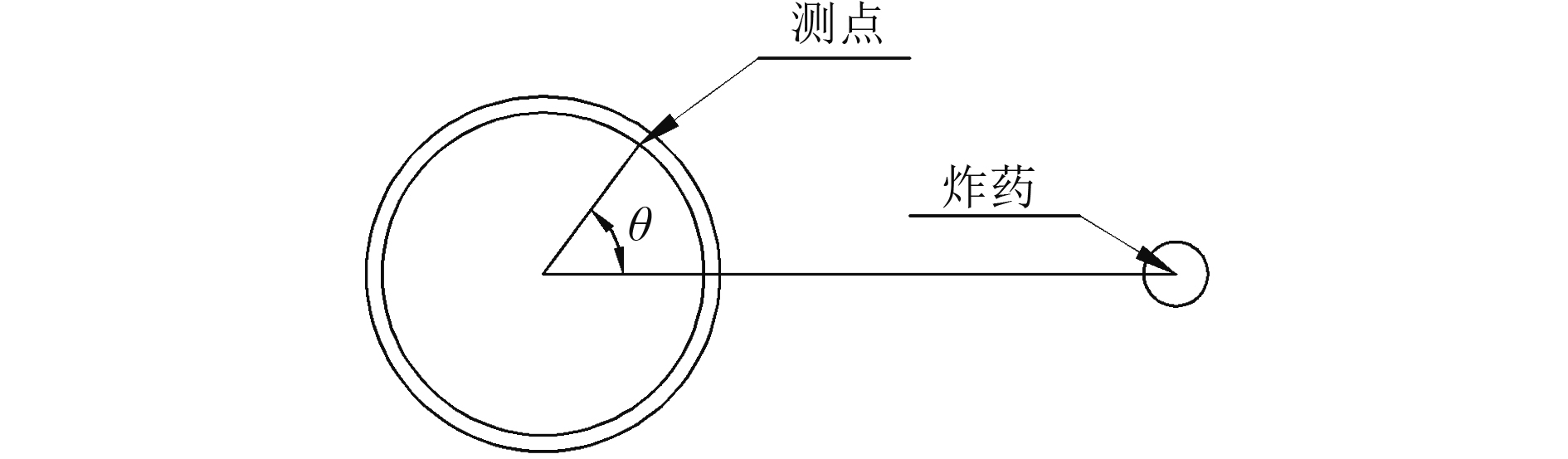
|
图 6 测点位置 Fig. 6 Positions of gauging points |

|
图 7 四个测点沿x方向位移随时间的变化 Fig. 7 x-direction displacements of the four gauging points against time |
由图7可知,不同板厚下,4个测点沿x方向位移随时间的变化趋势基本一致,对于测点A,随着冲击波的入射,其先向x轴负向移动,当t=0.0013 s时,位移最大,4种情况下最大位移分别为–55E-9m,–45E-9m,–35E-9m,–30E-9m。最大位移出现后,测点A开始向反方向移动,经过0.008 s振动后,逐渐回到原位置。对于测点C,其最大位移出现的时间略滞后于A点,这是因为A点位于迎爆面,而C点位于背爆面,其最大位移出现的时间为t=0.0014 s,4种壳板厚度下最大位移分别为45E-9m,35E-9m,30E-9m,25E-9m。可见,当h<0.04R时,若壳板厚度增加25%,最大位移约减小20%,而当h≥0.04R时,壳板厚度增加25%,最大位移约减小15%,一方面说明壳板厚度对圆柱壳的水下非接触爆炸响应有较大的影响,另一方面说明随着壳板厚度的增加,环肋圆柱壳最大位移减小的幅度逐渐变小。
对于B,D点,随着冲击波的的入射,其开始向x轴负向移动,4种壳板厚度下其最大位移几乎都不超过10E-9m,即壳板厚度对B,D点位移的影响较小。
5 爆炸距离的影响设计
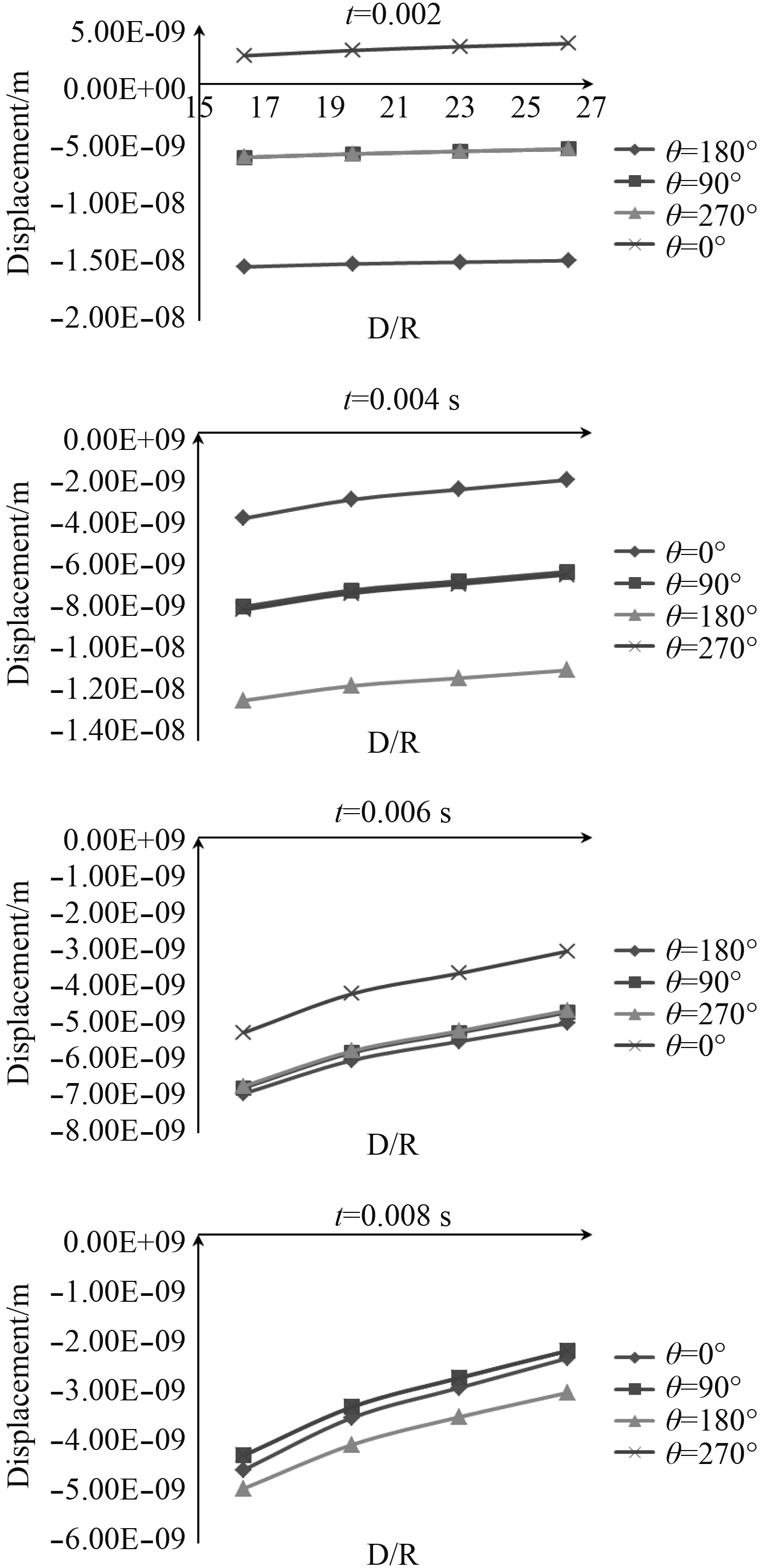
|
图 8 四个测点位移随外载荷距离的变化 Fig. 8 The displacements of four gauging points against load distance |
由图8可知,当t=0.002 s时,随着爆距的增加,4个测点位移-载荷曲线几乎是一条平直线,说明载荷距离对环肋圆柱壳冲击响应的影响不是发生在爆炸初期,这是因为冲击波以声速传递到环肋圆柱壳时,在爆距差别不大的情况下,其传递到环肋圆柱壳的时间相差很小。随着时间的推移,当t=0.004 s时,4个测点的位移随爆距的增大而减小,这是因为在该时刻下随着爆距的增大,在水的阻碍作用下,冲击波传递到圆柱壳的当量逐渐减小,当t=0.006 s,0.008 s时,位移-爆距曲线的斜率增大,说明位移减小的幅度增大,随着时间的推移,爆距对测点位移的影响逐渐增大,另外,位移-爆距曲线几乎为直线,说明位移随爆距的增大线性减小。
6 结 语本文基于Abaqus内嵌的以水下爆炸载荷计算方法和声-结构耦合方法为关键技术的水下爆炸分析法(AUA)对环肋圆柱壳在水下爆炸冲击下的响应进行了研究,得到以下结论:
1)当肋骨间距大于0.25倍环肋圆柱壳长时,肋骨不仅对其附近测点的变形有明显的抑制作用,也对肋骨中间的板壳起到了加强作用。
2)当d≥0.25L时,环肋圆柱壳最大变形量比
3)除了肋骨间距外,壳板厚度对圆柱壳的水下非接触爆炸响应也有较大的影响。当厚度小于0.04倍圆柱壳半径时,若壳板厚度增加25%,最大位移约减小20%,而当厚度大于0.04倍圆柱壳半径时,壳板厚度增加25%,最大位移约减小15%,即随着壳板厚度的增加,环肋圆柱壳最大位移减小的幅度逐渐变小。
4)在爆炸初期爆距对环肋圆柱壳冲击响应的影响不大,随时间的推移这种影响逐渐增大,环肋圆柱壳各测点变形随爆距的增大线性减小。
| [1] |
RUNGSIYAPHORNRAT S, KLASEBOER E, KHOO B C et al. The merging of two gaseous bubbles with an application to underwater explosions[J]. Computers and Fluids, 2003, 32: 1049-1074. DOI:10.1016/S0045-7930(02)00078-6 |
| [2] |
ZHANG A M, BAO Y N, BING Y S et al. Numerical simulation of bubble breakup phenomena in a narrow flow field[J]. Applied Mathematics and Mechanics, 2010, 31(4): 449-460. DOI:10.1007/s10483-010-0405-z |
| [3] |
张玮, 史少华. 水面舰艇舰员对水下爆炸冲击响应[J]. 爆炸与冲击, 2011, 31(5): 521-527. |
| [4] |
张阿漫, 王诗平, 汪玉, 等. 水下爆炸对舰船结构损伤特征研究综述[J]. 中国舰船研究, 2011, 6(3): 1-7. ZHANG A M, WANG S P, WANG Y, et al. Advances in the Research of characteristics of warship structural damage due to underwater explosion[J]. China ship research, 2011, 6(3): 1-7. DOI:10.3969/j.issn.1673-3185.2011.03.001 |
| [5] |
祝祥刚, 刘莹, 陈舸, 等. 水下非接触爆炸作用下的船体结构响应分析[J]. 计算机辅助工程, 2013, 22(2): 248-251. |
| [6] |
吴广明, 陈炜, 吴敌, 等. 水下非接触爆炸下船体爆炸弯矩简化计算方法[J]. 中国舰船研究, 2017, 12(3): 58-63. WU G M, CHEN W, WU D, et al. Calculation of explosion bending moment in hull girders subjected to non-contact underwater explosions[J]. Chinese Journal of Ship Research, 2017, 12(3): 58-63. DOI:10.3969/j.issn.1673-3185.2017.03.009 |
| [7] |
吴敌, 吴广明, 李正国, 等. 水下非接触爆炸冲击下舱段模型的仿真分析[J]. 舰船科学技术, 2016, 38(9): 37-41. WU Di, WU Guang-ming, LI Zheng-guo, et al. Numerical simulation analysis of cabin models subjected to underwater explosion shock wave[J]. Ship Science and Technology, 2016, 38(9): 37-41. |
| [8] |
肖锋, 谌勇, 朱大巍, 等. 水下非接触性爆炸下分层圆孔覆盖层动响应及抗冲击性能研究[J]. 振动与冲击, 2013, 32(19): 111-118. DOI:10.3969/j.issn.1000-3835.2013.19.020 |
| [9] |
赵延杰.近距及接触水下爆炸冲击波作用下结构毁伤的数值模拟[D]. 大连: 大连理工大学. 2013: 14.
|
| [10] |
李金河, 赵继波, 谭多望等. 炸药水中爆炸的冲击波性能[J]. 爆炸与冲击, 2009, 29(2): 172-176. DOI:10.3321/j.issn:1001-1455.2009.02.011 |
| [11] |
GEERS T L, HUNTER K S. An integrated wave-effects model for an underwater explosion bubble[J]. J. Acoust. Soc. Am, 2002, 111(4): 1584-1601. DOI:10.1121/1.1458590 |
 2020, Vol. 42
2020, Vol. 42
