对于近水面潜体,兴波阻力作为其总体阻力中最为重要的组成部分引起了学者们的广泛关注[1-2]。无论是潜艇在近水面的航行,还是水翼艇水下部分的运动,都涉及到潜体的兴波特性。特别是在潜体转向过程中,兴波阻力的变化对于舰船操纵性与稳定性有着十分重要的影响。因此,对于潜体转向过程中兴波阻力与升力变化的研究具有十分重要的工程意义。
在海洋工程领域中,面元法是求解三维势流问题时普遍使用到的方法,特别是Rankine源法的应用,凭借着频率规则、计算简单、能够灵活推广到非线性计算的特点,在处理三维兴波问题时有很大的应用空间。但是传统面元法在大网格规模计算的过程中存在着效率不高的问题,直接导致其求解大规模流场时效率低下,占用大量计算资源。为了解决这一缺陷,引入新算法对传统计算逻辑进行改进显然十分必要。
自从Rokhlin首次将快速多极子法应用到流体力学问题中[3],求解二维势流问题的计算效率得到了极大的提升,随着Greengard[4],Hackbusch[5],Cheng[6]对该算法的不断完善,将快速多极子法与其他方法结合便成为求解大规模势流问题的一大趋势。其中最为典型的是对边界元法的改进,结合后得到的快速多级子边界元方法已经在许多势流问题[7]、声学问题[8]、弹性力学问题[9]中得到应用。对于三维潜体的势流问题,快速多极子法也有相关应用[10-11]。
本文选择将多极子法与传统面元法结合,对有偏航角度的近水面潜体运动兴波特征进行研究,并且引入网格实时加密技术,在确保多极子面元法能高效精准求解潜体兴波问题的同时,在时间轴上采用实时步进,能够对潜体产生的复杂波形进行研究,以此发现并验证潜体非直线运动对于潜体产生的兴波阻力与升力的影响,以及自由表面处各波系相互间的干扰。
1 潜体近水面兴波问题描述 1.1 基本控制方程及初边界条件本文考虑的椭球潜体运动兴波流场示意图如图1所示。其中水深为无限深,静止平均自由水面长为L,宽为D。潜体为回转椭球体,长轴为
|
图 1 计算流场示意图 Fig. 1 Diagram of the computational fluid field |
| $ {\nabla ^2}\varphi = 0,z \leqslant \eta (x,y,t)\text{。} $ | (1) |
其中:
| $ \left\{ \begin{aligned} & {\frac{{\partial \varphi }}{{\partial t}}{\rm{ + }}g\eta {\rm{ + }}\frac{1}{2}{{\left| {\nabla \varphi } \right|}^2}{\rm{ = }}0,\;z = \eta (x,y,t)}\text{,}\\ & {\frac{{\partial \eta }}{{\partial t}}{\rm{ + }}\bar \nabla \varphi \cdot \bar \nabla \eta {\rm{ }} - {\rm{ }}\frac{{\partial \varphi }}{{\partial z}}{\rm{ = }}0,\;z = \eta (x,y,t)}\text{,}\\ & {\frac{{\partial \varphi }}{{\partial n}} = U(t) \cdot n,\quad \quad (x,y,z) \in {S_B}}\text{。} \end{aligned} \right. $ | (2) |
其中:
此外,假定潜体由静止状态启动,故在自由水面上的初始条件为:
| $\varphi = \frac{{\partial \varphi }}{{\partial t}} = \eta = 0,\quad (t = 0 )\text{。} $ | (3) |
假定潜体做水平面曲线运动,即椭球潜体始终以沿其长轴方向均匀速U运动,而其长轴与x轴夹角α做周期变化,具体表达式如下:
| $ \alpha = {\alpha _0} \cdot \cos (2{\text{π}} t/T)\text{。} $ | (4) |
其中:T为角度变化的周期,α0为初始时刻椭球长轴与x轴的夹角。显然,椭球潜体沿x轴方向推进,且|α|≤α0。因此定义α0为偏航角,用来表征潜体y方向摆动的幅度。在后续研究中选取T=π恒定,考察偏航角α0对于表面兴波特性的影响。
因此,潜体长轴与x轴夹角呈余弦函数变化,速度U始终恒定,即潜体运动路径也呈周期变化,即周期同样是T,轨迹如图2所示。

|
图 2 潜体运动路径 Fig. 2 Path of the submerged body |
采用面元法求解潜体兴波势流问题。首先对自由面和潜体表面边界进行离散,划分为N个面积分别为Si的面元,每个面元上布置强度分别为σi的面源;取每个面元的中心作为该面元的控制点。给定第一类或第二类边界条件,即已知任一面元Sj上控制点处的速度势
| $ \bar \phi ({x_j}) = \sum\limits_{i = 1}^N {\frac{{{\sigma _i}}}{{4{\text{π}} }}} \iint\limits_{{S_i}} {\frac{1}{r}{\rm{d}}S}\text{,} $ | (5) |
或
| $ \bar q({x_j}) = \sum\limits_{i = 1}^N {\frac{{{\sigma _i}}}{{4{\text{π}} }}} \iint\limits_{{S_i}} {\nabla \frac{1}{r}{\rm{d}}S}\text{。} $ | (6) |
其中:
可以将式(5)和式(6)简化为如下代数方程:
| $ {{A}}\sigma ={{ B}}\text{。} $ | (7) |
采用快速多极子法加速代数方程的计算,能够有效克服传统面元法的局限性。关于快速多极子面元法中核函数
在多极子面元法的基础上按照时间步进方法求解时域问题。已知tn时刻自由面上势函数φ[n]与波高函数η[n],根据式(5)~式(7)利用面元法求解得到面元源强,从而得到面元上的速度
| $ \frac{{{\varphi ^{[n + 1]}} - {\varphi ^{[n]}}}}{{\Delta t}} = {\left( {\frac{{\partial \varphi }}{{\partial t}}} \right)^{[n]}} \text{,} $ | (8) |
| $ \frac{{{\eta ^{[n + 1]}} - {\eta ^{[n]}}}}{{\Delta t}} = {\left( {\frac{{\partial \eta }}{{\partial t}}} \right)^{[n]}} \text{,} $ | (9) |
获得tn+1时刻自由面对应势函数φ[n+1]与波高函数η[n+1]。重复上述过程以完成时域问题求解在时间上的步进。
2.3 潜体受力系数定义对于自由表面选取四边形常数面元分割,总共有NF个单元。对于潜体表面选取三角形常数面元进行分割,总共有NB个单元。每个单元上压力分布分别为pi,其对应的诱导速度方向为向量ni,该向量在x,y,z方向的分量分别为nix,niy,niz。
在每个时间步中,可以求解得到整个流场中速度势与速度的分布,结合伯努利方程
| $ p = - \rho \frac{{{\rm D}\varphi }}{{{\rm D}t}} - \frac{1}{2}\rho {\left| {\nabla \varphi } \right|^2} + \rho \nabla \varphi \cdot U - \rho gz \text{,} $ | (10) |
即可计算出潜体表面各单元的压力分布。其中D/Dt为随体导数。潜体受到的升力与阻力可以用下式表示:
| $ {R_L} = - \sum\limits_{i = 1}^{{N_B}} {\iint_{{S_i}} {{p_i} \cdot {n_{iz}}{\rm{d}}S}} \text{,} $ | (11) |
| $ {R_{Dx}} = - \sum\limits_{i = 1}^{{N_B}} {\iint_{{S_i}} {{p_i} \cdot {n_{ix}}{\rm{d}}S}}\text{,} $ | (12) |
| $ {R_{Dy}} = - \sum\limits_{i = 1}^{{N_B}} {\iint_{{S_i}} {{p_i} \cdot {n_{iy}}{\rm{d}}S}} \text{。} $ | (13) |
式中,Si为潜体表面上的离散单元。进一步无量纲处理,可以得到相应升力与阻力系数:
| $ {C_L} = {R_L}/\frac{1}{2}\rho {U^2}{S_0} \text{,} $ | (14) |
| $ {C_{Dx}} = {R_{Dx}}/\frac{1}{2}\rho {U^2}{S_0} \text{,} $ | (15) |
| $ {C_{Dy}} = {R_{Dy}}/\frac{1}{2}\rho {U^2}{S_0} \text{。} $ | (16) |
其中S0为潜体表面积。从而,兴波总体阻力系数可通过x及y两个方向上的分量求得:
| $ \left| {{C_W}} \right| = \sqrt {{C_{Dx}}^2 + {C_{Dy}}^2} \text{。} $ | (17) |
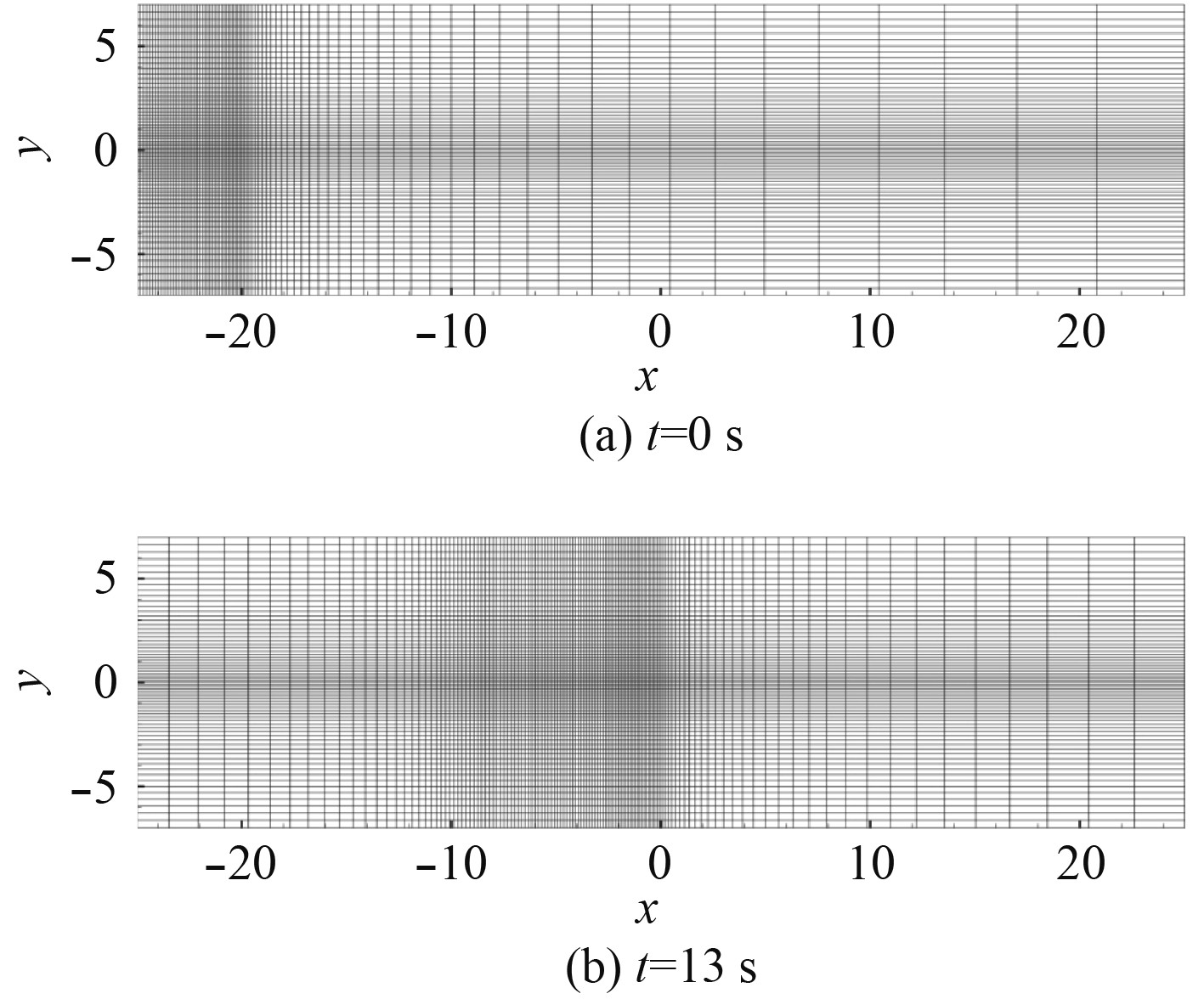
沈王刚等[11]文中已经验证了多极子面元法在求解潜体直线运动时域兴波问题的有效性。在上述方法的基础上,采取自由面实时加密,在潜体附近适当补充以确保计算精度与效率更高,更加节省计算资源。整个水池在网格加密的过程中遵循距离潜体越近网格越密的原则,在y方向上令边界处最疏,潜体中心处最密,网格大小以指数函数的形式变化。在x方向上网格密度变化同理,但尾流方向网格比来流方向更为密集,以准确捕捉尾流波形。自由面在x轴方向长50 m,y轴方向长14 m,以平面中心处为x-y平面坐标原点。选取2个时刻的自由面网格为例,如图3所示。
|
图 3 自由面网格实时加密 Fig. 3 Free surface mesh encryption in real time |
选取椭球体为回转椭球体,潜体长轴长度为1,短轴长度为0.2,划分网格时将两端与中心切面处加密,总体面元数为2 640,网格划分如图4所示。在文献[11]中已经证明了该划分方式已经达到了计算精度的要求。

|
图 4 椭球体表面网格 Fig. 4 surface grid of the ellipsoid |
对于水池的自由表面选取3种不同密度的网格,网格数量分别为250×70,375×210,500×140,定义网格密度为平均网格间距,故在50 m×14 m的自由面上对应的网格密度分别为0.2,0.133,0.1。
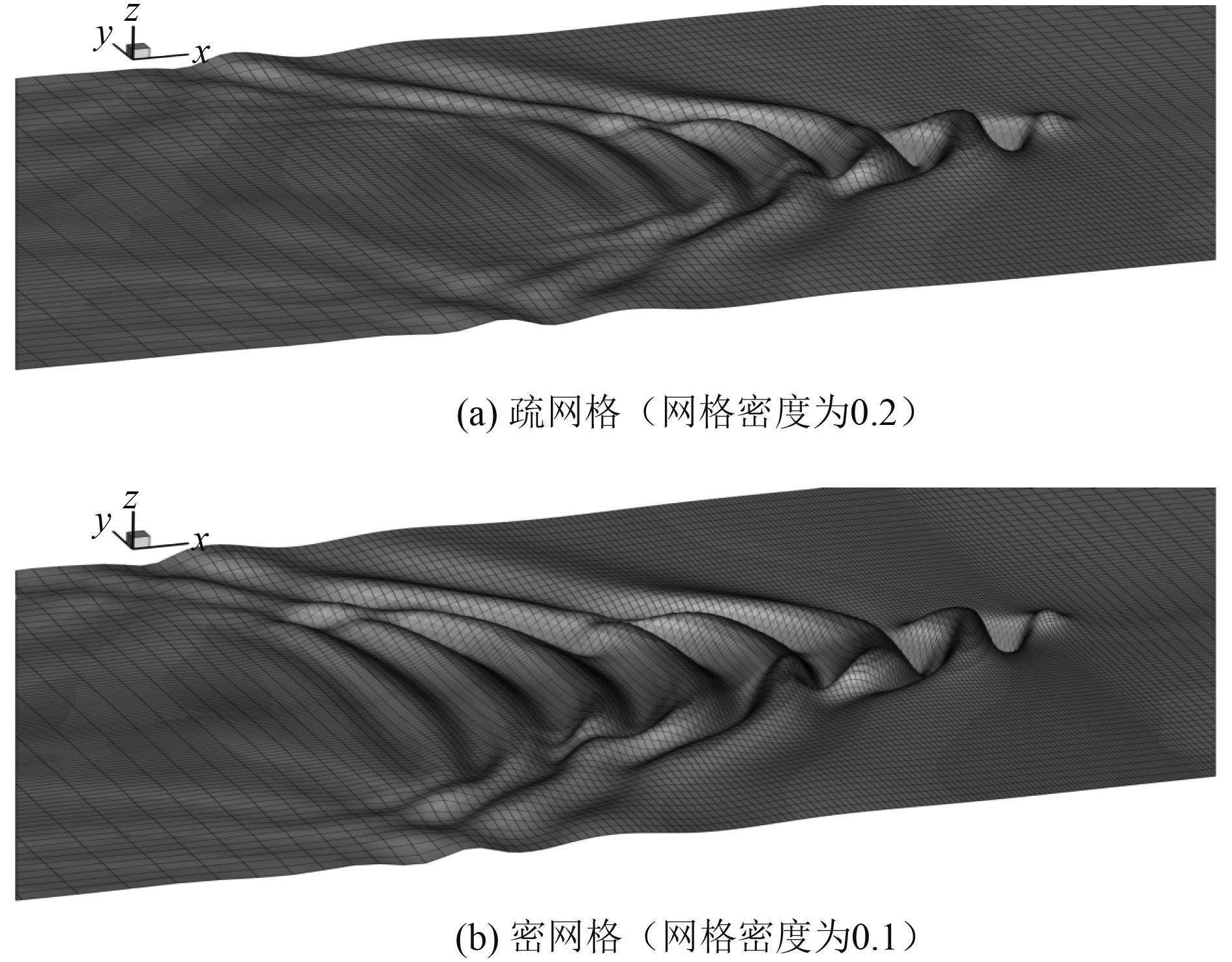
3种自由面网格下,椭球潜体中心距平静自由面h/l=0.16,潜体兴波的Froude数均为0.5,即速度U=1.566 m/s,偏航角度α0=π/9。其中网格密度为0.2与0.1的算例中,潜体在t=26 s时刻生成波形图如图5所示。可以明显观察到密度0.2网格的波浪,特别是在波高急剧变化的区域,光顺程度不及密度0.1网格,并且在潜体尾部一定距离处会损失很多波浪成分,尾部波浪衰减比较厉害。
|
图 5 t=26 s自由面波形及网格图像 Fig. 5 Free surfaces and grids at t=26 s |
3种网格得到的各水动力系数比较如图6所示。对于兴波阻力系数,0.2网格算例与0.133网格算例相差较大。y方向的CDy系数上,尽管变化周期相同,但幅值有20%左右的误差;在x方向的CDx系数上,变化趋势相同,每个周期中的最高点相近,但最低点仍有一定的误差。对于升力系数,0.2网格算例与0.133网格算例在幅度上同样具有较大差别。而网格密度0.1算例与网格密度0.133算例得到各项系数随时间的曲线基本重合,故可以认为网格密度0.1算例的计算结果可信,达到网格收敛。因此,后文中所有算例对自由表面离散均采用网格密度0.1,即数量为500*140的自由面网格。

|
图 6 不同密度网格下的水动力参数 Fig. 6 Hydrodynamic parameters at different grid density |
选取潜体为回转椭球体,潜体质心所在初始位置x/l=–20,y=0,椭球潜体中心距平静自由面h/l=0.16。潜体从t=0时刻开始,潜体有个加速过程,以避免自由水面突然的隆起,在t=2 s时刻达到指定速度后进行匀速正弦运动,运行速度U=1.566 m/s,对应Froude数为Fr=0.5。在时域上,选取时间步长0.04 s,步进次数650次,潜体共计运动时长26 s。
根据文献[11]中对于潜体平面直线定常运动的研究,可以得到潜体在匀速运动过程中,整体所受的升力、阻力系数如图7(a)所示。可以看出,在最初的2 s内,潜体从静止开始加速运动,之后的2 s中,由于加速度的变化,潜体附近流场在惯性的影响下,阻力与升力系数继续上升,然后略微下降,并在第4 s后基本达到稳定状态,从而升力、阻力等各项系数趋近于稳定值。因潜体沿着x轴方向运动,其在达到稳定状态后,x方向兴波阻力CDx为负值且基本保持不变。由于对称性,y方向兴波阻力CDy始终保持为0。
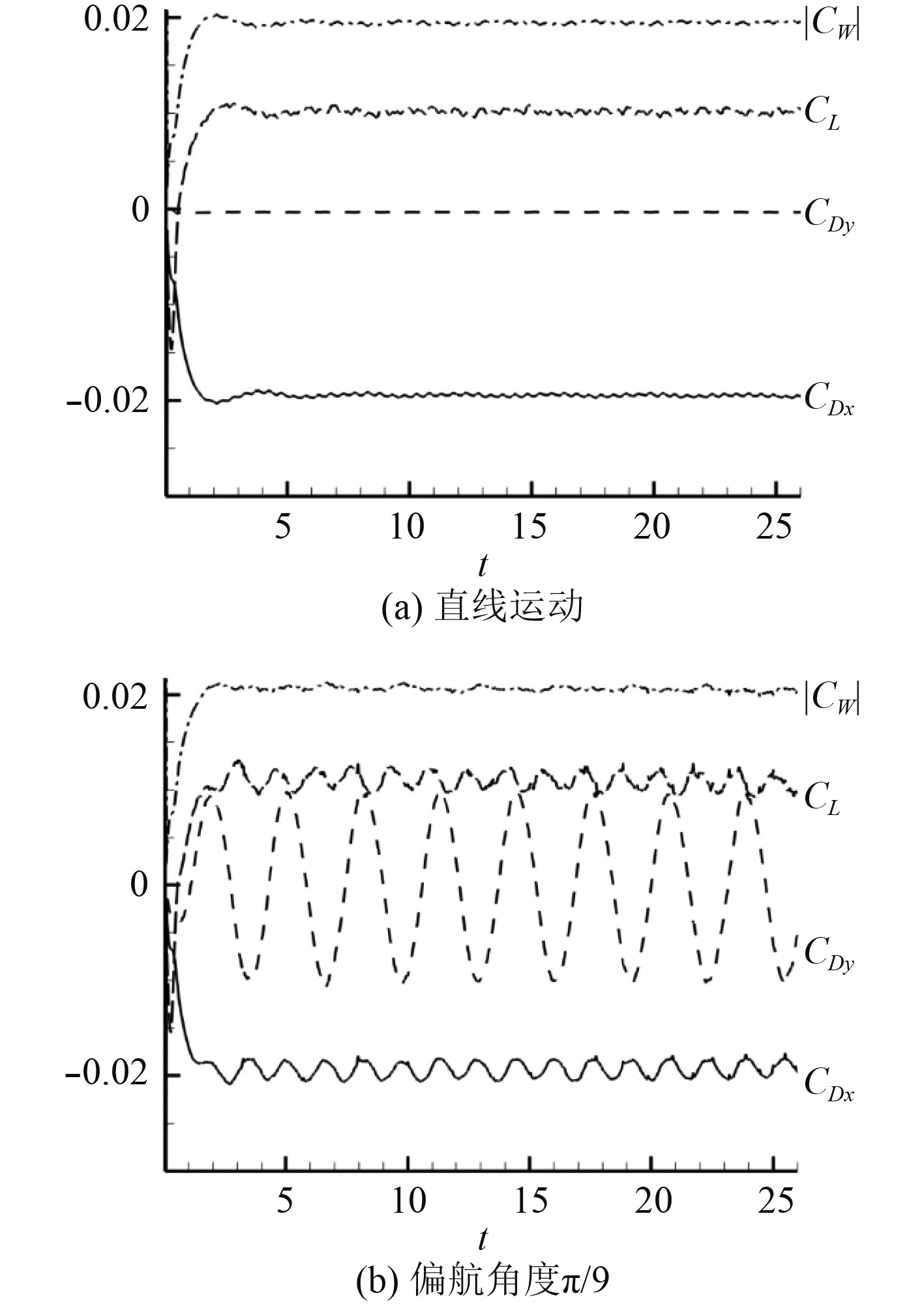
|
图 7 直线与偏航运动的各项水动力参数 Fig. 7 Hydrodynamic parameters of the rectilinear and sinusoidal motion |
为了研究平面曲线运动下潜体的兴波阻力,初始状态时椭球长轴与x轴夹角α0=π/9,即最大偏航角度为π/9,偏航角度变化周期为π,潜体运动特性如1.2节中所描述,其对应的升力与阻力系数如图7(b)所示。可以观察到与平面直线定常运动不同,潜体曲线运动从静止状态到加速完毕之后,因偏航角度周期性变化,潜体各项兴波阻力与升力系数同样呈现出周期性。其中y方向阻力系数CDy变化周期与潜体曲线运动周期一致,均为π。对于x方向的阻力系数,由于潜体在每一个运动周期中发生了2次左右方向上的偏转,故CDx的变化周期为潜体运动周期的一半。在偏航角为π/9的小角度偏航工况中,升力系数并无明显变化,甚至呈现平顺的稳定状态。
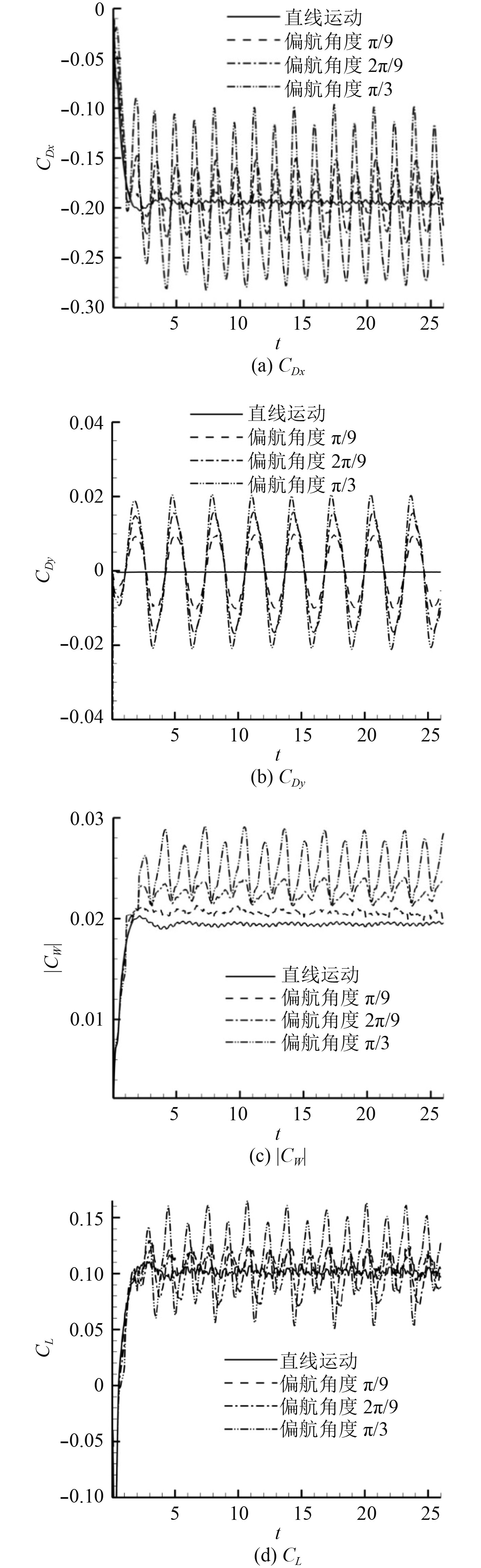
3.2 偏航角度对兴波阻力的影响在同样的深度与速度下,考虑3组不同偏航角度时潜体的兴波情况,初始偏航角度分别为π/9,2π/9,π/3,并将结果与潜体直线运动情况进行比较,如图8所示。对于每个水动力系数,规定每个周期中最大值的均值为平均最大值,同理可求得平均最小值,平均最大值与平均最小值的差即为其变化幅值。各个初始偏航角算例中,相应升力与兴波阻力变化均值、幅值情况列在表1与表2中。
|
|
表 1 升力与兴波阻力变化均值 Tab.1 The mean value of lift and wave resistance |
|
|
表 2 升力与兴波阻力变化幅值 Tab.2 The amplitudes of lift and wave resistance |
|
图 8 不同偏航角下的水动力参数 Fig. 8 Hydrodynamic parameters at different yawing angles |
图8(a)~图8(c)为阻力系数变化情况,在x方向上的分量CDx呈现出周期变化,均值与直线运动的稳定值十分接近。随着初始偏航角度的增大,其最大值逐渐增加,当角度达到π/3时,CDx在每个运动周期中会出现2个不同的正弦变化幅值,且潜体前进方向的左右侧会出现不对称性。在一个运动周期中,潜体在x方向上受到的阻力会经历一次左转极值与右转极值,并且在潜体偏航角较大时这2个极值并不相同。对于y方向分量CDy,始终以周期T呈正弦规律变化,并且均值为0。潜体y方向的运动受到偏航角的影响相对较小,但CDy这一项的最大值随着初始偏航角的增大仍呈现近似线性增长。
总体阻力|CW|均值随着偏航角度的增大而增加,当偏转角度为0和π/9时,2个分量在时域上有周期性变化,但|CW|基本呈一条稳定的直线。当角度达到2π/9和π/3时,兴波总阻力呈现出明显的周期性,由于CDx关于其均值存在不对称性,|CW|也同样具有显著的不对称性。此外,从表1与表2可以看出,当偏航角度达到π/3时,相比于潜体直线运动,总体兴波阻力均值增大了约30%,特别地,幅值变化高达10倍以上。由此可见,大偏航角曲线运动时,表面兴波对潜体所受阻力有着巨大的影响。
图8(d)为升力系数CL变化情况,可以看出升力的周期性变化十分明显,并且均值十分接近直线运动时升力的稳定值。随着初始偏航角度的增大,升力波动的幅度也逐渐增加;当角度达到π/3时,升力在每个潜体曲线运动周期中同样出现2个不同的变化幅值。根据表1与表2,在偏航角度达到π/3的情况下,和直线运动相比升力均值的变化基本保持在10%以内,但幅值变化剧烈,高达7倍以上。当偏航角较大时,表面兴波同样对潜体所受升力有着非常显著的影响。
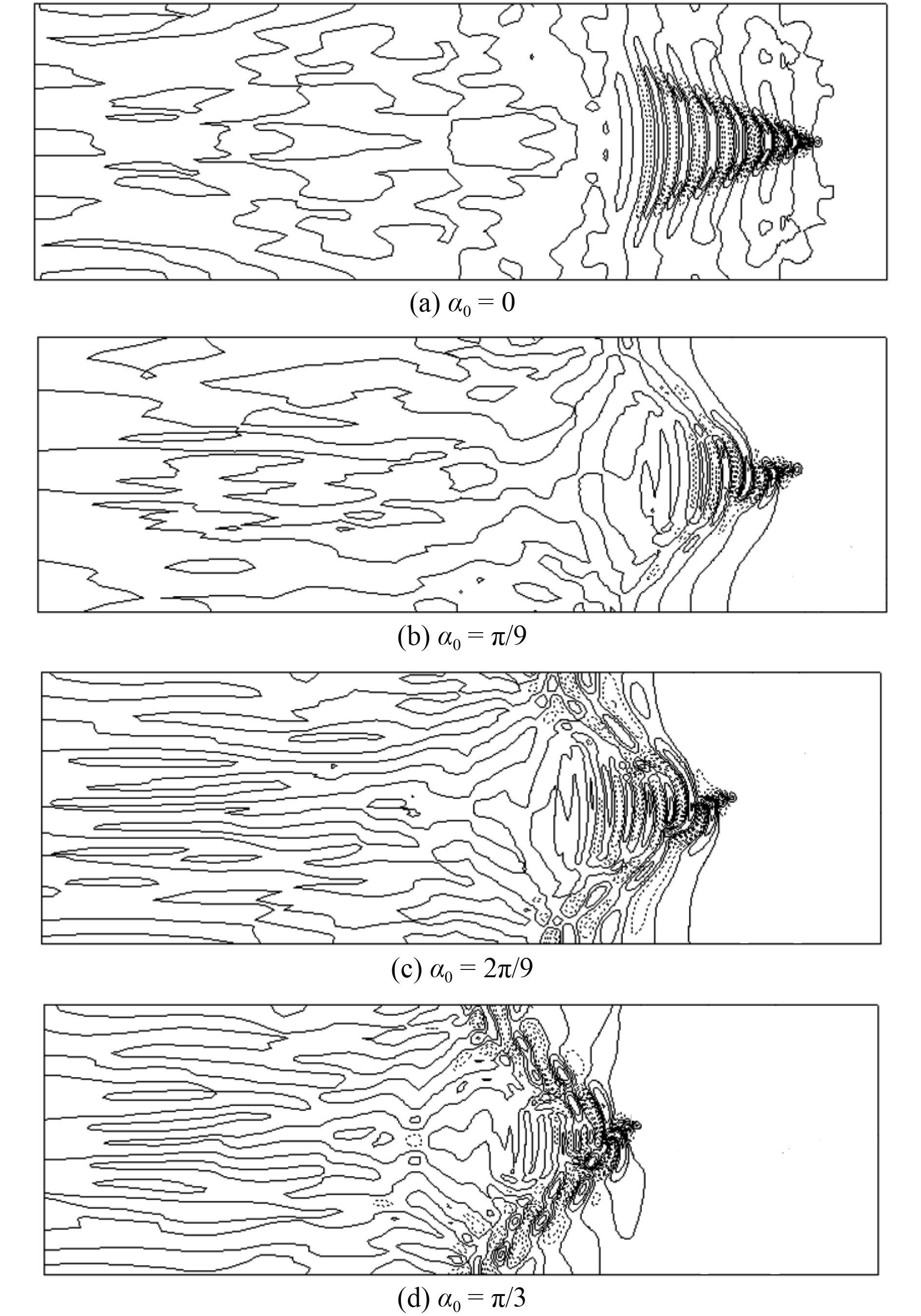
3.3 曲线运动潜体表面兴波波形研究对于不同的偏航角度,潜体兴波波面等高图如图9所示。当潜体做平面直线运动时,自由面上产生的兴波夹角为开尔文角,即θ=35°18′,如图9(a)所示。当潜体有偏航角度运动时,自由面上兴波夹角逐渐增大。偏航角度较小时,可以看出兴波夹角明显大于开尔文角,尾部兴波形状逐渐变得不规则,随着潜体将更多能量传递给表面兴波,其自身受到的兴波阻力也逐渐增加。当偏航角度达到π/3,兴波波系间的相互作用更为明显,自由面上波形变得十分复杂,可以明显看出潜体曲线运动所产生的表面波形不规则,多个波系间的相互作用显著,潜体尾部横波快速衰减,散波波形更为复杂,不能快速衰减且交替变化。表面兴波的显著差别表明了潜体做曲线运动过程中,更多的能量消耗传递到兴波中,因此潜体所受到的兴波阻力及升力也更大,且不对称性显著,与阻力和升力系数随时间变化曲线所展示的特性相符。
|
图 9 t=26 s时,不同偏航角下的船行波 Fig. 9 Ship wave of different yawing angles at t=26 s |
采用快速多极子面元法求解近水面潜体曲线运动时域兴波问题有着高效性与可靠性,通过本文所设置的算例及模拟结果分析,可以得到如下结论:
1)相比于潜体直线运动,偏航角度π/3时,潜体曲线运动所受的兴波总阻力均值增大了近30%,最大幅值增加超过10倍,表明表面兴波对潜体所受阻力影响非常显著。当偏航角较大时,表面兴波同样对潜体所受升力有着显著的影响,升力曲线波动的最大幅值相比直线运动也增加近7倍。
2)潜体在近水面曲线运动所产生的表面波系夹角随着偏航角的增大而增加,大偏航角时潜体所兴波系间相互干扰显著,自由面波形变得极为复杂,潜体曲线运动所受的兴波阻力激增,阻力及升力曲线出现大幅波动且不对称性。因此当潜体近水面曲线运动时,时域兴波研究对掌握潜体受力特性及运动控制都尤为重要。
| [1] |
韩端锋, 黄德波. 近水面潜体兴波阻力的数值预报和收敛性分析[J]. 船舶力学, 2005, 9(1): 29-35. HAN Duan-feng, HUANG De-bo. Numerical prediction and convergence analysis of wave resistance for submerged body near free surface[J]. Journal of Ship Mechanics, 2005, 9(1): 29-35. DOI:10.3969/j.issn.1007-7294.2005.01.005 |
| [2] |
杨向晖, 叶恒奎, 刘娟, 等. 潜体近水面航行兴波阻力计算[J]. 华中科技大学学报(自然科学版), 2008, 36(4): 129-132. YANG Xiang-hui, YE Heng-kui, LIU Juan, et al. Computation of the wave making resistance of submerged body moving beneath water surface[J]. J. Huazhong Univ. of Sci. & Tech. (Natural Science Edition), 2008, 36(4): 129-132. DOI:10.3321/j.issn:1671-4512.2008.04.035 |
| [3] |
ROKHLIN V. Rapid solution of integral equations of classical potential theory[J]. Journal of Computational Physics, 1985, 60(2): 187-207. DOI:10.1016/0021-9991(85)90002-6 |
| [4] |
GREENGARD L, ROKHLIN V. A fast algorithm for particle simulations[J]. Journal of Computational Physics, 1987, 73(2): 325-348. DOI:10.1016/0021-9991(87)90140-9 |
| [5] |
HACKBUSCH W, NOWAK Z P. On the fast matrix multiplication in the boundary element method by panel clustering[J]. Numerische Mathematik, 1989, 54(4): 463-491. DOI:10.1007/BF01396324 |
| [6] |
CHENG H, GREENGARD L, ROKHLIN V. A fast adaptive multipole algorithm in three dimensions[J]. Journal of Computational Physics, 1999, 155(2): 468-498. DOI:10.1006/jcph.1999.6355 |
| [7] |
LIN Z, LIAO S. Calculation of added mass coefficients of 3D complicated underwater bodies by FMBEM[J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(1): 187-194. DOI:10.1016/j.cnsns.2010.02.015 |
| [8] |
CHEN Z S, WAUBKE H, KREUZER W. A formulation of the fast multipole boundary element method (FMBEM) for acoustic radiation and scattering from three-dimensional structures[J]. Journal of Computational Acoustics, 2008, 16(02): 303-320. DOI:10.1142/S0218396X08003725 |
| [9] |
WANG Y, WANG Q, WANG G, et al. An adaptive dual-information FMBEM for 3D elasticity and its GPU implementation[J]. Engineering Analysis with Boundary Elements, 2013, 37(2): 236-249. DOI:10.1016/j.enganabound.2012.09.012 |
| [10] |
LIN Z, LIAO S. Calculation of added mass coefficients of 3D complicated underwater bodies by FMBEM[J]. Communications in Nonlinear Science & Numerical Simulation, 2011, 16(1): 187-194. |
| [11] |
沈王刚, 郑尧坤, 林志良. 多极子面元法近水面椭球体兴波时域研究[J]. 舰船科学技术, 2018(8): 14-22. SHEN Wang-gang, ZHENG Yao-kun, LIN Zhi-liang. Multipole panel method for the time-domain wave making research for ellipsoid near free surface[J]. Ship Science and Technology, 2018(8): 14-22. DOI:10.3404/j.issn.1672-7649.2018.08.003 |
| [12] |
LIU Y J, NISHIMURA N. The fast multipole boundary element method for potential problems: a tutorial[J]. Engineering Analysis with Boundary Elements, 2006, 30(5): 371-381. DOI:10.1016/j.enganabound.2005.11.006 |
| [13] |
NISHIMURA N. Fast multipole accelerated boundary integral equation methods[J]. Applied Mechanics Reviews, 2002, 55(4): 299-324. DOI:10.1115/1.1482087 |
| [14] |
YOSHIDA K. Applications of fast multipole method to boundary integral equation method[J]. Kyoto: Kyoto University, 2001. |
| [15] |
林志良. 比例边界有限元法及快速多极子边界元法的研究与应用[D]. 上海: 上海交通大学, 2010. LIN Zhi-liang. Research and Application of Scaled Boundary FEM and Fast Multipole BEM[D]. Shanghai: Shanghaijiaotong University, 2010. |
 2020, Vol. 42
2020, Vol. 42
