六自由度运动平台的发展水平标志着一个国家航空、航天、航海等领域的发达程度,尤其是我国近年来海上军事力量不断增强,对多自由度运动平台的开发设计需求就显得尤为突出。六自由度是由英国高级工程师Stewart于1965年提出的,因此也将六自由度运动平台称为Stewart平台[1]。Stewart平台属于一种并联运动机构[2],它具有运动精度高、响应速度快等特点,因而受到众多研究人员的重视。
随着工业技术的发展,Stewart平台的运用也越来越广泛,同时各方面的研究也越来越深入。最早将Stewart平台运用于操作装置的是Minskey[3],随后,澳大利亚学者Hunt教授于1978年提出,将并联机构运用于工业机器人结构[4],从而推动机器人产业的发展。由于我国工业起步较晚,导致六自由度平台的研究也相对薄弱,早期六自由度并联机构是从国外引进的,主要是运用在飞行模拟器上[5-6]。我国在机器人机构上的运用并联机构是1991年,当时燕山大学设计的第一并联机器人样机上采用了这一结构;次年,哈尔滨工程大学率先研制出的六自由度船舶运动模拟器通过国家鉴定[7]。六自由度液压运动平台在舰船上也得到了充分的运用,作为“三位一体”的海上舰船是现代军事领域的重要组成部分[8],因其工作环境的特殊性,需要在下水之前对其进行海上航行的动态模拟。目前,我国采用的就是利用Stewart平台搭建的并联多自由度摇摆平台[9]。
目前,针对并联Stewart平台的研究,主要是围绕结构优化、数学建模、工作特性及运动策略等方面。本课题来源于与高校合作,本文主要运用仿真软件对运动学和动力学、运动平台结构设计、关键部件等进行仿真分析研究,对研制六自由度平台具有重大的指导意义和实际应用价值。
1 平台结构设计和分析 1.1 设计参数1)负载指标
六自由度平台上面双功能桥梯是平台的负载;
负载总重5 t(不包括运送的货物重量);
负载的重心偏移量(以六自由度平台的中心为中心)为0.25 m,中心高(以平台上平面为基准)不大于0.5 m;
上平面大小:φ2 500 mm;
下平面大小:根据设计需求确定。
2)运动指标
六自由度液压运动平台应满足如表1所示运动指标,且每次运动最长时限为30 min。
|
|
表 1 六自由度液压运动平台的运动指标 Tab.1 Platform movement index |
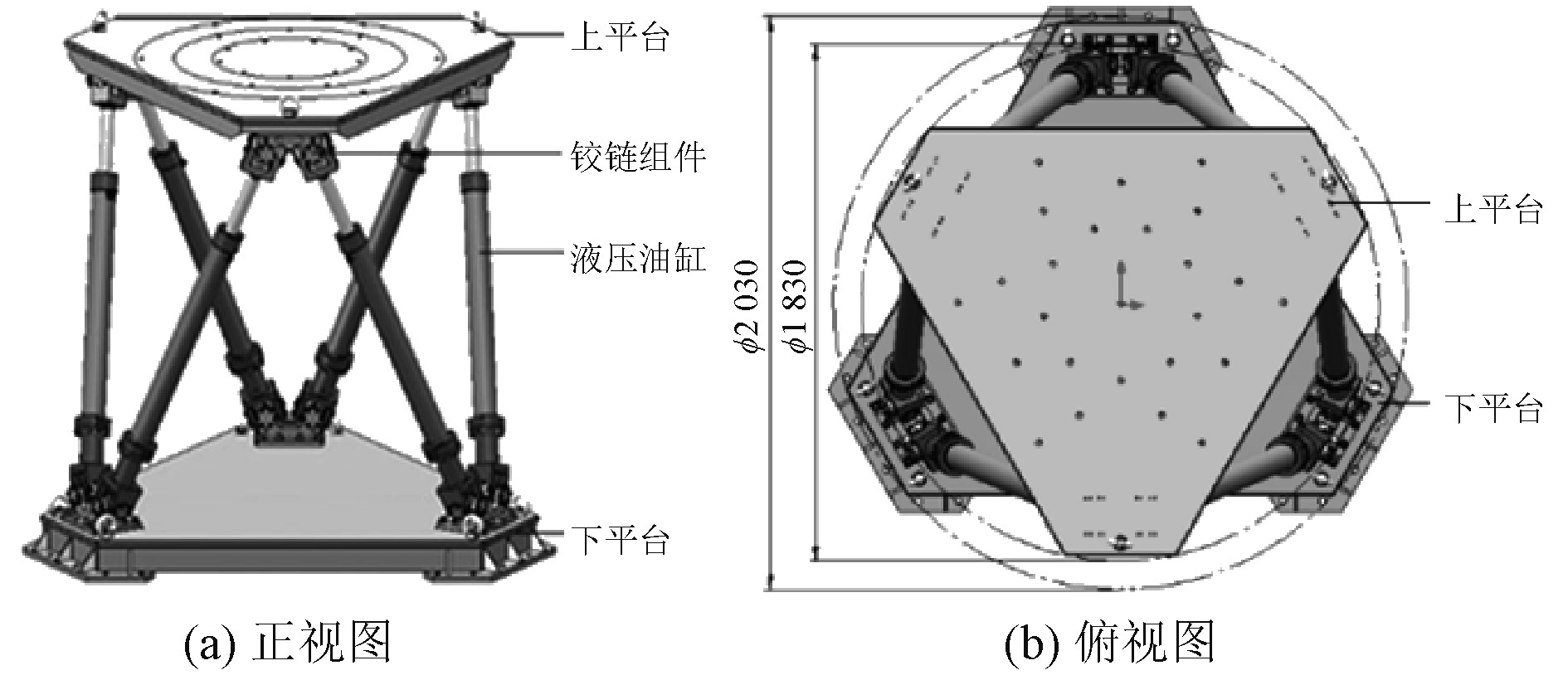
六自由度液压平台主要由上平台、下平台、液压油缸和铰链组件等部分组成,其结构如图1(a)所示,上平台随油缸运动,称之为动平台,下平台起支撑固定作用,称之为静平台。上、下平台通过6组液压油缸上下两端铰链组件相连接,上、下平台的铰接点均匀分布在大小不同的圆上,构成六边形。上平台外缘接于直径1 830 mm的圆,为了保证台体结构的稳定,同时尽量减少运动过程中活塞杆的伸缩量,使下平台外缘接于直径2 030 mm的圆,运动过程中承载物的重心位置投影始终在下平台的框架之内。由于上平台承载物重心位置的不确定性,如图1(b)所示。初始状态下,上、下平台的相对最小高度为1 750 mm,相对最大高度为2 050 mm。
|
图 1 六自由度液压平台体结构组成 Fig. 1 Structure composed of six degrees of freedom hydraulic platform |
6组液压油缸的移动副作为输入,推动6组活塞杆协调动作,使上平台灵活实现6个自由度的运动,从而使动平台在空间中呈现不同的位置和姿态。支座分别与上、下平台螺栓连接,其6个自由度被完全限制;十字节起到连接上、下平台与液压组件的作用,其自身的自由度对台体的整体自由度无影响,因此在计算过程中采用2个旋转自由度的万向节铰接点进行替代。把台体看作是由1个上平台、1个下平台、6组活塞杆和6组液压缸组成的简单运动机构,零件总数为14。
已知上平台与活塞杆构成6个万向节铰接点、下平台与液压缸构成6个万向节铰接点、活塞杆与液压缸构成6个移动副,且每个万向节铰接点限制4个自由度、每个移动副限制5个自由度,因此,台体的自由度为:
| $F = 6n - 4{p_1} - 5{p_2}=6 \times 14 - 4 \times 12 - 5 \times 6 = 6{\text{。}}$ | (1) |
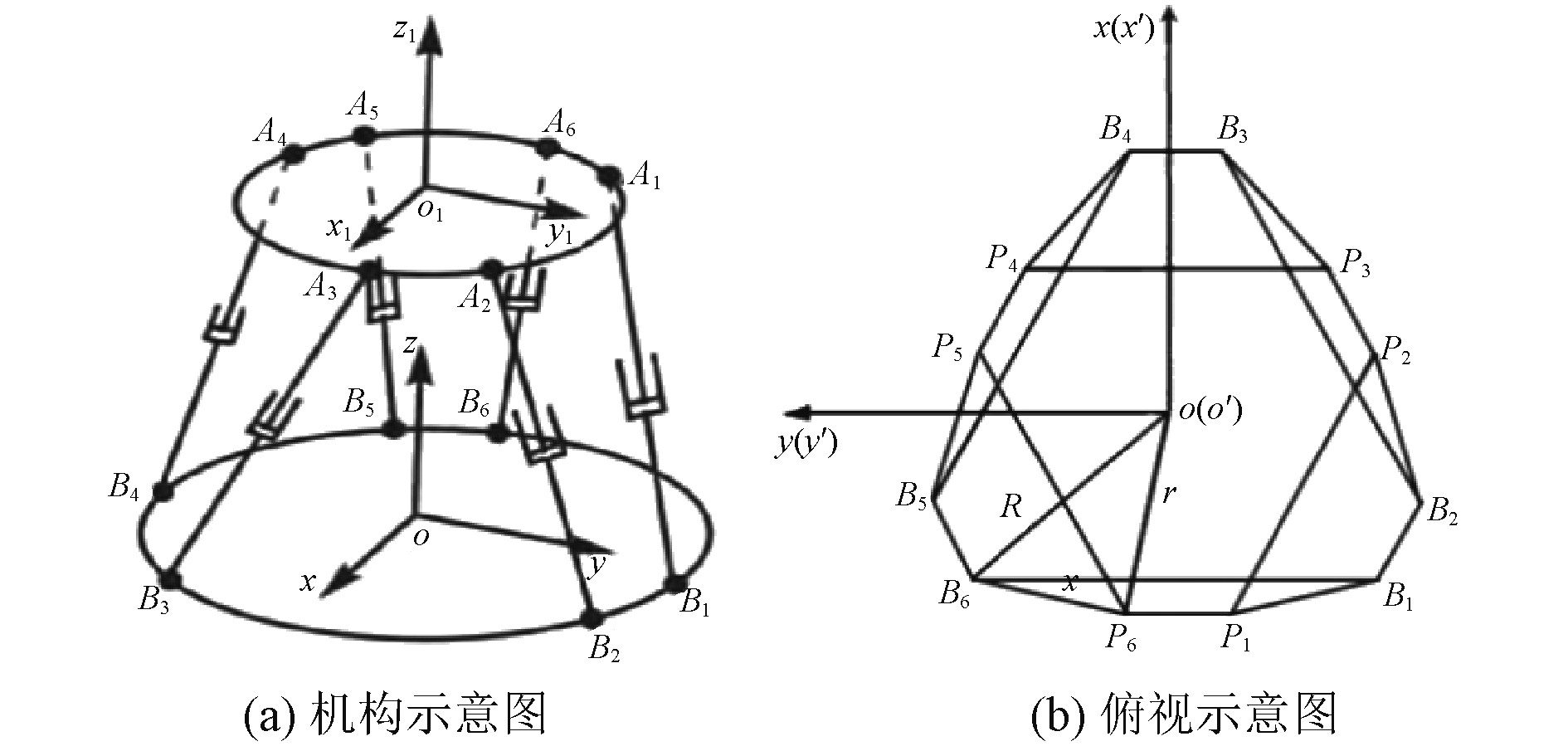
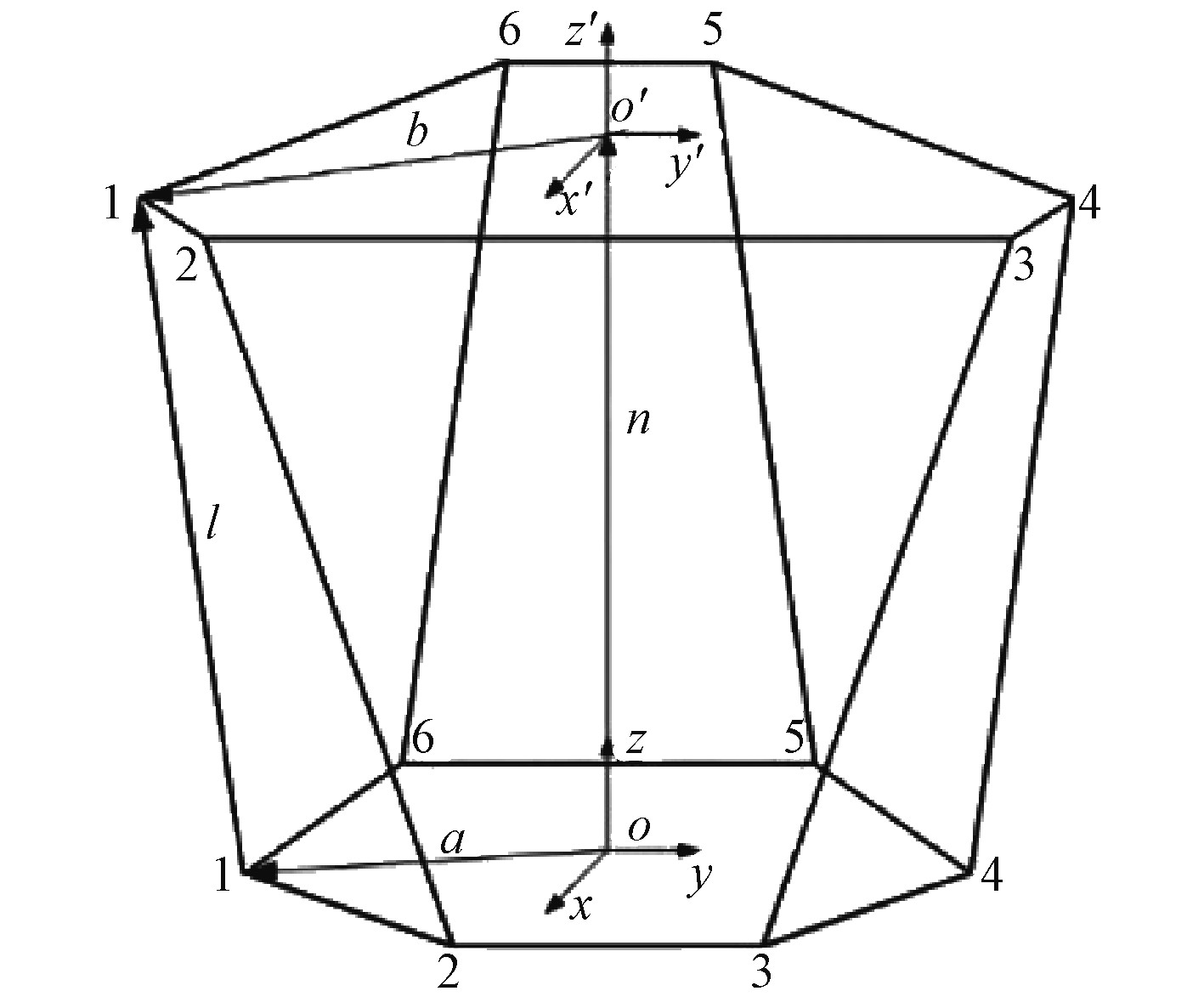
为了完成速度、加速度、受力分析、工作空间分析等工作,建立机构的坐标系如图2所示。该坐标系分为动坐标系和静坐标系,其中动坐标系OˊXˊYˊZˊ原点Oˊ位于动平台中心,而静坐标系OXYZ原点O位于静平台中心。
|
图 2 六自由度运动平台结构简图 Fig. 2 Structural diagram of a six-degree-of-freedom motion platform |
平台初始零位时,坐标轴OZ//OˊZˊ,OY//OˊYˊ,OZ与OˊZˊ重叠,当动平台位姿发生改变时,动平台位姿可用
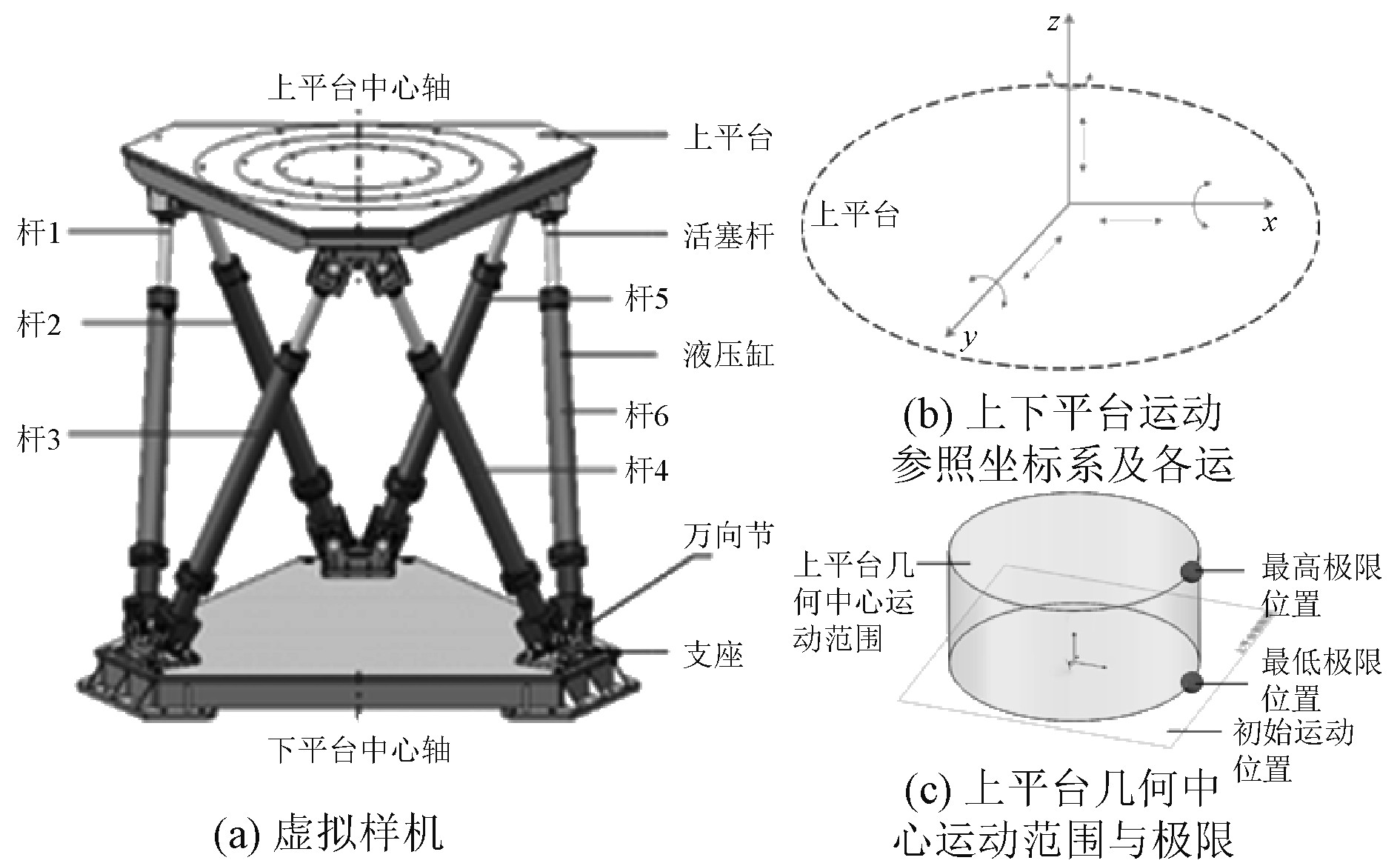
根据六自由度运动平台结构,在Soldworks Mottion中建立六自由度平台虚拟样机如图3(a)所示。从机构学上来分析,平台机构的六组液压油缸的伸缩运动是相互独立的,整个平台的运动具有6个自由度。建立动平台运动参照坐标系及各运动如图3(b)所示。技术参数动平台几何中心的x,y,z向最大位移分别为±300 mm,±300 mm和+300 mm,则动平台几何中心的标准运动范围模拟为底面直径600 mm,高300 mm的圆柱,如图3(c)所示。圆柱体的边缘即是上平台几何中心的运动极限位置。
|
图 3 虚拟样机 Fig. 3 Virtual prototype |
坐标变换矩阵结构为3×3,则有:
| ${{{H}}_{3 \times 3}} = \left[ {\begin{array}{*{20}{c}} {{C_\alpha }{C_\beta }}&{{C_\alpha }{S_\beta }{S_\gamma } - {S_\alpha }{C_\gamma }}&{{C_\alpha }{S_\beta }{C_\gamma } + {S_\alpha }{S_\gamma }} \\ {{S_\alpha }{C_\beta }}&{{S_\alpha }{S_\beta }{S_\gamma } + {C_\alpha }{C_\gamma }}&{{S_\alpha }{S_\beta }{C_\gamma } - {C_\alpha }{S_\gamma }} \\ { - {S_\beta }}&{ - {S_\beta }}&{{C_\beta }{C_\gamma }} \end{array}} \right]{\text{。}}$ | (2) |
其中cos简写为C,sin简写为S。
上式称为欧拉变换矩阵,则空间坐标变换公式也可以表示为:
| $O{P_{3 \times 1}} = {H_{3 \times 3}} \times O'{P'_{3 \times 1}} + OO'{\text{,}}$ | (3) |
其中
伸缩后杆长为:
| $ {L_i} = {\left[ {{{\left( {{x_i} - {x_{bi}}} \right)}^2} + {{\left( {{y_i} - {y_{bi}}} \right)}^2} + {{\left( {{z_i} - {z_{bi}}} \right)}^2}} \right]^{1/2}}{\text{,}} $ | (4) |
其中,
六自由度平台的正解方程组为:
| $ \begin{array}{l} {f_i}(\alpha ,\beta ,\gamma ,a,b,c)=\\ {\left[ {{{\left( {{x_i} - {x_{bi}}} \right)}^2} + {{\left( {{y_i} - {y_{bi}}} \right)}^2} + {{\left( {{z_i} - {z_{bi}}} \right)}^2}} \right]^{1/2}} - {L_i} = 0{\text{。}} \end{array} $ | (5) |
其中,
借助Matlab编程计算出平台的正解。
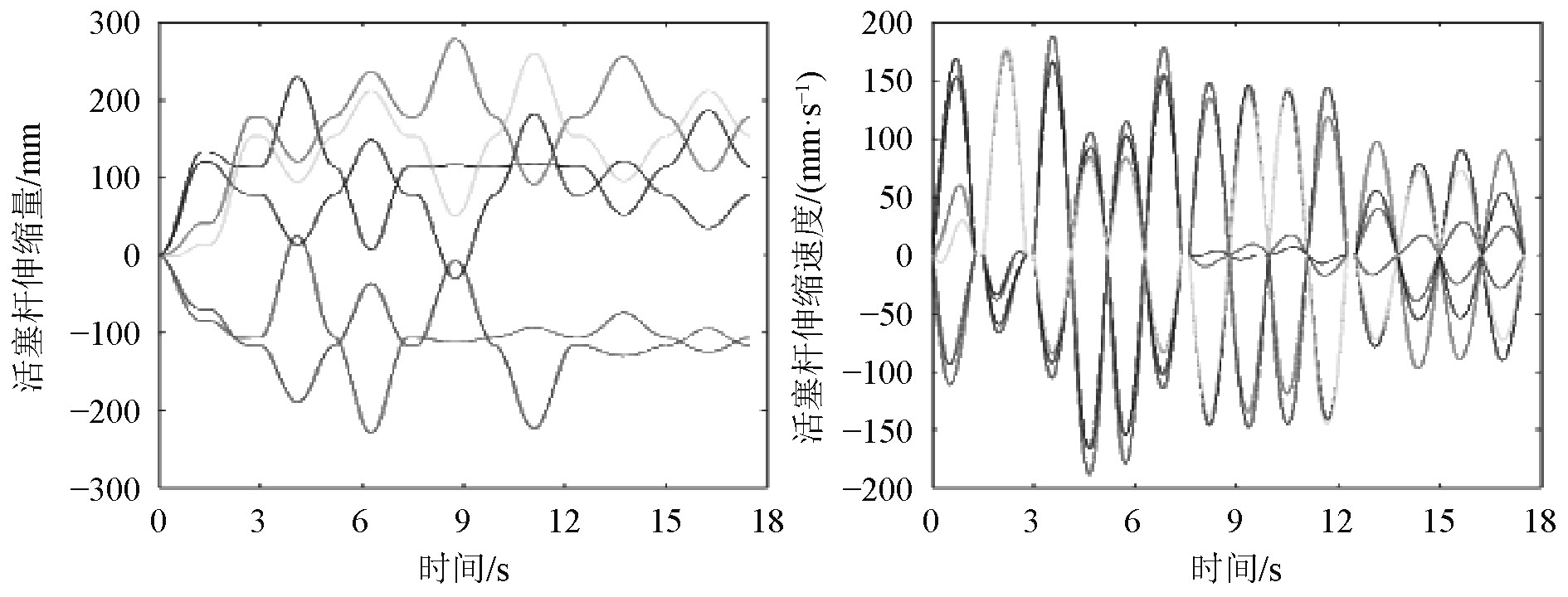
2.1 至最低、最高极限位置运动学计算台体开始运动时,拟定上平台的初始运动平面距离下平台的垂直距离为1 750 mm,1 695 mm,上、下平台的中心轴相重合,在Soldworks中测得上、下平台的初始位姿坐标及12个铰接点的坐标,并基于式1.1–1.3编写Matlab仿真程序代码,求出该活塞杆在不同阶段的伸缩量及伸缩速度如图4和图5所示。
|
图 4 至最低极限位置的杆长与速度变化 Fig. 4 Rod length and speed change to the lowest limit position |
|
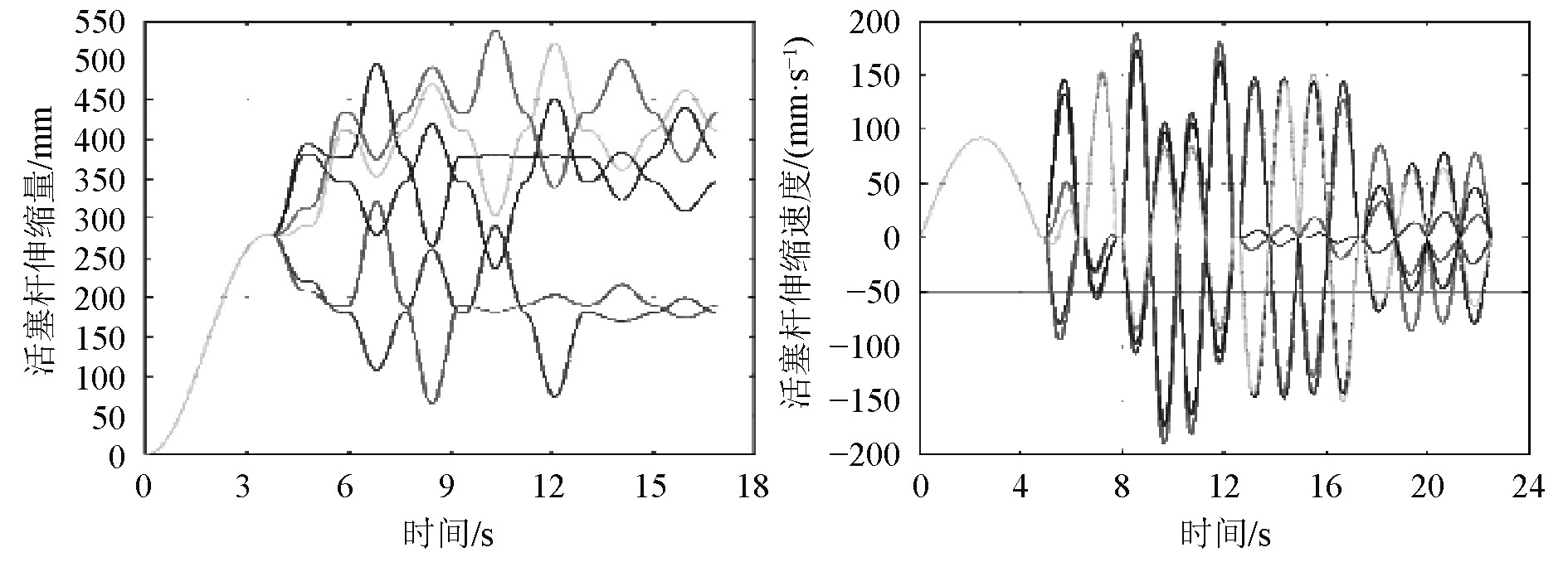
图 5 至最高极限位置的杆长与速度变化 Fig. 5 Rod length and speed change to the highest limit position |
由图4和图5可知,至最低极限位置的运动过程中,活塞杆的最大回缩量约为–229.8 mm,位于活塞杆4横摇–10°;最大伸长量约为280.7 mm,位于活塞杆1纵摇10°;最大回缩速度约为–188.7 mm/s,位于活塞杆4的横摇运动中;最大伸出速度约为188.7 mm/s,位于活塞杆4的横摇运动中;至最高极限位置的运动过程中,活塞杆相对于初始位置没有出现回缩现象,最大伸长量为540.2 mm,位于活塞杆1纵摇10°;最大回缩速度为–189.8 mm/s,位于活塞杆4的横摇运动中;最大伸出速度为189.8 mm/s,位于活塞杆4的横摇运动中。
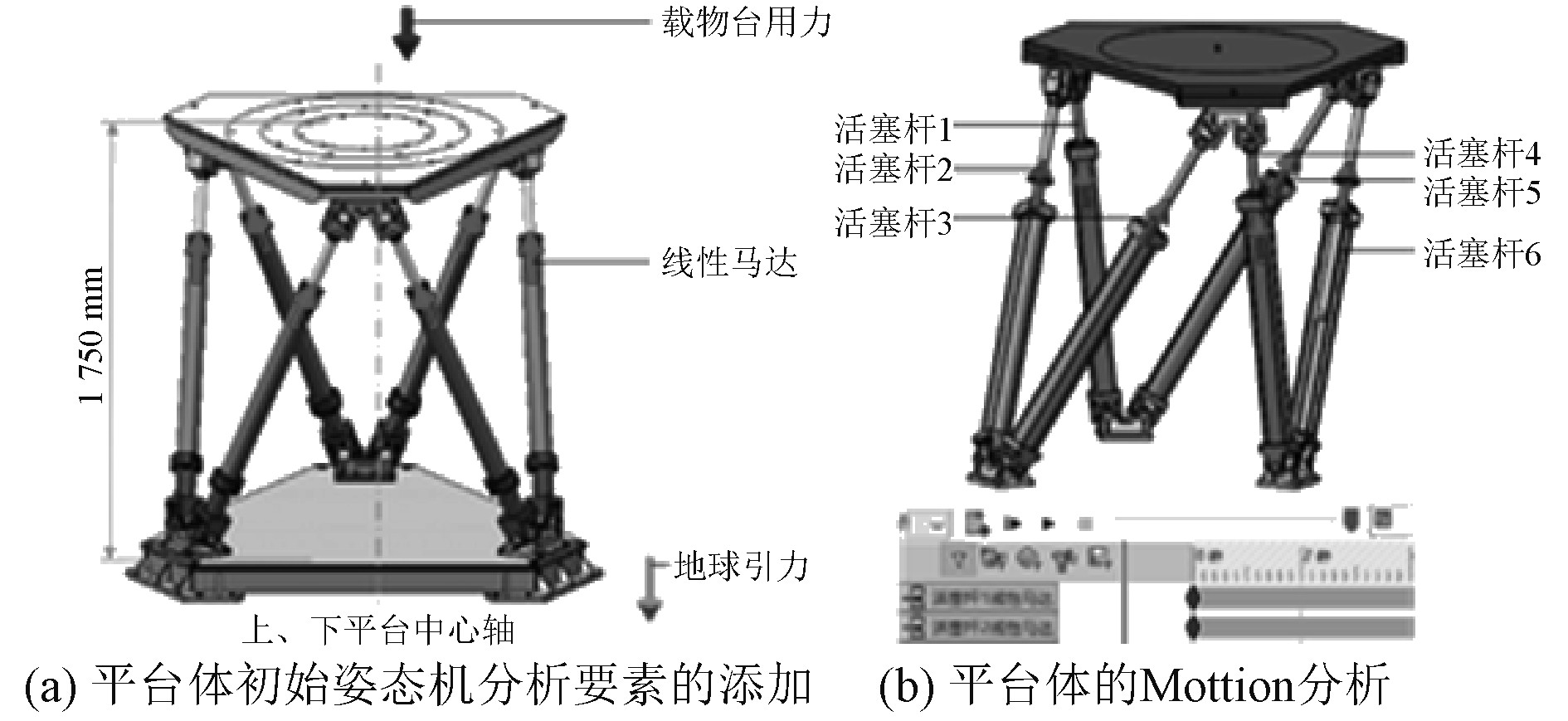
2.2 至最低、最高极限位置运动学仿真运动分析前的初始姿态,如图6(a)所示。拟定上平台的初始运动平面距离下平台的垂直距离为1 750 mm和1 695 mm,上、下平台的中心轴重合。在上平台表面添加60 kN的载物作用力,方向竖直向下,重心位置相对于上平台的上表面中心坐标分别偏移250 mm,250 mm,500 mm;考虑到上平台自重,添加50%的自重余量,将上平台质量设置为1 t,并添加地球引力,方向竖直向下。活塞杆与液压缸之间设为同心约束;万向节与活塞杆、万向节与液压缸之间设铰接约束;底部支座设为固定,以模拟下平台的作用;锁定顶部支座与上平台之间的相对位置;对上平台不做出单独约束以防止运动过程中发生冗余。将位置姿态反解计算出的活塞杆伸缩量数据输入线性马达,线性马达的伸缩量随时间变化如图6(b)所示。
|
图 6 平台体运动分析 Fig. 6 Analysis of platform body motion |
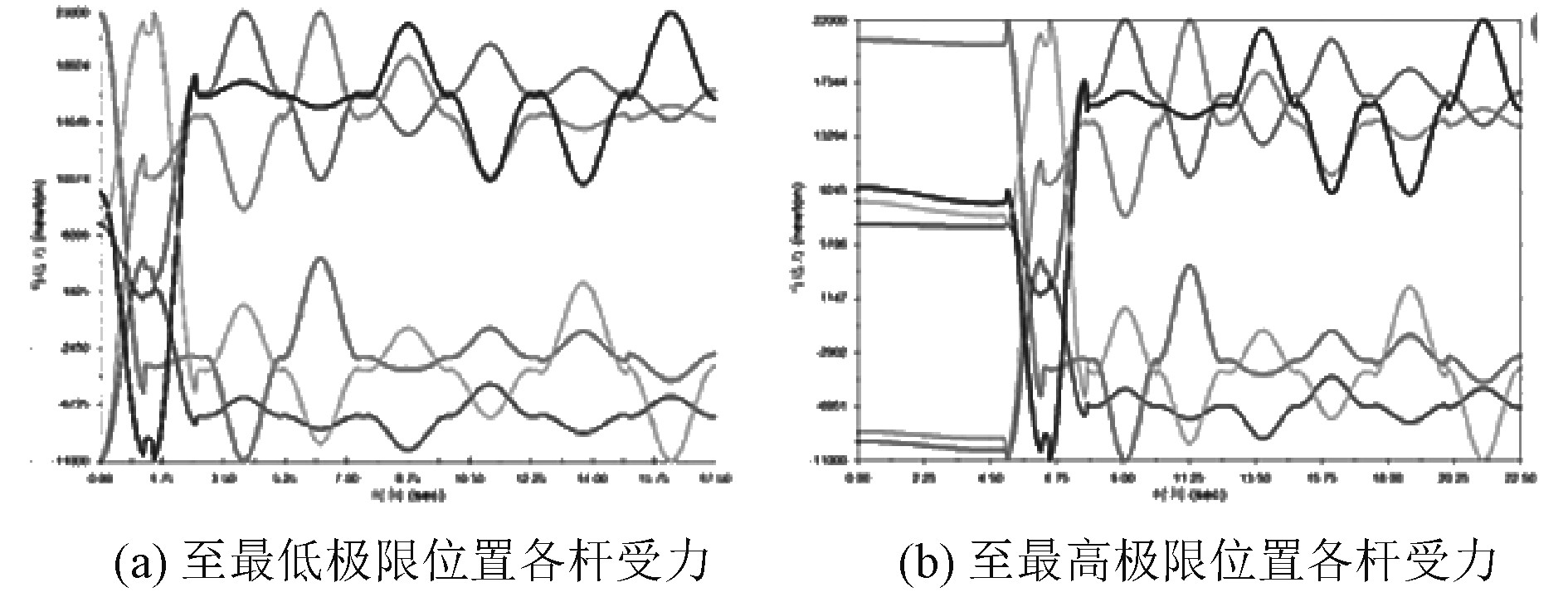
由图7(a)可知,上平台运动所需的最大推力发生在活塞杆2上,在上平台的横摇过程中,活塞杆2释放的推力急速增大,当上平台横摇10°时,活塞杆2回缩191.0 mm,输出推力最大,为26 383 N。同理,上平台的最大拉力发生在活塞杆1上,为–9955 N,对应上平台纵摇10°,对比运动学计算结果可知,此时活塞杆具有最大伸长量280.7 mm。
|
图 7 至极限位置各杆受力 Fig. 7 The force of pole to the limit position |
由图7(b)可知,上平台运动所需的最大推力发生在活塞杆2上,在上平台的横摇过程中,活塞杆2释放的推力急速增大,当上平台横摇10°时,活塞杆2伸长107.9 mm,其输出的推力最大,为26 117 N。同理,上平台的最大拉力发生在活塞杆1上,为–9392,对应上平台纵摇10°,对比运动学计算结果可知,此时活塞杆具有最大伸长量540.2 mm。
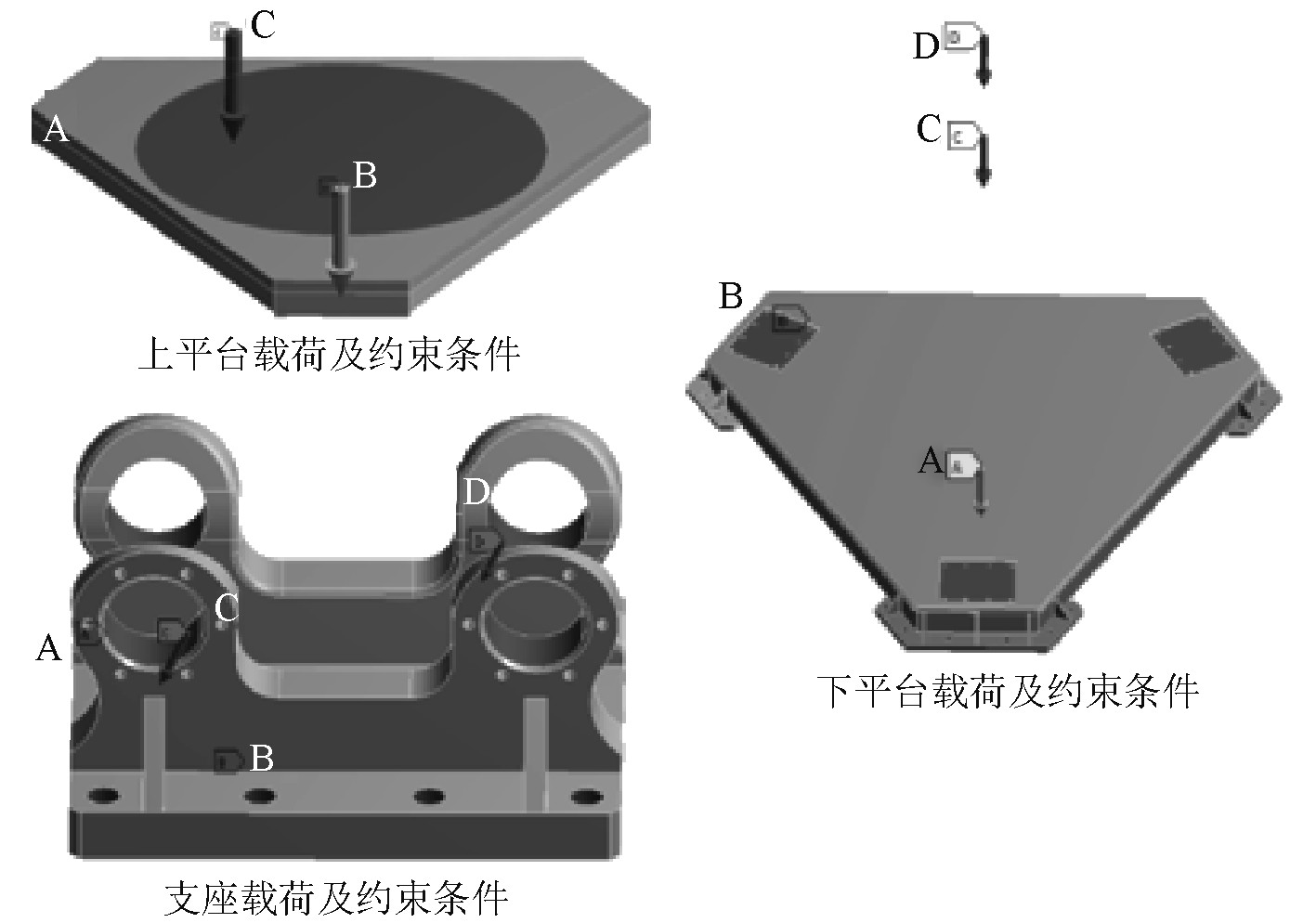
根据分析结果生成每个线性马达输出的马达力图解如图8和图9所示。
|
图 8 关键部件载荷及约束条件 Fig. 8 The load and constraints of key components |

|
图 9 关键部件有限元分析结果 Fig. 9 Results of finite element analysis of key components |
结合运动学计算与动力学仿真结果,得到台体的最终运动参数如表2所示。
|
|
表 2 台体最终运动参数 |
因为该组核心部件的材料均选用Q345,其屈服极限
误差分析的目的为根据上、下平台的位姿精度要求确定原始误差的范围,从而为铰链组件以及液压组件的设计提供设计依据。影响上平台的运动精度主要包括安装误差、定位误差及传动误差等,在只考虑几何误差的情况下,台体模型的复杂性对其运动精度的影响不大,因此只考虑定位误差及传动误差。分别将上平台的铰接误差记为
|
图 10 误差模型 Fig. 10 The model of error |
平台的位姿用向量表示为
参考相关文献,得到平台位姿误差计算公式:
| $ \delta E = {J_e}^{ - 1}\delta l + {J_m}^{ - 1}{J_m}\delta M {\text{。}} $ | (4.1) |
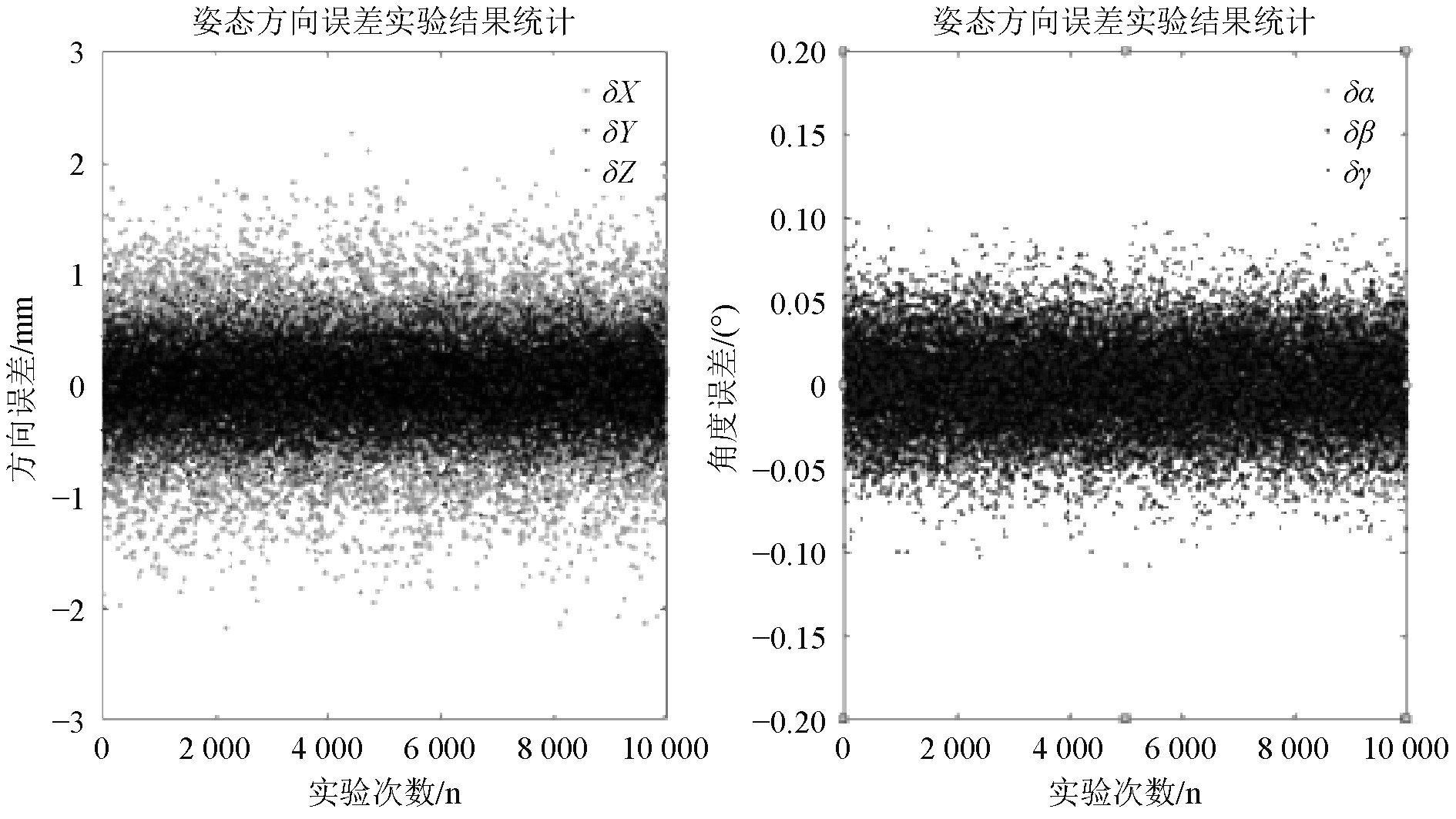
综合考虑设计制造公差、装配公差等,设铰接点误差范围为–0.5~0.5 mm,设活塞杆轴向误差范围为–0.2~0.2 mm,在设定范围内按照正态分布法则随机选取12×3=36个数据点记为12个铰接点的坐标误差,并随机选取6个数据点记为6根活塞杆的轴向误差。选取10 000组原始误差进行误差分析。其结果如图11所示。
|
图 11 平台位姿误差分布图 Fig. 11 Error distribution map of platform pose |
由图11可知,平台的姿态方向误差
通过对平台的结构、运动学及液压系统等几个方面的研究,运用SolidWorks与Matlab共同进行仿真计算和建模,从而有效地缩短产品的设计周期。同时,通过对系统的仿真分析,验证了系统整体结构设计的合理性。该模型中各性能指标都能达到设计要求,为六自由度运动平台的开发提供了良好的理论与技术支持。
此外,通过仿真动画直观地观察上平台的运动过程,把六自由度液压运动平台的运动学计算、参数优化等组合到一起,这是虚拟与现实相结合的先进性的体现,不仅能够为企业降低设计成本,同时还能够有效地提升设计人员的工作效率,为企业创造更多的经济效益。
| [1] |
黄晓敏. 基于matlab的六自由度平台研究[D]. 广州: 华南理工大学, 2013 HUANG Xiaomin. 6-DOF Platform research based on Matlab[D]. Guang zhou: South China University of Technology, 2013 |
| [2] |
曲中英, 翁正新. 基于Simulink的Stewart平台仿真研究[J]. 计算机仿真, 2013, 22(4): 264-268. QU Zhong ying, WENG Zheng xin. Stewart platform simulation research based on simulink[J]. Computer Simulation, 2013, 22(4): 264-268. |
| [3] |
MINSKY M. Mani pulator design vignettes[J]. MIT Al Memo No. 267. MITAI Laboratory 1972.
|
| [4] |
HUNT. Klnematic Geometry of Mechanis[M]. Oxford: Clarendon Press, 1978.
|
| [5] |
王晓明. 基于六维并联机构的空间光学载荷微振动环境模拟及指向稳定技术研究[D]. 长春: 中国科学院大学(中国科学院长春光学精密机械与物理研究所), 2019. WANG xiao ming. Research on micro-vibration environment simulation and pointing stability technology of the space optical payload based on six-DOF parallel mechanism[D]. Changchun Institute of Optics, Fine Mechanics and Physics Chinese Academy of Sciences, 2019. |
| [6] |
张智涛. Stewart类六自由度并联机构的研制[D]. 天津: 天津大学, 2009. ZHANG zhi tao. The research and manufacture of stewart parallel mechanism with 6-DOF[D]. Tian jin: Tianjin University, 2009. |
| [7] |
王鷁, 赵琳, 沈晓蓉, 等. 潜艇航行训练模拟器视景系统的设计与实现[J]. 哈尔滨工程大学学报, 2001, 22(2): 34–36. WANG Yi, ZHAO Lin, SHEN Xiao rong et al., Journal of Harbin Engineering University, 2001, 22(2). 34–36. |
| [8] |
陈雪丽, 张成义. 基于六自由度运动平台的潜艇模拟器的研究与仿真[J]. 舰船科学技术, 2001, 40(10A): 19-21. CHEN xue li, ZHANG cheng yi. Research and simulation of submarine simulator based on six degree of freedom motion platform[J]. Ship Science and Technology, 2001, 40(10A): 19-21. |
| [9] |
孟晓烨. 并联六自由度机构在舰船装备动态环境模拟中的应用[J]. 舰船科学技术, 2017, 39(4A): 67-69. MENG Xiao-ye. Application of parallel six degree of freedom mechanism in dynamic environment simulation of ship equipment[J]. Ship Science and Technology, 2017, 39(4A): 67-69. |
 2020, Vol. 42
2020, Vol. 42
