随着视频会议、云计算、物联网等新兴业务的快速发展,光纤通信容量的需求呈爆发式增长。光纤通信具有大容量、高速率、抗电磁干扰等优点,但同时也存在一些问题,如光电转换器件带宽有限、光纤色散及非线性效应等。这些因素会导致信号劣化,影响整体性能,并且随着通信速率的不断提升,这些问题会愈发严重。因此,研究人员提出了各种手段来解决这些问题,如利用先进的调制格式来提高频谱效率[1],以及在发射机和接收机端添加一系列的算法,补偿信号受到的各种损伤[2-3]。
最近,一种针对星座图的编码技术——星座整形,得到了广泛关注[4-5]。星座整形包括几何整形和概率整形。其中,概率整形由于只改变星座点概率分布而不改变星座点位置形状,应用更加灵活,对提升系统容量、改善误码性能等都有促进作用[6]。
本文阐述概率整形的原理,并通过互信息、误码率与信噪比的关系曲线,展示概率整形对系统性能的提升作用。搭建了10Gbaud 16QAM相干探测仿真系统,重点探究了概率整形在带宽受限情况下对系统误码性能和带宽容忍度的影响。
1 概率整形技术 1.1 概率整形原理概率整形的基本思想是改变各星座点的概率分布,对幅度较小的星座点赋以较高的概率,而对幅度较大的星座点赋以较小的概率。以16QAM信号为例,整体信号呈高斯分布,如图1所示。

|
图 1 概率整形前后星座图对比 Fig. 1 Comparison of constellations before and after probabilistic shaping |
由于星座点外圈之间的间隔相对于内圈之间更窄,在低信噪比条件下,外圈是误码高发区。而概率整形恰好是降低外圈星座点概率,增大内圈星座点概率。即增大误码性能好的星座点概率,而减小误码性能差的星座点概率,从而提升误码性能。此外,经过概率整形处理后,整体信号的平均功率得到降低,有助于解决光通信系统中的非线性效应带来的功率限制问题。
因此,通过概率整形编码,系统更接近实际信道特性,从而带来整形增益,使系统容量接近香农极限。
1.2 AWGN信道中概率整形性能分析以均匀分布和经过概率整形的16QAM信号为例,通过对比两者在加性高斯白噪声(additive white gaussian noise,AWGN)信道中的性能,来直观展示概率整形技术带来的性能改善。概率整形普遍使用的概率分布为麦克斯韦-玻尔兹曼(Maxwell-Boltzmann)分布,如下式:
| $ {P_X}\left( {\mathop x\nolimits_i } \right) = \frac{1}{{\sum\limits_{k{\rm{ = 1}}}^M {\mathop e\nolimits^{{\rm{ - }}v\mathop x\nolimits_k^2 } } }} \cdot \mathop e\nolimits^{ - v\mathop x\nolimits_i^2 } {\text{。}} $ | (1) |
其中:
互信息(Mutual Information,MI)是信息论中的一种重要的信息度量,表征一个随机变量中包含关于另一个随机变量的信息量,计算公式为:
| $ I\left( {X:Y} \right) = H(X) - H(X|Y) {\text{。}} $ | (2) |
其中:
按式(1)所述概率公式,求
| $ \left| \begin{gathered} {\rm{0}}{\rm{.0240 \;\; 0}}{\rm{.0535 \;\; 0}}{\rm{.0535 \;\; 0}}{\rm{.0240}} \\ {\rm{0}}{\rm{.0535 \;\; 0}}{\rm{.1190 \;\; 0}}{\rm{.1190 \;\; 0}}{\rm{.0535}} \\ {\rm{0}}{\rm{.0535 \;\; 0}}{\rm{.1190 \;\; 0}}{\rm{.1190 \;\; 0}}{\rm{.0535}} \\ {\rm{0}}{\rm{.0240 \;\; 0}}{\rm{.0535 \;\; 0}}{\rm{.0535 \;\; 0}}{\rm{.0340}} \\ \end{gathered} \right| {\text{,}} $ |
而当
| $ \left| \begin{gathered} {\rm{0}}{\rm{.0071 \;\; 0}}{\rm{.0349 \;\; 0}}{\rm{.0349 \;\; 0}}{\rm{.0071}} \\ {\rm{0}}{\rm{.0349 \;\; 0}}{\rm{.1731 \;\; 0}}{\rm{.1731 \;\; 0}}{\rm{.0349}} \\ {\rm{0}}{\rm{.0349 \;\; 0}}{\rm{.1731 \;\; 0}}{\rm{.1731 \;\; 0}}{\rm{.0349}} \\ {\rm{0}}{\rm{.0071 \;\; 0}}{\rm{.0349 \;\; 0}}{\rm{.0349 \;\; 0}}{\rm{.0071}} \\ \end{gathered} \right| {\text{。}} $ |
利用Matlab软件仿真上述2种概率分布信号与均匀分布信号在AWGN信道中的性能,得到不同信噪比条件下,互信息曲线如图2所示。

|
图 2 三种信号在不同信噪比下的互信息曲线 Fig. 2 The mutual information curves of three signals at different SNR |
可以看出,3种信号的互信息都会随着信噪比的增加而增加,最终稳定在信源熵值。高信噪比时,由于均匀分布信号的信源熵值最大,故其对应的互信息最大,而在低信噪比情况下,概率整形能提供更大的互信息。在不同信噪比区间,都会对应一种整形因子
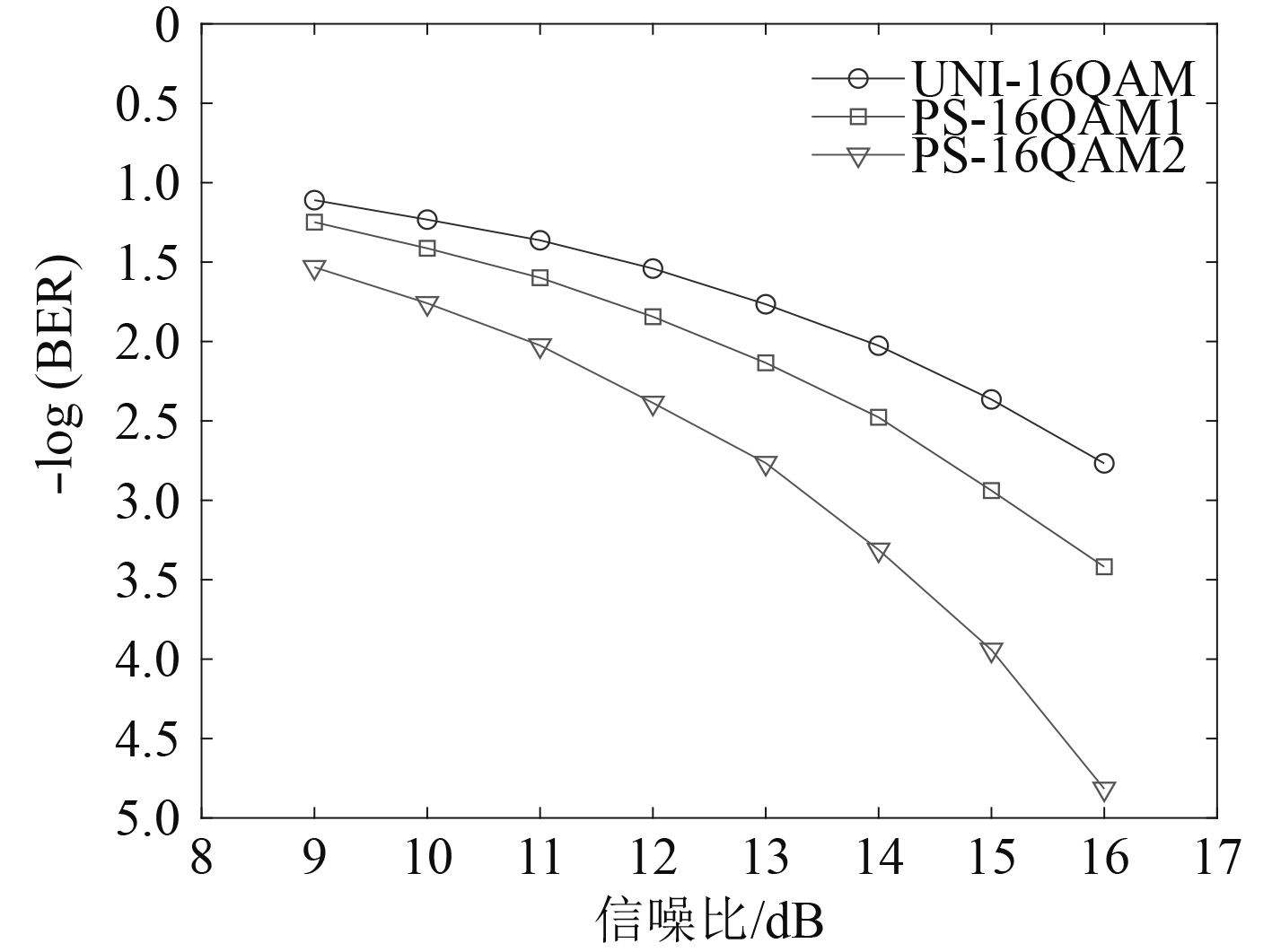
上述3种信号通过AWGN信道,信噪比与误码率关系曲线如图3所示。结果表明,经过概率整形后的信号对比均匀信号有更好的误码性能,且随着整形程度的增大,误码性能也会进一步提升。
|
图 3 三种信号在不同信噪比下的误码率曲线 Fig. 3 The BER curves of three signals at different SNR |
在理论研究中,通常假设系统各部分都是理想的,然而实际光纤通信系统受各方面因素作用,呈现为一个带宽受限的系统,因此有必要研究在带宽受限条件下概率整形能够带来的性能改善效果。
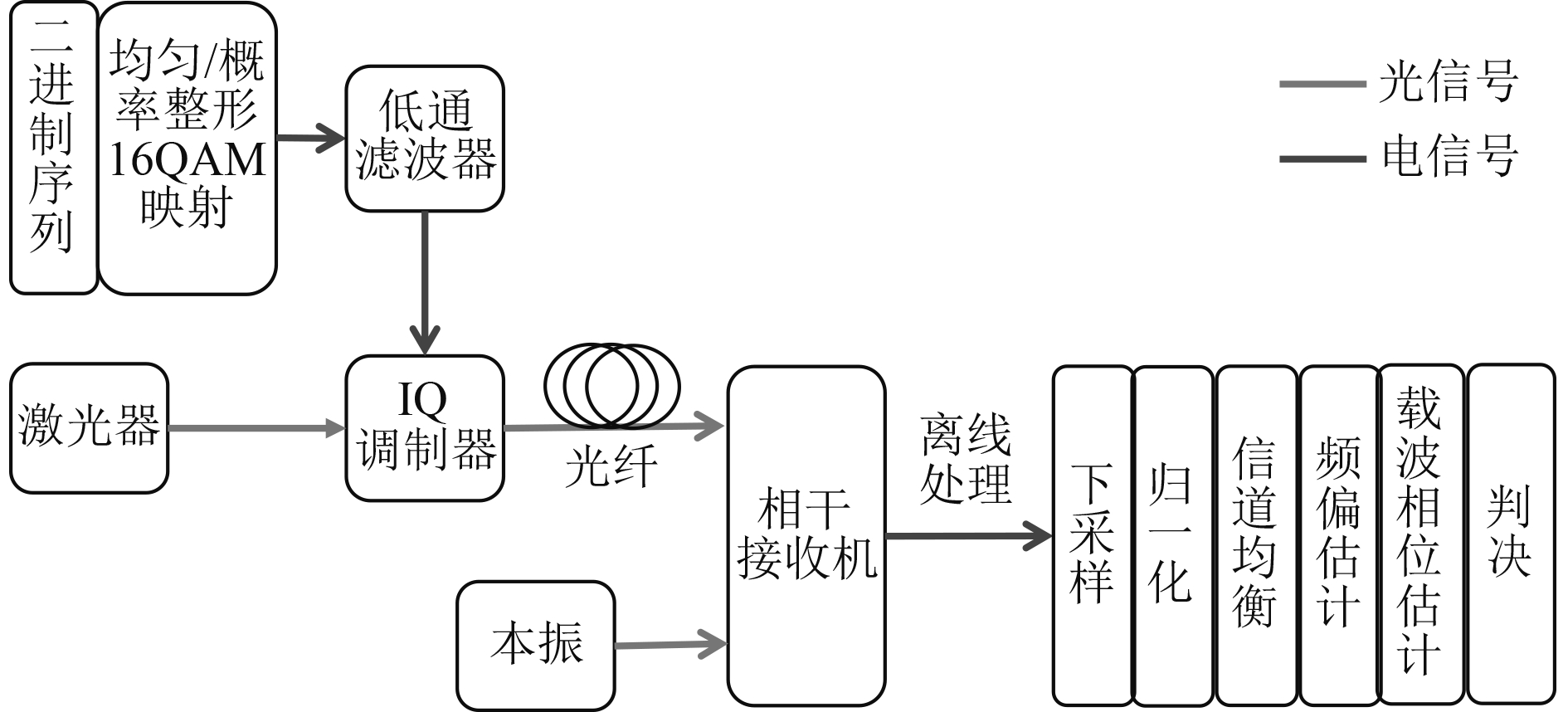
2.1 系统模型本文通过Matlab和VPI进行联合仿真,利用Matlab生成均匀分布和概率整形的信号,并在接收端对接收到的信号进行离线处理,并VPI中搭建整体光纤通信系统。整体系统框图如图4所示。同样以16QAM信号为例,由Matlab生成的10Gbaud基带均匀/概率整形16QAM信号经过一低通滤波器后,通过IQ调制器调制到光上,这里的低通滤波器用来模拟电光调制器的带宽限制。通过光纤传输后的信号光与本振光一起送入零差相干接收机进行解调。解调后的信号送入Matlab进行相应的离线处理。系统中,相关参数设置如表1所示。
|
|
表 1 仿真系统中各参数设置 Tab.1 General parameter table of simulation system |
|
图 4 系统框图 Fig. 4 The system diagram |
按表1所述设置相应参数,首先固定滤波器带宽为8 GHz,得到两信号误码率与光信噪比的关系曲线如图5所示。可以看出,在带限条件下,概率整形后的信号同样会带来误码率性能的提升,在3.8×10–3的误码门限下,能提供2 dB左右的性能提升。

|
图 5 误码率与光信噪比关系曲线 Fig. 5 The BER curves of two signals at different OSNR |
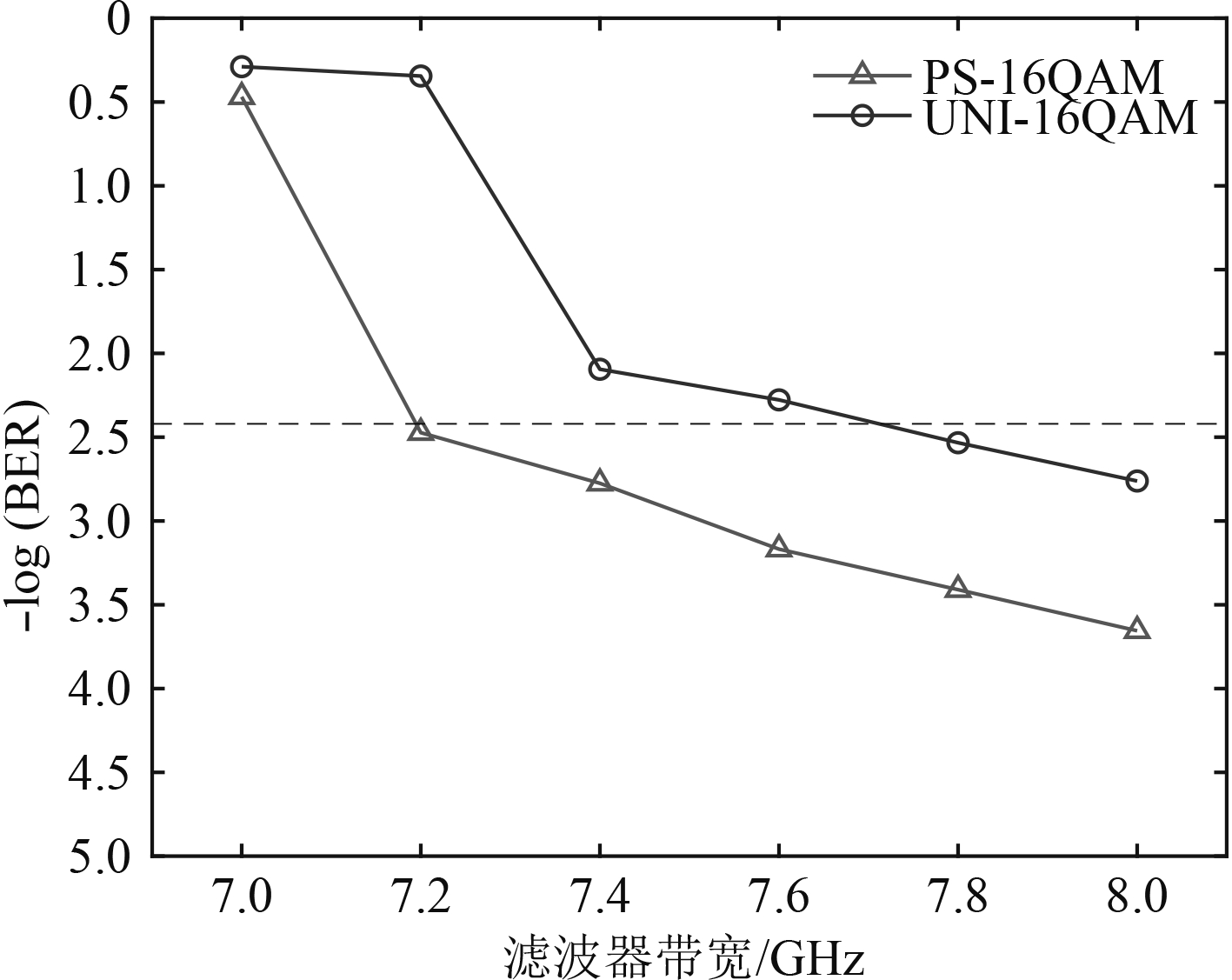
固定光信噪比为21 dB,调整滤波器带宽在7~8 GHz的范围内变化,得到两信号误码率与滤波器带宽的关系曲线如图6所示。可以看到,经过概率整形后的信号能够容忍更窄的带宽限制,在3.8×10–3的误码门限下,相较均匀分布信号能提供500 MHz左右的带宽容忍度提升。
|
图 6 误码率与滤波器带宽关系曲线 Fig. 6 The BER curves of two signals at different filter bandwidth |
概率整形是提升整体通信系统性能的一项重要技术。本文首先介绍概率整形的基本原理,并以AWGN信道为例分析其对通信系统的性能改善效果。随后,重点研究了概率整形在带限条件下的效果,通过Matlab与VPI进行了联合仿真。仿真结果表明,在带限光纤通信系统中,概率整形对系统误码性能以及带宽容忍度都有提升作用。
| [1] |
WINZER P J and Neilson D T . From scaling disparities to integrated parallelism: a decathlon for a decade[J]. Journal of Lightwave Technology, 2019, 35(5): 1099–1115.
|
| [2] |
SEB J. Digital coherent optical receivers: algorithms and subsystems[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2010, 16(5): 1164-1179. DOI:10.1109/JSTQE.2010.2044751 |
| [3] |
HAMJA A, UDDIN M S, SULTANA J, et al. DSP aided chromatic dispersion reckoning in single carrier high speed coherent optical communications, 2013 International Conference on Electrical Information and Communication Technology (EICT), Khulna, 2014: 1-5.
|
| [4] |
BOCHERER G, STEINER F, SCHULTE P. Bandwidth efficient and rate-matched low-density parity-check coded modulation[J]. IEEE Transactions on Communications, 2015, 63(12): 4651-4665. DOI:10.1109/TCOMM.2015.2494016 |
| [5] |
ZHANG S, YAMAN F. Constellation design with geometric and probabilistic shaping[J]. Optics Communications, 2017, 409: S0030401817307538. |
| [6] |
RENNER J, et al. Experimental comparison of probabilistic shaping methods for unrepeated fiber transmission[J]. Journal of Lightwave Technology, 2017, 35(22): 4871–4879.
|
 2020, Vol. 42
2020, Vol. 42
