汽轮发电机组因其较高的性价比和运行可靠性,被广泛应用于陆地电厂。一般认为,电网有功功率平衡、频率稳定主要由原动机控制主导。关于汽发机组的动态特性和控制策略,国内外学者进行了丰富的研究。IEEE工作组以机理分析结合实验的方式建立了锅炉-汽轮机-发电机功率传动特性模型,并被后续大量陆地电厂机组运行实践所证实[1]。文献[2-3]总结了机组汽门、锅炉协调控制的主要方法,利用西北电网算例研究了电网频率在不同方法作用下的区别。文献[4]研究了大型汽发机组的中压调节阀控制对蒸汽参数及流量的影响。
随着对机组运行特性中非线性因素的认识不断深入,将系统模型在某一平衡点小邻域内近似线性化的控制律设计方法已被非线性控制思想取代。有学者基于状态反馈线性化方法,设计了具有多性能指标的非线性控制律[5-6],进而针对再热式汽发机组数学模型优化了控制律的鲁棒性[7]。文献[8-9]基于机组汽门调节特性设计了预测控制律。文献[10]在设计炉机网协调控制的基础上,重点关注了电网典型性能指标的优化。文献[11]从电网组网层面对发电机组进行优化配置,提升了网络运行的经济性。
相比于陆地电网,船舶电力系统具有孤网运行、工况变换频繁且负荷变化范围大的特点,特别是兆瓦级船用负载的应用,使汽发机组功率调节率受限的影响更为突出、在调节过程中发生的工作点偏移更为显著。因此,为增加反馈控制律设计对船舶电力系统暂态过程的契合度、提高机组运行稳定性,本文充分考虑汽轮机突加负载后汽缸、汽阀和锅炉系统的响应特性,在陆用汽发机组研究成果的基础上,建立考虑汽缸效率变化的船舶汽轮发电机组数学模型。接着,采用零动态方法设计汽门、锅炉协调控制律,并通过数值仿真,验证该控制方法对电网受扰后频率稳定的有效性。
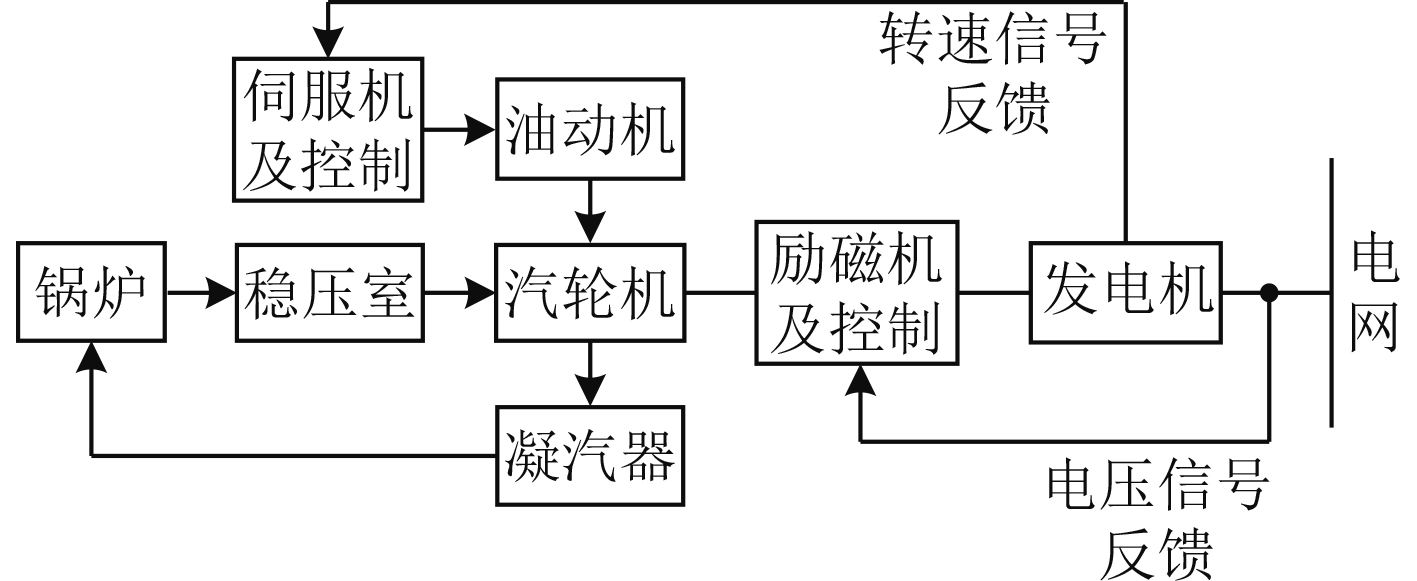
1 船舶汽轮发电机组建模汽轮发电机组由原动机、发电机及励磁系统组成。其中,油动机伺服系统接受机组转速信号反馈,进而控制汽阀、快速改变流量,并通过调节锅炉燃烧量改变工质蒸汽参数。机组连接结构如图1所示。
|
图 1 汽轮发电机组连接图 Fig. 1 Connection diagram of turbo-generator unit |
对于接入大电网的陆地电厂汽发机组而言,单机承载变化率通常较低,描述机组变负荷过程的数学模型通常忽略时间尺度较大的锅炉暂态。机组功率调节主要通过汽阀、励磁协调控制完成,汽缸容积效应时间常数
| $ \left\{ \begin{aligned} & \dot \delta = \omega - {\omega _0} {\text{,}}\\ & {T_J}\dot \omega = {P_m} - \frac{{{{E'}_q}{V_s}}}{{{{x'}_{d\Sigma }}}}\sin \delta - D(\omega - {\omega _0}) {\text{,}}\\ & {{T'}_{d0}}{{\dot E'}_q} = - {{E'}_q} + \frac{{{x_d} - {{x'}_d}}}{{{{x'}_{d\Sigma }}}}{V_s}\cos \delta + {E_f} {\text{,}} \\ & {T_H}{{\dot P}_m} = - {P_m} + {P_{m0}} + {u_P} {\text{。}} \end{aligned} \right. $ | (1) |
式中:δ为功角;ω为机组转速;
对于船舶电力系统分析而言,单机承载可能在较大范围内变化,此时主汽压调节过程不可忽略。当考虑汽压变化时,汽轮机实时有功功率
| $ {P_m} = {C_v}{p_T}{\eta _r} {\text{,}} $ | (2) |
| $ \left\{ \begin{array}{l} {T_{cv}}{{\dot C}_v} = - {C_v} + {u_{cv}} {\text{,}} \\ {T_G}{{\dot p}_T} = {G_B} - G {\text{,}} \\ {T_{GB}}{{\dot G}_B} = - {G_B} + {u_B} {\text{,}} \end{array} \right. $ | (3) |
| $ \left\{ \begin{array}{l} G = {k_{cv}}{C_v}\sqrt {{p_T} - {p_V}} {\text{,}} \\ {p_V} = {k_{pv}}{C_v}{p_T} {\text{。}} \end{array} \right. $ | (4) |
式中:
汽缸效率
| $ {\eta _r} = Ax_a^2 + B{x_a} + C {\text{,}} $ | (5) |
式中:
| $ \left\{ \begin{aligned} & {x_a} = \frac{u}{{{c_a}}} {\text{,}} \\ & \frac{1}{2}c_a^2 = \Delta h* = \frac{k}{{k - 1}}R{T_0}\left[1 - {\left(\frac{{{p_B}}}{{{p_T}}}\right)^{\frac{{k - 1}}{k}}}\right] {\text{。}} \end{aligned} \right. $ | (6) |
其中:
由于船舶电力系统大型用电负载的功率可与电站机组容量相匹敌,发电机组转速在遭遇诸如负荷突然离并网的大扰动后可能发生明显变化,进而导致效率
综合式(1)~式(6),即可得到计及汽压、效率变化的汽轮发电机组状态方程。为突出研究重点,考虑到同步发电机励磁控制的研究相对成熟,本文假定发电机采用性能优良的励磁控制器,使q轴暂态电势
| $ G = {k_{cv}}{C_v}{p_T} - {k_{cv}}{k'_{pv}}C_v^2{p_T} {\text{,}} $ | (7) |
式中
| $ \left\{ \begin{array}{l} {T_J}\dot \omega = {P_m} - {P_e} - D(\omega - {\omega _0}) {\text{,}} \\ {T_H}{{\dot P}_m} = - {P_m} + {C_v}{p_T}{\eta _r} {\text{,}} \\ {T_G}{{\dot p}_T} = - {k_{cv}}{C_v}{p_T} + {k_{cv}}{{k'}_{pv}}C_v^2{p_T} + {G_B} {\text{,}}\\ {T_{cv}}{{\dot C}_v} = - {C_v} + {u_{cv}} {\text{,}} \\ {T_{GB}}{{\dot G}_B} = - {G_B} + {u_B} {\text{。}} \end{array} \right.$ | (8) |
基于仿射非线性系统描述的非线性控制方法有若干种,不同方法对于控制目标各有侧重。其中,最优控制方法通过设计包含目标状态量集合的最优指标赋权矩阵,从而优化目标状态量集合在系统变工况过程中的暂态表现;鲁棒控制方法在系统模型中加入参数摄动或状态量扰动项,从而通过优化对应状态量的暂态指标抑制扰动。
而零动态控制方法直接关注系统外部动态,假定预期输出为零进而求解对应的系统输入。相比于最优控制和鲁棒控制,零动态方法契合于期望全程保持额定值的状态量调节,其设计过程较简明、物理意义清晰,适合用于设计汽发机组控制律。考虑式(8)所描述的汽轮机系统,设计零动态输出为转速、主汽压与额定值之差,以求得的输入信号进行动态控制,就可满足机组变负荷后的稳定需求,改善机组稳定水平。
2.2 控制律设计步骤由上节所确定的系统输出,有控制律设计步骤如下:
1)将系统模型式(8)改写为仿射非线性标准型式(9),系统输出记为
| $ {\dot {{x}}} = {{f}}({{x}}) + {{{g}}_1}({{x}}){u_1} + {{{g}}_2}({{x}}){u_2} {\text{,}} $ | (9) |
其中:
| $ {{x}}= \left[ \begin{array}{l} \omega \\ {P_m} \\ {p_T} \\ {C_v} \\ {G_B} \\ \end{array} \right]{\text{,}}\;\left\{ \begin{array}{l} {u_1} = {u_{cv}} {\text{,}} \\ {u_2} = {u_B} {\text{,}} \\ \end{array} \right.\;\;\;\left\{ \begin{array}{l} {y_1} = \omega - {\omega _0}{\text{,}} \\ {y_2} = {p_T} - {p_{T0}}{\text{,}} \end{array} \right. $ |
| $ {{f}}({{x}}) = \left[ \begin{aligned} &\frac{1}{{{T_J}}}{P_m} - \frac{1}{{{T_J}}}{P_e} - \frac{{D(\omega - {\omega _0})}}{{{T_J}}} \\ &- \frac{1}{{{T_H}}}{P_m} + \frac{1}{{{T_H}}}{C_v}{p_T}{\eta _r} \\ &- \frac{1}{{{T_G}}}{k_{cv}}{C_v}{p_T} + \frac{1}{{{T_G}}}{k_{cv}}{{k'}_{pv}}C_v^2{p_T} + \frac{1}{{{T_G}}}{G_B} \\ &- \frac{1}{{{T_{cv}}}}{C_v} \\ & - \frac{1}{{{T_{GB}}}}{G_B} \end{aligned} \right]{\text{,}} $ |
| $ {{{g}}_1}({{x}}) = \left[ \begin{array}{l} 0 \\ 0 \\ 0 \\ {}^{1}\!\!\diagup\!\!{}_{{{T}_{cv}}} \\ 0 \\ \end{array} \right]{\text{,}}\;\;\;{{{g}}_2}({{x}}) = \left[ \begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ {}^{1}\!\!\diagup\!\!{}_{{{T}_{GB}}} \\ \end{array} \right]{\text{。}} $ |
2)通过计算输出函数
| $\left\{ \begin{array}{l} {L_{{g_1}}}L_f^0{y_1} = {L_{{g_2}}}L_f^0{y_1} = {L_{{g_1}}}{L_f}{y_1} = {L_{{g_2}}}{L_f}{y_1} = 0 {\text{,}} \\ {L_{{g_1}}}L_f^0{y_2} = {L_{{g_2}}}L_f^0{y_2} = 0 {\text{,}} \\ \end{array} \right. $ |
| $ \left\{ \begin{array}{l} {L_{{g_1}}}L_f^2{y_1} \ne 0 {\text{,}} \\ {L_{{g_1}}}{L_f}{y_2} \ne 0 {\text{。}} \end{array} \right. $ |
其中Lie导数计算规则为:
| $\begin{aligned} &{{L_{{{f}}({{x}})}}y(x) = \frac{{\partial y(x)}}{{\partial {{x}}}}{{f}}({{x}}),}\\ &{{L_{{{g}}(x)}}{L_{{{f}}(x)}}y(x) = \frac{{\partial [{L_{{{f}}(x)}}y(x)]}}{{\partial {{x}}}}{{g}}(x)\; \cdots }{\text{。}} \end{aligned} $ |
依此类推。故
| $ {{z}} = \left[ \begin{array}{l} {\varphi _1} \\ {\varphi _2} \\ {\varphi _3} \\ {\psi _1} \\ {\psi _2} \\ \end{array} \right] = \left[ \begin{array}{l} {y_1} \\ {L_f}{y_1} \\ L_f^2{y_1} \\ {y_2} \\ {L_f}{y_2} \\ \end{array} \right]{\text{,}} $ |
| $ {\dot {{z}}} = \left[ \begin{array}{l} {{\dot \varphi }_1} \\ {{\dot \varphi }_2} \\ {{\dot \varphi }_3} \\ {{\dot \psi }_1} \\ {{\dot \psi }_2} \\ \end{array} \right] = \left[ \begin{array}{l} {\varphi _2} \\ {\varphi _3} \\ L_f^3{y_1} + {L_{{g_1}}}L_f^2{y_1}{u_1} + {L_{{g_2}}}L_f^2{y_1}{u_2} \\ {\psi _2} \\ L_f^2{y_2} + {L_{{g_1}}}{L_f}{y_2}{u_1} + {L_{{g_2}}}{L_f}{y_2}{u_2} \\ \end{array} \right]{\text{。}} $ | (10) |
3)计算零动态输入。令
| $ \left\{ \begin{array}{l} {{\dot \varphi }_3} = L_f^3{y_1} + {L_{{g_1}}}L_f^2{y_1}{u_1} + {L_{{g_2}}}L_f^2{y_1}{u_2} = 0{\text{,}} \\ {{\dot \psi }_2} = L_f^2{y_2} + {L_{{g_1}}}{L_f}{y_2}{u_1} + {L_{{g_2}}}{L_f}{y_2}{u_2} = 0 {\text{,}} \end{array} \right. $ |
可解出输入
| $ \begin{split} &\left\{ \begin{aligned} & {u_1} = - \left(\frac{{{T_{cv}}{T_H}{D^2}}}{{{T_J}{p_T}}} + {T_{cv}}{C_v}\frac{{\partial {\eta _r}}}{{\partial \omega }}\right)\frac{{\dot \omega }}{{{\eta _r}}} + \\ & \left(\frac{{{T_{cv}}{T_H}D}}{{{T_J}}} + {T_{cv}}\right)\frac{{{{\dot P}_m}}}{{{p_T}{\eta _r}}} - {T_{cv}}\frac{{{C_v}}}{{{\eta _r}}}\left(\frac{{{\eta _r}}}{{{p_T}}} + \frac{{\partial {\eta _r}}}{{\partial {p_T}}}\right){{\dot p}_T} + {C_v} {\text{,}} \\ & {u_2} = ({k_{cv}}{C_v} - {k_{cv}}{{k'}_{pv}}C_v^2){T_{GB}}{{\dot p}_T} + {G_B} + \\ &({k_{cv}}{p_T} - 2{k_{cv}}{{k'}_{pv}}{C_v}{p_T})\dfrac{{{T_{GB}}}}{{{T_{cv}}}}({u_1} - {C_v}) {\text{。}} \end{aligned} \right.\\[-14pt] \end{split} $ | (11) |
4)在式(11)控制律作用下,原系统式(8)转变为零动态系统如下式:
| $\left\{ \begin{array}{l} {T_{cv}}{{\dot C}_v} = - {C_v} + {u_{cv}} {\text{,}} \\ {T_{GB}}{{\dot G}_B} = - {G_B} + {u_B} {\text{,}} \end{array} \right.$ | (12) |
该系统可整理为:
| $ \begin{split} \left[ \begin{array}{l} {{\dot C}_v} \\ {{\dot G}_B} \\ \end{array} \right] =& \left[ \begin{array}{l} \begin{array}{*{20}{c}} { -{}^{1}\!\!\diagup\!\!{}_{{{T}_{cv}}}\;}&0 \end{array} \\ \begin{array}{*{20}{c}} 0&{ - {}^{1}\!\!\diagup\!\!{}_{{{T}_{GB}}}\;} \end{array} \\ \end{array} \right]\left[ \begin{array}{l} {C_v} \\ {G_B} \\ \end{array} \right] + \\ &\left[ \begin{array}{l} \begin{array}{*{20}{c}} {{}^{1}\!\!\diagup\!\!{}_{{{T}_{cv}}}\;}&0 \end{array} \\ \begin{array}{*{20}{c}} 0&{{}^{1}\!\!\diagup\!\!{}_{{{T}_{GB}}}\;} \end{array} \\ \end{array} \right] \left[ \begin{array}{l} {u_{cv}} \\ {u_B} \\ \end{array} \right] = {{Ax}} + {{By}} {\text{。}} \end{split} $ | (13) |
由线性系统稳定性判据可知,式(13)中常数矩阵A特征根全为负,故该零动态系统稳定。
3 仿真结果与分析利用PSCAD建立兆瓦级汽轮发电机组仿真模型,机组主要动态特性参数设置为:时间常数
|
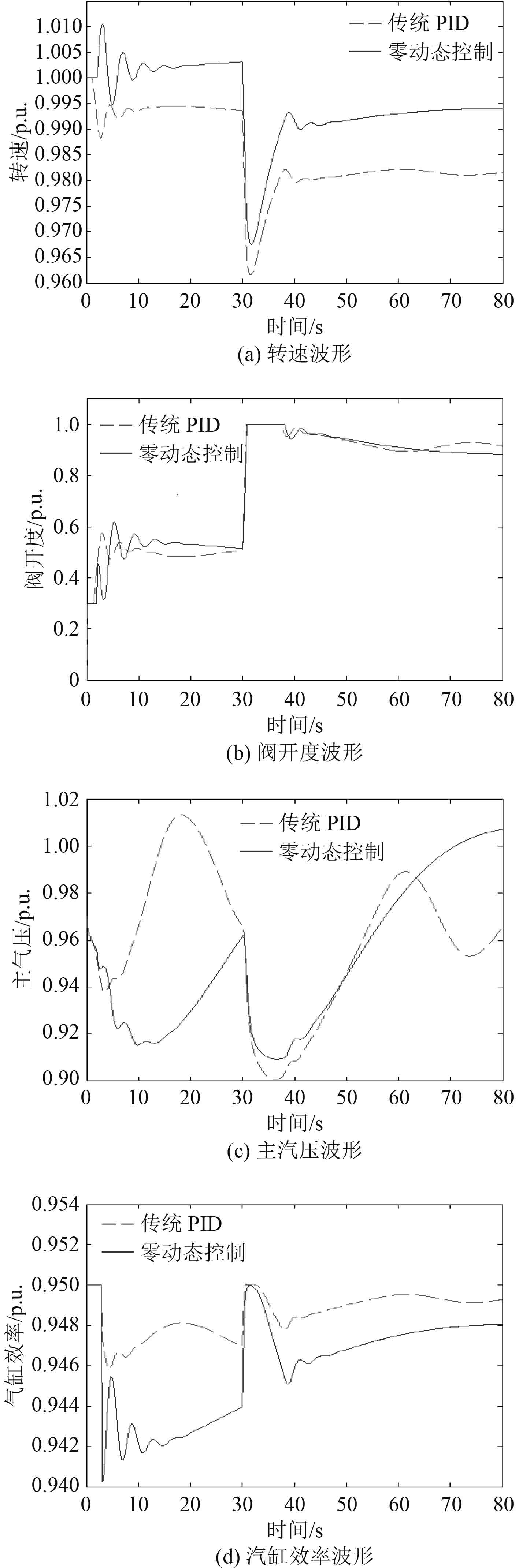
图 2 突加负载仿真波形对比 Fig. 2 Comparison of waveforms after sudden load |
由图2(a)可知,即便是重载情形,汽发机组转速在零动态控制律作用下依然能较好地逼近额定值。相比之下,PID控制器需要提高控制信号比例系数才能降低静态转速调整率,而这会增加系统的振荡风险、参数调整难度较大。由图2(b)和图2(c)可知,零动态控制较PID控制减少了暂态趋稳过程中的往复调节,这降低了电网因机组调节而发生受迫振荡的可能。由图2(d)可知,零动态控制作用下汽缸效率在稳态略低于PID控制0.15%~0.4%,这是由机组转速较高引起的。正常运行时汽缸效率通常位于速度比-效率特性曲线的单调减区间,该特性也有利于机组保持稳定。综上所述,相比于传统控制,采用零动态控制能更好地降低目标状态量的稳态偏差,有利于机组在负荷扰动后保持稳定。
4 结 语本文在陆用汽轮发电机组经典模型基础上,结合船舶电站变工况调节需求,建立了考虑汽缸效率变化的汽阀、锅炉协调控制模型。针对船舶电网电量稳定的控制目标,设计了汽压、转速零动态控制。负载阶跃仿真的结果表明,相较于传统PID控制,本文设计的零动态控制能使受控量在稳态更逼近设计值,同时能降低暂态过程中的往复调节,有利于维持系统稳定。
| [1] |
MELLO F P DE, ANDERSON P, DOUDNA J, et al. Dynamic models for fossil fueled steam units in power system studies[J]. IEEE Transactions on Power Systems, 1991, 6(2): 753-761. DOI:10.1109/59.76722 |
| [2] |
宋新立, 王成山, 刘涛, 等. 电力系统全过程动态仿真中的机炉协调控制系统模型研究[J]. 中国电机工程学报, 2013, 33(25): 167-172. SONG Xin-li, WANG Cheng-shan, LIU Tao, et al. Modeling of boiler-turbine coordinated control system in coal-fired power plants for power system unified dynamic simulation of transient, medium-term and long-term stabilities[J]. Proceedings of the CSEE, 2013, 33(25): 167-172. |
| [3] |
宋新立, 刘肇旭, 李永庄, 等. 电力系统稳定计算中火电厂调速系统模型及其应用分析[J]. 电网技术, 2008, 32(23): 44-49. SONG Xin-li, LIU Zhao-xu, LI Yong-zhuang, et al. Analysis on speed governing system model for fossil-fuel generating plant and its application in power system stability simulation[J]. Power System Technology, 2008, 32(23): 44-49. |
| [4] |
刘晓燕, 王文中, 欧阳杰, 等. 大型汽轮机中压调节阀参调供热研究[J]. 华电技术, 2018, 40(3): 9-12. LIU Xiao-yan, WANG Wen-zhong, OUYANG Jie, et al. Study on IP control valve of large-scale steam turbine engaged in heat supply regulation[J]. Huadian Technology, 2018, 40(3): 9-12. DOI:10.3969/j.issn.1674-1951.2018.03.003 |
| [5] |
李啸骢, 程时杰, 韦化, 等. 具有多性能指标的汽轮发电机非线性综合控制[J]. 中国电机工程学报, 2003, 23(4): 96-101. LI Xiao-cong, CHENG Shi-jie, WEI Hua, et al. Multi-index nonlinear integrated control for turbine generator unit[J]. Proceedings of the CSEE, 2003, 23(4): 96-101. DOI:10.3321/j.issn:0258-8013.2003.04.020 |
| [6] |
李啸骢, 程时杰, 韦化, 等. 中间再热式汽轮发电机组的多指标非线性综合控制器的研究[J]. 电网技术, 2004, 28(7): 1-6, 18. LI Xiao-cong, CHENG Shi-jie, WEI Hua, et al. Study on multi-index nonlinear integrated controller for reheat-type turbo-generator unit[J]. Power System Technology, 2004, 28(7): 1-6, 18. DOI:10.3321/j.issn:1000-3673.2004.07.001 |
| [7] |
陈明媛, 李啸骢, 从兰美, 等. 中间再热式汽轮发电机组的多指标非线性鲁棒综合控制[J]. 电力自动化设备, 2017, 37(10): 139-145. CHEN Ming-yuan, LI Xiao-cong, CONG Lan-mei, et al. Multi-index nonlinear robust control for reheat-type turbo-generator[J]. Electric Power Automation Equipment, 2017, 37(10): 139-145. |
| [8] |
蒋铁铮, 陈陈, 艾芊. 汽轮发电机汽门开度的分散非线性预测控制[J]. 中国电机工程学报, 2006, 26(20): 22-26. JIANG Tie-zheng, CHEN Chen, AI Qian. Study of decentralized nonlinear predictive control for steam valve of turbine-generator[J]. Proceedings of the CSEE, 2006, 26(20): 22-26. DOI:10.3321/j.issn:0258-8013.2006.20.004 |
| [9] |
蒋铁铮, 陈陈, 艾芊. 汽轮发电机主汽门开度的非线性最优预测控制[J]. 控制理论与应用, 2006, 23(3): 458-462. JIANG Tie-zheng, CHEN Chen, AI Qian. Nonlinear optimal predictive controller for main steam valve of turbine generator[J]. Control Theory & Application, 2006, 23(3): 458-462. DOI:10.3969/j.issn.1000-8152.2006.03.025 |
| [10] |
钟敏. 面向单元机组的炉机网协调控制[D]. 哈尔滨: 哈尔滨工业大学, 2016: 27-29. ZHONG Min, Boiler-turbine-grid coordinated control applied to unit plant[D]. Harbin Institute of Technology, 2016. |
| [11] |
余又红, 刘永葆, 孙丰瑞. 基于热经济学的舰船发电机组配置优化[J]. 海军工程大学学报, 2009, 21(4): 92-97. YU You-hong, LIU Yong-bao, SUN Feng-rui. Configuration optimization of marine generating units based on thermo-economics[J]. Journal of Naval University of Engineering, 2009, 21(4): 92-97. |
| [12] |
邓拓宇, 田亮, 刘吉臻. 供热机组锅炉储能与热网储能空间时间多尺度分析[J]. 中国电机工程学报, 2017, 37(2): 599-605. DENG Tuoyu, TIAN Liang, LIU Jizhen. Spatial and temporal multiscale analysis on energy storage in heat supply units'boiler and heat supply nets[J]. Proceedings of the CSEE, 2017, 37(2): 599-605. |
| [13] |
刘鑫屏, 田亮, 王琪. 供热机组发电负荷-机前压力-抽气压力简化非线性动态模型[J]. 动力工程学报, 2014, 34(2): 115-121. LIU Xinping, TIAN Liang, WANG Qi. Simplified nonlinear dynamic model of generating load-throttle pressure-extraction pressure for heating units[J]. Journal of Chinese Society of Power Engineering, 2014, 34(2): 115-121. |
| [14] |
卢强, 梅生伟, 孙元章. 电力系统非线性控制(第2版)[M]. 北京, 清华大学出版社, 2008: 309-311.
|
 2020, Vol. 42
2020, Vol. 42
