在渤海海域作业的某现役FPSO采取软刚臂单点系泊方式进行无应急解脱的永久式系泊。软刚臂单点系泊装置通过将FPSO与固定在海床上的固定塔架钢结构相连接,从而将FPSO系泊在指定的作业海域,并且具有风向标效应[1]。在风、浪、流环境载荷的联合作用下,FPSO可以围绕单点系泊装置的固定塔架旋转、横摇和纵荡,最终使FPSO受的系泊合外力最小并保证FPSO能够长期驻泊。
单点系泊装置导管架上方的将军柱是承受系泊力的主要构件之一,其结构特点为直径较大、焊口较长[2]。将军柱的主轴和斜撑在焊接的过程中很难控制焊接变形和保证焊接质量,在焊接点接头处由于焊接缺陷及结构几何不连续性等因素,通常会存在较高的应力集中。在系泊力这种交变载荷作用下焊接裂纹还会在使用过程中逐渐扩大,最后导致结构的破坏。由于在焊接过程中受到主观或者客观因素的影响,造成的焊接缺陷不仅影响将军柱的静强度,也会严重影响将军柱的疲劳寿命[3]。
因此,以渤海某单点系泊装置将军柱安全性评估为基础,建立将军柱有限元模型,使用AQWA软件对系泊过程产生的时域内的系泊力进行计算,得到疲劳计算载荷输入,并结合波浪散布图设计疲劳载荷周期谱,通过nCode软件计算结构的疲劳载荷最大循环次数,从而得到结构的疲劳寿命。
本文采用时间序列疲劳分析方法,提出一种基于波浪散布图长期海况下的疲劳计算方法,可为同类型的结构评估与疲劳设计提供参考。
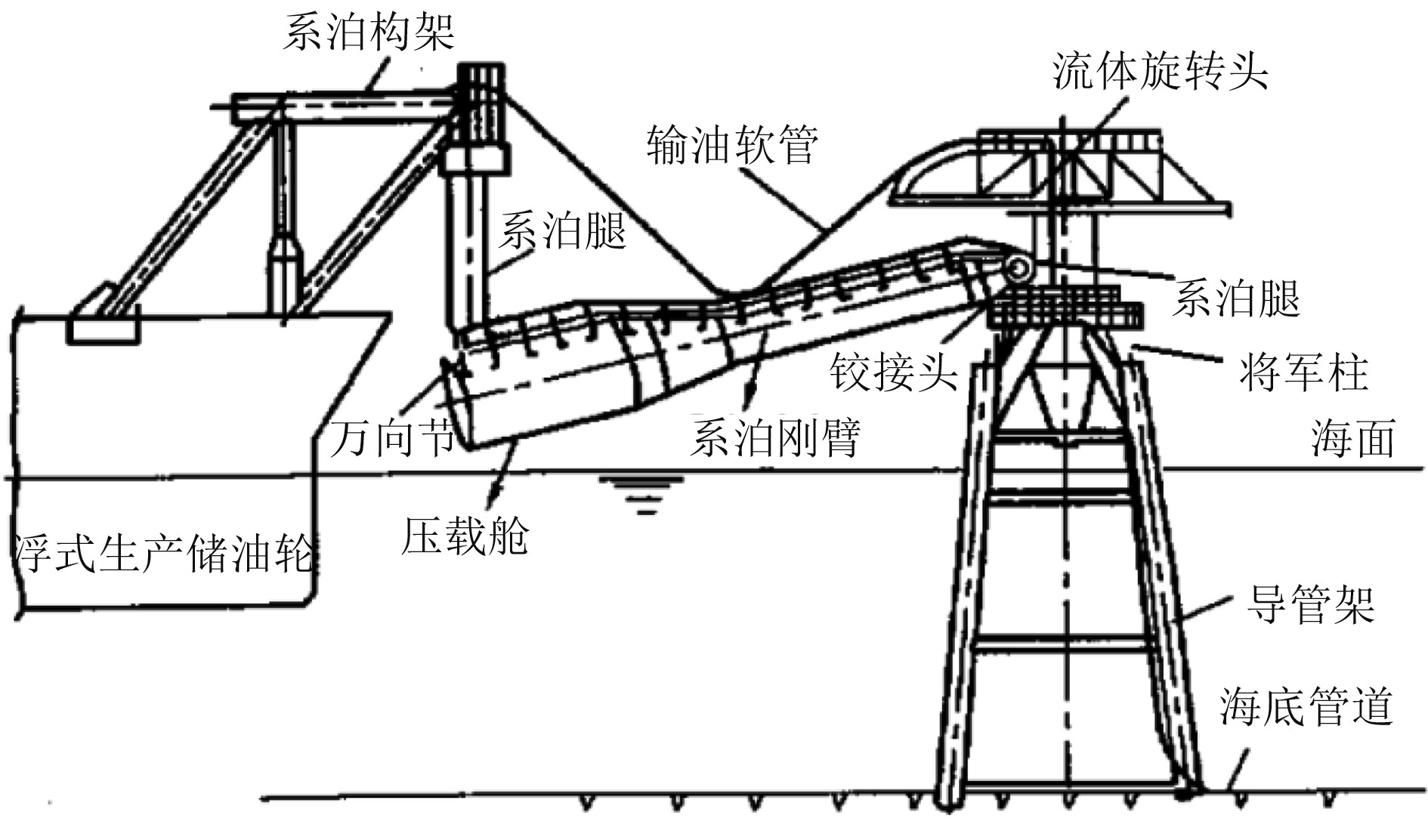
|
图 1 单点系泊装置示意图 Fig. 1 Single point mooring system sketch |
势流理论的假设前提是基于理想流体,流域的边界条件需要满足Laplace方程,将运动学和动力学边界条件线性化处理之后可以得到二维线性波运动的基本方程和边界条件为[4]:
| ${\left. {\frac{{{\partial ^2}\varnothing }}{{\partial {t^2}}} + g\frac{{\partial \varnothing}}{{\partial z}}} \right|_{z = 0}} = 0{\text{,}} $ | (1) |
| $\frac{{{\partial ^2}\varnothing}}{{\partial {{\rm{x}}^2}}} + \frac{{{\partial ^2}\varnothing }}{{\partial {{\rm{z}}^2}}} = 0 {\text{,}} $ | (2) |
| ${\left. {\frac{{\partial \varnothing }}{{\partial z}}} \right|_{z = - {\rm{d}}}} = 0 {\text{,}} $ | (3) |
| ${\left. { - \frac{1}{g}\frac{{\partial \varnothing }}{{\partial t}}} \right|_{z = 0}} = \eta {\text{。}} $ | (4) |
式中:
波动场的速度势函数
| $F = \mathop \int\!\!\!\int \nolimits_S^{} - pn{\rm d}s {\text{。}} $ | (5) |
式中,n为FPSO结构湿表面某点的外法线矢量。
1.2 多体耦合时域运动方程考虑环境载荷以及单点系泊装置系泊回复力对FPSO的联合作用,FPSO在时域内的运动方程为[5]:
| $\begin{split} & \mathop \sum \nolimits_{i = 1}^6 \left[ {{ M} + { A}\left( \infty \right)} \right]\ddot x\left( t \right) + \mathop \int \nolimits_0^t { r}\left( {t - \tau } \right)\dot x\left( \tau \right){\rm d}\tau + { D}\dot x\left( t \right) + \\ & { K}x\left( t \right) = {F^{\left( {1,2} \right)}}\left( t \right) + {F_W}\left( t \right) + {F_C}\left( t \right) + {F_{SPM}}\left( t \right){\text{。}} \end{split} $ | (6) |
式中:M为FPSO的质量矩阵;A(∞)为最大频率对应的附加水质量矩阵;r(t)为辐射阻尼的脉冲响应函数矩阵,附连水质量、辐射阻尼系数均采用三维势流理论应用源汇分布方法计算得到;D为FPSO慢漂阻尼矩阵;K为FPSO静水回复力刚度矩阵;F(1,2)(t)为1阶、2阶波浪载荷;FW(t),FC(t)分别为风流载荷;FSPM(t)为单点系泊系统提供的回复力。
1.3 雨流计数法将随机的时间-载荷历程曲线转化为一系列载荷循环的方法称为“循环计数法”。大量的实验结果表明,结构发生疲劳的损伤程度主要与循环应力范围大小及应力循环的次数这两点有关。因此,为计算将军柱的疲劳损伤,需要在将军柱所受到的时域系泊力载荷历程曲线中将那些对将军柱造成疲劳损伤的应力循环识别出来,然后统计其应力的大小,掌握应力范围的分布规律,即应力范围的大小与作用次数之间的关系,这种方法称为随机疲劳载荷计数。目前有很多种计数方法,而这些方法中最先进的一种方法称为“雨流计数法”[6]。
雨流计数法通过对AQWA计算得到的随时间变化系泊力历程曲线的每一部分都进行计数,并且只计数一次,大的应力幅值所造成的损伤不受截断它的小应力循环的影响,将截出的小应力循环叠加到较大的循环和半循环中。然后根据Miner线性叠加原理,通过将等幅实验得到的S-N中值曲线与雨流计数法处理过的应力结果相结合,便可以计算出将军柱结构的疲劳寿命。
1.4 线性系统变换理论船舶与海洋工程结构是一种典型的动力系统,作用在将军柱结构上的外载荷F(t)是系统的输入,将军柱由外载荷引起的交变应力X(t)则是系统的响应,关系如图2所示。

|
图 2 线性系统变换理论 Fig. 2 Linear system transform theory |
通过从外载荷的统计特性可以得到将军柱结构中交变应力的统计特性。
1.5 Miner线性累计损伤理论系泊载荷在整个结构寿命期间的长期分布由很多个短期海况造成的系泊力组成,且每一短期海况中将军柱所受到的应力范围由多级恒幅交变应力构成,设短期海况应力范围水平总共有n级,则对每一短期海况来说将军柱的疲劳累计损伤为:
| $ {D_{{L_i}}} = \mathop \sum \nolimits_{i = 1}^n {D_{\rm{i}}} {\text{。}} $ | (7) |
式中:Li为波浪散布图中第i海况作用的时间;
假设将军柱受到的应力范围在结构全寿命期的长期分布由k个短期海况系泊力引起的应力组成,那么整个系泊力载荷谱回复周期L期间将军柱所受到的疲劳累计损伤度为[7]:
| ${D_L} = \mathop \sum \nolimits_{{\rm{i}} = 1}^k {D_{{L_i}}}{\text{。}}$ | (8) |
式中:DL是度量钢结构疲劳累计损伤的一个无量纲值,当结构发生疲劳破坏时,其累计损伤度为1,即结构的DL值为1。
2 疲劳模型建立及计算 2.1 建立模型位于渤海的某单点系泊装置的设计寿命25年,是一座4腿导管架固定式软刚臂系泊系统。计算主要分析单点系泊固定塔架主要承力构件将军柱所受到的系泊力引起的结构疲劳。在Workbench中建立将军柱的三维有限元模型,忽略系泊头铸件和轴承等刚性机械构件,通过远程点(Remote point)的方式添加到模型中。其中将军柱主轴高6.7 m,甲板面积7.4 m。斜撑尺寸为φ914×30 mm,甲板腿尺寸为φ1143×50 mm,主轴尺寸为φ3500×50 mm。将军柱结构材料选用船用高强度钢GB-712 2012 EH36,材料性能如表1所示。
|
|
表 1 材料属性 Tab.1 Material property |
将军柱的主要结构如图3所示。图中箭头所指结构为固定塔架的系泊头,系泊头与将军柱刚性连接,为模型添加系泊力载荷时使用workbench中远程点建立远端边界MPC约束方程,其几何行为设置为刚性,对将军柱最下面4个钢桩进行固支约束。
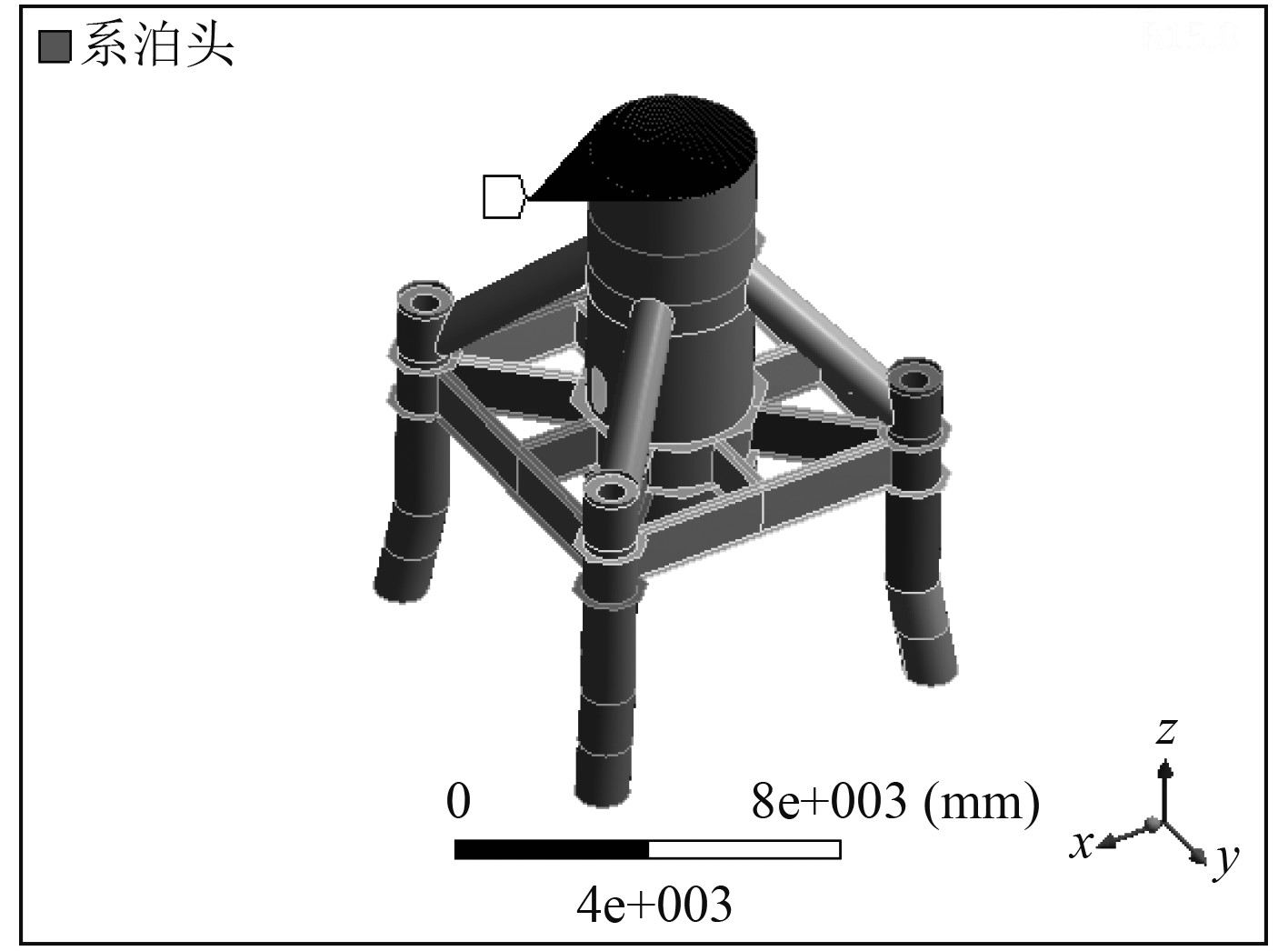
|
图 3 单点系泊将军柱疲劳计算模型 Fig. 3 King post fatigue analysis model |
在AQWA中建立软刚臂系泊系统的简化模型,其中单点系泊系统结构之间的轴承连接通过运动副的形式模拟。FPSO与系泊腿之间采用2个万向节和2个回转装置连接,释放3个转动自由度,系泊刚臂与系泊腿之间采用2个万向节连接,释放2个旋转自由度,系泊刚臂与将军柱的系泊头之间采用球铰接,释放3个旋转自由度。建立多体耦合分析模型之后划分结构网格,设置环境输入等相关参数,耦合分析模型计算网格如图4所示。由于水面以上部分网格对水动力计算没有影响,故只对FPSO水面以下部分进行网格划分[8]。

|
图 4 单点系泊装置与FPSO水动力模型 Fig. 4 Single point mooring system hydrodynamic model |
作用在将军柱主轴上的系泊力通过AQWA进行时域内水动力计算得到。AQWA的计算流程主要是基于线性波理论进行衍射分析得到结构的响应幅值算子(RAO)[9],再通过输入相应的风浪流参数进行时域响应分析得到系泊头时域内所受到的系泊力。
由于本文所述将军柱受到的系泊力变幅载荷频率远低于将军柱的固有频率,因此采用静应力疲劳分析的方法[10]。分别对波浪散布图上10个主要引起疲劳的海况进行水动力计算,得到每一个海况下作用在系泊头上的3个方向的系泊力。波浪分布如表2所示。作用在系泊头上的X,Y,Z方向的时域内系泊力大小如图5所示。
|
|
表 2 波高与周期分布 Tab.2 Wave load case |

|
图 5 系泊头时间-载荷曲线 Fig. 5 Mooring force time-load curve |
通过AQWA计算得到的时域系泊力计算结果,导出CSV格式文件,再导入到nCode Designlife疲劳计算软件中进行疲劳分析。
单个工况的时程曲线如图6所示。
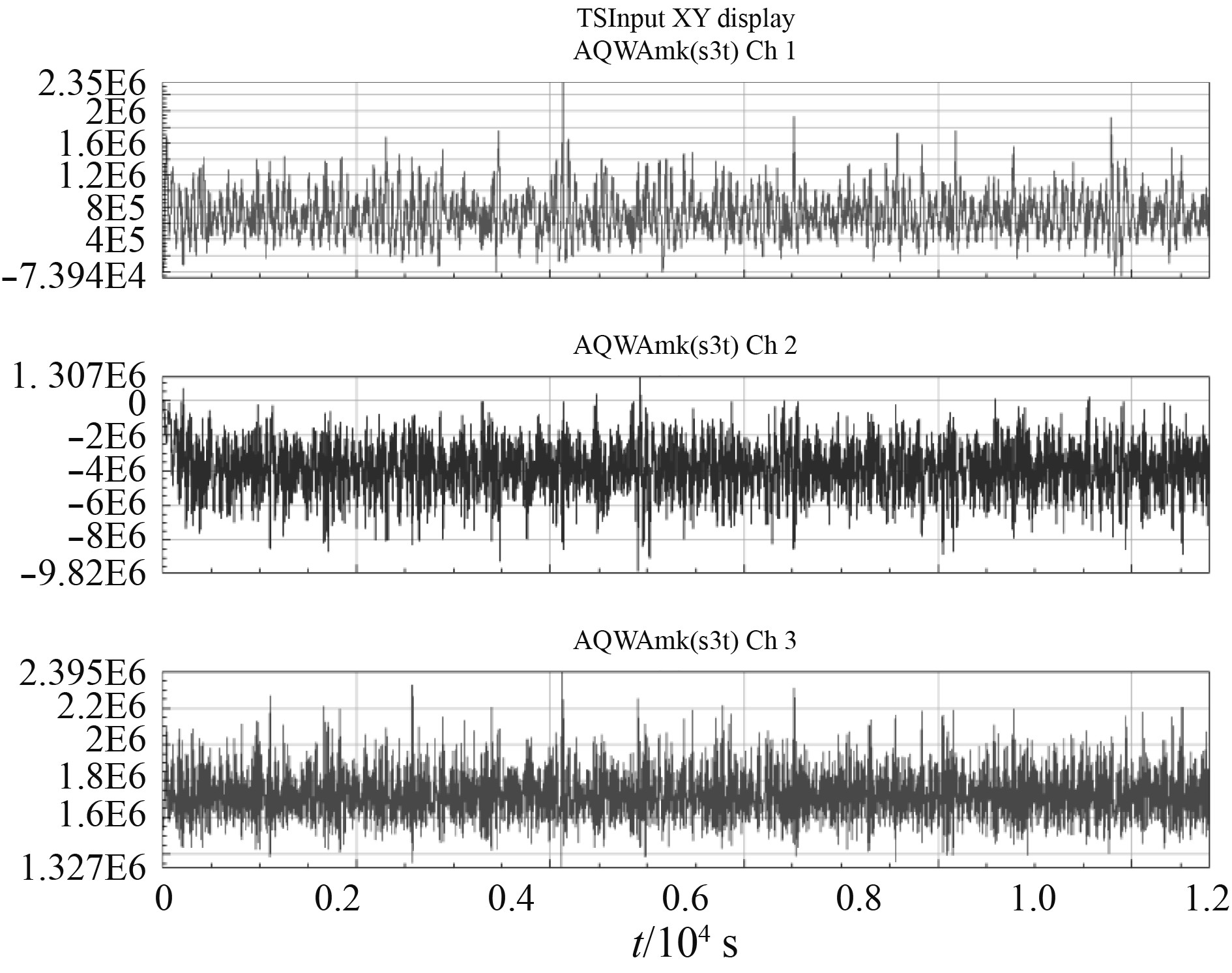
|
图 6 单海况时间-载荷曲线 Fig. 6 Single sea state time-load curve |
疲劳分析将长期分布海况模拟为3 600 s,通过将10个主要引起疲劳的海况按照出现的概率分为不同的时间段,每个短期海况时间段计算方法见下式:
| ${T_S} = 3\;600 \times P {\text{。}} $ | (9) |
其中:TS为短期单海况持续作用的时间,s;P为短期单海况出现概率。通过把每一段短期海况作用的时间-载荷历程相连接,建立长期海况的时间-载荷历程曲线。由于Miner线性累计损伤理论不考虑载荷的累加顺序[11],因此短期海况的时间-载荷历程曲线的连接顺序对载荷谱的建立不产生影响。长期海况下的系泊力载荷谱如图7所示。
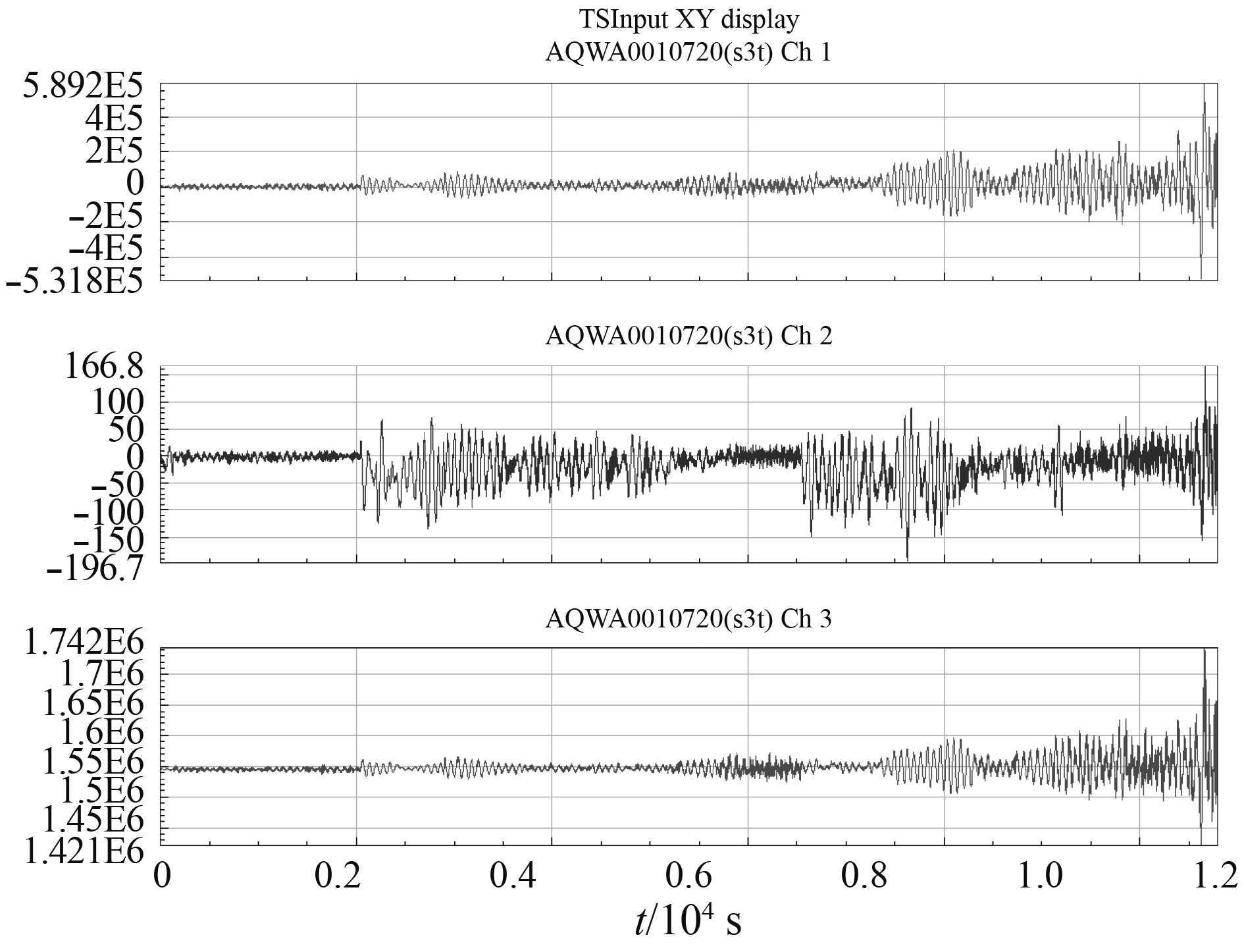
|
图 7 长期海况时间-载荷曲线 Fig. 7 Long-term sea state time-load curve |
以上述时域内变化的系泊力为一个疲劳循环周期,nCode可以计算一个疲劳循环周期下载荷造成的结构损伤和在该周期下的疲劳循环次数计算疲劳循环次数,通过将循环次数乘以单周期下载荷作用的时间(3 h),就可以得到结构的疲劳寿命[12]。
根据DNV(挪威船级社)规范的要求[13],使用古德曼(Goodman)修正法对平均应力进行修正,古德曼修正方法考虑了作用在结构上的平均应力、疲劳应力幅、材料性能等综合因素对疲劳寿命的影响。目前古德曼修正方法已广泛应用于疲劳强度设计中.
由于需要将有限元计算得到的应力,与材料S-N曲线中的应力进行等效转换,因此需要找到一个客观评价量——主应力。本文应力计算采用疲劳计算中最常用的危险面(Critical Plane)计算方法[14]。
通过输入EH36高强度钢的材料属性得到材料的S-K曲线,其中EH36高强度钢的极限强度为490 MPa[15]。应力幅值与循环次数的中值S-N曲线见图8所示。
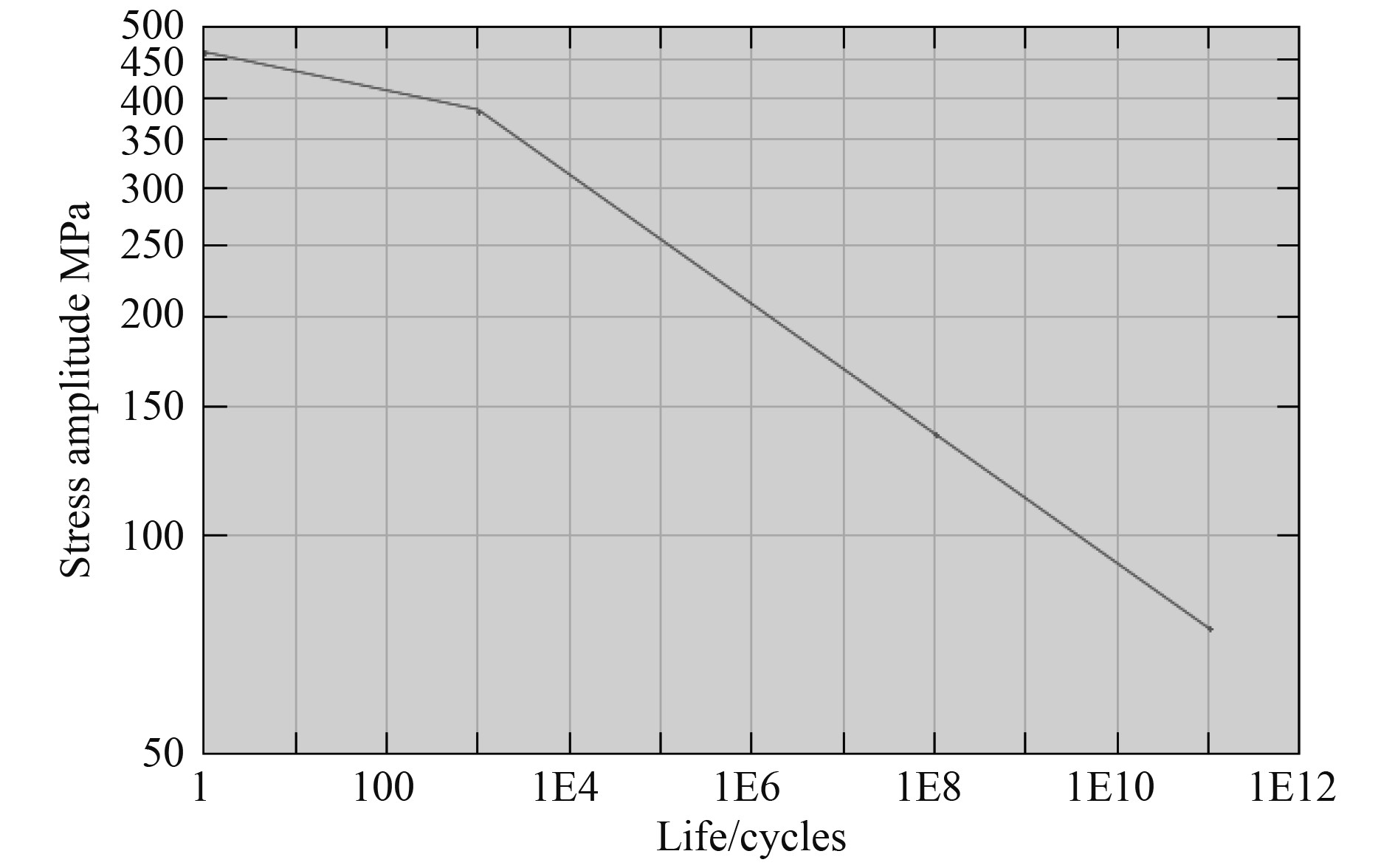
|
图 8 EH36高强度钢中值S-N曲线 Fig. 8 EH36 recommend S-N curve |
其管节点的疲劳寿命见表3。
|
|
表 3 最小寿命节点及位置 Tab.3 Joint fatigue life and damage |
计算结果表明,结构疲劳寿命最小的部位主要出现在将军柱的斜撑与主轴的连接处,根据CCS规范考虑2倍的安全系数[16],其最小寿命大于设计寿命25×2年,满足设计要求。

|
图 9 疲劳寿命全局图 Fig. 9 Fatigue life general sketch |

|
图 10 疲劳寿命局部放大图 Fig. 10 Fatigue life local sketch |
本文对渤海某FPSO单点系泊装置将军柱结构进行疲劳分析,提出一种固定结构在长期海况下疲劳损伤的计算方法。通过AQWA软件计算了疲劳海况作用下的系泊力载荷,在Workbench中建立将军柱的有限元模型,再利用nCode软件计算了结构的损伤及寿命。根据计算结果,本文得到以下结论:
1)疲劳寿命结果显示结构发生疲劳损伤的主要部位在将军柱的斜撑与主轴的连接处,设计中应着重考虑管节点连接部位的疲劳强度,其余部分疲劳损伤较小或所受应力幅值低于疲劳极限应力。通过增加该部位斜撑杆壁厚度,或者在斜撑内增加内衬板可以有效的延长结构的疲劳寿命。
2)通过将短期海况与波浪散布图结合,设计长期海况时间-载荷曲线,利用长期海况结构疲劳计算方法得到了将军柱的疲劳寿命,为相同类型的海上固定式结构物的结构设计及疲劳分析提供有益的参考及借鉴。
3)利用线性累计损伤理论计算得到了每个节点的疲劳损伤度,可以将波浪载荷导致的疲劳损伤结果与系泊力产生的损伤叠加,从而计算单点系泊装置将军柱在整个在位寿命期间的疲劳损伤,进一步评估结构的可靠性。
| [1] |
吕妍, 魏文普, 王佳, 等. FPSO原油外输溢油风险分析及风险评价[J]. 中国海上油气, 2013, 25(5): 89-92. |
| [2] |
董秀英, 张增华. 单点系泊导管架将军柱焊接新工艺[J]. 中国海洋平台, 1989(3): 25-28. |
| [3] |
刘杰鸣. 单点系泊导管架疲劳分析[J]. 中国海上油气: 工程, 2003, 15(3): 22-24. |
| [4] |
苏方磊. 水上软刚臂系泊FPSO水动力响应特性试验研究[D]. 大连: 大连理工大学, 2015.
|
| [5] |
余骁, 王允, 李慧. 软刚臂单点系泊系统系泊力计算两种方法对比[J]. 船海工程, 2018(1): 129-132. DOI:10.3963/j.issn.1671-7953.2018.01.029 |
| [6] |
刘洪涛 随机波浪荷载作用下海洋导管架平台疲劳寿命预测分析[D]. 天津: 天津大学, 2007.
|
| [7] |
Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design [Z]. API RP 2A-WSD, 21st, Dec 2000, IDT 2012.
|
| [8] |
WANG H R, WEI Y F, PAN F H, et al. On fatigue life of a single point mooring system on FPSO[J]. Ship & Boat, 2015. |
| [9] |
姚程. 基于AQWA的单点软刚臂系泊浮体的水动力响应研究[D]. 大连: 大连理工大学, 2017.
|
| [10] |
PAN J Y. Study on structural improvement and mooring line fatigue risk analysis for a single point mooring system[J]. International Psychogeriatrics, 2007, 26(1): 1-12. |
| [11] |
许津豪. 自升式平台桩腿动力响应及疲劳分析研究[D]. 广州: 华南理工大学, 2014.
|
| [12] |
Wen-Hua W U, Bai-Cheng L V, Yue Q J, et al. Research on analytical method of fatigue characteristics of soft yoke mooring system based on full-scale measurement[J]. CHina Ocean, 2017, 31(2): 230-237. DOI:10.1007/s13344-017-0027-0 |
| [13] |
DNV. Recommended practice, fatigue design of offshore steel structure [S]. Norway: Det Norske Veritas, 2001.
|
| [14] |
金嘉琦, 周巍, 王显荣, 等. 修井机作业平台的疲劳寿命研究[J]. 机械设计与制造, 2015(12): 132-134. DOI:10.3969/j.issn.1001-3997.2015.12.038 |
| [15] |
LIU J. Fatigue analysis for single point mooring jacket[J]. China Offshore Oil & Gas, 2003. |
| [16] |
海洋工程结构物疲劳强度评估指南[S]. 中国船级社, 2013.
|
 2020, Vol. 42
2020, Vol. 42
