2. 高新船舶与深海开发装备协同创新中心,上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep Sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China
水下运载器是一种能够运载工程技术人员和各种特殊装置到达海中特定位置,进行海底勘探、科学考察和近海底作业的重要设备[1-3]。随着计算机硬件、电池技术以及传感器技术的发展,各种类型的水下运载器被开发出来并承担起复杂多样的干预性任务,此类任务往往需要水下运载器具备水中定位这一重要功能,即在水下作业过程中依靠自身动力动态保持于水中某一确定位置[4-5]。
为了实现运载器在水中的定位,需要安装导航定位所需传感器及相应的推力执行机构,并通过适当的控制算法进行水中位置及姿态的自动调节。王芳等[6]对深水半潜式钻井平台进行了建模,设计了动力定位实时交互式仿真系统,从而模拟平台的水下定位。赵慎等[7]对AUV水下对接中的导航定位问题进行了概述并总结了导航定位方法和对所需传感器的性能的要求。王婷等[8]研究了水下航行器利用侧推和垂推实现自身升沉和旋转运动的动力定位方法。此外,为了使水下平台能够在不规则海流下保持悬停和姿态控制,Rahimah等[9]对水下平台的外形及推进系统进行了重新设计。Wei ZHANG[10]使用模糊PID方法来实现水下平台的姿态控制。
本文设计了一种水下自治平台的水平运动控制系统[11]。该水下平台用于从水面运载设备至海底布放,并从海底回收至水面指定位置。水下平台在上浮或下潜过程中,需要对平台的水平位置和姿态进行控制以保证平台始终位于水面超短基线系统(USBL)收发机稳定通信范围,并且能够在运动到指定位置进行设备布放或回收。该新型水下平台相比于常规水下航行器,其推进器布置方式特殊(见图1),且没有流线形封闭外壳,难以获取相关的水动力参数。此外,水下洋流的扰动也常随机变化导致其位置偏移。这些因素导致难以进行水下平台运动的精确建模,这种条件下水下平台的水平运动控制器设计成为了值得研究的问题。
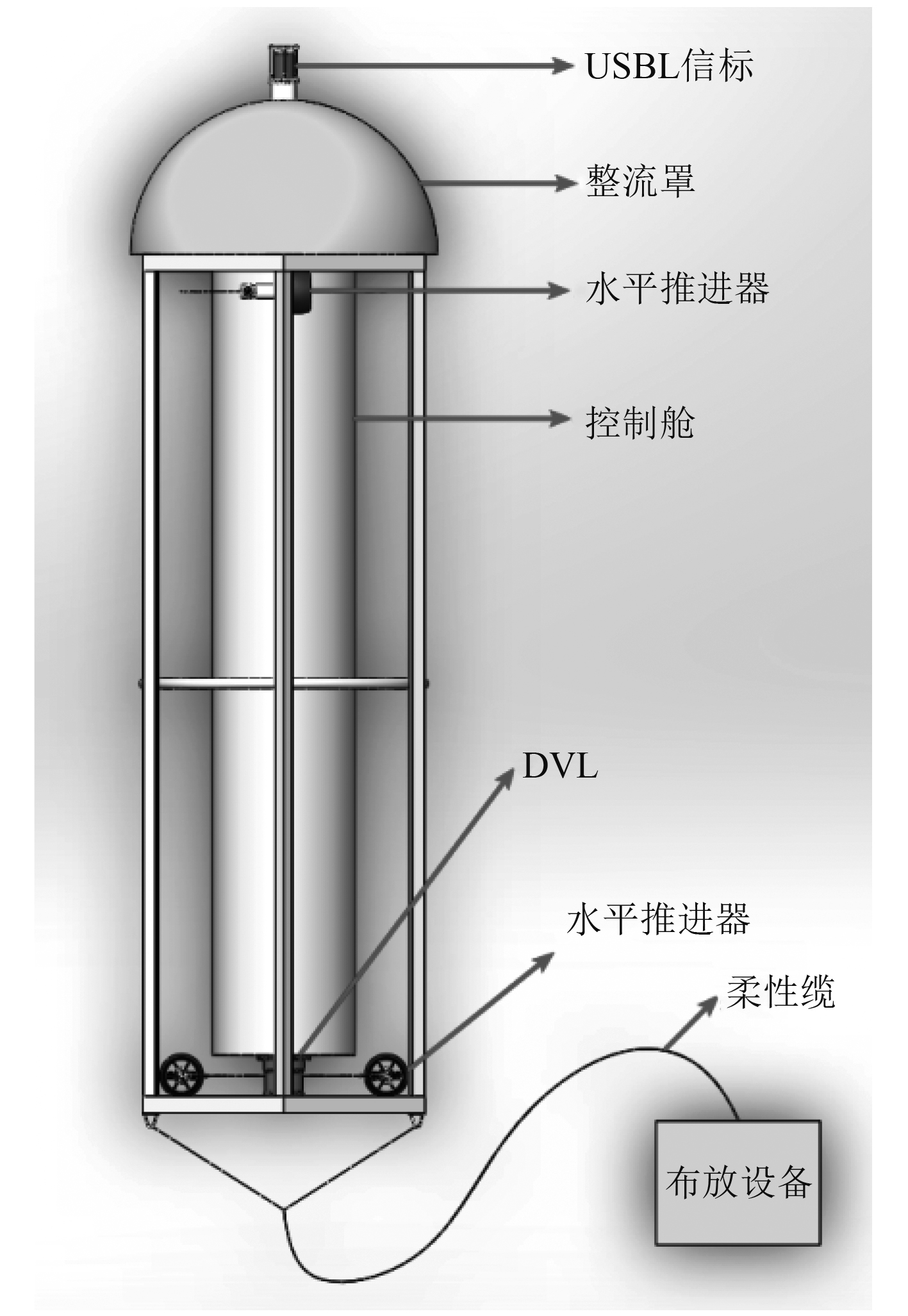
|
图 1 新型水下平台示意图 Fig. 1 Underwater platform schematic |
由上海交通大学设计及建造的升沉型水下平台是一种新型无缆水下自治平台,其示意图如图1所示。由于本文主要内容在于运动控制系统,图中仅保留水平控制相关零部件,平台主要参数见表1。平台顶端安装了USBL超短基线水下定位系统,该系统能够提供精确的位置跟踪和全双工数字通信功能。同时平台底部安装有多普勒测速仪(DVL),用于测量水下运载器在各个方向上的运动速度。
|
|
表 1 平台主要参数 Tab.1 The main parameters |
该水下平台的主要特点如下:1)整体几何形状为半球形整流罩加圆柱形本体,以减少上浮过程中的流体阻力;2)顶部半球形结构为浮力材料块,以获得上浮所需的正浮力;3)圆柱形本体内部为耐压圆柱筒体,其内部搭载锂电池系统而无需脐带缆供电。耐压筒体内部布置原则为重心尽可能低,因此平台具有良好的静稳性而无需主动进行横/纵倾控制;4)平台在水中具有足够正浮力,该浮力使平台在规定时间内上浮至悬停深度;5)下潜过程中平台下方采用柔性缆挂载设备,挂载后平台水中重量将大于其浮力。设备质量根据水中重量要求、下潜时间及功能需求另行设计;6)平台水平操纵性能:平台共配置4个水平推进器(图1)以控制水平位置以及平台姿态;7)平台导航/定位能力:平台基于惯性导航系统及多普勒测速仪(DVL)推算平台自身在下潜及上浮过程中的位置。平台顶部装有USBL定位信标,水面布放母船可追踪平台位置并发送给平台,平台惯性导航系统将根据USBL位置进行周期性修正。
从水面布放开始到完成一次布放及回收任务,平台工作流程分为下潜、座底、布放、上浮、回收几个阶段。首先平台与待布放设备由柔性缆连接,无动力下潜至海底。悬浮于布放设备上方等待水面上浮指令。平台上浮时将解锁柔性缆脱离布放设备并开始上浮。在平台上浮过程中需要对平台水平位置(预定位置)及艏向进行控制以避免随洋流等外力作用导致的水平位置漂移,最终平台浮出水面定位于预定位置等待回收。
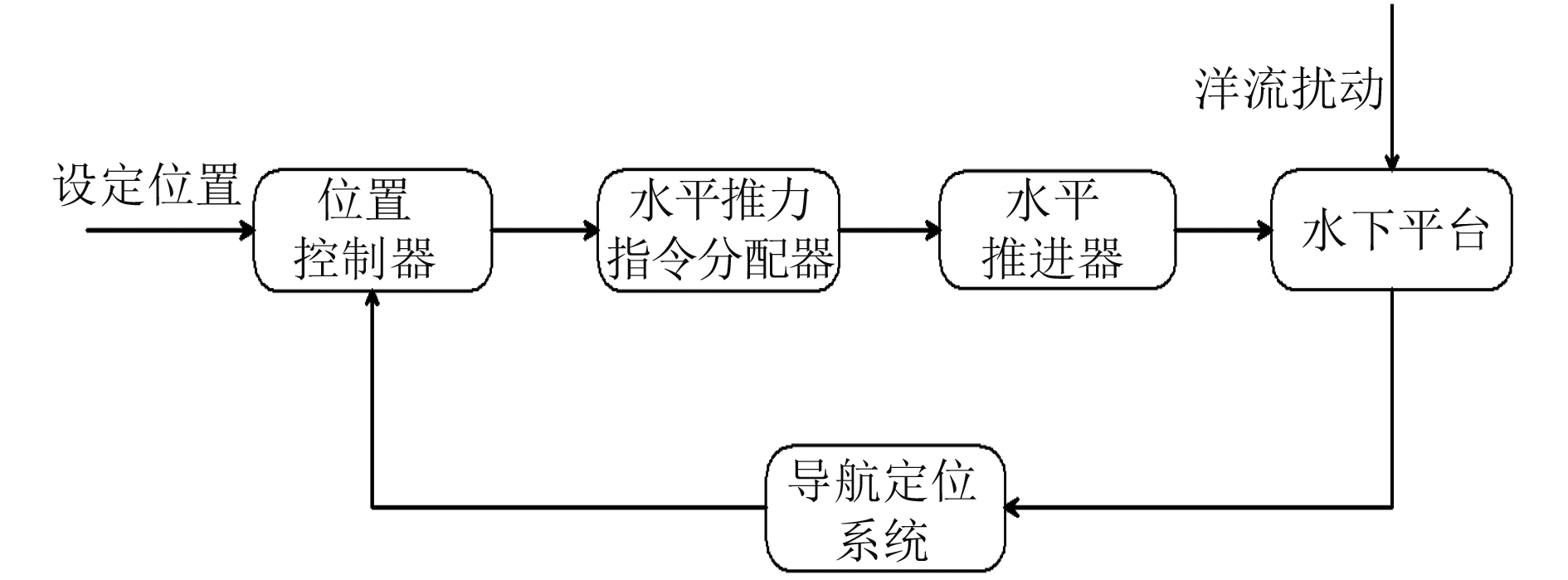
1.2 水平运动控制系统水平控制系统目的包括:1)使平台下潜和上浮过程中始终落入水面USBL收发机覆盖的圆锥体区域内,从而能够被跟踪并修正提供导航定位系统所需位置修正信息;2)平台出水位置与任务指定目标位置的水平误差不超过容许范围。
如图3所示,水平位置控制系统根据平台当前位置(由USBL/DVL/AHRS组合导航定位系统反馈)与设定位置之间的误差,产生纵向/侧向推力指令,并通过水平推力指令分配器给出各个水平推进器的推力,最后换算成各个推进器的控制电压。除了产生所需水平推力之外,水平推力分配器还需使平台保持预定艏向以避免其与布放设备之间的柔性缆产生扭结。
|
图 3 水平面运动控制系统结构图 Fig. 3 Structure of horizontal motion control system |
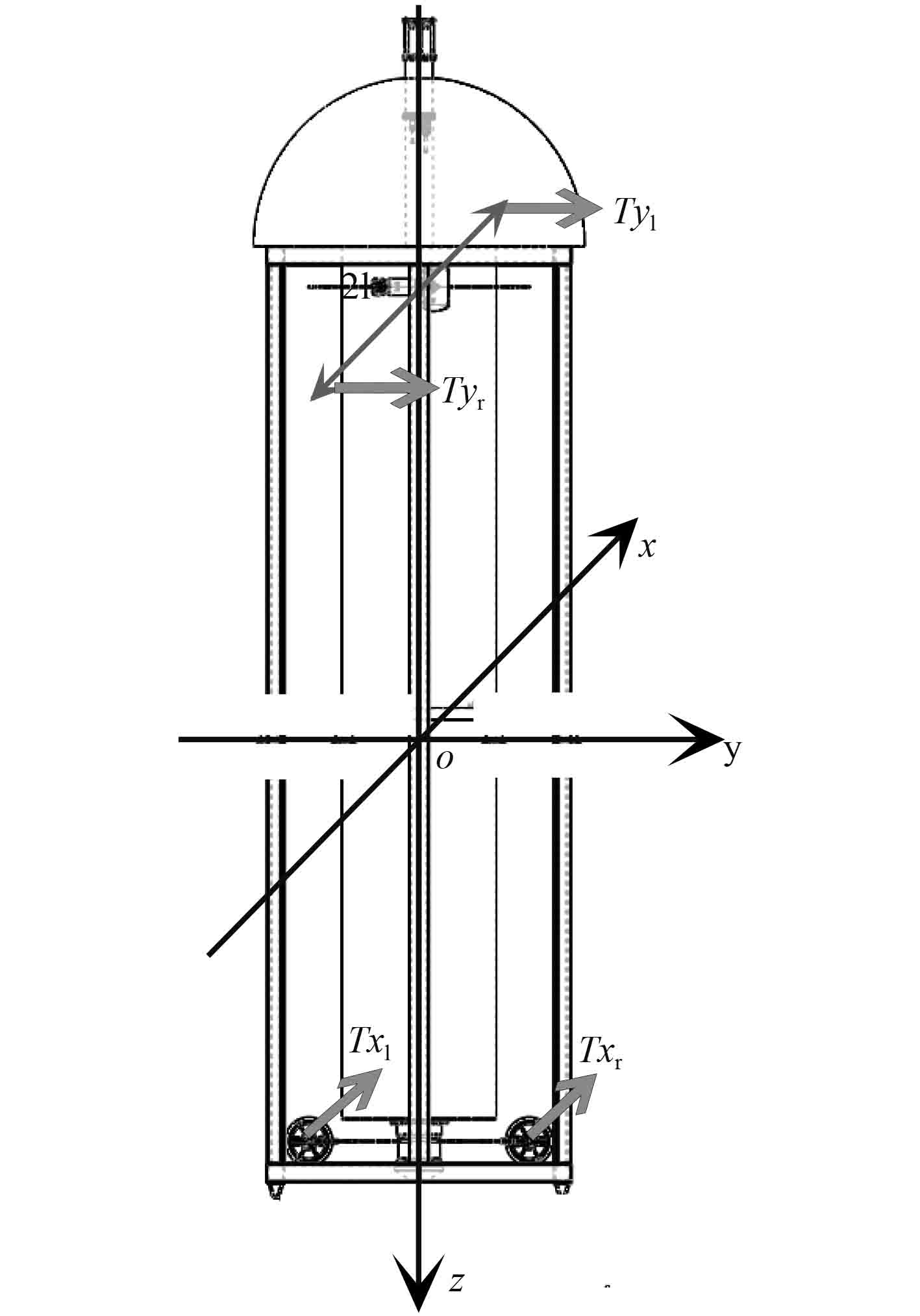
平台理想运动形式为垂向运动,采用不同于常规水下运载器载体坐标系定义方法。载体坐标系按如下方式定义(见图2):载体坐标系原点取在平台几何重心(浮心),Z轴为平台回转体的中心轴,且向下为正;X轴方向与平台底部水平推进器正推力方向一致;Y轴方向与平台顶部水平推进器正推力方向一致。
|
图 2 坐标系定义及推进器布置 Fig. 2 Coordinate system and thruster arrangement |
由于本文仅考虑水平位置控制,且重心浮心在一条垂直线上且重心位于浮心下方足够距离,可保证横/纵倾具有被动稳定性,因此运载器运动方程方程可简化为水平位置和艏向的三自由度运动方程。考虑到平台运动速度较小,忽略耦合项水动力阻尼系数。基于以上条件,平台水平运动方程可写为:
| $ \left\{ {\begin{array}{*{20}{l}} {{{M}}\dot v + {{C}}(v)v + {{D}}(v)v = \tau }{\text{,}} \\ {\dot \eta = {{J}}(\eta )v} {\text{,}} \end{array}} \right. $ | (1) |
这里:
| $ {{M}} = diag{\left\{ {m - X} \right._{\dot u}},m - {Y_{\dot v}},\left. {{I_z} - {N_{\dot r}}} \right\} {\text{,}} $ | (2) |
| $ {{C}}(v) = {{{C}}_{RB}}(v) + {{{C}}_A}(v) {\text{,}} $ | (3) |
| $ {{{C}}_{RB}} = \left[ {\begin{array}{*{20}{c}} 0&{ - mr}&0 \\ {mr}&0&0 \\ 0&0&0 \end{array}} \right] {{{C}}_A} = \left[ {\begin{array}{*{20}{c}} 0&0&{{Y_{\dot v}}v} \\ 0&0&{ - {X_{\dot u}}u} \\ { - {Y_{\dot v}}v}&{{X_{\dot u}}u}&0 \end{array}} \right] {\text{,}} $ | (4) |
| $ {{D}}(v) = - diag\left\{ {{X_u} + {X_{u\left| u \right|}}\left| u \right|,{Y_v} + {Y_{v\left| v \right|}}\left| v \right|,{N_r} + \left. {{N_{r\left| r \right|}}\left| r \right|} \right\}} \right. {\text{,}} $ | (5) |
| $ {{J}}(\eta ) = \left[ {\begin{array}{*{20}{c}} {\cos \psi }&{ - \sin \psi }&0 \\ {\sin \psi }&{\cos \psi }&0 \\ 0&0&1 \end{array}} \right] {\text{。}} $ | (6) |
水平位置控制算法流程如图4所示。控制器水平位置/首向误差

|
图 4 水平面运动控制系统原理图 Fig. 4 Schematic of horizontal plane motion control system |
定义位置/首向误差向量:
| $ \tilde \eta = {\eta _d} - \eta = {\left[ {{x_d} - x,{y_d} - y,{\psi _d} - \psi } \right]^{\rm T}}{\text{。}} $ | (7) |
推力控制律为:
| $ \tau = {{{J}}^{\rm T}}\left( {{{{K}}_p}\tilde \eta + {{{K}}_d}{\dot {\tilde {\eta}}} } \right) = {{{J}}^{\rm T}}{{{K}}_p}\tilde \eta - {{{J}}^{\rm T}}{{{K}}_d}{{J}}v{\text{,}} $ | (8) |
其中:
| $ \left\{ {\begin{array}{*{20}{l}} {{{{K}}_p} = {\rm diag}\left\{ {\left. {{k_{p1}},{k_{p2}},{k_{p3}}} \right\}} \right.}{\text{,}} \\ {{{{K}}_d} = {\rm diag}\left\{ {{k_{d1}},{k_{d2}},{k_{d3}}} \right\}}{\text{,}} \\ {{k_{pi}} > 0,{k_{di}} \geqslant 0{\rm{ }}i = 1,2,3} {\text{。}} \end{array}} \right. $ | (9) |
为证明上述控制器的全局稳定性,参考Fossen等关于PD控制的证明方法[12-14],构造Lyapunov函数如下:
| $ {{V}} = \frac{1}{2}{v^{\rm T}}{{M}}v + \frac{1}{2}{\tilde \eta ^{\rm T}}{{{K}}_p}\tilde \eta {\text{,}} $ | (10) |
对Lyapunov函数求导:
| $ \begin{gathered} {\dot {{V}}} = {v_T}{{M}}\dot v + {{\tilde \eta }^{\rm T}}{{{K}}_p}{\dot {\tilde {\eta}}} = \\ {v^{\rm T}}(\tau - {{C}}(v)v - {{D}}(v)v) + {{\tilde \eta }^{\rm T}}{{{K}}_p}{\dot {\tilde {\eta}}} {\text{,}} \end{gathered} $ | (11) |
将控制律表达式(8)代入上式,由
| $ \dot {{V}} = - {v^T}{{D}}(v)v - {{\dot {\tilde {\eta }}}^T}{{{K}}_d}{\dot {\tilde {\eta}}} \leqslant 0 {\text{。}} $ | (12) |
水下平台由于自身恢复力矩而无需考虑横/纵倾,因此水平推进器可以看成同一水平面布置(如图5),推进器与平台中心轴的距离为l,4个水平推进器(

|
图 5 水平推进器布置(俯视图) Fig. 5 Horizontal thruster arrangement (top view) |
根据平台水平推进器布置,推进器推力的合力应与控制力/力矩相等,各个推进器产生的推力应当满足式:
| $\left\{ {\begin{array}{*{20}{l}} {{f_1} + {f_2} = X} {\text{,}}\\ {{f_3} + {f_4} = Y}{\text{,}} \\ {({f_1} - {f_2} + {f_3} - {f_4})l = N} {\text{。}} \end{array}} \right.$ | (13) |
该方程有4个待求解的推力指令,仅有3个限制方程,从而有无穷组解。为了找到最优解(水平推进系统总功耗最低),需要对推力分配进行优化。参考(Fossen and Sagatun 1991a)中的能耗方程形式[15]:
| $ J(T) = \frac{1}{2}{T^{\rm T}}{{W}}T{\text{,}} $ | (14) |
| $ \left\{ {\begin{array}{*{20}{l}} {arg{\rm{ }} \mathop {\min }\limits_T J(T)} {\text{,}}\\ {s.t.{\rm{ }}\tau - {{B}}T = {{{O}}_{{\rm{3}} \times {\rm{1}}}}} {\text{,}}\\ {\left| {{f_i}} \right| \leqslant {f_{\max }}(i = 1,2,3,4)} {\text{。}} \end{array}} \right. $ | (15) |
其中,
| $ {{W}} = {{I}} = {\rm diag}\left\{ {1,1,1,1} \right\}{\text{,}}\;\;\;{{B}} = \left[ {\begin{array}{*{20}{l}} 1&1&0&0 \\ 0&0&1&1 \\ l&{ - l}&l&{ - l} \end{array}} \right]{\text{。}} $ |
为保证方程(15)有解需要对控制器产生的推力合力指令
| $\left\{ {\begin{array}{*{20}{c}} {{X / {2 + {N / {(4l) \leqslant {f_{\max }}}}}}} {\text{,}}\\ {{X / {2 - {N / {(4l) \leqslant {f_{\max }}}}}}}{\text{,}} \\ {{Y / {2 + {N / {(4l) \leqslant {f_{\max }}}}}}}{\text{,}} \\ {{Y / {2 - {N / {(4l) \leqslant {f_{\max }}}}}}}{\text{,}} \end{array}} \right.$ | (16) |
根据方程(15)中的不等式约束条件,定义函数:
| $\left\{ {\begin{array}{*{20}{l}} {{g_1}(f) = f - {f_{\max }} \leqslant 0} {\text{,}}\\ {{g_2}(f) = - f - {f_{\max }} \leqslant 0} {\text{,}} \end{array}} \right.$ | (17) |
使用Lagrange方法对方程(15)进行求解[17],定义函数
| $ \begin{gathered} L(T,\lambda ,\alpha ,\beta ) = \frac{1}{2}{T^{\rm T}}{{W}}T + {\lambda ^{\rm T}}(\tau - {{B}}T) + \\ \sum\limits_{i = 1}^4 {{\alpha _i}} {g_1}({f_i}) + \sum\limits_{i = 1}^4 {{\beta _i}} {g_2}({f_i}) {\text{,}} \end{gathered} $ | (18) |
根据KKT(Karush-Kuhn-Tucher)条件,以上方程的解
| $ \frac{{\partial L}}{{\partial T}}\left| {_{T = {T^*}} = } \right.{{W}}{T^*} - {{{B}}^T}\lambda + \alpha - \beta = {{{O}}_{{\rm{4}} \times {\rm{1}}}}{\text{,}} $ | (19) |
| $ \left\{ \begin{aligned} & {\frac{{\partial L}}{{\partial \lambda }}\left| {_{T = {T^*}} = \tau - {{B}}{T^*} = {{{O}}_{{\rm{3}} \times {\rm{1}}}}} \right.} {\text{,}}\\ & {{\lambda _i} \ne 0{\rm{ }}(i = 1,2,3)} \end{aligned} \right. $ | (20) |
| $\left\{ {\begin{array}{*{20}{l}} {{\alpha _i}{g_1}({f_i}) = 0}{\text{,}} \\ {{\beta _i}{g_2}({f_i}) = 0} {\text{,}}\\ {{\alpha _i},{\beta _i} \geqslant 0}{\text{,}} \\ {\left| {{f_i}} \right| \leqslant {f_{\max }}{\rm{ }}(i = 1,2,3,4)} {\text{,}} \end{array}} \right. $ | (21) |
在控制力
| $ {T^*} = {{{W}}^{ - 1}}{{{B}}^{\rm T}}{({{B}}{{{W}}^{ - 1}}{{{B}}^{\rm T}})^{ - 1}}\tau = {B^† }\tau {\text{,}} $ | (22) |
将平台实际参数代入上式,得到推力分配关系为:
| ${T^*} = \left[ {\begin{array}{*{20}{c}} {{f_1}*} \\ {{f_2}*} \\ {{f_3}*} \\ {{f_4}*} \end{array}} \right] = {B^† }\tau = \left[ {\begin{array}{*{20}{l}} {{1 / 2}}&0&{{1 / {(4l)}}} \\ {{1 / 2}}&0&{{{ - 1} / {(4l)}}} \\ 0&{{1 / 2}}&{{1 / {(4l)}}} \\ 0&{{1 / 2}}&{{{ - 1} / {(4l)}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} X \\ Y \\ N \end{array}} \right]{\text{。}}$ | (23) |
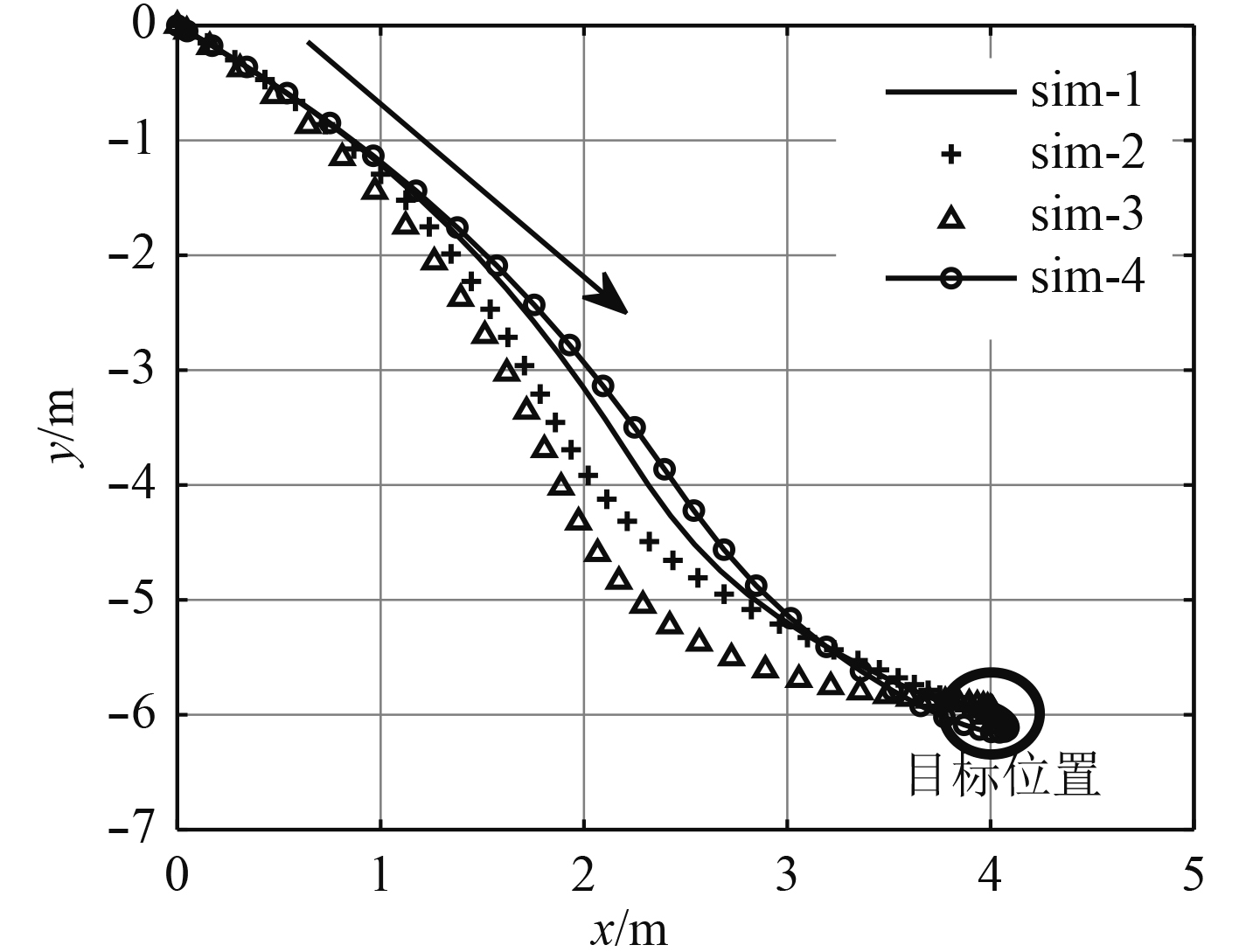
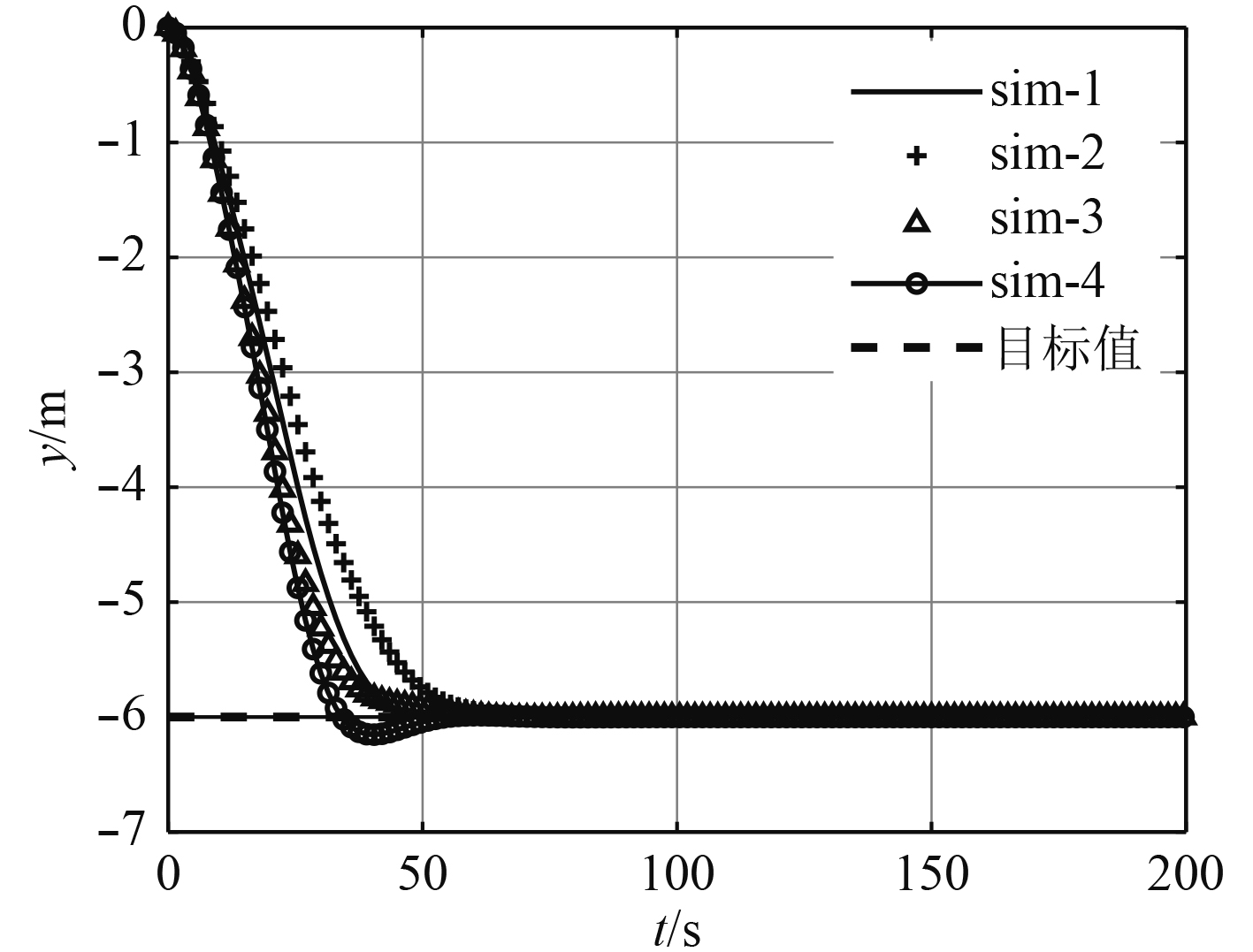
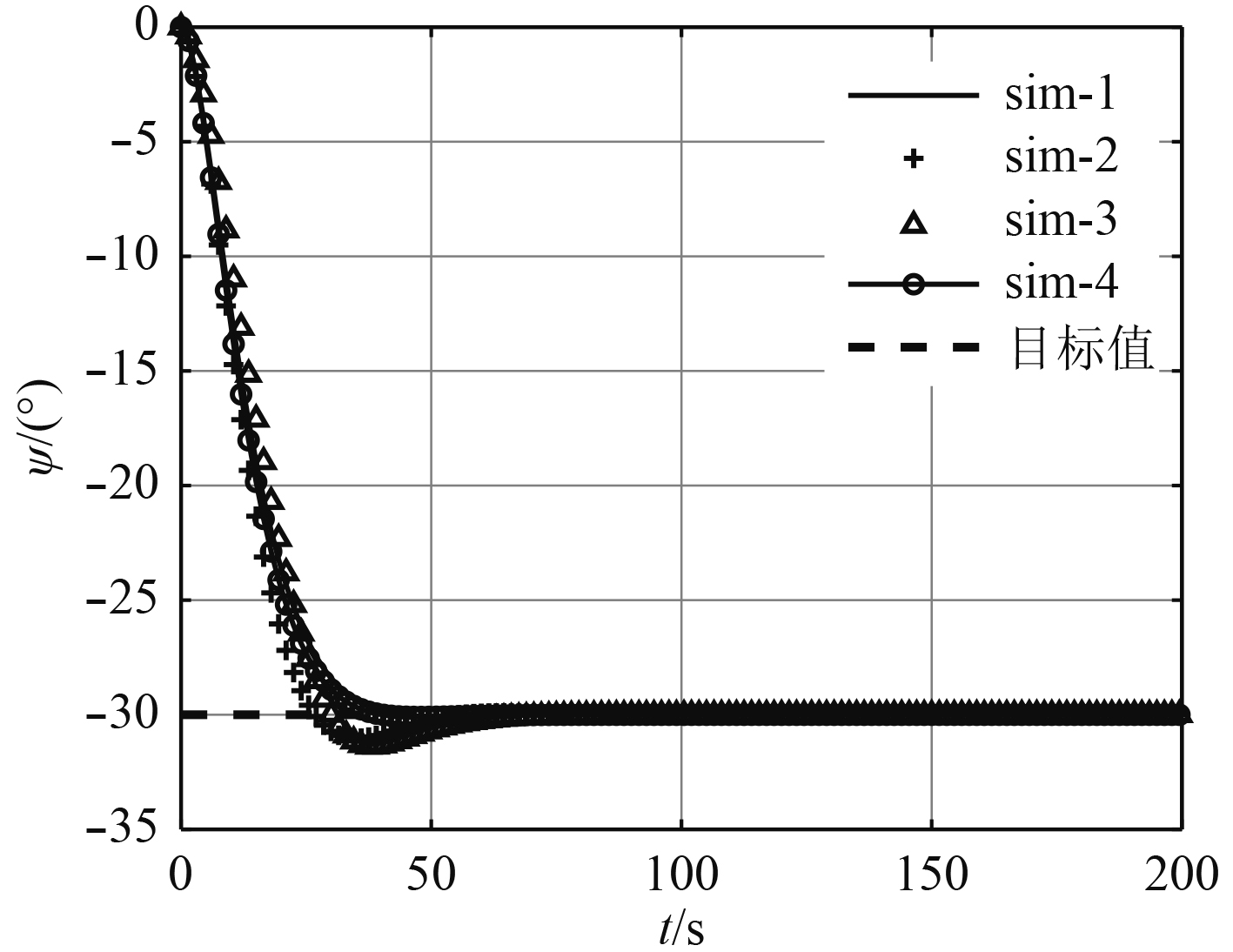
为了验证位置控制算法,进行了Matlab/Simulink定步长仿真,计算步长取为0.5 s,与平台组合导航系统的实际采样周期一致。此外,根据实际情况对推进器推力进行了饱和限制(限定推力范围),设定仿真总时长设为200 s。设定模型初始位置坐标为(0,0),初始艏向角为0°,目标位置坐标为(4,–6),目标艏向角为–30°。
由于平台外形的不规则,难以获取精确的模型参数。质量与惯性矩根据三维软件的设计图纸计算而来,平台模型经过简化处理后导入计算流体力学软件(如STAR-CCM+)得到剩下的水动力参数估计值,存在较大的不确定性。根据平台关于X-Y轴对称可知
|
|
表 2 仿真模型参数 Tab.2 Simulation model parameters |
由于参数的不确定性,随机选取了其中四组仿真结果,见图6~图9。从仿真结果可以看出,水平位置及艏向角均能实现稳定控制,且没有稳态误差。此外,从图中也可以看出控制器性能与参数选取具有一定关系,但均能实现稳定控制,实验中可以根据控制效果对参数进行进一步优化。本文在仿真中选取的控制器参数为:
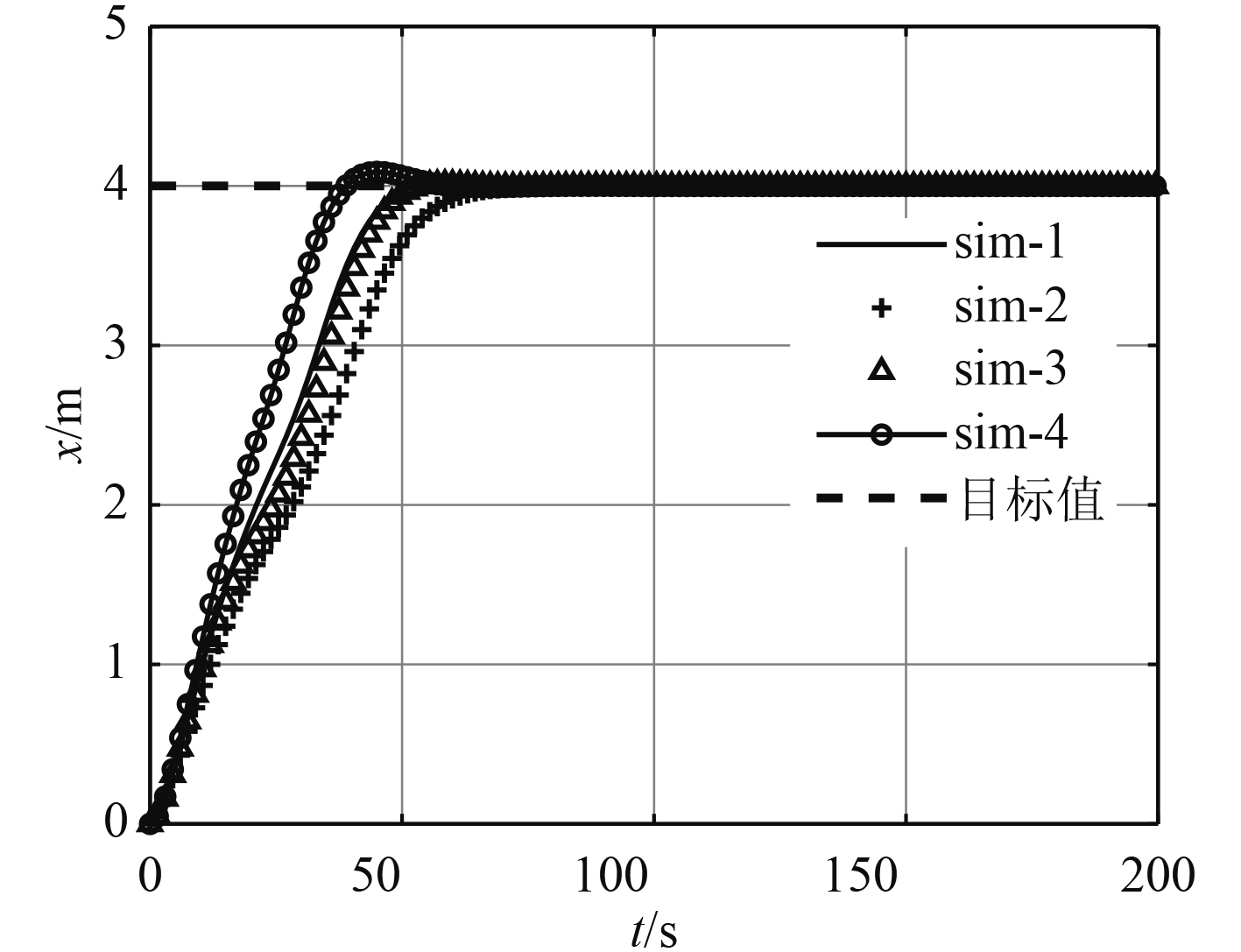
|
图 6 北向位置控制 Fig. 6 Northward position control |
|
图 9 水平位置控制 Fig. 9 Horizontal position control |
| $ \left\{ \begin{aligned} & {{{{K}}_p} = {\rm diag}\left\{ {150,150,\left. {15} \right\}} \right.}{\text{,}} \\ & {{{{K}}_d} = {\rm diag}\left\{ {40,40,50} \right\}} {\text{。}} \end{aligned} \right. $ |
|
图 7 东向位置控制 Fig. 7 Eastward position control |
|
图 8 首向控制 Fig. 8 Heading control |
本文设计了一种新型水下自治平台的水平面运动控制系统,其控制算法不依赖于模型参数,且能实现推进器功耗最低。对该平台进行的三自由度仿真结果表明:该方法不依赖与被控对象的模型参数,能够快速收敛到目标值且无稳态误差。此外该方法简单有效,参数意义明确,仿真与实验中都能够很方便的进行参数调节。
下一步,将应用水下平台湖试以进一步验证其有效性。
| [1] |
冯正平. 国外自治水下机器人发展现状综述[J]. 鱼雷技术, 2005, 13(1): 5-9. DOI:10.3969/j.issn.1673-1948.2005.01.002 |
| [2] |
徐玉如, 庞永杰, 甘永, 等. 智能水下机器人技术展望[J]. 智能系统学报, 2006, 1(1): 9-16. |
| [3] |
徐玉如, 李彭超. 水下机器人发展趋势[J]. 自然杂志, 2011, 33(3): 125-132. |
| [4] |
YAN Zheping,ZHOU Jiajia.Control technology of underwater unmanned vehicles[M].Beijing: National Defense Industry Press,2015: 4-15.
|
| [5] |
赵志高, 杨建民. 动力定位系统发展状况及研究方法[J]. 海洋工程, 2002, 20(1): 91-97. DOI:10.3969/j.issn.1005-9865.2002.01.017 |
| [6] |
王芳, 万磊, 徐玉如, 等. 深水半潜式钻井平台动力定位实时交互仿真系统[J]. 哈尔滨工程大学学报, 2011, 32(11): 1395-1401. DOI:10.3969/j.issn.1006-7043.2011.11.001 |
| [7] |
ZHAO S, QIAO C, WANG Y. On the navigation positioning technologies in AUV underwater docking[C]//Control Conference. IEEE, 2012: 4474-4479.
|
| [8] |
王婷, 宋保维. 水下航行器多推进器动力定位控制[J]. 兵工学报, 2006, 27(5): 845-850. DOI:10.3321/j.issn:1000-1093.2006.05.017 |
| [9] |
RAHIMAH J. Development of prototype remotely operated underwater vehicle[J]. 2011.
|
| [10] |
YANG Z Y, YANG H F. Research on fuzzy PID control of double closed-loop DC speed tuning system[J]. Application Research of Computers, 2011. |
| [11] |
HARROLD S O, LIAO D Z, YEUNG L F. An autonomous underwater platform[M]. 1997.
|
| [12] |
KÄLLSTRÖM C G. Guidance and control of ocean vehicles: By Thor I. Fossen. Wiley, Chichester (1996). ISBN 0-471-94113-1[J]. Automatica, 1996, 32(8): 1235. |
| [13] |
TANAKITKORN K, WILSON P A, TURNOCK S R, et al. Depth control for an over-actuated, hover-capable autonomous underwater vehicle with experimental verification[J]. Mechatronics, 2017, 41: 67-81. DOI:10.1016/j.mechatronics.2016.11.006 |
| [14] |
JIN S, KIM J, KIM J, et al. Six-degree-of-freedom hovering control of an underwater robotic platform with four tilting thrusters via selective switching control[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(5): 2370-2378. DOI:10.1109/TMECH.2014.2378286 |
| [15] |
FOSSEN T I, SAGATUN S I. Adaptive control of nonlinear systems: a case study of underwater robotic systems[J]. Journal of Robotic Systems, 1991, 8(3): 393-412. DOI:10.1002/rob.4620080307 |
| [16] |
OMERDIC E, ROBERTS G. Thruster fault diagnosis and accommodation for open-frame underwater vehicles[J]. Control Engineering Practice, 2004, 12(12): 1575-1598. DOI:10.1016/j.conengprac.2003.12.014 |
| [17] |
ABDI B, MIRZAEI M, GHARAMALEKI R M. A new approach to optimal control of nonlinear vehicle suspension system with input constraint[J]. Journal of Vibration & Control, 2017(1): 107754631770459. |
 2020, Vol. 42
2020, Vol. 42
