2. 中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110169;
3. 中国科学院大学,北京 100049
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
海洋探索的主要方式是母船携带AUV至指定位置,布放其进行水下作业,AUV完成任务后,人工回收至母船。母船式海洋作业流程经过数十年的经验累积,安全性、可靠性较高,但效率较低,人类已探索的海底只有5%,还有95%未知海底,海洋探索方式进入一个瓶颈期。
基于目前情况,美国、日本提出下一步设计规划,以及国际组织XPRIZE举办Shell Ocean Discovery(以下简称海洋探测大赛),旨在提高海洋探索的自主性、规模、速度、深度和分辨率,突破目前瓶颈。伍兹霍尔海洋研究所提出了“未来海洋作业三步走发展规划”[1],提出ASV(Autonomous Surface Vehicles,ASV)充当母船通信的中继信标协调AUV完成大范围、超视距作业,逐步实现AUV长时海洋探测工作。日本针对其周围海域提出了“自盘古”计划[2],使用ASV与水面艇协助AUV作业,并提出可在海床移动、采集样品的ROV(Remote Operated Vehicle,ROV),完成研究矿床成因等科研任务。海洋探测大赛是一项为期3年、耗资700万美元的全球竞赛,日本GEBCO-NF团队采用无人艇与AUV协同作业方案,高效完成在有限条件下对规定区域探测并赢得比赛冠军[3]。
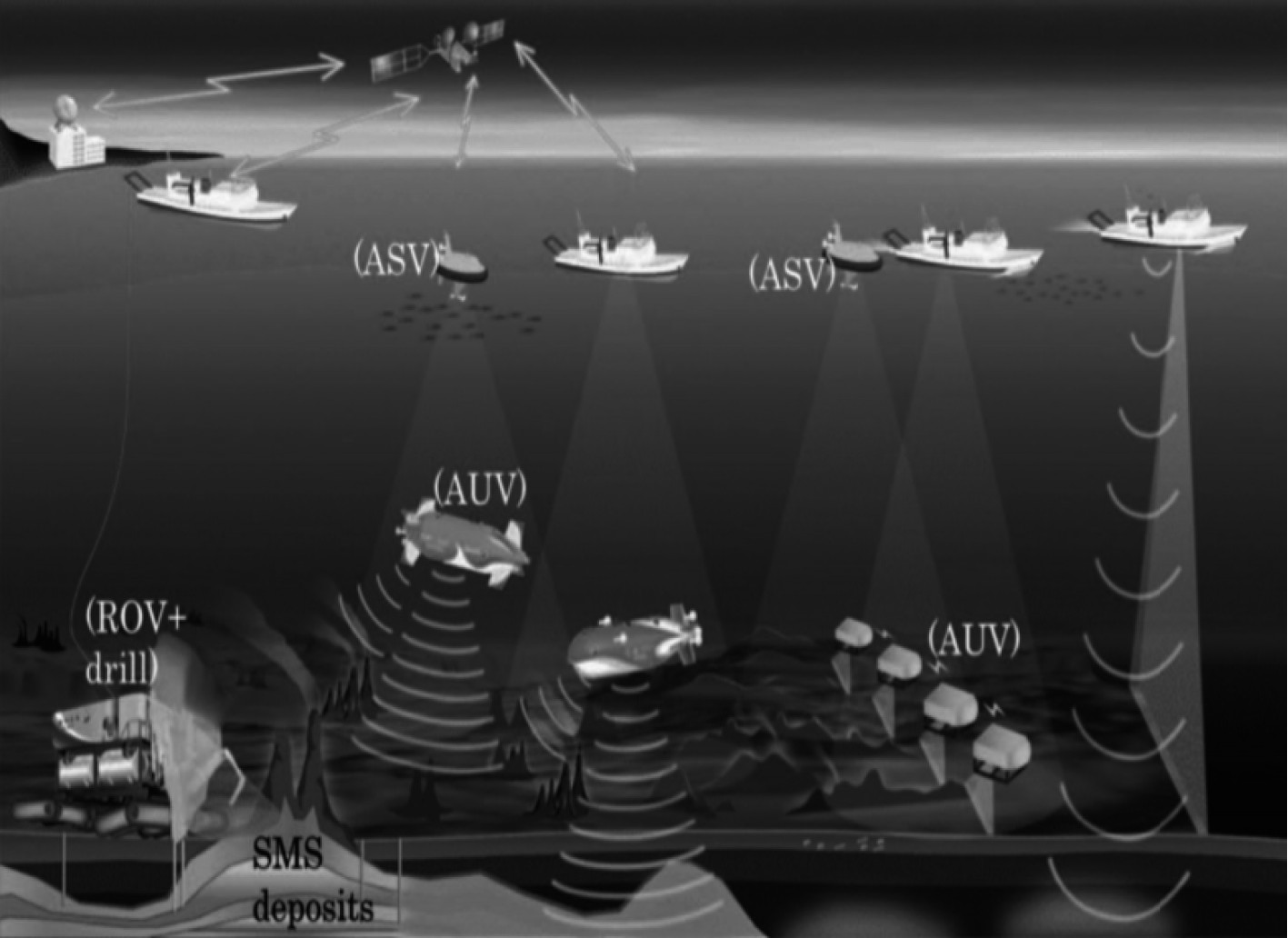
|
图 1 “自盘古”计划示意图 Fig. 1 Schematic illustration of the Zipangu project |
本文针对未来海洋探测,基于目前海洋技术水平,结合USV与AUV各自优势,弥补AUV携带能源有限、USV探测深度有限等缺陷,提出USV与AUV一体化系统概念设计,并针对一体化系统的需求提出一种三体船型USV。回收方案设计为USV水面动态回收AUV,并根据水面回收流程,以某便携式AUV为模型,研究AUV静水面航行的水动力特性分析,通过CFD软件分析结果、水动力简化模型理论推导以及外场水域试验数据对比,证明该CFD软件分析的可靠性和准确性。针对回收过程中USV尾流对AUV水面航行的影响进行了15种工况下的对比仿真分析,得出AUV回收最佳工况。
1 USV与AUV一体化概念设计USV与AUV一体化系统包括一对AUV与三体船型USV组合,USV具备运输、收放、补给、跟踪、通信、定位AUV的能力,在水下一定深度、一定面积进行USV与AUV协同作业。一体化系统作业模式包括定位作业流程、收放作业流程、通信作业流程、运载作业流程、艇载数据处理作业流程、补给作业流程。一体化系统适应于深远海的自主作业,作业期间无需母船直接协助,降低作业成本、提高作业效率。
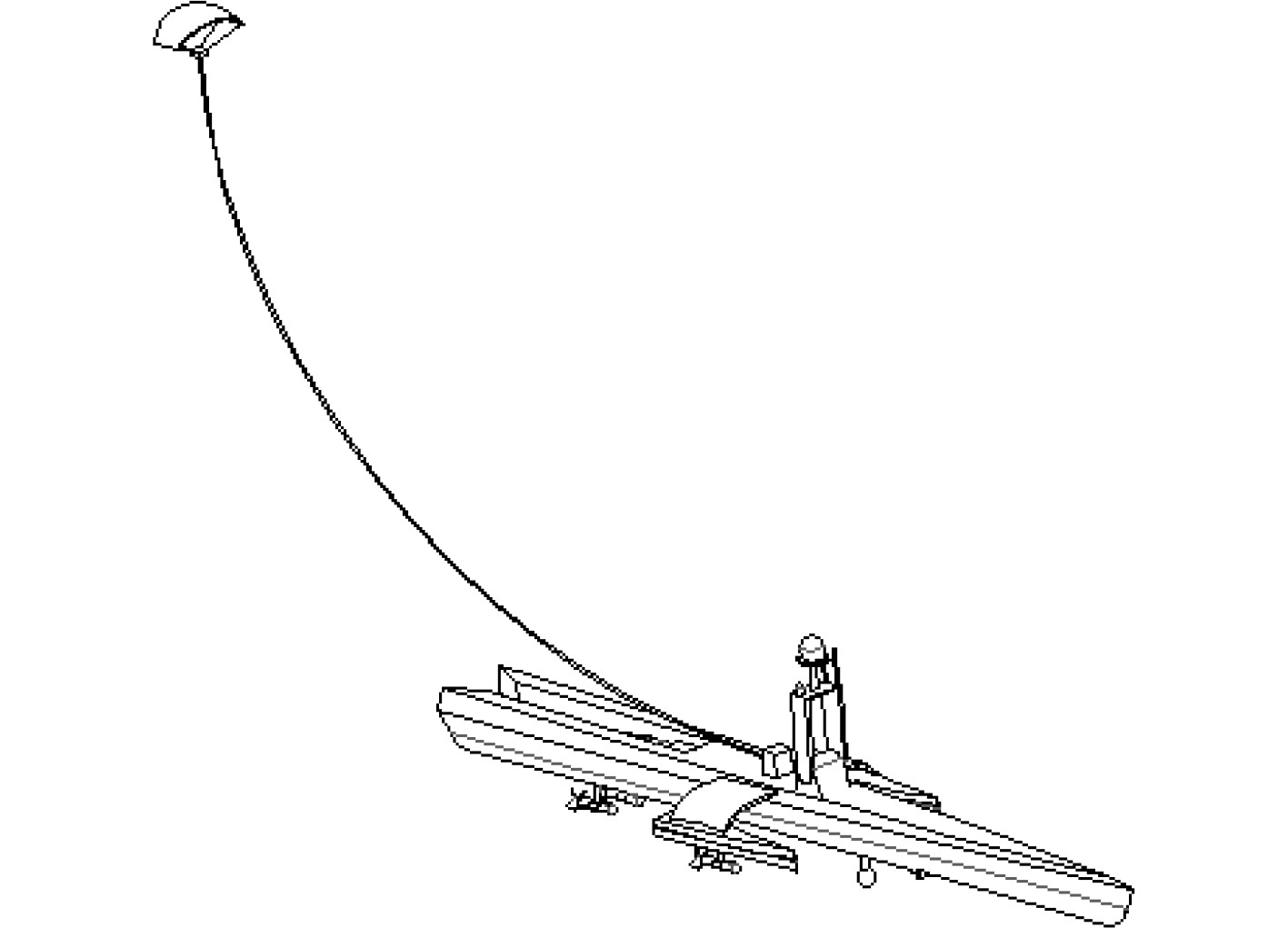
|
图 2 三体船示意图 Fig. 2 Schematic illustration of the trimaran |
收放作业流程分为AUV回收作业流程和AUV布放作业流程。

|
图 3 水面回收场景图 Fig. 3 Schematic illustration of the recovery scenario on the water |
1)回收作业流程
AUV在超短基线定位系统导航下归航至进入无线通信引导,AUV在无线通信下与USV同向航行,通过速度差进入USV主舱体;当AUV靠近USV尾部,导向板微调AUV前行方向,AUV首部触碰传送带,传送带上表面滚动方向朝向船首,AUV紧贴传送带进入主舱体,AUV首部碰触限位装置限位,限位信号经由艇载微型处理器处理,下达指令1传送带停止工作、下达指令2经由无线通信至AUV停止推进器工作、下达指令3夹紧装置固定AUV,完成收放作业流程回收作业。
2)AUV布放作业流程
夹紧装置停止工作,传送带上表面滚动方向朝向三体船船尾,AUV紧贴传送带进入水域,完成收放作业流程布放作业。
针对一体化系统AUV回收采取水面回收,相对于水下回收方式,其通信环境较恶劣、控制较复杂、回收装置限定条件较多[4 – 7]。水面回收优势是将水下三维对点转换为水面二维回收,并采取无线导引,增大回收成功概率。针对一体化作业要求多次收放AUV,水面回收对AUV外形无需改动,减少AUV额外功耗,USV尾部借鉴登陆舰尾部斜坡设计,便于运放AUV。
动态回收考虑USV在水面无法固定于一点、易受扰动,降低回收成功概率,故USV水面直线航行保证方向稳定性,AUV通过无线导引方式以较快于USV的速度同方向追赶,通过速度差实现进入USV后舱,提高回收成功概率。两者对接相对速度较小,同时减小碰撞力。水面回收的缺点是海浪对其影响较大,故便携式AUV回收应在低海况下进行,仿真环境设置为静水面环境。
1.2 其他作业流程定位作业流程包括中国北斗卫星导航系统定位USV以及USV超短基线定位AUV。通信作业流程包括水下通信、水面通信及卫星通信3部分,其中水下通信使用水声通信机完成信息传递,水面通信利用无线通信设备形成通信网络,卫星通信使用北斗通信系统,三者形成通信链路。艇载数据处理作业流程用于对USV接收数据进行相关分析得出下一步运行指令;运载系统是指AUV固定于USV主舱体,USV运输AUV至目标区域;补给作业流程对位于USV主舱体内的AUV进行无线充电。
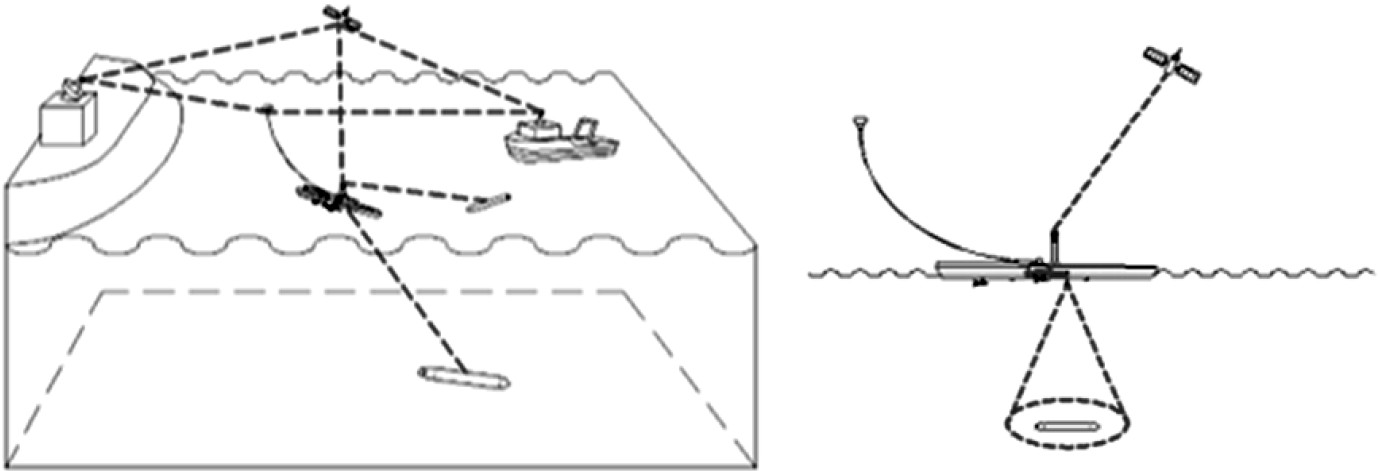
|
图 4 通信作业和定位作业场景图 Fig. 4 Schematic illustration of the communication and location work processes |
一体化系统作业模式作业流程为:AUV固定于USV主舱体,USV离开基站或母船,USV与基站或母船时刻通过无线通信或卫星通信保持数据、指令传输,USV自身位置通过定位作业流程北斗卫星定位;运输AUV至指定作业区域,USV收放作业流程布放AUV,AUV开始位于一定深度水域作业,无人水面艇超短基线定位作业流程定位AUV,USV通过水下通信相互传输信息至AUV,完成水下一定深度作业后,AUV上浮水面,USV收放装置回收AUV,AUV固定于USV主舱体,USV补给作业流程补给AUV,AUV通过无线数据传输系统传输原始数据,艇载数据处理作业流程处理原始数据,USV通过无线数据传输系统传输指令至AUV,完成一次作业流程,数次循环直至完成任务要求,USV返回基站或母船。
2 AUV静水面航行垂直面三自由度的水动力分析 2.1 AUV仿真模型参数设置针对USV水面回收AUV步骤,第1步AUV需要稳定在水面航行,以某便携式AUV为模型,通过STAR-CCM+水动力软件构建仿真模型。AUV质量75 kg,长度1776 mm,直径250 mm,静浮力0.5 kg,浮心距首部830 mm。

|
图 5 便携式AUV Fig. 5 Portable AUV |
AUV尾舵采用NACA0012翼型,弦长115 mm,展长110 mm,展弦比0.96。

|
图 6 AUV垂直面动网格 Fig. 6 AUV moving grid on vertical plane |
AUV仿真流域设定为45 m×4 m×5 m,本文在计算域内设置双重网格加密区,以提高体网格质量,在保证计算精度前提下,提高仿真环境模型计算效率。仿真流域网格基础值0.20 m;第1重自由液面加密区尺度为45 m×4 m×3 m,基础值0.06 m;第2重AUV计算加密区为3 m×1 m×1 m,基础值0.03 m。
2.2 案例分析根据之前试验情况以及以往工作经验,AUV稳定在水面航行必须保持上浮舵状态,否则AUV首部将呈现大幅震荡状态,不满足实际动态水面回收方案对AUV的航行要求,故仿真过程中需对不同舵角进行仿真计算,寻求最佳航行状态。选取舵角10°、推进力20 N为例。
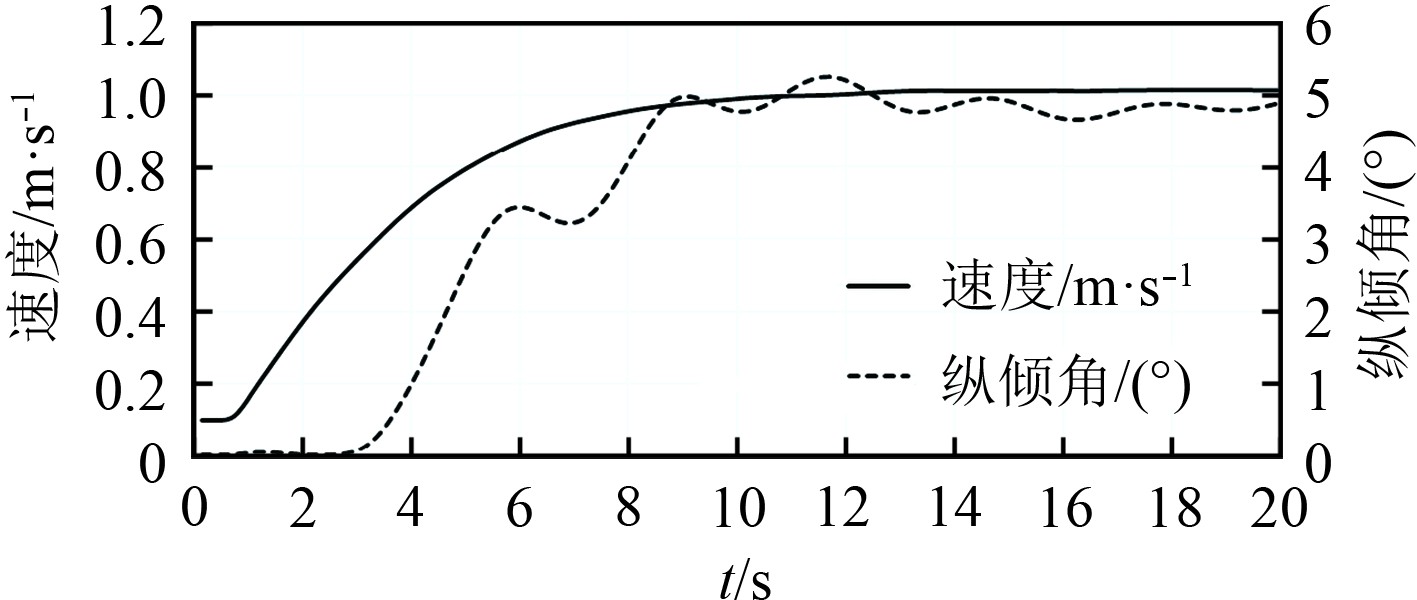
|
图 7 AUV纵倾角、速度变化曲线 Fig. 7 Variation curves of pitch and velocity of AUV |
仿真结果看,AUV仿真计算收敛后,最后速度和纵倾角稳定在一定数值范围内,水平前行运动,AUV的纵倾角与冲角相等,速度水平向前,符合实际航行现象。

|
图 8 AUV水面稳定航行 Fig. 8 AUV surface stability navigation |
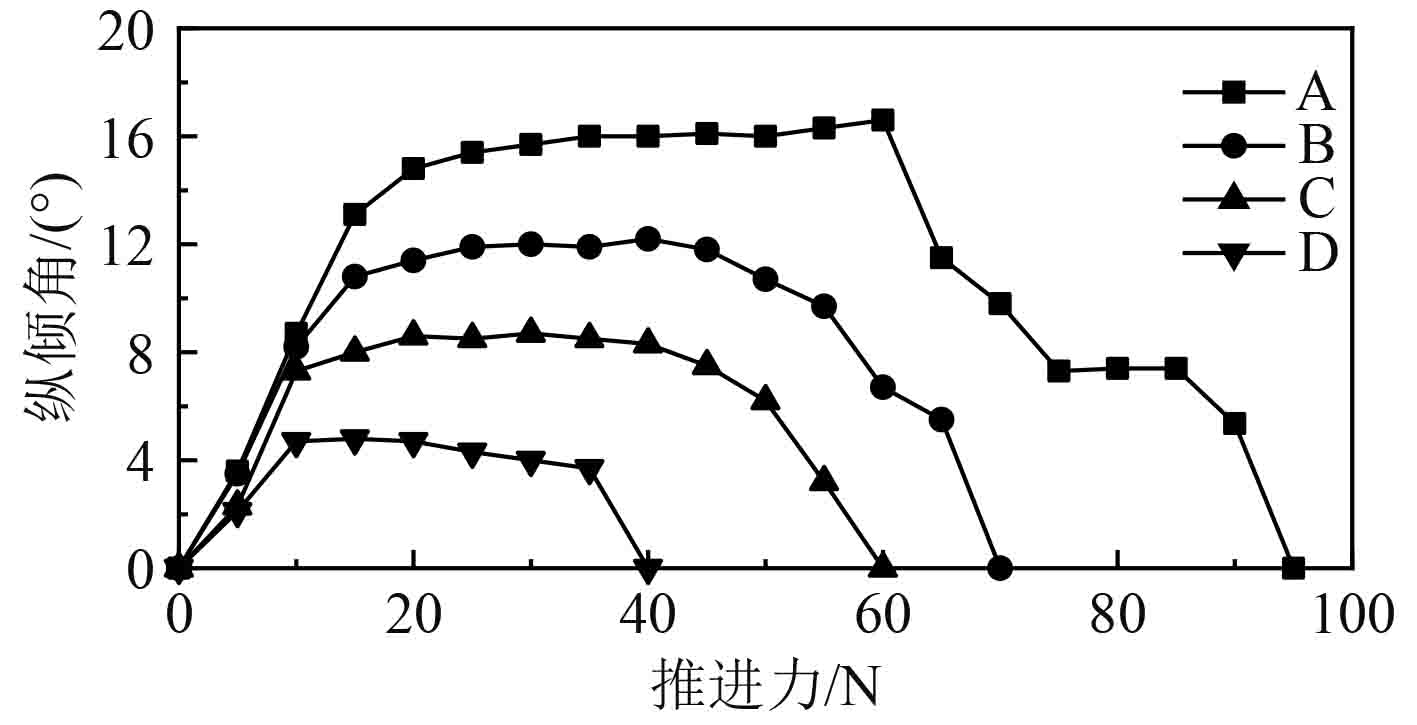
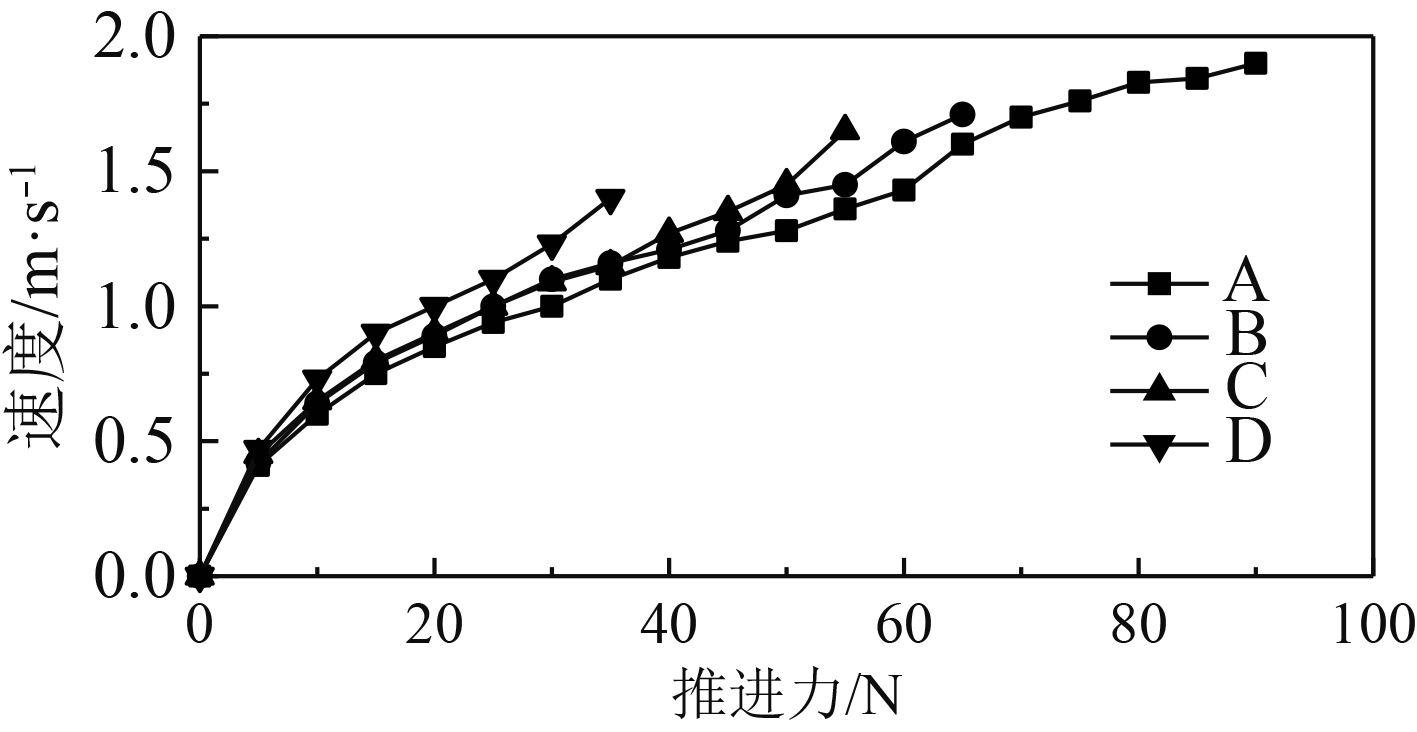
选取舵角5°,10°,15°,20°,25°五种工况分析,对AUV尾部处轴线方向施加5~100 N推进力,多种工况进行仿真计算,结果如图9和图10。其中A,B,C,D分别表示舵角10°,15°,20°,25°。
|
图 9 AUV舵角与纵倾角关系曲线 Fig. 9 Curve of relationship between rudder angle and pitch angle of AUV |
|
图 10 AUV推进力与稳定速度关系曲线 Fig. 10 Curve of relationship between rudder angle and constant velocity of AUV |
在相等舵角工况下,纵倾角随推进力增加先增大至平稳再减小,舵角越大纵倾角越大,大致呈现线形关系,AUV极限速度也随着舵角增大而增大,平均速度1.665 m/s。
2.4 AUV水面航行水动力建模本节主要根据仿真数据相关结论,构造AUV垂直面水动力模型,并进行水动力计算推导,并与仿真结果进行对比,验证仿真结果可靠性。
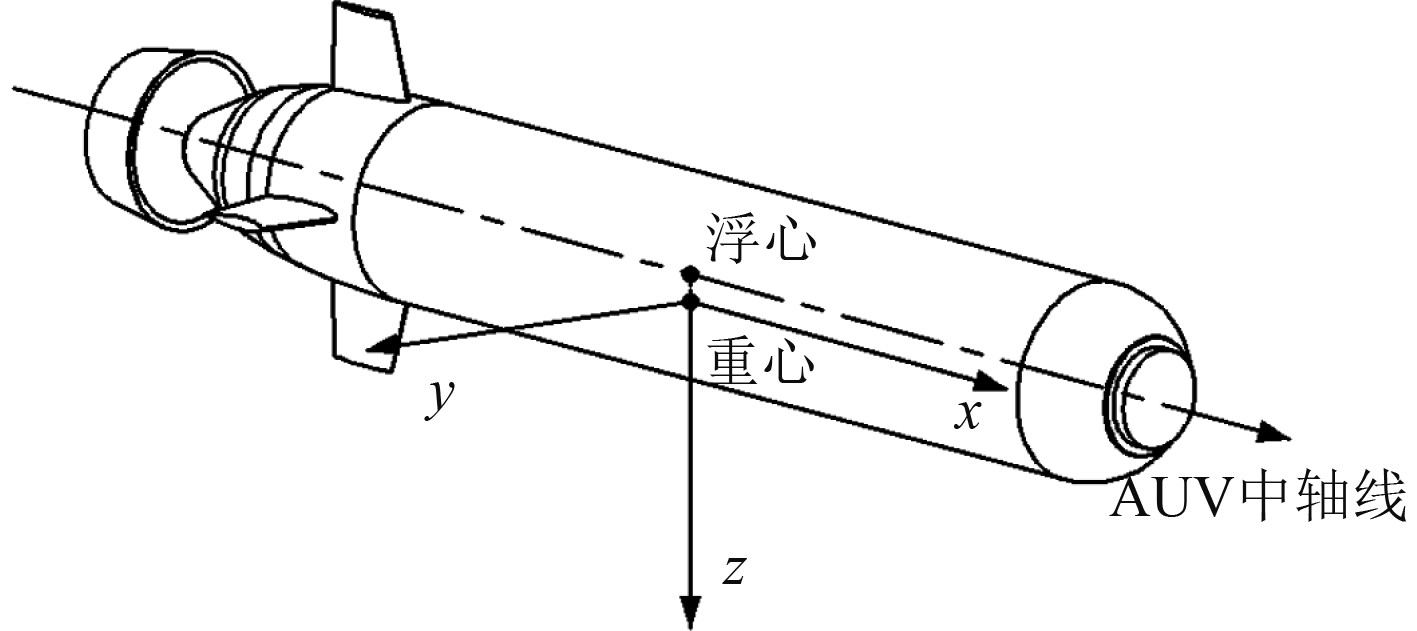
动系原点与AUV重心重合,AUV重心位于浮心正下2 mm,如图11所示。
|
图 11 AUV运动坐标系 Fig. 11 The moving coordinate system of AUV |
AUV一般运动方程建模,问题只考虑垂直面运动求解。
| $\left\{ \begin{array}{l} m\left( {\dot u + qw} \right) = X\text{,} \\ m\left( {\dot w - qu} \right) = Z \text{,} \\ {I_y}\dot q = M \text{。}\\ \end{array} \right.$ | (1) |
研究AUV水面匀速直线运动时,由于偏离
| $\left\{ \begin{array}{l} X = {X_0} + {X_u}u \text{,} \\ Z = {Z_0} + {Z_w}w + {Z_q}q + {Z_\delta }\delta \text{,} \\ M = {M_0} + {M_w}w + {M_q}q + {M_\delta }\delta \text{。} \\ \end{array} \right.$ | (2) |
式中:X0为AUV直线航行阻力;Z0为AUV上下不对称导致z轴方向力;M0为AUV前后不对称导致y轴力矩;Xu,Zw,Mw为速度系数;Zq,Mq为角速度系数;
由于动系原点与AUV重心重合,重心位于中心垂直动系
| ${M_P} = - P \cdot {x_P}\text{。}$ | (3) |
由静力学可知,当AUV俯仰运动时导致重力与浮力作用不在同一铅垂线上构成浮力扶正力矩,其中h为AUV稳心高,g为重力加速度。
| ${M_H}(\theta ) = ( - mgh + P)\sin \theta\text{。} $ | (4) |
当纵倾角不大时,取
| ${M_H}(\theta ) \approx {M_\theta }\theta\text{,} $ | (5) |
| ${M_\theta } = - mgh + P\text{。}$ | (6) |
由于螺旋桨轴线不与Gx轴重合,螺旋桨推力
| ${M_T} = {X_T} \cdot {z_T}\text{。}$ | (7) |
设定AUV弱机动运动,故忽略X方向等式,并代入水动力式,计及剩余静载、扶正力矩和桨力矩,并考虑AUV前后不对称时的垂直面操纵运动方程式:
| $\left\{ \begin{array}{l} (m - {Z_{\dot w}})\dot w - {Z_{\dot q}}\dot q - {Z_w}w - (mV + {Z_q})q \\ = {Z_0} + {Z_\delta }\delta + P\text{,} \\ ({I_y} - {M_{\dot q}})\dot q - {M_q}q - {M_{\dot w}}\dot w - {M_w}w \\ = {M_0} + + {M_\delta }\delta + {M_T}\delta + {M_P} + {M_\theta }\theta \text{。} \\ \end{array} \right.$ | (8) |
AUV水面匀速运动时,运动参数
| $\left\{ \begin{array}{l} {Z_\delta }\delta + P + {Z_w}w = 0\text{,} \\ {M_0} + {M_\delta }\delta + {M_T} + {M_P} + {M_\theta } + {M_w}w' = 0 \text{。} \\ \end{array} \right.$ | (9) |
上式水动力导数和运动参数都是有因次项,不便于比较,对上式进行无因次化,力遍除
上式相应无因次形式为:
| $\left\{ \begin{array}{l} {{Z'}_\delta }\delta + P' + {{Z'}_w}w = 0 \text{,} \\ {{M'}_0} + {{M'}_\delta }\delta + {{M'}_T} + {{M'}_P} + {{M'}_\theta }\theta + {{M'}_w}w' = 0\text{。} \\ \end{array} \right.$ | (10) |
通过仿真不同潜深的拘束船模试验测定,考虑自由水面对水动力系数的影响[8],校正后:
| $\left\{ \begin{array}{l} {{Z'}_w} \approx {{Z'}_{w\infty }} = - {\rm{0}}{\rm{.0007569}}\text{,} \\ {{M'}_w} \approx 1.1 \times {{M'}_{w\infty }} = {\rm{0}}{\rm{.0004304}}\text{,} \\ {{Z'}_\delta } \approx {{Z'}_{\delta \infty }} = 0.00063879 \text{,} \\ {{M'}_\delta } \approx {{M'}_{\delta \infty }} = 0.00046659 \text{。} \\ \end{array} \right.$ | (11) |
AUV水面俯仰定常运动时,可看作带纵倾角定深航行,定深深度近似为0,
| $ \theta = - \frac{{{{Z'}_\delta }}}{{{{Z'}_w}}}\delta - \frac{{P'}}{{{{Z'}_w}}} {\text{,}} $ | (12) |
代入相应数值,可得:
| $ \theta = 0.844\delta - 4.48 {\text{。}} $ | (13) |
对比仿真与计算数值,以及后续的外场水域试验数据,得出下表。
通过水动力计算纵倾角与仿真纵倾角对比,仿真稳定数值与水动力计算数值相差较小,仿真结果AUV稳定航行时纵倾角与舵角呈线形关系,纵倾角与AUV外形结构以及静浮力相关。
2.5 AUV垂直面极限速度求解AUV不同舵角下的极限速度,由公式化简可得:
| $\begin{split} {{M'}_0} + & {{M'}_P} + {{M'}_\delta }\left( - \dfrac{{{{Z'}_w}}}{{{{Z'}_\delta }}}\theta - \dfrac{{P'}}{{{{Z'}_\delta }}}\right) + {{M'}_T} + \\ & {{M'}_\theta }\theta + {{M'}_w}\theta = 0 \\ \end{split} $ | (14) |
将其中与速度相关水动力系数代入u计算:
| $\left\{ \begin{array}{l} P'(u) = \dfrac{{Pg\cos \theta }}{{\dfrac{1}{2}\rho {u^2}{L^2}}}\text{,} \\ {{M'}_0}(u) = \dfrac{{{M_0} + {M_P}}}{{\dfrac{1}{2}\rho {u^2}{L^2}}} \text{,} \\ {{M'}_\theta }(u) = \dfrac{{{M_\theta }}}{{\dfrac{1}{2}\rho {u^2}{L^2}}}\text{。} \\ \end{array} \right.$ | (15) |
| ${M_T}(u,\delta ) = {X_T}(u,\delta ) \cdot {z_T}\text{,}$ | (16) |
| ${X_T}(u,\delta ) = \left\{ \begin{array}{l} 39.47u - 19.87(\delta = {10^ \circ })\text{,} \\ 58.82u - 33.38(\delta = {15^ \circ })\text{,} \\ 70.48u - 46.26(\delta = {20^ \circ }) \text{,} \\ 79.73u - 53.23(\delta = {25^ \circ }) \text{。} \\ \end{array} \right.$ | (17) |
化简:
| $ {M_T}(u) = {X_T}(u,\delta ) \cdot {z_T} {\text{,}} $ | (18) |
代入公式:
| ${M'_0} + {M'_\delta }\delta + {M'_T} + {M'_\theta }\theta + {M'_w}w' = 0 {\text{,}} $ | (19) |
| $ \begin{split} {{M'}_0}(u) +& {{M'}_\delta }\left( - \dfrac{{{{Z'}_w}}}{{{{Z'}_\delta }}}\theta - \dfrac{{P'(v)}}{{{{Z'}_\delta }}}\right) + {{M'}_T}(u) + \\& {{M'}_\theta }(u)\theta + {{M'}_w}\theta = 0 {\text{。}} \end{split} $ | (20) |
代入系数以及不同舵角参数,求得:
在外场水域进行实际试验,AUV上浮下潜舵机转动角度范围在–20°~+20°;AUV内部安装有TCM5电子罗盘,时刻记录AUV纵倾角数值。AUV底部安装有DVL多普勒测速仪,时刻测量AUV速度。纵倾角、速度数值通过无线网线发送至岸基,试验人员可时刻观察AUV航行情况,保证试验安全进行。
考虑离岸水域水深较浅,为避免AUV下潜可能性,AUV从岸基出发时速度控制在1 m/s、上浮舵20°,监控AUV实际纵倾角数值,将AUV速度控制在平均速度1 m/s、均方差0.10 m/s、航行距离约50 m范围内,纵倾角稳定平均数值为11.0°,按照此步骤以此完成上浮舵角15°,10°,5°试验航行,平均纵倾角为7.4°,4.2°,在上浮舵为5°航行时,AUV航行状况不稳定。

|
图 13 三体船型USV模型 Fig. 13 Model of trimaran USV |
将实际航行数据与计算纵倾角、仿真纵倾角列于表1中,对比三者10°,15°,20°三种工况数据,证实了仿真模型以及水动力简化模型的可靠性与准确性,为第二步AUV追逐USV的仿真环境搭建提供基础。
|
|
表 1 AUV纵倾角对比表 Tab.1 Contrast of AUV pitch angles |
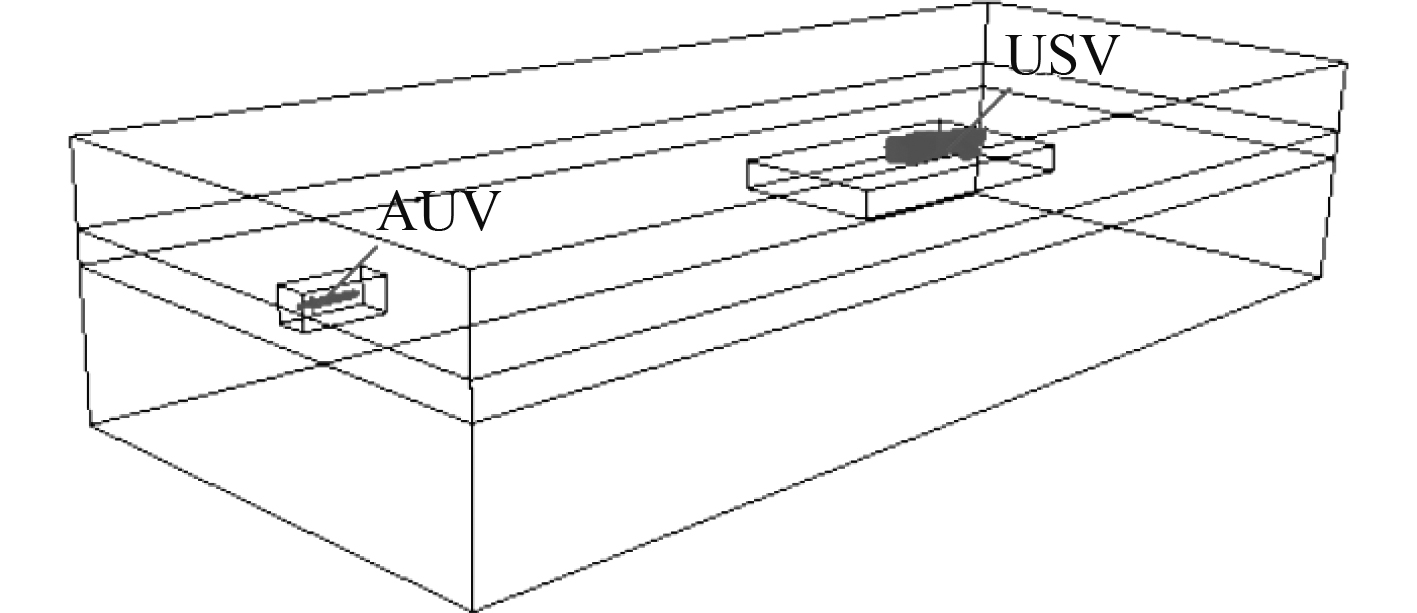
针对一体化系统对USV外形需求,以某便携式AUV为基准,选取三体船外形作为一体化系统USV。
|
图 14 水面回收仿真场景计算域 Fig. 14 Calculation domain of docking simulation on the water |
三体船相比单体船提高了船舶的稳定性和耐波性,可将推进器安装至2个侧体上,提高三体船的机动性,并考虑在回收AUV时,减小螺旋桨尾流对AUV航行影响,以及当回收失败时避免AUV撞击螺旋桨。相比双体船,三体船的主船体可提供运输空间,在船体尾部设计AUV回收装置。
|
|
表 2 三体船模型参数表 Tab.2 Parameter table of trimaran USV model |
USV的推进器布置在2个侧体上且低速航行,故数值仿真时可忽略螺旋桨尾流对AUV航行特性的影响,但航行过程中,不能忽略USV航行时尾流对AUV航行特性的影响。通过CFD仿真,对其影响进行判断。
3.1 动态仿真模型设定追逐仿真流域设定为40 m×16 m×8 m,并在计算域内针对AUV和USV设置双重网格加密区。仿真流域网格基础值0.20 m;第一重自由液面加密区尺度为40 m×16 m×1 m,基础值0.06 m;第二重AUV加密区为3 m×1 m×1 m,基础值0.03 m,USV加密区10 m×5 m×1 m,基础值0.03 m。
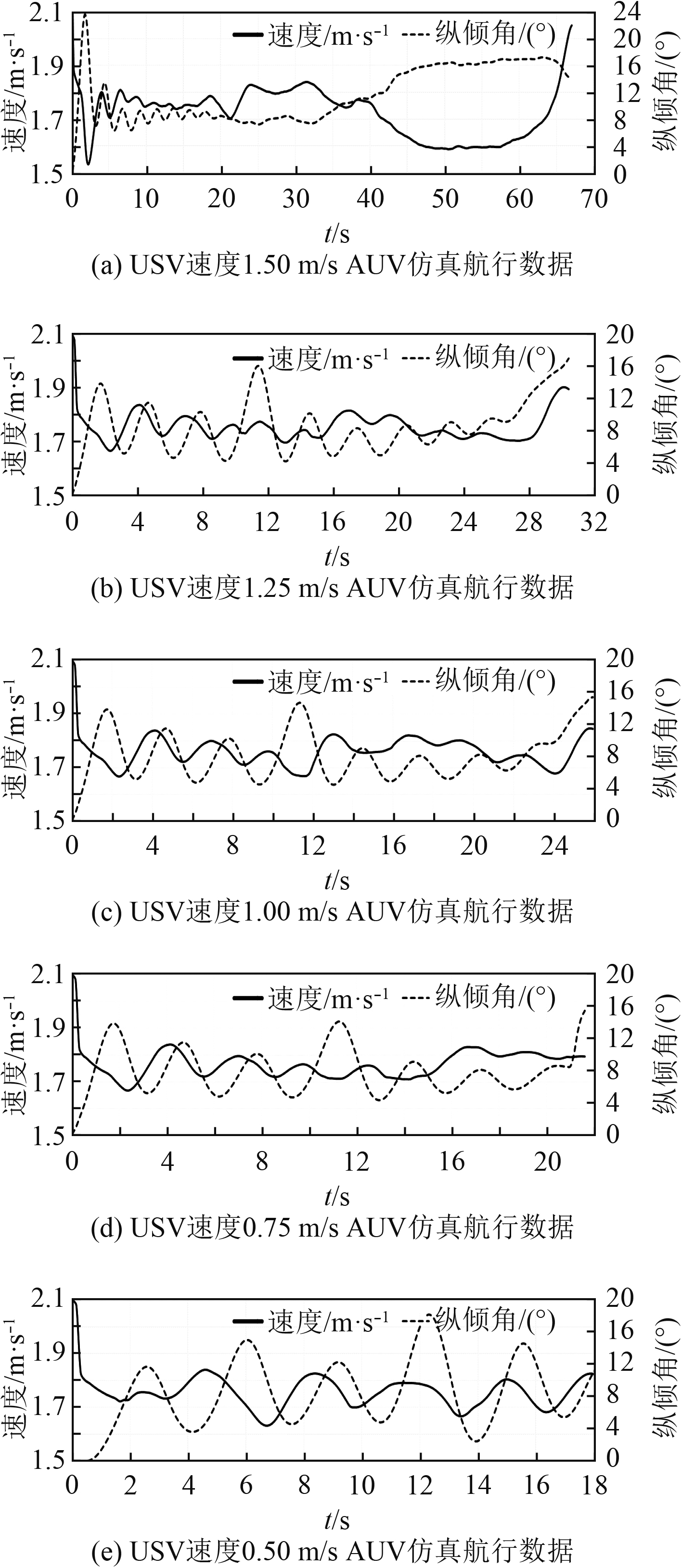
3.2 回收过程USV尾流对AUV速度1.75 m/s航行状态的影响USV仿真过程中保持速度约为0.5,0.75,1.00,1.25,1.50 m/s五种工况,AUV距离USV尾部20 m时两者同时前向运动,AUV工况选取舵角25°,仿真收敛速度1.75 m/s、纵倾角7.8°,AUV追逐USV过程中速度、纵倾角变化如图15所示,仿真停止条件是AUV碰触USV。
|
图 15 回收过程AUV速度1.75 m/s仿真航行数据 Fig. 15 AUV navigation data in docking simulation process at speed of 1.75 m/s |

|
图 16 回收过程仿真水面场景 Fig. 16 Surface water scene of recovery simulation process |
通过不同工况下仿真结果看,AUV在逐渐靠近USV过程中,AUV速度和纵倾角均发生变化。
1)靠近过程中AUV速度降低、纵倾角增大,速度差越近越明显;
2)AUV即将碰触USV尾部时,速度和纵倾角会发生突增,速度差越近越明显。
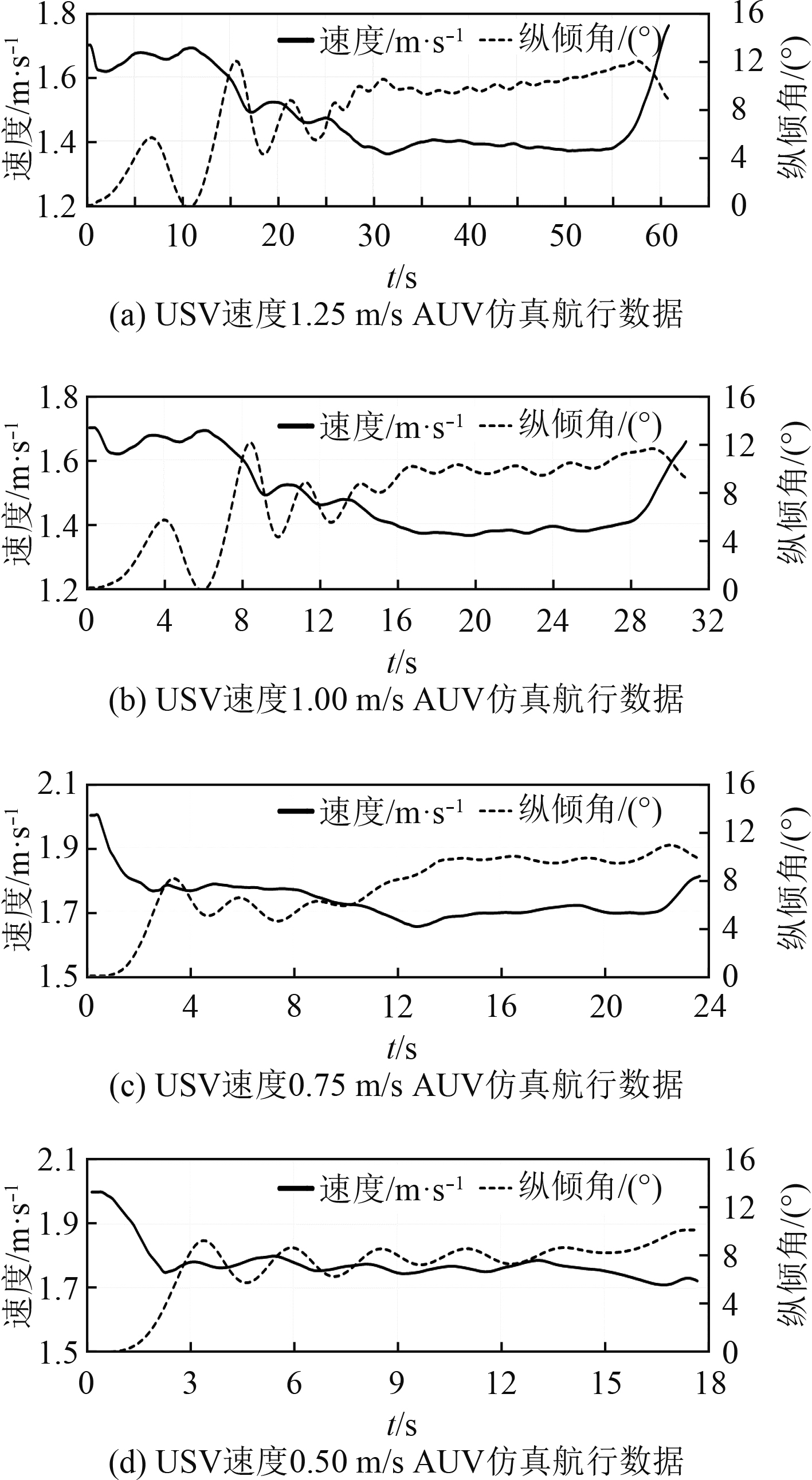
|
图 17 水面速度矢量图 Fig. 17 Velocity vector map on the water |
由于USV速度越快产生尾流对AUV影响越大,尾流扰动使AUV纵倾角增大速度降低。靠近USV时AUV速度突增,原因是USV后舱内壁产生正伴流现象,即其带动附近水域有向前运动趋势,导致流速相对于AUV速度差减小,AUV粘性水阻力随之减小,USV速度越快越明显,并且速度差较小时,AUV处在尾部区域相对时间也增加,速度突增幅度越大,2个原因导致速度差越小AUV靠近USV速度突增越明显。
由于纵倾角增加至约16°,回收过程中AUV底部有较大可能性率先碰触USV斜坡,由于AUV底部布置传感器等探测装置,对其将会产生损害,且考虑回收时AUV速度突增情况,故针对便携式AUV不建议使用AUV速度1.75 m/s工况回收。
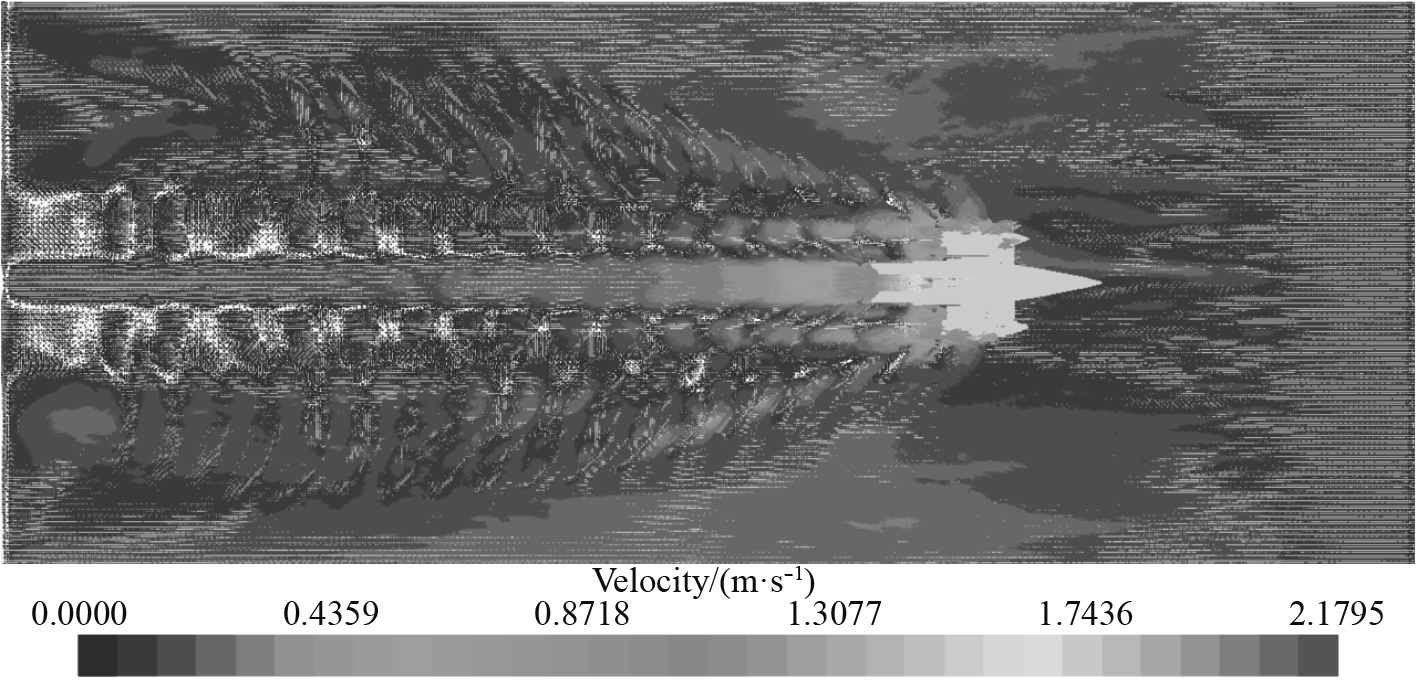
3.3 回收过程USV尾流对AUV速度1.50 m/s航行状态的影响USV仿真过程中保持速度约为0.5,0.75,1.00,1.25 m/s四种工况,AUV距离USV尾部15 m时两者同时前进方向运动,AUV工况选取舵角20°,仿真收敛速度1.50 m/s,纵倾角8.7°,AUV追逐USV过程中速度、纵倾角变化如图18所示,仿真停止条件是AUV碰触USV。
|
图 18 回收过程AUV速度1.50 m/s仿真航行数据 Fig. 18 AUV navigation data in docking simulation process at speed of 1.50 m/s |
分析结果与AUV1.75 m/s大致相同,AUV碰触USV时纵倾角较理想;USV在0.75 m/s,0.5 m/s速度突增较小,在此基础上USV速度越大,方向稳定性越强,USV工况在0.75 m/s时仿真结果针对一体化水面回收方案较理想。
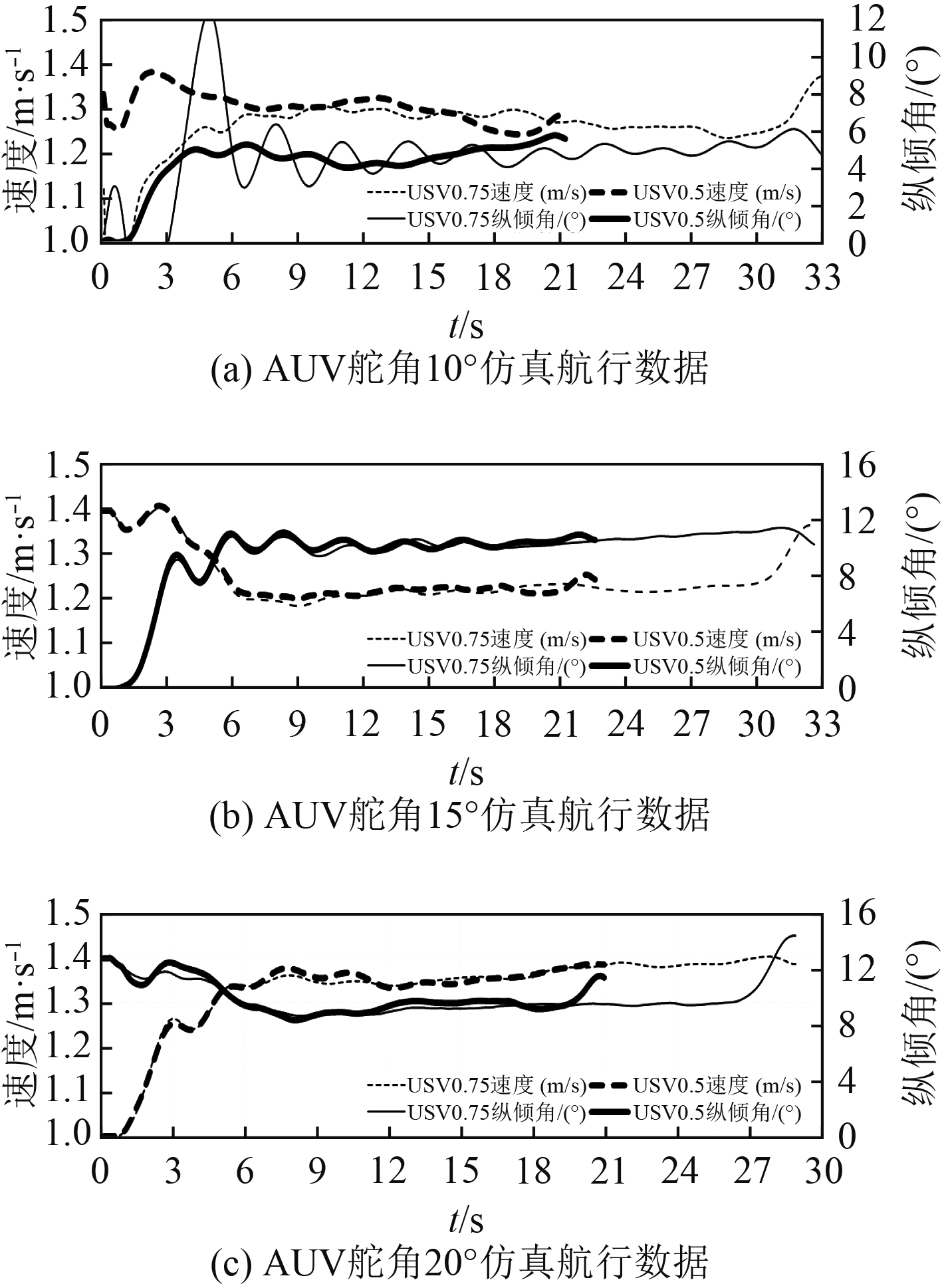
3.4 回收过程USV尾流对AUV速度1.25 m/s航行状态的影响鉴于上述仿真结果,相对速度差过小,AUV速度、纵倾角均有较大影响,对于舵角25°纵倾角过大,不适用于水面回收状态。针对AUV 1.25 m/s采用舵角10°,15°,20°三种舵角,USV速度0.5,0.75 m/s六种工况进行仿真对比,如图19所示。
|
图 19 回收过程AUV速度1.25 m/s仿真航行数据 Fig. 19 AUV navigation data in docking simulation process at speed of 1.25 m/s |
USV同速情况下,AUV回收时速度、纵倾角变化趋势、幅度基本相同,综合考虑前2种工况,优先选择纵倾角较小的20°舵角;USV速度0.75,0.5 m/s影响差别不大,故选取0.75 m/s。
4 结 语本文提出一种基于AUV与USV的一体化作业系统,面向该系统设计USV水面回收AUV作业流程,对回收过程中AUV的水面稳定航行特性进行了深入分析,USV航行尾流对其后方AUV航行在垂直面上三自由度的影响进行仿真分析。通过仿真计算及外场试验得出如下结论:
1)以某便携式AUV为模型进行水面垂直面三自由度航行水动力仿真,通过使用上浮舵角使AUV可在水面稳定水平前向航行,AUV的纵倾角与冲角相等,符合实际航行现象。
2)建立AUV水面航行水动力模型,求解出AUV舵角与AUV水面航行纵倾角呈线形关系,经过外场试验验证了水动力模型和仿真结果的准确性和可靠性。
3)以三体船型USV为仿真模型,进行动回收回收AUV水动力仿真分析,通过15种工况对比分析USV航行尾流对较高速AUV航行的垂直面三自由度影响,得出USV速度0.75 m/s航行、AUV舵角20°速度1.25~1.5 m/s回收可靠性最佳。
| [1] |
GERMAN C R, JAKUBA M V, KINSEY J C, et al. A long term vision for long-range ship-free deep ocean operations[J]. Persistent presence through coordination of Autonomous Surface Vehicles and Autonomous Underwater Vehicles, 2012, 134(1): 1-7. |
| [2] |
URABE T, URA T, TSUJIMOTO T, et al. Next-generation technology for ocean resources exploration (Zipangu-in-the-Ocean) project in Japan[C]. Oceans, 2015: 1–5.
|
| [3] |
ZWOLAK K, SIMPSON B, ANDERSON B, et al. An unmanned seafloor mapping system: The concept of an AUV integrated with the newly designed USV SEA-KIT[C]. Oceans, 2017: 1–6.
|
| [4] |
潘光, 黄明明, 宋保维, 等. AUV回收技术现状及发展趋势[J]. 鱼雷技术, 2008, 16(6): 10-14. DOI:10.3969/j.issn.1673-1948.2008.06.002 |
| [5] |
MENG LS, LIN Y, GU HT, et al. Study on dynamic characteristics analysis of underwater dynamic docking device[J]. Ocean Engineering, 2019, 180: 1-9. DOI:10.1016/j.oceaneng.2019.03.033 |
| [6] |
杜俊, 谷海涛, 孟令帅, 等. 面向USV的AUV自主回收装置设计及其水动力分析[J]. 工程设计学报, 2018. DOI:10.3785/j.issn.1006-754X.2018.01.008 |
| [7] |
曹和云, 倪先胜, 何利勇, 等. 国外潜载UUV布放与回收技术研究综述[J]. 中国造船, 2014, 55(2): 200-208. DOI:10.3969/j.issn.1000-4882.2014.02.023 |
| [8] |
施生达. 潜艇操纵性[M]. 国防工业出版社, 1995. 121–123.
|
 2020, Vol. 42
2020, Vol. 42
