锚链是锚泊系统的重要组成部分,连接着锚和船体,其运动特征和张力变化可直接表征舰船的锚泊状态。锚链可分为铺底段和悬链段两部分。铺底段锚链铺放在海底,其摩擦力和锚抓力共同提供了锚泊力[1]。悬链段锚链悬垂于海水中,底端的锚泊力和顶端的舰船所受外力综合作用于此。舰船锚泊时,悬链段时刻受到海流、波浪等海洋环境因素的影响[2],其运动特征和张力变化具有动态特性,在一定条件下将引起铺底段的应力变化,使舰船面临走锚的威胁,因而一直是舰船锚泊安全领域研究的热点。
当前,国内外学者多采用静力计算法对锚链悬链段进行分析,如经典悬链线方程法、抛物线理论以及分段外推法等[3-7]。经典悬链线方程属于超越方程,构建模型时通常将锚链的悬链段近似简化为抛物线[3],未考虑海流对锚链的作用力和锚链自身的弹性形变[4],与真实的锚链受力情况相差较大,特别是无法分析海流对于舰船走锚的影响。文献[5-6]在锚链动力性能分析中考虑了海流对锚链的作用力和锚链弹性形变的因素,但建模时同样也采用了易于计算的静力分析方法,忽略了水流力和弹性形变。现有文献在分析锚链运动特征和张力变化时,往往忽略海流等环境因素的干扰,尤其是在海流流速较大的情况下,计算结果将与实际情况存在一定的误差[7]。
鉴于此,本文基于拖曳系统运动模型的建立思想[8],采用集中质量法构建计入海流作用的锚链运动模型,进而进行仿真分析。
1 系统稳态模型构建本文仅考虑海流为定常流的情况,即海流中任何一点的压力、速度和密度等物理量都不随时间变化,且速度的方向始终由船首指向船尾。为简化分析,对锚链悬链段作如下假定:锚链为理想的弹性缆索,锚链上的张力和应变具有一一对应关系;忽略锚链的扭转运动,即锚链微元仅作3个自由度的运动;锚泊系统在运行过程中,锚链位于水面以下,并一直处于张紧状态,张力始终大于0,即不考虑锚链存在松弛时的情况;锚链的横截面是圆形。
1.1 坐标系建立为了便于分析锚链运动特征,引入2个右手坐标系,分别是惯性坐标系和锚链局部坐标系,其方向如图1所示。惯性坐标系

|
图 1 惯性坐标系与局部坐标系示意图 Fig. 1 Inertial and local coordinate |
以欧拉角表示锚链上任一点相对于惯性坐标系的姿态角,其中,
| $\left( {t,n,b} \right) = \left( {i,j,k} \right)\left[ D \right] {\text{。}} $ | (1) |
其中,
| $\left[ { D} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta \cos \psi }&{ - \cos \theta \sin \psi }&{\sin \theta } \\ {\sin \theta \cos \psi }&{ - \sin \theta \sin \psi }&{ - \cos \theta } \\ {\sin \psi }&{\cos \psi }&0 \end{array}} \right]{\text{。}}$ | (2) |
舰船与周围的海流有相对运动时,船体就会受到海流的作用力,这种作用力称为水动压力。船在锚泊时经常会受到水动压力的影响,水动压力的大小可按下式求取[9]:
| $ {F_w} = \frac{1}{2}{\rho _w}{C_w}LdV_w^2 {\text{。}} $ | (3) |
其中:
锚链的运动方程参考Ablow的模型[10]。假设锚链为连续的细长圆柱状缆索,材质均匀且具有各向同性,在整个锚链长度上平滑连续[11]。在海流作用下达到稳态时,锚链上任意一点的位置和张力不随时间变化。根据锚链在海洋中的实际情况,其受力可以分为重力与浮力的合力、流体水动力以及张力。根据锚链上任意一点的力平衡,可得矢量方程式:
| $ \frac{\partial }{{\partial S}}{{T}} + {{W}} + {{F}} = 0 {\text{。}} $ | (4) |
其中:
定义矢量
| $ \frac{\partial }{{\partial s}}{{T}} + S'\left( {{{W}} + {{F}}} \right) = 0 {\text{。}} $ | (5) |
| $ {{W}} = \frac{{\left( {m - {\rho _w}A} \right)g{{k}}}}{{S'}} {\text{。}} $ | (6) |
其中:
将式(2)代入式(6)中,得到在锚链局部坐标系下的展开式:
| $ S'{{W}} = - {w_1}\left( {\sin \theta {{t}} + \cos \theta {{n}}} \right) {\text{。}} $ | (7) |
其中,
将锚链截面等效为圆截面,其单位长度所受流体水动力为:
| $ \begin{split} {{F}} =\,& - \frac{1}{2}{\rho _w}d({\text{π}} {C_T}{{U}} \cdot {{t}}\left| {{{U}} \cdot {{t}}} \right|{{t}} + \\ & {C_N}\left| {{{U}} - ({{U}} \cdot {{t}}){{t}}} \right|({{U}} - ({{U}} \cdot {{t}}){{t}})) {\text{。}} \end{split} $ | (8) |
其中:
引入符号
| $ \begin{split} S'{{F}} =\,& - \frac{1}{{\sqrt {1 + eT} }}({\text{π}} {C_t}{U_t}\left| {{U_t}} \right|{{t}} + \\ & {C_n}{U_n}\sqrt {U_n^2 + U_b^2} {{n}} + {C_n}{U_b}\sqrt {U_n^2 + U_b^2} {{b}}) {\text{。}} \end{split} $ | (9) |
其中:
锚链的张力按下式进行展开:
| $ \frac{\partial }{{\partial s}}{{T}} = \left( {T{{t}}} \right)' = T'{{t}} + T\theta '{{n}} - T\psi '\cos \theta {{b}} {\text{。}} $ | (10) |
根据受力平衡,依据上文进行的锚链受力分析,所有作用力之和为0的原则,分别在锚链局部坐标系的3个方向上建立锚链动力平衡方程,具体表达式如下:
| $ \left\{ \begin{array}{l} T' - {w_1}\sin \theta - \sqrt {1 + eT} \pi {C_t}{U_t}\left| {{U_t}} \right| = 0 {\text{,}} \\ T\theta ' - {w_1}\cos \theta - \sqrt {1 + eT} {C_n}{U_n}\sqrt {U_n^2 + U_b^2} = 0{\text{,}} \\ - T\psi '\cos \theta - \sqrt {1 + eT} {C_n}{U_b}\sqrt {U_n^2 + U_b^2} = 0 {\text{。}} \end{array} \right. $ | (11) |
锚链在海流作用下的运动控制方程可写成如下的微分方程:
| $ M\frac{{\partial y}}{{\partial s}} = Q {\text{。}} $ | (12) |
将锚链上任一点的位置
| $ {{r}}' = x'{{i}} + y'{{j}} + z'{{k}} = \left( {1 + e} \right){{t}} {\text{,}} $ | (13) |
即可得到锚链上任意一点惯性坐标
| $\left\{ \begin{array}{l} x' = \left( {1 + e} \right)\cos \alpha \cos \beta {\text{,}} \\ y' = - \left( {1 + e} \right)\sin \alpha \cos \beta {\text{,}} \\ z' = - \left( {1 + e} \right)\sin \beta {\text{。}} \\ \end{array} \right.$ | (14) |
当应变
为了求解微分方程,需要确定边界条件。锚链底端为铺底段,包含了3个边界条件。根据稳态时受力平衡,锚链底端张力等于锚泊船所受海流水动力和悬链段锚链所受海流力之和,考虑到悬链段锚链所受海流力相比于锚泊船所受海流水动力极小,可以将其忽略。此外,底端锚链微元局部坐标系相对于惯性坐标系的2个方向角固定,即得到3个边界条件。3个边界条件的初值设定原则如下:根据舰船的水动力模型求解出锚泊船所受海流水动力,作为底端锚链微元张力初值;由于底端锚链微元水平铺在海底,其方向角分别为
舰船抛锚时,通常设置有足够长度的锚链以便有一段铺底锚链,使锚不产生上拔力,锚链会有一部分是直接铺放在海底[12]。锚链的悬链段可以采用上述模型进行分析,而铺底段显然不符合上述模型理论,一般可以近似地把这部分视为张力恒定的直线段计算。悬链段与铺底段的分界点随着锚链受力、水深和海流流速的不同而不断改变,确定分界点十分必要。对于这个问题,可以先放出与水深相等长度的悬链段,在一定流速的海流作用下,假设悬链段顶端微元位于水面,悬链段底端微元满足铺底条件,即方向角
基于上文建立的锚链运动模型,使用4阶龙格库塔法求解微分方程,对海流作用下锚链的运动特征和张力进行仿真,并与悬链线方程法进行比较和分析。
2.1 参数设置假设锚链长度足够使之存在铺底段,选用的海水、锚泊船和锚链等的物理参数设置见表1。
|
|
表 1 仿真过程主要参数 Tab.1 Major parameters in the simulation |
为比较海流的存在对锚链特征的影响,在以下情况下分别对本文所建立锚链运动模型和悬链线方程法[13-14]进行仿真和结果分析:
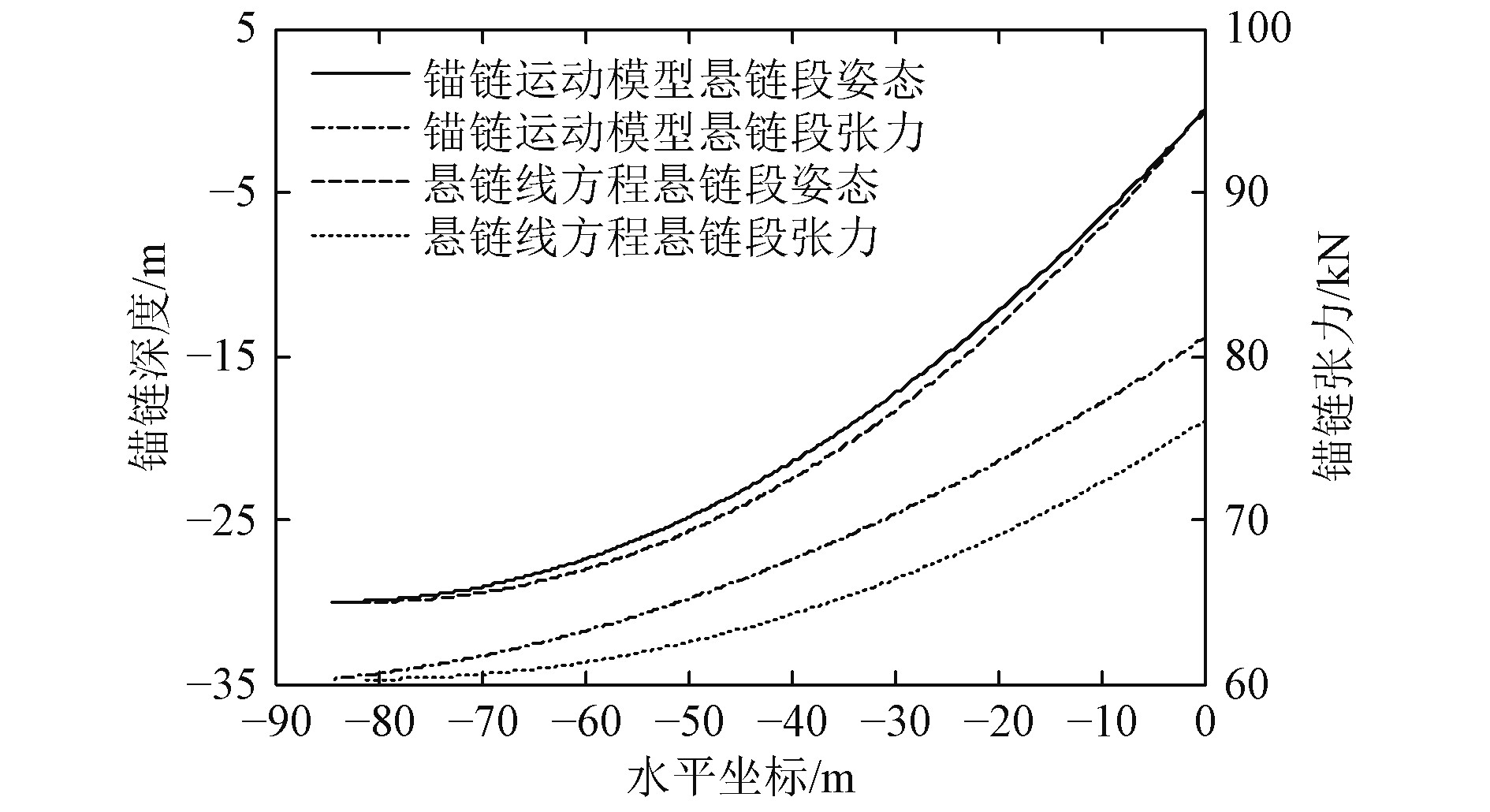
1)选择海流速度2 m/s,抛锚深度30 m,2种方法得到的锚链水中姿态和张力,结果如图2所示。
|
图 2 两种方法仿真结果对比 Fig. 2 Steady state of the anchor chain |
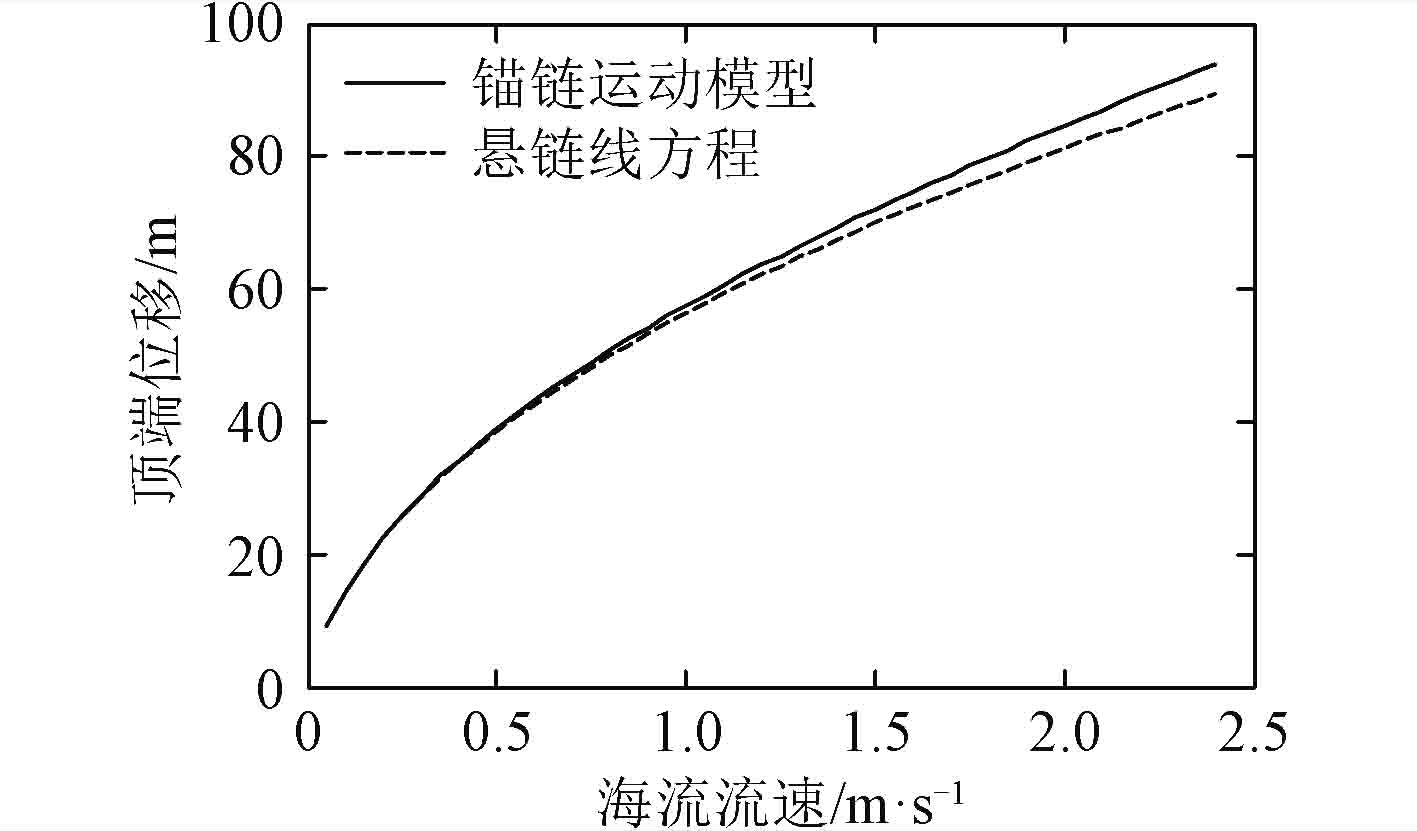
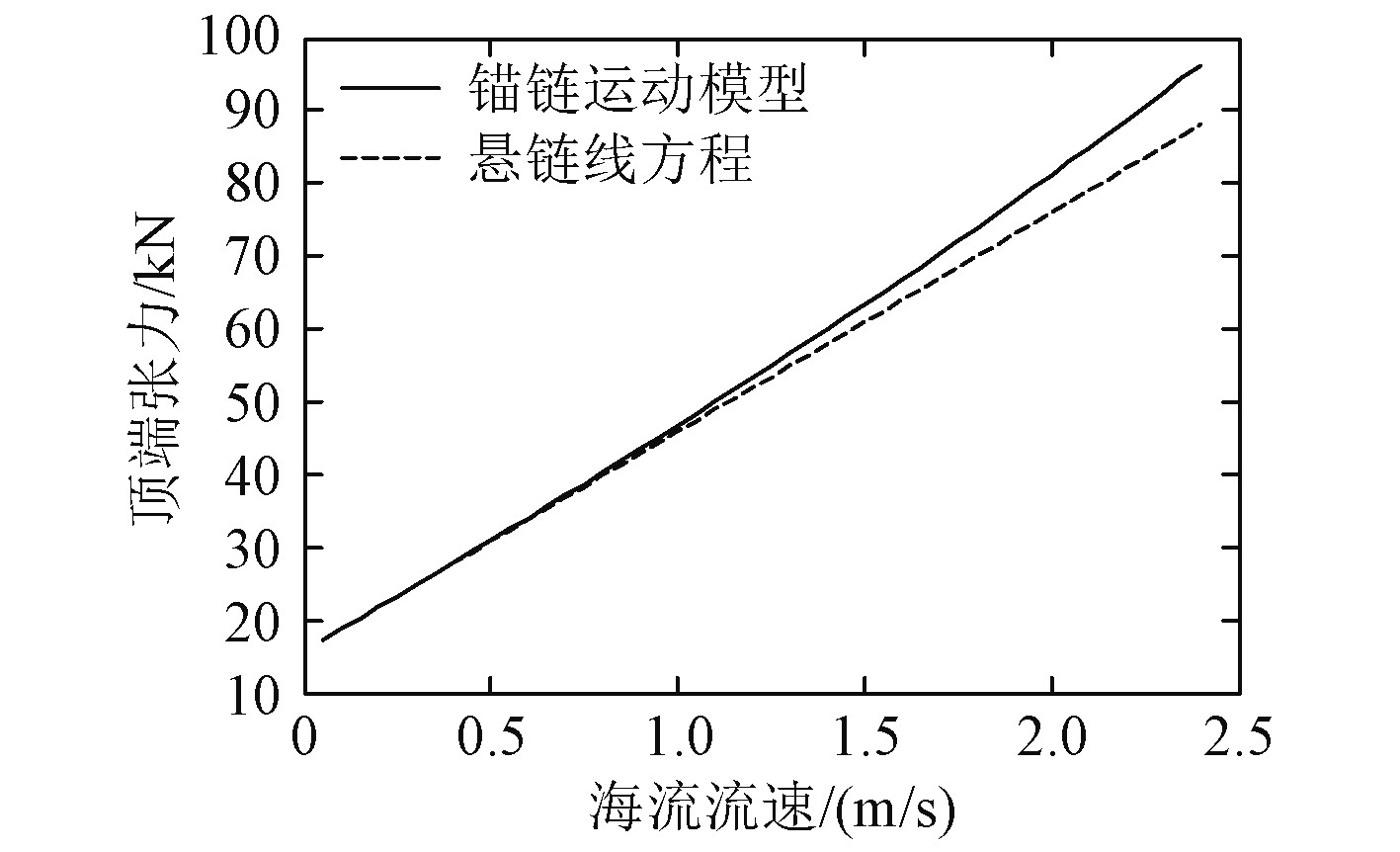
2)选择抛锚深度30 m,不同海流流速下2种方法得到的锚链顶端位移和张力,结果如图3和图4所示。
|
图 3 锚链顶端位移随海流流速变化 Fig. 3 Displacement change of the top chain with current |
|
图 4 锚链顶端张力随海流流速变化 Fig. 4 Tension change of the top chain with current |
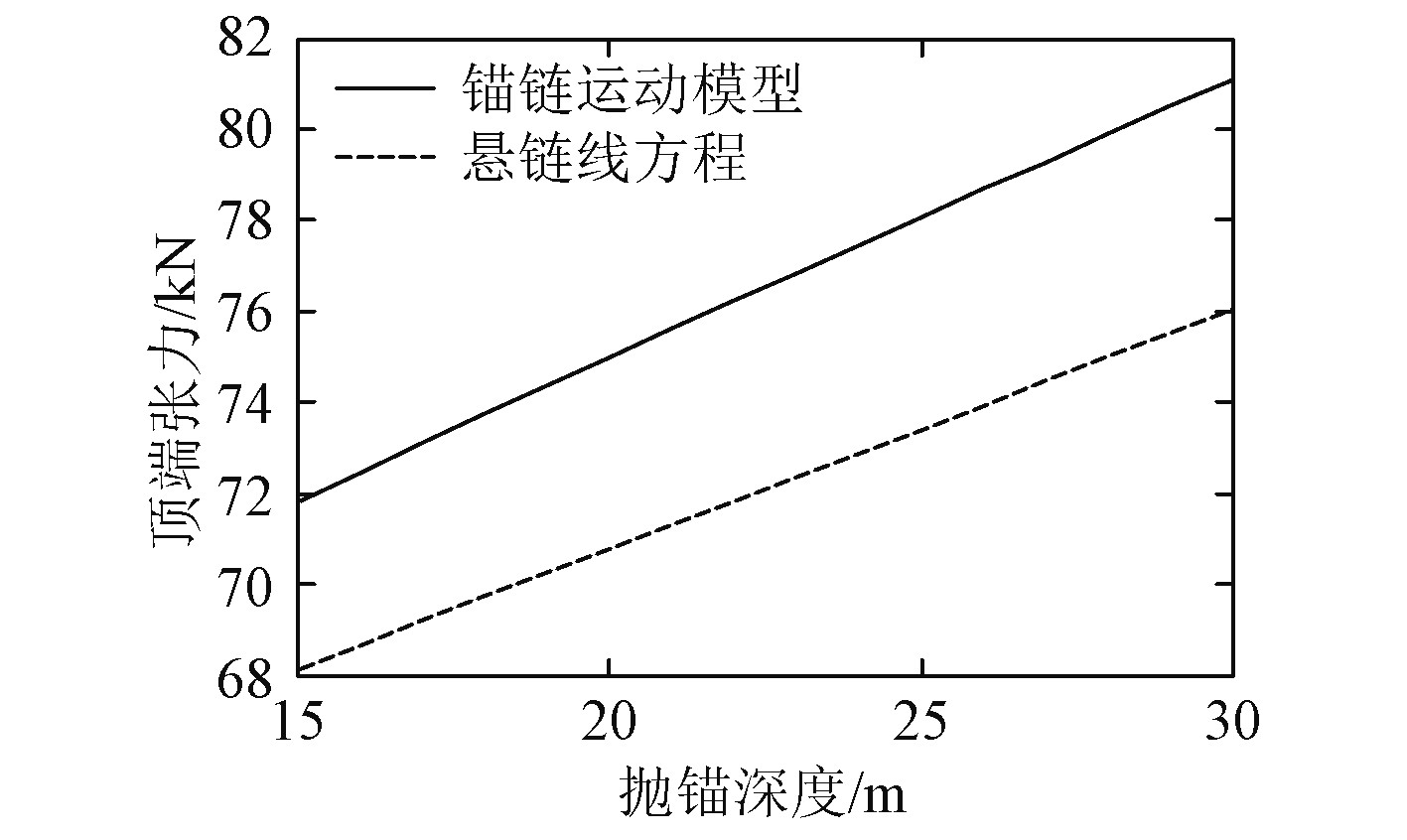
3)选择海流流速 2m/s,不同抛锚深度下2种方法得到的锚链顶端位移和张力,结果如图5和图6所示。

|
图 5 锚链顶端位移随抛锚深度变化 Fig. 5 Displacement change of the top chain with depth |
|
图 6 锚链顶端张力随抛锚深度变化 Fig. 6 Tension change of the top chain with depth |
由图2可知,采用本文锚链运动模型得到的悬链段水平长度为84.61 m,而采用悬链线方程得到的悬链段水平长度为81.27 m,二者存在差异。同时,随着距海底高度的增大,锚链张力逐渐增大,锚链受到的海流影响不断累积,2种方法结果的差值也逐渐增大,在达到水面时的结果分别为81.11 kN和76.03 kN,差值大于
由图3和图4可知,在相同抛锚深度下,海流流速不大时,海流对锚链顶端位移和张力的影响并不大,但随着流速的增大,海流对锚链的影响逐渐增大,2种情况下的差值越来越大。这是因为在海流和重力作用下,锚链所受的海流力和发生的弹性形变会随着流速的增大而增大,锚链悬链段在不断地张紧。据此可知,对于锚泊船来说,在海流流速较大时,采用悬链线方程计算的锚链顶端位移和张力会导致结果比实际情况小,这是不安全的。因而,在不同海流流速下不能忽略海流作用力对锚链的影响。
2.2.3 不同抛锚深度下锚链特征验证分析由图5和图6可知,在相同海流流速下,抛锚深度对锚链顶端位移和张力的影响一直较大,且随着抛锚深度的增大,影响更加显著,在抛锚深度30 m时,顶端位移相差4.11%,顶端张力相差6.68%。原因在于当抛锚深度增大时,锚链阻水面积相应增大,导致流体作用力增加,对锚链顶端的位移与张力产生一定影响。因而,在不同抛锚深度下也不可忽略海流作用力对锚链的影响。
2.3 锚链运动模型数值分析为检验海流速度对锚链姿态和张力的影响,在本文所建立的锚链运动模型基础上,选定抛锚深度为30 m,海流流速分别为0.5 m/s,1 m/s,1.5 m/s和2 m/s,分析锚链的姿态和张力变化情况,结果如图7和图8所示。
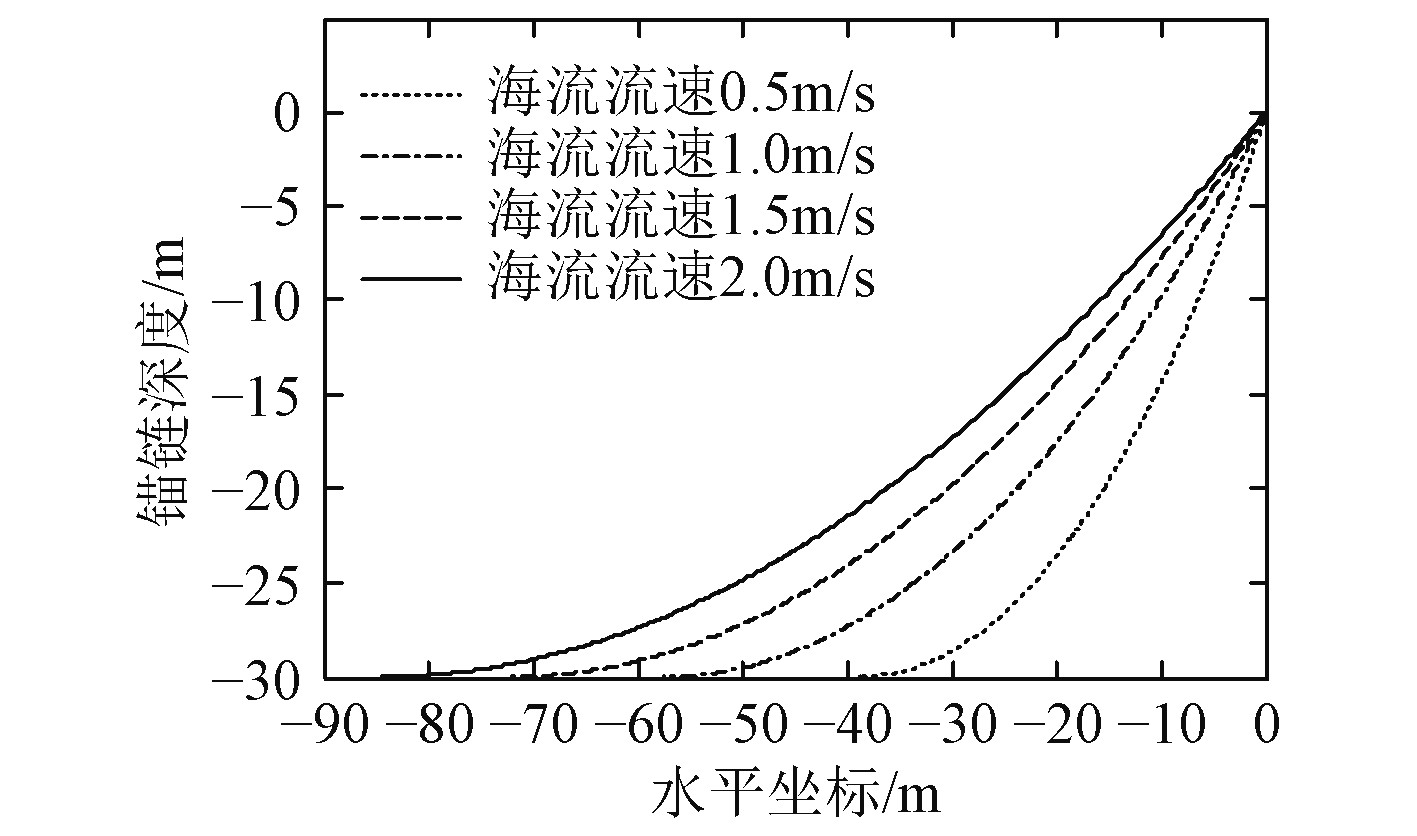
|
图 7 不同海流流速下锚链稳定姿态变化 Fig. 7 Steady state of the chain in different current |
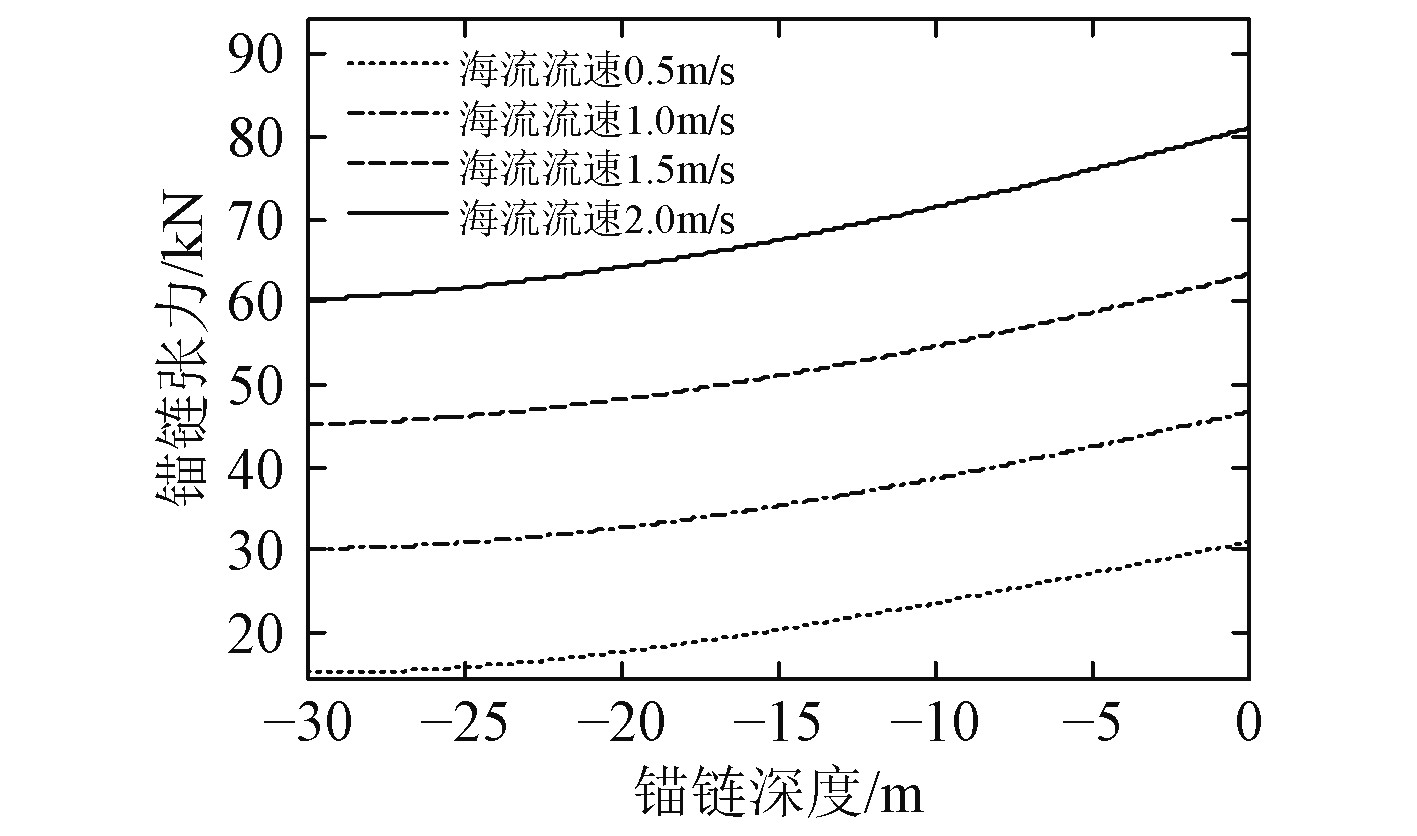
|
图 8 不同海流流速下锚链张力变化 Fig. 8 Tension change of the chain in different current |
由图7可知,抛锚深度相同时,随着海流流速的增大,锚链被拉起的长度逐渐增大,铺放海底的锚链相应缩短。这一过程也体现了海流是造成锚泊船走锚的重要因素,在进行建模时必须考虑海流作用。
2.3.2 海流作用下的锚链张力分析由图8可知,抛锚深度相同时,随着海流流速的增大,锚链各点的张力逐渐增大,且顶端锚链的张力增量最大,这是因为海流流速增大导致了锚泊船受到的水动力增大,底端锚链初始张力增大,同时锚链被拉起,悬链段长度增大,所受海流作用力和重力的累积效果越来越显著。
3 结 语本文针对传统锚链静力计算方法未计入海流作用这一问题,建立了海流作用下的锚链运动模型,对锚链悬链段的姿态和张力等进行仿真,并与悬链线方程方法比较和分析,得出以下结论:
1)海流作用力会对锚链运动产生影响,且随着海流流速的增大,海流对锚链的影响逐渐显著,特别是海流对锚链顶端张力、顶端位移的影响不可忽略。
2)当抛锚深度不变时,随着海流流速的增大,锚链悬链段的长度、顶端位移和锚链各点的张力逐渐增大,且顶端锚链的张力增量最大。
| [1] |
LIU H. Recent study of drag embedment plate anchors in China[J]. Journal of Marine Science and Applicationz, 2012, 11(4): 393-401. DOI:10.1007/s11804-012-1148-8 |
| [2] |
于洋, 蒋治强. 海流对深水锚泊船锚链静力特性的影响[J]. 中国航海, 2013, 36(1): 101-104. DOI:10.3969/j.issn.1000-4653.2013.01.022 |
| [3] |
郑瑞杰. 锚泊系统受力分析[D]. 大连: 大连理工大学, 2006
|
| [4] |
陈云鹤, 赵晶. 考虑水流力作用的锚链力计算方法[J]. 解放军理工大学学报自然科学版, 2016, 17(2): 116-120. |
| [5] |
YANG M D, TENG B. Static and Dynamic Analysis of Mooring Lines by Nonlinear Finite Element Method[J]. China Ocean Engineering, 2010, 24(3): 417-430. |
| [6] |
MA G, SUN L, KANG Y, et al. Effects of Different Influence Factors on Static and Dynamic Analysis of Mooring Line. 2015; 7(2): 95-102
|
| [7] |
郝春玲, 滕斌. 不均匀可拉伸单锚链系统的静力分析[J]. 中国海洋平台, 2003, 18(4): 18-21. DOI:10.3969/j.issn.1001-4500.2003.04.004 |
| [8] |
金良安, 苑志江, 迟卫, 等. 海洋拖曳系统对舰船操纵性能的影响[J]. 交通运输工程学报, 2013, 13(1): 47-54. JIN L A, YUAN Z J, CHI W, et al. Influence of Underwater Towed System on Ship Maneuverability[J]. Journal of Traffic and Transportation Engineering, 2013, 13(1): 47-54. DOI:10.3969/j.issn.1671-1637.2013.01.008 |
| [9] |
WU X, GUNNU G R S, MOAN T. Positioning capability of anchor handling vessels in deep water during anchor deployment[J]. Journal of Marine Science and Technology, 2015, 20(3): 1-18. |
| [10] |
ABLOW C M, SCHECHTER S. Numerical simulation of undersea cable dynamics[J]. Ocean Engineering, 1983, 10(6): 443-457. DOI:10.1016/0029-8018(83)90046-X |
| [11] |
张斌, 宋保维. 驻留型UUV锚泊系统运动建模与分析[J]. 哈尔滨工程大学学报, 2016, 37(4): 498-502. ZHANG B, SONG B W. Dynamic Modeling and Simulation of Mooring System for an Unmanned Underwater Vehicle[J]. Journal of Harbin Engineering University, 2016, 37(4): 498-502. |
| [12] |
周世良, 李泳龙, 李怡, 等. 基于弹性悬链线理论的斜坡式码头趸船系留设施受力计算方法[J]. 水运工程, 2014(1): 70-75. ZHOU S L, LI Y L, LI Y, et al. Calculation Method of Force on Mooring Facilities Attached to Pontoon for Sloping Wharf Based on Elastic Catenary Theory[J]. Port and Waterway Engineering, 2014(1): 70-75. |
| [13] |
王云龙, 张世富. 海上浮筒锚泊分析[J]. 船舶力学, 2011, 15(11): 1300-1305. WANG Y L, ZHANG S F. Mooring Analysis of Pontoon on Sea[J]. Journal of Ship Mechanics, 2011, 15(11): 1300-1305. DOI:10.3969/j.issn.1007-7294.2011.11.015 |
| [14] |
张强, 祝贵兵, 程向新, 等. 单点锚泊船锚链线水平摄动分析[J]. 舰船工程, 2016(3): 55-58. ZHANG Q, ZHU G B, CHENG X X, et al. Level Disturbance Analysis of Single Point Mooring Line[J]. Ship Engineering, 2016(3): 55-58. |
 2020, Vol. 42
2020, Vol. 42
