2. 海军工程大学兵器工程学院,湖北 武汉 430033
2. Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, China
随着海上斗争区域逐渐转向深海,深海潜伏式武器[1]等将逐渐登上战场。水下平台如潜艇作为水下隐蔽作战平台,将是运送和搭载该类武器的最佳平台之一。由于所研究的潜伏式武器口径大于现有鱼雷发射管口径,因此无法通过鱼雷发射装置[2]进行发射或布放。因此采用外部挂载的方式是潜艇等水下平台携带及施放潜伏式武器的有效方法之一。潜艇外搭载武器方面国外早已有一定的应用[3-5],国内也开展了部分研究[6]。在潜伏式武器以及水下平台外挂装置的总体论证研究中,武器施放后的初始运动规律是其所关注的重点之一,为此本文通过建立潜伏式武器施放后水下运动过程相关数学模型并进行仿真计算,对潜伏式武器施放后初始阶段的运动特性进行进行定量分析,从而为潜伏式武器及潜艇外挂装置的总体方案设计和论证提供理论依据。
1 潜伏式武器水下施放方案简介本文研究的武器水下施放的方案如见图1所示。该方案的运载装置外挂架通过连接紧固机构固定在潜艇底部,在潜艇航行到预定区域需投放武器时,首先通过艇内的仪器对武器进行初始发射参数设定。完成设定后,则通过运载装置的操纵控制设备首先对模块储放箱的底部挡板进行解锁,再通过液压开闭结构将底部挡板打开,这时武器在其负浮力的作用下离开外挂架,开始初始运动。本文主要对武器施放后的水下纵平面初始运动进行建模与仿真研究。

|
图 1 施放方案原理图 Fig. 1 Schematic diagram of the weapon underwater deployment |
在武器水下纵平面运动建模与仿真中,采用2种坐标系:固定坐标系

|
图 2 固定坐标系和运动坐标系 Fig. 2 Fixed coordinate system & moving coordinate system |
定系
动系
为了简化建模过程,建模中不考虑水下海流的影响。
2.2 潜伏式武器水下运动数学模型当武器施放后,武器在自身负浮力作用下作下沉运动。同时由于武器重心与浮心不在同一位置,武器还将绕其形心作旋转运动。因此该阶段的运动为武器整体向下运动的同时作绕自身的旋转运动,经推导,该阶段的纵平面运动方程如下:
横向力方程(
| $ \begin{split} & {{m}}\left[ {\mathop u\limits^ \bullet + wq + {z_G}\mathop q\limits^ \bullet - {x_G}{q^2}} \right] = \\ & \frac{1}{2}\rho {L^3}{X'_{\dot u}}\mathop u\limits^ \bullet + {X_u}u - \left( {W - B} \right)\sin \theta {\text{;}} \end{split} $ | (1) |
竖向力方程(
| $ \begin{split} & {{m}}\left[ {\mathop w\limits^ \bullet - u{q^2} - {x_G}\mathop q\limits^ \bullet - {z_G}{q^2}} \right] = \\ & \frac{1}{2}\rho {L^4}{{\rm{Z'}}_{\dot q}}\mathop q\limits^ \bullet + \frac{1}{2}\rho {L^3}{{\rm{Z'}}_{\dot w}}\mathop w\limits^ \bullet + \frac{1}{2}\rho {L^3}{{\rm{Z'}}_q}q + \frac{1}{2}\rho {L^2}{Z'_w}w +\\ & \left( {W - B} \right)\cos \theta{\text{;}} \end{split} $ | (2) |
纵倾力矩方程(
| $ \begin{split} & {J_y}\mathop q\limits^ \bullet + {\rm{m}}\left[ {{z_G}\left( {\mathop u\limits^ \bullet + wq} \right) - {x_G}\left( {\mathop u\limits^ \bullet - uq} \right)} \right] = \\ & \frac{1}{2}\rho {L^5}{M'_{\dot q}}\mathop q\limits^ \bullet + \frac{1}{2}\rho {L^4}{M'_{\dot w}}\mathop w\limits^ \bullet + \frac{1}{2}\rho {L^4}{M'_q}q + \frac{1}{2}\rho {L^3}{M'_w}w+\\ & \left( {{x_G}W - {x_C}B} \right)\cos \theta - \left( {{z_G}W - {z_C}B} \right)\sin \theta {\text{;}} \end{split} $ | (3) |
式中:
解以上方程可得在运动坐标系下的潜伏式武器任一时刻质心的加速度和绕质心的角加速度。
武器在固定坐标系下任一时刻的位置为:
| $ \begin{split} & {x_{\rm{G}}} = \int {{v_x}} {\rm{d}}t {\text{,}}\\ & {z_{\rm{G}}} = \int {v_z} {\rm{d}}t {\text{。}} \end{split} $ | (4) |
式中:vx、vz分别为武器在固定坐标系下x轴、z轴方向速度,可按下式计算:
| $ \left[ {\begin{array}{*{20}{l}} {{v_x}}\\ 0\\ {{v_z}} \end{array}} \right] = C_o^o {\text{。}} $ | (5) |
式中:
| $\begin{gathered} u = \int {\dot u{\rm{d}}t} {\text{,}} \\ w = \int {\dot w{\rm{d}}t} {\text{。}} \end{gathered} $ | (6) |
武器在任一时刻的姿态角为:
| $ \theta = \iint {\dot q{\rm d}{t^2}} {\text{。}} $ | (7) |
第一阶段的主要仿真参数为:武器初速度
将参数的初始值代入到仿真模型中进行运行仿真,得到武器的潜深曲线、速度
|
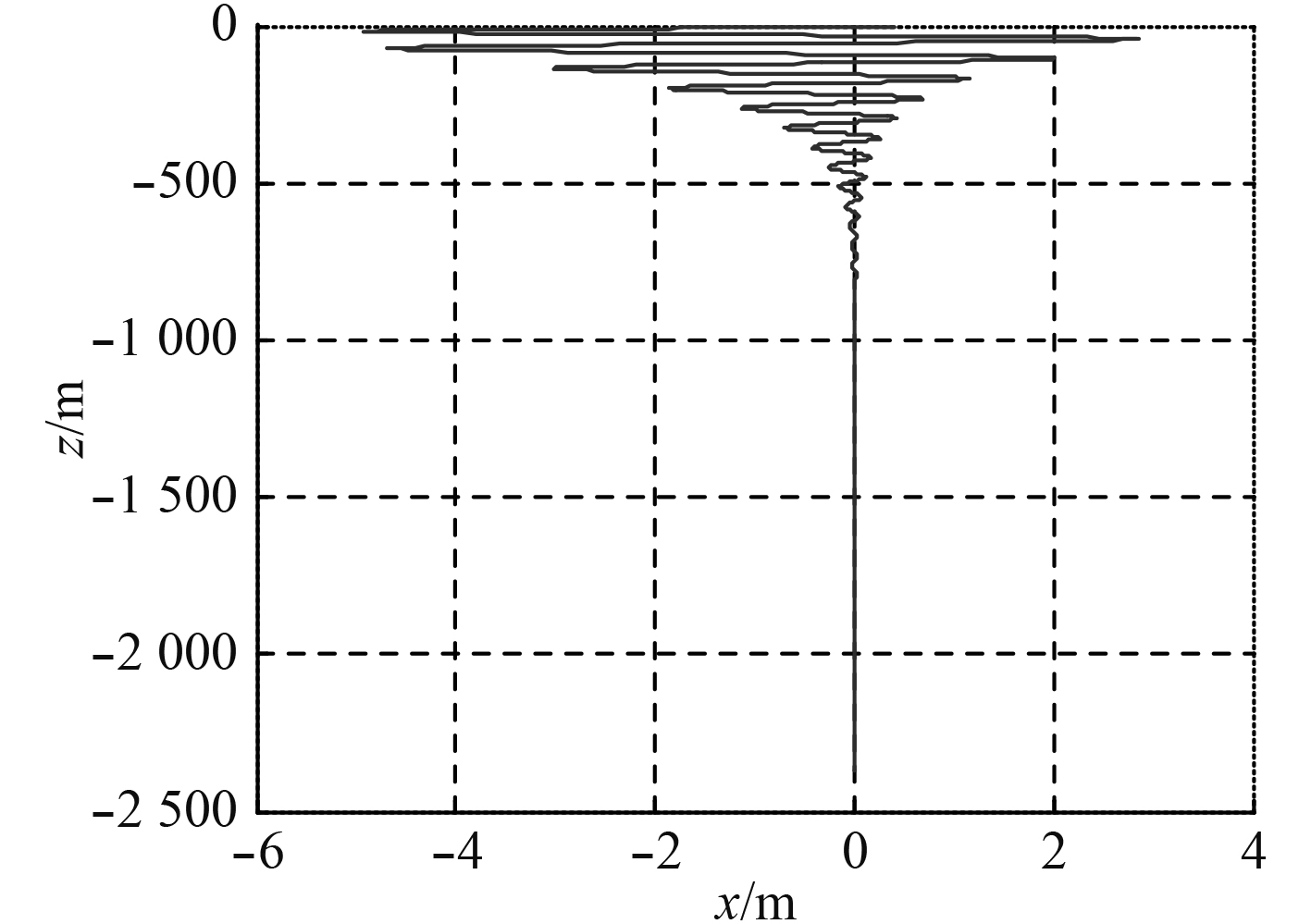
图 3 潜深曲线图 Fig. 3 The curve of the weapon diving depth in vertical plane |
|
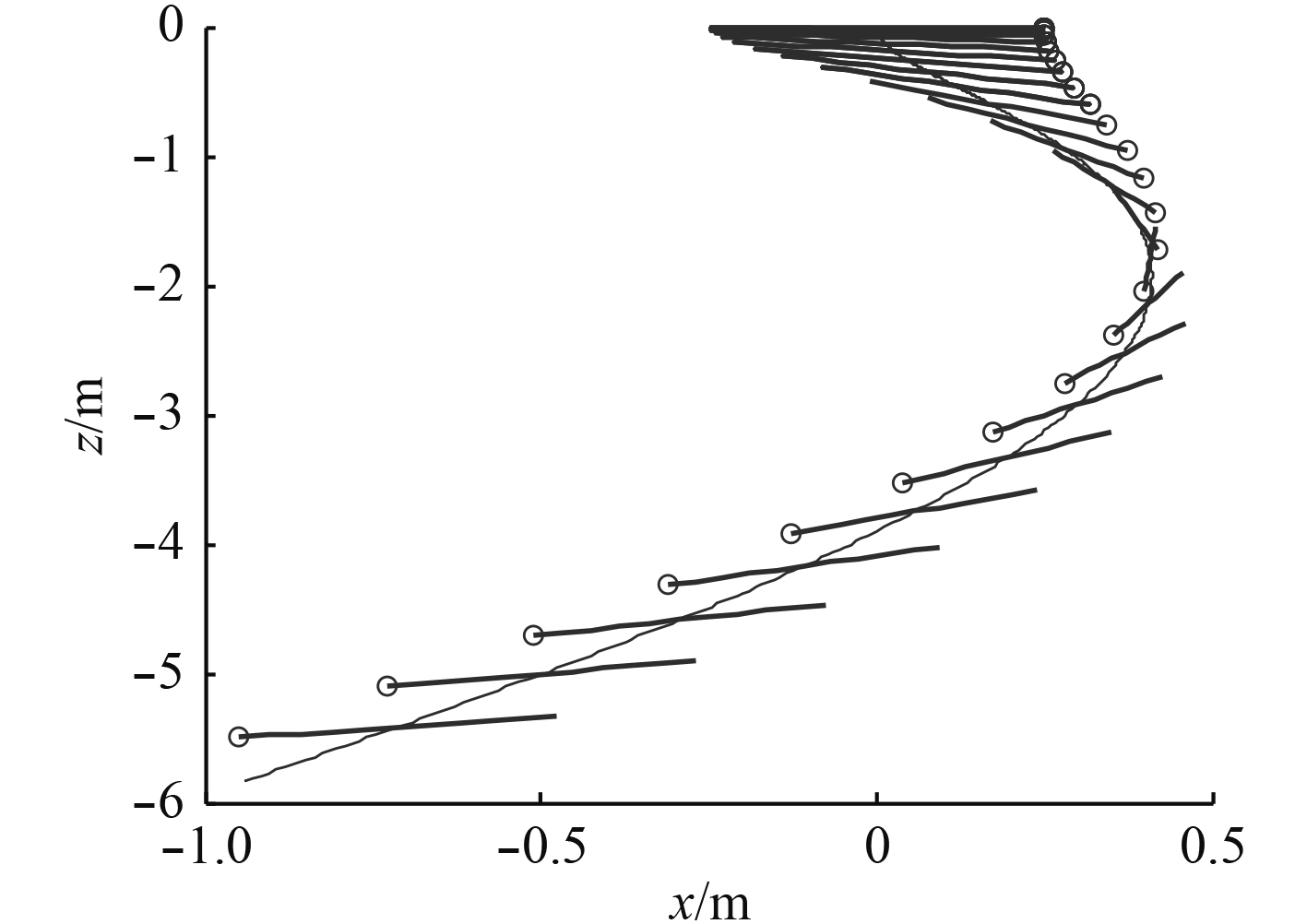
图 7 0-5 s内姿态变化图 Fig. 7 The weapon's movement posture changes in 5 s |
为了更加直观反映武器在下落时初始阶段的姿态变化,仿真中给出初始段(0–5 s)武器的姿态变化图(见图7),图中直线表示为武器中心轴线,圆圈表示武器底部。
从以上仿真结果可以看出:
1)武器在施放后,由于武器的重心与形心(动坐标原点)不重合,因此武器除了自身转动外(见图7),其重心还围绕施放点垂线作类似钟摆运动(见图3),并经过一段时间的摆动后,最终保持竖直下沉方向。
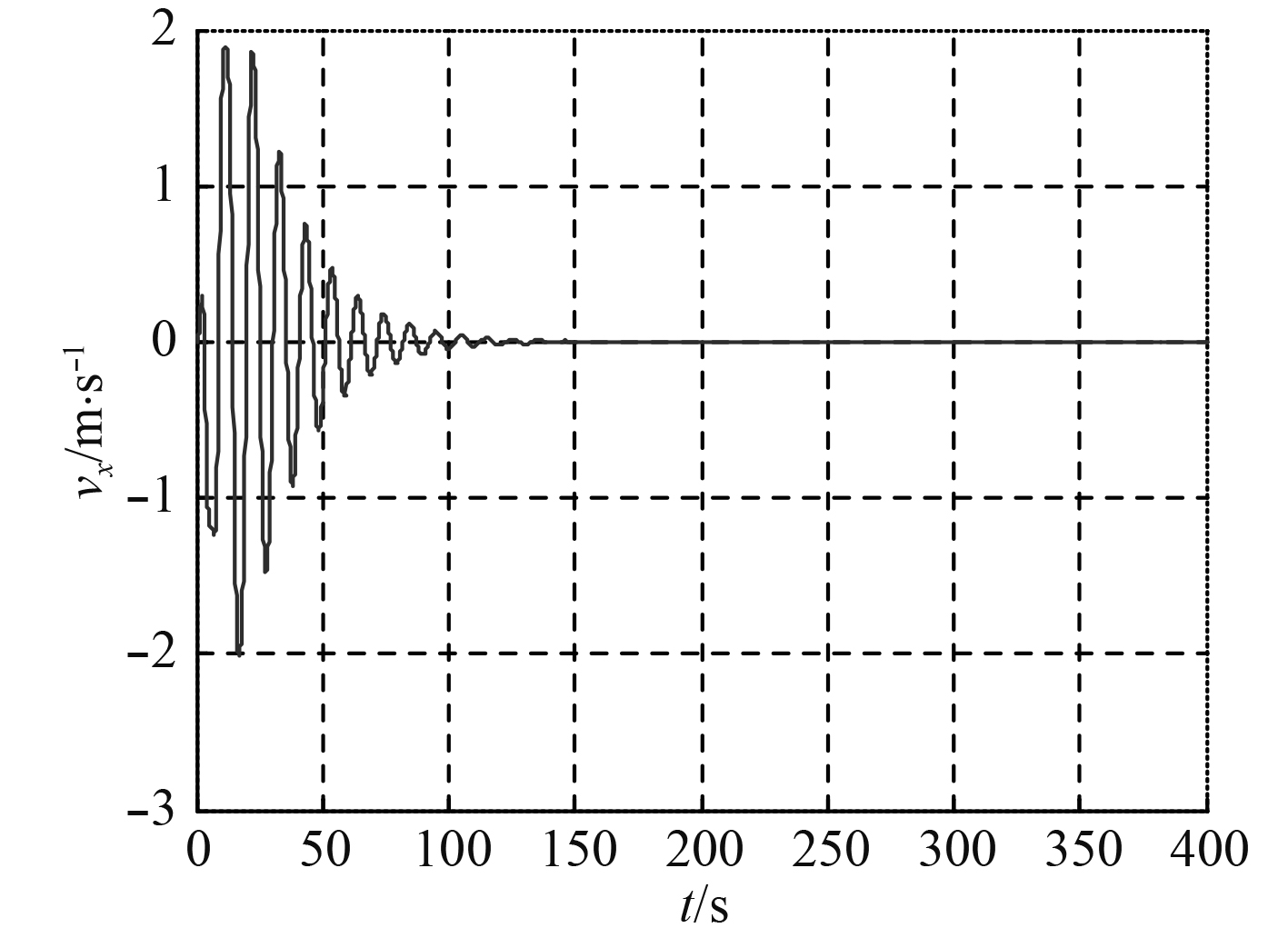
2)由武器在x轴方向的速度
|
图 4
|
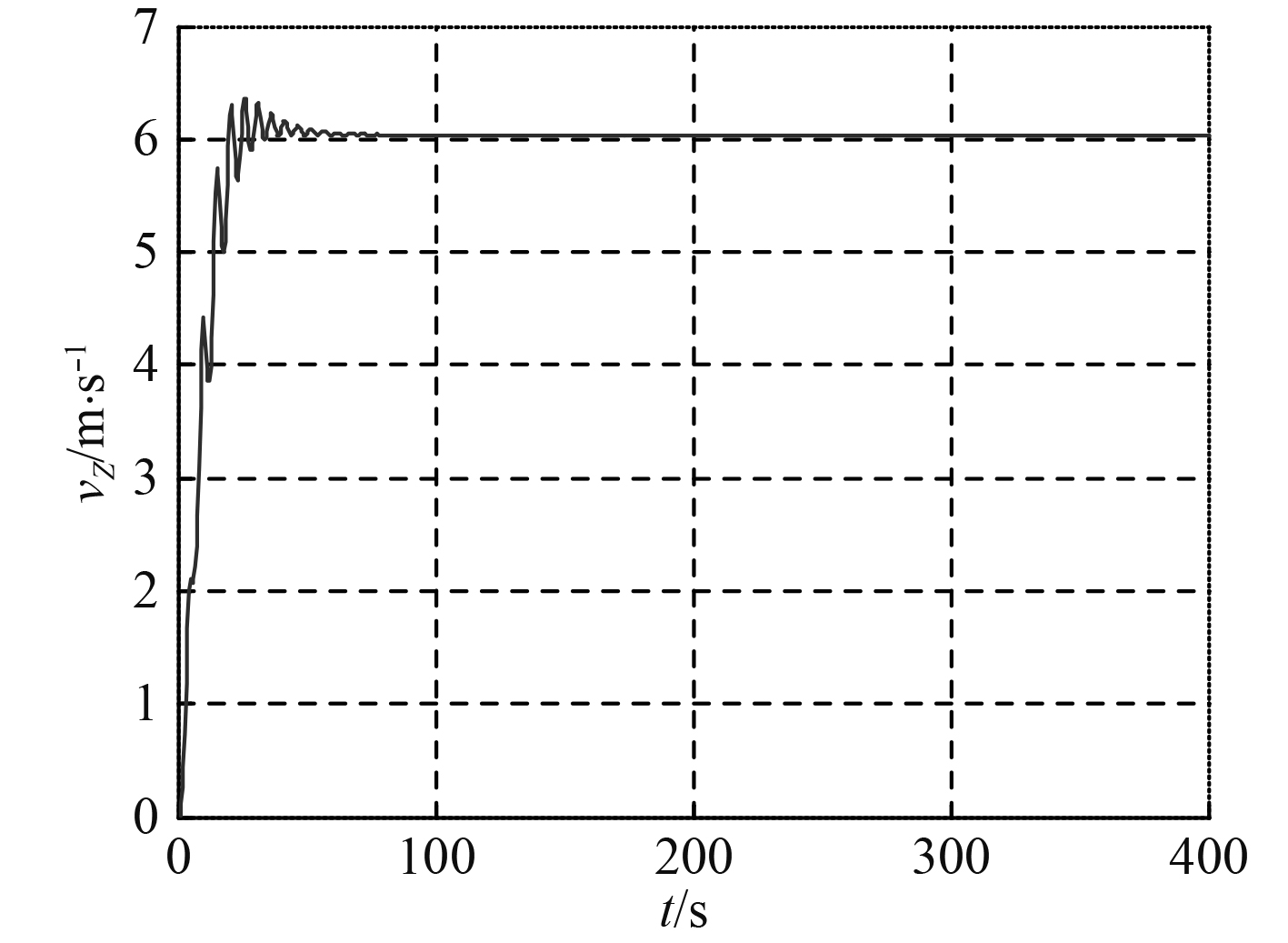
3)由武器在z轴方向的速度
|
图 5
|
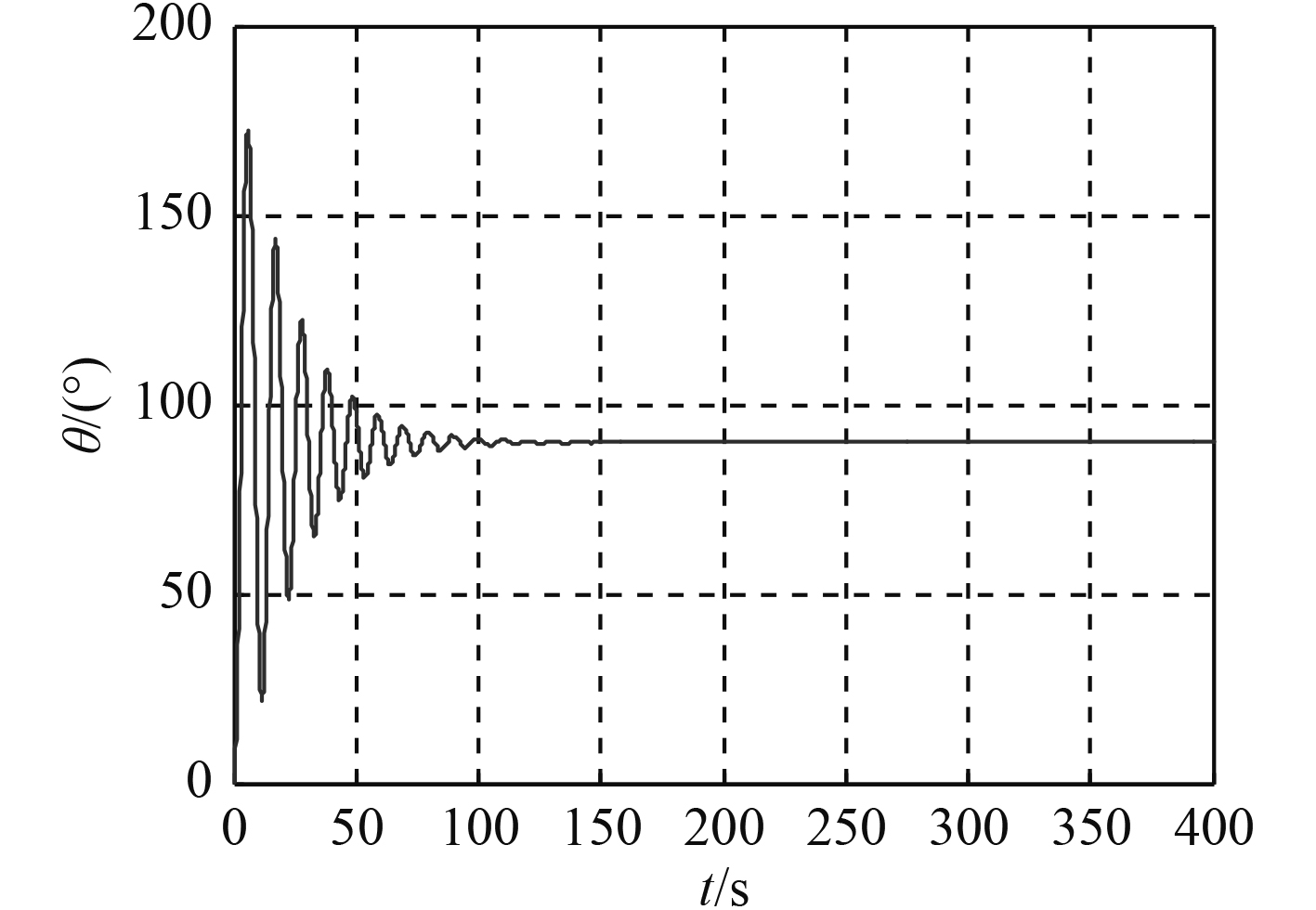
4)由纵倾角仿真曲线(见图6)可见,因武器绕自身转动,则纵倾角上则是在
|
图 6 纵倾角变化曲线 Fig. 6 The curves of the weapon's pitch angles |
为了进一步分析潜艇平台及武器的主要参数对其水下运动的影响,在标准参数仿真模型的基础上,逐一改变标准参数中的武器的负浮力、初始速度以及转动惯量,分别进行仿真以研究这些参数对武器的施放过程以及运动的影响规律。
1)改变武器负浮力的仿真
将武器的负浮力在标准参数基础上分别设定为减少20%(
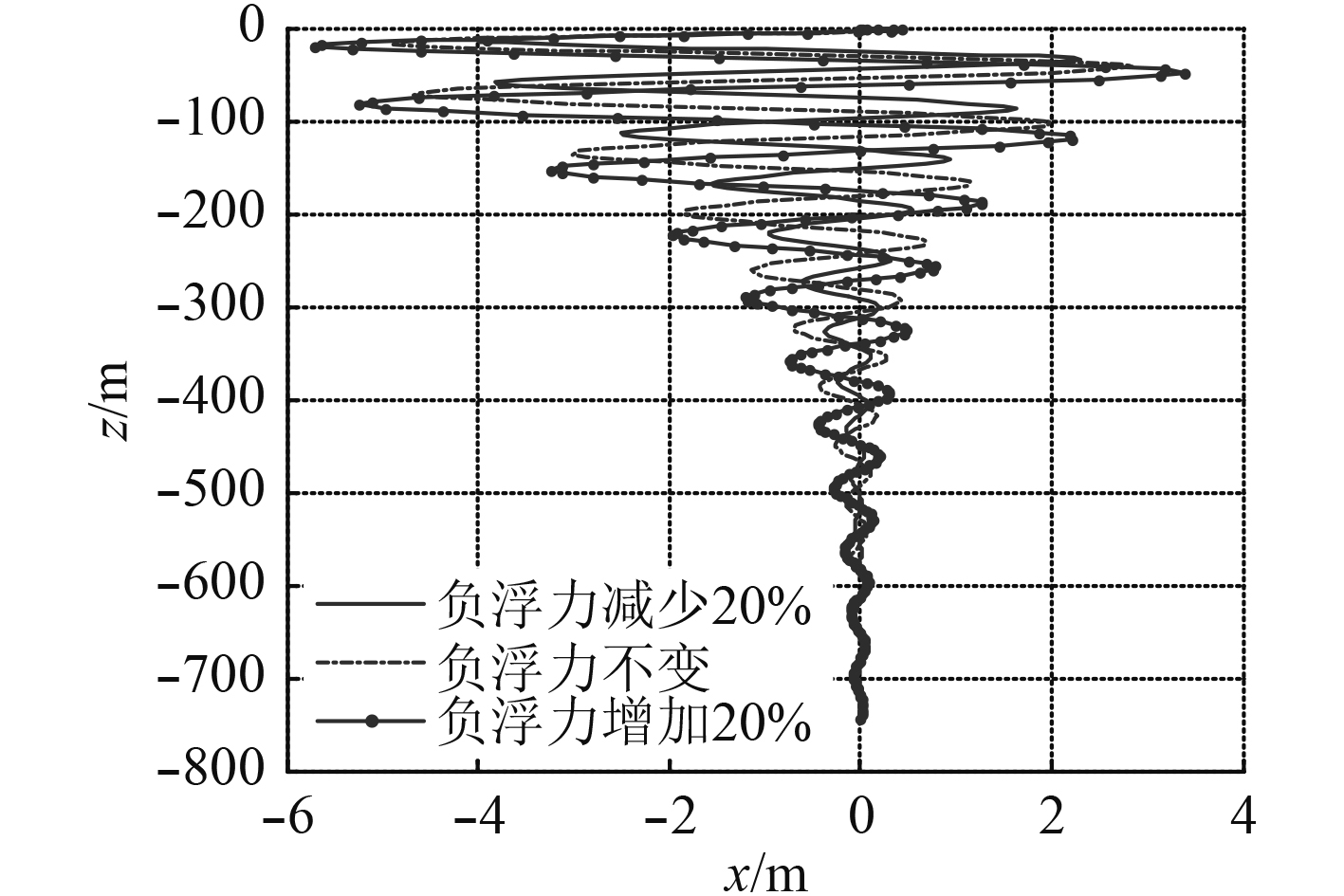
|
图 8 潜深曲线(变负浮力) Fig. 8 The curve of the weapon diving depth in vertical plane according to the negative buoyancy |

|
图 11 纵倾角变化曲线(变负浮力) Fig. 11 The curves of the weapon's pitch angles according to the negative buoyancy |
从仿真的结果可以看出:
武器的负浮力对武器的稳定后的z方向的运动速度
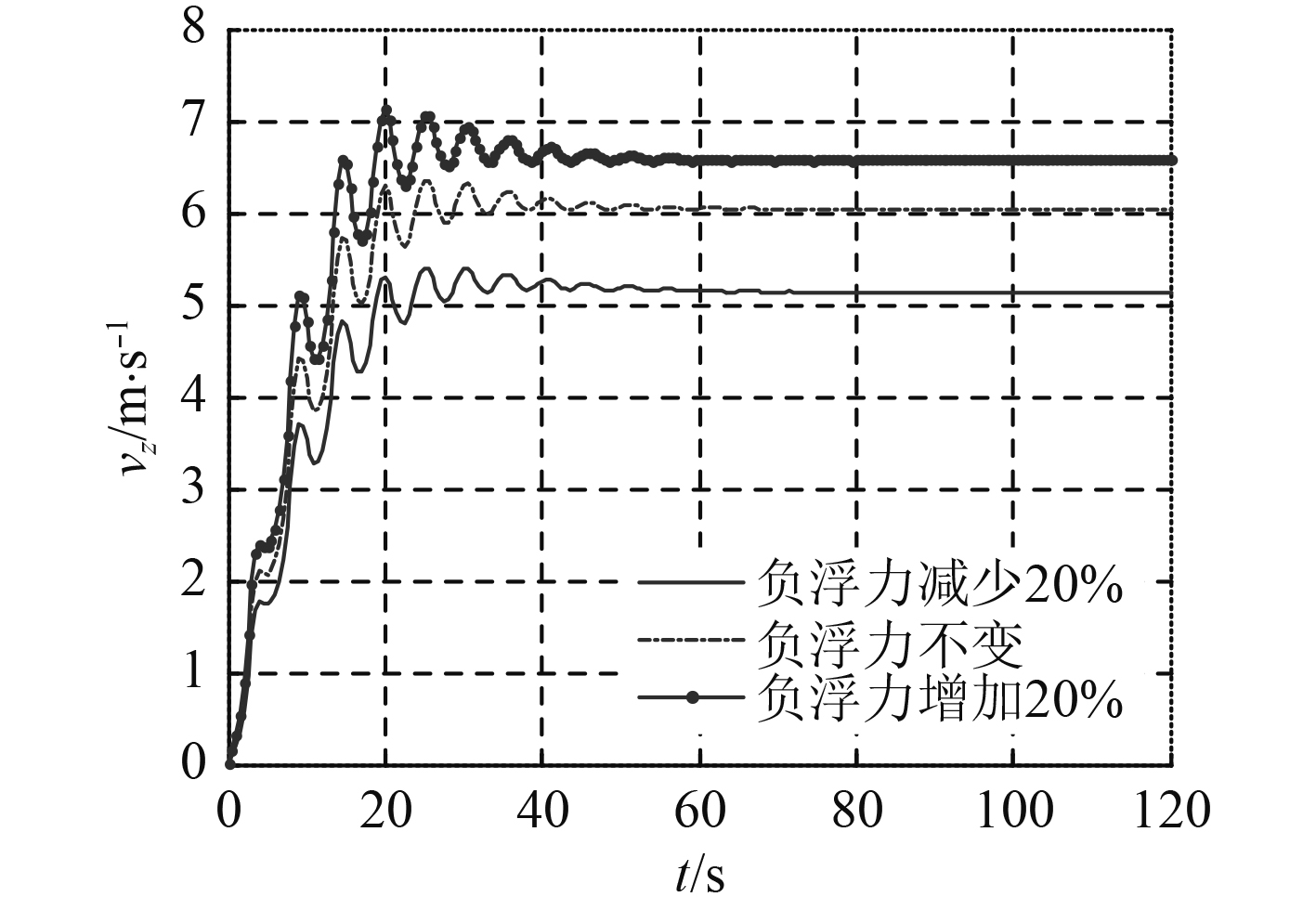
|
图 10
|
武器的负浮力对

|
图 9
|
2)改变武器初始速度的仿真
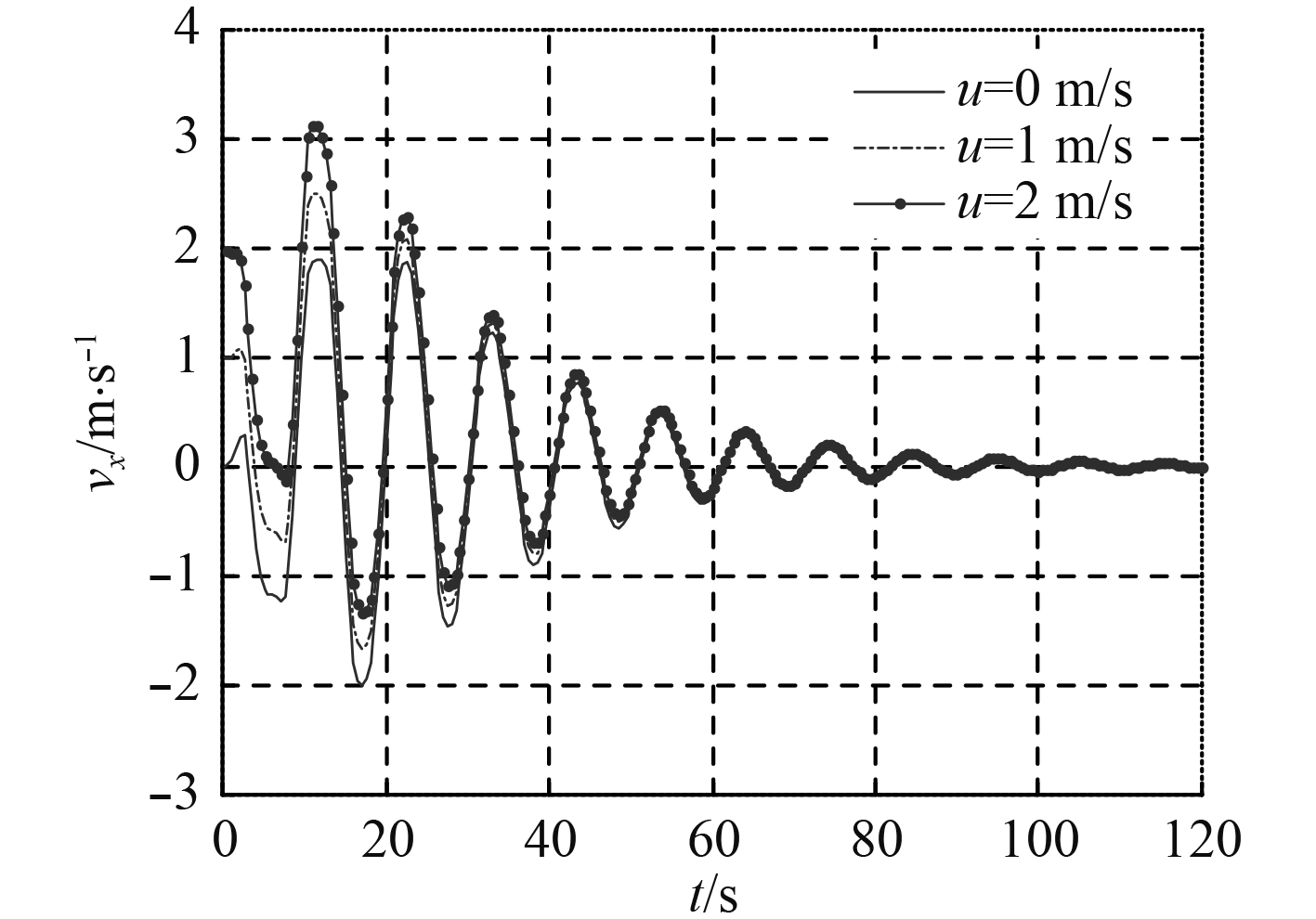
仿真中的武器初始速度可以认为是潜艇平台在运动中进行武器施放时武器在离开潜艇瞬间将带上的初速。将武器的初始速度分别设定为
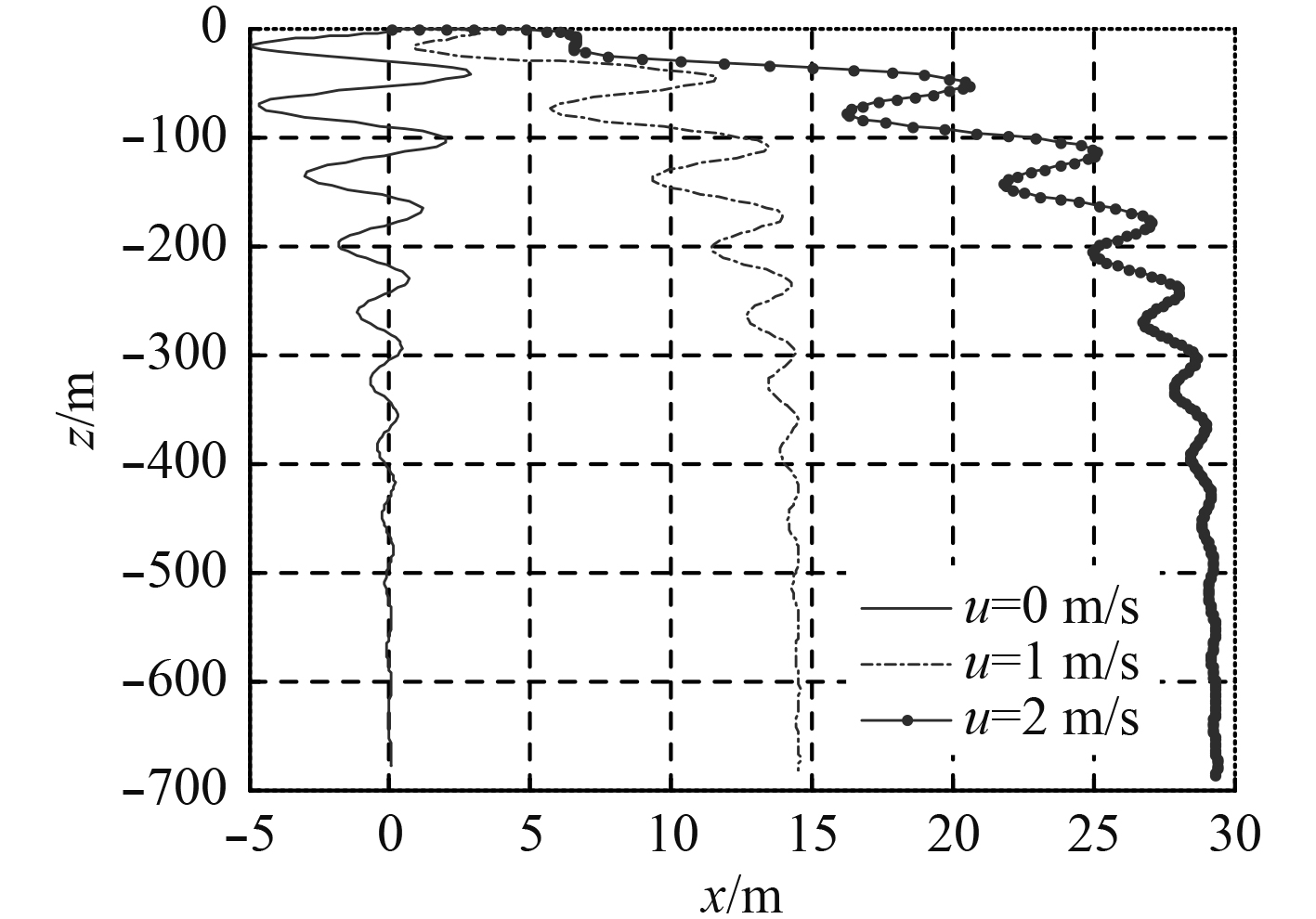
|
图 12 潜深曲线(变初速) Fig. 12 The curve of the weapon diving depth in vertical plane according to its initial velocity |

|
图 15 垂直面的纵倾角变化曲线(变初速) Fig. 15 The curves of the weapon's pitch angles according to its initial velocity |
|
图 13
|
从仿真的结果可见,改变武器的初始速度,主要对武器落点位置有影响,初始速度越大,武器落点离施放开始位置的距离越大,如初始速度

|
图 14
|
3)改变武器转动惯量的仿真
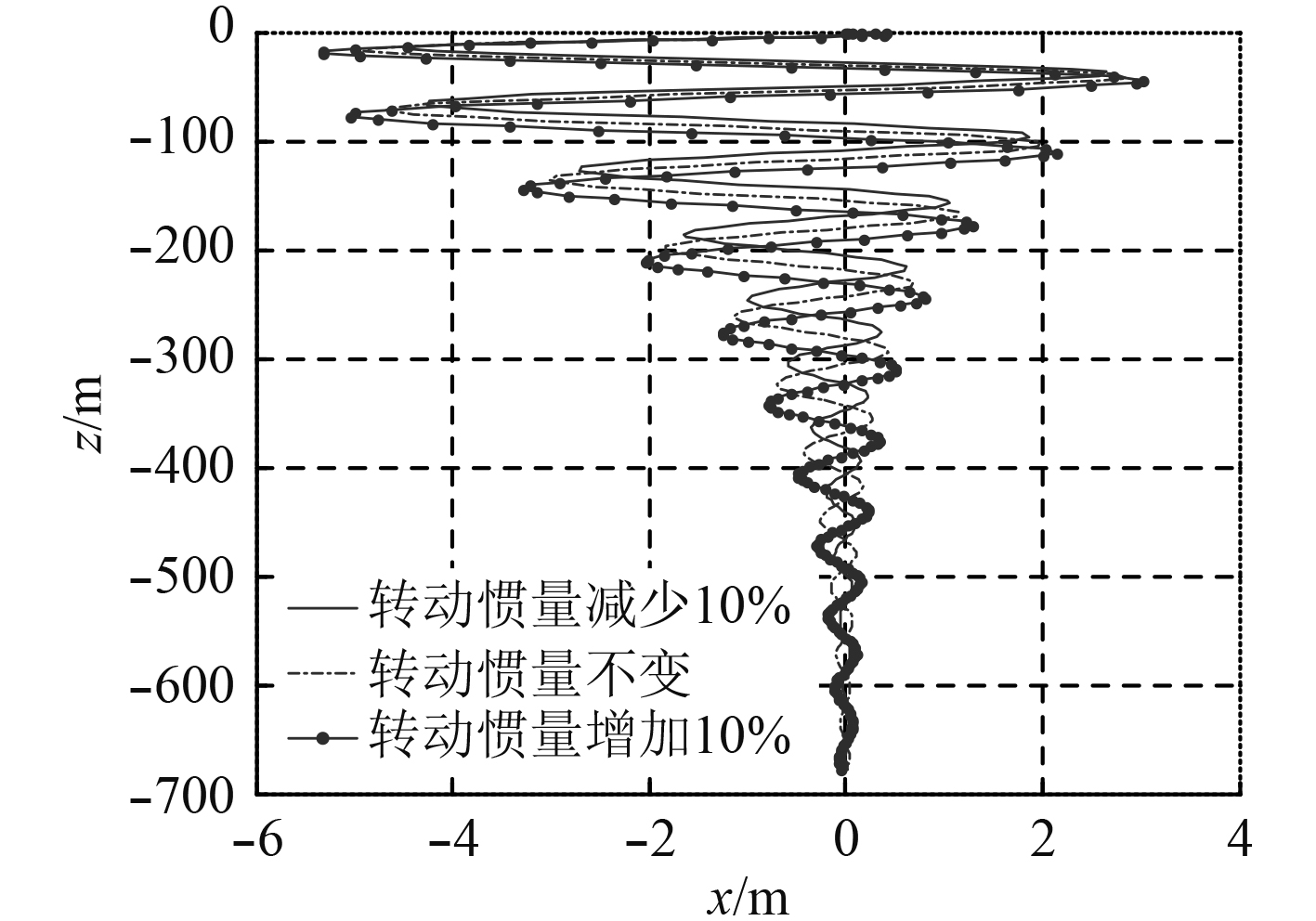
将武器绕y1轴的转动惯量标准参数基础上分别设定为减少10%(
|
图 16 潜深曲线(变转动惯量) Fig. 16 The curve of the weapon diving depth in vertical plane according to its moment of inertia |
|
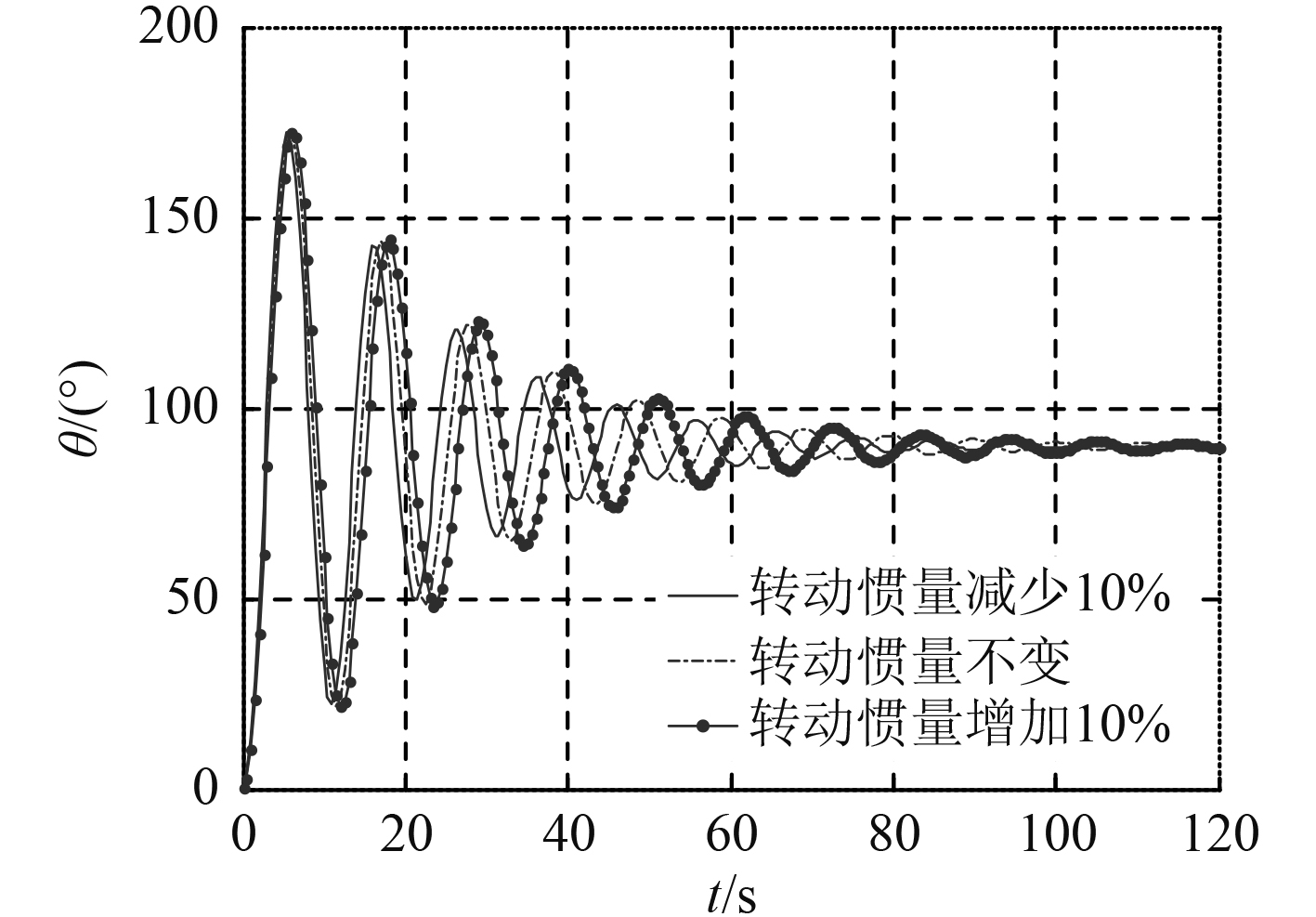
图 19 纵倾角变化曲线(变转动惯量) Fig. 19 The curves of the weapon's pitch angles according to its moment of inertia |
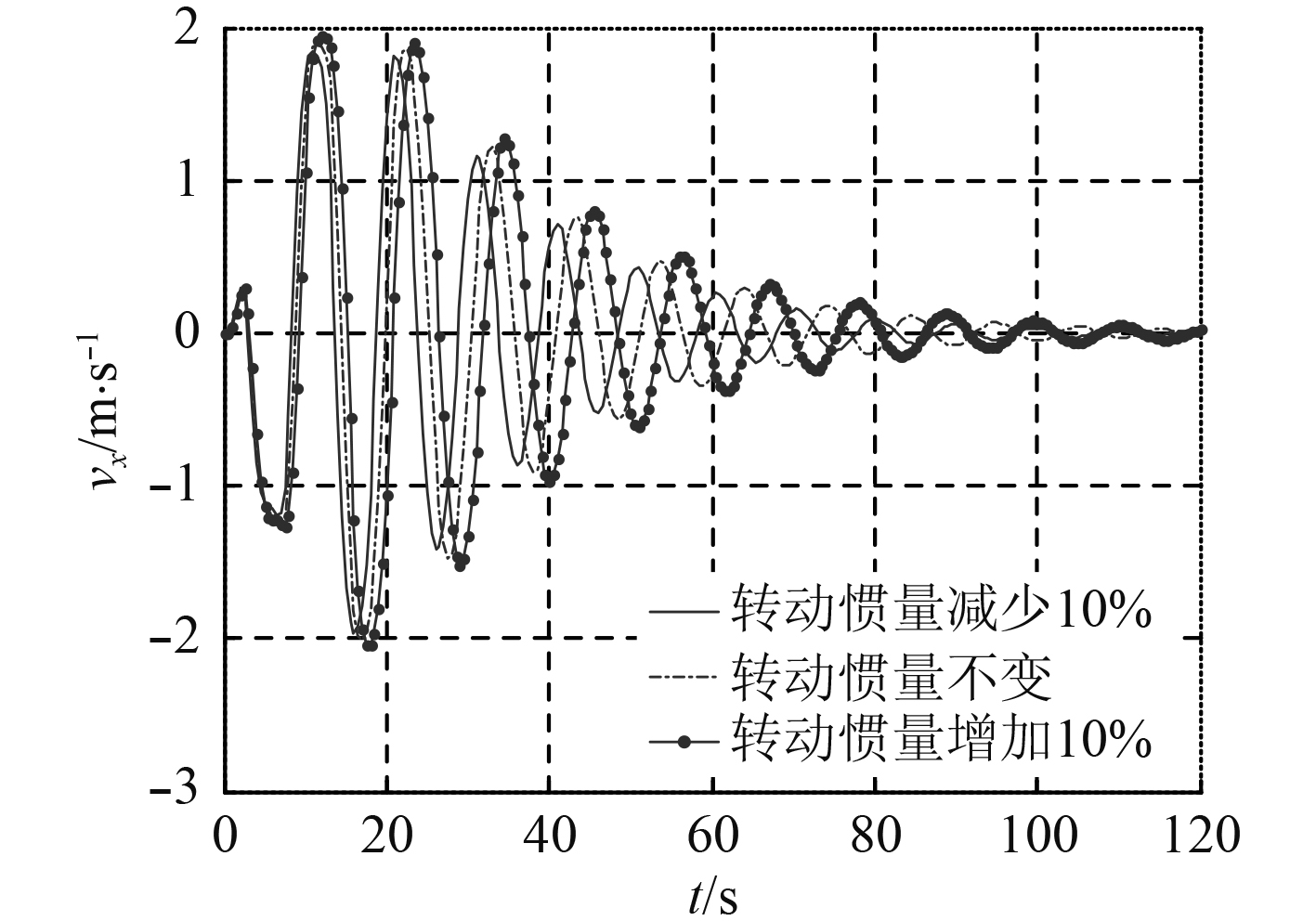
|
图 17
|
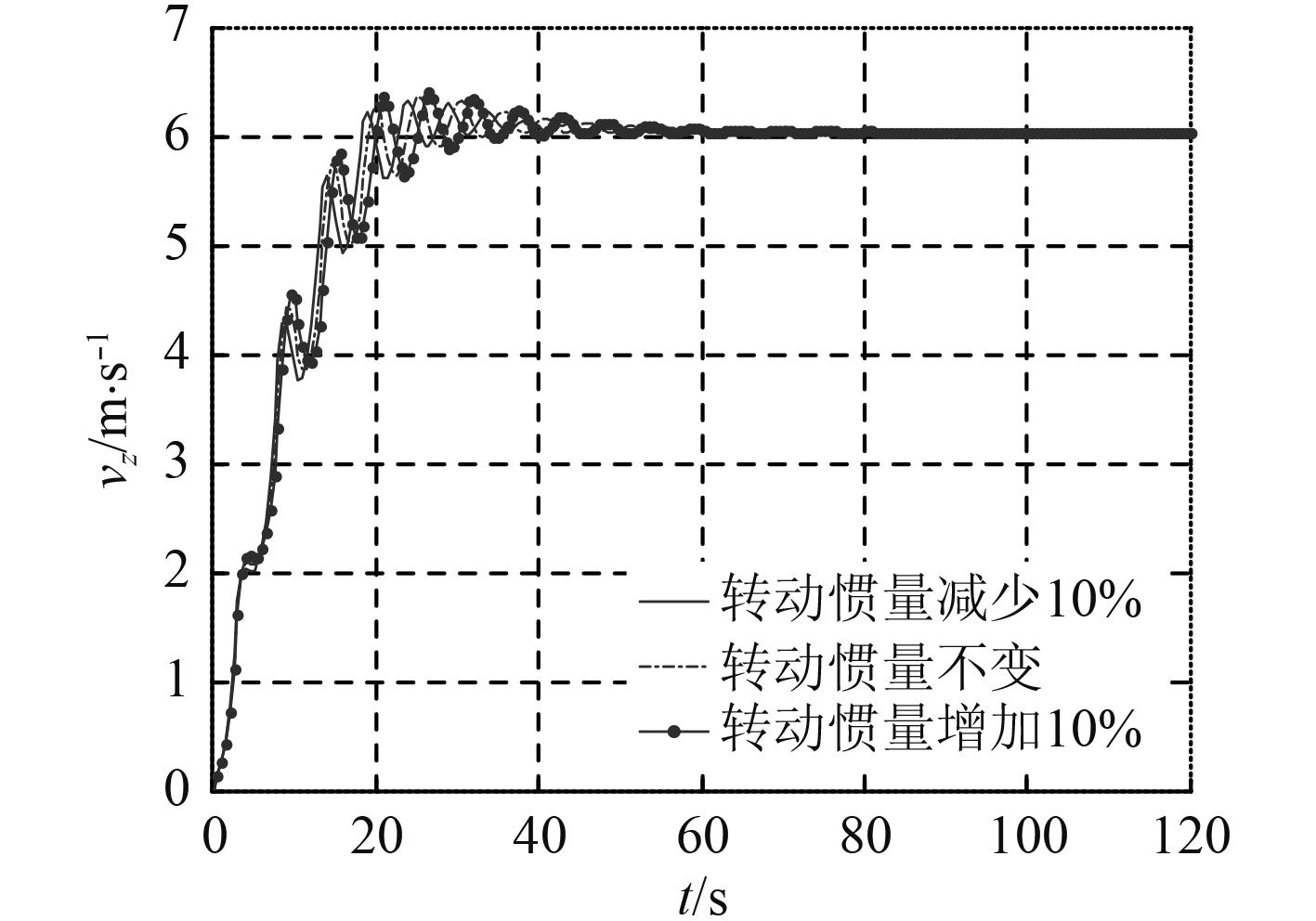
|
图 18
|
从仿真的结果可以看出,改变武器的转动惯量,
为了研究潜伏式武器水下施放后初始阶段的运动规律,建立潜伏式武器水下施放后的初始阶段运动模型并进行仿真分析。从仿真结果可知,无动力的潜伏式武器施放后,由于武器的重心和浮心不在其形心处,因此在投放后的武器初期运动为形心的下沉运动与绕形心钟摆式转动,这种摆动随着下沉深度加大幅度逐渐减小直至成垂直下沉状态。在这阶段中,武器水平初始速度、负浮力以及转动惯量等对其运动有影响。水平初始速度主要对武器落点位置有影响,初始速度越大,武器落点离施放开始位置的距离越大;负浮力对武器稳定后z方向的运动速度
| [1] |
宋保维, 朱信尧, 梁庆卫, 曹永辉. 潜伏式无人水下航行器概念设计[J]. 火力指挥与控制, 2010(8): 107-110. |
| [2] |
练永庆, 王树宗. 鱼雷发射装置设计原理[M]. 2012: 125~134.
|
| [3] |
范乃忠. 现代潜艇的外挂布雷装置[J]. 现代舰船, 1995, 6(2): 32-34. |
| [4] |
钱东. 美国未来的大型UUV-MANTA[J]. 鱼雷技术, 2003(1): 41-50. |
| [5] |
SIRMALIS J E. Pursuing the MANTA vision: recent at-sea technology demonstration results[C]. UDT 2001.
|
| [6] |
杨路春. 潜艇在有外部搭载情况下操纵性水动力导数的数值计算方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
| [7] |
MARTLON G, GRANT P. H. Standard Equations of motion for submarine simulation[R]. Naval Ship Research and Development Center, AD653861 June 1967.
|
 2020, Vol. 42
2020, Vol. 42
