泵喷推进器具有推迟空泡发生、降低辐射噪声[1]和提高推进效率等优点,目前已经广泛应用到潜艇和UUV等水下航行体中,学者们对其推进装置进行了广泛研究。Hong Gao等[2]基于CFD方法,采用单通道计算模型计算了后置定子泵喷推进器的水动力性能,分析了网格数量对计算结果的影响。饶志强[3]等采用混合网格技术对泵喷推进器的敞水性能进行了仿真,通过与实验值对比证明了CFD法的计算精度优于势流法。和普通螺旋桨类似,泵喷推进器的转子在旋转工作时会形成梢涡,引发梢涡空化,产生空化噪声。此外,梢涡还会引发转子和导管产生激振,形成结构振动噪声。因此对梢涡流动特性的研究是泵喷推进器性能研究的重要内容之一。时立攀[4]对泵喷推进器梢涡流动进行了计算,研究了梢涡对辐射噪声的影响。胡健[5]采用LES湍流模型对螺旋桨梢涡进行数值计算并较好地模拟螺旋桨梢涡形态。姬亚鹏[6]采用多种湍流模型对梢涡脉动量进行计算,结果表明基于DES湍流模型的计算结果与实验值最接近。蒲汲君[7]在三维水翼梢涡流场数值研究中,分析了不同湍流模型对梢涡流场计算结果的影响。宋明太[8]在椭圆水翼梢涡空化噪声研究中,通过梢涡空化噪声测试试验,验证了梢涡空化是导致螺旋桨辐射噪声增大的重要因素之一。
由于梢涡是泵喷推进器的重要噪声源,所以控制泵喷推进器梢涡是降低泵喷推进器辐射噪声的重要途径。为了控制转子和螺旋桨的梢涡强度,一般采取梢部卸载[9]的主动控制方法,但该方法对推进效率会产生较大的负面影响。泵喷推进器与航空发动压气机结构非常相似,都具有外部固定的环状导管和内部旋转工作的转子,转子叶梢都存在着复杂的涡系,航空发动机压气机在梢涡控制技术方面已经得到了长足发展,其中“处理机匣”是公认的比较成熟的流场被动控制技术之一。所谓“处理机匣”[10-11],即在转子叶梢附近的导管内壁上加工一定形状的凹槽,当转子叶片转动时,槽内流体发生抽吸和喷射,改变梢涡的强度和形态,从而可以达到控制梢涡强度的目的。
虽然航空发动机压气机处理机匣技术主要目的是通过控制梢涡提高压气机转子流场的稳定性,这虽然和泵喷推进器梢涡控制的目的不同,但都是控制梢涡诱发的不利影响。而且处理机匣技术不仅在高速压气机[12-13]中得到广泛应用,在低速压气机中也有大量应用,低速压气机的流体介质可以看成是不可压缩流体,与潜艇泵喷推进器流体介质处理方法相似,因此潜艇泵喷推进器可以借鉴压气机的处理机匣技术。本文在泵喷推进器导管内壁上设置凹槽用于控制梢涡流场,削弱梢部涡系强度,抑制转子梢涡空化的发生,形成一种泵喷推进器梢涡控制的新方法,对提高泵喷推进器的综合性能、降低潜艇等水下航行体的辐射噪声具有重要的理论意义和军事应用价值。
1 数学模型 1.1 研究对象研究对象为水下航行体的泵喷推进器,水下航行体的尾部外形如图1所示。为了消除缩尺比对计算数值的影响,采用实尺度模型进行计算。舵剖面形状采用NACA0010对称翼型,原始泵喷推进器为前置定子,转子为7叶,导管为减速型导管,转子叶梢与导管下表面间隙为2 mm。

|
图 1 水下航行器尾部示意图 Fig. 1 Diagram of the stern of the underwater vehicle |
为了研究凹槽对转子梢涡的影响,在转子梢部附近的导管内壁开设凹槽,凹槽的长度与转子梢部的轴向长度相等,槽宽和槽深都是8 mm,凹槽沿转子周向均匀分布,凹槽布置总数为120,如图2所示。

|
图 2 导管内壁凹槽布置形式 Fig. 2 Groove layout of duct inner wall |
SST
湍流脉动动能方程(k方程)为
| $ \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k{u_i}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\varGamma _k}\frac{{\partial k}}{{\partial {x_j}}}} \right) + {G_k} - {Y_k} + {S_k}{\text{;}} $ |
和湍流能量耗散率方程(ω方程)
| $ \frac{\partial }{{\partial t}}\left( {\rho \omega } \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho \omega {u_j}} \right) = \frac{\partial }{{\partial {x_j}}}\left( {{\varGamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right) + {G_\omega } - {Y_\omega } + {D_\omega } + {S_\omega }{\text{。}} $ |
其中:
DES模型通常被称为混合LES/RANS模型,是将RANS模型和LES模型的特点结合在一起。采用DES模型计算时,在边界层区域采用RANS模型,其他区域采用LES模型。这一特点极大地节省计算资源,在保证计算精度的前提下,所需网格数量比RANS模型多,但却比LES模型少。本文采用的DES模型基于SST
DES模型相对于SST
| $ {Y_k} = \rho {\beta ^*}k\omega {F_{DES}} {\text{,}} $ |
| $ {F_{DES}} = \max \left( {\frac{{{L_t}}}{{{C_{des}}{\Delta _{\max }}}},1} \right) {\text{。}} $ |
其中
| $ {\Delta _{\max }} = \max \left( {{\Delta _x},{\Delta _y},{\Delta _z}} \right){\text{。}} $ |
湍流尺度定义为
| $ {L_t} = \frac{{\sqrt k }}{{\beta *\omega }}{\text{。}} $ |
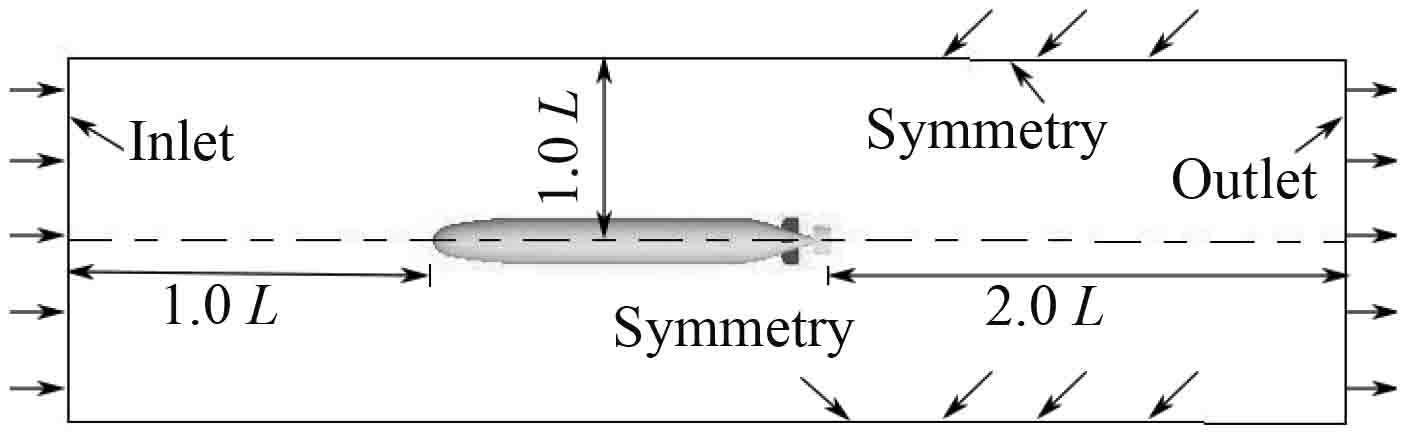
由于计算对象包括艇体部分,为了使计算数值更加准确,消除边界带来的不利影响,以水下航行器长度L为基准对计算域进行布置,计算域如图3所示。
|
图 3 计算域大小及边界条件示意图 Fig. 3 Diagram of computing domain size and boundary condition |
1)入口
入口端面距离水下航行器首端的距离是1 L,边界条件设置为速度进口。
2)出口
出口端面距离水下航行器尾端的距离是2 L,边界条件设置为压力出口,出口压力设置为未扰动时的压力。
3)四周壁面
四周壁面距离航行体中心轴线的距离是1L,边界条件设置为对称面。
航行体、导管、定子和转子边界条件都设置为无滑移壁面。
1.4 网格划分为了更好地控制网格数量,捕捉流场信息,提高网格质量,对水下航行体和泵喷推进器进行结构化网格划分。由于航行体和推进装置结构复杂,将计算域分为4部分进行网格划分,分别为推进器外域、推进器转子域、推进器定子导管域和导管凹槽域。转子、导管、凹槽和导管表面的网格如图4所示。导管凹槽域本是定子导管域的一部分,为了对导管凹槽加密的同时,又不至于大幅度增加网格数量,将导管凹槽从定子导管域中分离出来,单独对其进行网格划分。

|
图 4 计算域网格划分 Fig. 4 Grid division of computing domain |
泵喷推进器梢涡流场结构复杂,尤其是间隙涡和梢涡的相互干扰,促使主涡和二次涡相互影响,在一定程度上增强了流场的不稳定性,给数值模拟带来了一定困难。且在梢涡计算时,不同湍流模型对粘性耗散预报不同,这就造成计算结果差别很大。针对凹槽处理的泵喷推进器和原始泵喷推进器进行数值计算,转子网格数量667万,每个时间步长转子转动1.8°,选取SST
梢涡强度分布云图的计算结果如图5所示。可以看出,无论是采用DES湍流模型还是SST

|
图 5 不同湍流模型梢涡涡强分布云图 Fig. 5 Nephogram of tip vortex intensity distribution of different turbulent models |
为了更具体分析凹槽结构的梢涡控制效果以及2种湍流模型对梢涡计算结果的影响,取出2种泵喷推进器分别采用2种湍流模型在各△x处的梢涡强度计算数值进行比较,其中△x为梢涡截面与转子尾缘的轴向距离,结果如表1所示。
|
|
表 1 有无凹槽处理的泵喷推进器梢涡强度 Tab.1 Tip vortex intensity of pump jet thruster with groove and without groove |
由表1可知,在2种湍流模型下,带凹槽结构的梢涡强度明显低于原始泵喷推进器的计算数值,以△x =0.02处梢涡强度为例,在SST k-ω湍流模型下,导管凹槽泵喷推进器相对于原始泵喷推进器梢涡强度减小了39.22%,在DES湍流模型下,梢涡强度减小了26.94%。在其他2处截面,导管凹槽泵喷推进器梢涡强度也有明显降低,说明泵喷推进器导管内壁凹槽能够有效抑制梢涡,降低梢涡强度。
通过表1的数据还可以看出,以原始泵喷推进器和导管凹槽泵喷推进器△x =0.02处梢涡强度为例,原始泵喷推进器采用DES湍流模型的计算值比SST k-ω湍流模型增大约46.56%,带凹槽结构的泵喷推进器采用DES湍流模型的计算值比SST k-ω湍流模型增大约76.18%,进一步说明了DES湍流模型对梢涡强捕捉更加充分。究其原因,主要是因为SST k-ω湍流模型对湍流脉动进行了时均化处理,对旋涡运动等流动细节描述不准确。
2.2 不同时间步长梢涡计算结果为了研究时间步长对梢涡强度和凹槽效果等计算结果的影响,采用不同的时间步长T/n对2种泵喷推进器的梢涡流动进行计算,其中T为转子转动的周期,n为1周内的时间步数,n分别取200,720,1 800,即转子转动角度步长分别为1.8°,0.5°和0.2°。湍流模型选用分离涡,转子网格数量为667万,对原始泵喷推进器和装有凹槽的泵喷推进器的梢涡流动进行计算。3种时间步长条件下△x =0.02处的梢涡强度计算结果如表2和图6所示。
|
|
表 2 △x =0.02,不同时间步长梢涡计算数值 Tab.2 The calculated value of tip vortex with different time intervals at △x =0.02 |
|
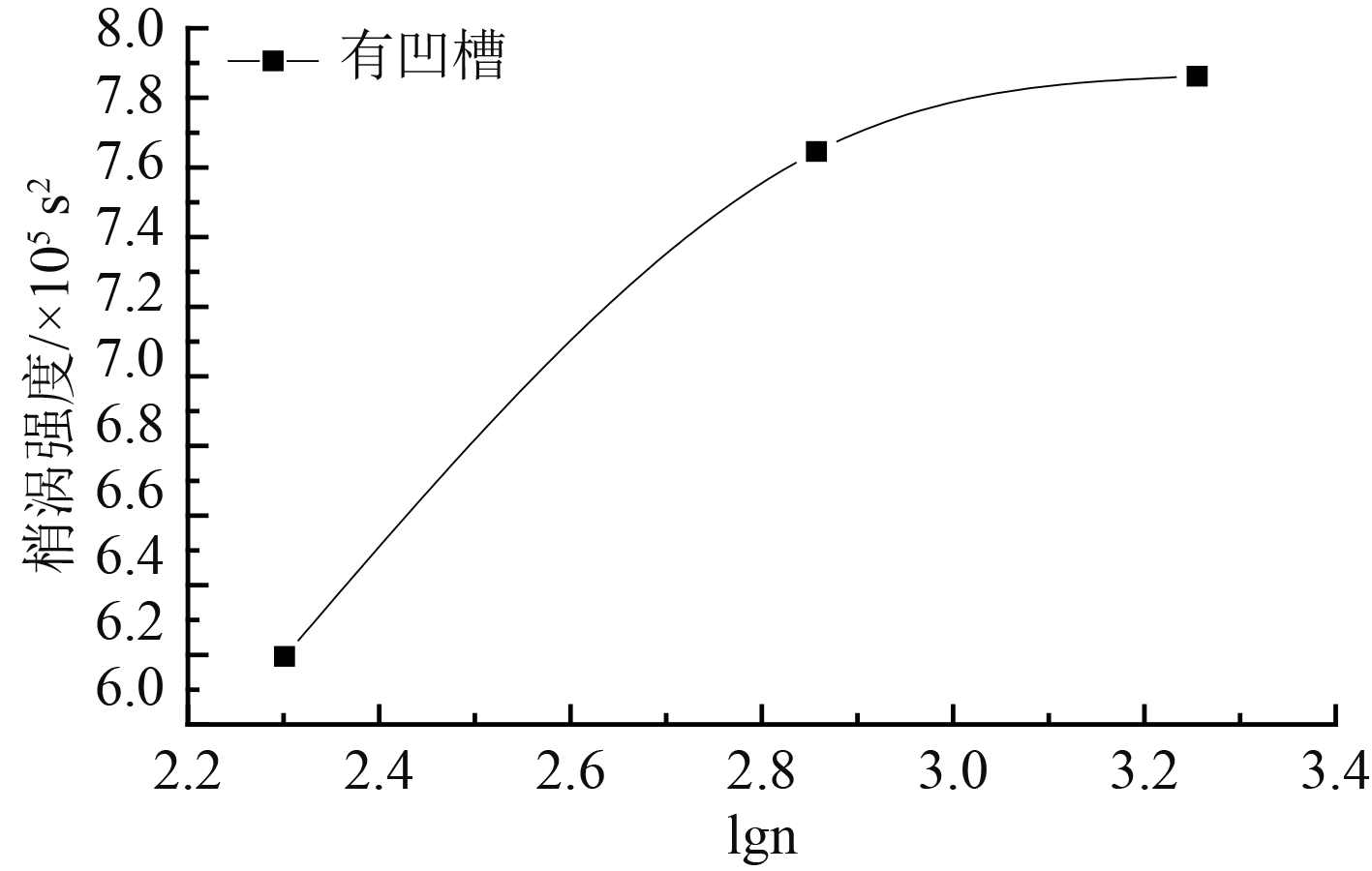
图 6 △x =0.02,不同时间步长梢涡强度分布曲线 Fig. 6 Tip vortex intensity distribution curve with different time intervals at △x =0.02 |
根据表2数据和图6涡强分布规律可以发现,转子转动角度步长在1.8°,0.5°和0.2°条件下,导管凹槽泵喷推进器相对于原始泵喷推进器梢涡强度计算值分别降低了26.94%,19.60%和23.82%,梢涡强度降低幅值在20%左右,说明导管凹槽抑制梢涡的作用比较明显。
由表2还可以看出,随着时间步长变小,梢涡计算值也逐渐变大。当步长从1.8°减小至0.5°时,梢涡强度计算值增大12.15%,步长继续减小至0.2°时,梢涡计算值仅增大1.15%,变化幅度较小,说明当步长减小至0.5°后,再继续减小步长对梢涡强度的计算结果影响很小,因此0.5°角度步长可以满足梢涡强度计算精度的要求。
2.3 不同网格尺度下梢涡计算结果网格尺度是影响计算数值的重要因素,对梢涡来说,转子网格尺度的变化对其数值的大小产生较大影响。为了验证导管凹槽是否有效的削弱梢涡强度,在保证其他因素相同的前提下,对转子网格进行不同程度加密,加密位置为转子梢涡生成区域。基于STAR-CCM+软件,选用DES湍流模型,采用非定常模式,转子转动角度步长为0.5°,对凹槽处理的泵喷推进器和原始泵喷推进器的梢涡流动进行计算。
各种网格数量时在△x =0.02 m位置处的梢涡计算数值如表3所示。可以看出,在3种网格尺度下,凹槽处理的泵喷推进器梢涡强度明显降低,说明凹槽处理的泵喷推进器有效的抑制梢涡的生成。
|
|
表 3 不同转子网格数量在同一位置处梢涡强度 Tab.3 Tip vortex intensity of rotor with different grid quantity at the same location |
从表3还可发现,当转子网格数量从479万增长至667万时,原泵喷推进器转子涡强增大58.28%,凹槽处理的泵喷推进器转子涡强增大58.64%,此时网格尺寸对计算结果影响较大,但当转子网格数量从667万增长至882万时,原泵喷推进器梢涡涡强计算值增大2.6%,凹槽处理的泵喷推进器梢涡涡强计算值增大5.6%,此时梢涡计算数值变化幅度较小。因此,转子网格控制在667万左右已经能够满足梢涡强度计算精度的需求。
为了进一步分析导管凹槽的效果,针对转子网格数量667万的工况进行进一步探究,△x =0.02 m,△x =0.03 m,△x =0.04 m位置处的梢涡计算数值如表4所示。可以看出,△x =0.02处的梢涡强度降低幅值高达19.60%,导管凹槽对转子梢涡削弱效果较为明显,且随着距离转子尾缘越远,梢涡削弱幅值先增大后减小。
|
|
表 4 转子网格667万,涡强对比数值 Tab.4 Comparison of tip vortex intensity by value when grid quantity is 6670000 |
本文在泵喷推进器导管内壁布置一系列凹槽,基于STAR-CCM+软件计算了不同网格数量、不同时间步长和不同湍流模型下的梢涡强度,分析了各种参数设置对梢涡计算结果的影响,初步验证了凹槽结构的梢涡控制效果,从而得出以下结论:
1)通过分析凹槽处理的泵喷推进器和原泵喷推进器在不同湍流模型、不同时间步长和不同转子网格数量下的计算结果,发现导管凹槽能够有效抑制转子梢涡强度。
2)通过对比分析发现,湍流模型、时间步长和网格数量对梢涡计算结果有较大影响,通过分析湍流模型、时间步长和网格数量对梢涡计算结果的影响规律,形成了导管凹槽梢涡抑制效果的数值计算方法。
3)本文针对基于凹槽结构的梢涡流动控制效果,重点讨论了湍流模型、网格数量和时间步长等参数对梢涡流动计算的影响,在讨论中,凹槽的形式和尺寸参数是固定的,而凹槽的形式和尺寸必定会对梢涡抑制效果产生影响,因此后续还需要开展凹槽的轴向长度、径向深度和周向宽度等参数对梢涡抑制效果的影响规律,为凹槽的优化选型奠定基础,以提高抑制梢涡强度和降低辐射噪声的效果。
| [1] |
朱锡清, 唐登海, 孙红星, 等. 船舶螺旋桨低频噪声研究[J]. 船舶力学, 2000, 15(1): 50-55. ZHU Xiqing, TANG Denghai, SUN Hongxing, et al. Study of frequency noise induced by propeller[J]. Journal of Ship Mechanics, 2000, 15(1): 50-55. |
| [2] |
GAO Hong, LIN Wanlai, DU Zhaohui. Numerical flow and performance analysis of a water-jet axial flow pump[J]. Ocean Engineering, 2008, 35(2008): 1604-1614. |
| [3] |
饶志强, 李巍, 杨晨俊. 定子参数变化对其前置定子导管桨性能的影响[J]. 上海交通大学学报, 2013. |
| [4] |
时立攀, 熊鹰. 导管型推进器设计及其水动力性能研究[D]. 武汉: 海军工程大学, 2015
|
| [5] |
胡健, 耿冲, 冯峰. 基于大涡模拟的螺旋桨梢涡数值分析[J]. 华中科技大学学报(自然科学版), 2017, 45(11): 68-73. |
| [6] |
姬亚鹏. 分离涡方法对梢涡中脉动量的数值模拟[D]. 上海: 上海交通大学, 2014.
|
| [7] |
蒲汲君, 熊鹰. 三维水翼梢涡流场数值研究[J]. 中国舰船研究, 2017, 12(1): 8-13. DOI:10.3969/j.issn.1673-3185.2017.01.002 |
| [8] |
宋明太, 刘进, 彭晓星, 等. 椭圆水翼梢涡空化噪声研究[C]// 全国水动力学研讨会. 2014.
|
| [9] |
邢文萍, 王天奎. 螺旋桨梢部卸载和叶片侧斜对降低脉动压力的作用[J]. 中国造船, 1983(2): 29-38. |
| [10] |
徐力平. 轴流压气机的旋转失速的生成及其主动控制. 英国应用力学前沿课题选介. 北京: 科学出版社, 1996.
|
| [11] |
朱俊强, 刘志伟. 轴流压气机的旋转失速的生成及其主动控制. 英国应用力学前沿课题选介. 北京: 科学出版社, 1996.
|
| [12] |
卢新根, 楚武利, 朱俊强, 等. 轴流压气机机匣处理研究进展及评述[J]. 力学进展, 2006, 36(2): 222-232. DOI:10.3321/j.issn:1000-0992.2006.02.006 |
| [13] |
卢新根, 楚武利, 张燕峰. 跨音速压气机间隙流与处理机匣相互作用分析[J]. 西安交通大学学报, 2006, 40(11): 1357-1360. DOI:10.3321/j.issn:0253-987X.2006.11.026 |
| [14] |
DEHGHAN M, BASIRAT TABRIZI H. Turbulence effects on the granular model of partical motion in a boundary layer flow[J]. The Canadian Journal of Chemical Engineering, 2014, 92(1): 189-195. DOI:10.1002/cjce.21812 |
 2020, Vol. 42
2020, Vol. 42
