2. 江苏新扬子造船有限公司,江苏 靖江 214532
2. Jiangsu NewYangzi Shipbuilding Co., Ltd, Jingjiang 214532, China
由于周期性变化气体和旋转装置的惯性力,船舶主机会产生侧向不平衡力和倾覆力矩[1],按照缸数及激振谐次的不同,可以导致主机机架H型或X型的振动。现代大型长行程、超长行程柴油机,由于冲程的加长,使柴油机的高度增加,主机顶部容易出现剧烈横向振动[2]。
同时,随着船舶大型化及高强度钢的大量使用,使得船体的刚度更低[3]。为减少排放,采用燃油效率高的新型低速柴油机,部分增加了气缸数,导致主机横向振动的激振频率更接近于上层建筑等部分船体结构的固有频率。针对上述问题,通常做法是在主机的排气侧(或操纵侧)安装顶部支撑。目前主机顶撑的结构形式,包括机械摩擦片式和液压式2种。机械式顶撑因其不可调节性,经常在船舶航行中由于过度的船体变形发生断裂破坏,而液压式顶撑的优势在于它具有自动补偿主机和船体间的相对变形的能力被广泛应用。本文主要讨论液压式顶撑在船体结构振动控制中的作用。
1 液压顶撑工作原理液压顶撑系统单元主要由液压缸单元、液压控制单元和直接安装在液压缸本体上的液压蓄能器组成[2]。在液压顶撑处于主动工作模式时,电磁阀关闭,当船体结构与主机间距离增大(见图1左),即液压活塞处于正冲程,液压缸内油压下降,液压油通过单向阀在蓄能器压力作用下流入液压缸,将液压缸内压力维持在初始压力值(约0.7 Mpa);当船体结构与主机间距离减小(见图1右),即液压活塞处于负冲程,液压缸内油压升高,此时单向阀阻止液压油返回蓄能器,若压力值大于安全阙值(2.6 Mpa/4 Mpa由型号决定),安全阀打开,液压油被引回蓄能器,从而将主机和船体结构间传递的力控制在允许范围内。在主动工作模式下,因液压油的不可压缩性,液压顶撑可以被简化为一个在拉伸和压缩时具有相同刚度的单轴弹簧,其阻尼效应相比可以忽略,主机和船体结构间实现弹性连接,将系统的固有频率提高到主机工作转速范围之外,发挥振动解调器的作用。

|
图 1 液压顶撑正、负冲程 Fig. 1 Positive and negative displacement |
当液压顶撑处于被动模式时,电磁阀打开。液压顶撑发生正、负冲程时,液压油避开单向阀而通过电磁阀实现在蓄能器和液压缸间的自由流动,同时伴随发生着振动能量的耗散。此时液压顶撑相当于阻尼器的作用,通过提供一定量的局部振动阻尼以减少振动响应。
综合上述分析,液压顶撑的动态特性可概括如表1所示。
|
|
表 1 液压顶撑的简化模型 Tab.1 Simplified model |
在分析复杂弹性体结构的振动响应时,一般是采用把结构离散为近似的多自由度系统的方法,然后通过求解多自由度系统得到结构在任意激励下的振动响应[4]。
多自由度系统的振动描述如下:
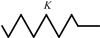
| $ \left[ { M} \right]\left\{ {\ddot v\left( t \right)} \right\} + \left[ { C} \right]\left\{ {\dot v\left( t \right)} \right\} + \left[ { K} \right]\left\{ {v\left( t \right)} \right\} = \left\{ {{ P}\left( \omega \right)} \right\}{e^{i\omega t}} {\text{。}} $ | (1) |
式中,
当液压顶撑处于主动工作模式时,液压顶撑近似简化为一维弹簧单元,增加系统刚度,且不考虑增加系统的阻尼。阻尼矩阵采用瑞利阻尼假设[5],其与质量矩阵或者刚度矩阵成比例,因为无阻尼振型对质量和刚度都是正交的。
| $\left[ { C} \right] = a\left[ { M} \right] + \beta \left[ { K} \right] {\text{。}} $ | (2) |
同时利用振型矩阵
单个模态的动力响应可表示为:
| $ {Y_n}\left( \omega \right) = \frac{{{p_n}\left( \omega \right)}}{{ - {m_n}{\omega ^2} + i{C_n}\omega + {k_n}}} {\text{。}} $ | (3) |
式中:
| $ {C_n} = 2{m_n}{\omega _n}{\xi _n} {\text{。}} $ | (4) |
当液压顶撑处于被动模式时,液压顶撑可简化为离散的一维粘性阻尼单元,额外增加系统阻尼,此时系统阻尼矩阵不再是比例阻尼矩阵,阻尼矩阵不满足振型正交条件,振型坐标运动方程之间将通过振型阻尼系数耦合,需采用直接积分法求解结构动态响应。
令
| $ \left[ { - {\omega ^2}{ M} + i\omega { C} + { K}} \right]\left\{ {u\left( \omega \right)} \right\} = \left\{ {{ P}\left( \omega \right)} \right\} {\text{,}} $ | (5) |
| $ \left[ { K} \right] = \left( {1 + i{ G}} \right)\left[ {{{ K}^1}} \right] {\text{。}} $ | (6) |
式中,
以某型原油船为例,该船选用的主机为MAN B&W 6G60ME-C9.5。装载状态选择压载到港工况,主机6阶H型倾覆力矩作为激振源,考察主机顶撑不同布置形式和工作模式的组合对船体结构振动响应的影响。
3.1 全船有限元模型利用MSC.Patran建立全船结构的有限元模型,质量分布方面,在船体结构上施加集中质量单元或者均布质量单元模拟,保证有限元模型质量分布与实船基本一致。附连水质量采用源汇分布法计算[9]。
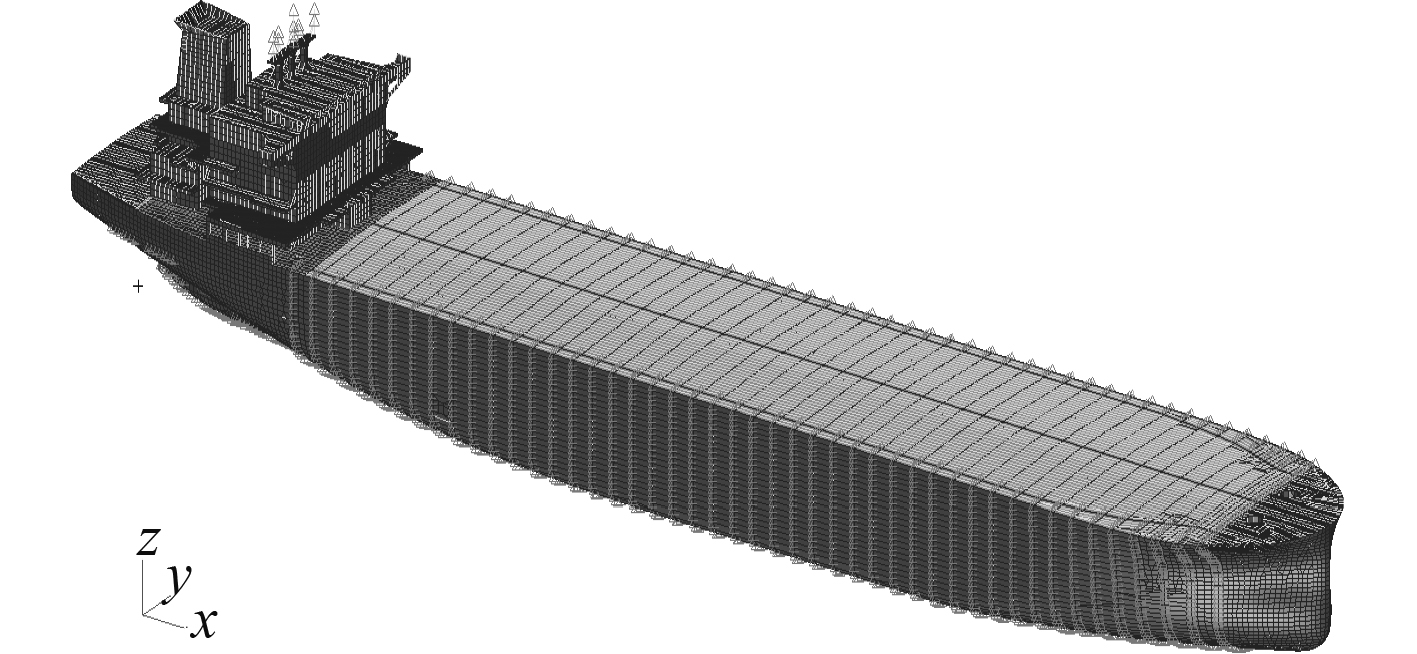
|
图 2 全船有限元模型 Fig. 2 Global ship FEM |
主机机架的外形尺寸及质心坐标参考主机规格书模拟。结合主机顶撑的动态特性,当主机顶撑处于主动工作模式时,其阻尼效应可以忽略,采用一维梁单元模拟并提供其实际的刚度值。当主机顶撑处于被动工作模式时,考虑主机顶撑不提供刚度,可利用一维阻尼单元模拟其阻尼值。
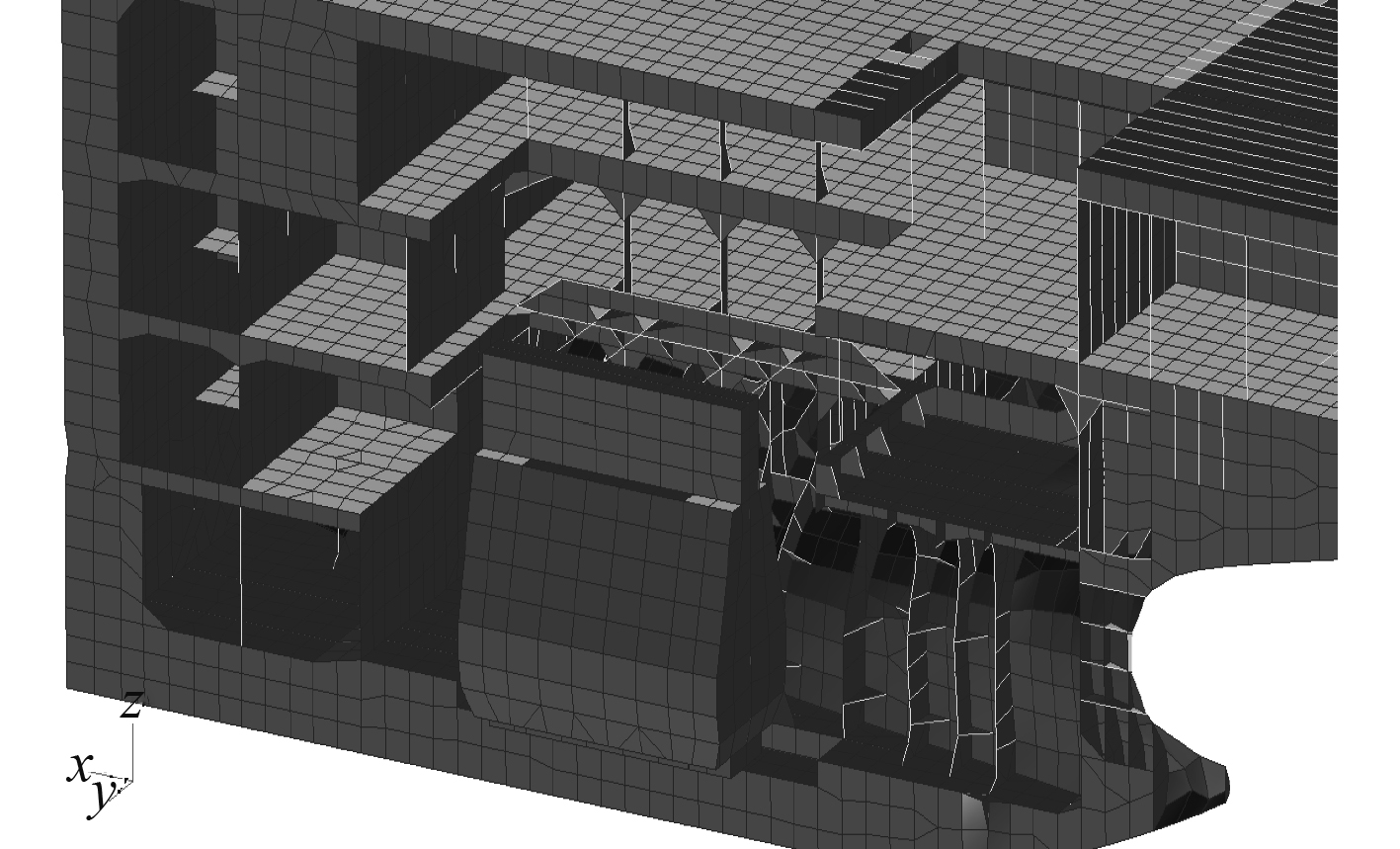
|
图 3 主机、机舱有限元模型 Fig. 3 Engine and engine room FEM |
为反映上层建筑的整体振动情况,选取上层建筑驾驶甲板中线与前端壁交点作为1号参考点。对于主机H型振动,选取主机机架顶部前端作为2号参考点。主机顶撑不同布置形式和工作模式的组合,如表2所示。
|
|
表 2 主机顶撑不同布置形式和工作模式的组合 Tab.2 Combinations different arrangements and different settings of top bracings |
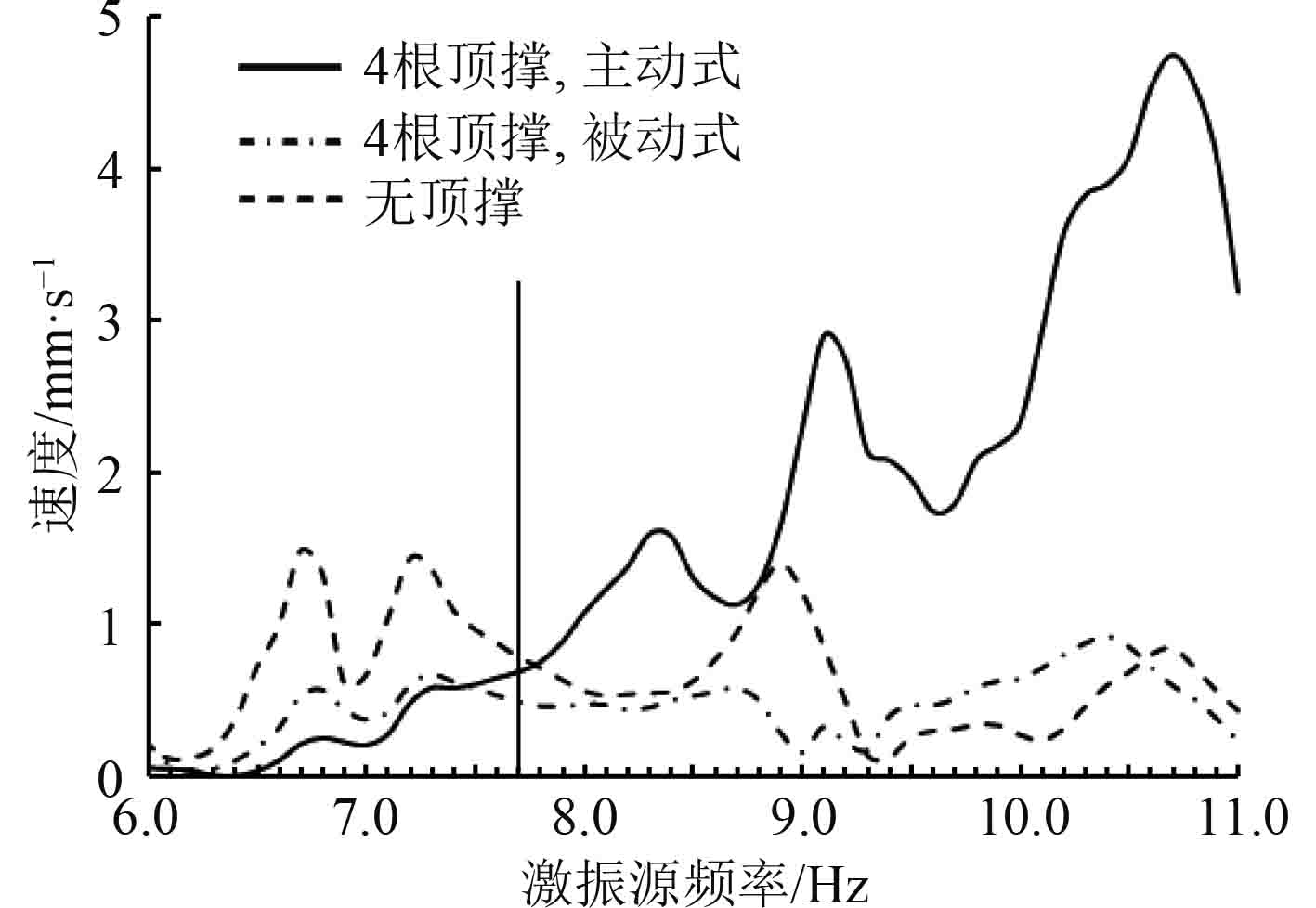
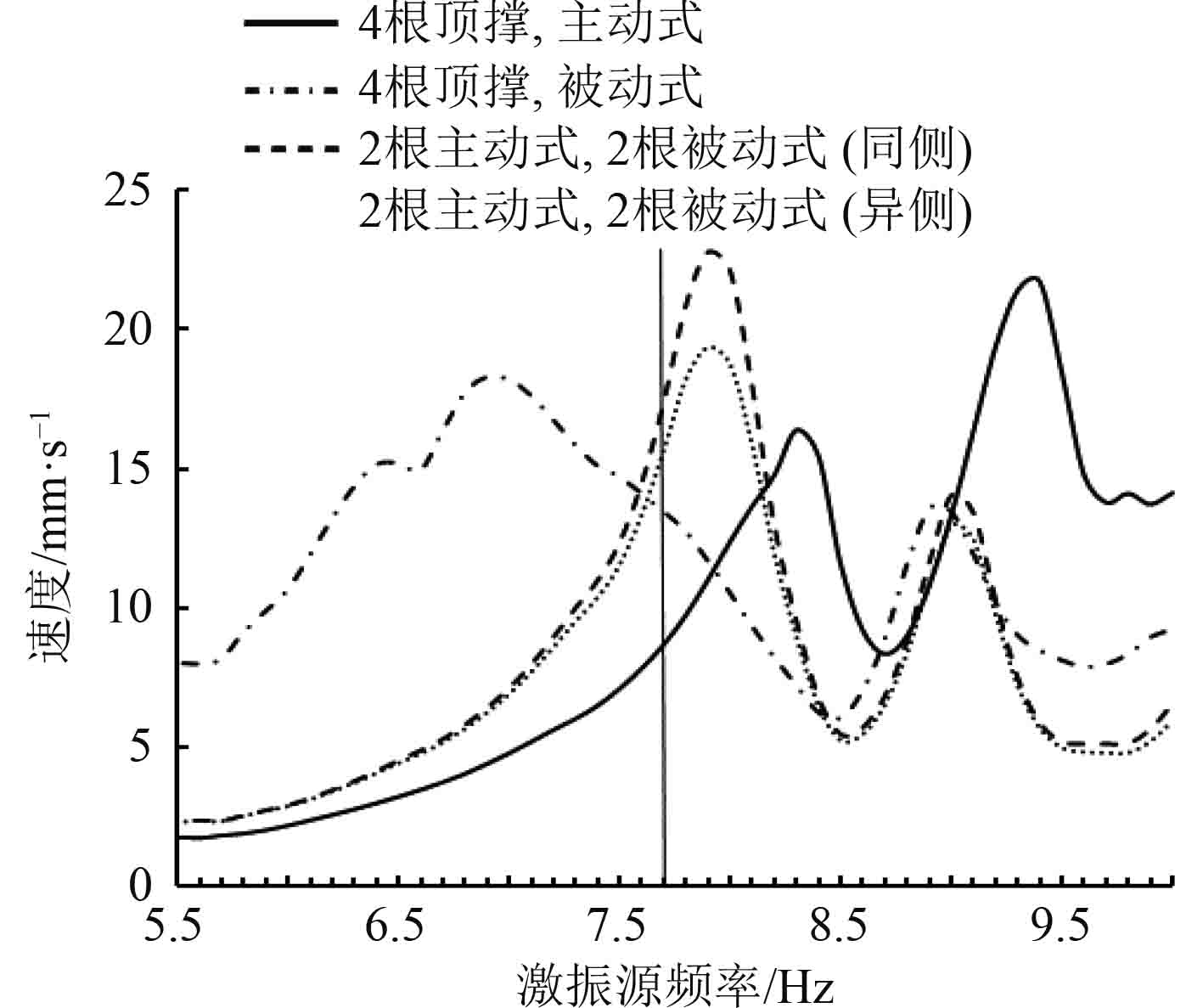
图4~图12所示的振动响应结果均为在主机6阶H型倾覆力矩下的响应峰值,主机6阶H型倾覆力矩的激励频率为7.72 Hz。
|
图 4 驾驶甲板前端中点纵向响应 Fig. 4 Navigation deck longitudinal response |
|
图 12 主机机架顶部前端横向响应 Fig. 12 Engine top transverse response |
对于上层建筑驾驶甲板前端中点(1号参考点),当主机顶撑布置在右单侧,工作模式分别为主动式和被动式,与无顶撑布置时的纵向和横向振动响应峰值如图4和图5所示。
|
图 5 驾驶甲板前端中点横向响应 Fig. 5 Navigation deck transverse response |
当主机顶撑左右双侧布置,工作模式分别为主动式和被动式时,驾驶甲板前端中点(1号参考点)的纵向和横向振动响应峰值如图6和图7所示。
|
图 6 驾驶甲板前端中点纵向响应 Fig. 6 Navigation deck longitudinal response |

|
图 7 驾驶甲板前端中点横向响应 Fig. 7 Navigation deck transverse response |
当主机顶撑主动式和被动式工作模式组合布置时,驾驶甲板前端中点(1号参考点)的纵向和横向振动响应峰值如图8和图9所示。
|
图 8 驾驶甲板前端中点纵向响应 Fig. 8 Navigation deck longitudinal response |

|
图 9 驾驶甲板前端中点横向响应 Fig. 9 Navigation deck transverse response |
1)与无顶撑布置相比,布置主机顶撑可以减小1号参考点的横向振动响应峰值;并且在常用转速附近,主机顶撑主动模式下1号参考点的横向响应值较小,对于纵向振动响应,在某转速以上响应值增加,主要原因是与主机顶撑相连接区域的船体结构刚度存在差异,使得主机机架系统的横向激励发生一定的扭转,从而导致纵向响应值增加。
2)当主机顶撑处于被动模式时,1号参考点的纵向与横向振动响应值在某转速以上也可以有效减小。
3)与右单侧布置主机顶撑相比,增加主机顶撑布置数量可以减小1号参考点的横向振动响应峰值。
4)2种主机顶撑主动模式、被动模式组合布置的方式对1号参考点的纵向与横向振动响应影响的差异均较小。
3.2.2 主机机架强迫振动响应计算结果主机顶撑不同布置形式和工作模式组合下的主机H型振动模态频率计算结果如表3所示。当主机顶撑在被动工作模式时,系统阻尼矩阵不再满足式(2)的解耦条件,需采用复模态(复特征值)的方法进行分析。
|
|
表 3 主机H型振动模态频率计算结果 Tab.3 Engine H-type natural frequency |
通过表3可以发现:
1)当主机顶撑为主动工作模式时,主机机架系统刚度增加,从而提高主机机架H型振动模态的频率;
2)当主机顶撑为被动工作模式时,对主机机架系统的刚度影响很小,所以其H型振动模态固有频率基本不变;
3)将无顶撑布置与单侧布置主动式顶撑相比,主机机架H型振动模态频率增加近30%,但随着主动式顶撑布置数量的增加,其增加幅度较小,主要因为此时主机系统刚度增加已不明显;
4)当主机顶撑主动式、被动式工作模式组合布置时,主机H型振动模态频率较右单侧主动式工作模式略有降低。
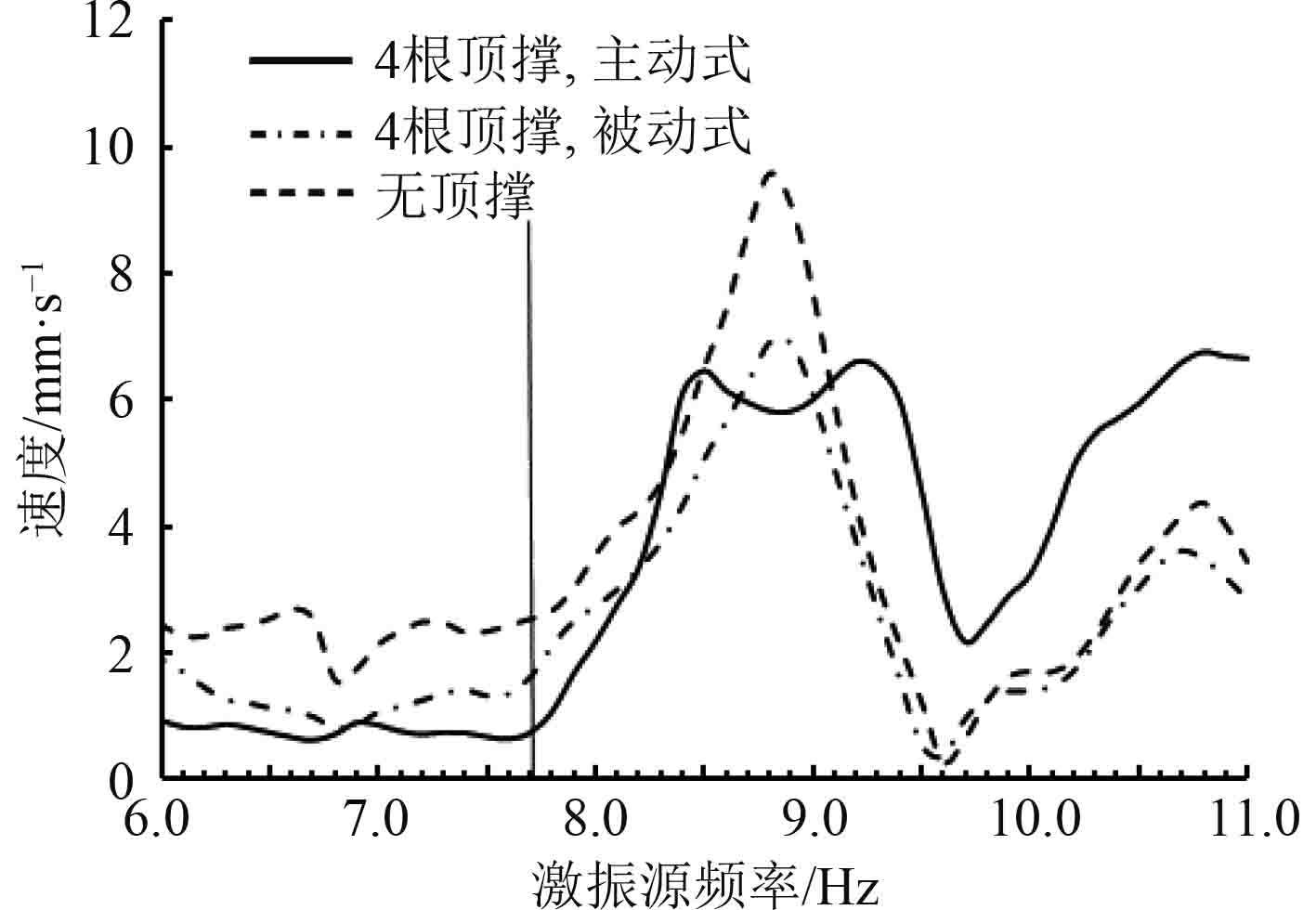
对于主机机架顶部前端(2号参考点),当主机顶撑布置在右单侧,工作模式分别为主动式和被动式,与无顶撑布置时横向振动响应峰值如图10所示。

|
图 10 主机机架顶部前端横向响应 Fig. 10 Engine top transverse response |
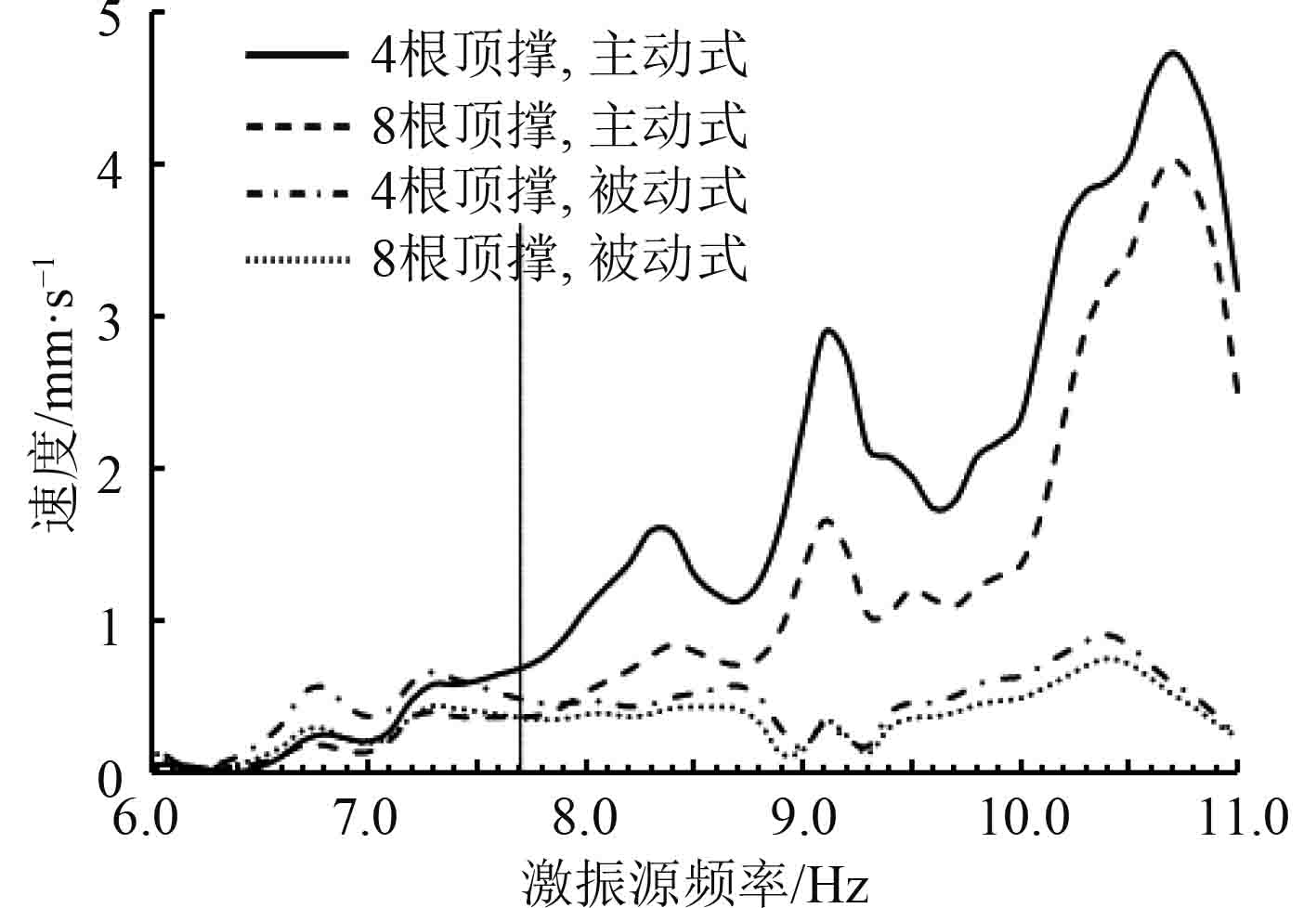
当主机顶撑左右双侧布置,工作模式分别为主动式和被动式时,主机机架顶部前端(2号参考点)横向振动响应峰值如图11所示。

|
图 11 主机机架顶部前端横向响应 Fig. 11 Engine top transverse response |
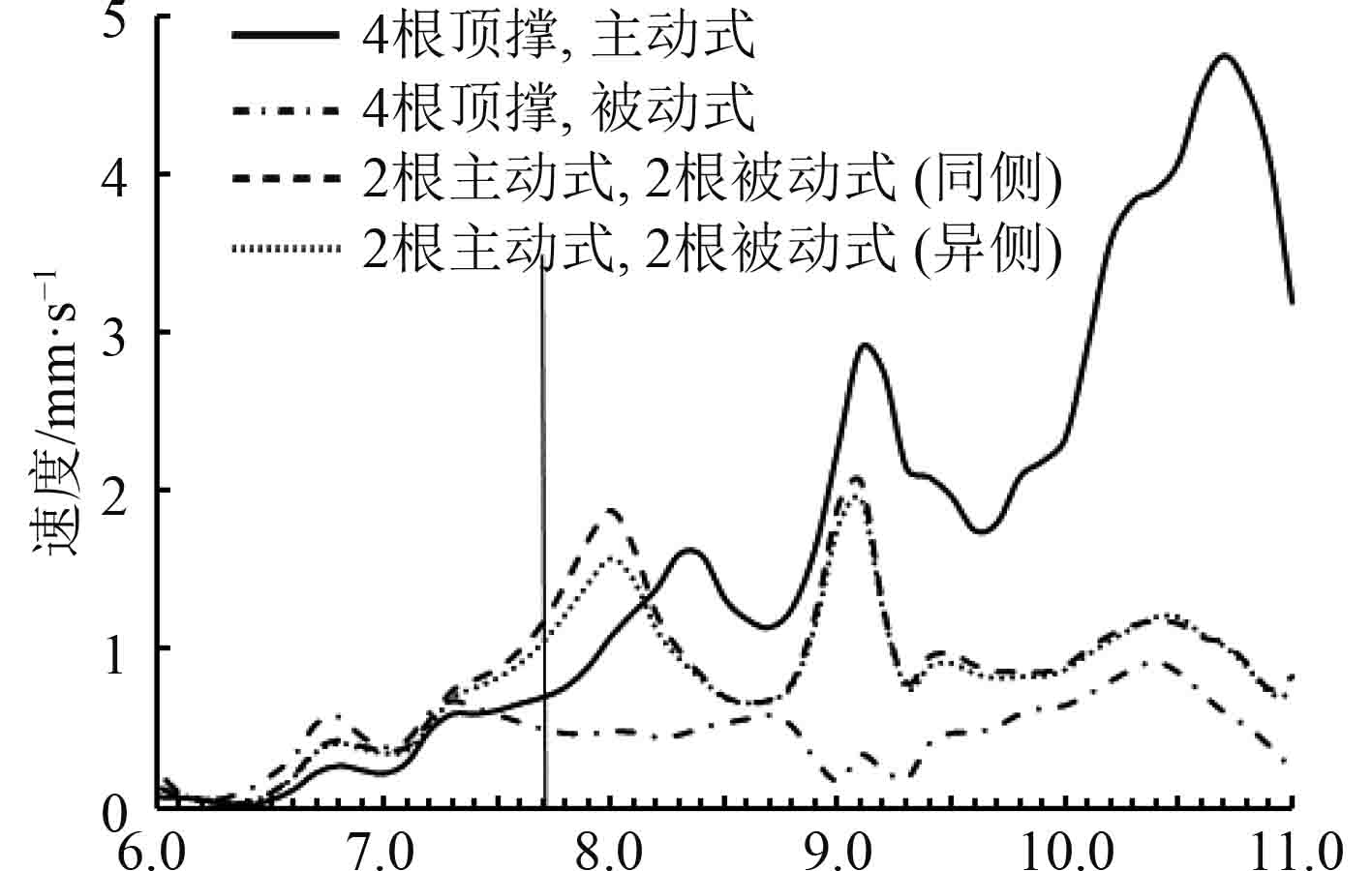
当主机顶撑主动式和被动式工作模式组合布置时,主机机架顶部前端(2号参考点)的横向振动响应峰值如图12所示。
1)布置主机顶撑可以有效减小主机机架的振动响应水平;同时主机顶撑主动模式可以提高最大响应峰值发生的频率。
2)与右单侧布置主机顶撑相比,增加主机顶撑布置数量可以减小主机机架的振动响应峰值,同时几乎不影响同一工作模式下最大响应峰值发生的频率。
3)主机机架在2种主机顶撑主动模式、被动模式组合布置方式下最大响应峰值发生的频率介于右单侧全部主动式和全部被动式之间。
4)通过设置主机临界转速点,实现在不同转速下主机顶撑工作模式的自动转换,可以一定程度上优化主机机架和船体结构的振动响应水平。主机顶撑在低于79 r/min可设置为主动模式,高于79 r/min可设置为被动模式。
4 结 语本文对主机液压顶撑在船体振动响应计算中进行模拟,并通过不同布置形式和工作模式的组合评估及分析了其在船体振动控制中的作用,得到以下结论:
1)基于主机顶撑工作原理,提出模拟主机顶撑不同工作状态特性的简化模型,主动模式时仅考虑其提供刚度,被动模式时仅考虑阻尼,以便船体振动响应分析时借鉴;
2)在船体振动响应分析时,当主机顶撑处于主动模式时采用模态叠加法,而主机顶撑处于被动模式时则采用直接积分法;
3)在主机顶撑工作于主动模式时,主机H型倾覆力矩作为激振源,可能会引起上层建筑纵向振动响应值增大,故在振动响应分析时需予以关注;
4)主机顶撑的布置可以改变主机机架和船体结构的振动响应水平。建议基于不同的装载工况,选择主机顶撑的布置形式,并考虑结合主机临界转速点,实现主机顶撑不同工作模式的自动转换。本文可为船体结构振动控制和船舶建造中主机顶撑调试提供参考,进而指导船体防振结构优化设计。
| [1] |
李香梅, 曹贻鹏, 闫力奇. 主机-船体耦合振动预测与特性研究[J]. 舰船科学技术, 2018, 40(3): 89-96. LI Xiang-mei, CAO Yi-peng, YAN Li-qi. Prediction and vibration characteristic analysis of diesel engine and cargo coupled system[J]. Ship Science and Technology, 2018, 40(3): 89-96. DOI:10.3404/j.issn.1672-7649.2018.03.016 |
| [2] |
李江波. 船舶主机选型与设计[D]. 大连: 大连海事大学, 2014.
|
| [3] |
马乔一. 1100TEU船振动和噪声研究及方案实施[J]. 船舶工程, 2015, 37(11): 34-39. |
| [4] |
徐医培, 李素有, 吴立言. 结构动态响应的求解方法分析[J]. 机械设计与制造, 2009(6): 12-14. DOI:10.3969/j.issn.1001-3997.2009.06.005 |
| [5] |
金咸定, 夏利娟. 船体振动学[M]. 上海: 上海交通大学出版社, 2011.
|
| [6] |
R. 克拉夫, J. 彭津. 结构动力学[M]. 北京: 高等教育出版社, 2017.
|
| [7] |
MSC. MSC Nastran 2013.1 Dynamic Analysis User‘s Guide[M]. Los Angeles, 2013.
|
| [8] |
MSC. MSC Nastran 2013.1 Quick Reference Guide[M]. Los Angeles, 2013.
|
| [9] |
张新伟, 吴小康, 陆利平. 40万吨矿砂船全船和局部振动研究[J]. 中国造船, 2011, 52(1): 26-38. ZHANG Xin-wei, WU Xiao-kang, LU Li-ping. Global and local vibration research on 400, 000DWT ore carrier[J]. Shipbuilding of China, 2011, 52(1): 26-38. DOI:10.3969/j.issn.1000-4882.2011.01.004 |
 2020, Vol. 42
2020, Vol. 42