2. 江苏自动化研究所,江苏连云港 222061
2. Jiangsu Automation Research Institute, Lianyungang 222061, China
采用焊接方式连接的海洋结构物由于焊缝区域及其焊趾区域存在较大的焊接温度产生较高的焊接应力场,焊接应力场对于海洋结构物结构性能以及服役时间件都产生很大的影响[1]。基于此,本文开展焊接残余应力及其释放研究。
焊接涉及的学科较为广泛,影响因素非常多,很难从数学上获得精确解。由于焊接残余应力测量受限于技术,数值仿真技术最早被用于研究焊接残余应力分布的规律。对于一维情况下的焊接残余应力产生的机制,1936年Boulton和Lancemartin[2]开展了数值仿真研究。进入60年代,Tall[3]利用计算机编程用于解决在一维空间沿着母材中线进行堆焊求解焊接残余应力分布的问题。针对于点焊接造成的焊接残余应力以及焊接变形,Alfredsson和Josefson [4] 采用FEM进行了系统的研究。B.Brickstad和B.LJosefson[5]针对于大直径不锈钢管-管多道对接焊焊接温度场及其应力场分布情况,对焊接影响参数进行数值仿真研究。针对于材料屈服强度对于纵向焊接残余应力及其分布规律的影响,Chin-HyungLee et al[6]对于同种和异种钢材焊接进行了数值仿真研究。P.Duranton et al[7]针对于316L不锈钢管对接焊的焊接过程采用网格自适应技术进行了数值模拟,详细介绍了热机械模拟过程以及方法。M.Adak et al[8]针对于焊接过程焊接参数开展了3种不同边界约束下、板厚以及网格模型对应力分布影响的研究。
国内对焊接残余应力数值模拟研究开始的时间较晚,楼志文等[9]通过自主编程有效模拟焊接过程中温度场和应力场变化。汪建华等[10]数值模拟管板接头焊接残余应力分布及其变形,对焊接接头变形以及板材开孔对于焊接残余应力分布影响进行研究。鹿安理等[11]在商用软件的基础上,结合计算机技术开发了用于焊接数值仿真的有限元软件。刘川和张建勋[12]通过采用动态子结构方法,将焊接位置划分为线性以及非线性弹塑性区进行焊接残余应力计算,有效提高了计算准确性。傅定发等[13]采用有限元法研究了6061薄壁铝合金不同焊接顺序影响下的焊接残余应力分布。李良碧等[14]采用有限元法计算了深海耐压环肋圆柱壳结构的焊接残余应力和残余变形,同时针对于耐压结构极限承载能力和稳定性进行了研究。徐磊等[15]对潜水器的耐压球壳焊接残余应力分布情况进行了有限元计算,并研究耐压球壳极限承载力。邓德安等[16]基于Sysweld软件,探究了横向拘束对焊接残余应力的影响,横向约束可以明显降低横向残余应力,在焊缝端部尤为明显。
对于焊接时,试件初始边界约束对焊接残余应力及其在后续拉伸载荷作用下释放影响的研究较少。本文首先采用数值仿真和试验相结合的研究方法,通过数值仿真计算得到焊接过程中不同边界约束下的应力场,在此基础上,开展焊接试验验证;最后开展边界约束对于焊接残余应力释放的影响研究。
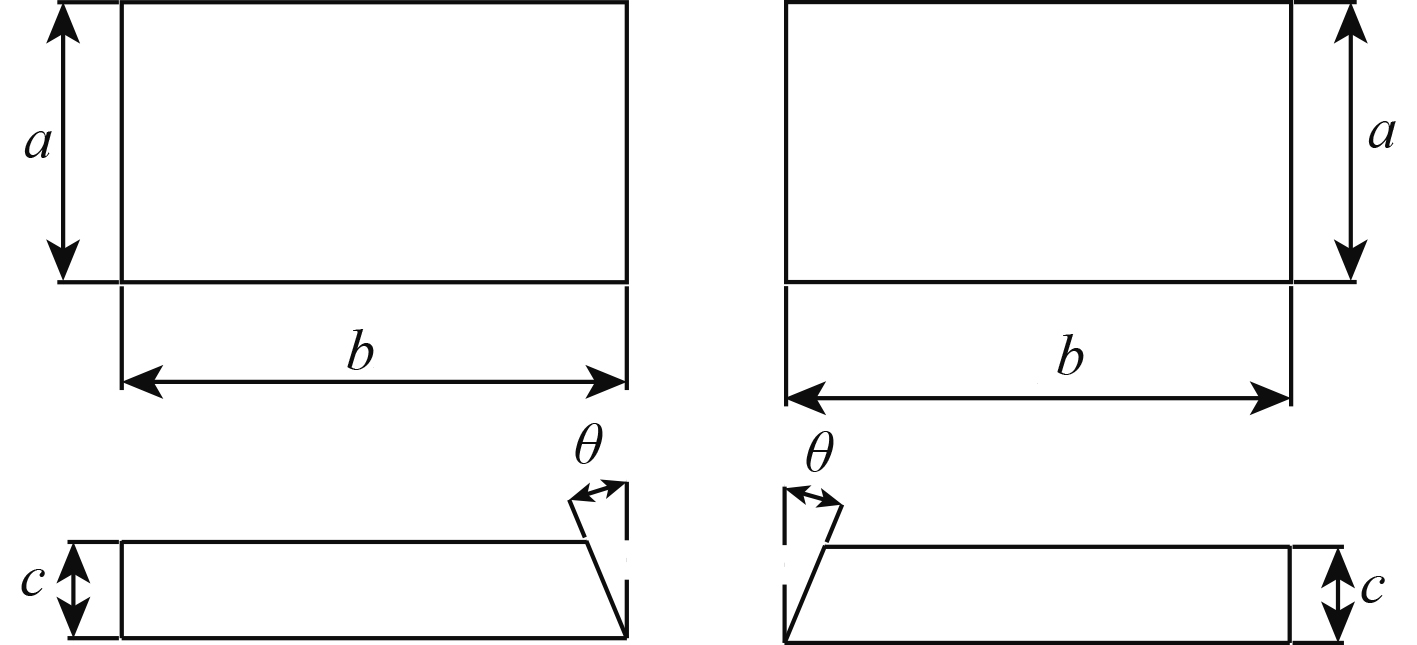
1 焊接残余应力有限元计算 1.1 温度场计算采用CO2气体保护焊进行平板对接焊,试件材料为AH36船用高强钢,焊道V型坡口,板厚9 mm,见图1和表1。根据船厂AH36钢焊接工艺,试件开V型坡口,正面依次焊3道,最后从反面清根处理后再补焊接1道。
|
图 1 焊接试件示意图 Fig. 1 Schematic diagram of thin-plate welding test piece |
|
|
表 1 焊接试件相关尺寸 Tab.1 Related dimensions of thin plate welding test piece |
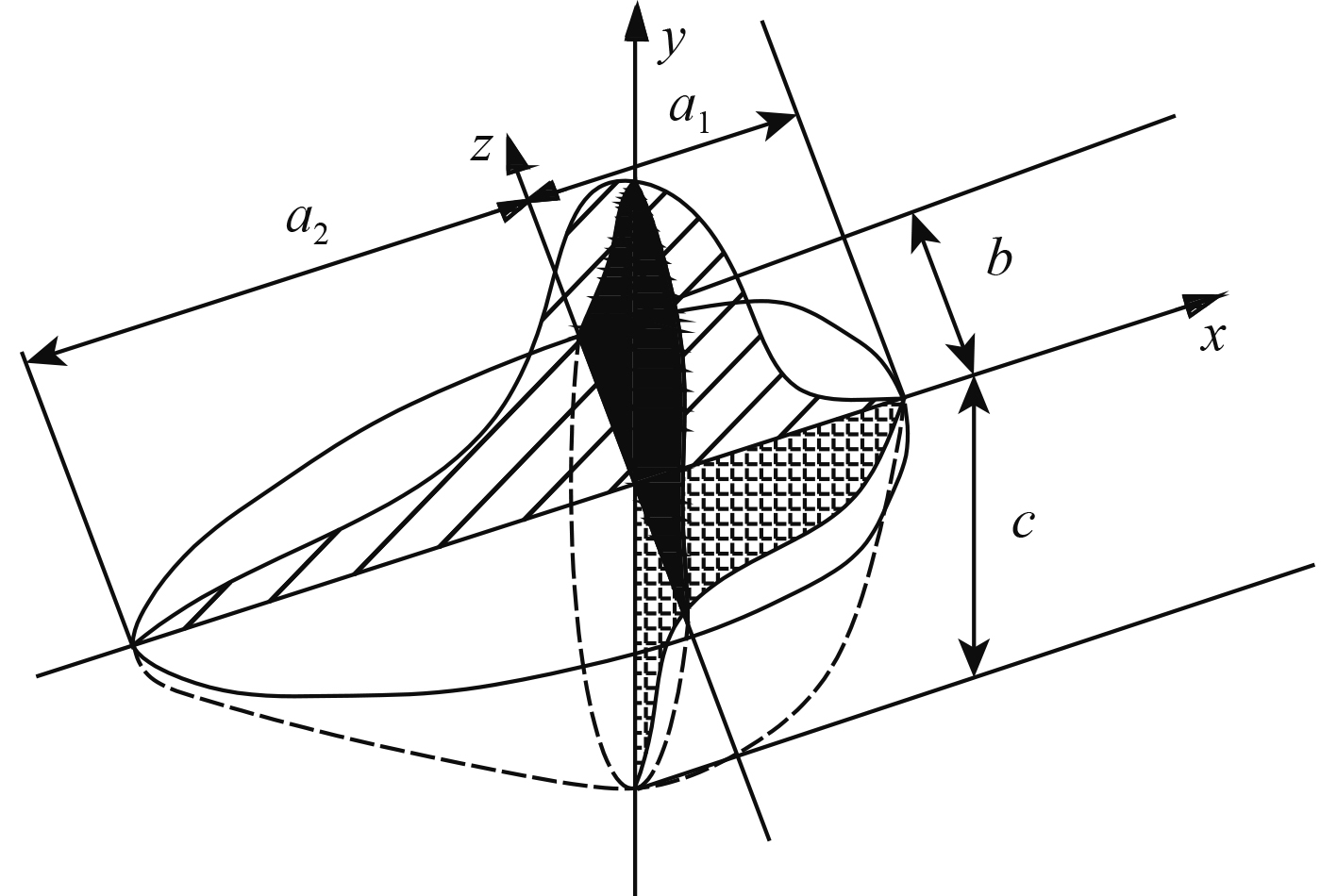
采用Abaqus,有限元模型单元类型选用三维8节点实体单元。焊缝区域进行了网格加密,有限元网格尺寸1 mm左右,焊趾位置到两端有限元网格尺寸从1~4 mm逐渐变大,从而节约计算时间。热源模型采用双椭球热源如图2所示。前半部分热源分布为:
|
图 2 双椭球热源模型 Fig. 2 Double ellipsoid heat source model |
| $ \begin{split} & q(x,y,z) =\\ & \frac{{6\sqrt 3 {f_1}Q}}{{{\text{π}} {a_1}bc\sqrt {\text{π}} }}\exp \left( - 3\frac{{{x^2}}}{{{a_1}^2}}\right)\exp \left( - 3\frac{{{y^2}}}{{{b^2}}}\right)\exp \left( - 3\frac{{{z^2}}}{{{c^2}}}\right) {\text{,}} \end{split} $ | (1) |
后半部分热源分布为:
| $ \begin{split} & q(x,y,z) = \\ & \frac{{6\sqrt 3 {f_2}Q}}{{{\text{π}} {a_2}bc\sqrt {\text{π}} }}\exp \left( - 3\frac{{{x^2}}}{{{a_2}^2}}\right)\exp \left( - 3\frac{{{y^2}}}{{{b^2}}}\right)\exp \left( - 3\frac{{{z^2}}}{{{c^2}}}\right){\text{。}} \end{split} $ | (2) |
式中:
在焊缝区域,采用生死单元法模拟焊道中焊料的焊接成型过程。采用Fortran语言将如表2所示的焊接试验中记录的焊接电流和电压作为数值计算的参数,输入用于编写双椭球热源模型,嵌入到Abaqus软件中,实现模拟焊接过程中热源移动情况。由于试件进行4层焊接,每层焊接设置1个起始节点,根据每层焊接时间,控制生死单元法同移动热源移动速度相一致。
|
|
表 2 试件焊接相关参数 Tab.2 Welding related parameters of test piece |
初始温度取为室温25 ℃,为模拟焊接过程中金属与周围介质的对流换热,并设置初始对流换热系数为50
三维瞬态温度场控制方程为:
| $ {\rm{c}}\rho \frac{{\partial {\rm T}}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {k\frac{{\partial {\rm T}}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {k\frac{{\partial {\rm T}}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {k\frac{{\partial {\rm T}}}{{\partial z}}} \right) + Q {\text{。}} $ | (3) |
式中:
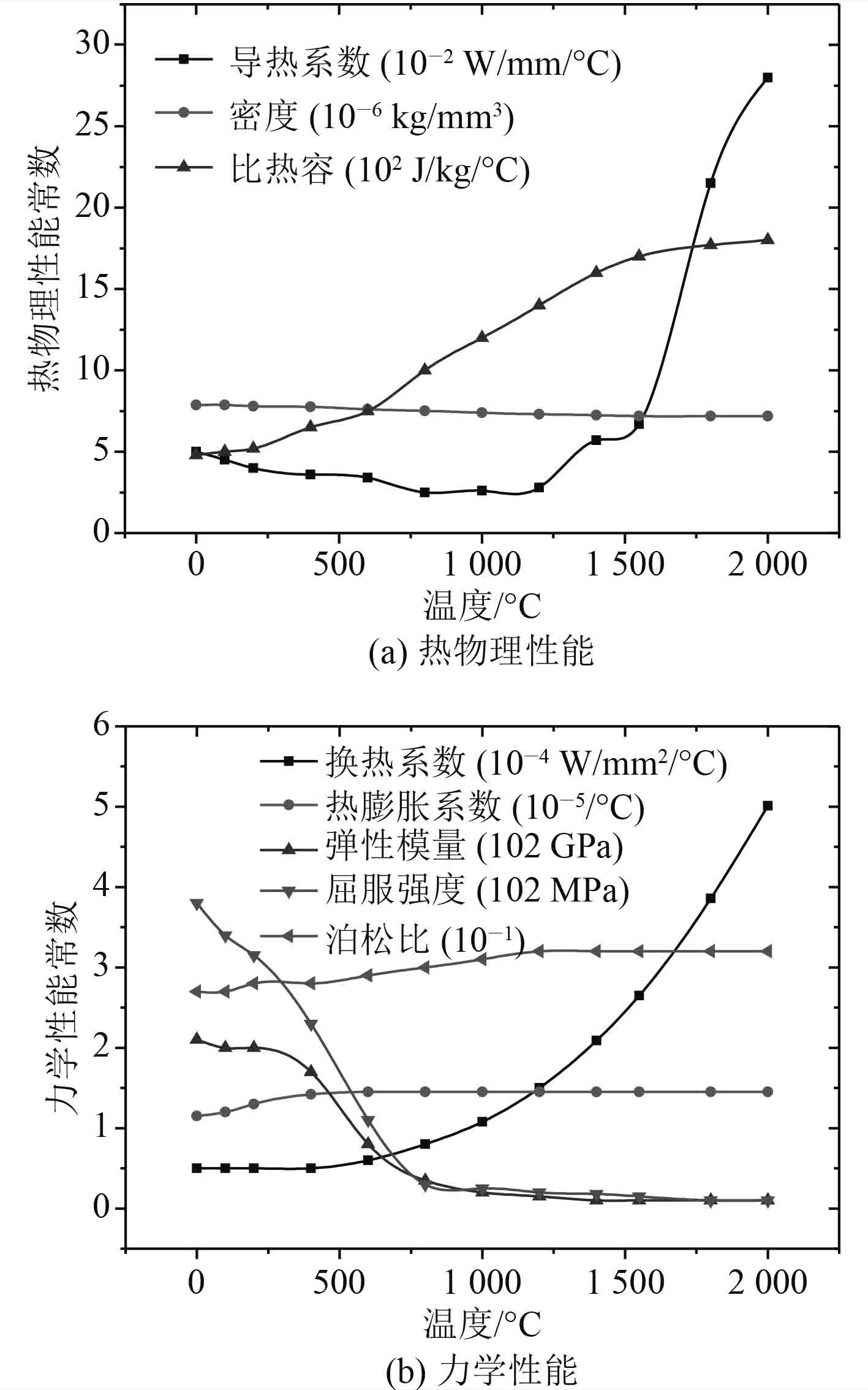
|
图 3 AH36钢随温度变化的材料性能 Fig. 3 Temperature-dependent material properties of AH36 |
模拟焊接温度场过程中,对每层焊接结束后,冷却60 s,然后进行下一层焊接,更加贴近焊接现场过程。正面第一层焊料填充结束以及试件全部焊接结束试件温度场分布情况,如图4所示。
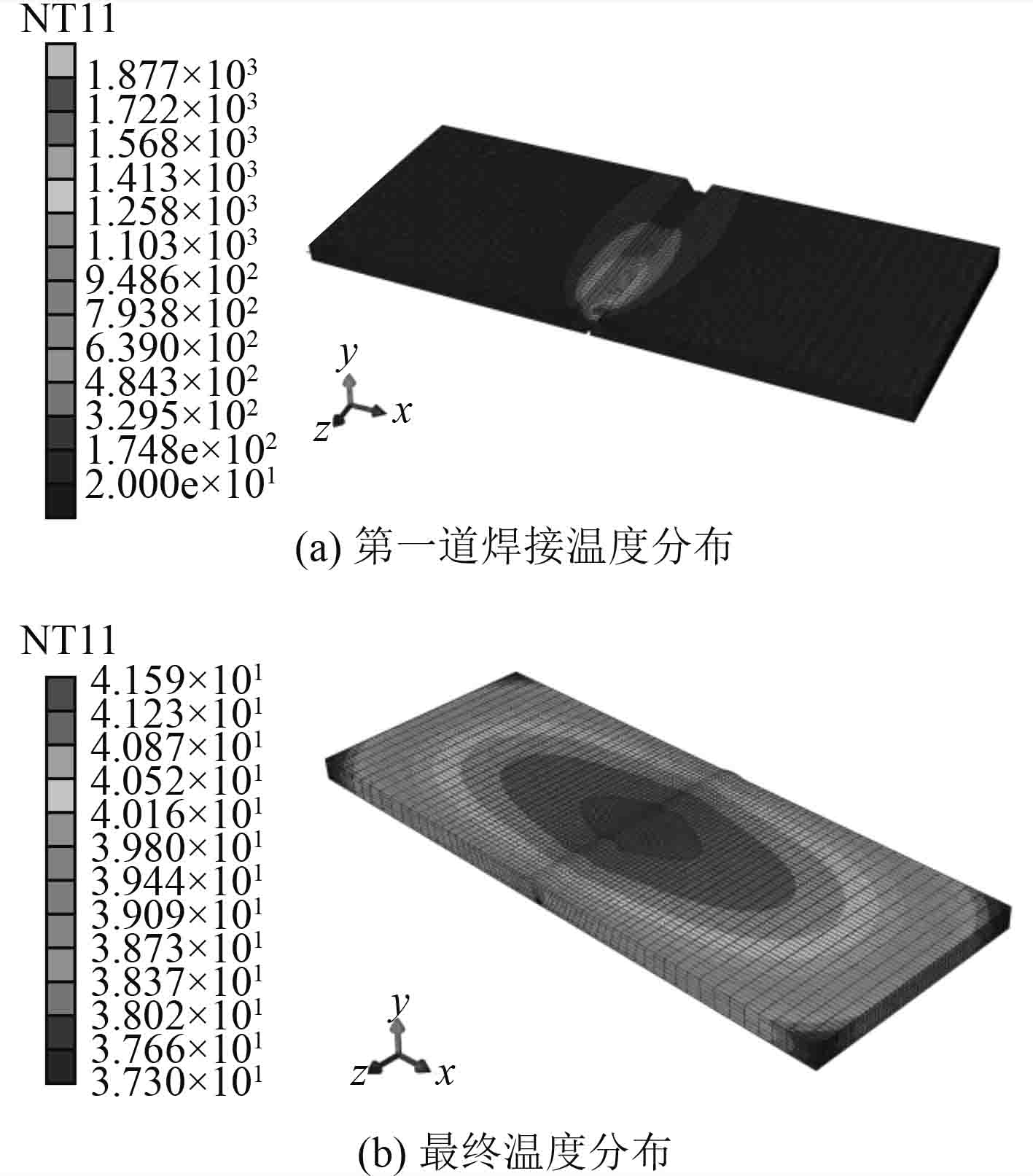
|
图 4 CO2气体保护焊试件温度变化图 Fig. 4 Temperature distribution diagrams of plate CO2 gas shielded test piece |
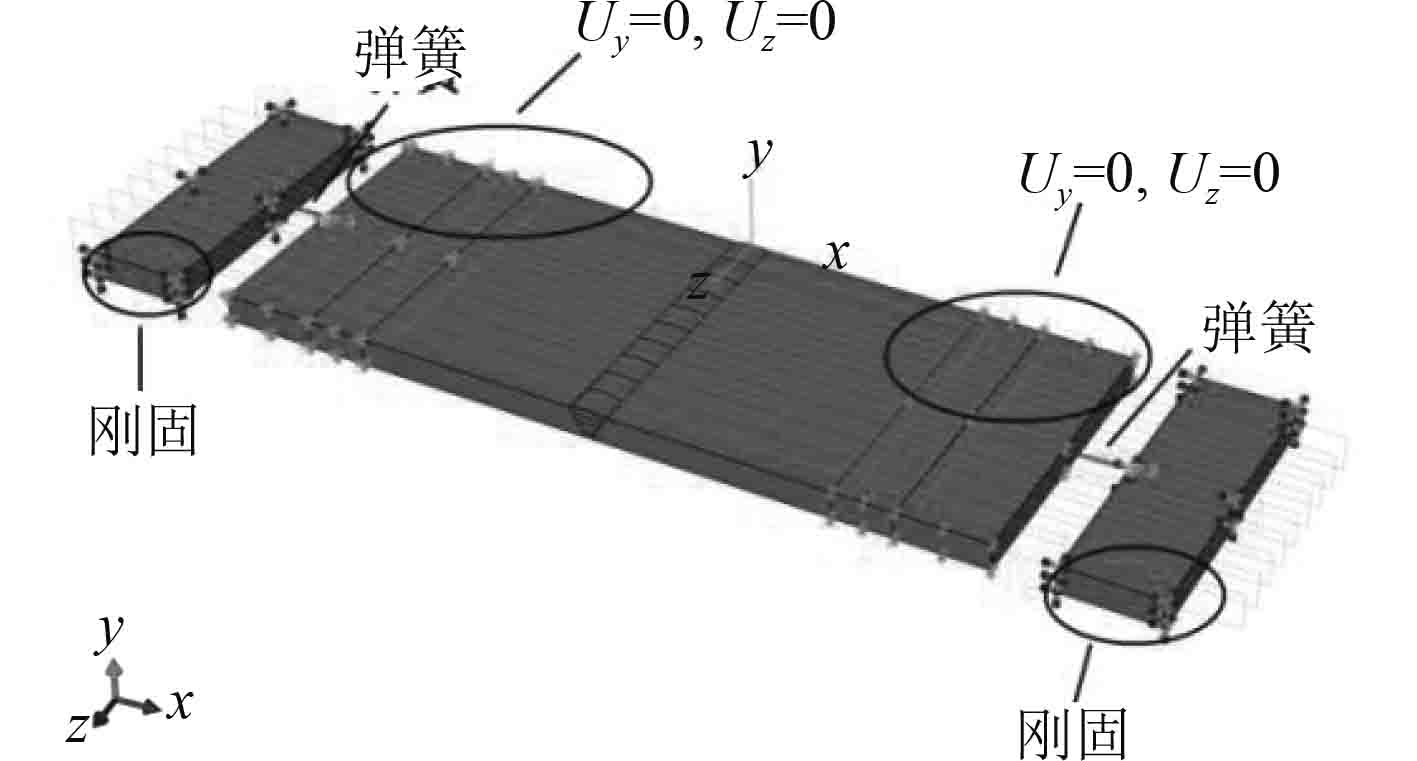
焊接过程中,常规的焊接方式一般是对母材进行二次切割,用于研究焊接位置焊接残余应力分布情况。二次切割会造成焊接残余应力二次分布,对于后续研究拉伸载荷作用下焊接残余应力释放有影响。因此,本文设计的试验装配方式选择试件两边采用楔形块压紧固定。该约束方式对试件垂向位移进行了限制,水平方向约束主要依靠楔形块与试件表面静摩擦力进行约束。水平方向的约束既不是可以自由趋近,也不是刚性固定,所以有限元计算时边界条件采用水平方向施加弹簧约束。
对焊接试件两端分别设置一个刚性物体,物体两端边界约束完全刚性固定,将焊接件以及刚性物体靠近的2个面,分别对2个面进行面内节点耦合到1个节点。在耦合点之间加载一个轴向单自由度的弹簧单元进行弹簧约束。焊接件表面选择部分区域模拟焊接试验装配方式进行约束,有限元模型的弹簧约束如图5所示。
|
图 5 边界条件和弹簧约束 Fig. 5 Boundary conditions and spring constraints |
为考虑弹簧刚度对计算结果的影响,分析了弹簧刚度系数为0 N/mm,
|
|
表 3 不同边界约束汇总表 Tab.3 Summary of different boundary constraints |
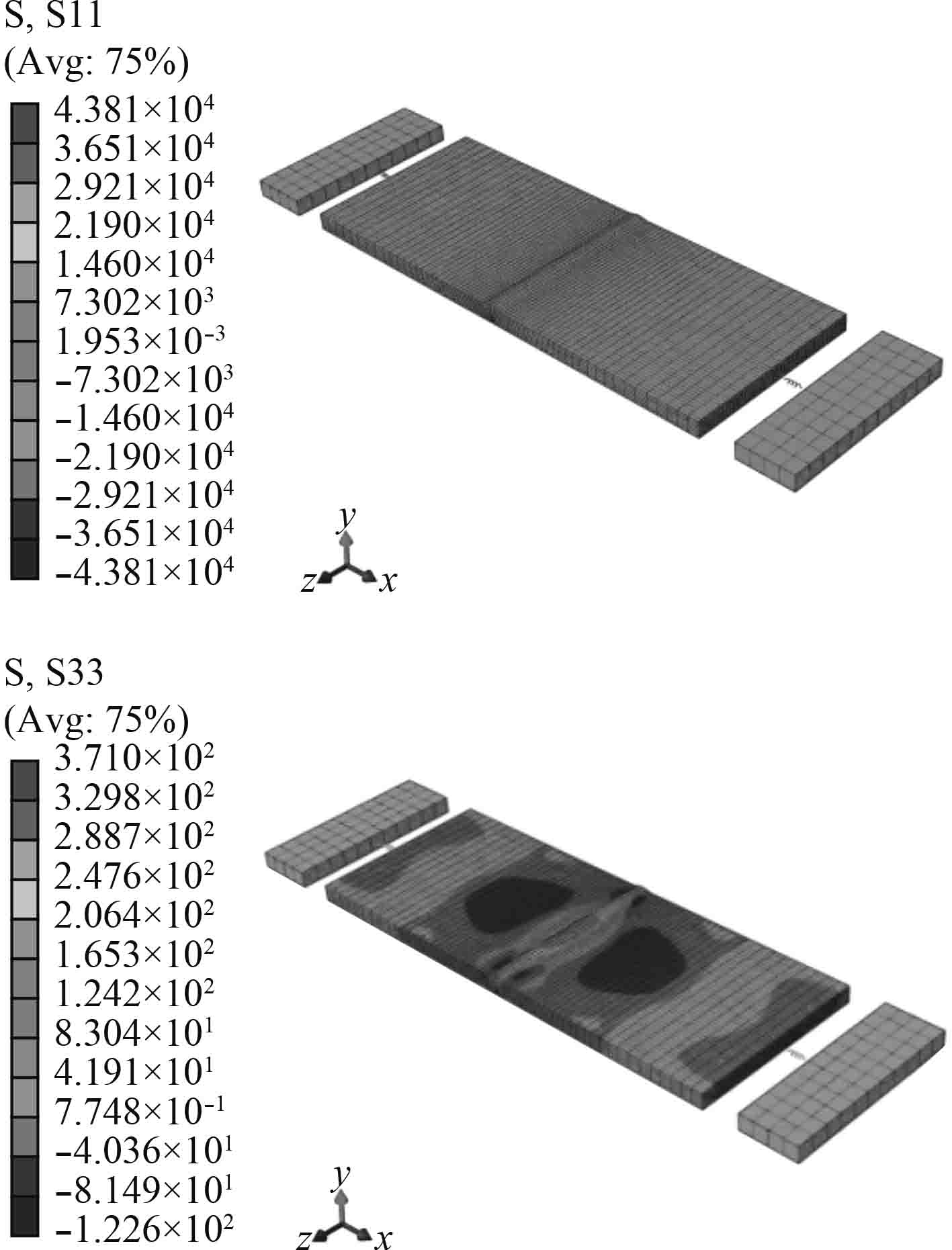
边界条件3情况下的初始焊接残余应力分布情况如图6所示。
|
图 6 横向和纵向焊接残余应力分布图(边界条件3) Fig. 6 Transverse and longitudinal welding residual stress distribution of plate(Boundary condition 3) |
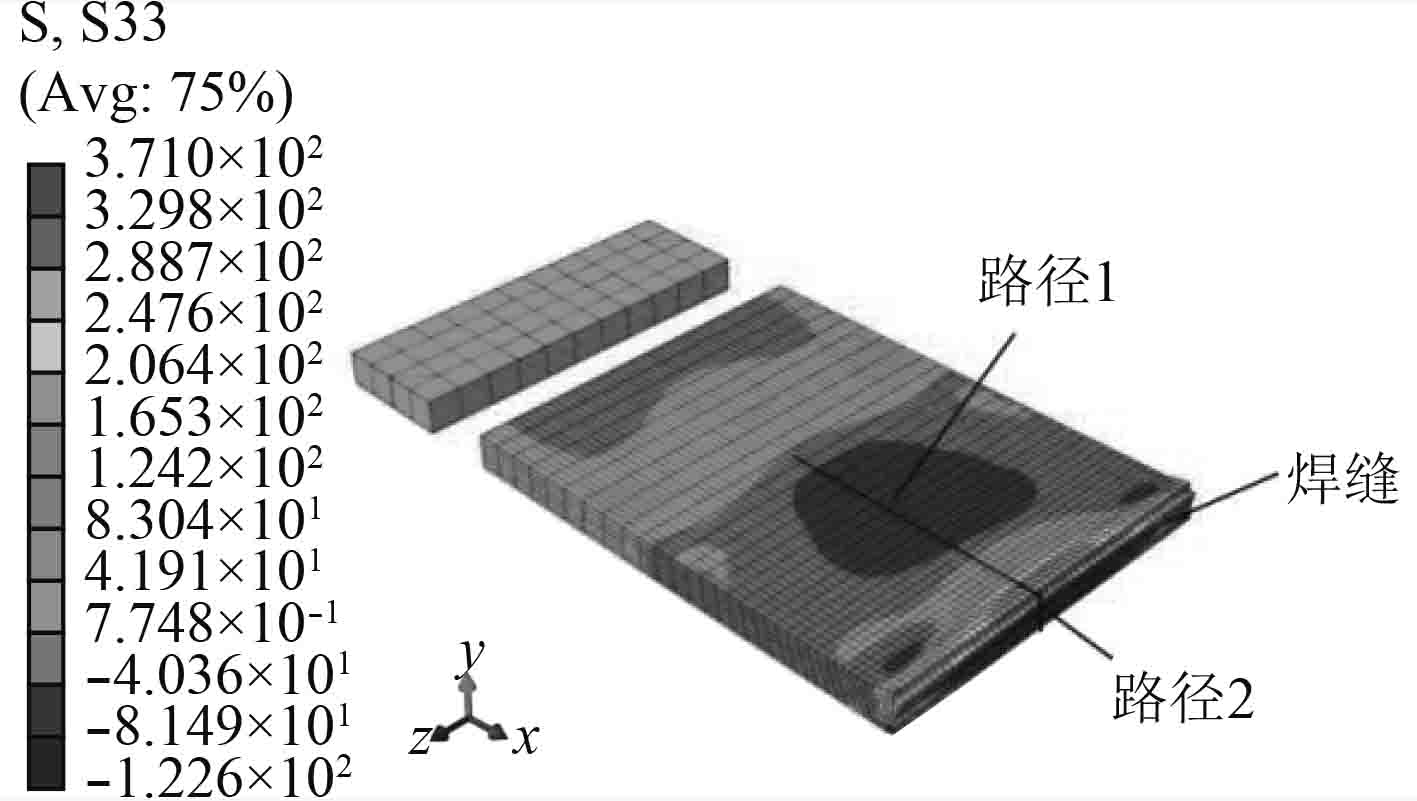
为了更好地分析焊接残余的应力分布情况,选择2条路径分析焊接残余应力分布,具体路径如图7所示。路径1为远离焊缝方向,位于试件上表面,从焊缝中点沿着垂直于焊接方向;路径2为焊缝深度方向,从试件上表面的焊缝中点位置沿着板厚方向向下。
|
图 7 焊接残余应力路径选择 Fig. 7 Path selection of welding residual stress |
焊接残余应力在循环载荷作用下释放的规律需要研究确定材料循环塑性本构模型,包括屈服表面、流动准则以及硬化准则。非线性硬化准则包括非线性随动硬化准则和等向硬化准则[19]。
非线性随动硬化准则主要描述随着后应力
| $ \dot \alpha = \sum\limits_i {\left[ {{C_i}\frac{1}{{{\sigma _0}}}(\sigma - \alpha ){{\dot {\bar \varepsilon} }^{pl}} - {\gamma _i}\alpha {{\dot {\bar \varepsilon} }^{pl}}} \right]} {\text{。}} $ | (4) |
式中:
|
|
表 4 非线性随动硬化模型参数与温度关系 Tab.4 Mechanism of welding residual stress release |
等向强化准则[18]将描述随着等效应力
| $ {\sigma ^0} = {\sigma _{10}} + {Q_{\inf }}(1 - {e^{ - b{{\bar \varepsilon }^{pl}}}}) {\text{。}} $ | (5) |
式中:
|
|
表 5 等向硬化模型参数与温度的关系 Tab.5 Mechanism of welding residual stress release |
焊接试验过程在船厂焊接实验室中进行,严格按照船厂现场施工工艺进行焊接,焊接工艺选择CO2气体保护焊,焊接过程中记录每层相关焊接参数。
2.2 残余应力测试试验试验数据选择路径1试件表面位置距离焊缝中心距离3 mm,12 mm,23 mm,37 mm,54 mm和75 mm 6个点作为研究对象,对测点位置进行电解腐蚀液腐蚀去除机械残余应力以便于测量焊接残余应力。使用PROTO公司生产的iXRD型残余应力仪测量焊接残余应力,得到焊接残余应力。
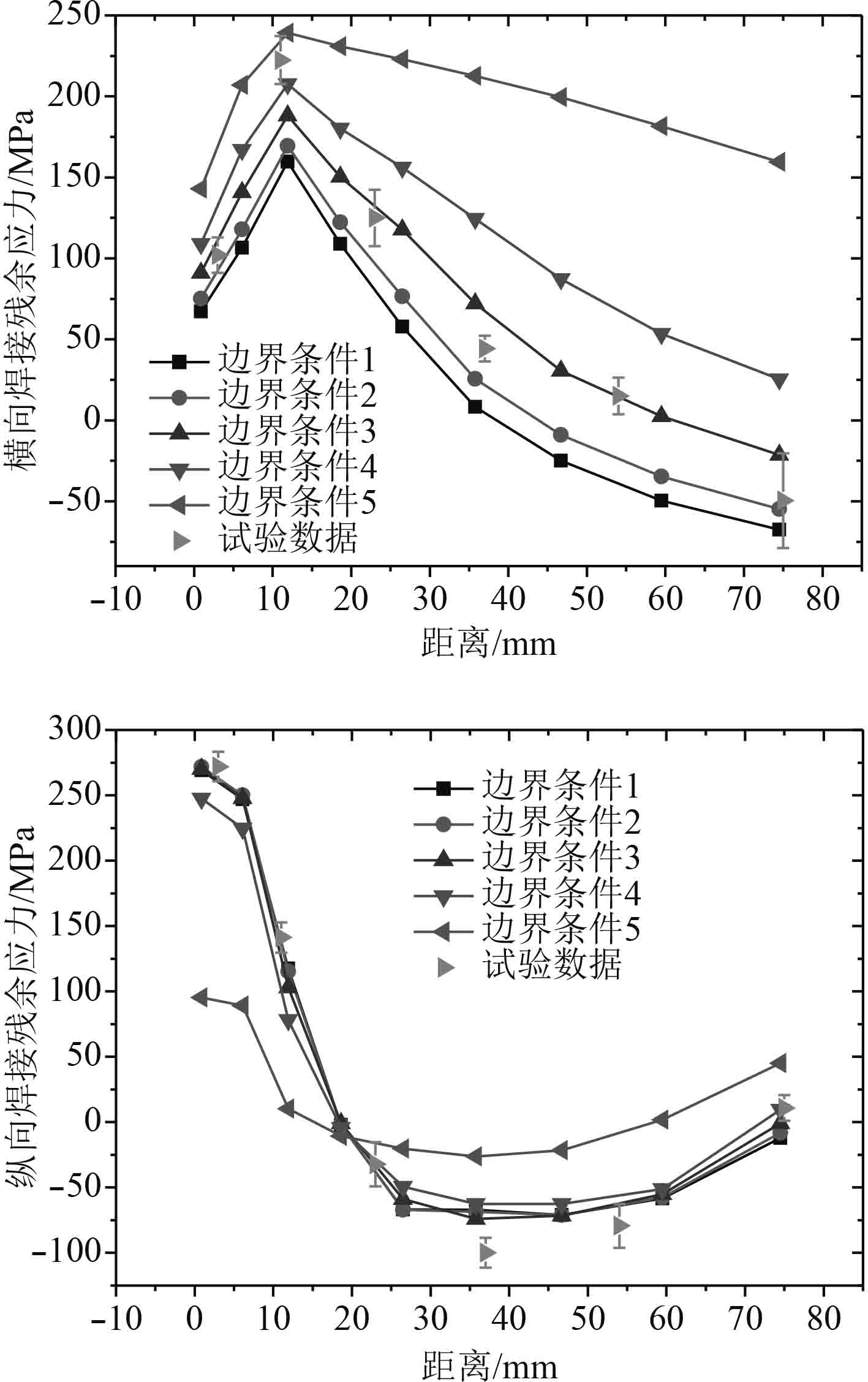
3 不同边界约束的影响 3.1 不同边界约束对初始焊接残余应力的影响通过有限元法计算焊接残余应力分布情况,根据试验选择的测点,对路径1典型节点数值仿真结果进行输出,进而通过数值仿真结果对比试验结果,如图8所示。
|
图 8 路径1横向和纵向焊接残余应力情况 Fig. 8 Welding residual stress distribution along the the transverse and longitudinal directions of path 1 |
从图8可以看出,不同边界约束下,路径1横向和纵向残余应力沿着距离焊缝中心距离分布的总体趋势大致相同。横向焊接残余应力随着距离焊缝距离的增加先增加,在12 mm焊趾附件位置达到峰值,然后随着距离增加逐渐降低。
随着试件焊接初始边界约束的增强,路径1横向残余应力逐渐增大。以最大值为例进行说明,边界条件1(自由趋近)情况下为160 MPa,边界条件5(刚性固定)为251 MPa。
随着边界约束的增加,纵向焊接残余应力最大值一般出现在焊缝中心位置,边界条件1(自由趋近)情况下为269 MPa,边界条件5(刚性固定)为95 MPa;然后应力逐渐降低,由拉应力变为压应力,呈先减小后缓慢增大的规律。
试验数据与边界条件3有限元计算数据之间的误差较小,认为边界条件3情况有限元数值能够有效的模拟试验结果。
图9表示沿着厚度方向的路径2上焊接残余应力的分布情况。不同边界约束下,其总体分布规律也是相同的,呈现出板厚中部的焊接残余应力最大,上下表面的残余应力相对小些的规律。主要是由于试验过程中焊接工艺选择先正面焊3道反面焊1道,所以上下表面的焊接残余应力并不是关于板厚中心对称的,横向和纵向焊接残余应力最大值一般出现在距离上表面6.5 mm处。
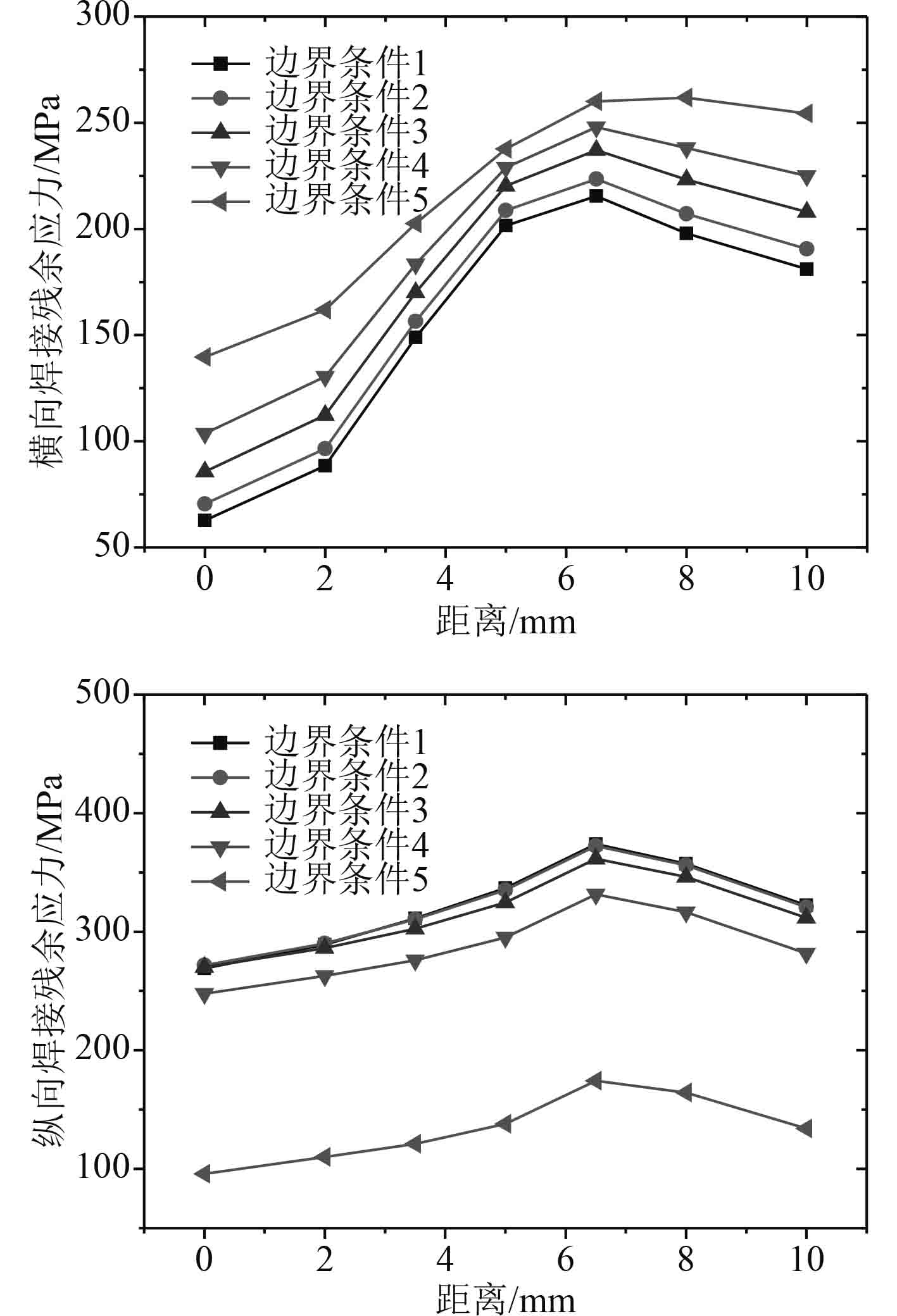
|
图 9 路径2横向和纵向焊接残余应力分布情况 Fig. 9 Welding residual stress distribution along the transverse and longitudinal directions of path 2 |
随着焊接边界约束的增加,路径2上的横向焊接残余应力增加。以最大值为例进行说明,边界条件1(自由趋近)情况下为215 MPa,边界条件5(刚性固定)情况下为260 MPa。
随着约束的增强,路径2上的纵向焊接残余应力变化规律相较于横向焊接残余应力相反,表现为逐渐降低。以最大值为例进行说明,边界条件1(自由趋近)情况下为373 MPa,边界条件5(刚性固定)情况下为174 MPa。
3.2 不同边界约束对焊接残余应力释放的影响焊接过程中边界约束对于后续循环拉伸载荷作用下的释放也会产生影响。开展3种初始边界约束条件作用下的焊接残余应力释放情况研究,弹簧弹性刚度依次设计为50 000(边界条件2)、200 000(边界条件3)和500 000 N/mm(边界条件4)。刚固试件两端加载循环拉伸载荷,为了更好地研究焊接残余应力释放情况,现在对于加载载荷应力幅值设置3种情况:100 MPa,150 MPa以及200 MPa,载荷施加频率1 Hz,应力比0.1。通过加载循环载荷1,2,5,10,20,30,40和50次通过有限元软件模拟焊接残余应力在3种加载条件下的释放情况。
为便于定量分析,选取2个考察点,分别是路径1距离焊缝中心距离12 mm处(B点)以及厚度方向距离焊缝表面6.5 mm处(G点)。
如图10~图12所示,无论是试件表面还是内部,在循环载荷作用下,焊接残余应力都会出现明显释放现象,循环载荷加载10次以前,焊接残余应力释放更加明显。
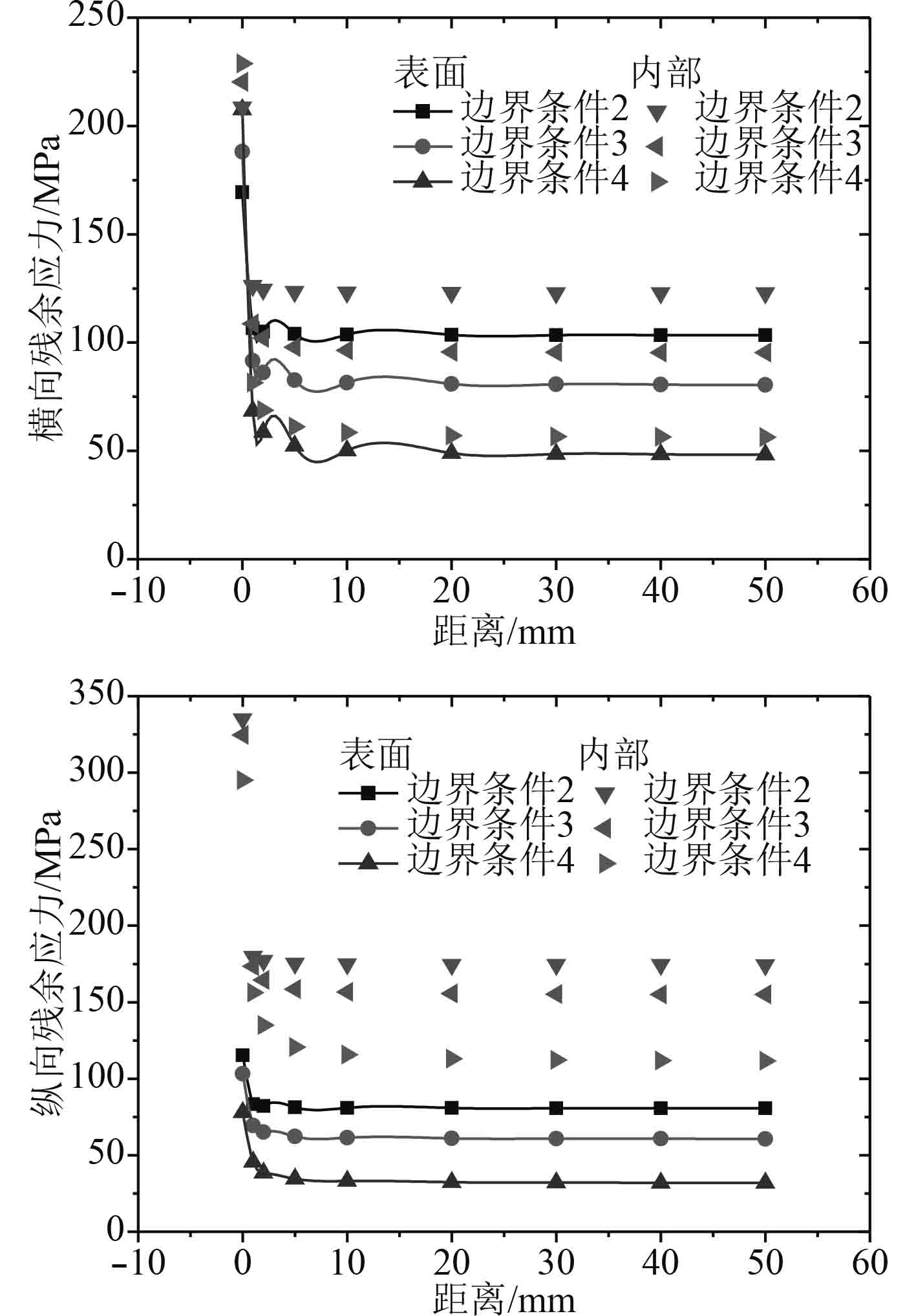
|
图 10 表面和内部两点横向和纵向焊接残余应力释放情况(100 MPa) Fig. 10 Transverse and longitudinal residual stress release at both surface and interior(100 MPa) |
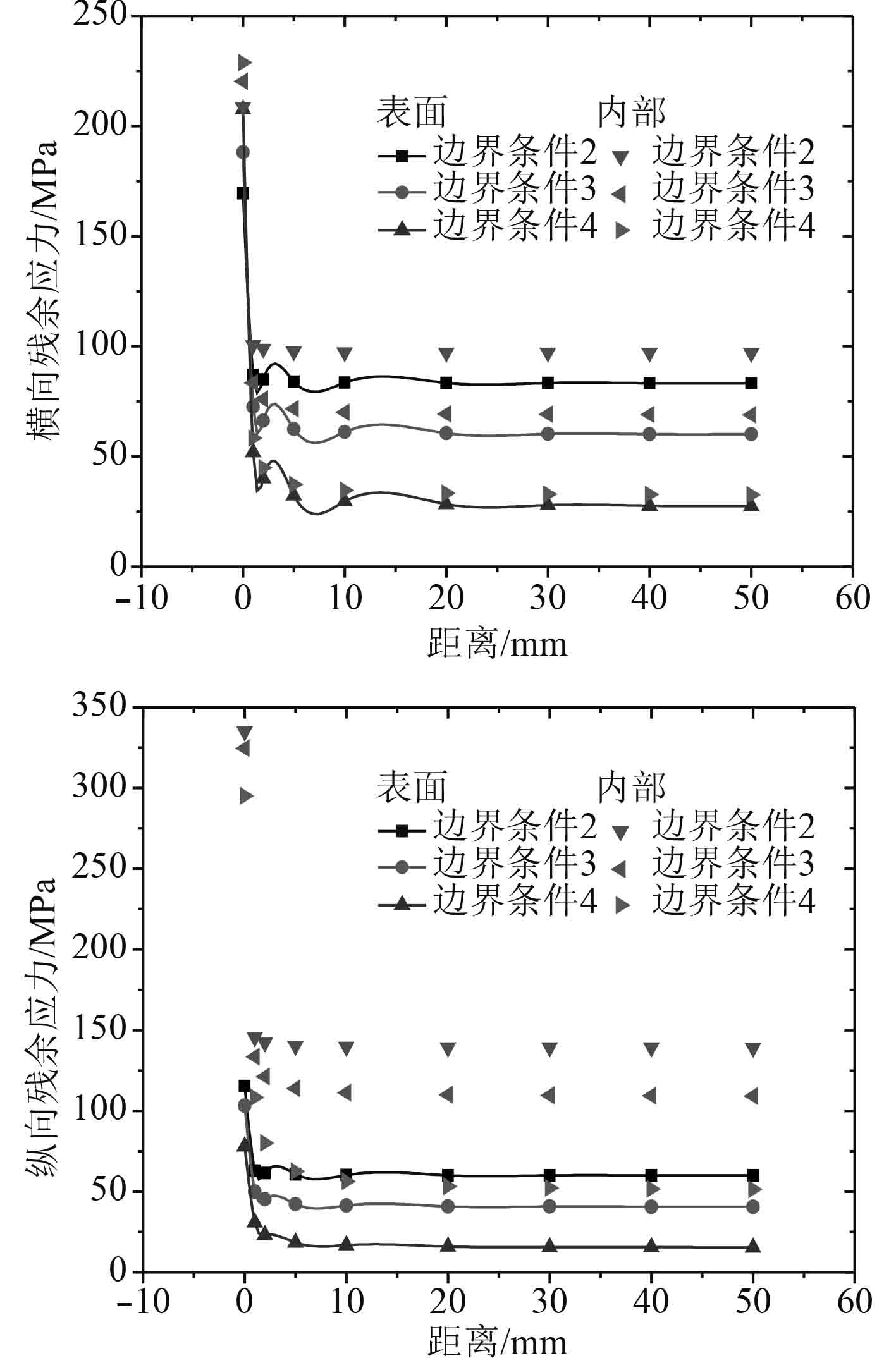
|
图 11 表面和内部两点横向和纵向焊接残余应力释放情况(150 MPa) Fig. 11 Transverse and longitudinal residual stress release at both surface and interior(150 MPa) |
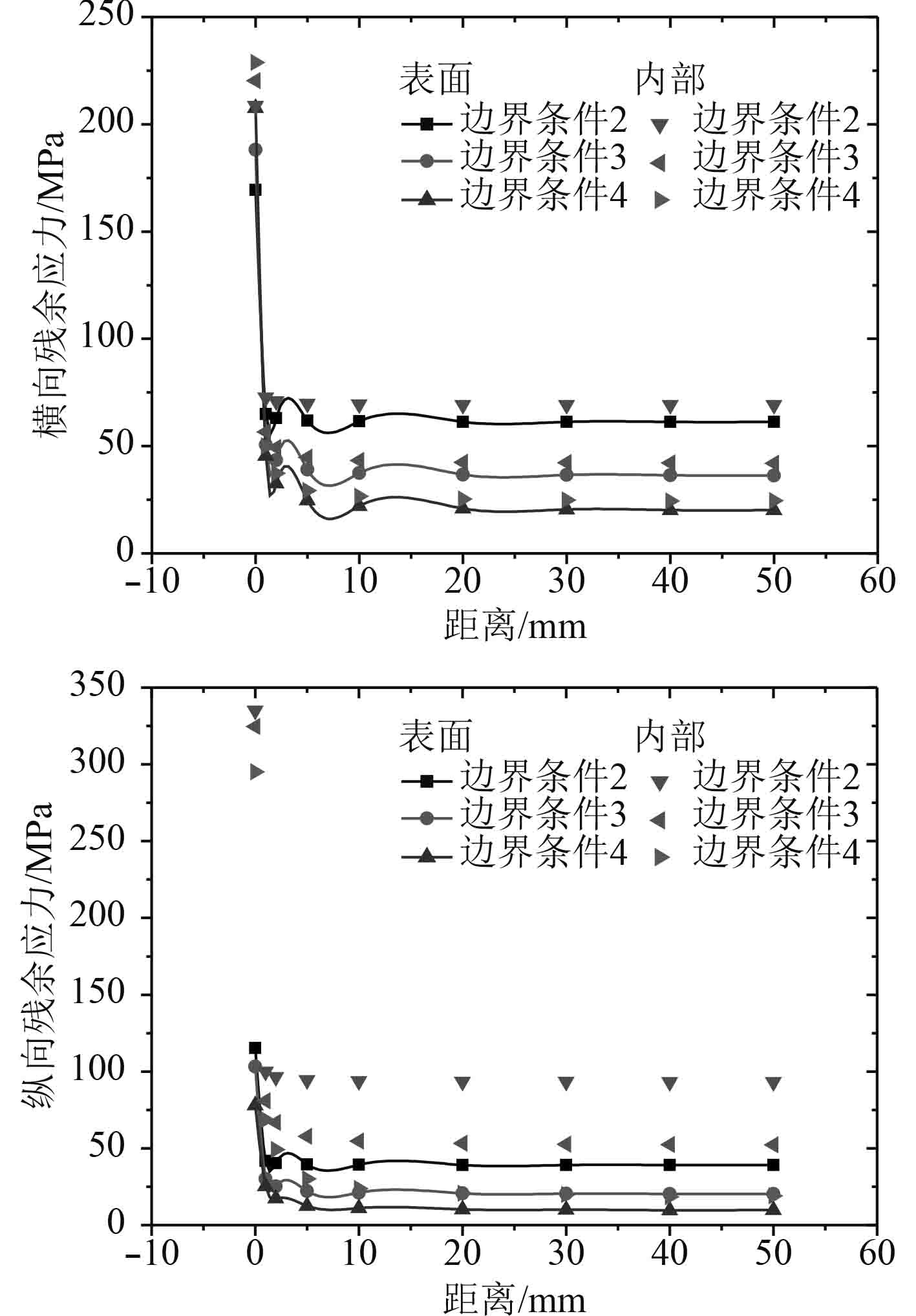
|
图 12 表面和内部两点横向和纵向焊接残余应力释放情况(200 MPa) Fig. 12 Transverse and longitudinal residual stress release at both surface and interior(200 MPa) |
以150 MPa作用下,3种边界条件焊接残余应力释放情况为例,边界条件2作用下,B点初始焊接残余应力169 MPa,在拉伸应力150 MPa循环加载1次后降低至87 MPa,释放率49%;加载2次,焊接残余应力降至85 MPa,释放率50%;加载50次,横向焊接残余应力降低为83 MPa,释放率51%,第一次循环拉伸载荷作用下的残余应力的释放量占总的释放量95%。边界条件3作用下,B点初始焊接残余应力188 MPa,拉伸应力为150 MPa情况下,加载1次拉伸载荷后应力降至73 MPa,释放率61%;加载2次,焊接残余应力为66 MPa,释放率65%;加载50次,焊接残余应力为60 MPa,释放率68%,第1次循环焊接残余应力的释放量占总的释放量90%;边界条件4作用下,B点初始焊接残余应力208 MPa,拉伸应力150 MPa循环加载1次残余应力降至52 MPa,释放率75%;加载2次,焊接残余应力为40 MPa,释放率81%;加载50次,焊接残余应力为28 MPa,释放率87%,第一次循环释放量占总的释放量87%;内部点横向焊接残余应力释放规律类似于表面点,纵向焊接残余应力类似于横向焊接残余应力释放规律。随着初始焊接情况下边界约束的增强,后续拉伸载荷作用下焊接残余应力释放越多;随着边界条件约束增强,第一次循环释放量占总的50次循环释放量比例逐渐下降(见表6)。
|
|
表 6 B点焊接残余应力释放情况表(150 MPa) Tab.6 Table of welding residual stress release of B point(150 MPa) |
本文采用热弹塑性有限元方法计算了不同边界约束条件下AH36高强钢对接焊的焊接残余应力及其释放情况。主要结论如下:
1)路径1和路径2上的横向焊接残余应力均受边界约束影响较大,且约束越强残余应力越大;纵向焊接残余应力受边界约束影响与横向残余应力相反,约束越强残余应力越小。
2)横向焊接残余应力最大值出现在距离焊缝中心12 mm的焊趾区域附近,而纵向焊接残余应力最大值出现焊缝中心位置。
3)3种边界约束条件,随着边界约束增强,加载同样循环次数,无论横向还是纵向焊接残余应力释放程度增加。
4)随着边界约束增加,加载同样循环载荷,最终焊接残余应力数值更低,第1次循环释放量占总的50次循环释放量比例逐渐增加。
| [1] |
WEBSTER G A, EZEILO A N. Residual stress distribution and their influence on fatigue lifetimes[J]. International Journal of Fatigue, 2001, 23(1): 375-83. |
| [2] |
BOULTON N S, MARTIN L. Residual stresses in arc-welded plates[J]. Institute of Mechanical Engineers, 1936, 133: 245-339. |
| [3] |
TALL L. Residual Stress in welded plates-a theoretical study[J]. Welding journal, 1964, 43(1): 10-23. |
| [4] |
ALFREDSSON K S, JOSEFSON B L. Harmonic response of a spot welded box beam-influence of welding residual stresses and deformation[J]. Springer Berlin Heidelberg, 1992, 2(6): 277-287. |
| [5] |
BRIEKSTAD B, JOSEFSON B L. A parametric study of residual stresses in multi-pass butt-welded stainless steel pipes[J]. International Journal of Pressure Vessels and Piping, 1998, 75(1): 11-25. DOI:10.1016/S0308-0161(97)00117-8 |
| [6] |
LEE C H, CHANG K H. Numerical analysis of residual stress in welds of similar or dissimilar steel weld mental under superimposed tensile loads[J]. Computational Materials Scienee, 2007, 40(4): 548-556. DOI:10.1016/j.commatsci.2007.02.005 |
| [7] |
DURANTON P, DEVAUX J, ROBIN V, et al. 3D modeling of multiple welding of a 316L stainless steel pipe[J]. Journal of Materials Processing Technology, 2004, 32(153-154): 457-463. |
| [8] |
ADAK M, GUEDES C. SOARES Effects of different restraints on the weld-induced residual deformations and stresses in a steel plate[J]. International Journal of Advanced Manufacturing Technology, 2014, 71(1-4): 699-710. DOI:10.1007/s00170-013-5521-9 |
| [9] |
楼志文, 童云生, 阂行. 瞬态温度场和热弹塑性场的有限元分析[J]. 西安交通大学学报, 1981, 15(8): 1-8. |
| [10] |
汪建华, 钟小敏, 戚新海. 管板接头三维焊接变形的数值模拟[J]. 焊接学报, 1995, 16(3): 140-145. |
| [11] |
鹿安理, 史清宇, 赵海燕, 等. 厚板焊接过程温度场、应力场的三维有限元数值模拟[J]. 中国机械工程, 2001, 12(2): 183-186. DOI:10.3321/j.issn:1004-132X.2001.02.019 |
| [12] |
刘川, 张建勋. 基于动态子结构的三维焊接残余应力变形数值模拟[J]. 焊接学报, 2008, 29(4): 24-27+117. |
| [13] |
FU D F, ZHOU C Q, LI C, et al. Effect of welding sequence on residual stress in thin-walled octagonal pipe-plate structure[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(3): 657-664. DOI:10.1016/S1003-6326(14)63108-3 |
| [14] |
李良碧, 万正权. 焊接残余变形对深海耐压环肋圆柱壳稳定性的影响[J]. 船舶力学, 2016, 20(1-2): 120-126. |
| [15] |
徐磊, 黄小平, 王芳. 焊接残余应力对深潜器耐压球壳承载能力的影响[J]. 船舶力学, 2017, 21(7): 864-872. |
| [16] |
邓德安, 任森栋, 李索, 等. 多重热循环和约束条件对P92钢焊接残余应力的影响[J]. 金属学报, 2017, 53(11): 1532-1540. DOI:10.11900/0412.1961.2017.00007 |
| [17] |
DRAGISTAMENKOVIĆ, Ivana VASOVIĆ. Finite element analysis of residual stress in butt welding two similar plates[J]. Scientific Technical Review, 2009, 1(1): 57-60. |
| [18] |
DUNNE F, PETRINIC N. Introduction to Computational Plasticity[M]. Oxford University Press, Oxford, 2005.
|
| [19] |
Chin-Hyung LEE, Kyong-Ho CHANG, et al. Finite element modeling of residual stress relaxation in steel butt welds under cyclic loading[J]. Engineering Structures, 2015(103): 63-71. |
 2020, Vol. 42
2020, Vol. 42
