0 引　言

风速风向是船舶气象仪观测的重要气象要素之一，相对风是指以船舶为参考，相对于系泊或航行船舶观测到的风，真风是指以大地正北为参考的自然界实际风。船舶等移动平台上相对风和真风的测量精度，与多种因素有关，包括传感器技术指标、安装位置、船舶姿态等等。胡桐等^[1]采用计算机流体力学仿真方法分析船体周围钝体绕流气流场的分布情况，建立了相对风偏差校正模型。王国峰等^[2]分析了船舶运动状态下传感器倾角的变化对测风结果的影响，提出了一种基于空间模型的测量误差补偿算法。李志乾等^[3]分析了船舶相对风和航速航向误差对真风计算的影响，提出了真风解算误差的修正方法。周扬等^[4]采用模块化设计方法，通过软硬件结合，自动识别两种测风传感器和2种航向来源实现真风解算。周亦武等^[5]分析了船舶摇摆状态下测风误差产生的机理，提出了基于多变量非线性数据拟合及动态补偿的校正方法。郭颜萍等^[6]采用基于小波变换和最小二乘支持向量机相结合的方法估算船面风速和风向。上述工作分别从不同方面，针对船舶相对风或真风测量误差，提出了改进的方法并进行了仿真试验验证，但并未涉及通过融合算法提高船舶气象仪相对风的测量精度。实际上，相对风对于提高真风解算准确性和保障船舶的安全航行意义重大。

由于船体本身以及其上建筑物和其他设备的影响，船体各处的风速、风向的分布值是复杂和不均匀的^[7]，单只传感器测得的数据不全面，只能代表局部。大型船舶通常选择2个或2个以上的监测点安装测风传感器，与单传感器系统相比，多传感器系统具有增强系统生存能力、扩展空间覆盖范围、提高信息可信度等优点，特别是可以通过对来自多个传感器的信息加以有效融合，取长补短，从而有效提高信息探测性能^[8-9]。加权平均法是将多个传感器提供的冗余信息进行加权平均后作为融合值。卡尔曼滤波是1960年Kalman RE提出的一种最优化自回归数据处理算法，在测量方差已知的情况下能够从一系列存在测量噪声的数据中，估计动态系统的状态^[10-11]。本文将基于这2种方法进行融合算法的研究。考虑到在船舶正常向前航行过程中，测风传感器通常情况下都是迎风的，这意味着，如果以船舶水平面为参考坐标系，以船首向为零度，那么测风传感器相对船舶测量的风向通常分布在第一、四象限内，本文着重探讨这种迎风状态下相对风测量数据融合的处理方法。

1 加权融合算法 1.1 系统描述方程

设随机线性离散系统的方程为：

$ {x_k} = A{x_{k - 1}} + B{u_{k - 1}} + {w_{k - 1}}{\text{，}} $

(1)

$ {z_k} = H{x_k} + {v_k} {\text{。}} $

(2)

式中： ${x_k}$ 为k时刻的系统状态； ${u_k}$ 为k时刻对系统的控制量，由于本系统没有控制量，因此 ${u_k}$ =0； ${z_k}$ 为k时刻的测量值； ${w_k}$ 为过程激励噪声， ${v_k}$ 为观测噪声。假设各参数为相互独立、正态分布的白色噪声，满足：

$ p(w)\sim N(0,{ Q}){\text{，}} $

(3)

$ p(v)\sim N(0,R) {\text{。}} $

(4)

式中： $ Q$ 表示过程噪声协方差矩阵， $ R$ 为观测噪声协方差矩阵。

1.2 加权平均算法

在船舶气象仪相对风的测量过程中，为了克服单个传感器的不确定和局限性，往往采用两个或两个以上的测风传感器同时报告其大小和方向，充分利用每个传感器的测量信息，才能更准确地获得船上真实的相对风。在对多个传感器的数据进行融合时，加权平均算法是较为常用的处理方法，即按照一定原则给每个传感器制定权重，然后通过加权融合所有的局部测量值，从而得到一个全局的最优估计值^[12]。假设系统中有n个传感器 ${s_1}$ ， ${s_2}$ ，…， ${s_n}$ ，第 $i$ 个传感器在 $k$ 时刻的状态估计值表示为 ${\hat x} _k^i$ （ $i = 1,2,...,n$ ），各个传感器的权重系数分别表示为 ${w_1},{w_2},...,{w_n}$ ，则采用加权平均算法得到的K时刻全局状态估计值 ${{\tilde x} _k}$ 可表示为：

${{\tilde x} _k} = \sum\limits_{i = 1}^n {{w_i}x_k^i}, $

(5)

${\text{且有}}\sum\limits_{i = 1}^n {{w_i} = 1}{\text{。}} $

(6)

算数平均值方法是加权平均算法的一种特殊形式，它将各个传感器的权重系数选取的相等，由式（6）可得， $w \displaystyle\sum\limits_{i = 1}^n {1 = 1} $ ，进而得到 $w = \dfrac{1}{n}$ ，则式（5）化为：

$ {{\tilde x} _k} = \sum\limits_{i = 1}^n {{w_i}x_k^i} = \frac{1}{n}\sum\limits_{i = 1}^n {x_k^i} {\text{。}} $

(7)

这种方法简单直观，最终得到的融合值亦包含系统中所有传感器的测量信息，但却忽略了传感器因自身差异而导致的测量误差大小不一的问题。例如，传感器自身的精度高低可能不同；再如某些情况下由于观测点周围气流受到干扰而造成测量值误差偏大等。考虑到这些情况，算数平均值方法得到的融合值能够比测量偏差较大的传感器效果好，但是与测量偏差较小的传感器相比还是有一定差距。因此，为了获取更为准确的融合值，有必要对上述方法加以改进。

2 改进的融合算法 2.1 基于动态权值的加权平均融合

基于动态权值的加权平均融合算法，由各观测时刻的测量数据实时计算各个传感器的权值，从而能够实现权值的动态分配，破除权值分配的绝对化。该算法把每个传感器测量值的加权系数分为静态因子和动态因子两部分，静态因子是由传感器自身参数确定的固定值，动态因子则根据当前状态参数不断改变。融合值 ${{\tilde x} _k}$ 通过下式计算：

$ {{\tilde x} _k} = \sum\limits_{i = 1}^n {({w_{iS}} + {w_{iD}})x_k^i} {\text{。}} $

(8)

式中： $x_k^i$ 为k时刻第 $i$ 个传感器的测量值， ${w_{iS}}$ 和 ${w_{iD}}$ 为传感器的静态加权因子和动态加权因子，由式（6）可知：

$ \sum\limits_{i = 1}^n {({w_{iS}} + {w_{iD}}) = 1} {\text{。}} $

(9)

静态加权因子的大小取决于传感器自身性能。传感器自身误差小，则其观测的数据精确度高，因此其测量值的加权系数相应的取大；反之传感器自身误差大，则其测量值的加权系数相应的取小。由此可见，静态加权因子与传感器自身误差成反比，设传感器的误差△_i=[δ₁ δ₂…δ_m]^T，定义 $w{'_{iS}} = 1/\left(\sqrt {\Delta _{{i}}^{\rm{T}}{\Delta _{{i}}}} \right)$ 。动态加权因子的确定基于参与融合的传感器测量值与一个参考基准的偏差，并与这个偏差成反比^[13]。设当前参考基准值为 ${\overline x _k}$ ，则定义 $w{'_{iD}} = 1/\left(\left| {\left| {x_k^i - {{\overline x }_k}} \right|} \right|\right)$ 。为了满足式（9），使各传感器的加权系数之和为1，引出一个调整系数 $r$ ，则融合值 ${{\tilde x} _k}$ 的计算公式为：

$ \begin{split} & {{\tilde x} _k} = \sum\limits_{i = 1}^n {({w_{iS}} + {w_{iD}})x_k^i} =\\ & \sum\limits_{i = 1}^n {(w{'_{iS}} + w{'_{iD}}) \cdot r \cdot x_k^i} =\\ & \sum\limits_{i = 1}^n {\left(\frac{1}{{\sqrt {\Delta _{\rm{i}}^{\rm{T}}{\Delta _{\rm{i}}}} }} + \frac{1}{{\left| {\left| { x_k^i - {{\overline x }_k}} \right|} \right|}}\right) \cdot r \cdot x_k^i} {\text{。}} \end{split} $

(10)

$ {\text{其中}},\;r = \frac{1}{{\displaystyle\sum\limits_{i = 1}^n {\left(\frac{1}{{\sqrt {\Delta _{\rm{i}}^{\rm{T}}{\Delta _{\rm{i}}}} }} + \frac{1}{{\left| {\left| { x_k^i - {{\overline x }_k}} \right|} \right|}}\right)} }} {\text{。}}\hspace{56pt} $

(11)

一般地将系统中参与融合的各传感器测量值的算数平均值作为 ${\overline x _k}$ ，即令

$ {\overline x _k} = \frac{1}{n}\sum\limits_{i = 1}^n {x_k^i} {\text{。}} $

(12)

2.2 离散卡尔曼滤波器

卡尔曼滤波器由一组递归数学公式描述，其提供了一种高效可计算的方法来估计过程的状态，并使估计均方误差最小。卡尔曼滤波器首先估计过程中某一时刻的状态，然后以量测更新的方式获得反馈。因此卡尔曼滤波器可以分为状态更新过程和量测更新过程2个部分。状态更新方程负责向前推算当前状态变量和估计误差协方差，为下一个时间状态构造先验估计。量测更新方程负责反馈，它在状态更新方程中的先验估计基础上，结合新时刻的量测信息来产生后验估计。卡尔曼滤波器包含下面5个公式，其中2个状态更新方程，3个量测更新方程^[14]。

状态更新方程：

向前推算状态变量

$ {\hat x_{k}^ - } = A{{\hat x} _{k - 1}} + B{u_{k - 1}}{\text{；}} $

(13)

向前推算误差协方差

$ P_k^ - = A{P_{k - 1}}{A^{\rm T}} + Q{\text{；}} $

(14)

量测更新方程：

计算卡尔曼增益

$ {K_k} = P_k^ - {H^{\rm T}}{(HP_k^ - {H^{\rm T}} + R)^{ - 1}}{\text{；}} $

(15)

由观测量更新估计

$ {{\hat x} _k} = {\hat x_{k }^ - } + {K_k}({z_k} - H{\hat x_{k}^ - } ) {\text{；}} $

(16)

更新误差协方差

$ {P_k} = (I - {K_k}H)P_k^ - {\text{。}} $

(17)

2.3 基于动态权值和卡尔曼滤波的融合算法

从式（10）可以看到，基于动态权值的加权平均融合算法的关键在于参考基准值 ${\overline x _k}$ 的确定，其选取的原则是尽可能地反映环境真实值。采用式（12）得到的参考基准值 ${\overline x _k}$ 只是采用当前测量值对测量要素当前状态的一个大略估计，如果能在参考基准值 ${\overline x _k}$ 的计算中糅合进历史测量值信息，采用卡尔曼滤波技术更新参考基准值 ${\overline x _k}$ ，使其本身及其变化趋势更接近环境真实值，那么基于动态权值的加权平均融合算法的融合效果将会更好^[15]。卡尔曼滤波是一种线性最小方差估计，算法采用递推形式在时域内滤波，只要获知上一时刻状态的估计值以及当前状态的观测值就可以计算出当前状态的估计值，因此不需要记录观测或者估计一些历史信息，适用于对多维随机过程进行估计，这个估计可以是对当前目标位置的滤波，也可以是对于将来位置的预测。为了使基于动态权值的加权平均融合算法得到的融合数据精度更高，首先将参与融合计算的各传感器测量值的平均值进行卡尔曼滤波，然后再将其作为参考基准值 ${\overline x _k}$ 参与后续计算，即令

$ {\overline x _k} = {{\hat x} _k} = {\hat x_{k }^ - } + {K_k}({z_k} - H{\hat x_{k}^ - } {\text{，}}$

(18)

其中， ${z_k}$ 的取值为当前时刻各传感器测量值的算术平均：

$ {z_k} = \frac{1}{n}\sum\limits_{i = 1}^n {x_k^i} {\text{。}} $

(19)

将式（18）代入式（10），得到新的融合公式：

$ \begin{split} & \mathop {{x_k}}\limits^\sim = \sum\limits_{i = 1}^n {\left(\frac{1}{{\sqrt {\Delta _{\rm{i}}^{\rm{T}}{\Delta _{\rm{i}}}} }} + \frac{1}{{\left| {\left| { x_k^i - {{\overline x }_k}} \right|} \right|}}\right) \cdot r \cdot x_k^i} =\\ & \sum\limits_{i = 1}^n {\left(\frac{1}{{\sqrt {\Delta _{\rm{i}}^{\rm{T}}{\Delta _{\rm{i}}}} }} + \frac{1}{{\left| {\left| { x_k^i - {{{\hat x} }_k}} \right|} \right|}}\right) \cdot r \cdot x_k^i} =\\ & \sum\limits_{i = 1}^n {\left(\frac{1}{{\sqrt {\Delta _{\rm{i}}^{\rm{T}}{\Delta _{\rm{i}}}} }} + \frac{1}{{\left| {\left| { x_k^i - {\hat x_{k}^ - } - {K_k}({z_k} - H{\hat x_{k }^ - } )} \right|} \right|}}\right) \cdot r \cdot x_k^i} {\text{。}} \end{split} $

(20)

由于式（18）中 ${\overline x _k}$ 是采用卡尔曼滤波处理得到的，因此比式（12）中的 ${\overline x _k}$ 在作为权值调整基准时更具参考价值，因而采用式（20）得到的融合值的准确度将会提高。

3 试验验证与结果分析 3.1 试验数据的获取

世界气象组织建议，安装测风传感器时尽量靠近安装平台的前部并且具有一定的高度^[16]，据此在船上选择风场开阔区域安装3台测风传感器。在主桅杆上部横杆两侧对称安装2台螺旋桨式测风传感器，分别称为左舷测风传感器、右舷测风传感器，记作S₁、S₂。在首甲板的开阔区域，首尾中心线上焊接1基座，基座上安装1根支撑杆，其高度与主桅杆上部横杆与首甲板的垂直高度相等。超声波测风传感器安装于该支撑杆上，称为船首测风传感器，记作S₃。船首测风传感器距离左舷和右舷测风传感器的水平距离约为13 m。3台传感器距离海平面的垂直距离均约25 m。3台测风传感器精度如表1所示。

表1中V均为实测风速值。在船舶正常航行条件下，分别采集3台测风传感器的相对风速和相对风向，采样周期均为2 s。抽取2016年3月实船航行的测风数据进行试验验证与分析。

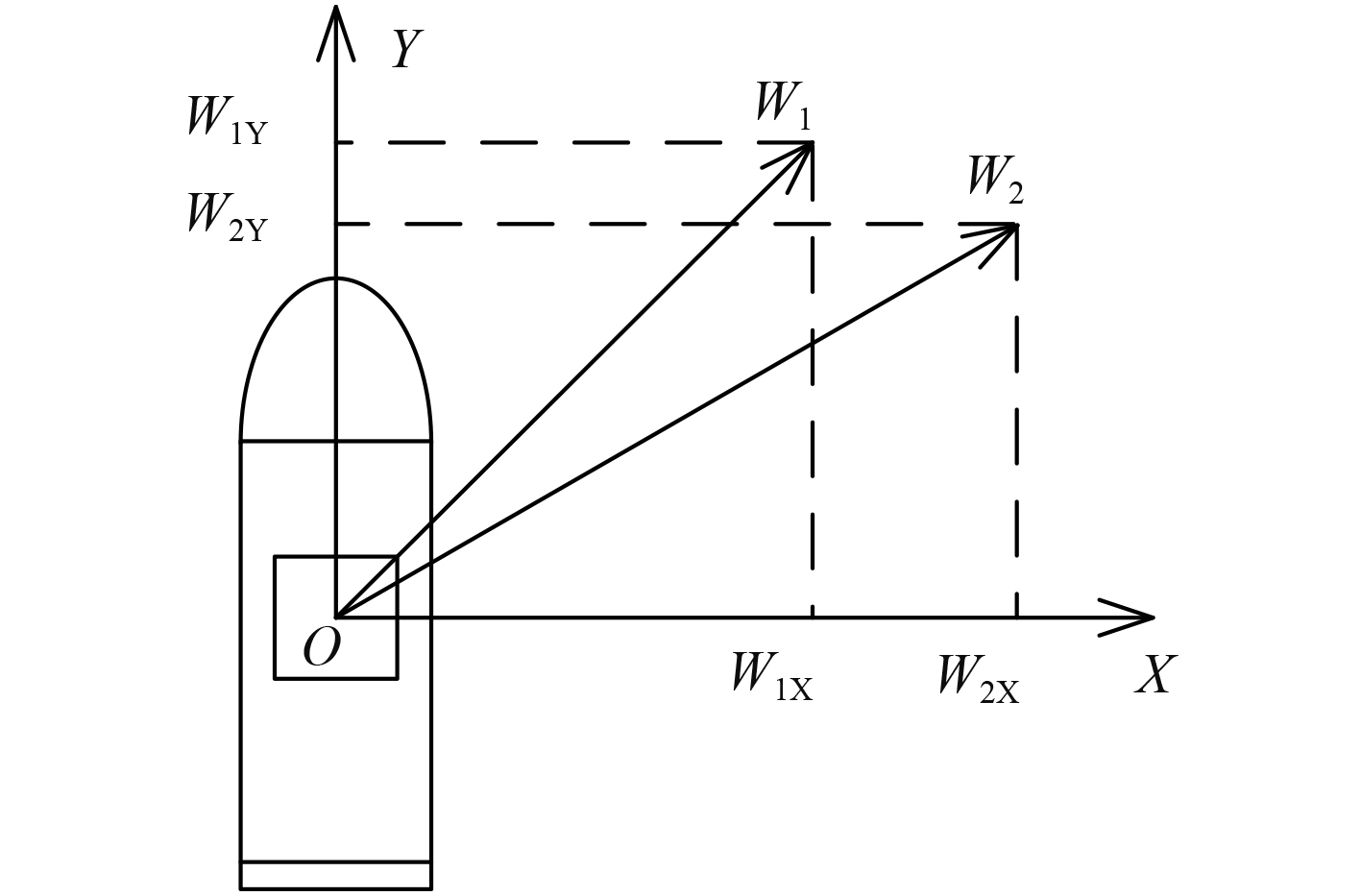
3.2 试验数据的处理

如图1所示，以船舶首尾线为Y轴，船首为正向，与其垂直的横向为X轴，右舷为正向，在船舶所在的水平面内建立直角坐标系，分别将主桅杆上横杆两侧传感器的相对风数据沿X轴、Y轴进行分解，得到X轴方向的2个风速分量：W_1X，W_2X；以及Y轴方向的2个风速分量W_1Y，W_2Y。

试验数据处理包括3个步骤：采用融合算法公式求出W_1X，W_2X的平均值W_X；采用融合算法公式求出W_1Y，W_2Y的平均值W_Y；利用矢量法则求出W_X和W_Y的合成风速、合成风向。由于位于船首的超声波测风传感器精度更高，且所处风场更为开阔，因此这里将其测量数据作为标准值。分别计算传感器1测量值、传感器2测量值、融合值与标准值的误差^[17]。

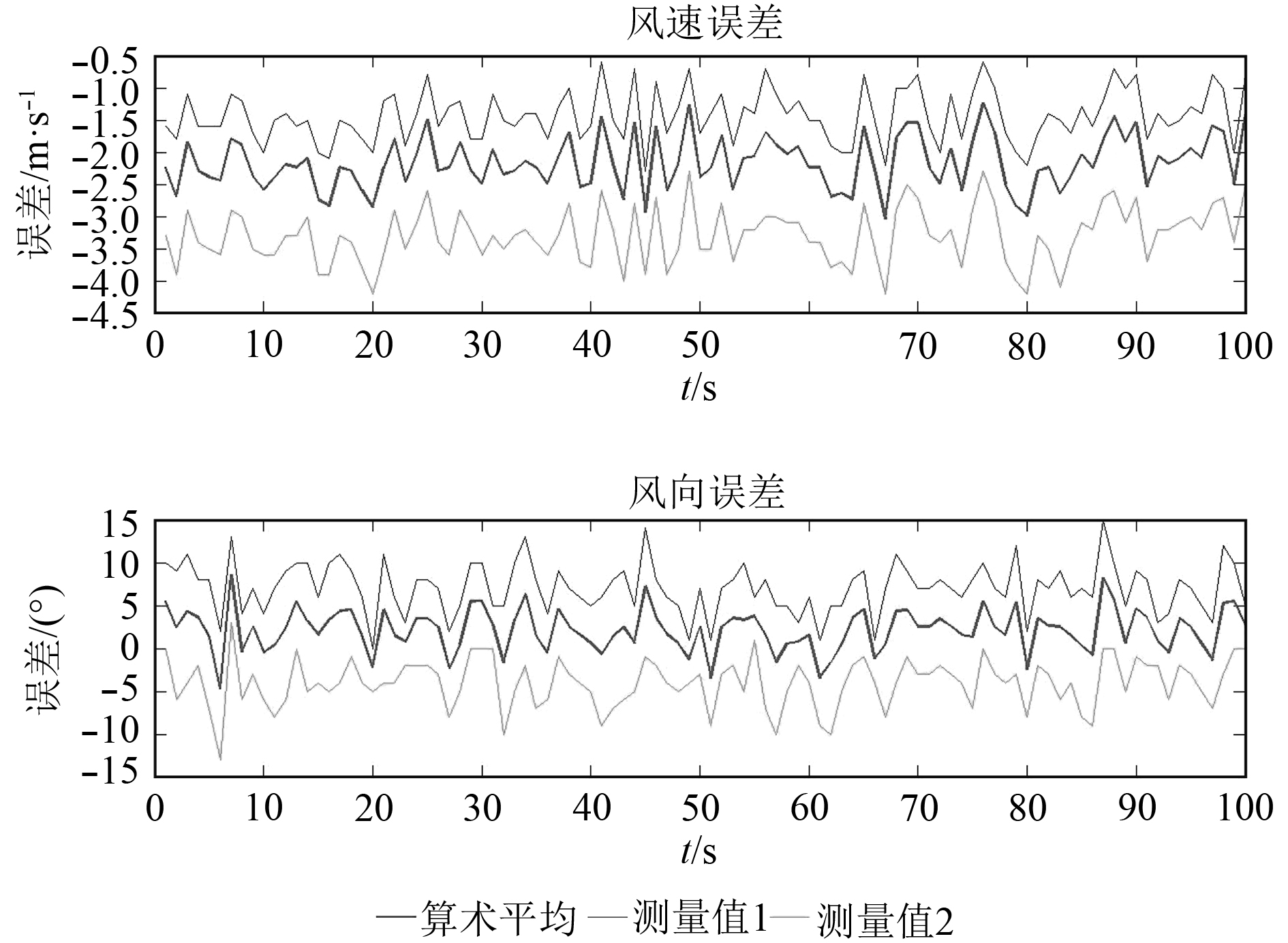
3.3 验证结果与分析

1）验证算术平均融合算法。采用Y述的三个步骤进行数据处理，即采用式（7）求出W_1X，W_2X的平均值W_X；采用式（7）求出W_1Y，W_2Y的平均值W_Y；利用矢量法则求出W_X和W_Y的合成风速、合成风向。图2为算数平均融合值、S₁测量值和S₂测量值对比标准值的误差曲线，包括风速误差和风向误差。可以看出，算术平均融合后，风速、风向的误差均小于传感器2，但是大于传感器1的误差。分析可知，采用算术平均融合算法，虽然综合了2个传感器的测量值，改善了测量误差相对大的传感器的测量效果，但是由于没有区分测量值的优劣进而倚重更有利的测量信息，因此其融合后的误差仍然较大。

2）验证基于动态权值的融合算法

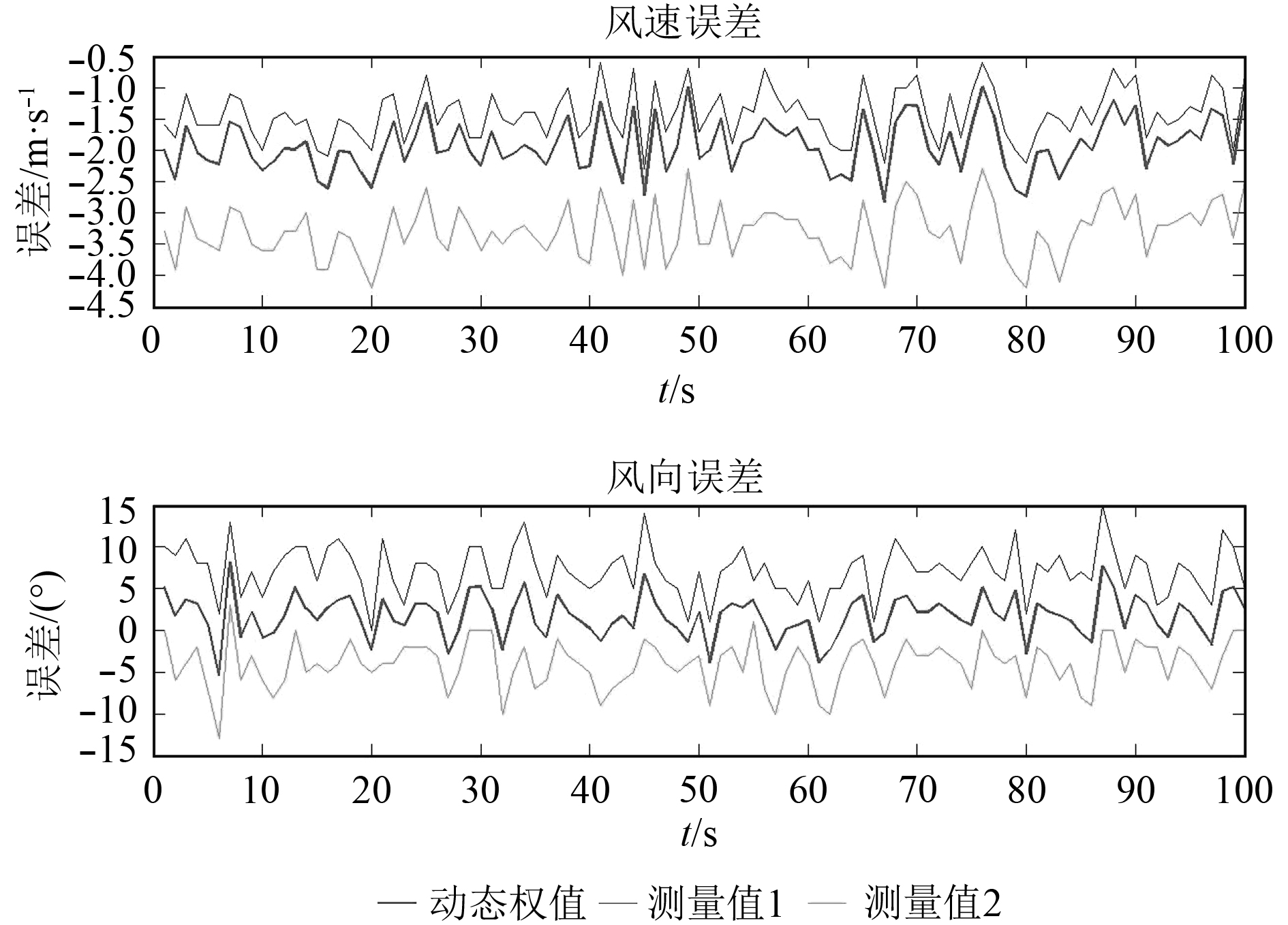
同样采用上述的3个步骤进行数据处理，不同的只是把式（7）换成了式（10）。计算结果表明，动态权值融合后，风速均方根误差为1.6 m/s，较上述算术平均融合误差减小0.7 m/s；风向均方根误差为5.0°，较上述算术平均融合误差减小0.8°。图3为动态权值融合值、S₁测量值和S₂测量值对比标准值的误差曲线。分析可知，动态权值融合避免了权值均分固定不变的绝对化，每次融合计算之前，把当前时刻各个传感器的加权平均值作为基准值，将传感器的测量值与这个基准值比较，并根据比较结果的优劣算出该传感器参与融合计算的权值，这样准确度高的数据将分配到更多的权重，因此融合精度有所改善。

3）验证基于动态权值和卡尔曼滤波的融合算法

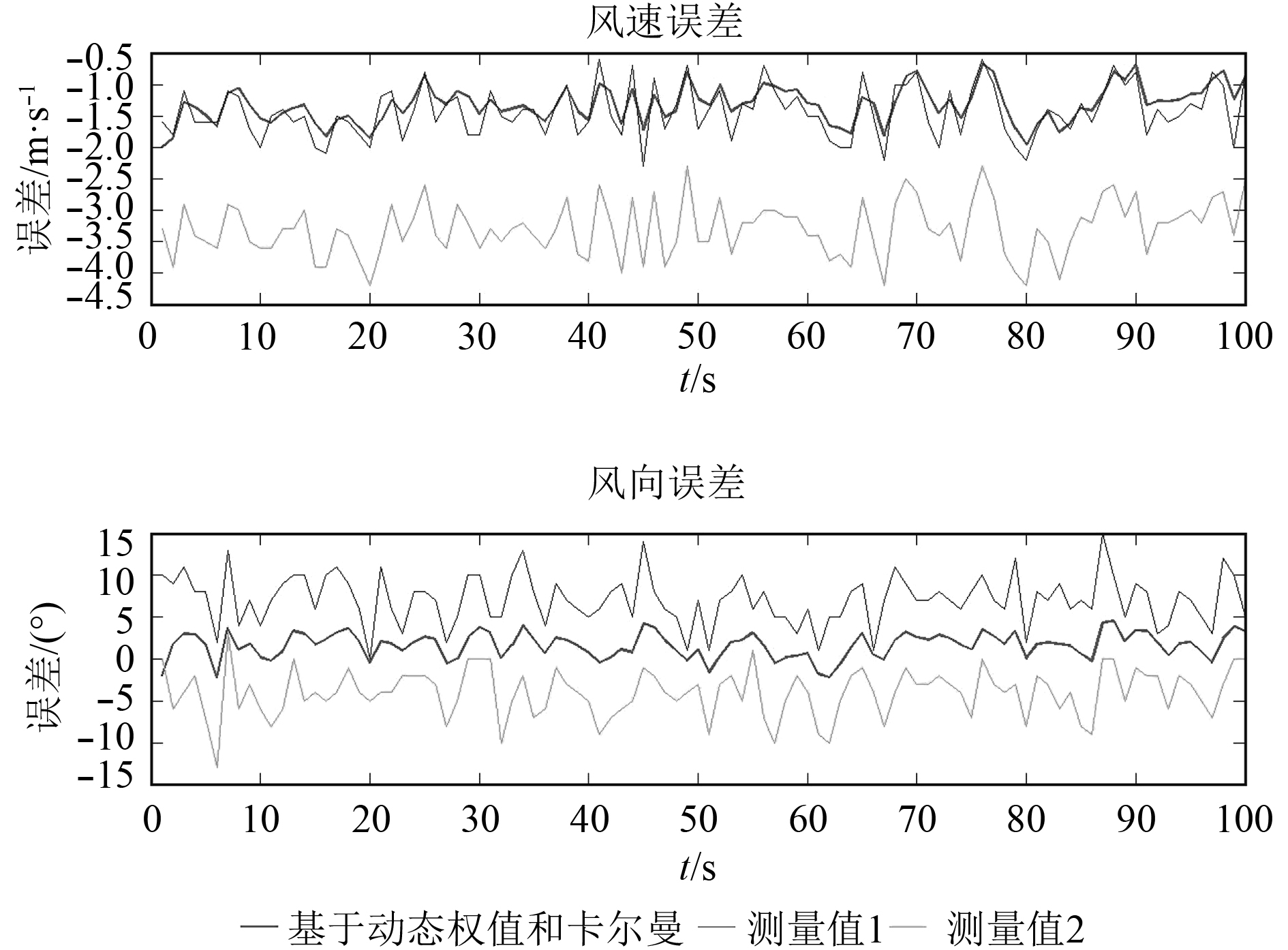
同样采用上述的3个步骤进行数据处理，不同的只是把式（10）换成了式（20）。计算结果表明，采用基于动态权值和卡尔曼滤波的融合算法，风速均方根误差为1.3 m/s，较动态权值融合误差减小0.3 m/s；风向均方根误差为2.8°，较动态权值融合误差减小2.1°。图4为基于动态权值和卡尔曼滤波的融合值、S₁测量值和S₂测量值对比标准值的误差曲线。分析可知，准确度的进一步提高归功于卡尔曼滤波，由于每次融合前先将各传感器的算术平均值经过卡尔曼滤波后再作为对比的基准值，因此使得到的基准值糅合进了测量值的历史信息，对风速、风向数据的预估结果值更稳定，从而使作差后的优劣判断参考性更强，对于权值的动态分配更准确。

将算数平均融合记为算法1，将动态权值融合记为算法2，将基于动态权值和卡尔曼滤波融合记为算法3。表2列出了S₁测量值、S₂测量值、3种算法的融合值相对标准值的均方根误差。可以看出，3种算法的误差逐次降低，其中前2种算法的融合结果比传感器2好，但是不及具有更好表现的传感器1；第3种算法的融合结果则超越了表现更好的传感器1。

图5为3种融合算法的误差曲线。可以看出，相比算法1和算法2，算法3的风向误差显著降低，而风速误差尽管有所改善，但是不太理想。分析可知，这是由于船首测风传感器，始终处于迎风状态，相对于S₁和S₂的风速偏大，造成作为标准值的风速值偏大，所以导致风速误差较大且为负。而正是由于风速较大，获得的风向反而更精准，因此作为标准值的风向值更接近真实环境值，所以风向误差的融合结果更为理想。

4 结　语

针对船舶气象仪测风传感器相对风的融合计算问题，提出了一种基于动态权值和卡尔曼滤波的融合算法。与权值固定的平均权值融合算法相比，该算法使风速误差减小约0.07*V（V为实测风速值），风向误差降低约2°。这是由于该算法先将测量值进行优劣判断再据此对权值进行自适应调整，因而能够有效地去粗取精并提高测量精度。与单纯的动态权值融合算法相比，该算法使风速误差减小约0.03*V（V为实测风速值），风向误差降低约1°。这是由于该算法引进卡尔曼滤波优化作为参考对比的基准值，糅合了测量值的历史信息，克服了仅仅采用当前采样周期数据进行权值调整的局限性，所以能够进一步改善权值，提高数据融合精度。综上该算法能够实时自适应分配权重，有效降低加权融合值的误差，从而为船舶气象仪相对风的测量提供了一种有效且实现简单的数据融合算法。