2. 高新船舶与深海开发装备协同创新中心,上海 200240;
3. 船舶和海洋工程水动力湖北省重点实验室,湖北 武汉 430074;
4. 武汉第二船舶设计研究所,湖北 武汉 430064
2. Collaboration Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China;
3. Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics, Wuhan 430074, China;
4. Wuhan Second Ship Design and Research Institute, Wuhan 430064, China
全球气候变暖最重要的一个因素就是人类活动造成的温室气体(GHG)排放,在所有的温室气体排放量中,航运业占了相当大的比例,其中CO2占2.9%,NOx占14%~15%,SOx占16%[1]。2018年4月国际海事组织(IMO)海上环境保护委员会第72次会议(MEPC 72)通过了关于减少船舶温室气体排放的“巴黎协定”,该协定要求到2030年,每个运输单位的二氧化碳排放量至少较2008年降低40%,并争取在2050年实现70%的降低。对于船舶制造和营运而言,如何降低温室气体排放已经成为一个不得不考虑的问题。同时,随着金融危机对航运业的影响,运价下跌、货量减少,船东们为了能够获得利润必须想方设法提高营运效率,降低成本。纵倾调节技术在不改变船舶载重和航速的前提下,仅改变船舶航行过程中的纵倾角,进而改变其航行阻力,能够起到节能减排的作用。与其他节能减排方式相比,纵倾调节技术具有易于实现、成本低廉、效果明显等优点[2]。
随着计算机技术的发展,计算流体力学(CFD)也得到了飞速的发展。相比模型试验,数值模拟具有费用低、周期短、无尺度效应等优点,且无需考虑船模加工精度和船模变形的影响,并可获得较为详细的流场信息。徐杰等[3-4]采用直接求解RANS方程的方法对20艘散货船的绕流场和阻力进行了数值模拟,通过与试验结果的详细对比,得出结论:只要选取合适的湍流模型,数值模拟结果能够达到较高的精度,能满足工程应用。余建伟等[5-6]就渔政船在各航速下船体阻力进行了理论计算和船模试验验证研究,对理论计算中的船体压阻力、黏性阻力等数据分析,并提出分成分计算来简化船舶阻力计算的思路。
纵倾优化研究方面,涂海文等与中国船级社开发一套纵倾优化软件并用于指导实船压载,通过对比得出4%~6%的节能效果;Salma Sherbaz等[7]通过对MOERI Container Ship进行数值仿真,并与试验结果比较,分析了集装箱船在纵倾调节过程中阻力各成分的变化趋势。毛文雷等[8]应用Rankine源自由面势流理论计算不同纵倾下船舶兴波阻力系数以及总阻力系数,应用三维面元法计算规则波中的波浪增阻,并针对实海域进行了増阻预报,得出一定的尾倾能减小兴波阻力和总阻力的结论。本文运用计算流体力学方法求解180000DWT散货船在设计状态不同纵倾角下阻力值和流场信息,通过模型试验验证阻力计算的准确性,并比较同纵倾状态下阻力值,得到船舶设计状态的阻力最佳纵倾。进一步计算出模型对应状态兴波阻力,通过各个阻力成分流场细节的分析和比较,得到了船舶纵倾优化过程中阻力变化的主导因素。
1 研究对象文中计算模型选用180 000 t散货船,该船具有肥大型球鼻首,实船设计吃水为16.5 m,设计航速v=15 kn,此状态Froude数为Fn=0.1447。按照缩尺比λ=55进行换算后各尺寸如表1所示。
|
|
表 1 船舶主要参数 Tab.1 The main characteristics of ship |
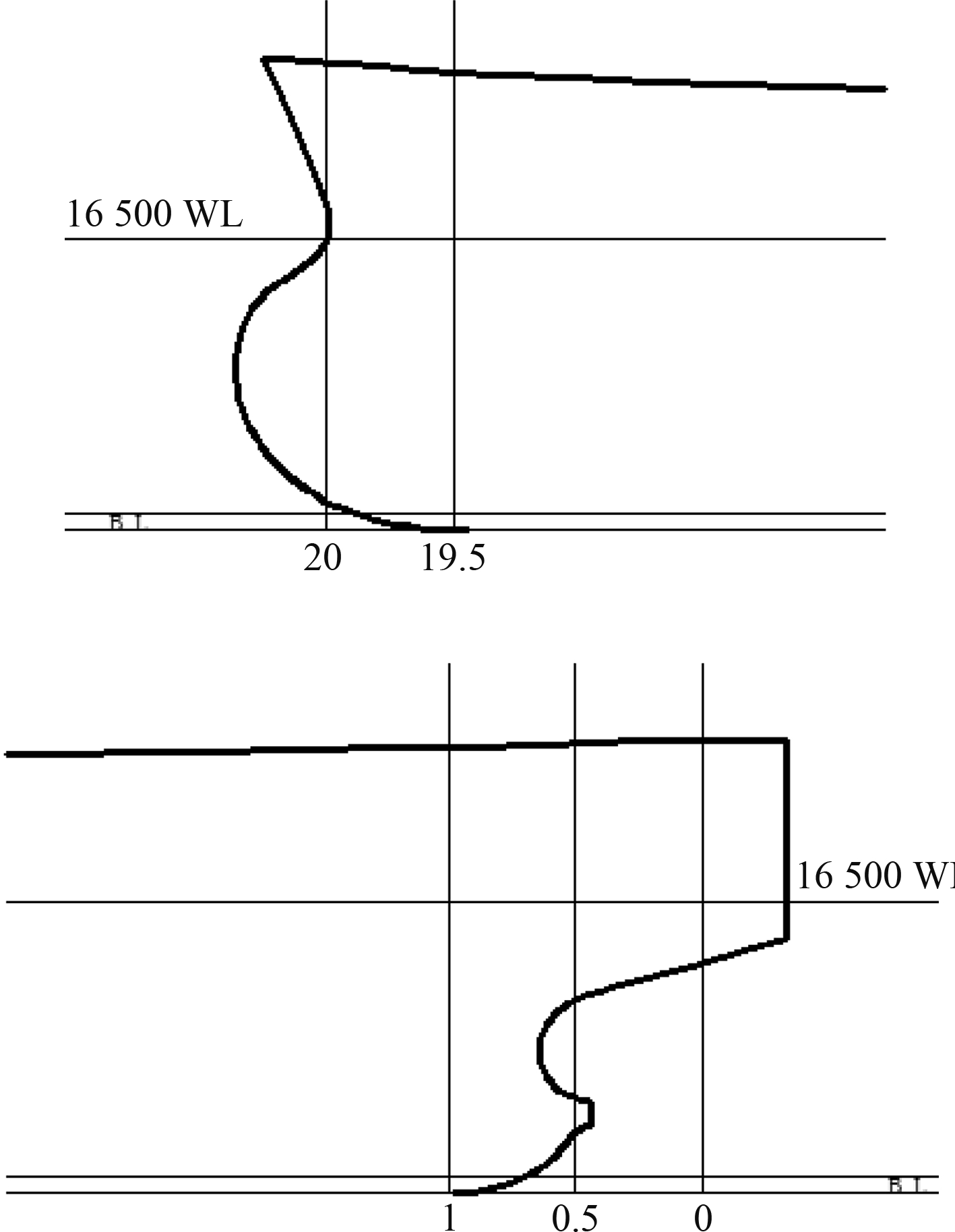
平浮时首尾对应位置如图1所示。在研究的过程中,保证排水量不变的前提下分别对船舶进行不同的纵倾角调整,结合实船航行工况,分别为首倾0.804°,0.603°,0.402°,0.201°;尾倾0.251°,0.503°,0.754°,1.005°。
|
图 1 平浮时设计吃水位置 Fig. 1 The place of design draft in even keel condition |
数值计算三维模型选用UG建模,如图2所示。

|
图 2 计算模型 Fig. 2 Calculation model |
采用RANS控制方程组,包括连续性方程和动量守恒方程[9],分别如下:
连续性方程
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial (\rho {u_i})}}{{\partial {x_i}}}{\rm{ = }}0 {\text{,}} $ | (1) |
动量守恒方程
| $ \begin{split} & \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_j}}} = - \frac{{\partial \rho }}{{\partial {x_i}}} +\\ & \left. {\frac{\partial }{{\partial {x_i}}}\left[ {\mu (\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}) - } \right.\frac{2}{3}\mu \frac{{\partial {u_l}}}{{\partial {x_l}}}{\delta _{ij}}} \right] \!+\! \frac{\partial }{{\partial {x_j}}}\left( { - p\overline {{u'_i }{u'_j}} } \right) \!+\! \rho {f_i} {\text{。}} \end{split} $ | (2) |
式中:ui为流体时均速度分量;p为流体压强;fi为流体体积力分量;ρ为流体密度;μ为流体的粘性系数;附加应力记为
针对肥大型球鼻艏船舶,选用SST κ-ω湍流模型封闭方程组数值预报都能达到比较高的精度[10-11]。其方程如下:
雷诺应力的涡粘性模型
| $ {\tau _{\tau ij}} = 2{\mu _\tau }\left( {{S_{ij}} - {S_{nn}}{\delta _{ij}}/3} \right) - 2\rho \kappa {\delta _{ij}}/3{\text{。}} $ | (3) |
式中:
| $ \mu \tau = \rho \kappa /\omega {\text{。}} $ | (4) |
| $ \begin{split} & \frac{{\partial \rho \kappa }}{{\partial t}} + \frac{\partial }{{\partial {x_j}}}\left[ {\rho {\mu _{\rm{j}}}\kappa {\rm{ - }}\left( {\mu + {\sigma ^*}{\mu _\tau }} \right)\frac{{\partial \kappa }}{{\partial {\chi _{\rm{j}}}}}} \right]{\rm{ = }}\\ & {\tau _{\tau ij}}{S_{ij}} - {\beta ^*}\rho \omega \kappa {\text{,}} \end{split} $ | (5) |
| $ \frac{{\partial \rho \omega }}{{\partial t}} \!+\! \frac{\partial }{{\partial {x_j}}}\left[ {\rho {\mu _{\rm{j}}}\omega {\rm{ - }}\left( {\mu \!+\! \sigma {\mu _\tau }} \right)\frac{{\partial \omega }}{{\partial {\chi _{\rm{j}}}}}} \right]\!{\rm{ = }}\alpha \frac{\omega }{\kappa }{\tau _{\tau ij}}{S_{ij}} \!- \beta \rho {\omega ^2} {\text{。}} $ | (6) |
计算中两相流模型选用VOF模型方程[12]
| $ \frac{{\partial {\rm{C}}}}{{\partial t}} + \overrightarrow u \cdot \nabla C = 0 {\text{。}} $ | (7) |
其中:
考虑到船舶对称性,建立半船模型。数值模拟计算域船长方向5倍船长,其中船前方取1倍船长,船后方约3倍船长;船宽方向取2倍船长,水深方向取1倍船长。如图3所示。
|
图 3 计算域示意图 Fig. 3 Computational domain |
计算域的离散通过ICEM网格划分工具来完成,全局采用六面体结构网格,网格结构类型采用H-C型网格,即纵向为H型网格,横向为C型网格。由于壁面附近的流动船体表面曲线变化较大,在靠近船体处网格适当加密;自由面需要捕捉波形,靠近自由面附近网格较密,流场底部网格较稀。网格总数200万左右,y+值在80左右。船体表面网格如图4所示。

|
图 4 船体表面网格 Fig. 4 The mesh of ship |
计算过程中边界条件设置如下:计算域前方为速度入口并设定来流速度,其中空气域湍流强度为0.1%,湍动粘度比为1%;水域湍流强度为1%,湍动粘度比为1%。计算域后方设为压力出口,计算区域的上方设为速度入口。底面与侧面设定为壁面边界条件,船体表面为壁面边界条件,中间为对称面边界条件。
采用k-ω湍流模型封闭方程组,速度压力的耦合方法为SIMPLE方法。压力的插值方法采用体积力加权方式。动量项和体积分数项均采用2阶迎风差分格式。自由表面的求解选用了欧拉隐式VOF法[12]。
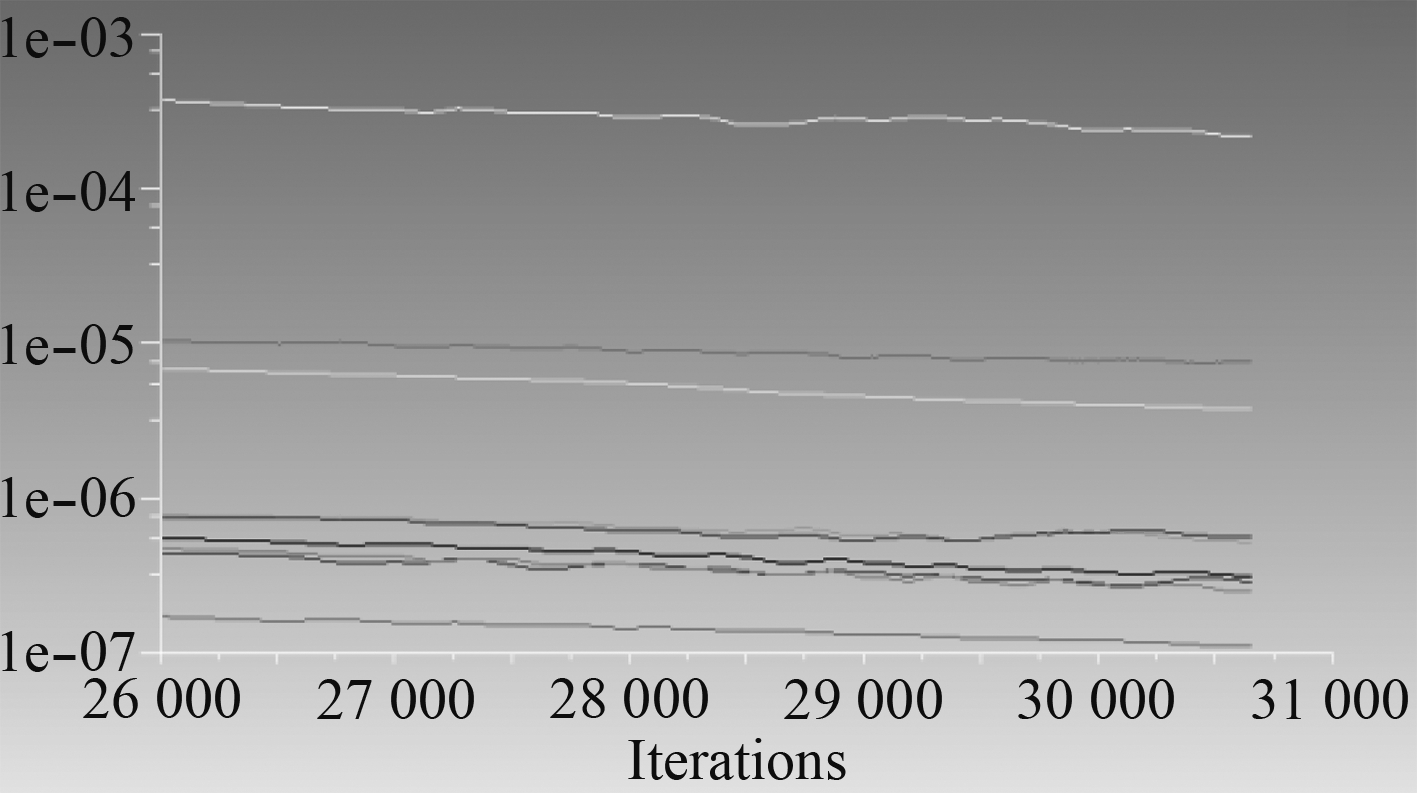
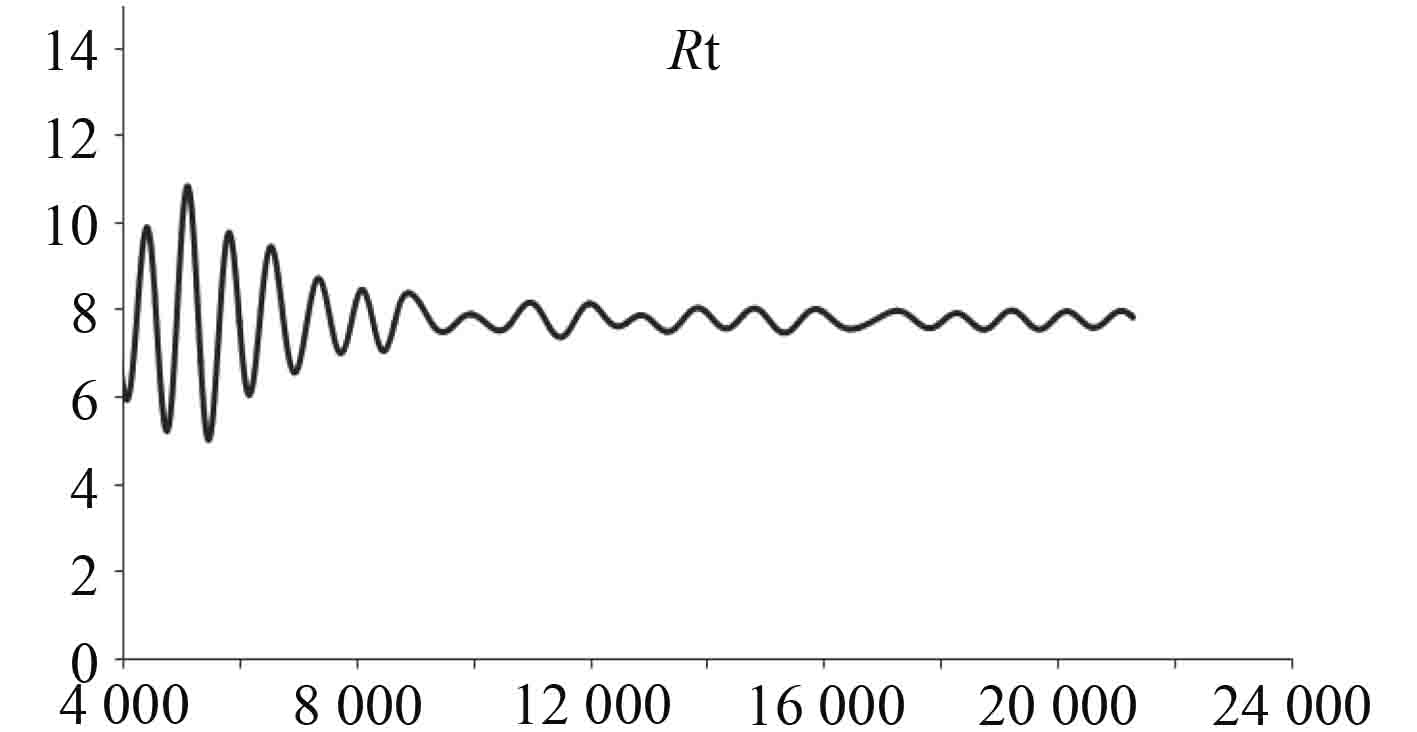
4 阻力计算及试验验证按照上述设置求解各纵倾角下船舶阻力,计算100 s左右趋于稳定,稳定后残差收敛曲线和阻力收敛曲线如图5和图6所示。
|
图 5 残差收敛曲线 Fig. 5 Residual convergence curve |
|
图 6 阻力收敛曲线 Fig. 6 Resistance convergence curve |
模型试验选择华中科技大学船模试验水池完成,该水池长175 m,宽6 m,水深4 m,模型如图7所示。

|
图 7 船舶模型 Fig. 7 Ship model |
保证船舶排水量相等前提下对船舶进行不同的角度调整,分别为首倾0.804°,0.603°,0.402°,0.201°;尾倾0.251°,0.503°,0.754°,1.005°,为方便表述,将首倾角度定义为负,尾倾角度定义为正。将不同倾角下模型试验所得数据与计算数据对比如表2及图8所示。
|
|
表 2 计算数据与模型试验数据对比 Tab.2 Comparison of calculations and model test data |
|
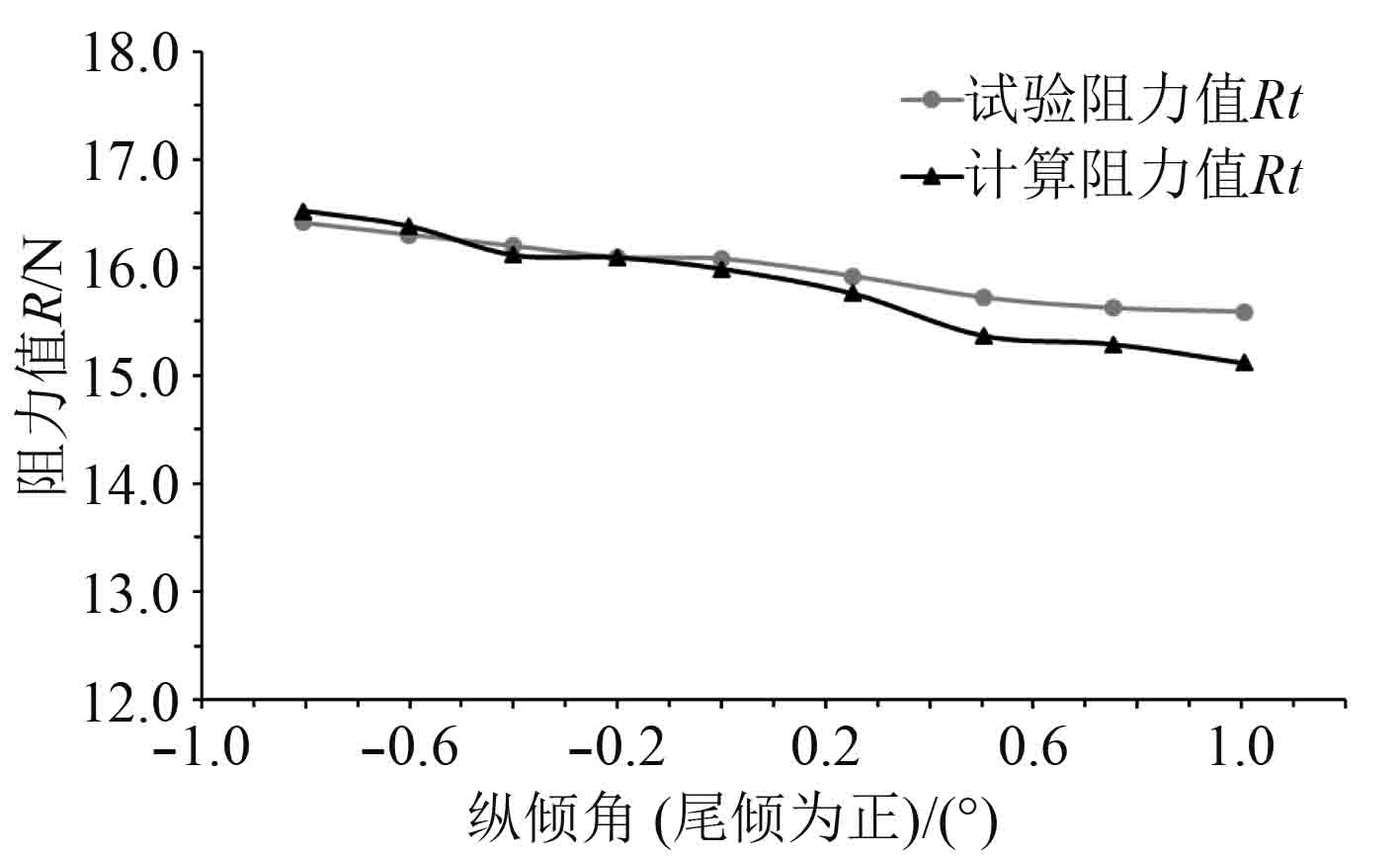
图 8 计算数据和模型试验数据 Fig. 8 Data of calculations and model test |
将计算值与试验值比较,可得计算值与实验值吻合度较高,最大误差为3.034%,并且阻力随倾角变化趋势与试验一致。通过总阻力的比较,证明选用上述网格以及边界条件的合理性。
通过对CFD仿真结果分析可知,船舶在尾倾1.005°时阻力值最小。船舶从平浮向首倾调整过程中,阻力随着首倾角的增大不断增大,在首倾角为–0.804°时达到最大,相对平浮增大3.353%;在平浮向尾倾调整过程中,阻力随着纵倾角增大而减小,在尾倾角为1.005°时效果最好,相对平浮减小5.449%。
5 阻力成分分析通过上述分析可知,船舶在纵倾调节过程中阻力变化明显,最大时与平浮相差5.449%。为了研究船舶阻力变化过程中各阻力成分的变化情况,采用同样的网格和边界条件选用无粘流模型计算船舶的兴波阻力,计算所得总阻力减去兴波阻力即为船舶的粘性阻力。将所得结果如表3及图9所示。为了得到船舶纵倾优化倾角变化过程中阻力变化的主导因素,将结果表述为不同倾角下总阻力变化量中分阻力变化量所占的比例:
|
|
表 3 不同倾角阻力成分比较 Tab.3 Comparison of resistance component on different trim condition |
|
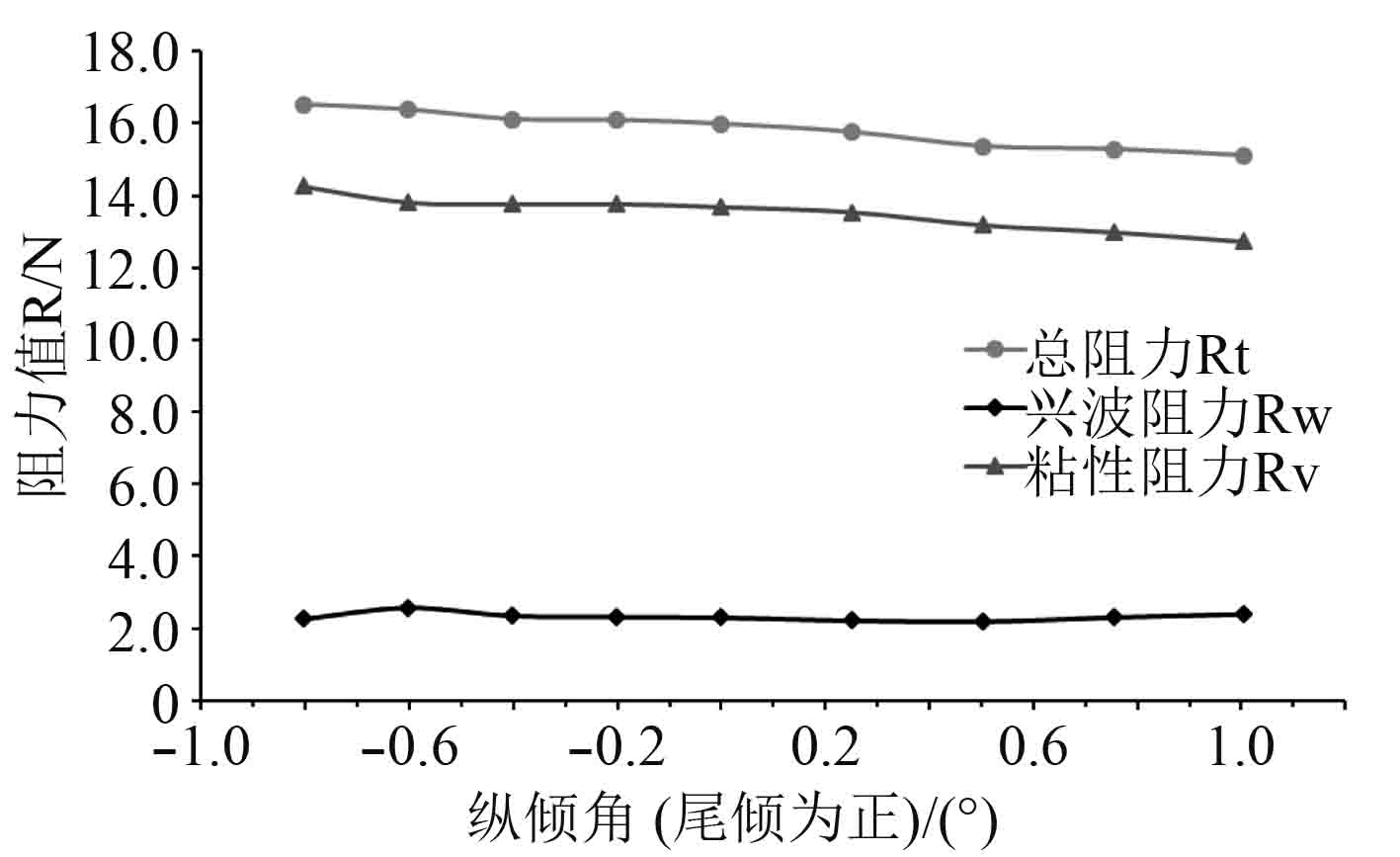
图 9 不同倾角阻力成分比较 Fig. 9 Comparison of resistance component on different trim condition |
| $ \begin{split} & {\text{分阻力在总阻力变化量比例}} = \frac{{\Delta {\text{分阻力}}}}{{\Delta {\text{总阻力}}}} =\\ & \frac{{{\text{纵倾后分阻力}} - {\text{平浮时分阻力}}}}{{{\text{纵倾后总阻力}} - {\text{平浮时总阻力}}}} * 100\% {\text{。}} \end{split} $ |
上述表述中分阻力指兴波阻力或粘性阻力,计算所得结果如表3所示。各分阻力变化量所占比例如图10所示。

|
图 10 各阻力成分变化量比 Fig. 10 Change of different resistancecomponent on trim |
分析数据可以看出,在模型总阻力不断变小(由首倾向尾倾变化)过程中,粘性阻力变化占比越来越大,可以说明本散货船纵倾造成阻力变化主要是由于粘性阻力发生较大变化引起。本船吃水已超过球鼻艏以及尾封板底部,在纵倾过程中湿面积变化不明显,因此可以推测粘性阻力变化可能是由于纵倾造成模型水下形状发生变化,引起粘压阻力变化造成。
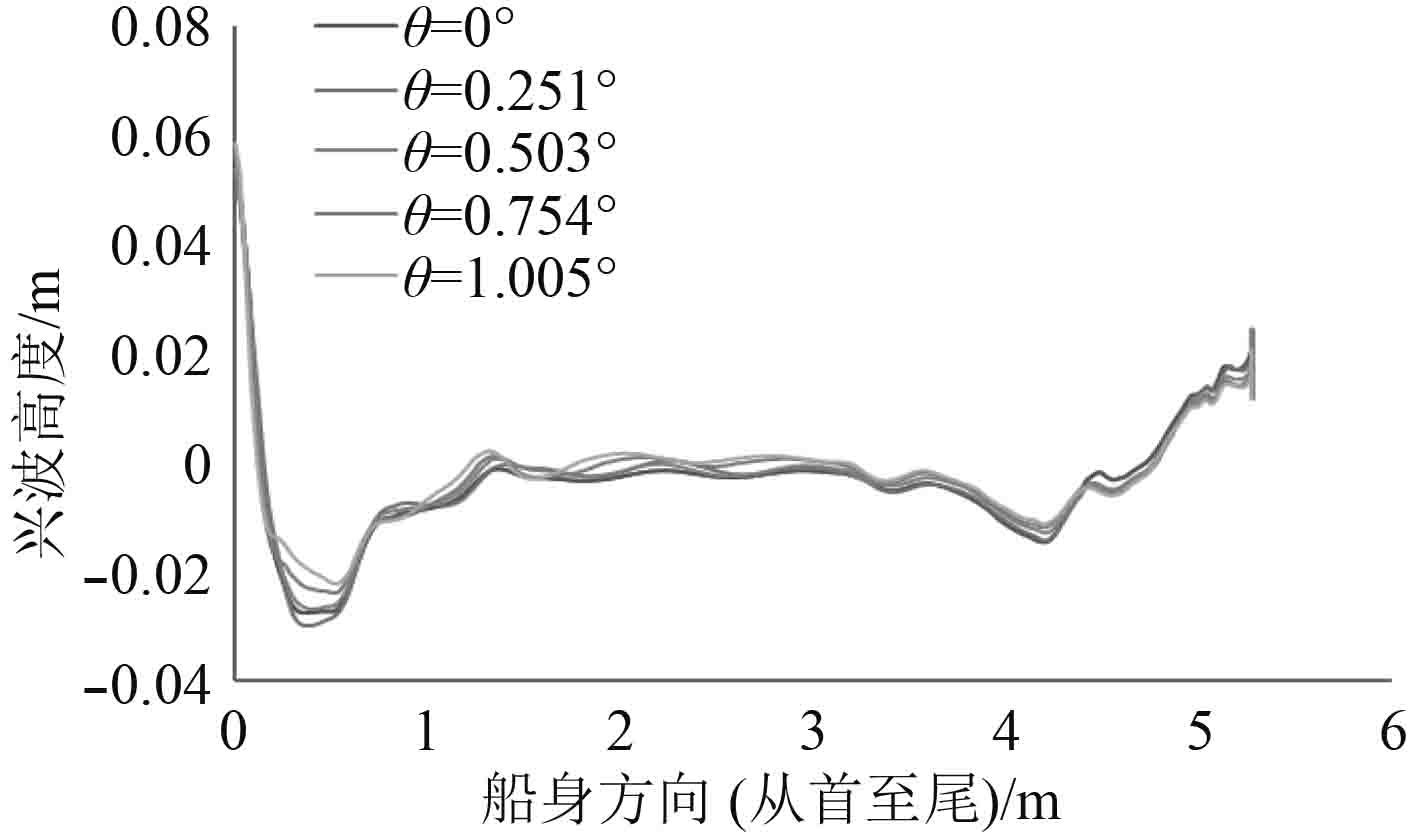
从Fluent中导出不同倾角计算稳定后波高沿船长方向分布数值,如图11和图12所示。图中船首为横坐标轴原点处,船尾沿着横坐标增大方向。比较计算所得兴波阻力值与波高图,可得其大小趋势吻合。

|
图 11 不同首倾波高变化 Fig. 11 Wave profile of trim by bow |
|
图 12 不同尾倾波高变化 Fig. 12 Wave profile of trim by stern |

|
图 13 θ=–0.804°兴波云图 Fig. 13 Wave making contour of θ=–0.804° |

|
图 14 θ=–0.603°兴波云图 Fig. 14 Wave making contour of θ=–0.603° |

|
图 15 θ=–0.402°兴波云图 Fig. 15 Wave making contour of θ=–0.402° |

|
图 16 θ=–0.201°兴波云图 Fig. 16 Wave making contour of θ=–0.201° |

|
图 17 θ=0°兴波云图 Fig. 17 Wave making contour of θ=0° |

|
图 18 θ=0.251°兴波云图 Fig. 18 Wave making contour of θ=0.251° |

|
图 19 θ=0.503°兴波云图 Fig. 19 Wave making contour of θ=0.503° |

|
图 20 θ=0.503°兴波云图 Fig. 20 Wave making contour of θ=0.503° |

|
图 21 θ=1.005°兴波云图 Fig. 21 Wave making contour of θ=1.005° |
本文主要研究散货船纵倾优化过程中阻力的变化情况,以及总阻力的变化量中不同阻力成分所占比例。通过计算阻力值与试验值以及变化趋势的对比,验证网格和边界条件的合理性,采用相同的网格计算兴波阻力,总阻力中减去兴波阻力余下部分为粘性阻力。通过比较得出如下结论:
1)比较不同纵倾状态总阻力可知,对于本散货船设计吃水而言,模型尾倾状态有明显减阻效果,且在一定范围内随着尾倾角增大减阻效果加强。
2)通过不同阻力成分的比较可知,该散货船在纵倾优化过程中,总阻力的改变量中粘性阻力占很大比例,兴波阻力变化量较小。可得针对本散货船而言,纵倾优化过程中粘性阻力的改变为总阻力改变的主导因素。
| [1] |
赵博. 航运业的2050[J]. 中国船检, 2018, 217(06): 20-23. ZHAO Bo. 2050 In the shipping industry[J]. China Ship Inspection, 2018, 217(06): 20-23. |
| [2] |
SUN J, TU H, CHEN Y, et al. A study on trim optimization for a container ship based on effects due to resistance[J]. Journal of Ship Research, 2016, 60: 30-47. DOI:10.5957/JOSR.60.1.150022 |
| [3] |
徐杰、俞汲、黄少锋, 等. 散货船阻力预报中湍流模型的应用. 中国造船, 2011, 52(增刊1).
|
| [4] |
马峥, 黄少锋, 朱德祥. 湍流模型在船舶计算流体力学中的适用性研究[J]. 水动力学研究与进展: (A辑), 2009(2): 207-216.
|
| [5] |
余建伟, 缪国平, 朱仁传. 基于CFD的船舶阻力计算与预报研究[D]. 上海: 上海交通大学.
|
| [6] |
倪崇本, 缪国平, 朱仁传. 基于CFD的船舶阻力性能综合研究[D]. 上海: 上海交通大学.
|
| [7] |
SHERBAZ S, Wenyang Duan. Ship trim optimization: assessment of influence of trim on resistance of MOERI container ship[J]. Scientific World Journal 2014, 6 pages
|
| [8] |
张志荣, 赵峰, 李百齐. k-ω湍流模式在船舶粘性流场计算中的应用. 船舶力学, 2002, 7(1)
|
| [9] |
Y PAN, SA KINNAS. A viscous/inviscid interactive approach for the prediction of performance of hydrofoils and propellers with nonzero trailing edge thickness[J]. Journal of Ship Research, 2011, 55(1): 45-63. |
| [10] |
Y PAN, X DONG, Q ZHU, et al. Boundary-element method for the prediction of performance of flapping foils with leading-edge separation[J]. Journal of Fluid Mechanics, 2012, 698: 446-467. DOI:10.1017/jfm.2012.119 |
| [11] |
TU H, YANG Y, ZHANG L, et al. A modified admiralty coefficient for estimating power curves in EEDI calculations[J]. Ocean. Eng, 2018, 150: 309-317. DOI:10.1016/j.oceaneng.2017.12.068 |
| [12] |
HIRT C W, NICHOLS B D. Volume of Fluid (VOF) Method for the dynamics of free boundary[J]. Journal of Computational Physics, 1981, 39: 201-225. DOI:10.1016/0021-9991(81)90145-5 |
 2020, Vol. 42
2020, Vol. 42
