2. 海军工程大学 舰船与海洋学院,湖北 武汉 430033
2. College of Naval Architecture and Ocean Engineering, Naval University of Engineering, Wuhan 430033, China
在周向非均匀伴流场中运转的螺旋桨将产生周期性的激振力,通常分为由于非定常螺旋桨叶载荷通过轴系传递到船体的轴承力和由于螺旋桨诱导的压力场经过水传递至船体表面的表面力。螺旋桨激振力是船体尾部结构振动的主要激励源,因此预报螺旋桨非定常水动力性能进而确定激振力,对于研究双轴双桨双舵与尾部附体耦合振动特性具有重要意义。
目前CFD方法预报螺旋桨的非定常水动力性能已发展到了相当高的水平,利用CFD方法预报螺旋桨激振力变得越来越普遍。Krasilnikov等[1]使用RANS方法研究了斜流条件下的吊舱螺旋桨受力情况;Gaggero等[2]分别使用RANS方法和面元法分析了斜流中的螺旋桨,通过与试验数据对比说明了2种方法的能力和限制;Liefvendahl等[3]使用LES和动网格方法研究了艇桨组合模型的螺旋桨脉动压力、扭矩和单叶片载荷,分别从时域和频域对计算结果进行了分析,TIAN等[4]使用LES方法和动网格技术计算了桨叶表面压力脉动和非定常螺旋桨推力,并对其进行频谱分析,观察到表面压力谱峰与轴频谐波的关系,来流不均匀程度显著影响非定常推力频谱,傅慧萍[5]通过Fluent软件计算了螺旋桨推力的脉动情况,沈海龙等[6]使用CFD方法模拟了均匀及非均匀伴流中不同螺旋桨的非定常水动力性能,预报结果与试验结果吻合较好;丁科等[7]通过RANS和VOF方法,求取了“船+桨”系统的螺旋桨激振力,得到了螺旋桨激振力在叶频和倍叶频处存在明显的线谱,马超等[8]基于CFD软件,对艇体后螺旋桨进行三维非定常湍流计算,分析螺旋桨周围压力场的变化特点及对艇体的影响,获得了螺旋桨转动1周过程中轴承力的变化规律;张漫等[9]使用滑移网格模型预报螺旋桨的非定常水动力性能;陈如星等[10]基于CFX的滑移网格技术预报伴流场下螺旋桨的非定常水动力性能,将计算结果与建议值进行了比较分析,表明该方法可有效预报螺旋桨激振力。
目前的研究主要是将计算或试验得到的伴流场作为来流条件施加于螺旋桨,将螺旋桨置于船后,并考虑船体兴波和船体纵向运动后航态变化的较少。针对以上研究现状,本文以一全附体船舶为研究对象,基于CFD技术,建立叠模、考虑船体兴波及航态变化条件下螺旋桨激振力的数值计算方法。同时,对螺旋桨推力和船底板压力的平均值和脉动幅值进行进一步对比分析。
1 控制方程及计算方法 1.1 粘性流场计算方程RANS方程是粘性流体运动学和动力学的控制方程,文中以它作为求解船体粘性兴波流场的基本方程。其具体形式如下:
| $ \begin{split} & \frac{\partial }{{\partial t}}(\rho {u_i}) + \frac{\partial }{{\partial {x_j}}}(\rho {u_i}{u_j}) = - \frac{{\partial p}}{{\partial x{}_i}} +\\ & \frac{\partial }{{\partial {x_j}}}\left[ {{\mu _0}\left(\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}\right) - \frac{2}{3}{\mu _0}\frac{{\partial {u_l}}}{{\partial {x_l}}}{\delta _{ij}}} \right] +\\ & \frac{\partial }{{\partial {x_j}}}( - \rho \overline {u_i^{'}u_j^{'}} ) + \rho {f_i} {\text{。}} \end{split} $ | (1) |
式中:ρ为流体密度;μ为流体粘度;为p静压;fi为单位质量的质量力;ui,uj为速度分量。
湍流模式为Realizable k-ε模型[11],其方程形式如下:
湍流脉动动能方程(k方程)
| $ \begin{split} & \frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_j}}}(\rho k{u_j}) = \frac{\partial }{{\partial {x_j}}}\left[ {\left({\mu _0} + \frac{{{\mu _t}}}{{{\sigma _k}}})\frac{{\partial k}}{{\partial {x_j}}}\right)} \right] + \\ & {G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k}{\text{;}} \end{split} $ | (2) |
湍流能量耗散率方程(ε方程)为
| $ \begin{split} & \frac{\partial }{{\partial t}}(\rho \varepsilon ) + \frac{\partial }{{\partial {x_j}}}(\rho \varepsilon {u_j}) = \frac{\partial }{{\partial {x_j}}}\left[ {(\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}})\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \\ & \rho {C_1}{S_\varepsilon } - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\nu \varepsilon } }}{C_{1\varepsilon }}\frac{\varepsilon }{k}{C_{3\varepsilon }}{G_b} + {S_\varepsilon } {\text{。}} \end{split} $ | (3) |
式中:
采用流体积法(Volume of Fluid Method,VOF)计算船体兴波。
1.2 船体运动求解船体所受力和力矩为:
| $ {{F}} = \int_S {([\tau ] - p[I])} \cdot {{n}}{\rm d}S - m{{g}}{\text{,}} $ | (4) |
| ${{{m}}_{\rm{C}}} = \int_S {({{r}} - {{{r}}_{\rm{C}}})([\tau ] - p[I])} \cdot {{n}}{\rm d}S {\text{。}} $ | (5) |
式中:F和mC分别为作用在船模上的力和力矩矢量;[τ]为剪切应力;p为压力;n为船体表面外法线方向;m为船体的质量;rC为船模重心处的位置矢量,下标C为船模的转动中心(重心),r为船模表面任意一点的位置矢量。
根据牛顿第二定律,船模运动的六自由度控制方程[12]表达式如下:
| $ \frac{\rm d}{{{\rm d}t}}(m{{{v}}_{\rm{C}}}) = {{F}} {\text{,}} $ | (6) |
| $ \frac{\rm d}{{{\rm d}t}}([{M_{\rm{C}}}] \cdot {{{\omega }}_{\rm{C}}}) = {{{m}}_{\rm{C}}} {\text{。}} $ | (7) |
式中:vC为船模平动速度矢量;[MC]为惯性矩张量;ωC为船模转动的角速度矢量。
在数值模拟中,作用在船模上的力和力矩可由式(4)和式(5)得到,其运动的速度、角速度及位置、姿态等可以通过式(6)和式(7)求解、积分得到。
2 计算设置 2.1 计算模型分别设计叠模、考虑自由面兴波但船体固定和释放船体纵摇垂荡自由度3种情况,如图1所示。
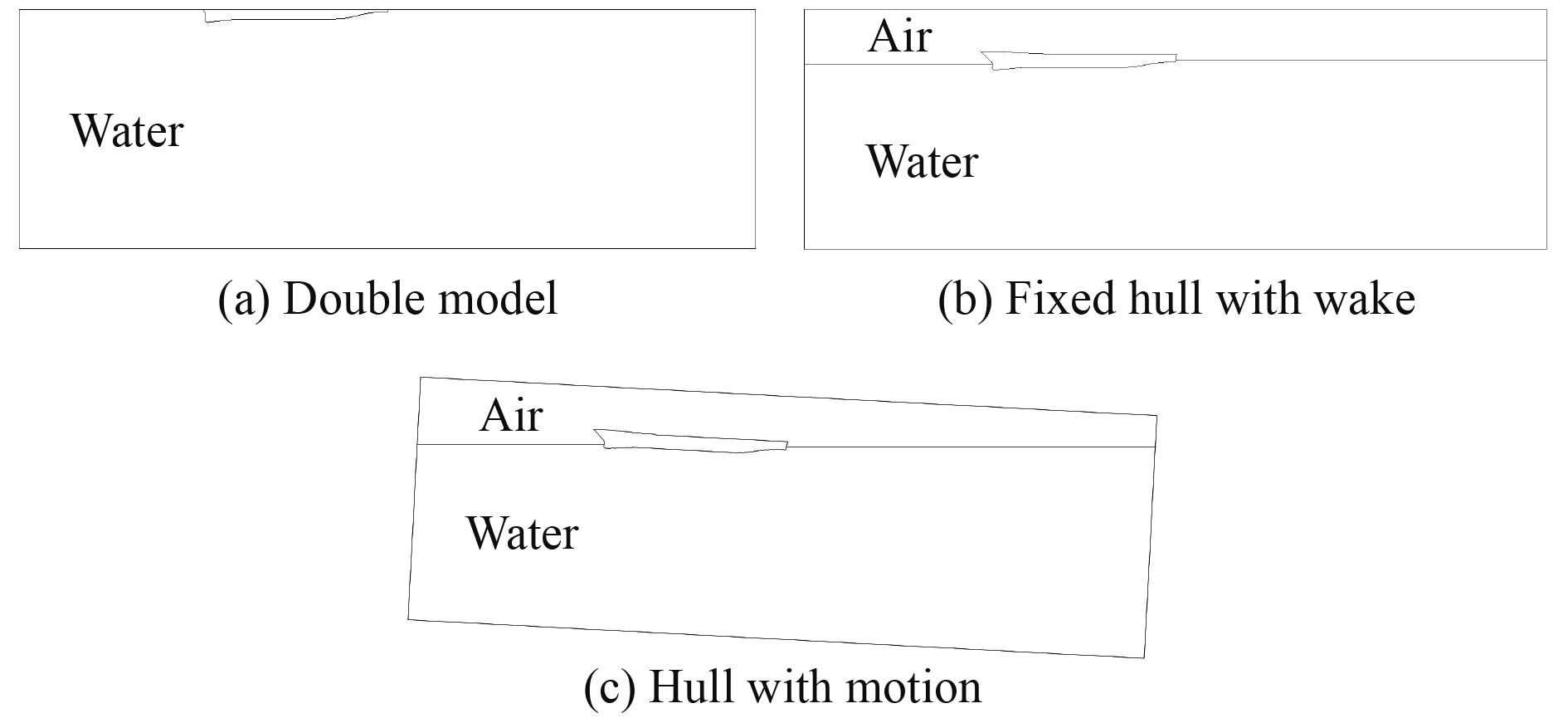
|
图 1 计算的3种情况 Fig. 1 Three cases of computation |
使用的CFD计算软件STAR CCM+对三种情况下的螺旋桨非定常力和船底板脉动压力进行计算。由于左右对称,计算区域只取一半,前端位于首部上游约1倍船长处,设为速度入口;后端位于尾部下游约2倍船长处,设为压力出口;侧壁位于左舷约1倍船长处,设为速度入口;中纵面设为对称面;底部位于龙骨下方约1倍船长处,设为速度入口;顶部叠模时位于水线处,设为对称面,考虑兴波时位于甲板上方约1倍船长处,设为速度入口;船体设定为壁面。螺旋桨的旋转域与外域通过Interface连接。计算区域及船体表面的网格划分如图2所示。网格划分采用非结构化网格,网格数量叠模时约180万,考虑兴波时约200万,计算时间步长为0.000 2 s。
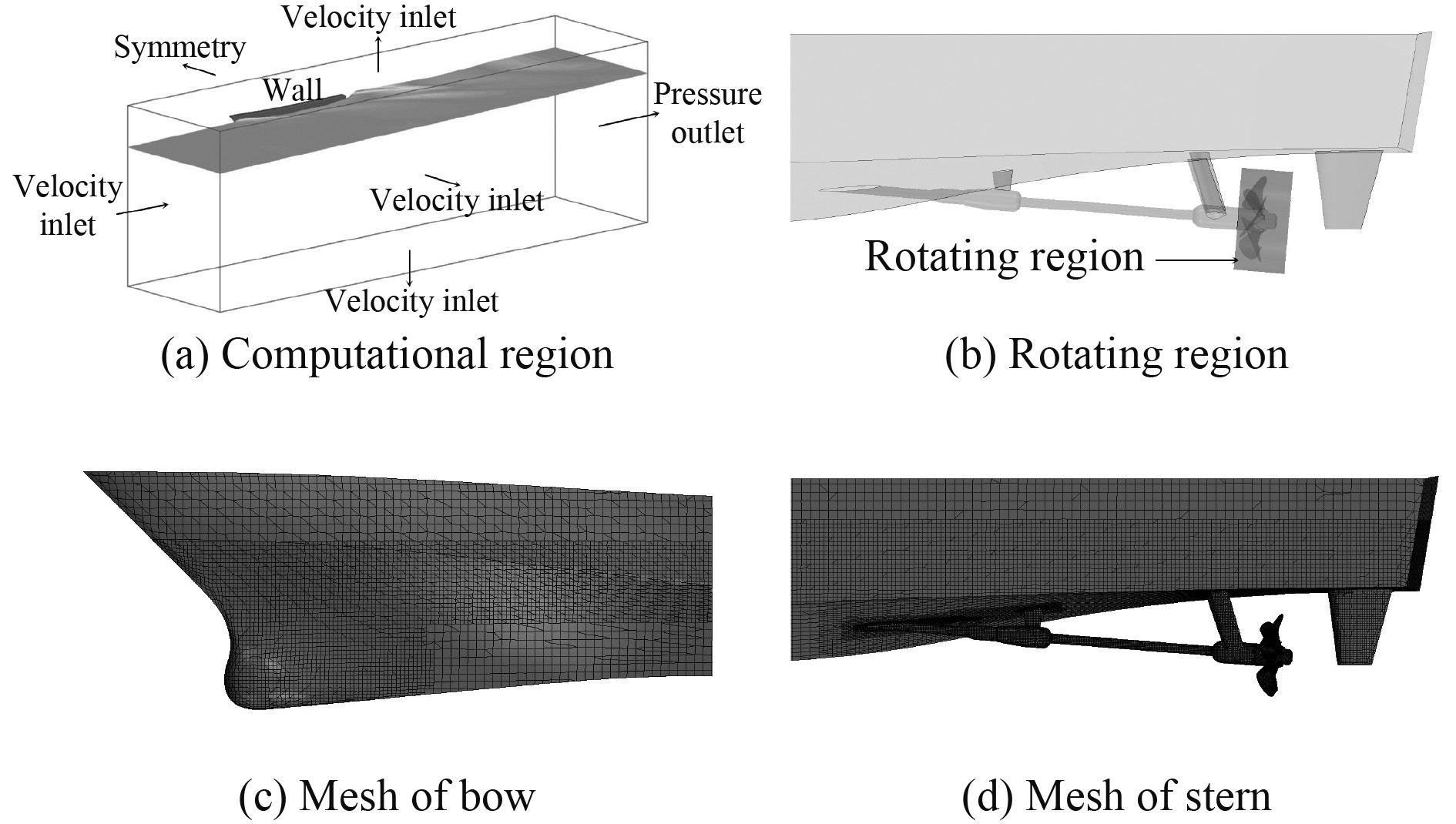
|
图 2 计算区域及网格划分 Fig. 2 Computational region and mesh |
计算时,选取模型速度为3.732 m/s,螺旋桨转速为927 r/min。监控螺旋桨的推力,在桨轴正上方的船底板处从尾封板到前尾轴架设置20个监测点,监测相应位置的压力变化。
3 数值计算结果分析 3.1 螺旋桨推力分析考虑兴波时的船体兴波波型如图3所示。待螺旋桨推力变化规律稳定后,取0.5 s的推力计算结果,如图4所示。可见考虑兴波时推力的平均值有所减小,考虑航态时更小,与叠模相比分别减小1.37%和6.00%。
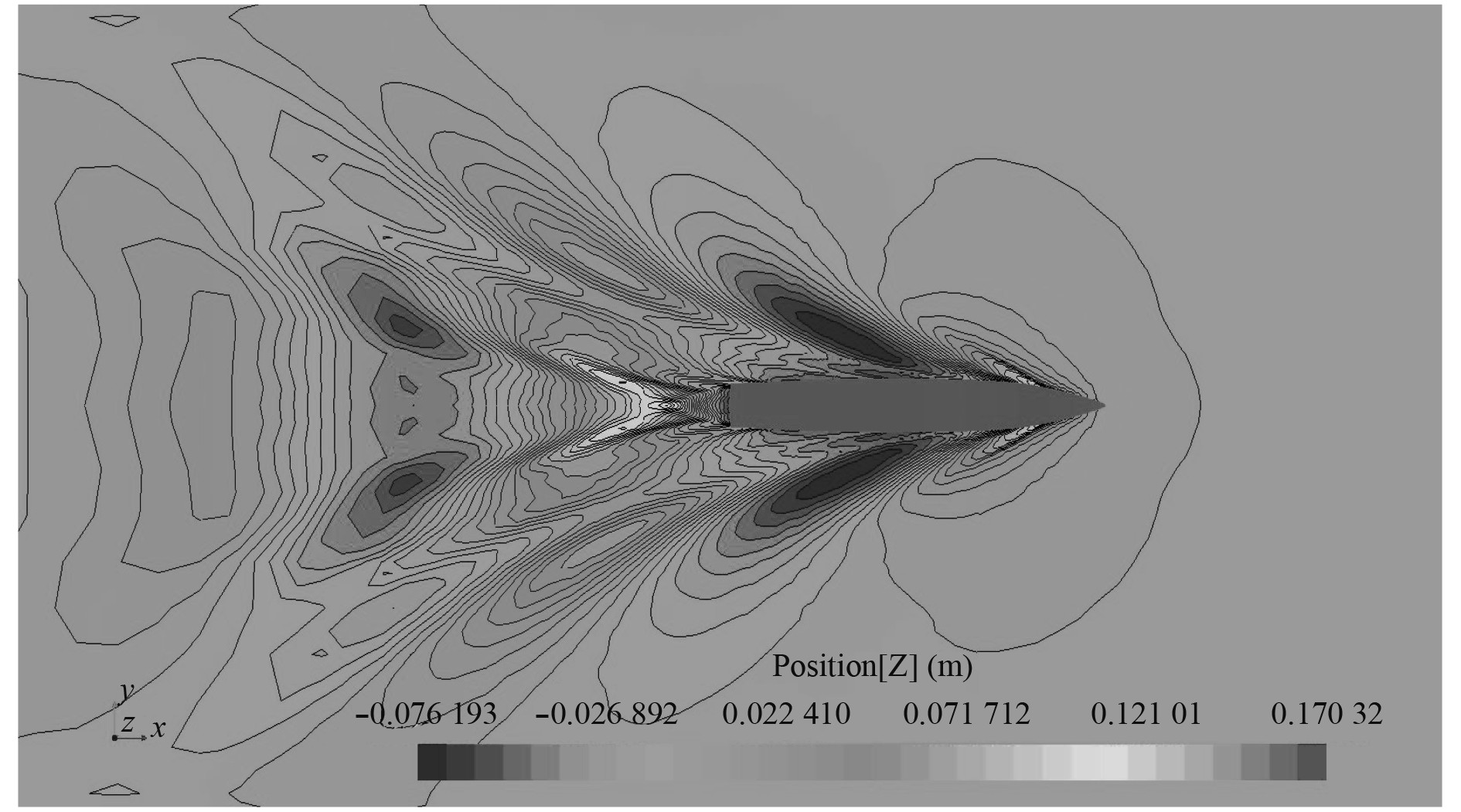
|
图 3 船体兴波波型 Fig. 3 Hull wake pattern |

|
图 4 推力计算结果 Fig. 4 Calculation result of thrust |
减小的原因可用兴波及航态变化导致的流场变化来解释。3种情况下过桨轴线的纵剖面上的速度分布如图5所示。可见情况2和情况3的速度依次增大,螺旋桨进速系数增大,推力系数减小。
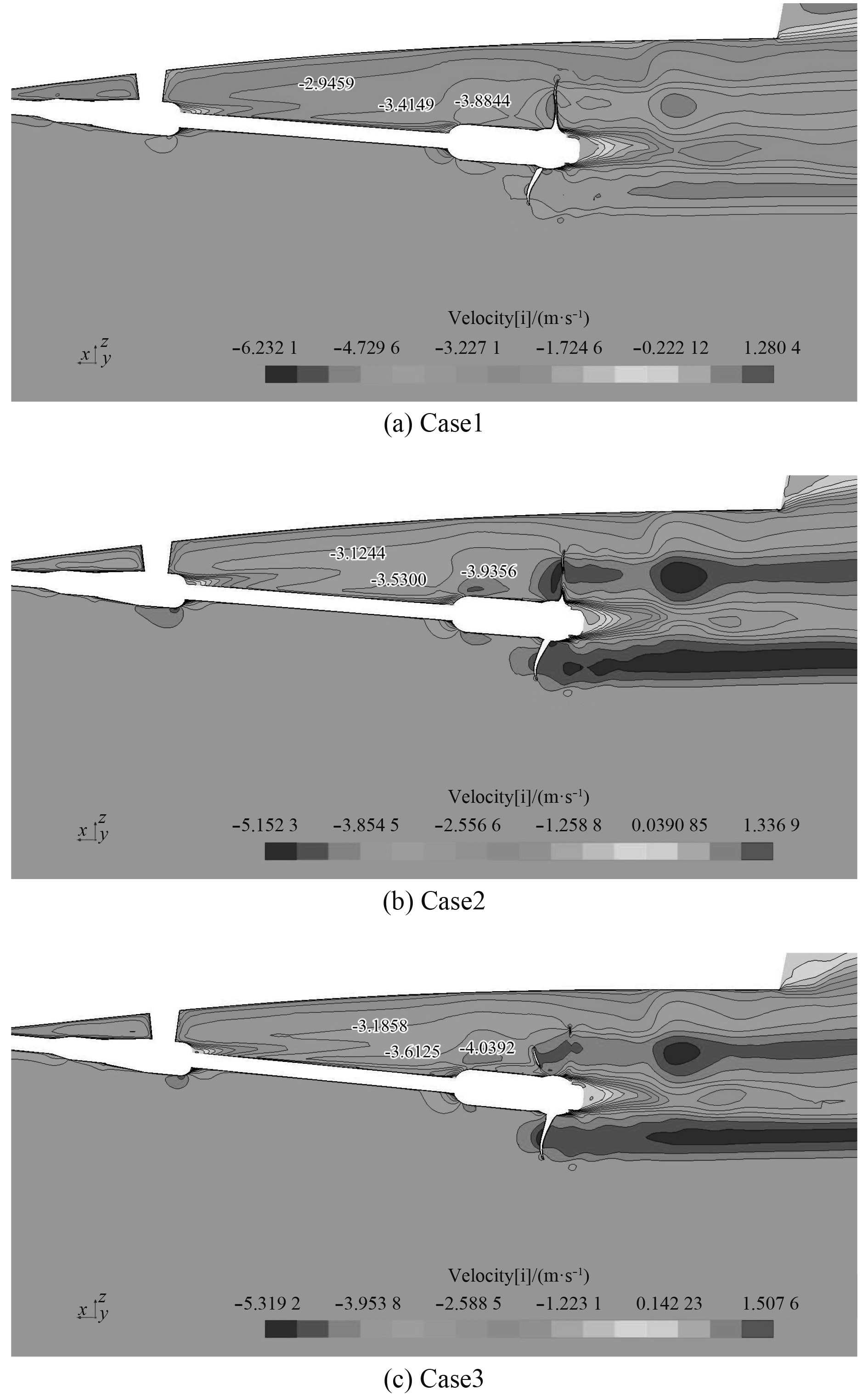
|
图 5 推力计算结果 Fig. 5 Calculation result of thrust |
螺旋桨推力的功率谱密度如图6所示。从图中可分辨出1~5倍叶频,3种情况下1,2倍叶频出峰值较为接近,与叠模相比分别,考虑兴波和航态时1倍叶频处峰值分别减小6.95%和25.81%。推测其原因为:从情况1到情况3,越来越接近真实情况,对计算的限制条件逐渐减弱,限制条件对流场的干扰也逐渐减弱,来流不均匀程度减弱,因此推力脉动的幅值减小。

|
图 6 推力的功率谱密度 Fig. 6 PSD of thrust |
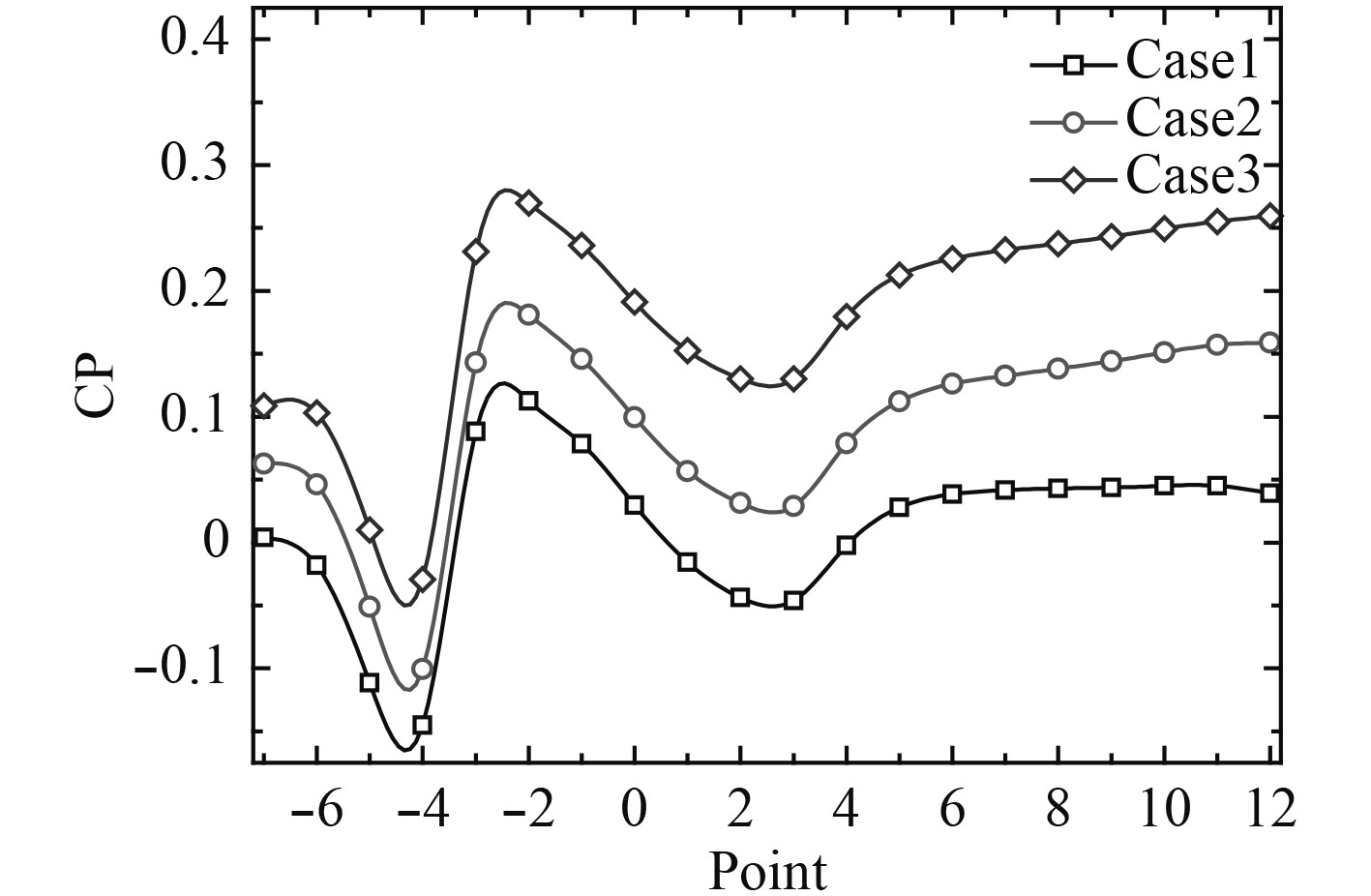
船底板压力平均值随位置的变化如图7所示。其中0点代表将盘面正上方,“-”代表船尾方向,“+”代表船首方向。可见情况2和情况3的平均压力比情况1依次增大,该现象也可以用流场速度变化来解释。
|
图 7 船底板压力平均值 Fig. 7 Average pressure on hull bottom |
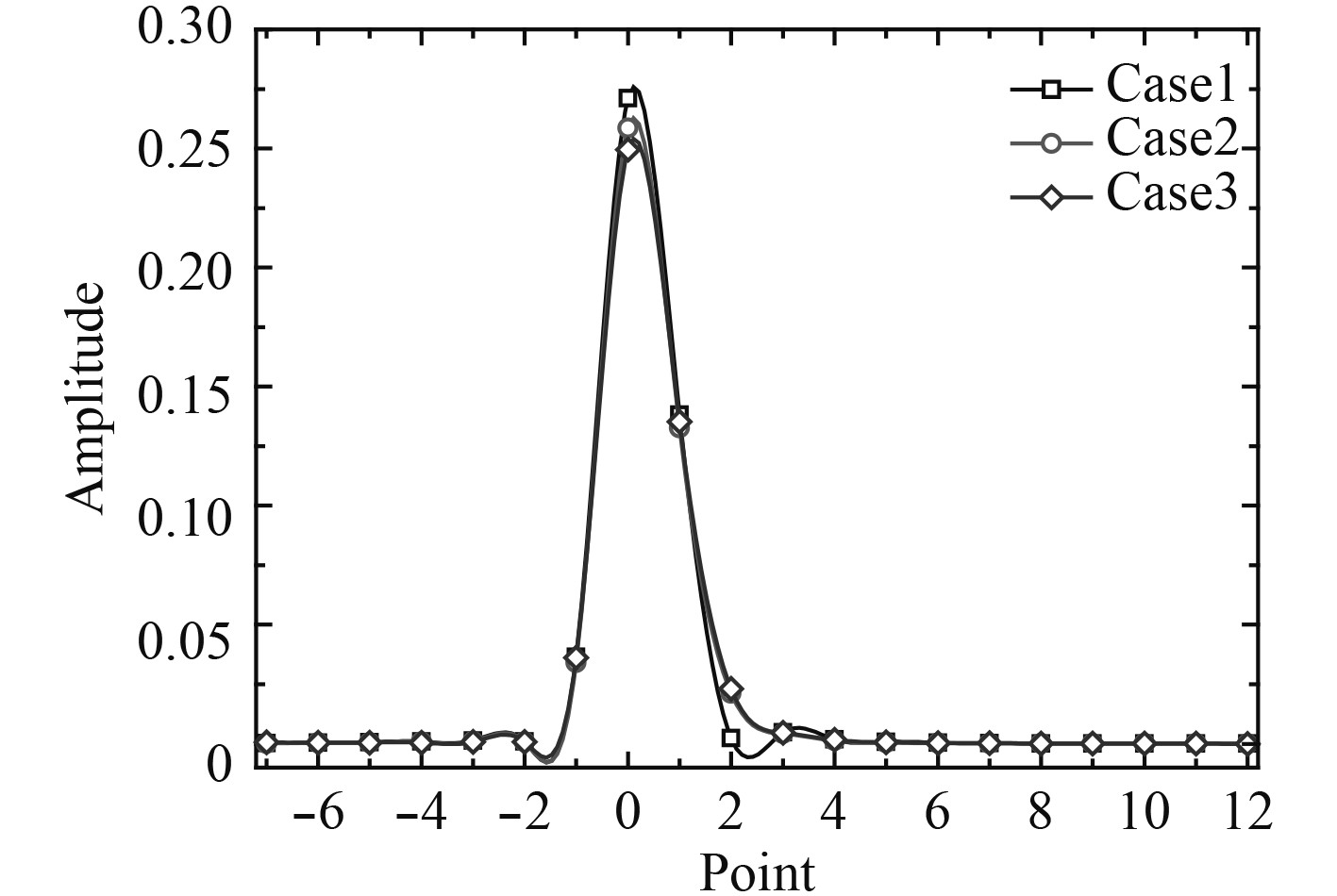
船底板脉动压力1倍叶频处峰值随位置的变化如图8所示。可见桨盘面处船底板压力脉动最为强烈,向艏艉方向迅速减小,在“±2”点前后,脉动已较小并基本不变。其中3种情况下桨盘面处脉动幅值变化规律与推力相似,推测原因同样为来流不均匀程度的减弱。
|
图 8 一倍叶频处峰值 Fig. 8 Peak at BPF |
本文采用RANS方法建立船后螺旋桨激振力的数值计算方法,开展了3种情况下螺旋桨推力、船底板脉动压力的数值分析,得到如下结论:
1)考虑兴波及航态变化时,由于流速变化,螺旋桨推力平均值减小,船底板压力平均值增大;由于来流不均匀程度的变化,1倍叶频处峰值减小。
2)考虑兴波及航态变化时,计算得到的激振力更加接近真实情况,但由于激振力在频域中较为接近,为节约计算量,计算时可不考虑船体兴波及航态变化。
| [1] |
KRASILNIKOV V, ZHANG Z, HONG F. Analysis of unsteady propeller blade forces by RANS[C]//Proc First International Symposium on Marine Propulsors, Trondheim, Norway June 2009.
|
| [2] |
GAGGERO S, VILLA D, BRIZZOLARA S. RANS and panel method for unsteady flow propeller analysis[J]. J Hydrodyn, 2010, 22(5, Suppl. 1): 564-569. |
| [3] |
LESFVENDAHL M, TROENG C. Computation of cycle-to-cycle variation in blade load for a submarine propeller using LES[C]//Proc Second International Symposium on Marine Propulsors, Hamburg, Germany 2011.
|
| [4] |
TIAN Jin, YANG Haosen, ZHANG Zhenguo, et al. LES-based numerical analysis of surface-pressure fluctuations and unsteady thrust of a marine propeller[C]//Inter-noise, Australia 2014.
|
| [5] |
傅慧萍. 船桨整体及螺旋桨诱导的船体表面脉动压力计算[J]. 哈尔滨工程大学学报, 2009, 30(7): 728-734. DOI:10.3969/j.issn.1006-7043.2009.07.002 |
| [6] |
沈海龙, 苏玉民. 船体粘性非均匀伴流场中螺旋桨非定常水动力性能预报研究[J]. 水动力学研究与进展, 2009, 24(2): 232-241. |
| [7] |
丁科, 王永生, 魏应三. 船艉螺旋桨激振力的数值预报[C]//第十一届全国水动力学学术会议暨第二十四届全国水动力学研讨会并周培源诞辰110周年纪念大会, 无锡, 2012.
|
| [8] |
马超, 肖锋, 张志谊, 等. 艇体非均匀伴流场下螺旋桨压力场[J]. 噪声与振动控制, 2013, 4(2): 49-53. |
| [9] |
张漫, 黎胜. 基于滑移网格技术计算螺旋桨水动力性能研究[J]. 船海工程, 2013, 42(5): 25-29. DOI:10.3963/j.issn.1671-7953.2013.05.006 |
| [10] |
陈如星, 周瑞平, 林晞晨. 基于CFX的螺旋桨激振力数值预报研究[J]. 武汉理工大学学报, 2014, 36(7): 74-79. |
| [11] |
SHIH T H, LIOU W W, SHABBIR A, et al. A New k-ε eddy-viscosity model for high reynolds number turbulent flows-model development and validation[J]. Computers Fluids, 1995, 24(3): 227-238. DOI:10.1016/0045-7930(94)00032-T |
| [12] |
吴乘胜, 陈雄, 孙立宪, 等. 静水中自由船模拖曳CFD模拟方法研究[J]. 船舶力学, 2010, 14(8): 823-833. DOI:10.3969/j.issn.1007-7294.2010.08.001 |
 2020, Vol. 42
2020, Vol. 42
