2. 河南省水下智能装备重点实验室,河南 郑州 450015
2. Henan Key Laboratory of Underwater Intelligence Equipment, Zhengzhou 450015, China
推进剂是固体火箭发动机的能源,推进剂在固体火箭发动机燃烧室内燃烧产生高温高压的燃气,燃气通过拉法尔喷管以高速向后喷出,从而获得反作用推力,使飞行器克服飞行中各种阻力,达到一定的飞行速度或射程,完成预定任务[1]。
燃速是固体推进剂的重要参数,是推进剂研究和生产过程中的必测参数。国军标中规定了2种燃速测试方法[2],即靶线法和水下声发射法,二者都是在测试温度和压力不变的条件下测试规定长度固体推进剂药条的燃烧时间,由此计算出推进剂的平均燃速,以平均燃速表示推进剂出厂的标准燃速[3]。该测试方法与测试样本与固体推进剂在固体火箭发动机燃烧室中的燃烧存在很大差异,导致推进剂的实际工作燃速与出厂燃速存在较大差异。本文针对某型固体火箭发动机改性双基推进剂出厂轴向燃速和动态燃速存在差异的情况,较为全面地分析了影响推进剂燃速的主要因素,提出基于最小二乘法固体推进剂的动态燃速辨识方法。
1 燃速基本理论 1.1 燃速定义燃速是固体推进剂的重要性能参数,决定了装药的燃气生成量、固体火箭发动机产生的推力。如果推进剂的结构和理化性能各向同性,推进剂燃烧表面同时点燃,则认为全部的燃烧表面将沿其法线方向,以相同的燃烧速度向着推进剂内部退移,即推进剂燃烧表面按平行层燃烧规律逐层燃烧,这种燃烧规律称为几何燃烧规律[4]。
假设在dt时间内,推进剂燃烧表面沿其法线法向退移了距离de,推进剂燃烧速度定义为:
| $ \dot r = \frac{{{\rm d}e}}{{{\rm d}t}} {\text{。}} $ |
目前,最常用的固体火箭推进剂燃速定律是指数燃速定律和萨摩菲尔燃速定律。指数燃速公式最常用于双基和改性双基推进剂,萨摩菲尔燃速定律适用于AP复合推进剂。由于本文以改性双基推进剂为例,因此采用指数燃速定律。
| $ r = a{p^n} {\text{。}} $ |
式中:
燃速系数
1)推进剂组分对燃速的影响
研究表明,少量的燃速稳定剂和催化剂可以明显改变推进剂的燃速,在相同压强条件下,
2)初温对燃速的影响
推进剂初温是影响燃速的重要因素,初温通过改变推进剂固相预热区和凝相反应区的热平衡影响推进剂燃烧速度[5],单位体积的推进剂从初温
为定量计算初温对燃速的影响,引入燃速的温度敏感系数,即一定压强条件下,温度改变1 K(或1 ℃)所引起的燃速相对变化量。
| $ {\alpha _T} = {\left[ {\frac{1}{{\dot r}}\frac{{\partial \dot r}}{{\partial {T_i}}}} \right]_p} {\text{,}} $ |
在压强相同的情况下,上式可写为:
| $ {\alpha _T} = \frac{{{r_2} - {r_1}}}{{{r_1}({T_2} - {T_1})}} {\text{。}} $ |
3)密度对燃速的影响
由式
4)压强对燃速的影响
根据稳态燃烧理论,压强增加,将提高气相到固体表面的温度梯度,从而增强对燃面的热传导,导致燃速增大。研究表明,固体推进剂的瞬态燃速是由压强随时间的变化率决定的,大幅快速降压可以使瞬态燃速减小至零,导致熄火;而大幅快速升压则导致燃速激增,进而导致压强迅速上升,甚至使发动机爆炸。
5)燃速的加速度效应
在一些特定的应用场合,要求固体火箭发动机随着导弹进行高速旋转,有的转速甚至高达上万转。实验表明,旋转加速度使固体火箭推进剂的燃速增大[6]。
2 静态燃速与动态燃速差异分析针对某型自由装填固体火箭发动机整机地面静止试验时的动态燃速与药厂标注静态燃速存在差异的现象进行试验分析,排除了催化剂、初温、密度和和燃速加速度效应的影响。
固体火箭发动机所用双基推进剂或改性双基推进剂药柱为压伸成型,装药出厂标准燃速采用《GJB770B-2005火药试验方法》中“方法706.1燃速靶线法”的药条进行测试,其测试试样见图1,燃速测试结果主要体现为轴向燃速。而固体火箭发动机实际工作过程中装药实际燃烧方向见图2,其体现为径向燃速。固体火箭发动机实际装药和靶线法测试所取试样在尺寸、燃烧方向和燃烧室压强上存在差异。为了获得准确的固体火箭发动机内弹道理论计算曲线,需要对推进剂药柱的动态燃速进行辨识。

|
图 1 燃速测试装药燃烧方向示意图(轴向燃烧) Fig. 1 Burning direction of test burning rate charge (axial burning) |

|
图 2 装药实际燃烧方向示意图(径向燃烧) Fig. 2 Schematic diagram of actual combustion direction of charge (radial combustion) |
固体火箭发动机燃烧室压强分为上升段和平衡段两段计算。压强上升段按下式计算[7]:
| $ {{t}} = \frac{{{{{V}}_{{\rm{c}}0}}}}{{(1 - {\rm{\nu }}){{k}}{{\left(\dfrac{2}{{{{k}} + 1}}\right)}^{\frac{{{{k}} + 1}}{{{{k}} - 1}}}}{{{C}}^*}{{At}}}}\ln \frac{{1 - {{\left(\dfrac{{{{{P}}_{{{ig}}}}}}{{{{{P}}_0}}}\right)}^{1 - {\rm{\nu }}}}}}{{1 - {{\left(\dfrac{{{{{P}}_{}}}}{{{{{P}}_0}}}\right)}^{1 - {\rm{\nu }}}}}} {\text{。}} $ |
式中:
平衡段的压强按照以下公式进行计算:
| $ {{{P}}_0} = {\left({{\rm{\rho }}_{{p}}}{{{U}}_1}{\rm{\varepsilon }}{{{C}}^*}\frac{{{{{A}}_{{b}}}}}{{{\rm{\mu }}{{\rm{\sigma }}_{{f}}}{{{A}}_{{t}}}}}\right)^{\frac{1}{{1 - {\rm{\nu }}}}}} {\text{。}} $ |
式中:
通过对比理论计算模型的压力曲线与地面静止试验曲线的偏差可以评估理论计算模型与实测曲线偏差的最小平方和(最小二乘法[8]),获得最佳动态燃速。压强偏差的最小平方和为:
| $ r = \sum\limits_{i = 1}^N {({P_i} - {P_i}'} {)^2} {\text{。}} $ |
式中:
对同一批尺寸和基础理化性能检测合格的装药,以地面静止试验的压强曲线为基准,理论计算模型中参数除燃速外,其他均取地面静止试验中所用装药的实际参数。因此可以通过分析理论计算模型的压强曲线和地面试车的压强曲线之间的差异辨识出动态燃速。
为了减少点火压力峰和点火压强下降段对统计结果的影响,首先,将实测有效压强曲线和理论计算压强曲线初始段“时间统一”,统计区间的时间起点取平直段和上升段的拐点,取测试压强曲线和理论计算压强曲线峰值对应工作时间最短的时间点为统计区间的时间终点,在此时间范围内间隔0.01 s计算实测有效压强曲线和理论计算压强曲线压强偏差的平方和,压强偏差的平方和最小的动态燃速为该批次装药的动态燃速。
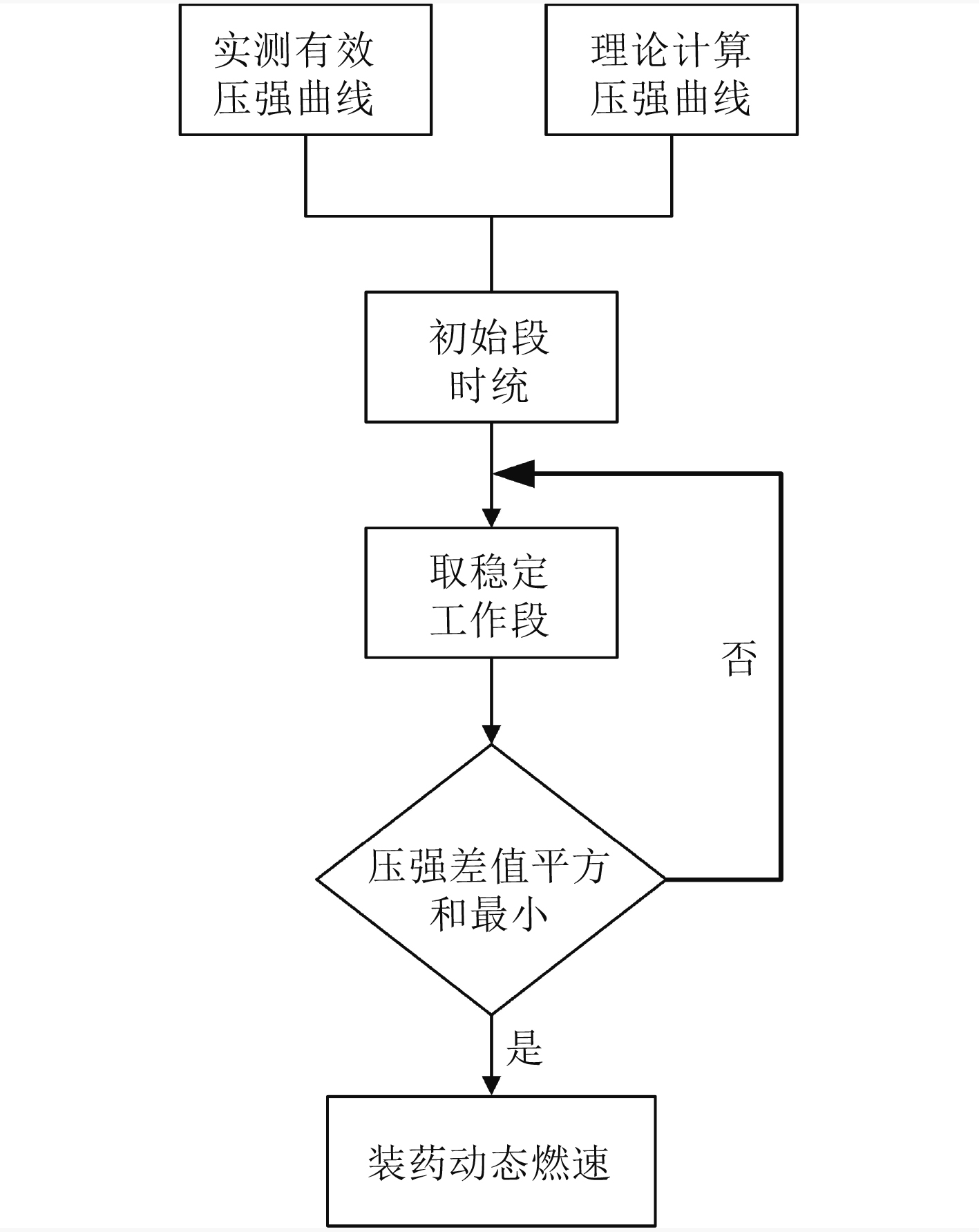
|
图 3 动态燃速辨识流程图 Fig. 3 Flow chart of dynamic burning rate identification |
某型固体火箭发动机辨识前测试压强曲线与理论计算压强曲线如图4所示。可知理论计算燃速比测试燃速偏高,理论计算过程所用参数均为推进剂实测值,可排除药型偏差、喉径和温度等因素,初步定位为静态燃速和动态燃速存在偏差所致。对多批改性双基推进剂运用最小二乘法辨识出装药的动态燃速如表1所示。辨识前静态燃速计算压强与测试压强残差最大值为2.7509,辨识后动态燃速计算压强与测试压强残差最大值为0.2947。通过动态燃速辨识,有效提高了理论计算结果与实验测试结果的吻合度。
|
|
表 1 动态燃速辨识结果 Tab.1 identification results of dynamic burning rate |

|
图 4 静态燃速计算压强与测试压强曲线对比 Fig. 4 Comparison between calculated pressure and test pressure curve of static burning rate |
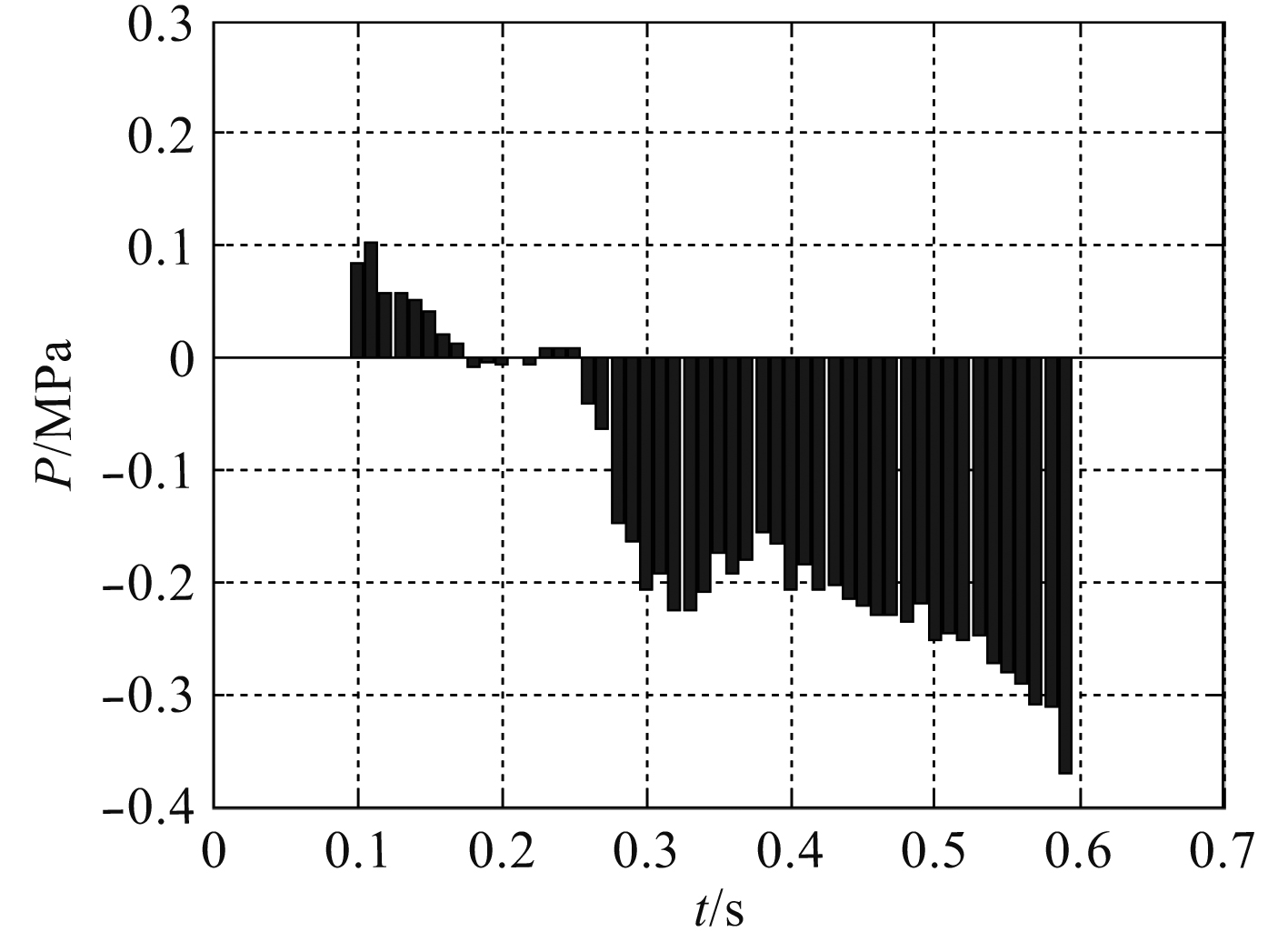
|
图 5 辨识前压强偏差分布直方图 Fig. 5 Histogram of pressure deviation distribution before identification |
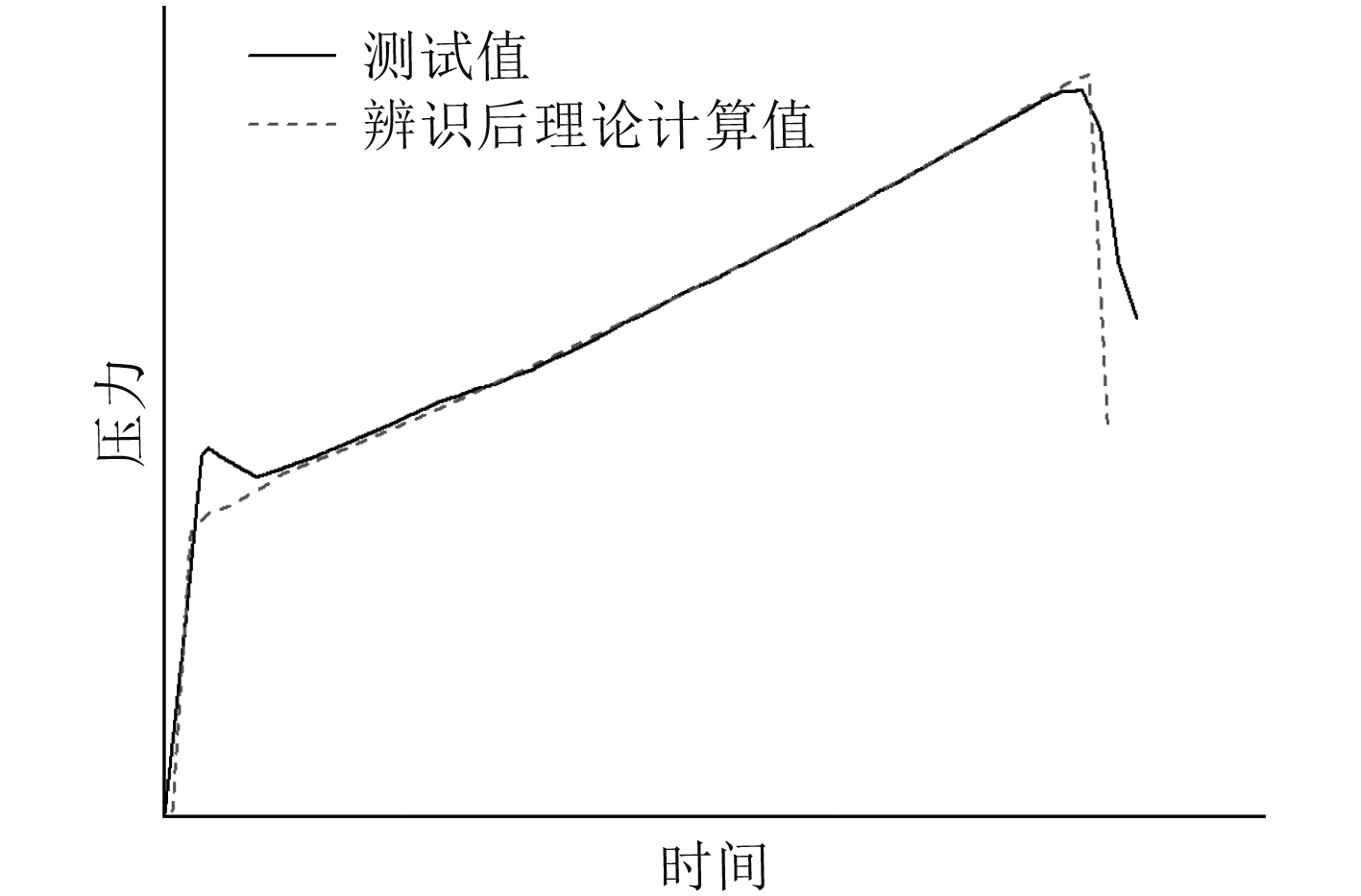
|
图 6 动态燃速计算压强与测试压强曲线对比 Fig. 6 Comparison between calculated pressure and measured pressure curve of dynamic burning rate |
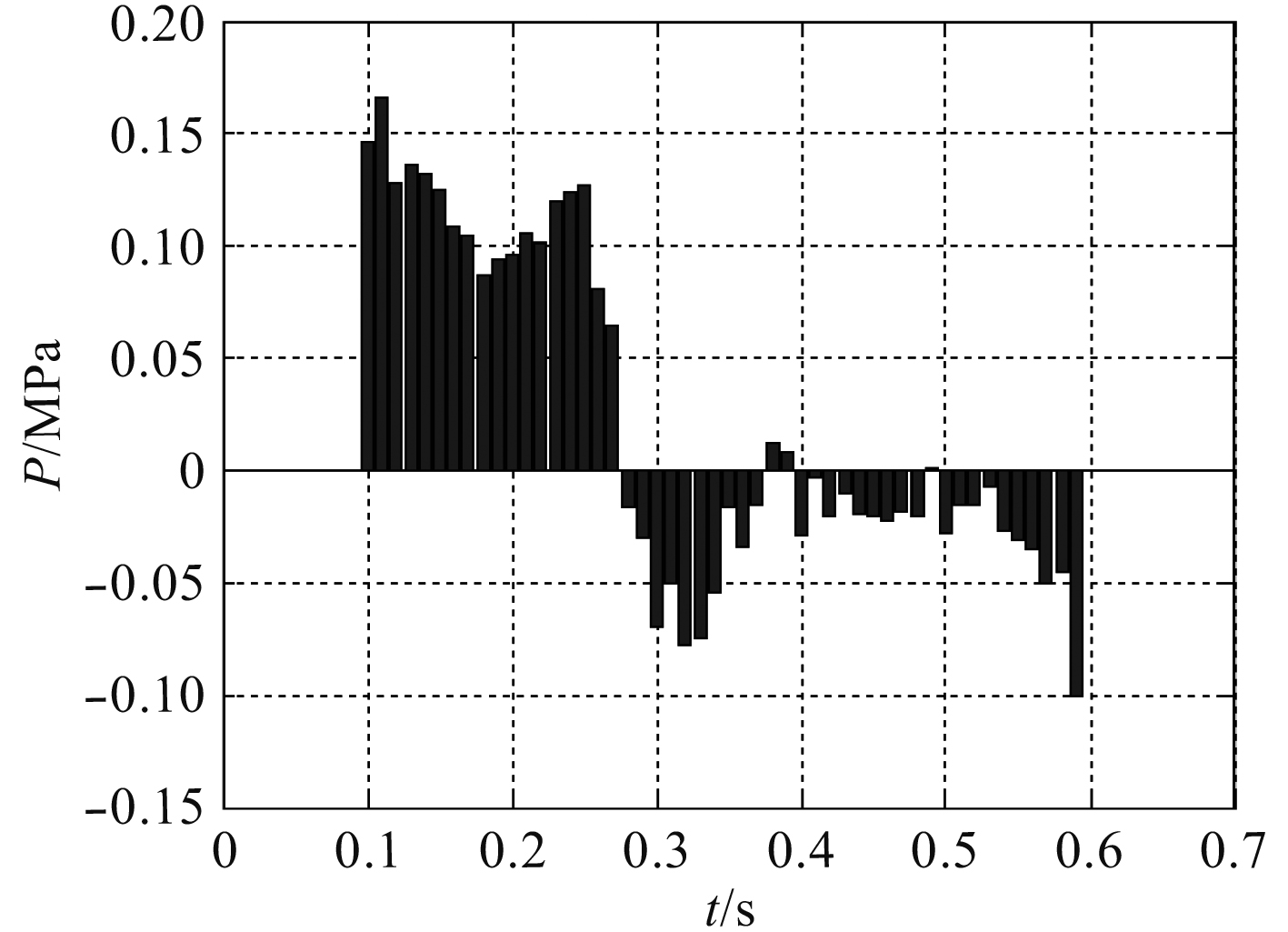
|
图 7 辨识后压强偏差分布直方图 Fig. 7 Histogram of pressure deviation distribution after identification |
本文针对某型固体火箭发动机改性双基推进剂静态燃速和动态燃速存在差异的情况,较为全面分析了影响推进剂燃速的主要因素,提出基于最小二乘法固体推进剂的动态燃速辨识方法。通过分析,得到如下结论:
1)改性双基推进剂出厂的
2)基于最小二乘法辨识出的固体火箭发动机装药燃速为动态燃速,利用该燃速可有效提高理论计算模型的预示精度;
3)根据多批装药动态燃速辨识结果可知,本文提出的动态燃速辨识方法具有较强的准确性和工程应用价值。
| [1] |
李葆首. 固体推进剂性能[M]. 西安: 西北工业大学出版社. 1990, 12.
|
| [2] |
中国国家军用标准GJB770B-2005: 火炸药实验方法: 燃速测试方法706.1靶线法和706.2水下声发射法[S].
|
| [3] |
裴庆, 赵凤起, 等. 固体推进剂燃速测试技术研究进展[J]. 火炸药学报, 2015, 38(3): 9-14. PEI Qing, ZHAO Fengqi, et al. Research progress in the burning rate measurement technology of solid propellant[J]. Chinese Journal of Explosives & Propellants, 2015, 38(3): 9-14. |
| [4] |
武晓松, 陈军, 等. 固体火箭发动机原理[M]. 北京: 兵器工业出版社, 2011.
|
| [5] |
马凯歌. 固体推进剂准动态燃速测试方法研究[D]. 西安: 西安电子科技大学, 2012. MA Kaige. Research on Test Method for Quasi-dynamic Burning Rate of Solid Propellant[D], Xi An: Xi Dian University, 2012. |
| [6] |
唐金兰, 刘佩进. 固体火箭发动机原理[M]. 北京: 国防工业出版社, 2013.
|
| [7] |
李咸海, 王俊杰. 潜地导弹发射动力系统[M]. 哈尔滨: 哈尔滨工程大学出版社, 2000.
|
| [8] |
贾小勇, 徐传胜, 白欣. 最小二乘法的创立及其思想方法[J]. 西北大学学报(自然科学版), 2006(3): 507-511. JIA Xiaoyong, XU Chuansheng, BAI Xin. The invention and way of thinking on least squares[J]. Journal of Northwest University (Natural Science Edition), 2006(3): 507-511. DOI:10.3321/j.issn:1000-274X.2006.03.040 |
 2020, Vol. 42
2020, Vol. 42
