0 引　言

虽然卫星通信是陆地对远洋船舶通信中的主要手段，但由于海上降雨频繁，Ka、Ku等卫星通信的高频段信号波长与雨滴直径较为接近，雨水会对信号造成严重衰减^[1]。因此，需要另外一种可靠的通信方式作为恶劣天气条件下卫星通信失效时的备用手段。能够实现陆地对远洋船舶通信的另一方式就是利用超低频频段信号进行通信。虽然超低频通信的信息传输速率较低，但其信号稳定，传播距离远，为陆地对远洋船舶传递导航信息、指令信息提供了可能。

但是，使用该频段信号通信的最大问题是环境的干扰噪声很大。由于船体中电缆网络布线复杂，用电设备拥挤集中，信道中存在大量的工频、射频以及雷电脉冲干扰^[2]，这些干扰通过天线主瓣和副瓣方向进入接收机后，严重影响了目标信号的接收。同时，由于发射接收天线的体积受限，天线的增益也较低，所以信号的能量受限。因此，如何对干扰进行有效地抵消，是超低频远洋通信成功的关键。

常用的削弱干扰影响的技术手段主要有滤波法，它可以有效地滤除带外噪声，但是对带内的噪声是无效的。对于工频和射频这类固定频率的干扰，可以使用基于经验小波变换的电力线干扰抑制技术来克服^[3-4]，但其算法复杂，特别是小波基的选取较为困难，往往依据经验而定。相对简单地，可以在硬件电路上使用指定频率陷波器来除去固定频率的噪声^[5]，但是干扰信号频率的偏移易使抑制效果下降。为此，有学者提出利用特征子空间投影法（Eigen-subspace Projection，ESP）进行空间滤波^[6-8]，通过分离信号与干扰的子空间的方法能够对强干扰信号形成较好的抑制效果。

本文根据ESP算法的特点，提出一种主天线与参考天线正交布设的多通道接收模型，并提出了一种基于传统ESP算法的改进方法来抑制带内干扰。传统的ESP算法直接利用参考天线估计干扰子空间，这对于估计一些在参考天线上投影分量较小的干扰是不准确的。改进后的算法结合了阻塞信号的思想，它能够最大程度地消除主天线信号中的期望信号，保留主天线之间具有强相干性的干扰^[9]，并用这部分信号来优化对干扰子空间的估计，使得算法对干扰有更强的抑制效果。

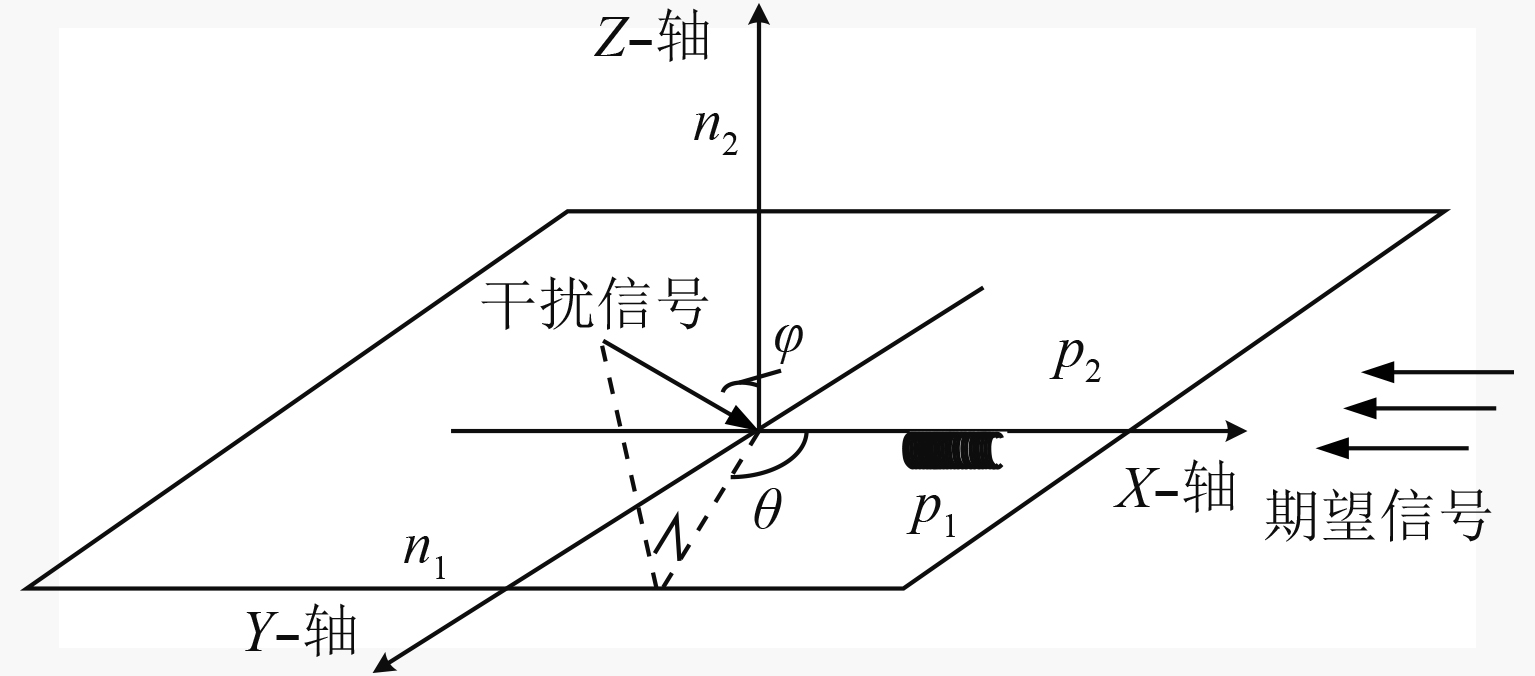
1 天线与信号模型 1.1 天线建模

本文提出一种新形式的接收天线布设方法。如图1所示，主接收天线p₁，p₂与参考天线n₁，n₂在空间中正交放置。由于采用的是磁性天线，其增益在磁芯方向最大，正交于磁芯方向最小。因此，当主天线磁芯对准陆地发射天线来波方向时，参考天线中期望信号的成分最少。n₁，n₂两根参考天线理论上能接收到除了主天线方向以外空间中的所有干扰信号。同时，该模型设计了p₁，p₂两根主天线，因为主天线方向的一些干扰信息可以通过对两根主天线信号进行阻塞处理的方法获得，联合参考天线信号估算干扰子空间可以使结果更准确。

1.2 信号建模

在接收模型中，某根主天线在某一时刻接收到信号可表示为：

$ \begin{split} {x_p}\left( n \right) = & s\left( n \right)\; + \;\sum\limits_{j = 1}^K {{P_X}\left( {{\theta _{{w_j}}}} \right){w_j}\left( n \right)} + \sum\limits_{k = 1}^L {P\left( {{\theta _{{r_k}}}} \right){r_k}\left( n \right)} +\\ & {n_\alpha }{\kern 1pt} {\kern 1pt} \left( n \right) + {n_i}\left( n \right) {\text{。}} \end{split} $

(1)

其中：

$ \begin{split} & {P_X}\left( {{\theta _{{w_j}}}} \right) = \cos {\theta _{{w_j}}} {\text{，}} \\ & {P_X}\left( {{\theta _{{r_k}}}} \right) = \cos {\theta _{{r_k}}} {\text{。}} \end{split} $

(2)

式中： $\left( {\varphi ,\theta } \right){\kern 1pt} $ 为某一干扰信号与期望信号的极坐标角度关系； ${P_X}\left( \cdot \right)$ 为投影运算符号，表示信号向X轴方向上投影； $s\left( n \right){\kern 1pt} $ 为期望信号； ${w_j}\left( n \right){\kern 1pt} $ 为第 $j{\kern 1pt} $ 个工频干扰； ${r_k}\left( n \right){\kern 1pt} $ 为第 $k{\kern 1pt} $ 个射频干扰； ${n_\alpha }\left( n \right){\kern 1pt} $ 为大气噪声； ${n_i}\left( n \right){\kern 1pt} $ 为背景噪声。

在超低频频段，人造干扰是噪声的主要成分^[10]，其主要表现为船舶上的电力线干扰和电机工作产生的干扰。电力线干扰主要表现为50 Hz的单音信号以及奇次谐波干扰，其幅度可高于底噪几十分贝。在通信时选择合适的通信频率即可直接避开电力线干扰，但其造成的杂散干扰依然可能对通信产生影响。大气噪声的主要成分是雷电噪声，其在时域中的表现形式一般是突发的脉冲信号，电机在工作时也可能会产生类似的干扰噪声，它们都会提高频带内的噪声底限，从而降低期望信号的信噪比，射频干扰可能源于某一电机或是其他通信用户。因为超低频频段信道可用带宽小，仅靠避开存在干扰的频段很难保证持续地大容量的通信，所以在通信时这部分干扰必须被有效抑制。

由于参考天线与主天线结构相同，且接收到的信号几乎不包含目标成分，则Y轴方向的参考天线在某一时刻收到的信号可以近似地表示为：

$ \begin{split} & {x_{ref}}\left( {n - \tau } \right) = \sum\limits_{j = 1}^k {{P_Y}\left( {{\varphi _{{w_j}}},{\theta _{{w_j}}}} \right){w_j}\left( {n - \tau } \right)} + {n_i}\left( {n - \tau } \right) +\\ &\;\sum\limits_{j = 1}^L {{P_Y}\left( {{\varphi _{{r_k}}},{\theta _{{r_k}}}} \right){r_j}\left( {n - \tau } \right)} + {n_\alpha }{\kern 1pt} \left( {n - \tau } \right){\text{。}} \end{split} $

(3)

其中：

$ \begin{array}{l} {P_Y}\left( {{\varphi _{{w_j}}},{\theta _{{w_j}}}} \right) = \sin {\theta _{{w_j}}}\sin {\varphi _{{w_j}}} {\text{，}} \\ {P_Y}\left( {{\varphi _{{r_k}}},{\theta _{{r_k}}}} \right) = \sin {\theta _{{r_k}}}\sin {\varphi _{{r_k}}} {\text{。}} \end{array} $

(4)

式中： $\tau {\kern 1pt} $ 为到达参考天线的时延。但由于超低频电磁波信号的波长可达100至1 000万千米，远大于磁性天线的间距，所以 $\tau {\kern 1pt} $ 可以近似地被忽略，得到。

$ {x_{ref}}\left( {t - \tau } \right) \approx {x_{ref}}\left( t \right){\text{。}} $

(5)

2 干扰抵消算法 2.1 传统的ESP算法

特征子空间投影算法通过子空间的分解与投影来消除目标信号中的干扰噪声，其基本思想已经出现在各类学科应用当中，如雷达干扰抵消器^[4]，面部特征检测^[6]等。算法流程如下：

假设共有 $M$ 根天线，其中有 $K$ 根主天线， $M - K$ 根参考天线，则天线阵列信号为：

$ {{X}} = {\left[ {{{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_M}} \right]^{\rm T}} {\text{。}} $

(6)

其中，主天线阵列信号为 ${{{X}}_p} = {\left[ {{{{x}}_1},{{{x}}_2}, \cdots ,{{{x}}_K}} \right]^{\rm T}}{\kern 1pt} $ ，参考天线信号为 ${{{X}}_r} = {\left[ {{{{x}}_{K + 1}},{{{x}}_{K + 1}}, \cdots ,{{{x}}_M}} \right]^{\rm T}}{\kern 1pt} $ 。设第 $i$ 根参考天线在某时刻 $t$ 以及前 $M$ 个时刻采样所获得的数据构成矢量为：

$ {{{x}}_{ref,i}} = {\left[ {{x_{ref,\;i}}{{\left( t \right)}_{\kern 1pt} },{x_{{\kern 1pt} ref,\;i}}\left( {t - 1} \right), \cdots ,{x_{ref,\;i}}\left( {t - M} \right)} \right]^{\;\rm T}}{\kern 1pt} {\text{。}} $

(7)

首先，构建接收信号的协方差矩阵：

$ {\hat R_{ref}} = \;\frac{1}{{{N_{ref}}}}\;\sum\limits_{i{\kern 1pt} = {\kern 1pt} 1}^{{N_{ref}}} {{{{x}}_{ref,\;i}}} {\kern 1pt} {{{x}}_{ref,\;i}}^{\rm H}\;{\text{。}} $

(8)

对 ${{\hat { R}}_{\;ref}}{\kern 1pt} $ 进行特征分解（Eigenvalue decomposition，EVD），得到特征值 $\lambda {{\kern 1pt} _1}{\kern 1pt} ,\;\lambda {{\kern 1pt} _2}{\kern 1pt} ,{\kern 1pt} \; \cdots \;,\;\lambda {{\kern 1pt} _M}{\kern 1pt} $ 以及与特征值相对应的特征向量 ${V_1}{\kern 1pt} ,\;{V_2}{\kern 1pt} ,{\kern 1pt} \; \cdots \;,\;{V_M}$ 。其中会有几个明显较大的特征值对应于空间中的强干扰，取这些特征值所对应的特征向量构成干扰子空间 ${{S}}{\kern 1pt} $ ，余下的 $M - r{\kern 1pt} $ 个特征向量构成信号和噪声子空间 ${{G}}{\kern 1pt} $ 。最后，只要取一路信干噪比最大的主信号投影到信号和噪声子空间 ${{G}}{\kern 1pt} $ 上，即可得到剔除干扰后的序列为：

$ {{{y}}_{out}} = {{{x}}_p} - {{S}}{{{S}}^H}{{{x}}_p}{\rm{ = }}\left( {{{I}} - {\hat { S}}{{{\hat { S}}}^H}} \right){{{x}}_p}{\rm{ = }}{{{P}}_S}{{{x}}_p}{\text{。}} $

(9)

式中 ${{{P}}_S}{\kern 1pt} $ 即为对噪声子空间投影的投影算子。

可见，利用ESP算法虽然能抵消干扰，但在实际过程当中，可能会出现干扰与目标信号夹角较小的情况，此时只使用参考天线信号求得的投影算子对这部分干扰的抑制效果不佳。因此，提出一种改进的ESP算法。

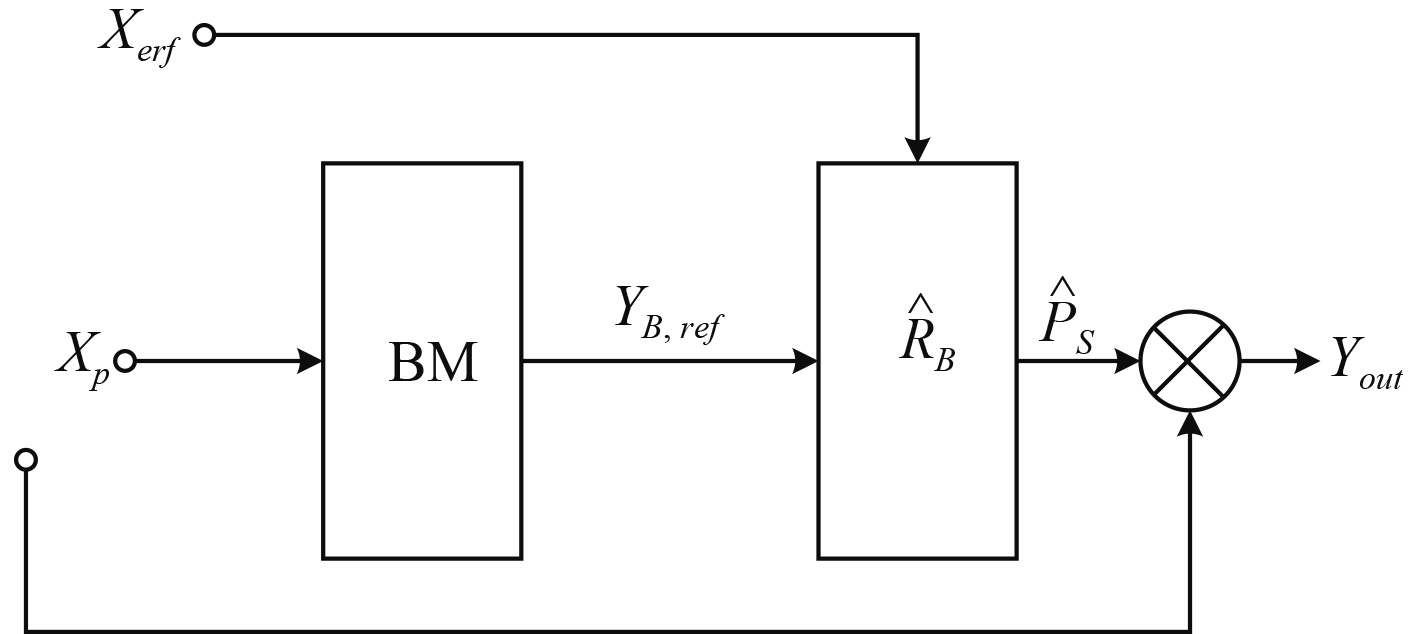
2.2 改进的ESP算法

改进后的算法原理框图如图2所示。该算法结合了阻塞信号的方法对干扰子空间进行联合优化估计，因此将该方法称为B-ESP方法。算法主要分为两部分。

2.2.1 系数约束自适应的阻塞矩阵

因为超低频电磁波在自由空间中的衰减约为1 dB每兆米^[11]，所以每一路天线中的期望信号可以被视为完全相同。设共有 $N$ 根磁性天线，一次处理的数据点数为 $M{\kern 1pt} $ ，则阵列天线的输入信号 ${{X}}{\kern 1pt} $ 是一个 $N \times M{\kern 1pt} $ 维矩阵， ${{b}}_i^{\rm T}{\kern 1pt} $ 代表一般的阻塞矩阵 ${{{B}}^{\rm T}}$ 的第i行，当所有的i都满足：

$ {{b}}_i^{\rm T} \cdot {{1}} = 0{\text{，}} $

(10)

且 ${{b}}_i^{\rm T}$ 之间线性无关时，经过阻塞处理后的信号

$ {{{Y}}_b} = {{{B}}^{\rm T}}{{X}} {\text{，}} $

(11)

是一个 $(N - 1) \times M{\kern 1pt} $ 维矩阵，且其中包含的期望信号的成分被完全抵消。但实际上，使用式（10）提出的阻塞矩阵会造成期望信号的泄漏，继而在后续步骤中造成对干扰空间的错误估计，影响干扰抵消结果。

在实验中发现，即便是在间隔1 m内的2根天线，收到的信号依然存在不能忽略的能量偏差。分析其原因，一是因为2根主天线难以做到严格的平行，因此期望信号落在主天线上的投影分量不尽相同。另外，每一路天线的电感以及运放电路的增益也难以做到完全相同，这也导致了采集到的各路信号的能量存在差异。为此，本文对原阻塞矩阵进行了改进。设初始矩阵

$ {{B}} = \left[ {\begin{array}{*{20}{c}} 1&{ - 1}&0& \cdots &0 \\ 0&1&{ - 1}& \ddots &0 \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0& \cdots &0&1&{ - 1} \end{array}} \right] {\text{，}} $

(12)

是一个 $\left( {K - 1} \right) \times N{\kern 1pt} $ 维的矩阵，它的作用是使相邻的两路输入信号在时域中互相抵消期望信号成分，并合成一路输出。改进后的阻塞矩阵为：

$ {{{B}}_M} = \left[ {\begin{array}{*{20}{c}} 1&{{\alpha _1}}&0& \cdots &0 \\ 0&1&{{\alpha _2}}& \ddots &0 \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0& \cdots &0&1&{{\alpha _{K - 1}}} \end{array}} \right] {\text{。}} $

(13)

设 ${{{b}}_i}$ 代表阻塞矩阵 ${B_M}$ 的第i行，则对于 $\alpha $ 的问题求解被描述如下：

$ \left\{ \begin{array}{l} \min {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} SIN{R_F}\left( {{{{b}}_i}{{{X}}_p},f} \right) {\text{，}} \\ {\rm s.t.}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\xi _d} < {\alpha _i} < {\xi _t} {\text{。}} \end{array} \right. $

(14)

其中：

$ SIN{R_F}\left( {{{x}},f} \right) = 10\lg \frac{{{P_s}}}{{{P_n}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\rm dB} \right) {\text{。}} $

(15)

式中： ${P_s}{\kern 1pt} $ 为期望信号的功率； ${P_n}{\kern 1pt} $ 为频率 $f{\kern 1pt} $ 处带宽 $B{\kern 1pt} $ 范围内干扰噪声的平均功率。 ${\xi _d}{\kern 1pt} $ 和 ${\xi _t}{\kern 1pt} $ 被用于限制 $\alpha {\kern 1pt} $ 的范围。因为天线在被制作时已经尽量保证了它们的一致性，所以 $\alpha {\kern 1pt} $ 的调整范围是微小的。因此，控制 $\alpha {\kern 1pt} $ 的范围有利于更快地获得最优解。得到的结果

$ {{{Y}}_{B,ref}} = {{{B}}_M}^{\rm T}{{{X}}_p} {\text{，}} $

(16)

作为辅助估计干扰子空间的参考信号被输入到下一级中。

2.2.2 联合优化估计干扰子空间

利用改进的阻塞矩阵输出的信号作为一路参考信号，结合参考天线的信号联合估计干扰子空间，将式(8)修正为：

$ {{\hat { R'}}_{ref}} = \frac{1}{{M - K + 1}}\left( {\sum\limits_{i = 1}^{{N_{ref}}} {{{{x}}_{ref,\;i}}} {\kern 1pt} {{{x}}_{ref,\;i}}^H + {{{Y}}_{B,ref}}{{{Y}}_{B,ref}}^{\rm H}} \right){\text{。}} $

(17)

${{\hat { R'}}_{ref}}{\kern 1pt} $ 是优化估计后的协方差矩阵。按照ESP算法，进行EVD即可求得新的干扰子空间。

最后，总结出B-ESP算法具体步骤如下：

步骤1　利用系数约束自适应阻塞矩阵处理主天线信号，得到阻塞后的输出信号 ${{{Y}}_{B,ref}}{\kern 1pt} $ ；

步骤2　将 ${{{Y}}_{B,ref}}{\kern 1pt} $ 与参考天线阵列信号 ${{{X}}_r}{\kern 1pt} $ 组成新的参考信号阵列，求得优化估计后的协方差矩阵 ${{\hat { R'}}_{ref}}{\kern 1pt} $ ；

步骤3　对 ${{\hat { R}}'_{ref}}{\kern 1pt} $ 做EVD处理，求解干扰子空间，得到新的投影算子 ${{{P}}'_S}$ ；

步骤4　取一路信干噪比最大的主信号进行投影即可得到结果 ${{{y}}_{out}} = {{{P}}_S}{{{x}}_p}{\kern 1pt} $ 。

3 仿真及实测结果验证

为验证算法有效性，本文分别用模拟和实测的数据算法的效果进行了验证。

3.1 仿真

使用数学计算软件Matlab，按照1.1节提出的信号与天线模型对算法进行仿真验证。假设期望信号 $s(t){\kern 1pt} $ 是130 Hz的单音信号；工频干扰为50 Hz和150 Hz的单音信号；射频干扰为载频132 Hz的最小频移键控（Minimum shift keying，MSK）调制信号，其频谱展宽可将期望信号完全淹没；大气噪声 ${n_\alpha }{\kern 1pt} {\kern 1pt} \left( t \right){\kern 1pt} $ 和背景噪声 ${n_i}{\kern 1pt} {\kern 1pt} \left( t \right){\kern 1pt} $ 设置为高斯白噪声。这里只研究一个干扰在不同入射角度情况下算法的表现效果，因此设置除了MSK信号以外的所有干扰信号的 $\varphi {\kern 1pt} $ 和 $\theta {\kern 1pt} $ 都为45°，采样频率为 ${f_c} = 1\;000\;{\rm Hz}{\kern 1pt} $ 。

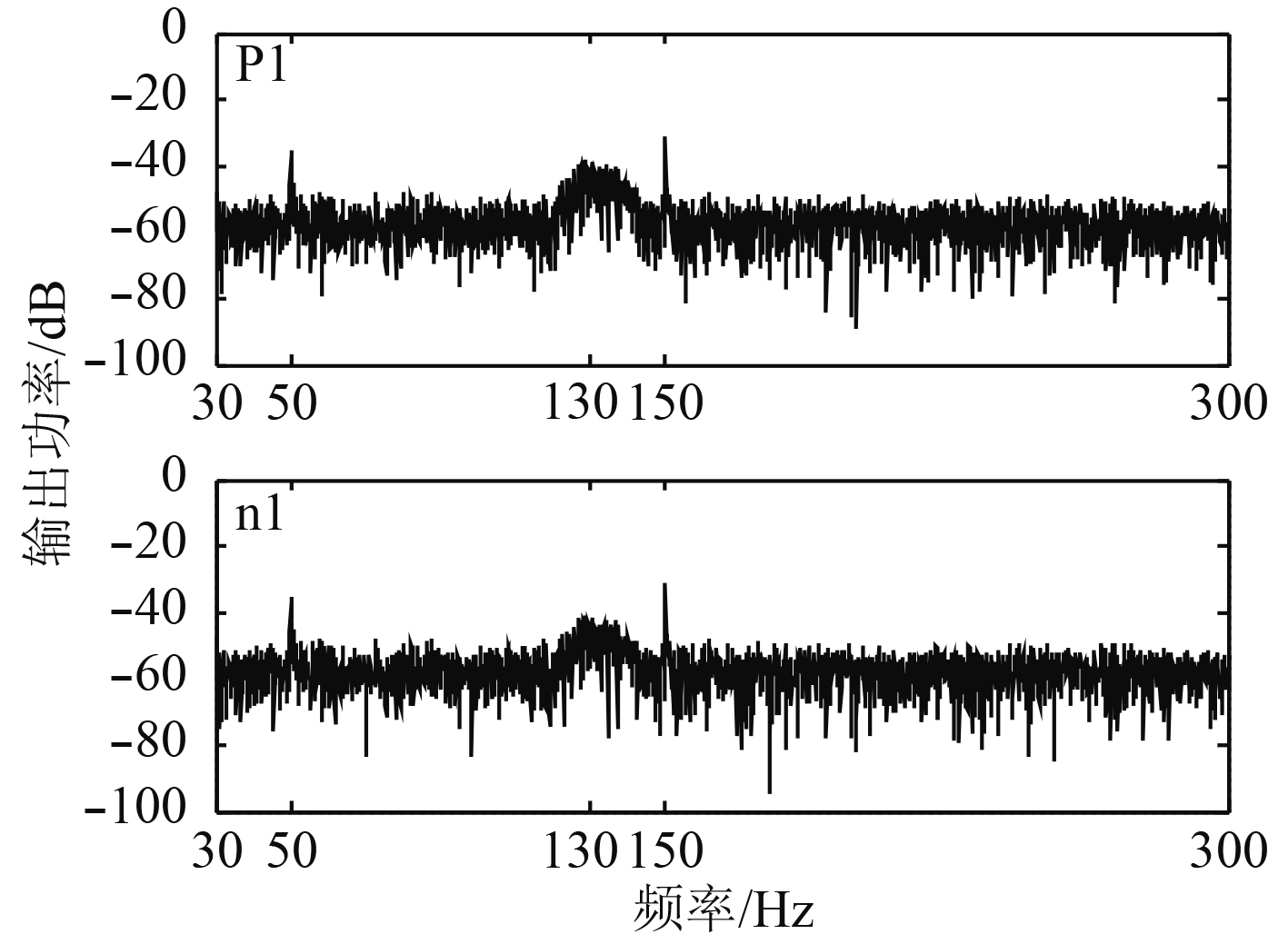
图3为主天线n₁和参考天线p₁接收到的信号的功率谱。可以看到，期望信号在功率谱中被MSK信号完全淹没。

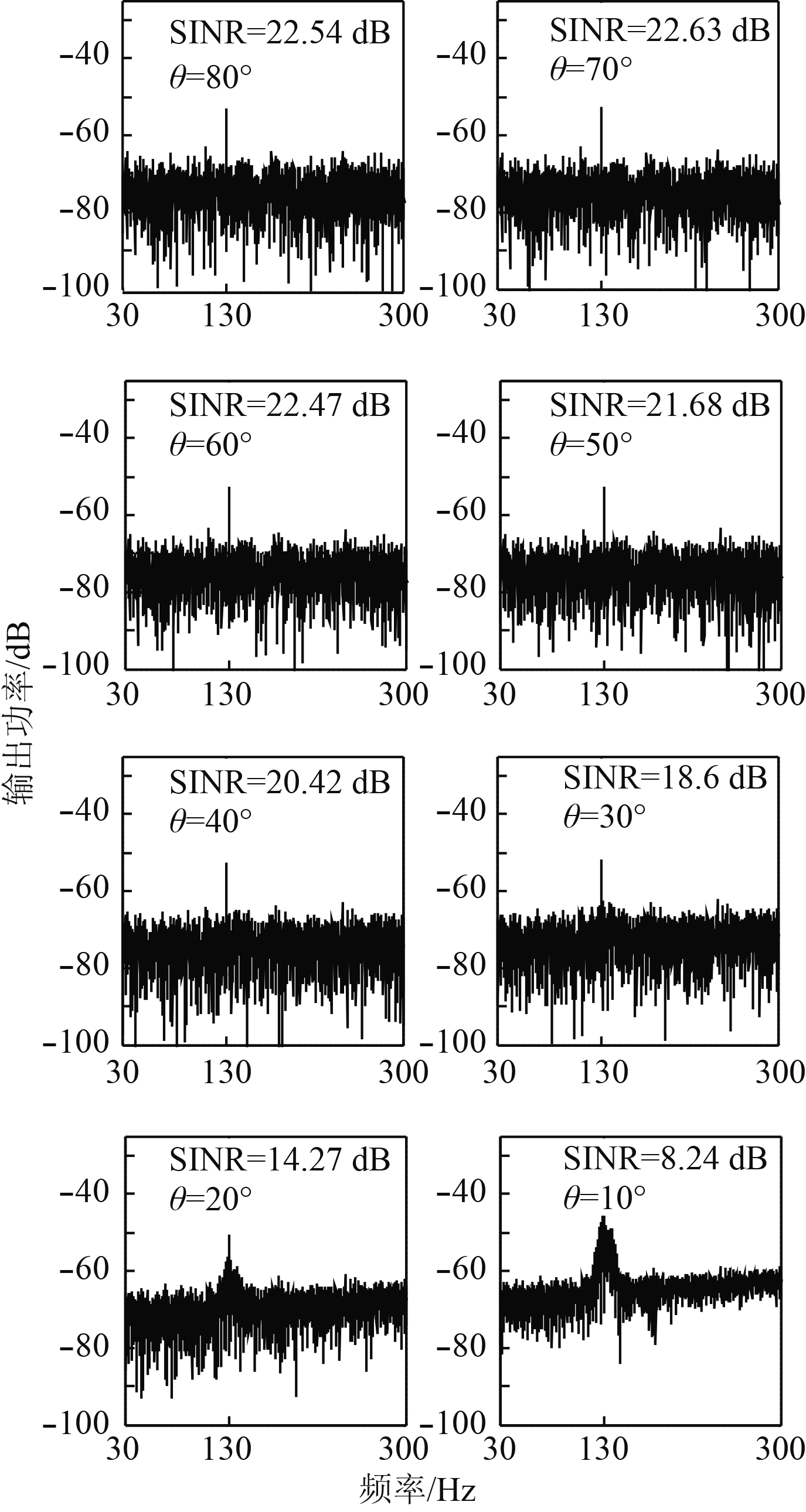
采用传统的ESP方法处理不同入射角度的干扰信号。设 $\varphi {\kern 1pt} $ 为45°不变， $\theta {\kern 1pt} $ 从80°～10°递减，共进行8次仿真，结果如图4所示。可以看到，在 $\theta {\kern 1pt} $ 的角度较大时， $\theta {\kern 1pt} $ 的改变并不会明显地影响算法的效果。但是，在 $\theta < 40^\circ {\kern 1pt} $ 以后，随着干扰与主天线的夹角 $\theta {\kern 1pt} $ 逐渐减小，传统的ESP算法的性能表现开始有明显下降。当 $\theta = 10^\circ {\kern 1pt} $ 时，ESP算法以几乎没有效果。此种情况下，用提出的B-ESP算法处理信号，得到的结果如图5所示。

图5（b）是图5（a）的局部放大图。可以明显看到，颜色最深的实线所代表的B-ESP算法有效地抵消了MSK信号形成的干扰，130 Hz的期望信号被成功恢复，且相比于ESP算法的输出结果信干比提升了13.28 dB。因此，仿真实验证明，所提出的算法与理论情况相符。

3.2 实验

为进一步验证提出算法的效果，本文采用图6所示的天线结构。

在3.1中设置的实验条件下采集数据并处理。2种算法在不同干扰角度的情况下的输出结果的性能被记录在表1中。

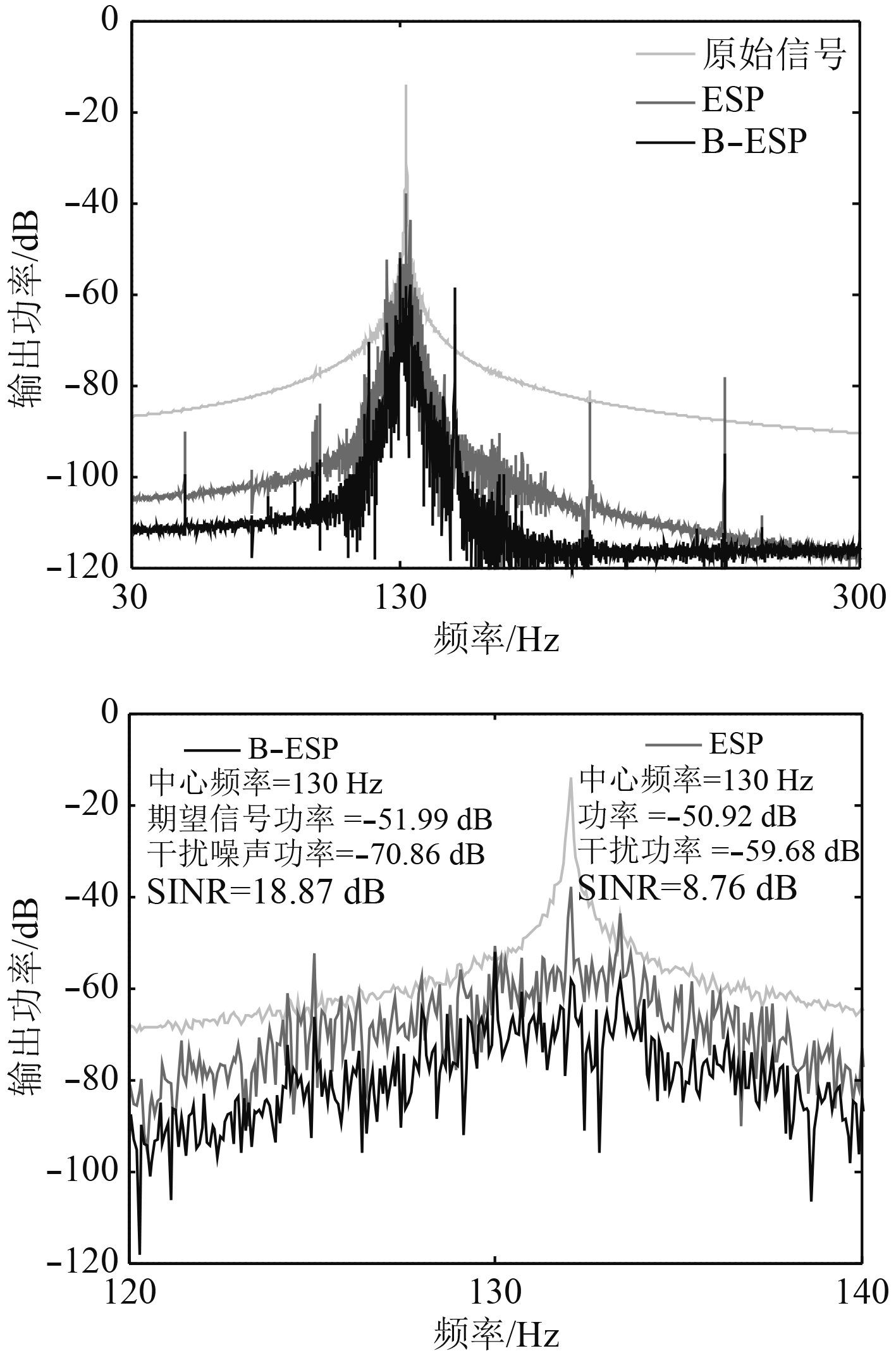
可以看到，2种算法对干扰干扰都具有抑制效果，但是本文提出的B-ESP算法对干扰的抑制效果明显好于传统的ESP算法，特别是在干扰与主天线的夹角较小的情况下。并且，B-ESP算法的输出结果随着 $\theta {\kern 1pt} $ 的变化不显著，说明其具有较好的鲁棒性。在 $\theta = 15^\circ {\kern 1pt} $ 时，改进的算法的输出结果相比于传统算法，信干比提升了10.11 dB，输出结果如图7所示。其性能参数也被标注在了图上。可见，B-ESP算法比ESP算法抵消了更多的干扰，对于信号的改善更明显。

4 结　语

本文描述了超低频通信时存在的问题，提出了使用多天线阵列结合ESP算法解决此问题。首先对天线阵列和其接收信号进行了仿真建模，简单介绍了ESP算法并对其提出了改进。提出的B-ESP算法结合了系数约束自适应阻塞矩阵，提取了主天线上抑制干扰的有用信息，联合参考天线信号优化了对干扰子空间的估计。仿真和实验结果表明，改进后的算法相比于传统算法，能够在干扰与主天线角度较小的情况下抵消更多的干扰，同时更具有鲁棒性，具有较好的实践应用价值。本文存在的主要问题是未在更复杂的干扰环境下对改进后的算法进行实验验证，下一步将对此提出改进。