光纤水听器的研究始于20世纪70年代末[1]。目前备受关注的是干涉型光纤水听器,在对干涉型光纤水听器的信号解调技术的研究中,被动零差检测方式更适于大规模水听器阵列,其主要包括2种方法,一种是相位载波生成法(PGC),其动态范围较小。另外一种方法是Koo K P提出的3×3耦合器法[2],相比于PGC法,3×3耦合器法不需要引入载波且动态范围更大,因此,受到了国内外众多学者的广泛关注。Sheem S K以3×3耦合器作为干涉仪输出端提高了灵敏度[3]。Todd M D提出并改进了反正切方法,消除了耦合器不理想特性对解调结果的影响[4]。何俊理论分析并实验计算出了3×3耦合器的3路输出信号相位差[5]。张晓峻对微分交叉相乘(DCM)解调方法进行了仿真分析[6]。毛欣对基于3×3耦合器解调方法的分析结果表明,DCM法动态范围大于反正切法[7]。宋美杰针对3×3耦合器法干涉仪的偏振态调节的不足,借鉴相位载波生成法的经验,提出了一种新的解调算法[8]。可以看出,3×3耦合器解调方法是目前学者们的研究热点,但是对于3×3耦合器反正切解调方法中耦合器相位差特性偏差对解调效果的影响,以及对于不同类型信号的解调效果的研究,还有待补充。
本文介绍了基于不理想3×3耦合器的两路输出信号进行解调的方法,推导出了解调算法的输出信号表达式,利用Simulink建立了基于此种方法的解调系统模型。首先仿真分析了反正切相位扩展效果和耦合器相位差特性偏差对解调的影响,然后仿真分析了该方法对单频、线性调频信号的解调效果。最后,搭建了一个基于此算法的干涉型光纤水听器解调系统进行实验验证。解调结果表明,基于该解调算法的干涉型光纤水听器解调系统解调效果稳定可靠,能基本满足光纤水听器实际应用要求。
1 基于3×3耦合器的反正切解调原理3×3耦合器具有独特的光学特性,理想情况下,基于3×3耦合器的迈克尔逊干涉仪各路输出信号的相位差刚好为120°,在实际情况下,3×3光纤耦合器相位差特性不理想,故不能严格保证为120°,其误差越大,解调结果中的谐波分量越高,失真越严重。
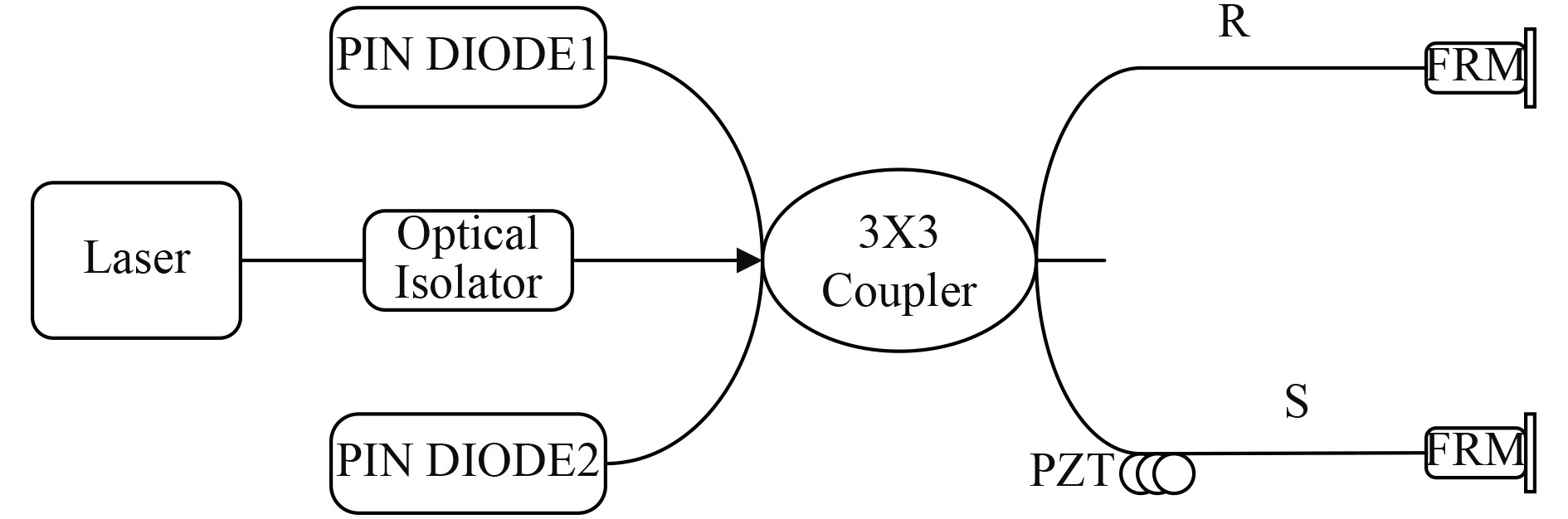
图1中Laser表示激光源,Optical Isolator表示光隔离器,PIN Diode表示光电转换模块,FRM表示法拉第旋转镜,PZT表示压电陶瓷传感器,R,S分别表示参考光纤、传感光纤,其中传感光纤绕在PZT上,用特定电信号调制PZT来模拟声信号。如图1所示,2个光电二极管接收到的信号可表示为:
|
图 1 基于3×3耦合器的迈克尔逊干涉仪结构 Fig. 1 Michelson interferometer structure based on 3×3 coupler |
| $ {V_1}\left( t \right) = {A_1} + {B_1}\cos \left[ {\varphi \left( t \right) - \alpha } \right] {\text{,}} $ | (1) |
| $ {V_2}\left( t \right) = {A_2} + {B_2}\cos \left[ {\varphi \left( t \right) + \alpha } \right] {\text{。}} $ | (2) |
其中:
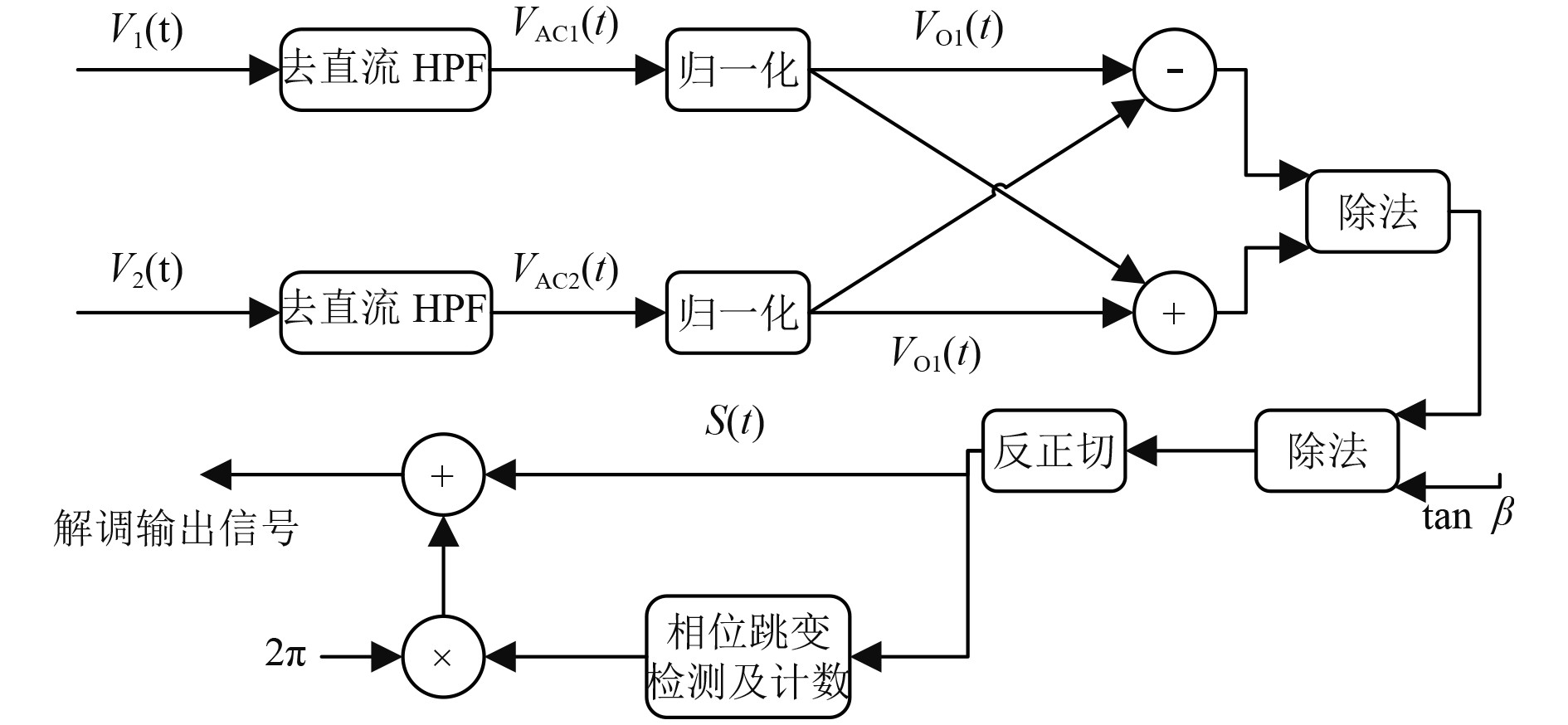
如图2所示,两路信号再经过去直流高通滤波器后可表示为:
|
图 2 基于3×3耦合器的解调方法 Fig. 2 Demodulation method based on 3×3 coupler |
| $ {V_{AC1}}\left( t \right) = {B_1}\cos \left[ {\varphi \left( t \right) - \alpha } \right] {\text{,}}$ | (3) |
| $ {V_{AC2}}\left( t \right) = {B_2}\cos \left[ {\varphi \left( t \right) + \alpha } \right] {\text{。}} $ | (4) |
根据式(3)和式(4)的结果分别计算出这两路信号的幅度,并做如下归一化处理:
| $ {V_{O1}}\left( t \right) = {{{V_{AC1}}\left( t \right)}/{{B_1}}} = \cos \left[ {\varphi \left( t \right) - \alpha } \right] {\text{,}} $ | (5) |
| $ {V_{O2}}\left( t \right) = {{{V_{AC2}}\left( t \right)}/{{B_2}}} = \cos \left[ {\varphi \left( t \right) + \alpha } \right] {\text{。}} $ | (6) |
对上述两式进行相减和相加运算可得到:
| $ {V_{O1}}\left( t \right) - {V_{O2}}\left( t \right) = 2\sin \left[ {\varphi \left( t \right)} \right]\sin \alpha {\text{,}} $ | (7) |
| $ {V_{O1}}\left( t \right) + {V_{O2}}\left( t \right) = 2\cos \left[ {\varphi \left( t \right)} \right]\cos \alpha {\text{。}} $ | (8) |
将式(7)和式(8)相除,可以得到如下结果:
| $ \frac{{{V_{O1}}\left( t \right) - {V_{O2}}\left( t \right)}}{{{V_{O1}}\left( t \right) + {V_{O2}}\left( t \right)}} = \tan \left[ {\varphi \left( t \right)} \right] \cdot \tan \alpha {\text{。}} $ | (9) |
在实际应用中,干涉仪输出信号的相位差特性不理想,并不是理想的120°,这种偏差将会降低解调算法的可解调动态范围,为了降低这种偏差造成的影响,可以对式(9)做如下处理:
| $ S(t) = \arctan \left[ {\tan \varphi \left( t \right) \cdot \tan \alpha /\tan \beta } \right] {\text{。}} $ | (10) |
其中,
另外,当
| $\Delta \varphi = \varphi (k) - \varphi (k - 1) {\text{。}} $ | (11) |
其中,
本文利用Simulink建立了基于3×3耦合器的两路输出信号进行解调的仿真模型。为观察反正切输出结果与相位扩展效果,设定

|
图 3 相位扩展 Fig. 3 Phase extension |
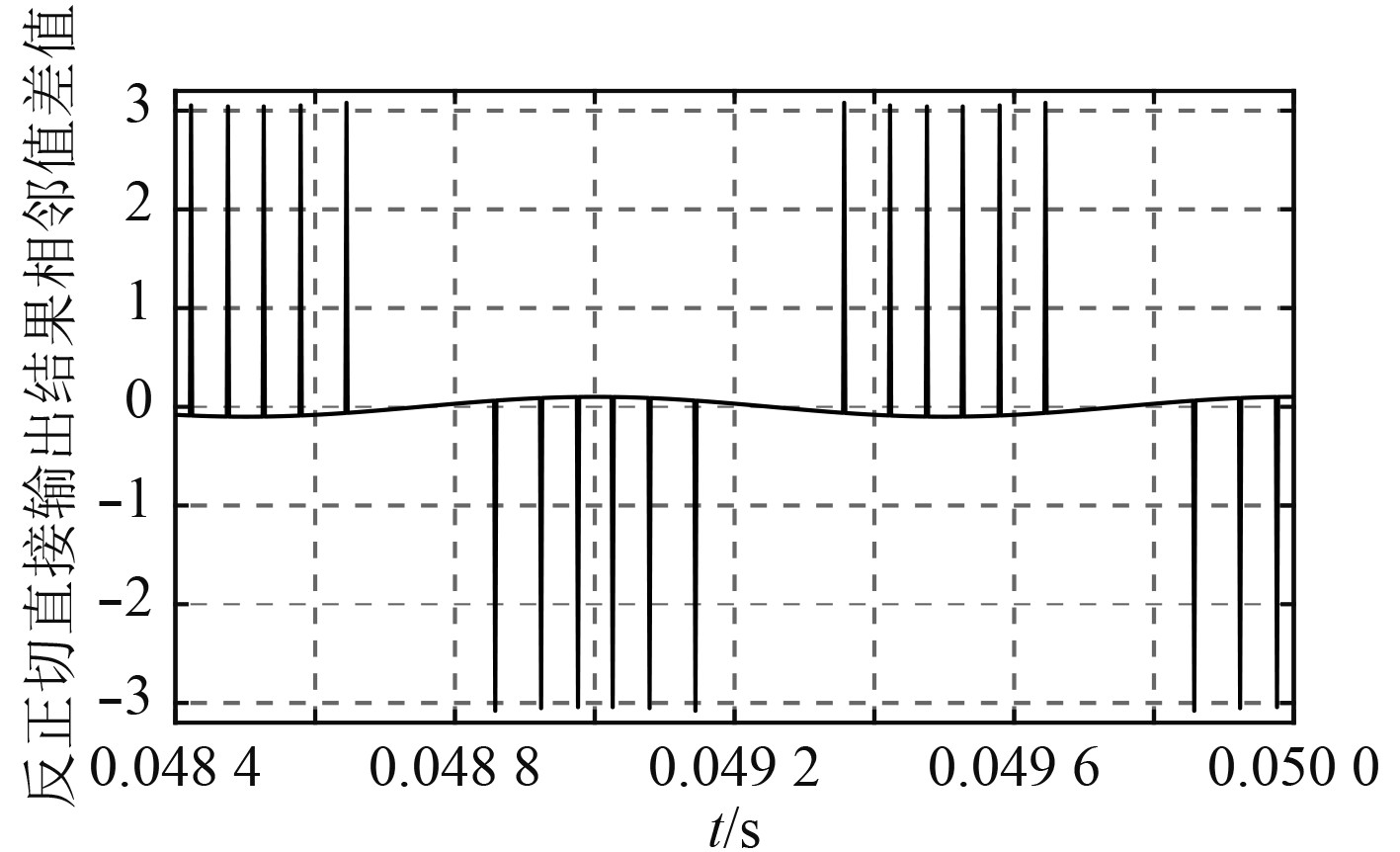
|
图 4 相邻差值 Fig. 4 The difference between adjacent results |
如图3所示,反正切直接输出结果值域为

|
图 5 解调信号的时域图和频谱图 Fig. 5 Waveform and spectrum diagram of demodulation signal |
理想的3×3耦合器的输出信号具有120°的相位差特性,根据文献[5]可知,实际情况下,3×3耦合器的输出信号相位差与理想值之差在1°以内,本文对
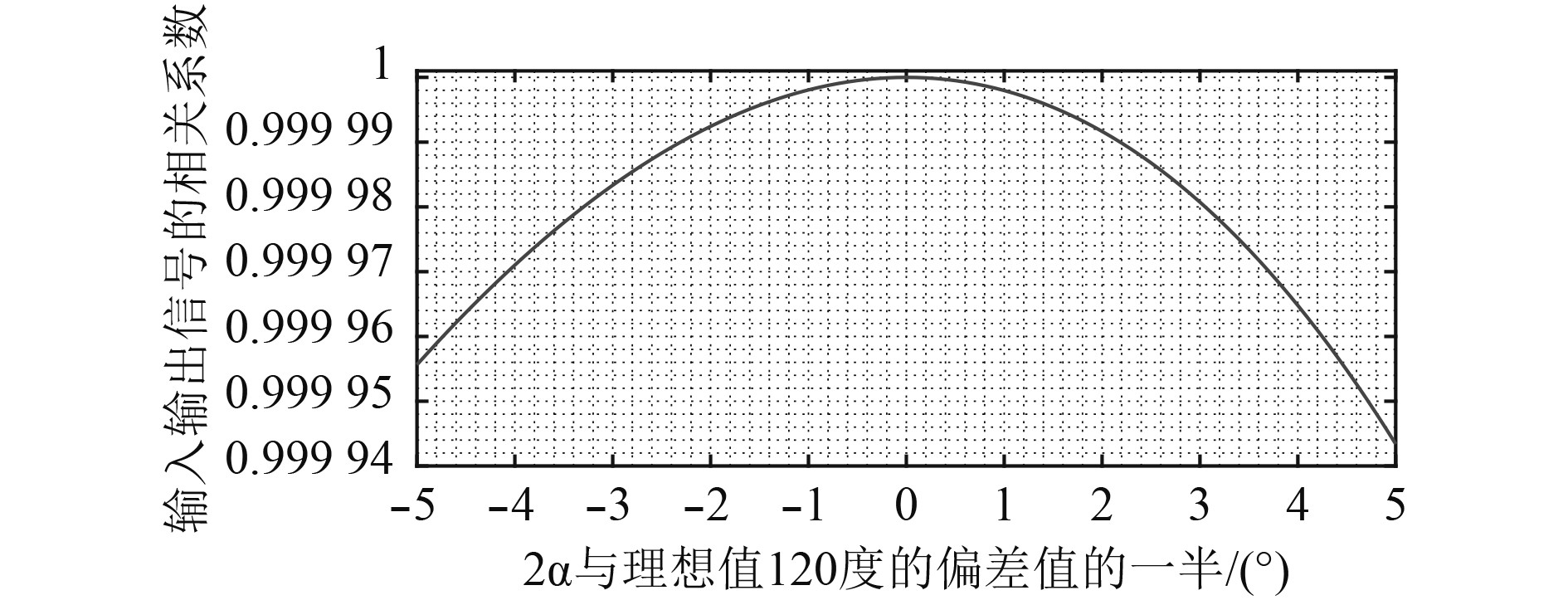
|
图 6 相关系数与偏差值的关系 Fig. 6 The relationship between correlation coefficient and deviation value |
当3×3耦合器的输出信号之间的相位差与120°的偏差在10°以内时,采用本文所用解调方法得到的输出信号与输入信号的相关系数在0.999 94~1之间,这说明在这样的偏差情况下,解调结果未失真,证明本解调算法能够消除3×3耦合器的输出相位差偏差带来的影响。
2.3 对单频信号的解调 2.3.1 不同幅度下的解调效果干涉仪输出信号是一种调频信号,根据卡森估算公式,可知,输出信号的有效频谱宽度为:
| $ B{\rm{ = }}2(D + 1){f_s} {\text{。}} $ | (12) |
根据式(12)和奈奎斯特定理,为了解调信号不失真,模数转换器的采样率应该满足如下条件:
| $ {f_{sam}} > 4(D + 1){f_s}{\rm{ = }}4{D_{\max }}{f_s} {\text{。}} $ | (13) |
其中

|
图 7 信号幅度上限 Fig. 7 Upper limit of signal amplitude |
当采样频率为625 kHz,输入信号频率固定在1 kHz时,对不同幅度信号进行解调,仿真得到相关系数曲线如图8所示。
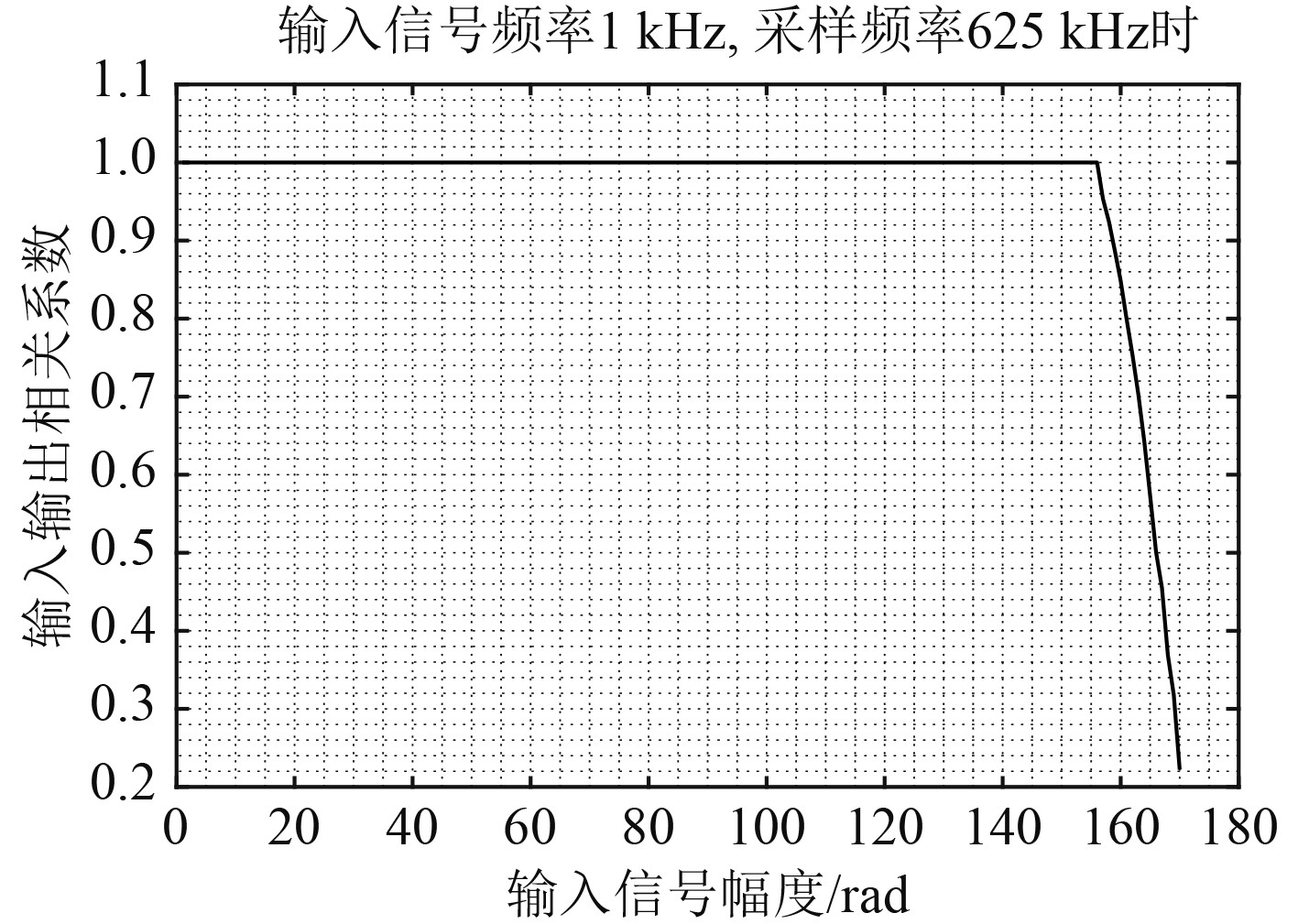
|
图 8 不同幅度条件下的相关系数 Fig. 8 Correlation coefficients under different amplitude conditions |
令输入信号
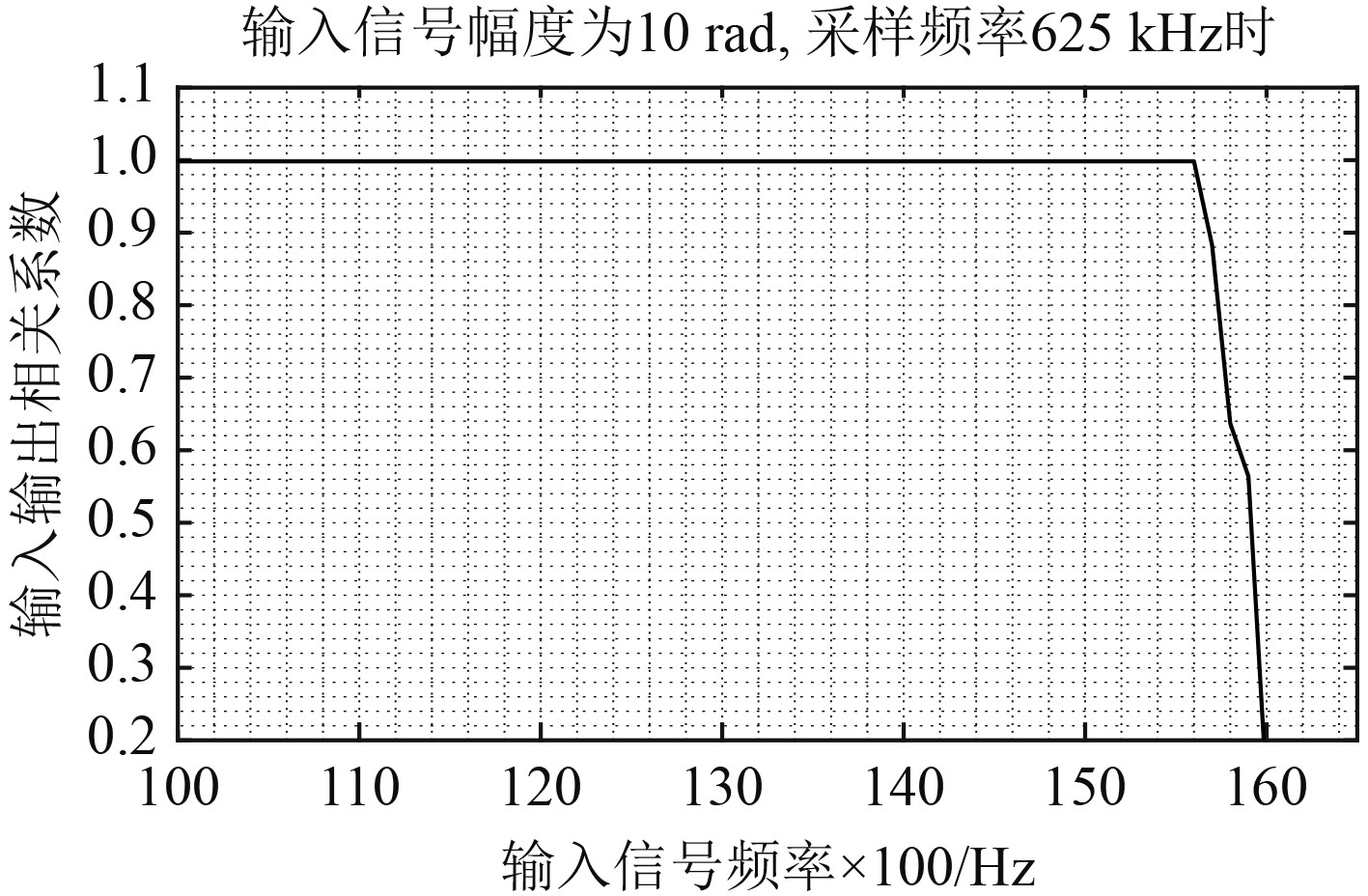
|
图 9 不同频率条件下的相关系数 Fig. 9 Correlation coefficients under different frequencies conditions |
由图8和图9可知,当输入信号为单频信号时,在一定频率、幅度范围内,输入输出信号的相关系数能保持在0.99以上,即能无失真解调。当频率、幅度继续增大至不满足条件式(13)时,相关系数小于0.99,解调结果失真,无法还原出输入输入信号。
2.4 对线性调频信号的解调线性调频信号是指瞬时频率随时间线性变化的信号,本文采用线性调频信号初始相位为零,幅度为10 rad。解调系统采样率为625 kHz。
2.4.1 不同带宽情况下的解调效果当输入线性调频信号的中心频率为定值时,对不同带宽情况下的解调效果进行仿真分析。
2.4.2 不同中心频率情况下的解调效果当输入线性调频信号的带宽为定值时,对不同中心频率情况下的解调效果进行仿真分析,结果如图10和图11所示。
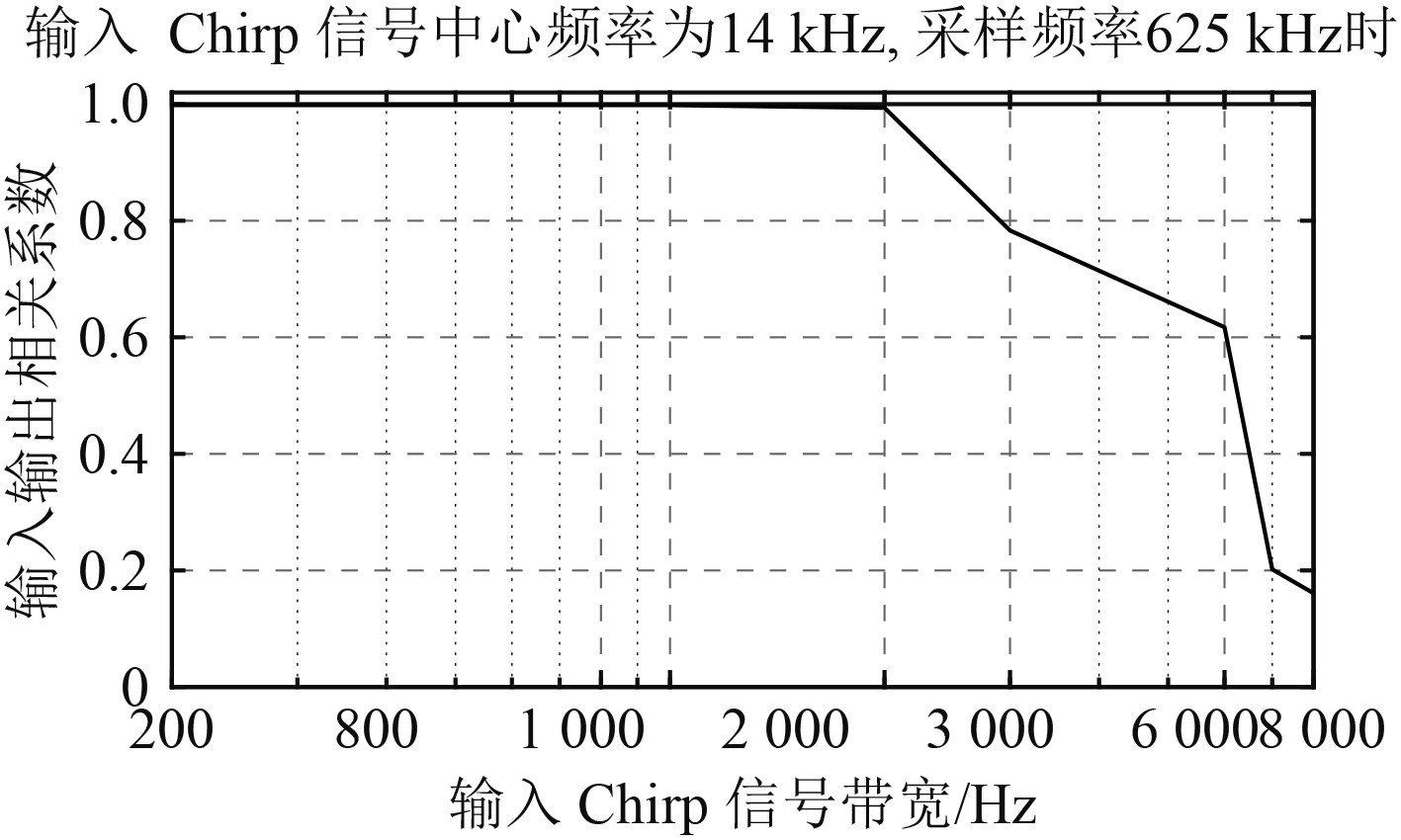
|
图 10 不同带宽条件下的相关系数 Fig. 10 The correlation coefficients under different bandwidth conditions |
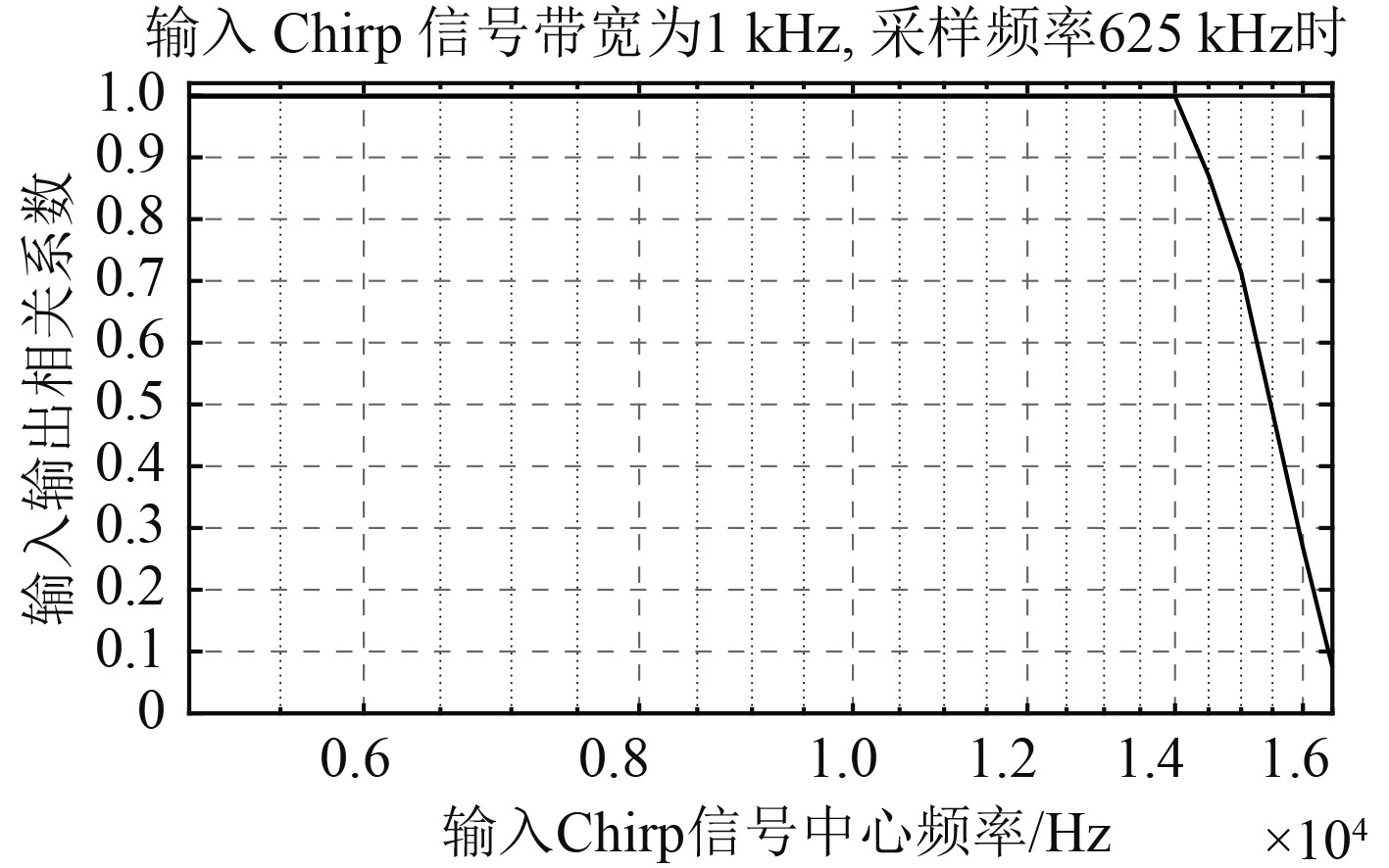
|
图 11 不同中心频率条件下输入输出信号相关系数 Fig. 11 The correlation coefficient at different center frequencies |
由图10和图11可知,当输入信号为线性调频信号时,相关系数的变化趋势与单频信号相似,在一定的带宽、中心频率情况下,相关系数均在0.99以上,解调无失真,当带宽、中心频率继续变化至不满足条件式(13)时,解调即失真。观察图8~图11可知,无论输入是单频信号,还是多频信号,只要信号频率、幅度满足条件式(13),就能实现无失真解调。
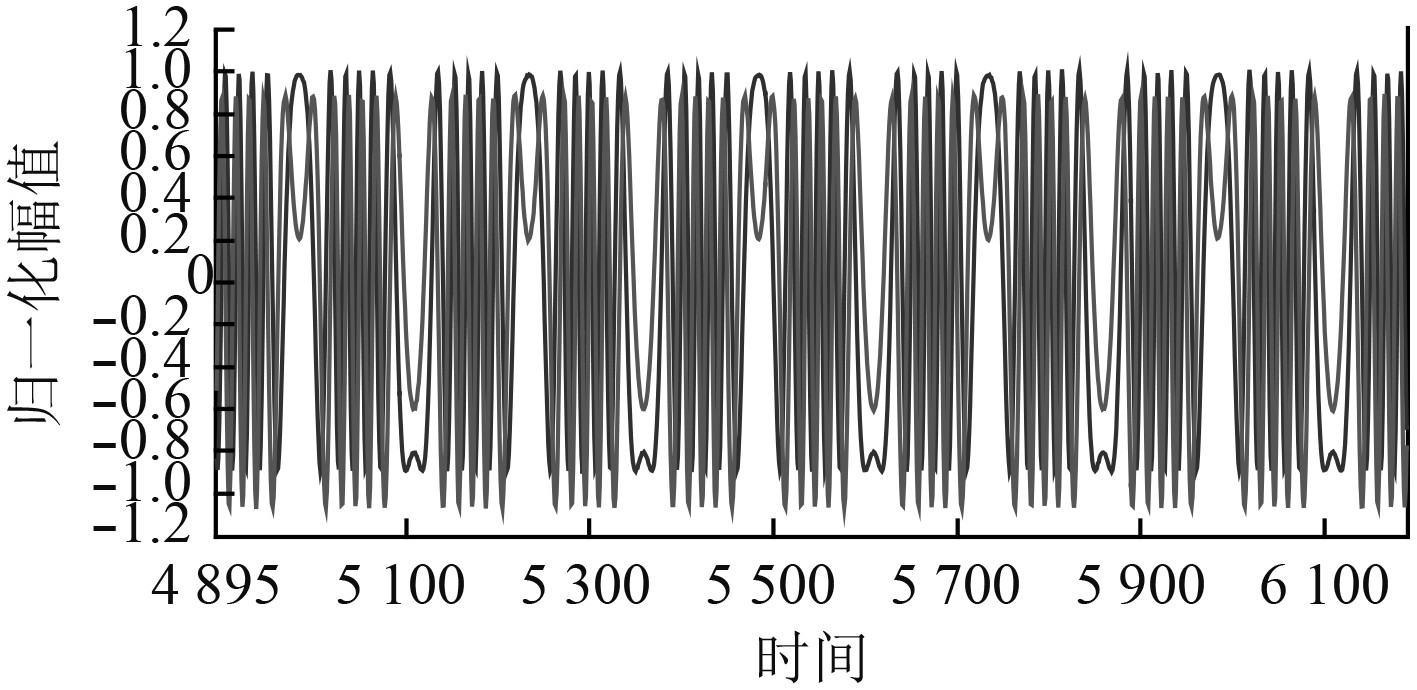
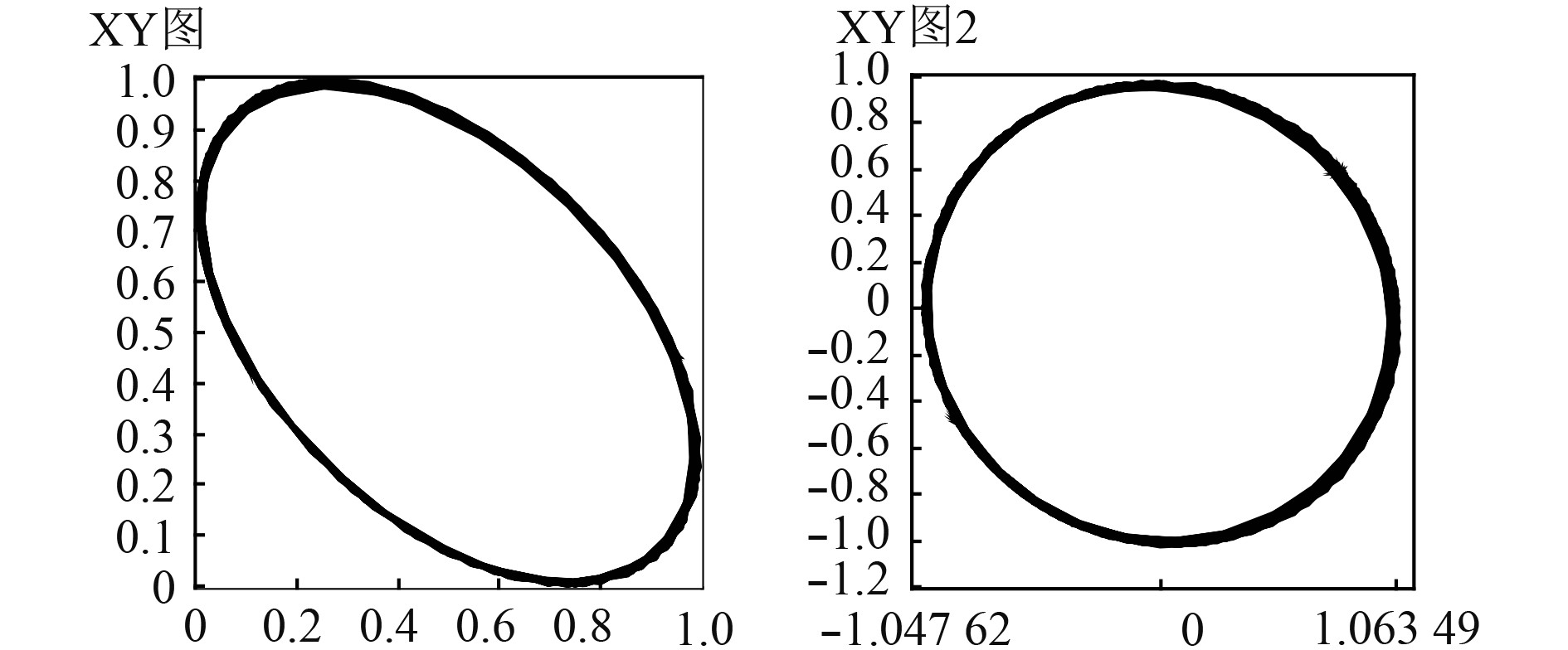
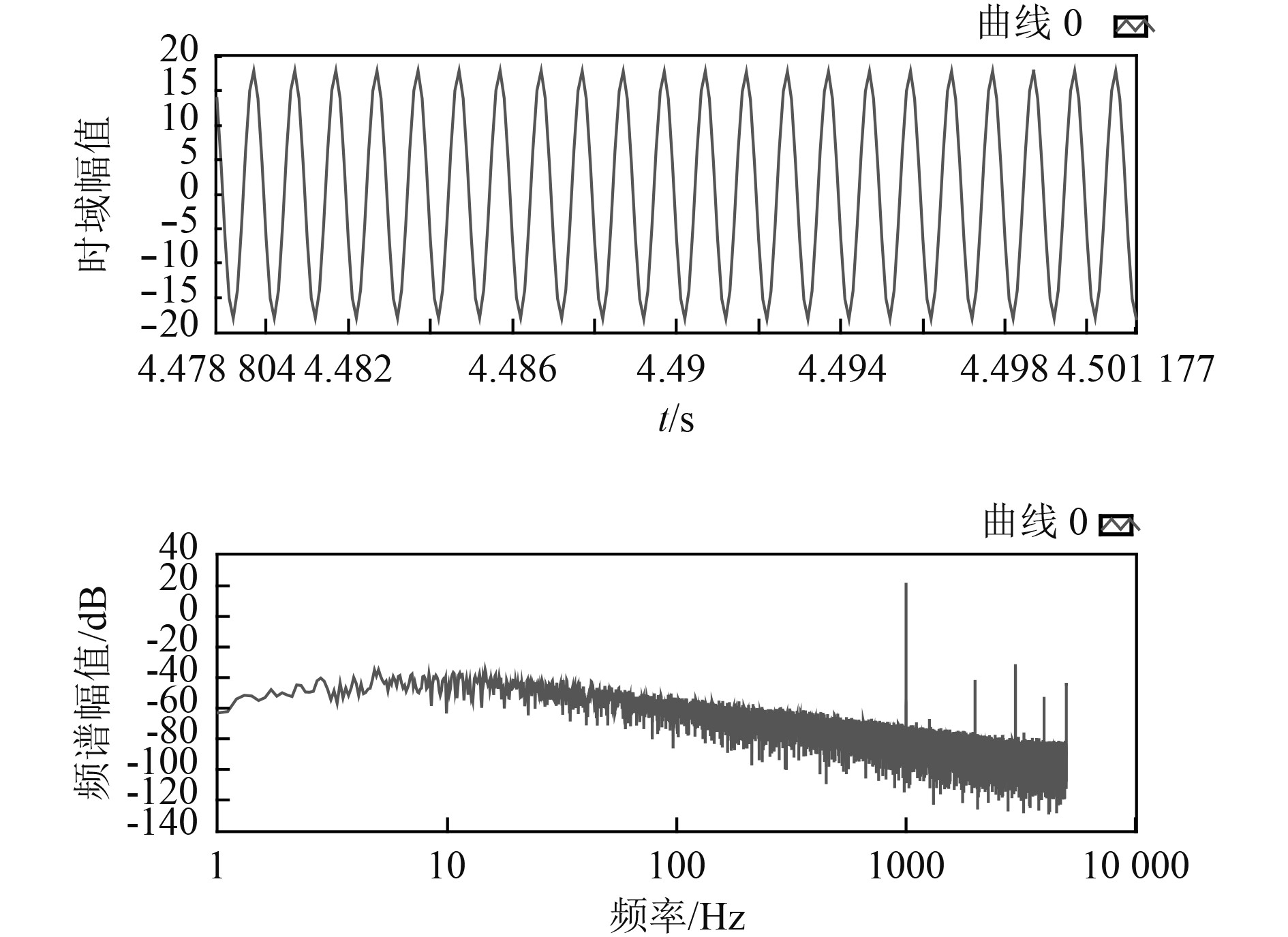
3 实验结果为了验证本文解调算法的实际解调效果,本文进行了模拟水声信号解调。通过对补偿干涉仪的压电陶瓷加载驱动电压信号来模拟水声信号。本系统采用RIO稳定光源,输出功率稳定度≤0.1 dB,补偿干涉仪使携带传感信息的传感光与参考光进行干涉,传感信息以余弦的形式调制在干涉光波信号的相位上。光电转换器将光信号转换为电信号,每通道电输出信号本底噪声≤5 mV,光插入损耗≤14 dB,以XILINX公司XC5VLX50T系列FPGA芯片为核心来实现解调算法,系统输出采样率为10 kHz,数据精度为14 bit,通过FPGA对采样数据进行解调,并将解调结果送至上位机,通过Labview2014程序进行显示和分析。实验中待测信号是1 kHz,18 rad的正弦信号,去直流及归一化处理前后的两路相位信号以及李萨如图如图12和图13所示,解调输出时域图和频谱图如图14所示,输出信号幅度稳定在17.9~18.1 rad之间,频率为1 kHz,基波信号幅度与最大谐波幅值差大于30 dB,解调结果准确可信,由频谱图可知本解调系统1 kHz处的动态范围大约为90 dB。
|
图 12 干涉仪输出信号 Fig. 12 Two output signals of the interferometer |
|
图 13 去直流及归一化处理前后的李萨如图 Fig. 13 Lissajous diagram of two interference signals |
|
图 14 输出信号波形和频谱 Fig. 14 The waveform and spectrum of the output signal |
本文介绍了一种利用3×3耦合器的两路输出信号进行解调的方法,推导了输出信号表达式,利用Simulink建立了解调模型。由仿真结果可知,系统动态范围下限决定于系统本底噪声,可以通过提高系统采样率来增大系统动态范围上限,进而提高系统动态范围。对单频、线性调频信号进行了解调仿真,仿真结果与式(13)所描述的不失真解调条件相符,当输入信号频率、幅度不满足该条件时,解调结果即失真。最后,搭建了基于此方法的数字化解调系统进行算法验证。实验结果表明,基于该解调方法的干涉型光纤水听器解调系统能够无失真解调出输入的模拟水声信号,且谐波性能好、解调结果准确可靠。本文研究内容对干涉型光纤水听器数字化解调系统设计具有一定的理论指导价值。
| [1] |
BUCARO J A. Fiber-optic hydrophone[J]. The Journal of the Acoustical Society of America, 1977, 62(5): 1302-1304. DOI:10.1121/1.381624 |
| [2] |
K OO, K. P.. Passive stabilization scheme for fiber interferometers using (3×3) fiber directional couplers[J]. Applied Physics Letters, 1982, 41(7): 616. DOI:10.1063/1.93626 |
| [3] |
SHEEM S K, GIALLORENZI T G, KOO K P. Optical techniques to solve the signal fading problem in fiber interferometers[J]. Applied Optics, 1982, 21(4): 689-693. DOI:10.1364/AO.21.000689 |
| [4] |
TO DD, M. D, SEAVER M, BUCHOLTZ F. Improved, operationally-passive interferometric demodulation method using 3×3 coupler[J]. Electronics Letters, 2002, 38(15): 784. DOI:10.1049/el:20020569 |
| [5] |
何俊, 肖浩, 冯磊. 基于3×3耦合器的迈克尔逊干涉仪相位特性分析[J]. 光学学报, 2008, 28(10). HE Jun. XIAO Hao. FENG Lei. Analysis of phase characteristics of Michelson interferometer based on 3×3 coupler[J]. Acta Optica Sinica, 2008, 28(10). DOI:10.3321/j.issn:0253-2239.2008.10.023 |
| [6] |
张晓峻, 康崇, 孙晶华. 3×3光纤耦合器解调方法[J]. 发光学报, 2013, 34(5). ZHANG Xiaojun. KANG Chong. SUN Jinghua. 3×3 fiber coupler demodulation method[J]. Chinese Journal of Luminescence, 2013, 34(5). |
| [7] |
毛欣, 黄俊斌, 顾宏灿. 采用3×3耦合器的分布反馈式光纤激光传感器解调技术[J]. 发光学报, 2017(3). MAO Xin. HUANG Junbin. GU Hongcan. Using 3×3 coupler distributed feedback fiber optic laser sensor demodulation technology[J]. Chinese Journal of Luminescence, 2017(3). |
| [8] |
宋美杰, 于廷宽. 一种基于3×3耦合器的光纤相位解调算法[J]. 光通信技术, 2019, 43(5): 51-53. SONG Meijie, YU Tingkuan. An optical fiber phase demodulation algorithm based on 3×3 coupler[J]. Optical Communication Technology, 2019, 43(5): 51-53. |
 2020, Vol. 42
2020, Vol. 42
