压缩感知(Compressive Sensing,CS)[1-3]理论作为一种新兴的信号处理理论,当信号在某个正交变换域内具有稀疏性时,便可以以远低于奈奎斯特采样速率的频率对其欠采样,然后通过非线性重构算法大概率恢复原始稀疏信号。基于CS的信道估计方法是利用水声信道多径分布的稀疏特性,将信道估计问题转化为稀疏信号的重构问题,通过CS重构算法可精确恢复信道响应。已有不少学者将其应用于通信系统的信道估计中。COTTER和RAO提出了应用于单载波通信系统的基于匹配追踪(Matching Pursuit,MP)算法[4]的稀疏信道估计[5-6]。WANG等将上述基于MP的稀疏信道估计方法拓展到MIMO-OFDM多载波通信系统[7]。C.R等在文献[8]的基础上深入研究了基于CS的稀疏信道估计方法,提出了一种OFDM频域信道估计算法并分析了各种稀疏重构算法的优劣。但是这类方法主要研究的是静态稀疏信号,忽略了信号的动态稀疏特性,对于时变信道的估计精度不高。静态CS理论唯有通过增加测量次数才能获得静态时的重构效果,考虑到单次CS重构算法的复杂度,通常难以实际应用。而分布式压缩感知理论的提出,解决了传统静态CS的局限性。它是一种动态CS理论,通过利用多个信号的共同稀疏性进行联合重构,大大提高了稀疏重建性能,进而提高了水声信道估计的精度。因此本文在分布式压缩感知理论的框架下,考虑到水声通信信道具有时变稀疏性以及统计上的动态性,对同步正交匹配追踪算法进行改进,构造一种时域联合的信道估计方法,进一步提高了水声信道的信道估计性能。
1 分布式压缩感知理论及联合稀疏模型DCS理论的研究对象是具有联合稀疏特性的信号集,通过挖掘各稀疏信号之间的相关性结构,采取联合恢复信号的策略,因此能够获得更好的稀疏信号重构效果。联合稀疏模型(Joint Sparsity Models,JSM)中常用的主要有JSM-1型和JSM-2型。
1)JSM-1型
在JSM-1型中,被观测信号集中每个信号都由公共稀疏部分和各自独立的稀疏部分组成。公共稀疏部分和各自独立的稀疏部分都可以通过同一个稀疏基进行稀疏表示。
2)JSM-2型
与JSM-1模型不同,JSM-2模型中所有信号间都具有相同的稀疏支撑集而只是非零系数不同。在本模型中,所有原信号都可以通过同一个稀疏基构造。SOMP算法也是基于该模型。
2 基于联合稀疏模型的CS信道估计 2.1 系统模型基于CS的OFDM信道估计方法,其核心思想是将OFDM信道估计问题转化为稀疏信号重构问题,通过CS重构算法加以解决。具体表示为:
| $ {{{Y}}_P} = {{{X}}_P}{{{F}}_P}{{h}} + {{{W}}_P} = {{Ah}} + {{{W}}_P} {\text{。}} $ | (1) |
式中:对于接收端来说,
然而此类方式在解决问题时虽然简单实用,但未充分考虑水声通信信道的缓变特征且若能充分利用各时刻信道响应的公共稀疏特性,则能进一步提高OFDM系统信道估计的性能。
基于此,相关文献在DCS理论框架下通过SOMP算法解决JSM-2模型下的联合稀疏恢复问题来实现水声信道的信道估计问题。
由式(3),若考虑连续T个OFDM符号时间内的信道估计,则
| $ \left\{ {\begin{array}{*{20}{c}} {{{Y}}_P^{(1)} = {{A}}{{{h}}^{(1)}} + {{W}}_P^{(1)}}{\text{,}} \\ {{{Y}}_P^{(2)} = {{A}}{{{h}}^{(2)}} + {{W}}_P^{(2)}} {\text{,}}\\ \vdots \\ {{{Y}}_P^{(T)} = {{A}}{{{h}}^{(T)}} + {{W}}_P^{(T)}} {\text{。}} \end{array} } \right. $ | (2) |
其中,
针对式(2)的联合稀疏模型,构造如下的优化问题来求解联合信道估计:
| $ \begin{array}{l} {\hat{ H}} = \arg \min \sum\limits_{t = 1}^T {{{\left\| {{{{h}}^{(t)}}} \right\|}_1}} {\text{,}} \\ {\rm s.t.}\sum\limits_{t = 1}^T {\left\| {Y_P^{(t)} - A{h^{(t)}}} \right\|} _2^2 \leqslant \varepsilon {\text{。}} \\ \end{array} $ | (3) |
式中,
SOMP算法作为一种在OMP算法基础上改进的贪婪算法,主要应用与JSM-2模型。SOMP算法在每次迭代中同样仅选取与残差最匹配的原子进行支撑集的更新,通过多次快速迭代完成对信号集的联合恢复。
然而实际的水声通信信道在多个OFDM数据符号内路径时延可能会发生改变,甚至可能发生路径的生灭现象,基于SOMP算法的时域联合信道估计假定在几个连续数据符号内信道共享相同的路径时延集很难完全满足实际情况。此外,各符号间存在独立稀疏多径特性,与JSM-1模型相匹配。
在DCS理论的JSM-1模型中,每个信号都由公共稀疏部分和独立稀疏部分组成,因此可以将信道路径时延分为公共信道抽头和动态信道抽头分别考虑。在这种分离的基础上,本文提出一种改进的SOMP算法来重建时变稀疏信道。首先在所有OFDM数据符号中同时检测稀疏信道的公共信道抽头,然后将公共信道抽头的路径时延集作为动态信道抽头跟踪过程中的初始化集,目的是为了跟踪动态信道抽头并消除初始化集中的错误抽头。
现结合逐符号OFDM信道估计模型,给出基于改进SOMP算法的OFDM信道估计流程,其步骤如下:
1)输入
接收导频信号
2)公共信道抽头检测
| $ {{\bf{\Lambda }}_0} = SOMP({{{Y}}_P},{{A}},K) {\text{。}} $ | (4) |
3)动态信道抽头检测
初始化:索引集
迭代过程:第t次迭代。
步骤1 找出残差
| $ \begin{array}{*{20}{l}} {\lambda _t^{(i)} = \arg {{\max }_j}\left| {\left\langle {{{{A}}_j},{{r}}_{t - 1}^{(i)}} \right\rangle } \right|} {\text{,}}\\ {{{\varGamma }}_t^{(i)} = {{\varGamma }}_{t - 1}^{(i)} \cup \lambda _t^{(i)}} {\text{,}}\\ {{{\varPhi }}_t^{(i)} = {{\varPhi }}_{t - 1}^{(i)} \cup {{{A}}_{\lambda _t^{(i)}}}} {\text{。}} \end{array} $ | (5) |
步骤2 利用LS算法求出每个符号内的信道冲激响应。
| $ {\hat{ h}}_t^{(i)} = \arg \min {\left\| {{{Y}}_P^{(i)} - {\bf{\Phi }}_t^{(i)}{{{h}}^{(i)}}} \right\|_2} {\text{。}} $ | (6) |
步骤3 仅保留
步骤4 更新残差。
| $ {{r}}_t^{(i)} = Y_P^{(i)} - {\bf{\Phi }}_t^{(i)}{\hat{ h}}_t^{(i)} {\text{。}} $ | (7) |
步骤5 判断是否满足条件
4)输出
各OFDM符号对应的信道冲激响应估计值
在本文的仿真系统中,OFDM系统子载波总数设为256,保护间隔长度为64点循环前缀,单个OFDM符号插入的导频数量根据资料选择32个导频。导频插入方式依据信道估计方式而定,传统LS信道估计采用等间隔的梳状导频插入,而基于CS的信道估计全部采用随机导频插入。所有调制方式均采用QPSK调制,且无信道编码,接收端假定已完全同步。
本文所提JSM-1模型中的公共稀疏多径仅幅度随时间变化,各符号内的动态稀疏多径则随机生成。所有稀疏多径彼此独立,增益服从零均值的复高斯分布并按指数规律衰减。假设信道长度
基于以上系统仿真参数设置,做以下几组仿真:
1)不同信道长度对估计算法性能影响
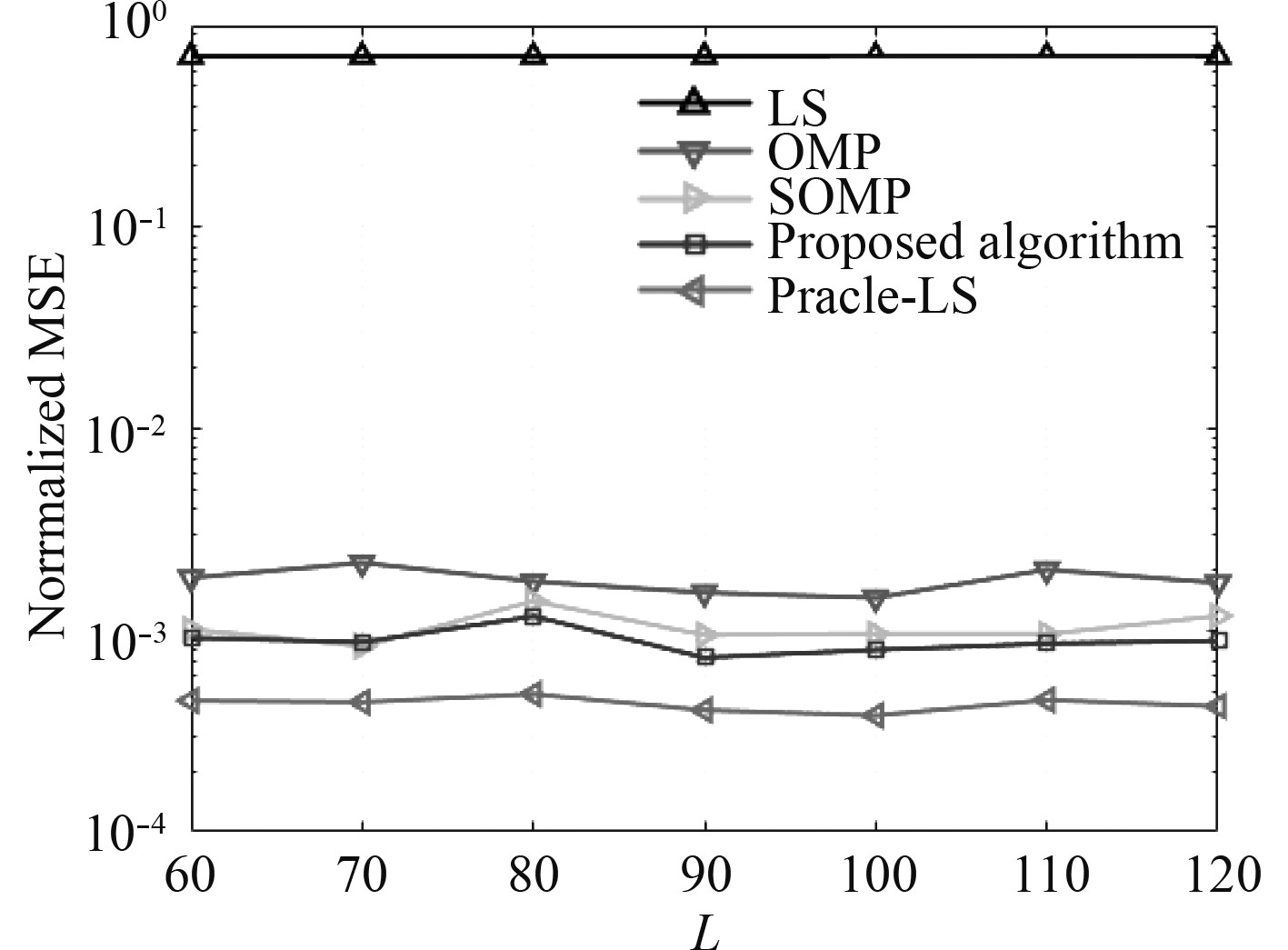
本部分主要研究了不同信道长度对估计算法性能的影响。仿真选定信噪比为30 dB,信道长度在60~120之间变化,变化间隔为10。图1给出了仿真结果。图中除了本文所提算法外,还有LS,OMP,SOMP以及Oracle-LS算法作为对比算法。可以发现,信道长度的变化对信道估计算法的性能没有较大的影响。
|
图 1 不同信道长度下的归一化均方误差 Fig. 1 The NMSE with different channel lengths |
2)公共信道抽头数对信道估计算法性能影响
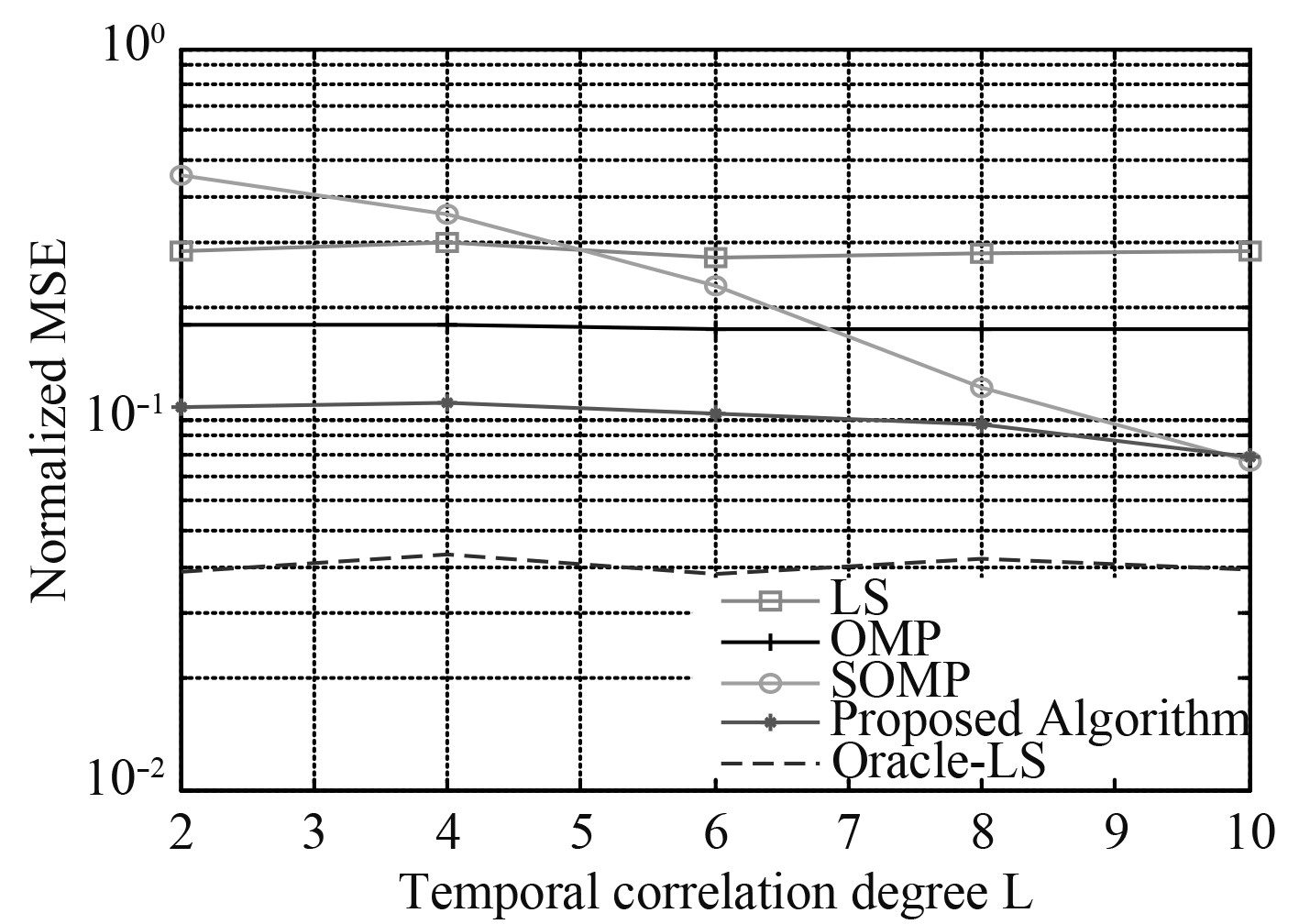
本次仿真中设信道最大稀疏度K=10,用时间相关度L表示公共信道抽头数,具体数值在2~8之间变化,图2给出了仿真结果。图中除了本文所提算法外,还有LS、OMP、SOMP以及Oracle-LS算法作为对比算法。可见,所有算法中受时间相关度L影响最大的是SOMP算法,其余算法均无较大影响。本文所提算法由于包含了动态信道抽头检测,因此L的变化仅影响算法的计算复杂度,对算法性能影响不大。至于SOMP算法,由于其默认共享相同路径时延集,因此当L增大时,相同的路径时延数增大,算法性能变好,反之算法性能减弱。可以看到,当L=K=10时,信道退化为JSM-2模型,此时本文所提算法也退化为SOMP算法,因此两者的估计性能相当。
|
图 2 不同时间相关度下的归一化均方误差 Fig. 2 The NMSE with different temporal correlation degree L |
3)不同信噪比下多种算法的NMSE及BER曲线
本组仿真比较了本文所提算法在内的多种算法的信道估计性能,具体评价指标采用归一化均方误差和误比特率这2个参数。
图3和图4分别是NMSE和BER的仿真结果。在这2组仿真中,公共信道抽头数和信道最大稀疏度分别被设置为L=8和K=10,参与对比的信道估计算法有LS,OMP,SOMP以及Oracle-LS算法。为保证LS算法性能,导频插入方式为均匀间隔为8的梳状导频,其余CS算法均采用随机导频。

|
图 3 不同信噪比下的归一化均方误差 Fig. 3 The NMSE with different SNR |
|
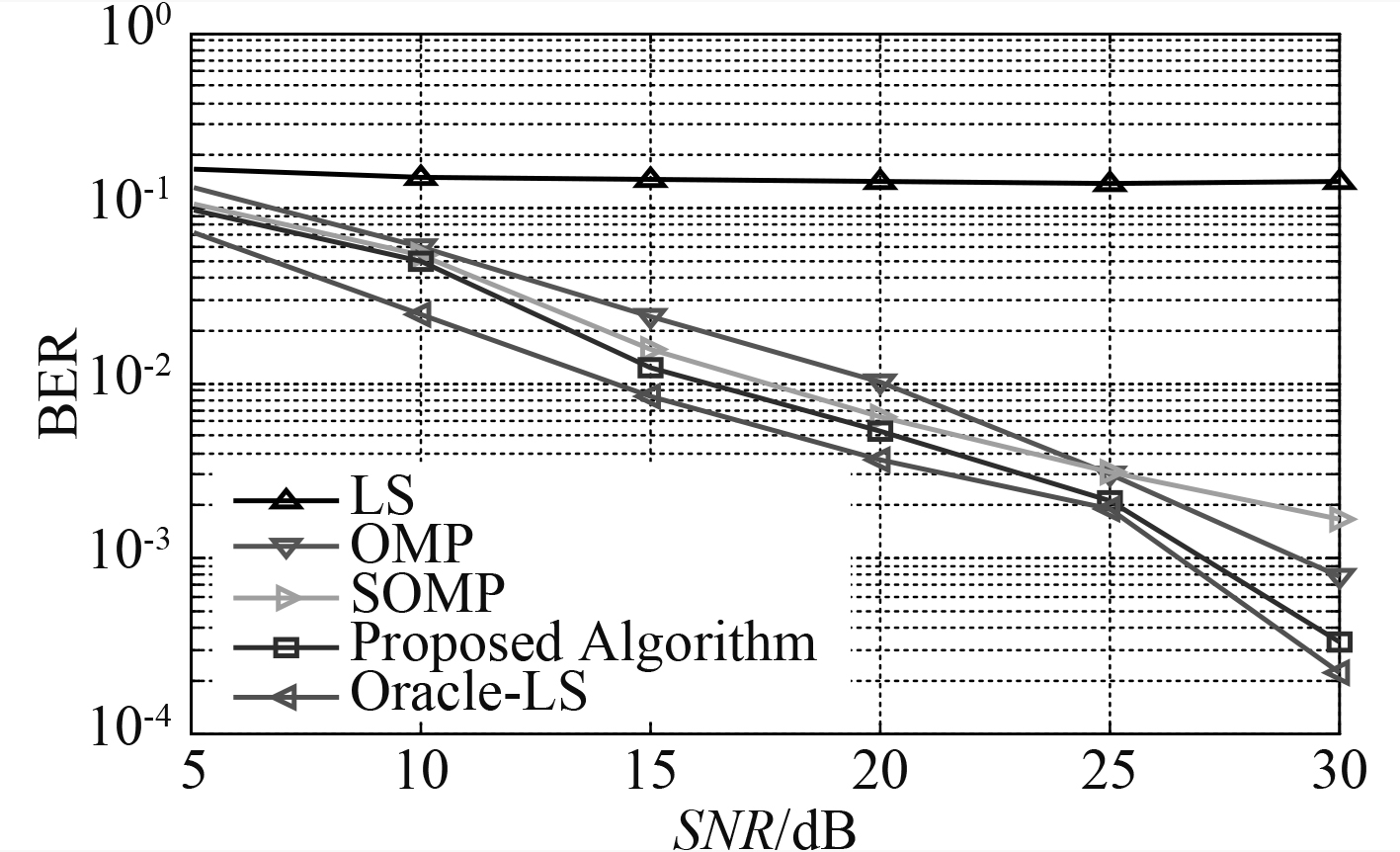
图 4 不同信噪比下的误比特率 Fig. 4 The BER with different SNR |
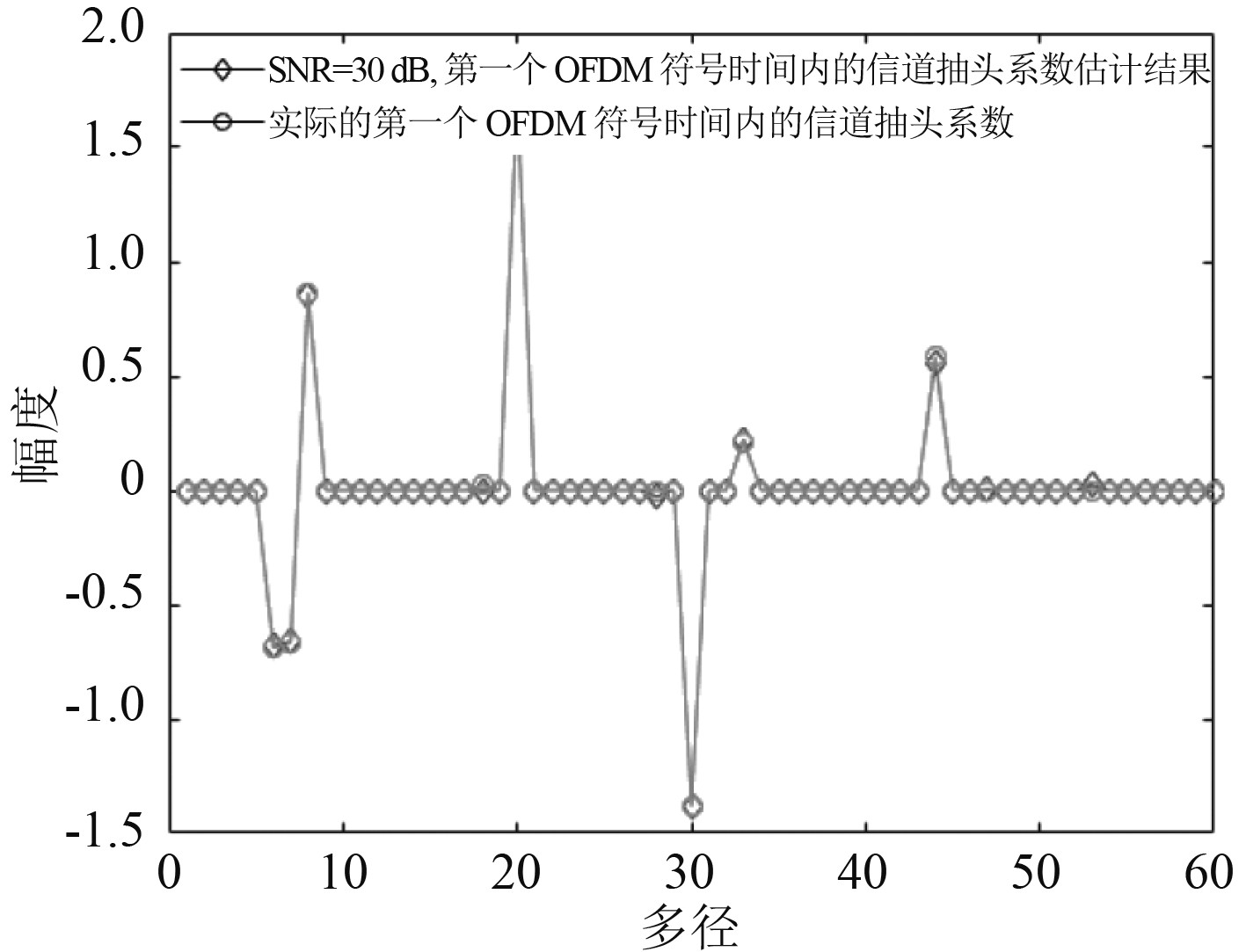
从图3和图4不难发现,NMSE和BER的性能曲线基本趋于一致。其中,LS算法作为传统算法,由于导频数小于信道长度且算法本身估计稀疏路径时受噪声影响较大,因此估计性能最差。对于基于CS的信道估计,SOMP算法在信噪比较低时对于OMP算法有较大优势。然而当信噪比增大时,由于SOMP算法模型在时变信道下的固有缺陷,性能提升效果有限,而OMP算法在高信噪比环境下受噪声影响较小,每次重构信道都可以进行完整K次迭代,因此高信噪比环境下性能更优。至于本文中所提出的改进SOMP算法,由于考虑了对动态信道的抽头检测,因此效果好于OMP和SOMP算法,与前文数学分析的结果相一致。此外,本组仿真中的对比算法Oracle-LS是时变稀疏信道多径时延集已知时的LS估计,此结果是LS准则下的理论极限值。图5将所提算法在信噪比30 dB下,第1个OFDM符号时间内的信道估计结果与原始信道对比,可以发现两者数据基本重叠,估计性能良好。
|
图 5 所提算法信道估计结果与原信道对比 Fig. 5 The comparison between channel estimation result of the proposed algorithm and the original channel |
本文主要研究了基于改进的SOMP水声通信信道联合估计方法。首先阐述了分布式压缩感知理论及联合稀疏模型,分析了现有的基于SOMP算法的时域联合信道估计方法未曾考虑信道时变性的缺陷,并提出了一种基于JSM-1模型的改进SOMP算法用于联合恢复信道估计。仿真结果表明,本文所提算法在时变信道环境下相比现有逐符号CS信道估计算法具有更大的性能优势,且算法复杂度更低。
| [1] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [2] |
CANDÈS E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [3] |
CANDÈS E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30. DOI:10.1109/MSP.2007.914731 |
| [4] |
MALLAT S G, ZHANG Z. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [5] |
COTTER S F, RAO B D. Matching pursuit based decision-feedback equalizers[C]// IEEE International Conference on Acoustics, Speech, and Signal Processing, 2000: 2713-2716.
|
| [6] |
COTTER S F, RAO B D. Sparse channel estimation via matching pursuit with application to equalization[J]. IEEE Trans Wireless Commun, 2002, 50(3): 374-377. DOI:10.1109/26.990897 |
| [7] |
WANG D, HAN B, ZHAO J, et al. Channel estimation algorithms for broadband MIMO-OFDM sparse channel[C]// IEEE 2003 International Symposium on Personal, Indoor and Mobile Radio Communications. 2003: 1929-1933.
|
| [8] |
LI W, PREISIG J C. Estimation of rapidly time-varying sparse channels[J]. IEEE Journal of Oceanic Engineering, 2008, 32(4): 927-939. |
 2020, Vol. 42
2020, Vol. 42
