船舶舵装置、通海阀件、盖板等部件均采用液压驱动方式,具有可靠性高、驱动力矩大的优点,但活塞等运动件在行程末端仍具有较高的速度,致使运动部件以较大的速度撞击止挡部件,产生较大的冲击振动和噪声,影响机械设备的安全性和可靠性,甚至影响到船舶的辐射噪声。针对该问题,周志才等[1]对盖板启闭装置的结构参数进行了多参量联合优化分析,优化结果表明撞击速度可以减小46.5%~50.84%。赖浩凯[2]利用无冲击电磁换向阀对盖板启闭装置中原液压系统进行改造,降低启闭装置在开启时的冲击加速度和冲击力。但上述研究对液压驱动机构改动较大,导致机械结构和液压系统相对复杂,且无法完全消除冲击振动和噪声。
在液压油缸内增加缓冲装置不仅可以降低活塞等运动件在行程末端的速度,而且对液压驱动机构改动较小。缓冲装置的结构参数会影响其缓冲性能,不同结构参数对缓冲性能的影响程度不一,因此需要合理选取油缸缓冲装置的结构参数[3-5]。
本文提出在液压油缸内设计缓冲装置,建立含负载条件下缓冲装置的数学模型,研究不同结构参数对缓冲性能的影响,为后续船舶液压驱动机构液压油缸的缓冲装置设计提供理论基础。
1 缓冲装置数学模型已有研究表明,圆柱形缓冲装置在缓冲过程中容易引发较大的液压冲击,造成机器振动、噪声和磨损;圆锥形缓冲装置引发的液压冲击相对较小,但存在缓冲压力建立迟缓、相同缓冲长度下造成缓冲不足的问题[6]。本文提出在液压油缸内设计圆柱形变节流面积缓冲装置以降低缓冲过程中的液压冲击,同时达到较好的缓冲效果。缓冲装置结构简图如图1所示,其主要参数包括缓冲套与缓冲腔的单边间隙δ,缓冲套大端直径
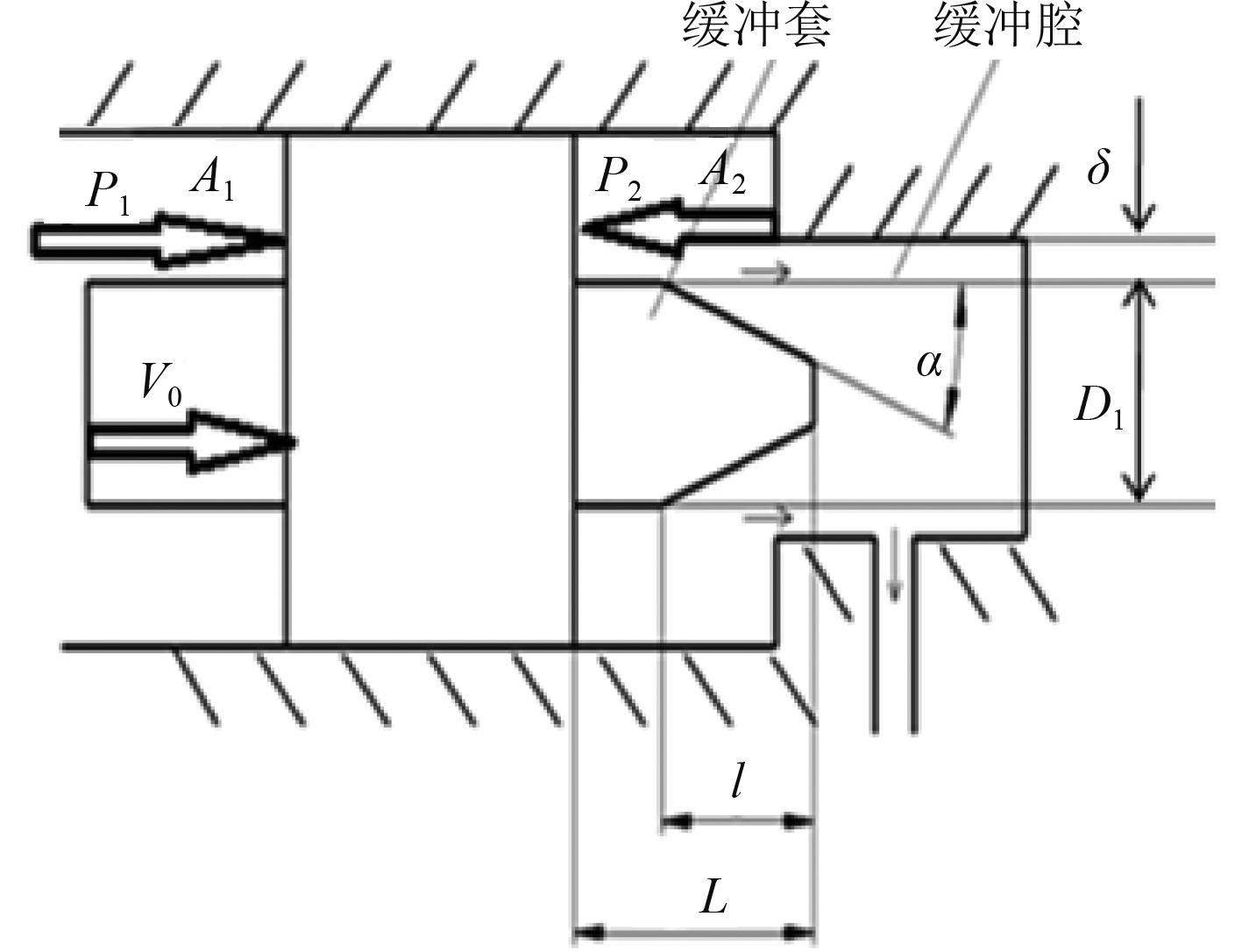
|
图 1 缓冲装置结构简图 Fig. 1 Structure diagram of buffering device |
取
| $ {p_1}{A_1} - {p_2}{A_2} - F = ma {\text{。}} $ | (1) |
式中:
由流体连续性方程可得缓冲腔排出的液体流量为:
| $ Q = {v_x}{A_2} {\text{。}} $ | (2) |
式中:
| $ Q = {C_q}A\sqrt {\frac{{2\left| {\Delta p} \right|}}{\rho }} {\text{。}} $ | (3) |
式中:
| $ \left| {\Delta p} \right| = \frac{{{Q^2}\rho }}{{2{C_q}^2{A^2}}} = \frac{{{{({v_x}{A_2})}^2}\rho }}{{2{C_q}^2{A^2}}} {\text{。}} $ | (4) |
缓冲套进入缓冲孔之后,过流面积变化如下:
| $ \begin{array}{l} { A} = \left[ {3\left[ \begin{array}{l} 0.004\;36D_1^2\arccos \left[ {1 - \dfrac{{{L_2}\tan \alpha }}{{{{{D_1}}}/{2}}}} \right] - \\ \dfrac{{{D_1}}}{2}\sin \left[ {\arccos \left[ {1 - \dfrac{{{L_2}\tan \alpha }}{{{{{D_1}}}/{2}}}} \right]} \right] \times \\ \left(\dfrac{{{D_1}}}{2} - {L_2}\tan \alpha \right) \\ \end{array} \right] + {A_3}} \right] \times {10^{ - 6}} {\text{。}} \end{array} $ | (5) |
式中:
将缓冲过程分为2个阶段,分析如下:
1)从缓冲腔压力开始形成到进油压力
| $ {p_2} = \frac{{A_2^2\rho v_0^2}}{{2{C_q}^2{A^2}}} {\text{。}} $ | (6) |
2)从进油压力
| $ {v_x} = \sqrt {v_{x - 1}^2 - 2{a_x}\Delta {L_x}} {\text{。}} $ | (7) |
将式(7)与式(4)联立求得第2阶段的缓冲腔压力变化方程如下:
| $ {p_2} = \frac{{A_2^2\rho (v_{x - 1}^2 - 2{a_x}\Delta {L_x})}}{{2{C_q}^2{A^2}}} {\text{,}} $ | (8) |
联立式(1)、式(7)求得:
| $ {a_x} = \frac{{2{C_q}^2{A^2}(F - {p_{1\max }}{A_1}) + A_2^3\rho v_{x - 1}^2}}{{2(A_2^3\rho \Delta {L_x} - {C_q}^2{A^2}m)}} {\text{。}} $ | (9) |
将上述2个阶段合并为一个整体后,可得到不同
采用AMESim软件搭建如图2所示的仿真模型,模拟液压油缸运动的全过程。
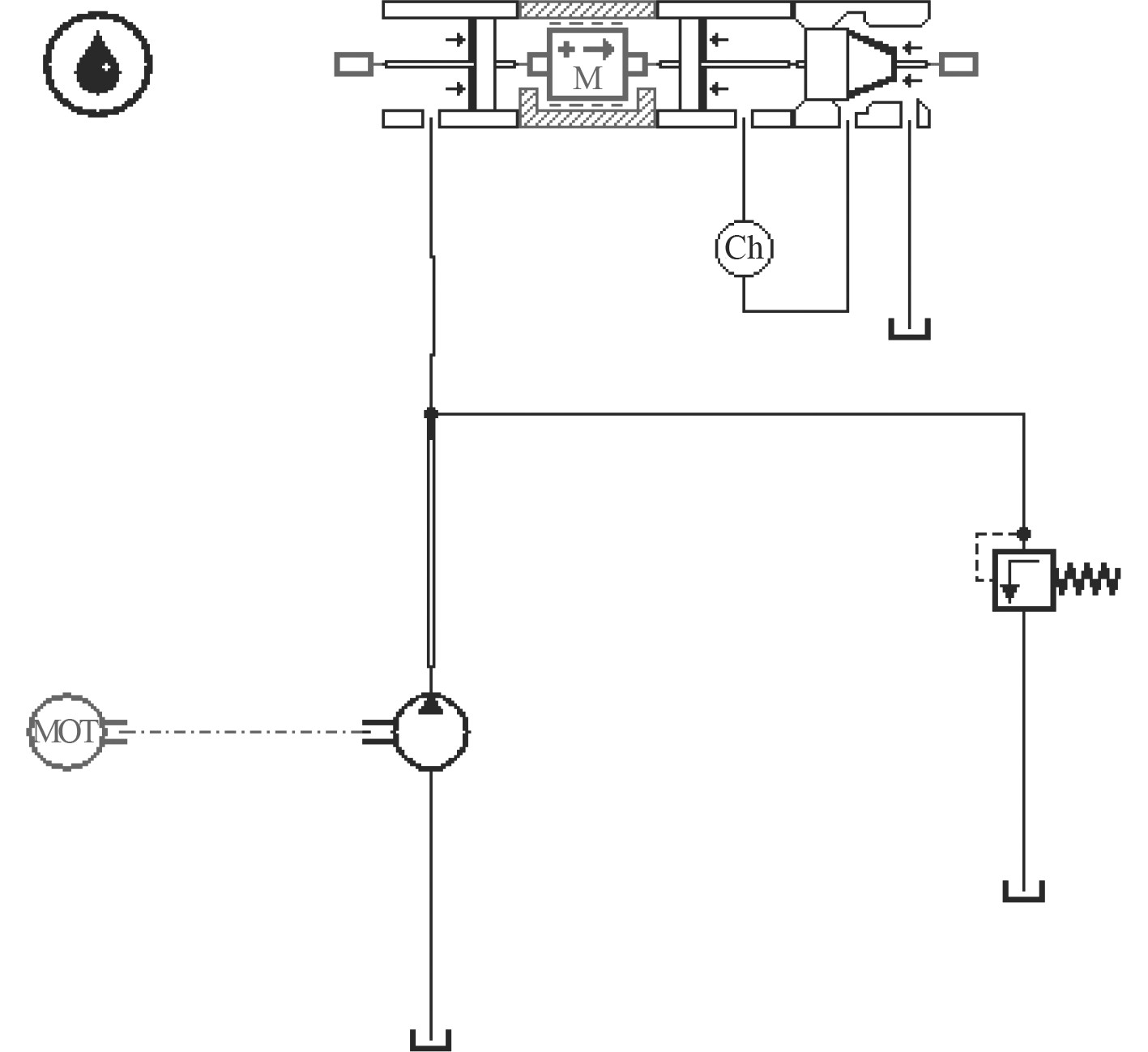
|
图 2 AMESim仿真模型 Fig. 2 Simulation model of AMESim |
仿真参数设置如表1所示。
|
|
表 1 仿真参数 Tab.1 Simulation parameters |
分别讨论缓冲套与缓冲腔的单边间隙δ、缓冲套大端直径
在仿真模型中,单边间隙δ分别设为0.12 mm,0.14 mm,0.16 mm,0.18 mm,0.2 mm,其他参数保持不变,分析其对缓冲效果的影响。
从图3可以看出,不同单边间隙下,缓冲腔压力整体变化趋势一致,不同曲线的差别较小。随着活塞位移增加,缓冲腔压力逐步上升,在347 mm附近达到峰值(此时缓冲套圆柱段即将进入缓冲腔),随后迅速恢复到稳态压力值。单边间隙越小,缓冲腔压力增加越早且峰值压力越大,但均没有出现较大的液压冲击。
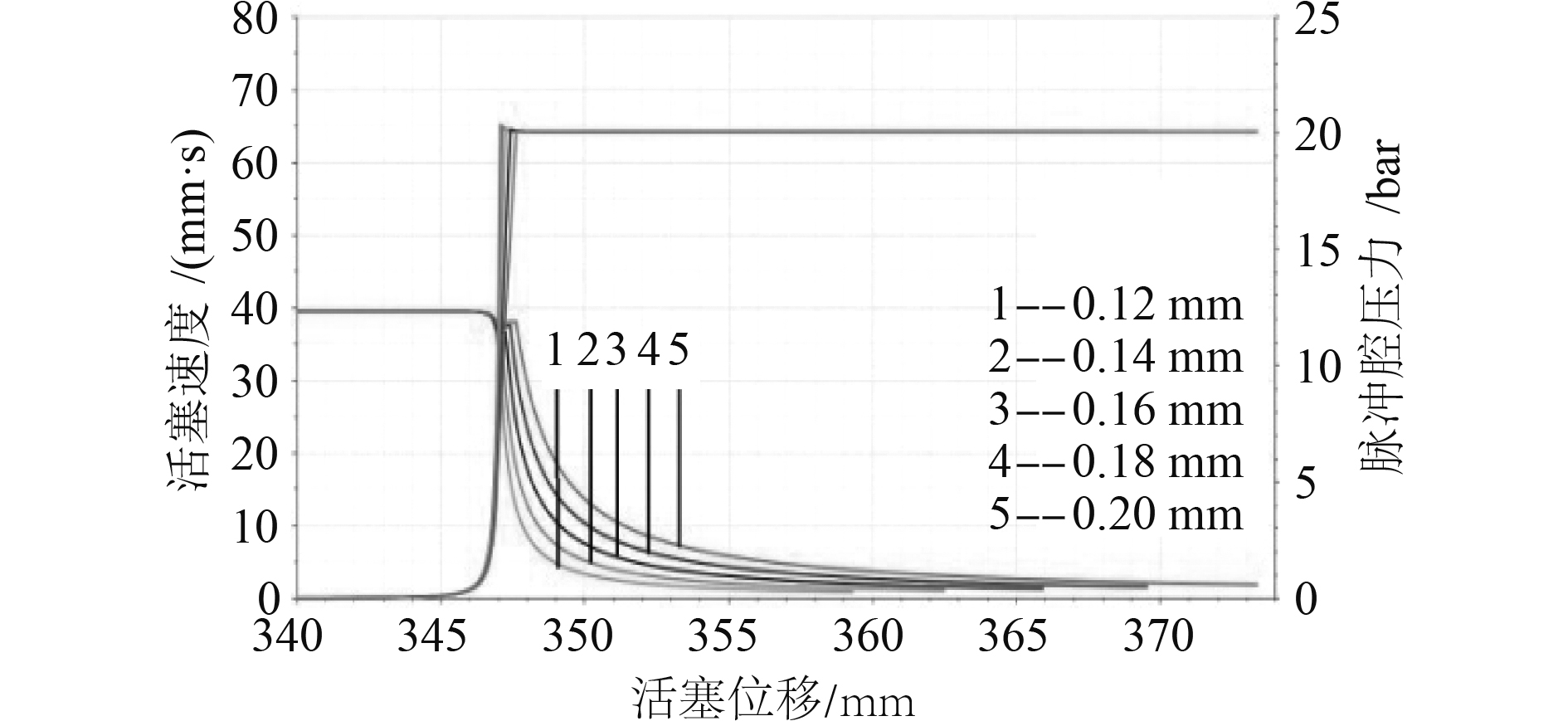
|
图 3 不同单边间隙下活塞速度与缓冲腔压力随活塞位移变化曲线 Fig. 3 Curves of buffering cavity pressure and piston velocity changes with piston displacement under different unilateral clearances |
不同单边间隙下,活塞速度整体变化趋势一致;先匀速后变减速,这与理论分析是一致的。活塞速度在347 mm附近开始下降,这与缓冲腔压力增大的趋势相对应。单边间隙越小,活塞越早开始减速,且速度下降越快,活塞最终的速度也越小。
2.2 缓冲套大端直径在仿真模型中,单边间隙δ设为0.12 mm,缓冲套大端直径
由图4可知,缓冲套大端直径对缓冲性能的影响与单边间隙对缓冲性能的影响相似,不同缓冲套大端直径所对应的活塞速度、缓冲腔压力变化曲线差别较小。
|
图 4 不同缓冲套大端直径下活塞速度与缓冲腔压力随活塞位移变化曲线 Fig. 4 Curves of buffering cavity pressure and piston velocity changes with piston displacement under different diameters at large end of buffering cover |
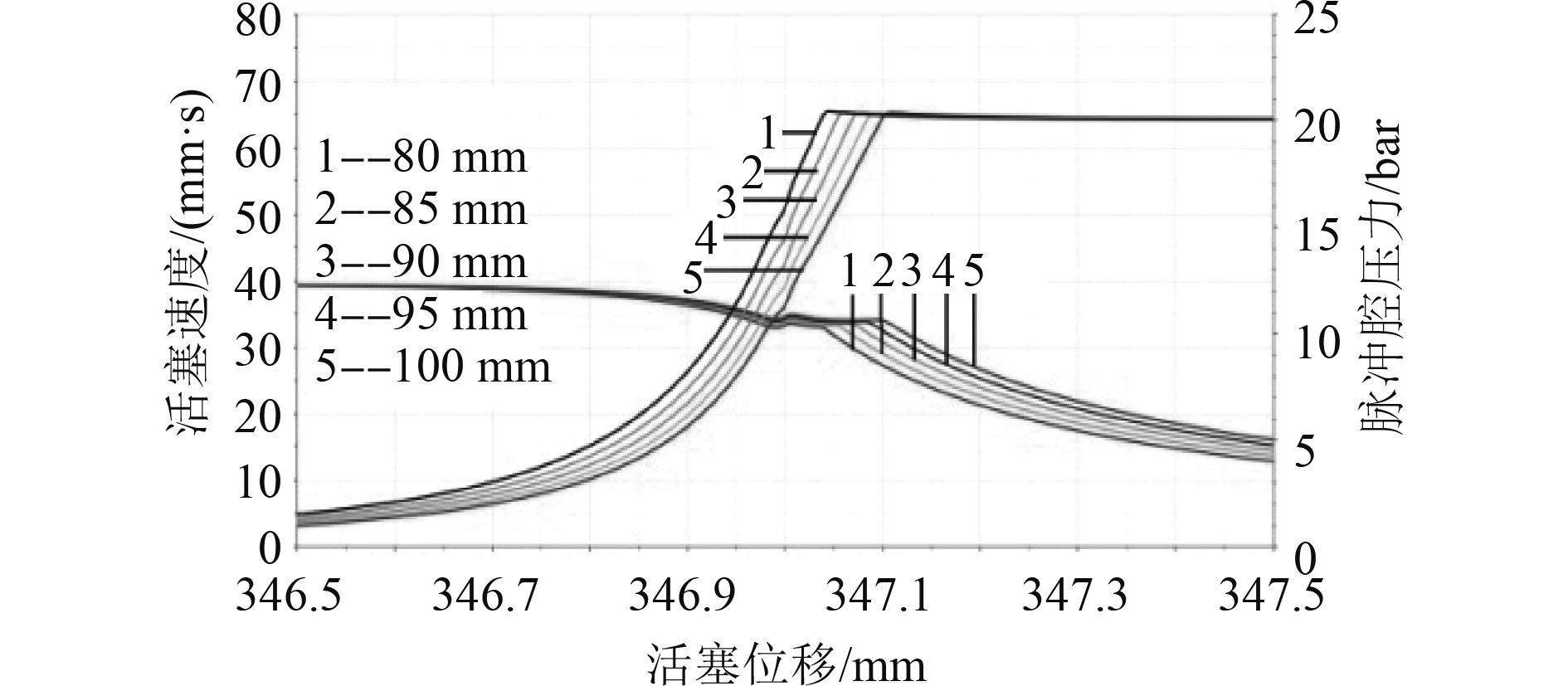
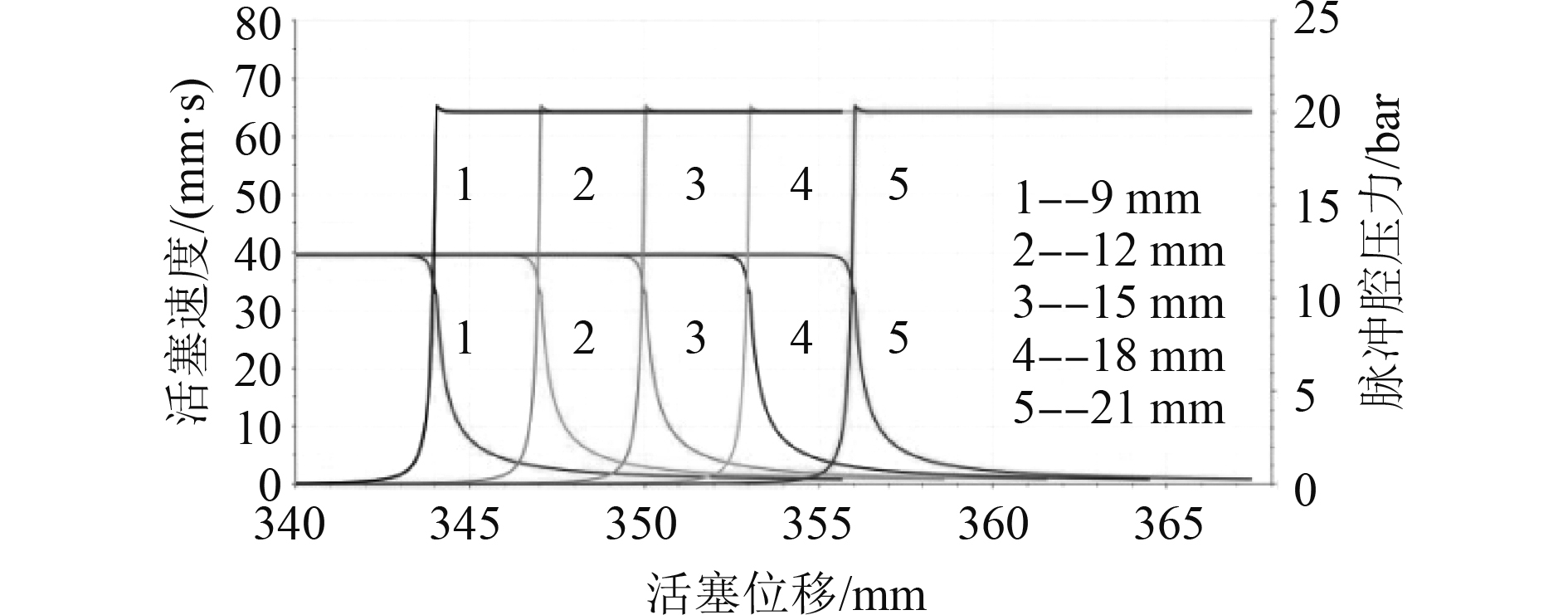
在仿真模型中,单边间隙δ设为0.12 mm,缓冲套大端直径设为80 mm,圆锥段长度l分别设为9 mm、12 mm、15 mm、18 mm、21 mm,其它参数保持不变,分析圆锥段长度对缓冲效果的影响。
由图5可知,不同圆锥段长度所对应的缓冲腔压力、活塞速度曲线的整体变化趋势一致,但活塞速度下降的起始点和缓冲腔压力上升的起始点的位置不同。即圆锥段长度仅对缓冲套圆柱段进入缓冲腔的时间有影响,对活塞速度、缓冲腔压力的幅值没有影响。
|
图 5 不同圆锥段长度下活塞速度与缓冲腔压力随活塞位移变化曲线 Fig. 5 Curves of buffering cavity pressure and piston velocity changes with piston displacement under different cone lengths |
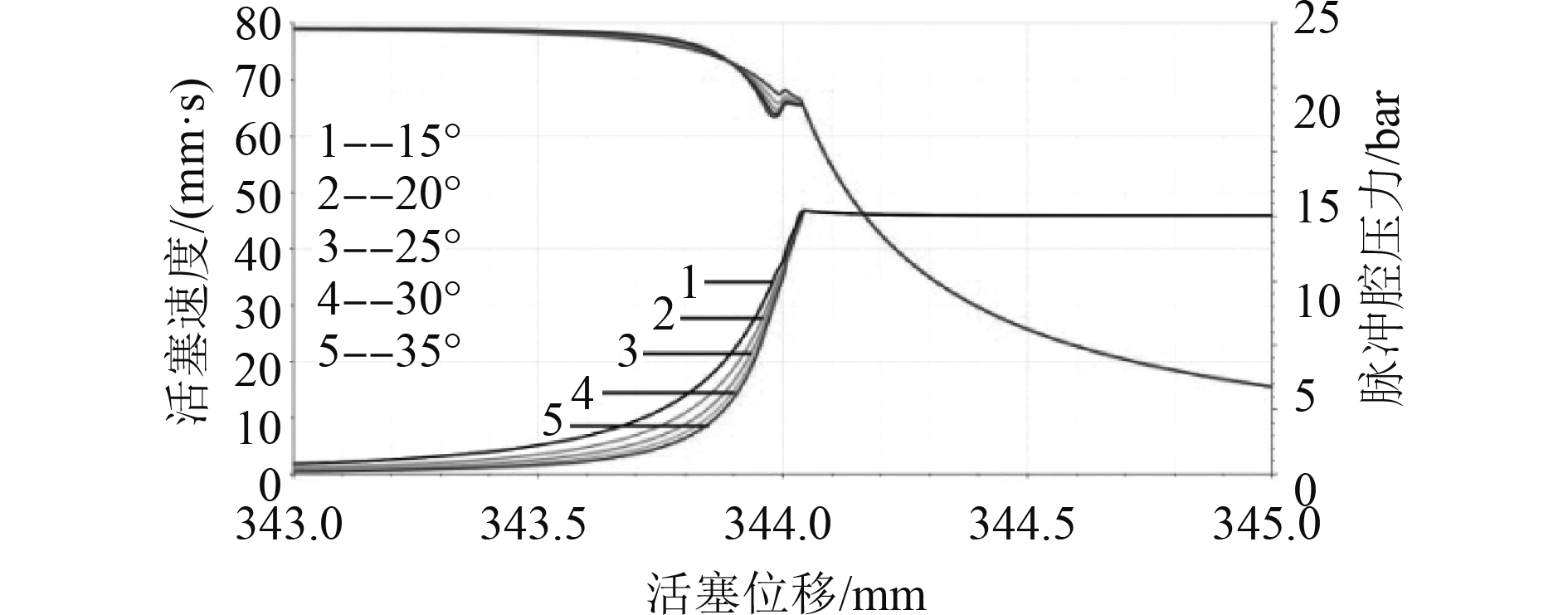
在仿真模型中,单边间隙δ设为0.12 mm,缓冲套大端直径设为80 mm,圆锥段长度l设为9 mm,锥角分别设为15°,20°,25°,30°,35°,分析锥角对缓冲效果的影响。
锥角会影响缓冲套与缓冲腔之间的过流面积,致使不同锥角下的缓冲腔压力、活塞速度随活塞位移的变化关系存在差异。从图6可以看出,不同锥角下的缓冲腔压力曲线整体趋势一致,锥角越小,缓冲腔压力增加越早,压力变化越平缓。不同锥角下的活塞速度曲线差别不大。
|
图 6 不同锥角下活塞速度与缓冲腔压力随活塞位移变化曲线 Fig. 6 Curves of buffering cavity pressure and piston velocity changes with piston displacement under different cone angles |
通过以上分析,并综合考虑现有液压机的结构尺寸及零部件加工装配、结构强度等影响因素,对圆柱形变节流面积缓冲装置进行了优化设计,其结构参数如表2所示。
|
|
表 2 缓冲装置结构参数 Tab.2 Structure parameters of buffering device |
根据上述参数,进行仿真,得到如图7所示的缓冲过程中缓冲腔压力、活塞速度随活塞位移的变化曲线。
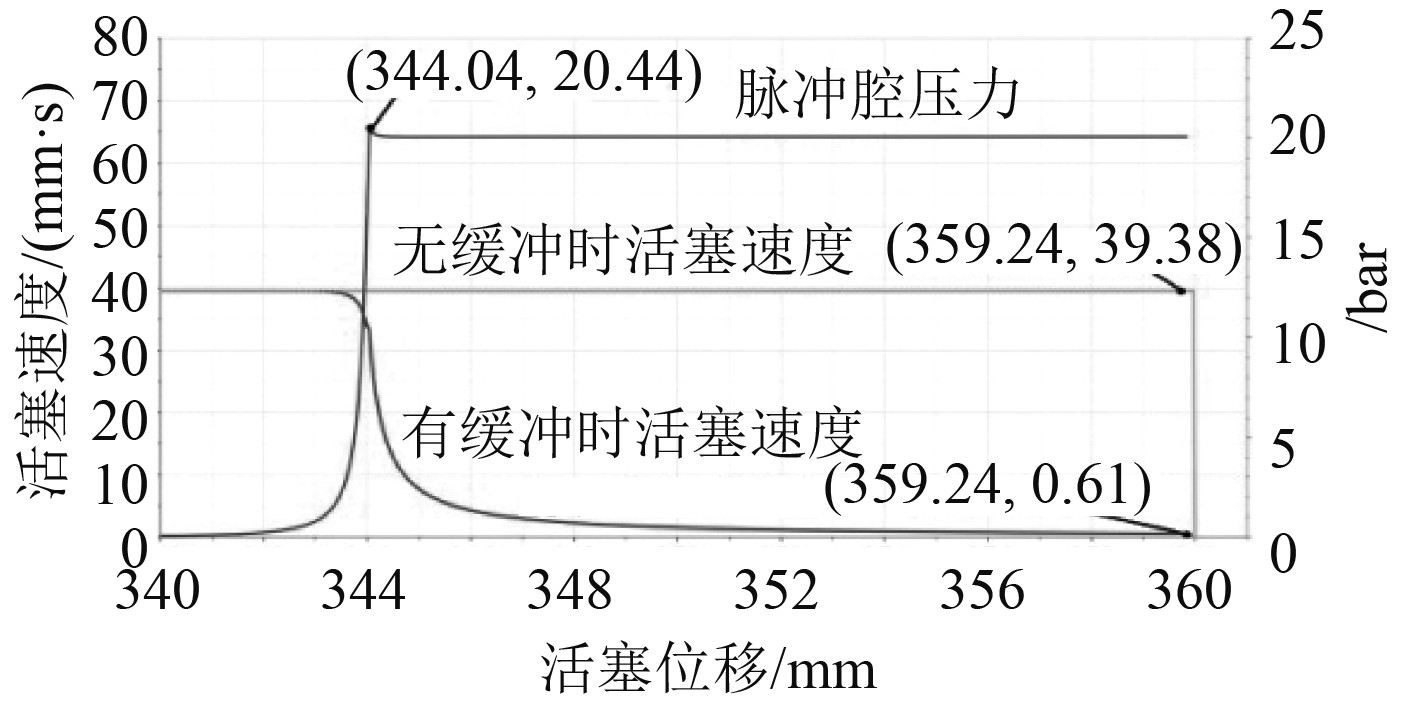
|
图 7 活塞速度与缓冲腔压力随活塞位移 Fig. 7 Curves of buffering cavity pressure and piston velocity changes with piston displacement |
可以看出,无缓冲时,活塞在到达行程终点前作匀速运动,在行程终点处速度骤降为0。增加缓冲装置后,活塞初始为匀速运动,到344 mm附近速度开始作变减速运动,并持续到行程终点。缓冲腔压力随着活塞位移增加逐步上升,在344 mm附近达到峰值(20.44 bar),随后迅速恢复到稳态压力值(20 bar)并持续到行程终点。有缓冲与无缓冲相比,活塞在到达行程终点前的速度(盖板与止挡板的撞击速度)下降约为98%,缓冲过程较为平缓,没有出现较大的液压冲击。
4 结 语针对圆柱形变节流面积缓冲装置,建立其数学模型对其进行受力分析和运动学分析,将缓冲过程分为2个阶段,得到了含负载条件下缓冲腔压力、活塞速度随活塞位移的变化关系。对该缓冲装置进行参数设计并计算缓冲装置的缓冲性能,结果表明:
1)单边间隙对缓冲腔压力和活塞速度的影响最大,缓冲套大端直径、锥角的影响次之,圆锥段长度对缓冲性能的影响最小。
2)有缓冲与无缓冲相比,活塞在到达行程终点前的速度(盖板与止挡板的撞击速度)下降约为98%,缓冲过程较为平缓,没有出现较大的液压冲击。
| [1] |
周志才, 吴新跃, 谢最伟. 基于ADAMS/Insight的某传动机构参数优化[J]. 机械工程师, 2011(6): 64-66. DOI:10.3969/j.issn.1002-2333.2011.06.030 |
| [2] |
赖浩凯, 楼京俊, 孙炯, 等. 基于ADAMS和AMESim软件的舰艇某装置启闭建模及优化[J]. 中国舰船研究, 2014, 9(3): 105-108+122. DOI:10.3969/j.issn.1673-3185.2014.03.016 |
| [3] |
赵伟, 黄钰曌, 俞浙青, 等. 高速液压缸活塞式缓冲机构的研究[J]. 中国机械工程, 2014, 25(8): 1033-1036. DOI:10.3969/j.issn.1004-132X.2014.08.008 |
| [4] |
邓经纬, 曹楚君. 基于AMESim油缸缓冲装置优化设计[J]. 机床与液压, 2017, 45(10): 122-125. DOI:10.3969/j.issn.1001-3881.2017.10.032 |
| [5] |
王传瑶, 王勇勤, 罗远新, 等. 液压缸缓冲动态特性对比研究[J]. 液压与气动, 2017(10): 89-95. DOI:10.11832/j.issn.1000-4858.2017.10.015 |
| [6] |
吴仁智, 徐君, 张洪伟. 圆柱形变节流面积缓冲结构的缓冲性能分析[J]. 中国工程机械学报, 2013, 11(3): 211-215. DOI:10.3969/j.issn.1672-5581.2013.03.006 |
| [7] |
梁全, 谢基晨, 聂利卫. 液压系统Amesim计算机仿真进阶教程[M]. 北京: 机械工业出版社, 2016.
|
 2020, Vol. 42
2020, Vol. 42
