2. 西北工业大学 动力与能源学院,陕西 西安 710072;
3. 先进航空发动机协同创新中心,北京 100191
2. School of Power and Energy, Northwestern Polytechnical University, Xi'an 710072, China;
3. Collaborative Innovation Center of Advanced Aero-Engine, Beijing 100191, China
离心叶轮机械在运行过程中的强噪声辐射严重危害了工作人员的身心健康,也对设备安全运行带来了隐患。从噪声产生机理上分析,风机的噪声分为叶轮内部湍流运动激发的湍流噪声,叶片壳体偶极子源激发的偶极子源噪声,还有气动力激励壳体振动产生的振动噪声。前两类可以归为气动噪声,后一类归为结构噪声[1]。目前绝大多数研究集中在气动噪声上,且大多表现为离散单音特性[2-6]。此方法利用CFD技术求解非定常流场获取噪声源信息,基于Lighthill声比拟理论及其特殊方程(求解固定壁面声场的Curle方程,求解旋转运动声场的FW-H方程等)以及求解涡流噪声的Powell涡流声理论等诸多气动噪声预测方法获取远场声压。主要分为2个步骤:1)近场非线性流场的CFD瞬态计算,得到叶片和蜗壳表面的脉动力,即获取噪声源时域数据;2)以叶片和蜗壳表面的脉动力快速傅里叶变换(FFT)得到的频域解作为点声源激励,采用Lighthill声比拟理论及其特殊方程形式得到远场声压。Younis等[3]应用非定常雷诺时均应力方程(URANS方程)和FW-H方程对某型多翼离心风机叶片单极子和偶极子噪声进行了数值预测和分析;Khelladi等[7]通过URANS和 Lowson公式结合的方法,求解了某型离心风机叶轮叶片和扩压器叶片单极子和偶极子源激发产生的气动噪声;Suarez等[8]结合URANS和Powell涡声理论对某型后向离心叶轮和蜗舌间隙对风机噪声的影响进行了研究和分析;Liu等[9]创造性地结合大涡模拟(LES)、FW-H方程和Powell涡声理论等方法对带有蜗壳的离心风机叶片和蜗壳偶极子源离散单音噪声和涡流引发的四极子宽频噪声进行了数值预测研究,为了在计算中考虑叶轮和蜗壳的固体边界对声波传播的影响,Tournour[10]和Cai[11]等采用声学边界元法求解远场噪声,但是求解得到的噪声是建立在自由场边界基础上的,预测精度有损失。为了考虑复杂边界(叶片和蜗壳边界)对声传播的影响,张建华等[12]提出了一种基于声学有限元方法,此方法将风机的气动噪声预测分为2个主要步骤:1)基于URANS求解叶片和蜗壳偶极子噪声源;2)通过频域变换和Galerkin方法离散求解FW-H方程,并成功地对此风机气动噪声进行了数值预测。本文将采用此方法获得风机的离散单音噪声。事实上风机的非定常流动诱发的噪声属于流固耦合噪声,叶轮和蜗壳是弹性体结构,尤其在大型风机中蜗壳的振动不可忽略。风机的振动噪声研究文献较少,Koopmann[13]首次提出了一种基于边界元(BEM)计算和实验测量相结合的预测方法;Cai[11]和 Liu[14]发展这种方法,并数值预测了工业用离心风机蜗壳振动声辐射。张建华[15]基于声学有限元方法(FEM)并考虑蜗壳壁面对声波的散射和反射作用,结合流固声单向耦合方法数值预测了壳体振动声辐射。事实上,带有壳体的大型离心风机噪声主要分为气动噪声和振动噪声,风机在运行过程中的噪声是多种噪声源激发的噪声的相互抑制和相互叠加,然而,很少有学者对风机的噪声进行定量的分析。本文针对大型船用离心风机多噪声源(叶轮偶极子源、壳体偶极子源、结构振动激励源)激励特点,对上述多噪声源进行定量预测和分析,确定主要的噪声分量。
1 离心风机噪声计算模型 1.1 离心风机模型参数以某船用离心风机为研究对象,该风机依据使用环境不同,分为2种安装状态:进出口开口和进出口连接有封闭长管道,本文所研究的风机处在第1种安装环境下,该风机具体参数见表1。
|
|
表 1 风机参数 Tab.1 Parameters of marine centrifugal fan |
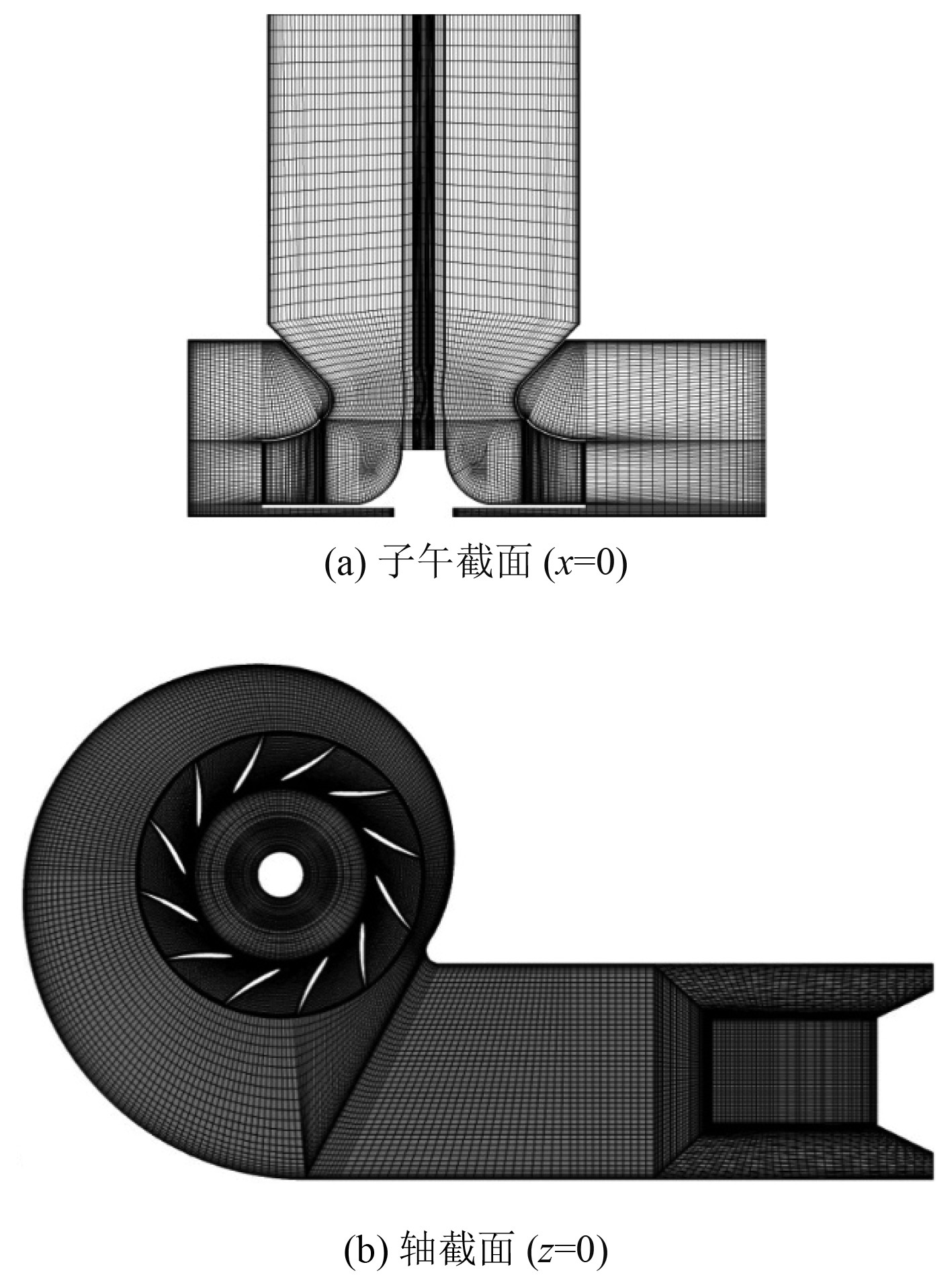
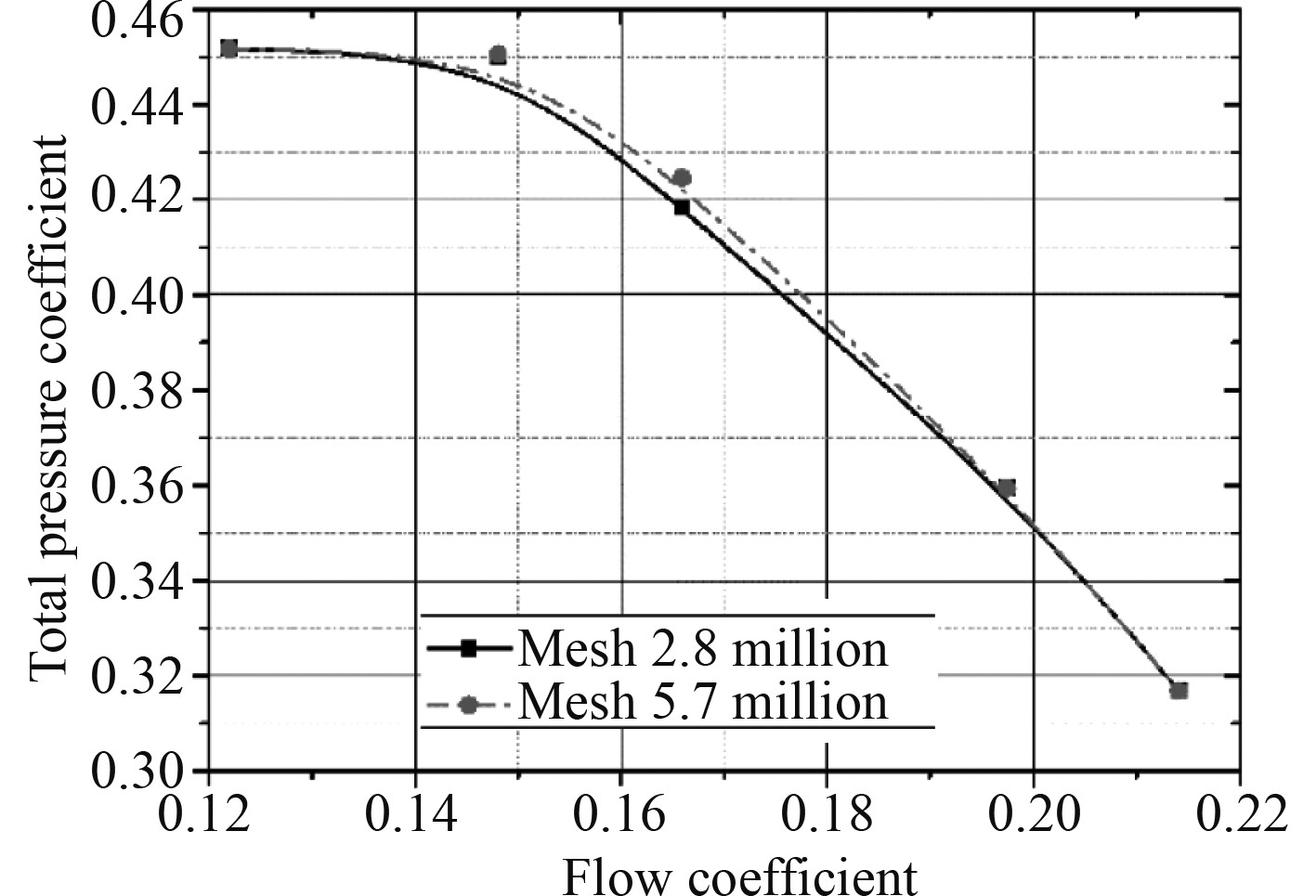
为了获得较为精确的计算结果,风机内部的流动结构全部采用ICEM划分较高正交性的六面体结构化网格。风机网格采用多计算域处理,按照安装结构分为4个组成部分:风机进口管道和集流段计算域(包含深入叶轮内静止的气流空腔区域),NACA65翼型叶轮计算域、蜗壳流体通道计算域(带有前后空腔),出口延伸段和节流阀计算域。为了尽可能降低计算模型和样机之间误差的影响,网格构建过程中考虑了集流段与叶轮进口之间的径向间隙、叶轮厚度以及集流段厚度,网格细节见图1。图2显示了风机的总压升系数随流量变化曲线,网格数增加1倍后,总压升基本保持不变,此曲线进一步证明了网格数超过280万后,网格达到无关解。
|
图 1 风机网格剖面图 Fig. 1 Grid section of blade and hub |
|
图 2 网格无关解验证 Fig. 2 Validation of grid independent |
基于商业软件Ansys CFX求解连续方程、动量方程和Standard k-ε湍流控制方程。各控制方程均采用有限元体积法离散。特征风机的叶尖马赫数(叶轮叶尖周向速度和当地声速之比)小于0.3,风机内部的流动被认为是不可压缩的,风机进出口温差几乎没有变化,流动是绝热的,计算中忽略能量方程;基于高阶格式(high revolution)离散差分控制方程,双时间步长全隐式格式以及二阶后向欧拉差分离散非定常计算的时间项,基于压力的耦合求解算法获得连续方程和动量方程的解[16]。为了加速非定常计算收敛过程,通常以定常流场的稳态解为初场。非定常时间步长为5.7089E-5 s(每个叶片通道设定30个时间步)。收敛判定:定常计算要求所有求解方程RMS残差降到10–5以下;非定常要求监测点变量呈现完整的周期性波动。计算得知,当叶轮转过5 400个时间步,即叶轮转动15圈后,设定的监测点达到完整的周期性波动,认定计算收敛。
1.3 噪声计算模型 1.3.1 气动噪声计算采用URANS耦合FW-H方程的方法求解该船用离心风机的气动噪声和振动噪声辐射。前期的研究显示,对于本文研究的低马赫数的离心风机气动噪声,叶片和蜗壳表面的偶极子源是主要噪声源[12]。因此,计算中忽略声源信息中与叶轮和蜗壳内部湍流运动相关联的四极子声源项和与排挤流体体积关联的单级子叶片厚度声源项,仅保留周期性非定常压力脉动激发的偶极子声源项。
计算旋转叶片偶极子源产生的基频及其谐波噪声时,需要对叶片偶极子源噪声进行特别处理,以适合 Helmholtz 方程的求解。本文使用Lowson公式对叶片的基频气动声源进行建模,基于等效声源的方法将叶片分为20段,将非定常流场计算稳定收敛后提取的叶片壁面压力脉动时域数据按照各部分进行面积分得到对应的3个方向的时域力,随后对所得3个方向的时域力进行FFT变换转换为计算所需的频域力,作为叶片偶极子声源,最后基于Lowson公式计算自由场辐射声。壳体气动噪声的计算分为2个重要步骤:1)求解风机内部的非定常流场,获得稳定收敛后的蜗壳壁面的非定常时域压力脉动数据,经过Fourier变换得到压力脉动的频域分量,作为偶极子声源项;2)基于Helmholtz方程的频域形式求解带有上述蜗壳表面偶极子声源项的非齐次波动方程。
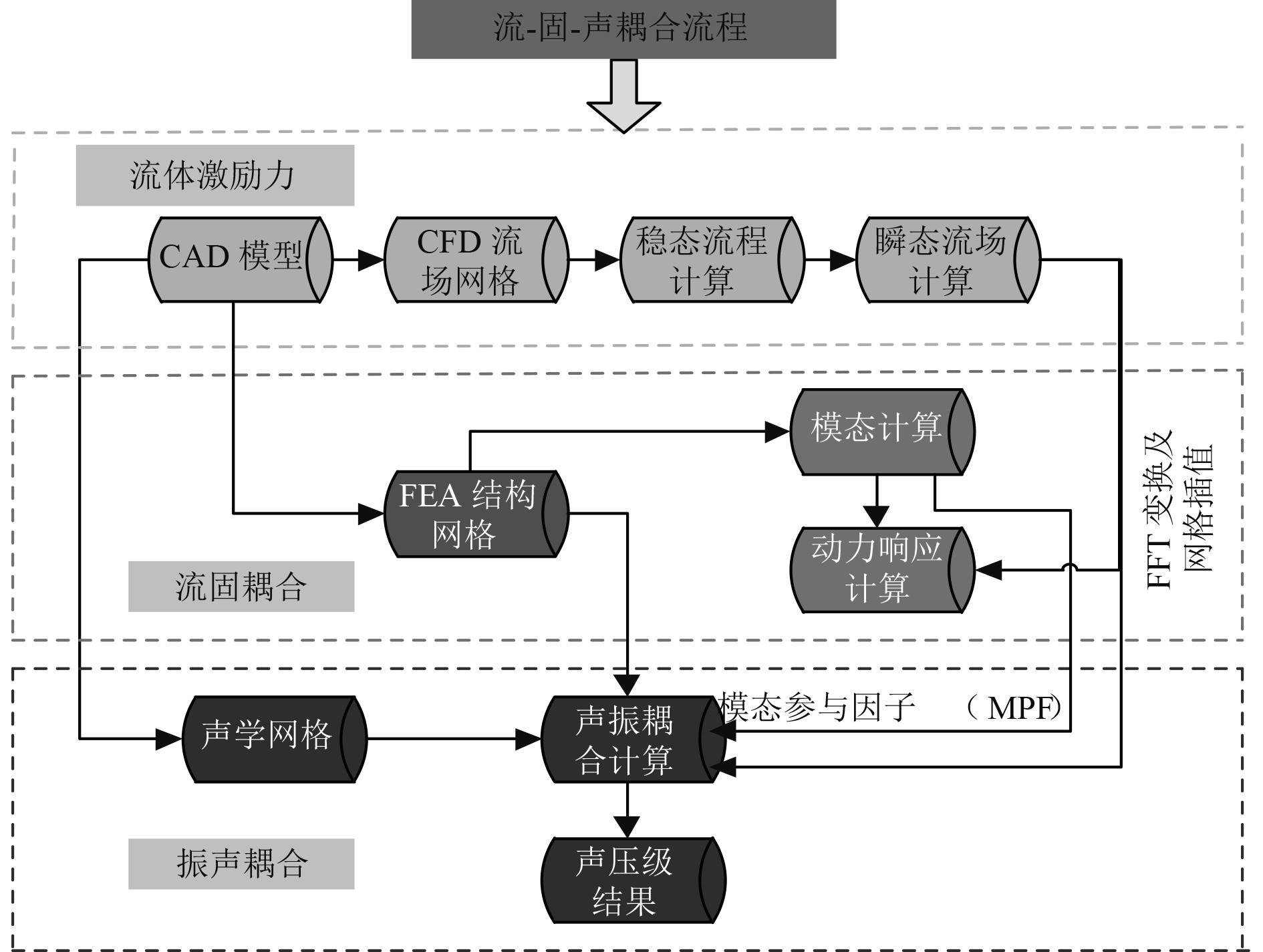
1.3.2 振动噪声计算壳体的振动噪声以壳体表面的振动速度或振动加速度为边界条件(壳体的振动加速度通过单向流固耦合计算获得,详细过程参考文献[17])。基于模态叠加法求解蜗壳的各阶模态参与因子,采用振动-噪声耦合计算方法获取壳体的振动噪声辐射,图3给出了流-固-声耦合计算流程示意图。
|
图 3 振声耦合流程示意图 Fig. 3 The flow chart of numerical evaluation method of casing vibro-acoustic coupling |
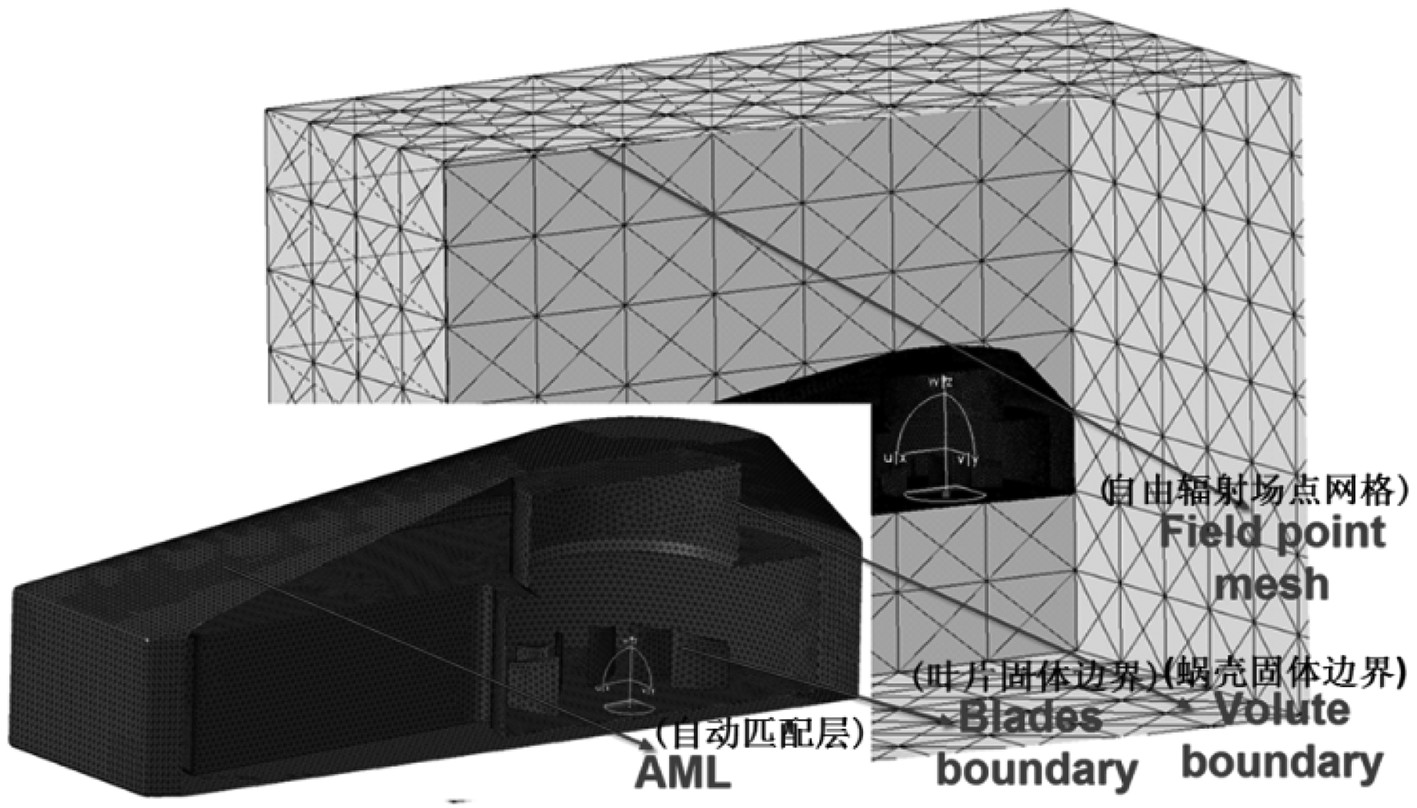
频域的Helmholtz波动方程基于声学有限元方法离散,建模中考虑了叶片和蜗壳固壁对声波的散射和反射作用[12],图4给出了划分完成的声学有限元网格。该网格采用非结构化的四面体网格,网格尺寸最大值为18 mm,总的网格数为1 600 094。为了保证许可最大频率下的空间求解精度,该声学网格单元长度
|
图 4 船用离心风机声学有限元网格 Fig. 4 Acoustic mesh of marine centrifugal fan |
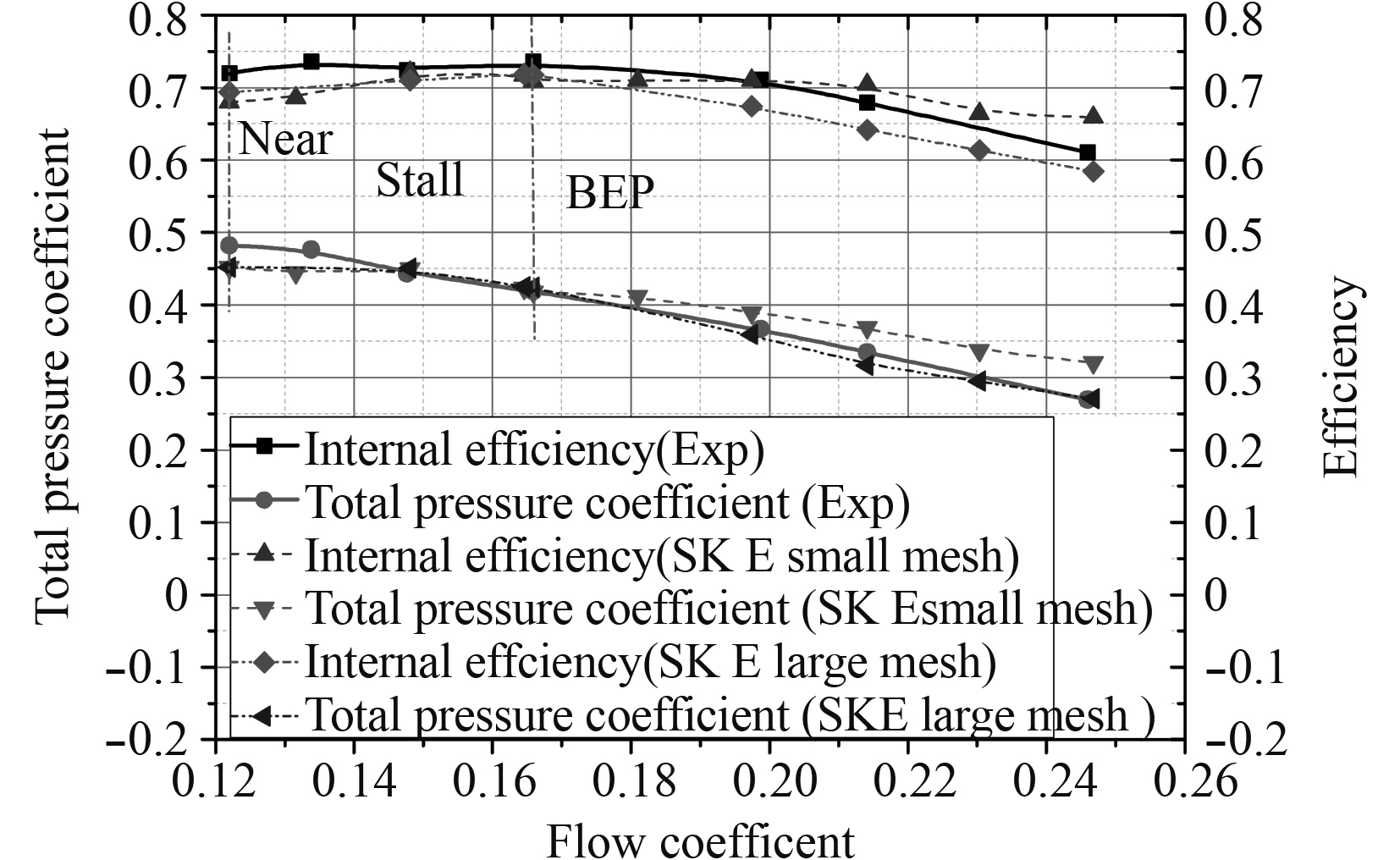
为了对数值计算模型进行验证,图5给出了风机气动性能数值和实验的对比曲线。定义无量纲的流量系数φ、总压系数ψ,效率η计算公式为:
|
图 5 风机气动性能曲线对比 Fig. 5 Comparison between numerical and experimental curves |
| $ \varphi = \frac{{{\rm{4}}{Q_{\rm{v}}}}}{{{\text{π}} {D^{\rm{2}}}{u_{\rm{2}}}}}, \psi = \frac{{{P_{\rm{t}}}}}{{\rho u_{\rm{2}}^{\rm{2}}}}, \eta = \frac{{{P_{\rm{t}}} \cdot {Q_{\rm{v}}}}}{{{P_{\rm{w}}}}} {\text{。}} $ | (1) |
其中:
在设计转速下(2920 r/min)的最大效率点(BEP)对应的流量为Q=3.361 kg/s(φ=0.166)和总压升 PT=3182 Pa(ψ=0.420)。从图可以看出,计算和实验性能曲线吻合良好,两者具有相同的趋势:风机全压升随着流量的增大而减小。在近设计点附近((φ=0.149~0.20)计算值和实验值误差最小。
风机蜗壳偶极子源激发的单音噪声主要来源于蜗壳表面的非定常压力脉动[3-6]。因此,对风机壳体壁面压力脉动的验证是确定噪声源计算准确性的关键。蜗舌部位为起始点(0°位置),沿蜗壳周向逆时针方向非均匀的布置11个测量截面,各截面角度分布如表2所示。每个轴向截面(Z/B=0.17,0.27,0.34,0.75,B表示蜗壳轴向宽度;Z表示测点到蜗壳后板的距离)非均匀分布4个轴向点位。
|
|
表 2 壳体周向测点角度坐标分布 Tab.2 The distribution of angle coordinates of measurement points on volute |
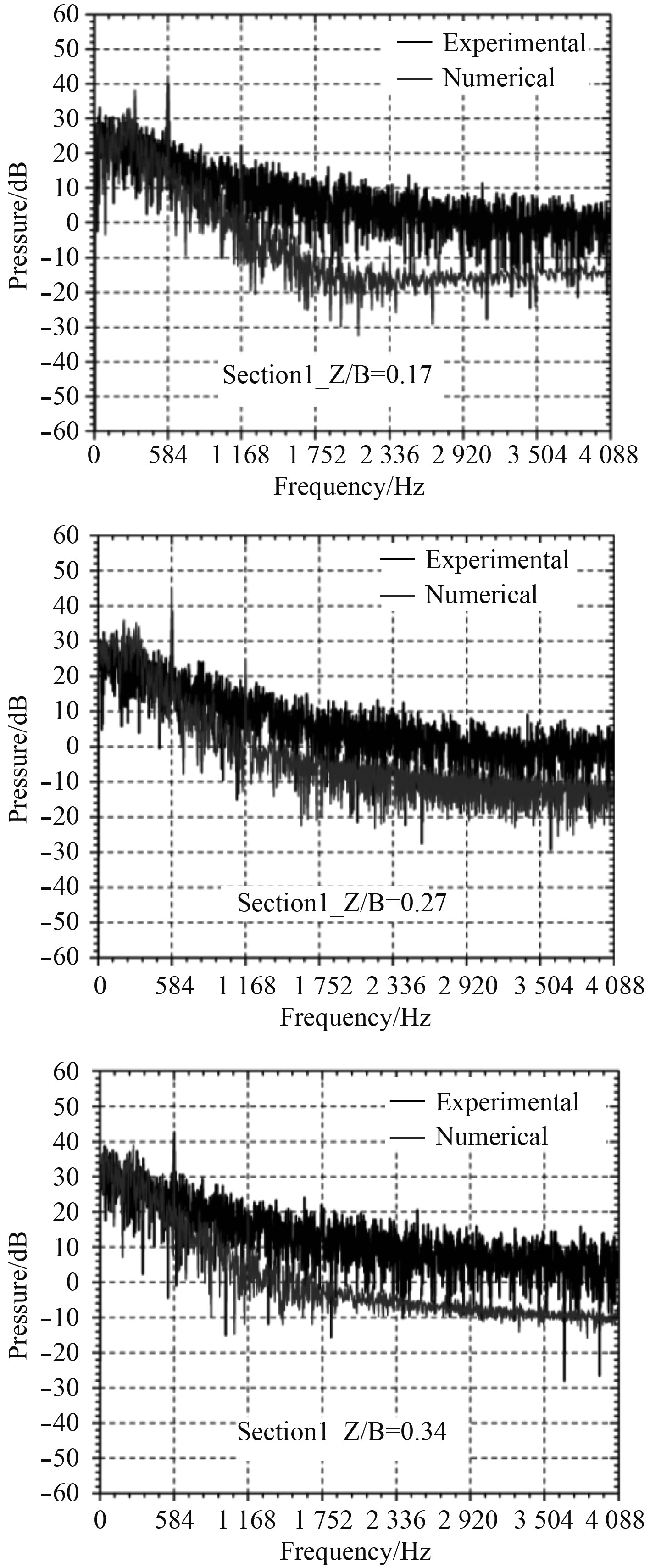
由于不同点位频谱波形具有相似性,仅给出压力脉动最为强烈的蜗舌截面(P1,蜗舌上周向0°)3个点位频谱图实验和计算结果对比。图6给出了蜗壳壁面P1截面叶轮叶轮出口点位压力脉动频谱图。在P01点位的所有的数值和实验测量频谱中,叶轮出口范围内(Z/B=0.07~0.36),叶片通过频率(BPF,基频对应584 Hz)处观察到明显的峰值,且在基频上,计算和实验吻合较好。这表明对于最为关注的基频噪声,噪声源计算模型是可靠的,详细实验和计算分析过程参考文献[12]。
|
图 6 蜗壳壁面P01截面压力脉动频谱 Fig. 6 Power spectra of casing pressure fluctuation at three measurement points with the flow rate BEP Point 01 |
为了定量的确定噪声源强度,定义一个周期时间内固定节点的偶极子强度如下:
| $ {I_d}_s = \sqrt {\frac{1}{N}{{\sum\limits_{i = 1}^N {\left( {{{\left. {\frac{{\partial {p_s}}}{{\partial t}}} \right|}_i}} \right)} }^2}} {\text{,}} $ | (2) |
经过FFT变换后,上式转变为:
| $ {I_d}_s = \sqrt {\frac{1}{N}{{\sum\limits_{i = 1}^N {\left( {{{\left. {\omega {p_s}} \right|}_i}} \right)} }^2}} {\text{。}} $ | (3) |
其中:N为总时间步数,
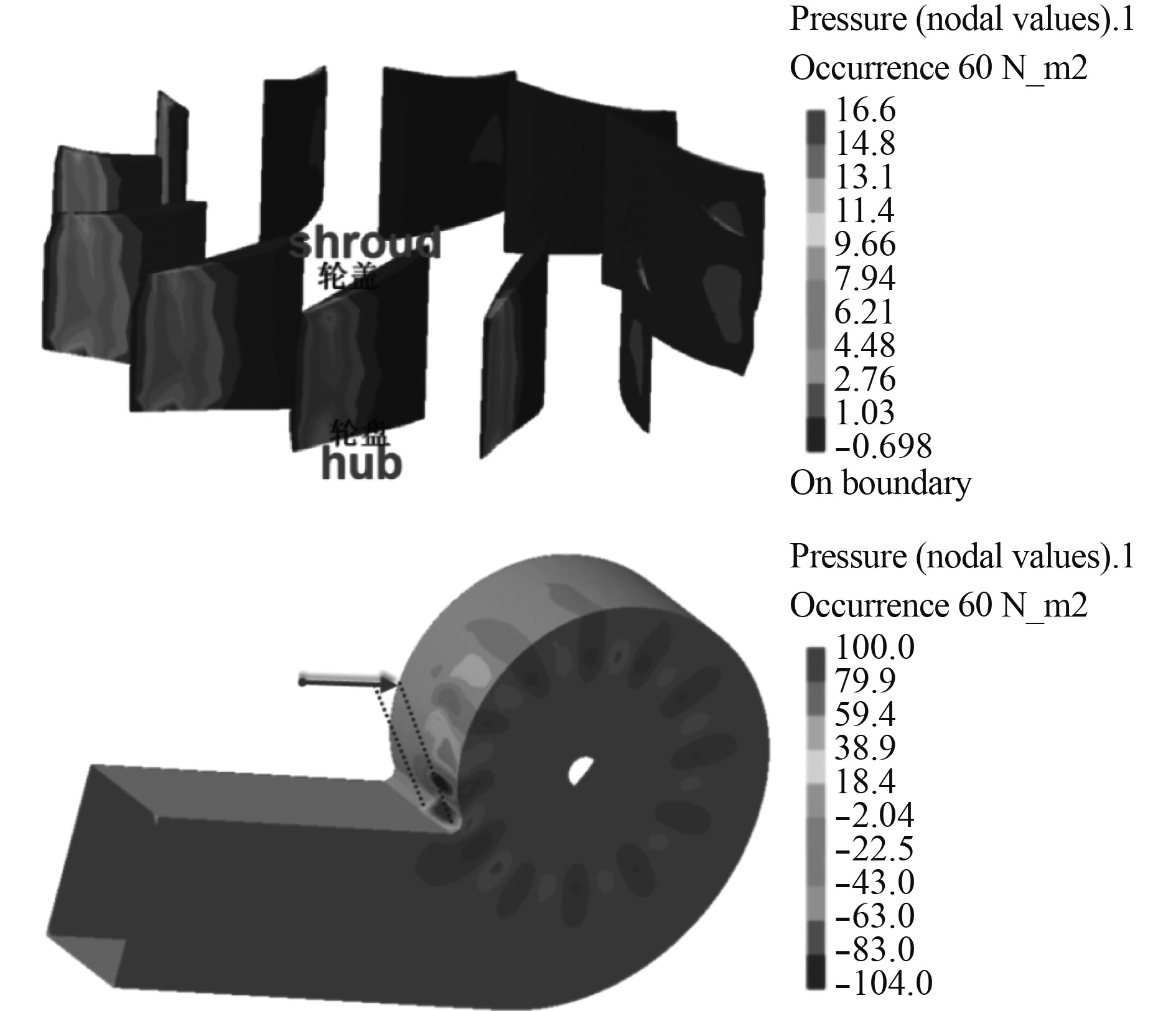
|
图 7 基频下偶极子源强度分布:(a)叶片;(b)蜗壳 Fig. 7 The distribution of acoustic dipole sources intensity:(a)blades;(b)volute |
定义测点频谱声压级(SPL)公式为:
| $ {L_{pi}}(\omega ) = 20\lg (p{}_i(\omega )/{p_{ref}}) {\text{。}} $ | (4) |
式中:
依据3步计算法获得壳体振动噪声辐射:1)计算振动激励源(壳体壁面压力脉动)并将其插值和FFT变换后加载到结构有限元网格上;2)计算振动噪声源(流固耦合计算);3)将壳体振动速度或是加速度作为计算边界,基于模态叠加法进行振声耦合计算。
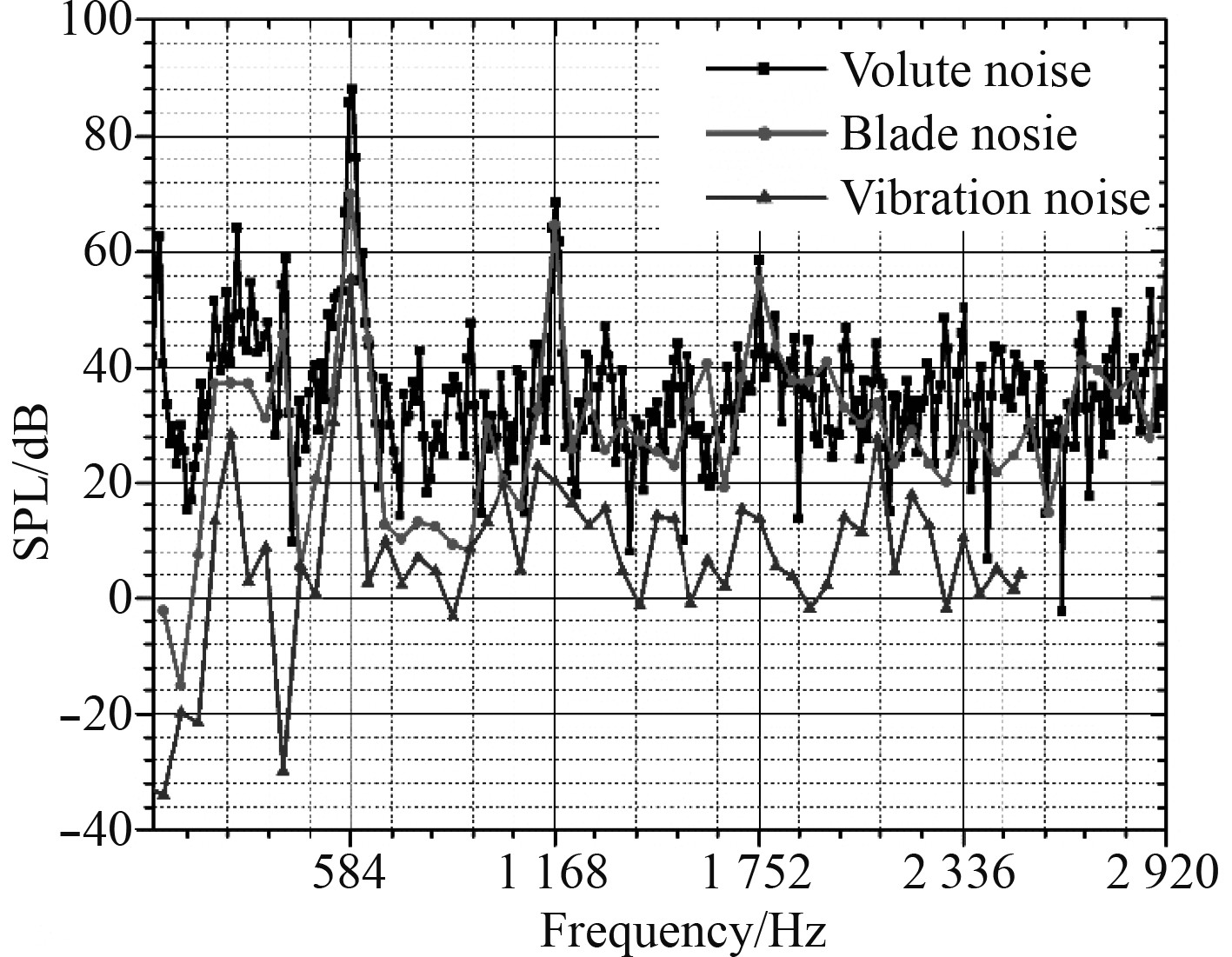
图8给出了设计流量下(BEP),距离风机管道出口1 m处45°测点不同激励力(叶片偶极子源、蜗壳偶极子源、蜗壳结构振动响应)的噪声频谱。可以看出,任意一种激励力下,基频及其谐波的噪声分量幅值较高,基频的噪声分量均占据主导地位,壳体基频噪声最大约为87 dB,叶片噪声次之约为71 dB,壳体振动噪声最小约为57 dB。可见,对于进出口未连接长管道的离心风机,蜗壳基频振动噪声远小于基频气动噪声(相差30 dB)。
|
图 8 距离风机出口1 m,45°测点噪声频谱 Fig. 8 Sound pressure level at measured points distance to outlet 1meter, 45° |
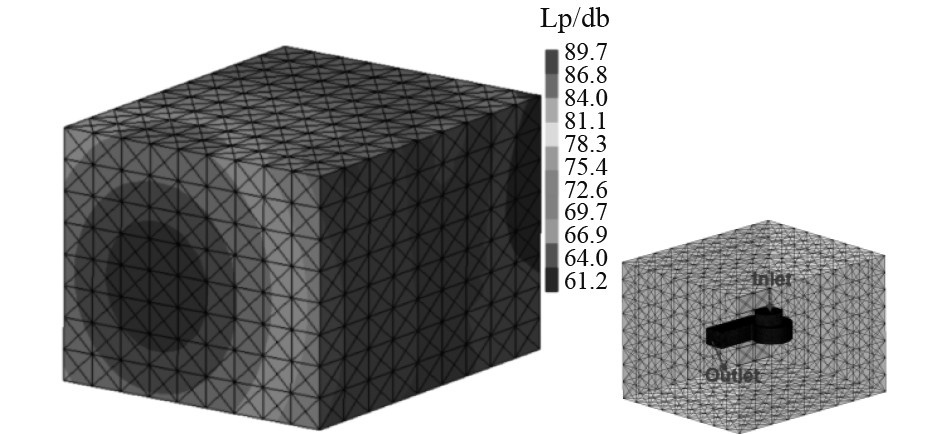
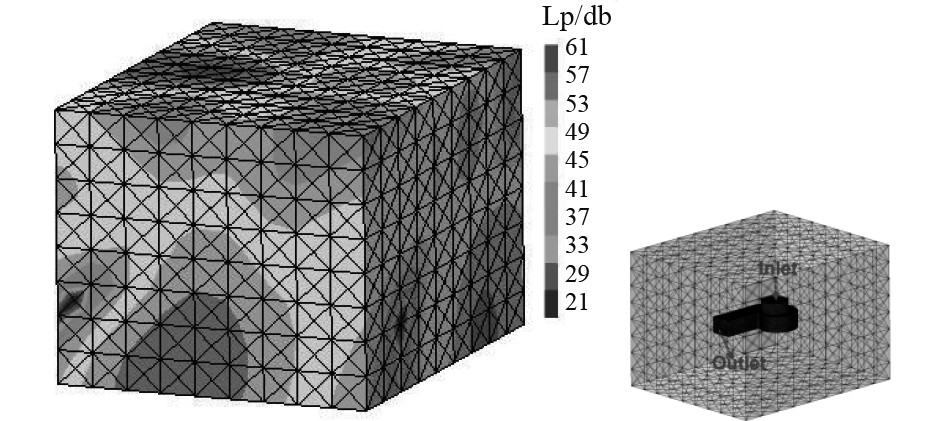
图9~图11 给出了风机叶轮基频气动噪声、壳体基频气动噪声和壳体基频振动噪声的场点声压分布。可以清晰观察到,气动噪声主要从出口管道传播,噪声辐射较为集中;振动噪声在进出口区域均观察到明显的高噪声辐射区;噪声辐射较为分散。虽然前文的分析表明壳体的气动噪声最高,但是真实风机噪声是3种噪声的相互干涉、相互叠加,尤其是叶片和壳体气动噪声的叠加作用。图12给出了叶片和壳体气动噪声耦合叠加的场点声压分布。可以看出,不管如何叠加,风机的噪声依然以基频分量为主,场点的最大总基频噪声声压级约为90.6 dB,略高于壳体基频气动噪声(89.7 dB),并且这两部分噪声分量的叠加并没有改变原有的声场指向性,噪声依然主要从风机管道出口向外辐射声能量。

|
图 9 叶片基频(584 Hz)噪声场点的声压分布(BEP) Fig. 9 Sound pressure distributions of blade noise at BPF(584 Hz) |
|
图 10 壳体基频(584 Hz)噪声场点的声压分布(BEP) Fig. 10 Sound pressure distributions of casing noise at BPF(584 Hz) |
|
图 11 壳体基频(584 Hz)振动噪声场点声压分布(BEP) Fig. 11 Sound pressure distributions of vibrational noise of casing at BPF(584 Hz) |

|
图 12 叠加后风机基频(584 Hz)噪声场点的声压分布(BEP) Fig. 12 Sound pressure distributions of field points of fan BPF noise |
1)对于进出口开口的船用离心风机结构,其主要噪声源可以分为壳体表面偶极子源、叶片表面偶极子源、壳体振动激励源。研究表明,风机的噪声以基频为主,且风机的壳体偶极子源激发产生的基频气动噪声最为突出,87 dB;其次是叶片偶极子源激发产生的叶片基频噪声,71 dB;蜗壳振动激发产生的基频振动噪声最小,57 dB。
2)风机气动噪声主要从管道出口向外辐射,且噪声辐射能量集中;壳体振动激发产生的振动噪声,在进出口区域均发现高能辐射区,且噪声辐射能量分散。
3)真实风机中3种噪声是相互干涉、相互叠加作用,尤其是叶片和壳体气动噪声的叠加。研究表明,噪声叠加使总噪声辐射增加了0.9 dB,但是声场的指向性没有发生变化。
| [1] |
WRIGHT S E. The acoustic spectrum of axial flow machines[J]. Journal of Sound and Vibration, 1976, 45(2): 165-223. DOI:10.1016/0022-460X(76)90596-4 |
| [2] |
BALLESTEROS-TAJADURA R, VELARDE-SUÁREZ S, HURTADO-CRUZ JUAN P. Noise Prediction of a Centrifugal Fan: Numerical Results and Experimental Validation[J]. ASME Journal of Fluids Engineering, 2008, 130(9): 1-12. |
| [3] |
YOUNSI M, BAKIR F, KOUIDRI S, et al. Numerical and experimental study of unsteady flow in centrifugal fan[J]. Proceeding of the Institution of Mechanical Engineers, Part A, Journal of Power and Energy, 2007, 221(7): 1025-1036. DOI:10.1243/09576509JPE445 |
| [4] |
JEON WH. A numerical study on the effects of design parameters on the performance and noise of a centrifugal fan[J]. Journal of Sound and Vibration, 2003, 265(1): 221-230. DOI:10.1016/S0022-460X(02)01582-1 |
| [5] |
PARAMASIVAM K, RAJOO S, ROMAGNOLI A, et al. Tonal noise prediction in a small high speed centrifugal fan and experimental validation[J]. Applied Acoustics, 2017, 125(04): 59-70. |
| [6] |
PREZELJ J, NOVAKOVIĆ T. Centrifugal fan with inclined blades for vacuum cleaner motor[J]. Applied Acoustics, 2018, 140(05): 13-23. |
| [7] |
KHELLADI S, KOUIDRI S, BAKIR F, et al. Predicting tonal noise from a high rotational speed centrifugal fan[J]. Journal of Sound and Vibration, 2008, 313(1-2): 113-133. DOI:10.1016/j.jsv.2007.11.044 |
| [8] |
SUAREZ S V, TAJADURA R B, MORROS C S, FRANWS J F. Numerical prediction of the aerodynamic tonal noise in a centrifugal fan[C]. ASME Fluids Engineering Division Summer Meeting, Montreal, Canada, July, 2002.
|
| [9] |
LIU Qiuhong, QI Datong, TAN Hongtao. Computation of aerodynamic noise of centrifugal fan using LES approach, acoustic analogy and vortex sound theory[J]. Proc. ImechE, Part C: Journal of Mechanical Engineering Science, 2007, 221(11): 1321-1332. DOI:10.1243/09544062JMES609 |
| [10] |
TOURNOUR M, EL HACHEMI Z, ALEX R. Investigation of the tonal noise radiated by subsonic fans using the aero-acoustic analogy[C]. Proceeding of Fan Noise International Symposium, Senlis, France: CETIM, 2003.
|
| [11] |
J.C. CAI, D.T. QI. A quantitative study of the blade passing frequency noise fan[J]. Journal of Vibration Engineering, 2012, 14(3): 1200-1211. |
| [12] |
Jianhua ZHANG J, Wuli CHU, Haoguang ZHANG, et al. Numerical and experimental investigations of the unsteady aerodynamics and aero-acoustics characteristics of a backward curved blade centrifugal fan[J]. Applied Acoustics, 2016, 110(3): 256-267. |
| [13] |
KOOPMANN G H, NEISE W CUNFARE K A. Fan casing noise radiation[J]. ASME Journal of Vibration and Acoustics, 1991, 113(1): 37-42. DOI:10.1115/1.2930152 |
| [14] |
F.A. LU, X.J WANG,, D.T. QI, J.C. CAI. Study of the tonal noise of a centrifugal fan at the blade passing frequency. Part II. vibroacoustics[J]. Journal of Low Frequency Noise, Vibration and Active Control, 2011, 30(2): 89-105. DOI:10.1260/0263-0923.30.2.89 |
| [15] |
张建华. 船用离心风机内部非定常流动诱发噪声产生机理及其降噪策略研究[D], 西安: 西北工业大学, 2016.
|
| [16] |
Jiancheng CAI, Datong QI, Fu′an LU. Study of the tonal noise of a centrifugal fan at the blade passing frequency Part II. Vibroacoustics[J]. Journal of Low Frequency Noise Vibration and Active Control, 2010, 29(4): 253-266. DOI:10.1260/0263-0923.29.4.253 |
| [17] |
ZHANG Jian-hua, CHU Wu-li, DONG Xing-jie, et al. Numerical investigation of internal fluid-induced volute vibration in a marine centrifugal fan[J]. Mechanical Science and Technology for Aerospace Engineering, 2016, 35(4): 523-530. |
 2020, Vol. 42
2020, Vol. 42
