2. 中国科学院机器人与智能制造创新研究院, 辽宁 沈阳 110016;
3. 中国科学院大学,北京 100049
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Science, Shenyang 110016, China;
3. University of Chinese Academy of Science, Beijing 100049, China
认识、开发和利用海洋是建设海洋强国的基础,在各种海洋技术中,水下自主机器人(Autonomous Underwater Vehicle,AUV)能在一般潜器不能达到的水域自主进行工作,被广泛应用在科研考察[1]、水下作业[2]和军事活动中。AUV发展的关键技术包括提高续航能力技术、水下高速通信技术、精确导航定位技术、高级自主决策技术和运动控制技术等。在诸多关键技术中,运动控制技术尤为重要,只有具备了精准度高,鲁棒性强的运动控制方法AUV才能在远洋、深海、恶劣的海况环境下自主地完成任务。水下自主机器人难以控制的主要原因有:机器人高度的非线性、时变的动态特性,水动力系数的不确定性,各自由度运动间的耦合性,存在未知水流的扰动等。从国内外公开发表的相关论文来看,经典控制理论、现代控制理论和智能控制中的很多控制方法都在AUV的运动控制中有所应用,相关研究也取得了一定的成果,主要研究包括PID控制方法,滑模变结构控制,模糊控制、鲁棒控制、神经网络控制、反步法等[3]。反步法又称为反演控制技术,其核心思想是把复杂的非线性系统分解为不超过系统阶数的子系统,然后分别为子系统设计李雅普诺夫函数和中间虚拟控制量,一直反演到整个系统的控制器设计,该方法在设计不确定系统的鲁棒控制器方面具有一定的优越性,国内外很多学者在AUV动力学模型的基础上对该方法在AUV运动控制中的运用进行了研究,但由于动力学模型难以获得、控制量求解过程存在“微分爆炸”现象,使得反步法较难在实际控制中得到应用[4-6]。鲁棒控制基于状态空间模型的频率设计方法提出了从根本上解决控制对象模型不确定性和外界扰动不确定性问题的有效方法,R. Yang基于该方法设计了AUV航向控制器,并通过试验验证了方法的有效性[7]。文献[8]利用线性化后的AUV模型设计了H∞鲁棒控制器并仿真验证了方法的有效性。神经网络控制方法以神经元理论为基础,模拟人类大脑神经元间相互连接的结构,通过网络节点间的权值建立关联,模仿人脑存储和信息处理方式对数据实现分布式存储和并行处理,该方法可以处理水下机器人强非线性问题,但系统输入输出间的映射关系无法直观表达,通常需要与其他控制方法结合使用[9]。滑模变结构控制(SMC)具有快速响应、对参数变化及扰动不灵敏的特性,因此近年来在水下机器人运动控制中受到较多的关注,Anthony J等针对AUV的速度、航向和升沉运动分别设计了SMC控制器,仿真结果显示该方法具有较强的鲁棒性[10];David Bryan Marco等将SMC方法成功应用在了ARIES AUV中,在实际航行试验中获得了较好的控制效果[11],但该方法需要基于系统模型进行设计。PID控制算法在各种控制方法中发展最为成熟,控制器设计可以不基于系统模型,被广泛应用在工业界各种控制系统中,目前水下航行器普遍采用该算法进行航行控制,但该控制器参数一旦确定将不会跟随系统状态进行改变,不具有自调整特性,因而很多时候不能满足控制需求。模糊控制器同样可以不基于系统模型进行设计,且容易对非线性系统和时变系统实现鲁棒控制,因此在很多领域已得到应用。本文在不基于系统模型进行控制器设计的背景下,研究了一种参数自调整模糊PID控制算法,并通过仿真和航行试验对算法进行了验证。
1 问题描述AUV水下运动是十分复杂的空间六自由度运动,工程应用中通常简化水平面和纵垂面运动间的耦合特性,针对两平面的运动分别设计控制器。通过泰勒级数展开法对水动力系数线性化处理,忽略质量系数矩阵中的耦合项后,可以得到平面内AUV的动力学模型如下:
| $ { A}\left[ {\begin{array}{*{20}{c}} {{{\dot v}_r}} \\ {\dot r} \\ {\dot \psi } \end{array}} \right] = {{B}}\left[ {\begin{array}{*{20}{c}} {{v_r}} \\ r \\ \psi \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{Y_\delta }} \\ {{N_\delta }} \\ 0 \end{array}} \right]{\delta _r}\left( t \right){\text{。}} $ | (1) |
| $ { A} = \left[\!\! {\begin{array}{*{20}{c}} {{{m}} - {Y_{{{\dot v}_r}}}} \!\!&\!\! 0 \!\!&\!\! 0 \\ 0 \!\!&\!\! {{I_{zz}} - {N_{\dot r}}} \!\!&\!\! 0 \\ 0 \!\!&\!\! 0 \!\!&\!\! 1 \end{array}} \!\!\right],{ B} = \left[\!\! {\begin{array}{*{20}{c}} {{Y_{{v_r}}}} \!\!&\!\! {{Y_r} - m{U_0}} \!\!&\!\! 0 \\ {{N_{{v_r}}}} \!\!&\!\! {{N_r}} \!\!&\!\! 0 \\ 0 \!\!&\!\! 1 \!\!&\!\! 0 \end{array}} \!\!\right]{\text{。}} $ |
式中:m为航行器质量,
PID控制本身的算法设计并不依赖于系统的模型,但算法的参数需要根据实际系统进行整定,是一种经典的基于反馈的线性控制器。该算法应用在非线性系统时,通常采用分段线性化的方法,在不同的工作点上分别设计控制器参数,从而实现对系统不同工作状态的控制,但工作点附近系统状态并非始终稳定,造成所获得的控制器参数难以始终保持较好的控制效果,为此有必要对传统PID算法进行改进,提高控制算法的适用性和鲁棒性。
2.1 数字PID算法在模拟系统中,PID控制器的算法表达式为:
| $ {{u(t)}} = {k_p} \cdot e\left( t \right) + {k_i} \cdot \mathop \int \nolimits_0^t e\left( t \right) \cdot {\rm d}t + {k_d} \cdot \frac{{{\rm d}e\left( t \right)}}{{{\rm d}t}} {\text{。}} $ | (2) |
式中:u(t)为控制器输出信号;e(t)为被控系统的偏差信号;kp,ki,kd为控制器参数,计算机控制系统需要对式(2)进行离散化处理,用数字形式的差分方程代替连续系统的微分方程。AUV的航向控制中,e(t)为AUV航向偏差,该数值根据目标航向和惯性组合导航单元中获得的当前航向信息计算获得。控制器参数需要根据AUV的载荷状态,航行速度进行调整,调整过程较为困难,所获得的参数往往不能总是令人满意。为了使控制器参数具有一定的自调整能力,将控制器参数引入一个调整量,使原始参数改变为:
| $ \left\{ {\begin{array}{*{20}{c}} {{k_{p1}} = {k_p} + \Delta {k_p}} {\text{,}}\\ {{k_{i1}} = {k_i} + \Delta {k_i}} {\text{,}}\\ {{k_{d1}} = {k_d} + \Delta {k_d}} {\text{。}} \end{array}} \right. $ | (3) |
模糊控制自1974年首次被应用在加热器控制后,在世界各地、各行各业得到了广泛的应用,比较典型的应用包括飞船飞行控制、机器人控制、汽车速度控制、核反应堆控制等[12]。模糊控制是模糊集合理论的重要应用,基于Mamdani模糊模型表示的模糊系统设计包括以下几个过程:
1)确定模糊控制器的输入变量。输出变量和论域:
通常把输入变量的个数称作模糊控制的维数,控制器的维数越高则相应的控制效果会越好,但相对实现起来也更加困难,计算复杂度也越高,通常选用误差和误差的微分作为控制输入构成二维模糊控制器。论域范围的选取对控制品质有重要的影响。论域太大,系统会对某些输入数值响应迟钝,同时解模糊处理时空闲区域较大;论域过小,实际数据分布特征又可能没有被反映出来。因此需要根据实际系统反复推敲确定以上信息。
2)模糊化和解模糊
模糊化是将精确量转化为模糊量的过程,是一种主观评价,可以将测量值转化成主观量值的评价。模糊控制的输入和输出空间就是分别由控制规则中的前提语言变量和结论语言变量构成的,语言变量又称为模糊标记,一般包括{负大、负中、负小、零、正小、正中、正大},对应的英文书写形式为{NB、NM、NS、Z、PS、PM、PB}。解模糊是从输出论域所定义的模糊控制作用空间到精确控制作用空间的映射,比较常用的方法有质心法、最大隶属度法、和系数加权平均法。最大隶属度法忽略了过多的参数,不能反映真实情况,常用于简单系统,质心法比较合理,但在系统复杂度高时,为了提高实时性可以用系数加权平均法代替该方法[13]。质心法计算公式如下:
| $\frac{{\mathop \sum \nolimits^ {x_i} \cdot {\mu _n}\left( x \right){\rm d}x}}{{{\mu _n}\left( x \right)}} {\text{。}}$ | (4) |
3)确定模糊规则和推理方法
模糊控制规则是模糊控制器设计的核心,整套的规则是基于长期的实践经验,并通过不断的修正完善所形成的一套有效的控制策略。一般来说,模糊控制规则先通过专家经验和控制工程知识来确定,随后根据实际操作人员控制过程来完善。模糊推理同样是控制器中的关键部分,具有模拟人基于模糊概念的推理能力。存在如下多输入多规则:
如果A1且B1,那么C1;
否则如果A2且B2,那么C2
否则如果An且Bn,那么Cn
已知A'且B''则C''的计算过程如下:
| $ \begin{split} & C' = (A'{\rm and}B')^\circ \left( {\left[ {({A_1}{\rm{and}}{B_1}} \right) \to {C_1}} \right] \cup \cdot \cdot \cdot \cup \\ & \left[ {({A_n}{\rm{and}}{B_n}} \right) \to {C_n}]) = {C_1}^{\rm{'}} \cup {C_2}^{\rm{'}} \cup \cdots \cup {C_n}^{\rm{'}} \end{split} $ | (5) |
其中
→”是命题联结词符号。“
4)模糊输入量和输出量变换
将精确量向模糊论域转化的时需要进行尺度变换,而将输出论域内的数值转化到实际控制值的过程同样需要进行尺度变换,变换的方法可以是线性的,也可以是非线性的,不同的方法对控制效果影响较大。
2.3 模糊PID控制算法使用误差和误差的微分作为控制输入的模糊控制器具有类似于PD控制器的特性,该控制器能够获得良好的系统动态特性,但无法消除静态误差。此外,控制器模糊控制规则整定困难,需要基于大量的经验和试验,工作量巨大,很难实现。水下机器人控制凝结了前人大量的工作和智慧,对于不同的航行工况往往总结了一套较为理想的PID控制参数。为了能够在继续发挥原有控制器的作用的同时对控制效果进行改善,可以使用模糊控制器对原始PID的参数进行调整,使之具有一定的自适应特性,此时模糊控制器的控制规则可以根据PID控制器参数的整定原理进行设计,并根据实际需求进行调整,相对比较容易。在AUV的航向控制中,选定航向误差ψe及其导数作为模糊控制器的输入量,设计模糊控制规则如表1~表3所示。
|
|
表 1 比例系数Δkp控制规则表 Tab.1 Scale factor control rules of Δkp |
|
|
表 2 积分系数Δki控制规则表 Tab.2 Integration coefficient control rules of Δki |
|
|
表 3 微分系数Δkd控制规则表 Tab.3 Differential coefficient control rules of Δkd |
确定了模糊控制规则后,另外一个需要解决的关键问题是模糊控制输入量和输出量的变换问题,在AUV的航向控制中,目标航向的变化范围在0~360°范围内,因此不同控制命令下,航向偏差变化范围不同且差别较大,这样使用固定的线性变换方法不在适用,因此采用公式(6)对误差数据进行非线性量化处理。该尺度变换函数两端疏松中间密集的特点与偏差大时控制较粗,偏差小时控制较细的思想相一致。
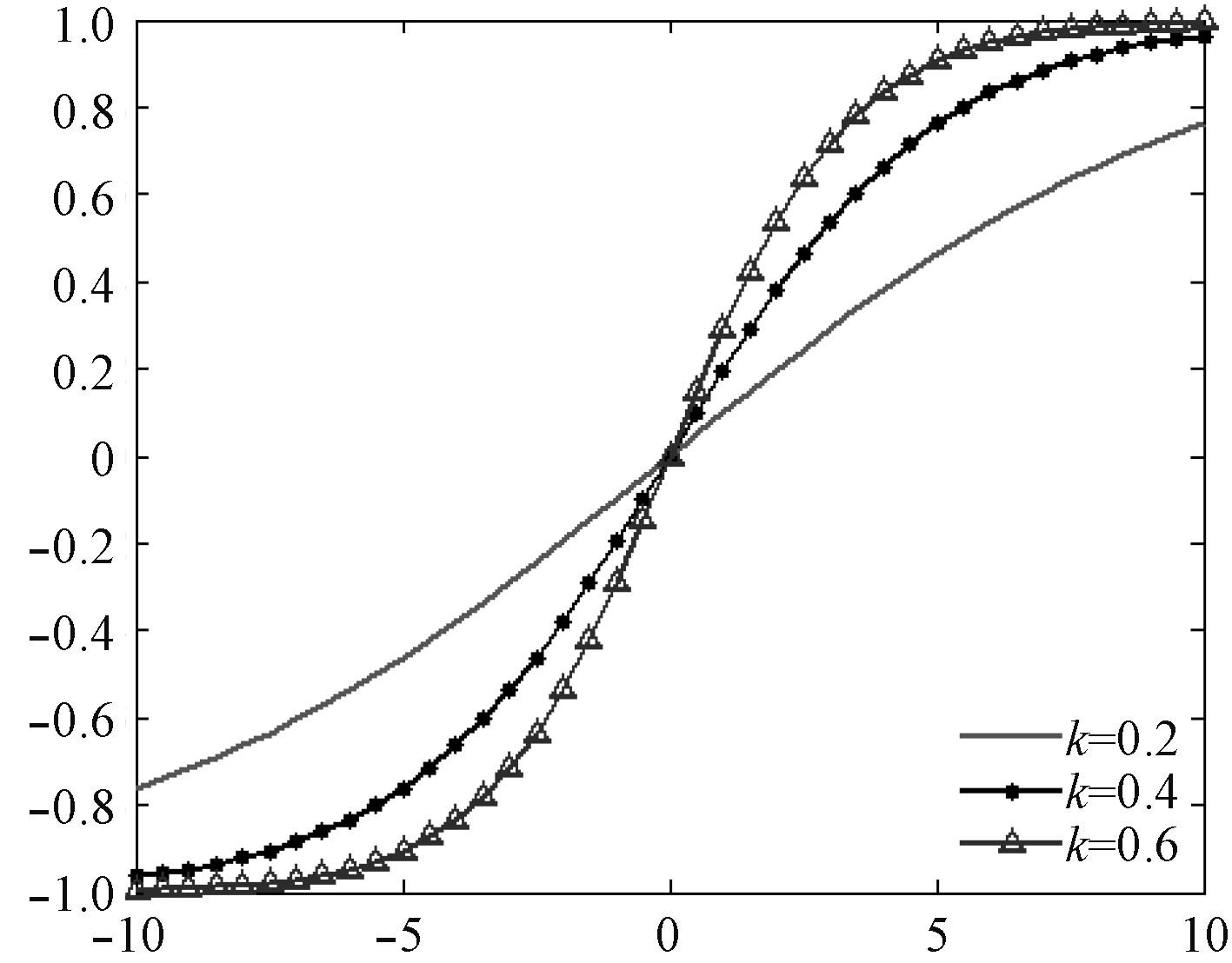
| $ {{y(x)}} = \frac{2}{{1 + {e^{ - kx}}}} - 1 {\text{。}} $ | (6) |
式中k>0,用于调节函数曲线形状的参数。图1为参数对曲线形状的影响。可以看出,在k取不同的值的时候,函数映射关系会随之改变,这样,可以根据需求,通过对参数k的调整实现对精确控制范围的调整。模糊输出部分采用典型的线性变换方法,根据控制需求设定比例系数即可。
|
图 1 尺度函数曲线 Fig. 1 Scaling function curve |
模糊PID控制器中,模糊控制规则和输入输出量的尺度变换方法对控制效果有重要的影响,其中PID控制器参数的模糊控制规则可以使用一般的模型进行调整,但尺度变换函数的参数调整通常需要结合实际航行条件进行调整,下面分别基于Matlab仿真软件和某型AUV数字仿真平台对控制器特性进行仿真验证。
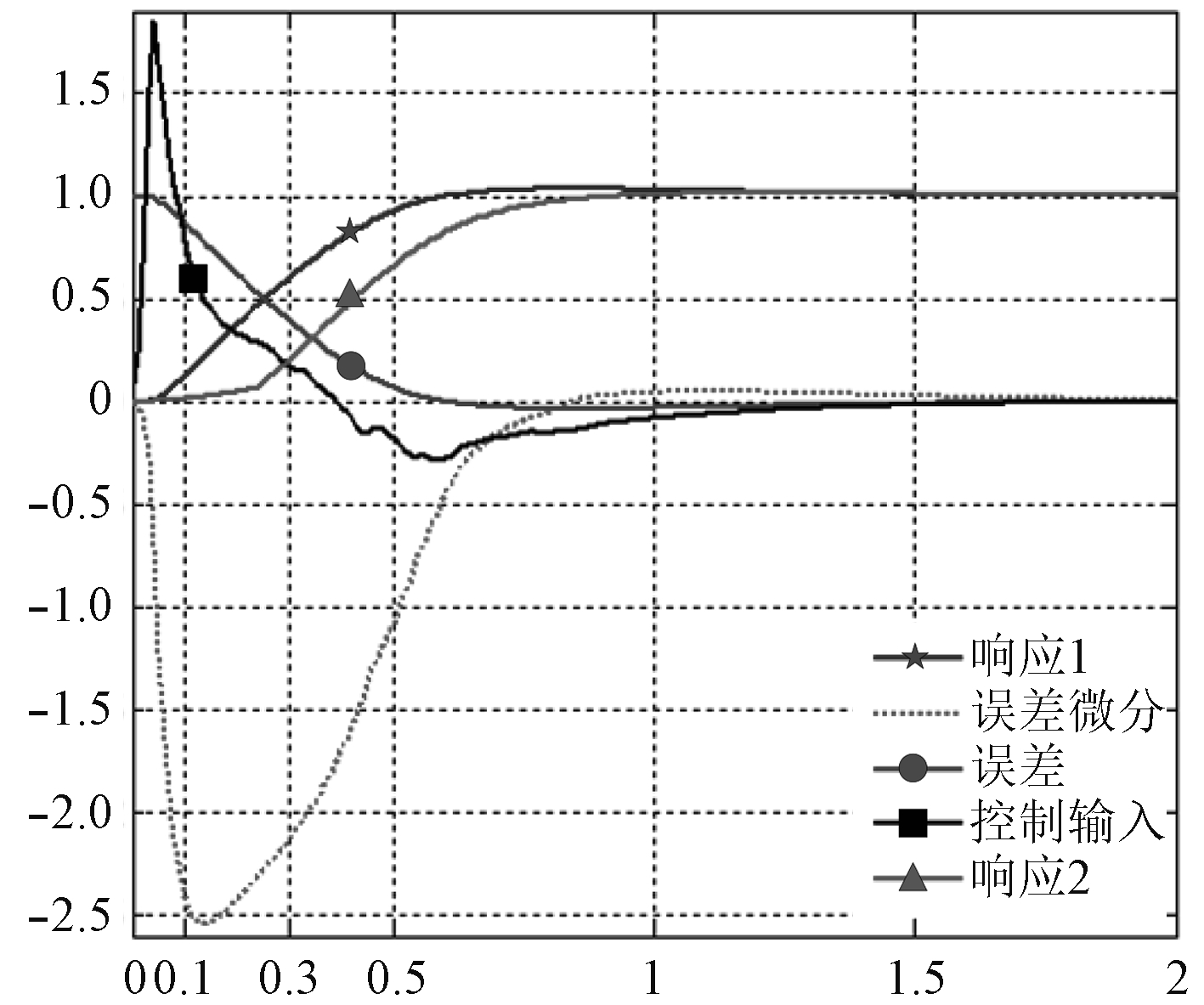
3.1 Matlab仿真该部分主要对2.3部分模糊控制规则的性能进行验证,控制规则表中“A/B”表示规则调整前使用A控制规则,该规则对应图2中的系统响应曲线“响应1”,规则调整后使用B规则,相对应的系统响应曲线为“响应2”。对方程(1)进行变换处理,代入某径航行器参数获得航向开环传递函数如下[14]:
|
图 2 系统输入与响应 Fig. 2 System input and response |
| $ {\rm{G}}\left( {\rm{s}} \right) = \frac{{4.718 s + 13.48}}{{0.158\;3{s^3} + 1.587{s^2} + s}} {\text{。}} $ | (7) |
PID控制器参数设定为:kp=1.107,ki=0,kd=0.12,得到如图2所示的系统输入和响应曲线。图中响应1曲线超调量较大,超调量3.5%,稳态时间3.21 s。为了降低系统超调并提高系统稳态时间,对响应1相对应系统控制输入、控制误差、误差的微分进行分析,各曲线如图2所示。瞬态响应阶段,为了尽快跟踪设定值,控制输入应较大,而为了减小超调,在响应没有跟上设定值时就应该降低输入,图中输入曲线满足这一规律。但注意到,在0.5~1 s过程中,误差已经趋于零时,误差的微分仍然较大,因此,在原控制规律的基础上,需要适当降低控制输入数值的大小,在比例系数规则表和微分系数规则表中对相应模糊输出进行适当的调小处理。调整后仿真得到响应2曲线。相比响应1、响应2超调量减少到1.6%,稳态时间为2.3 s,相比降低了0.91 s,但响应时间却有所增加。以上可知,在不同的使用需求下,可以通过适当调整模糊控制规则来得到不同的控制品质。
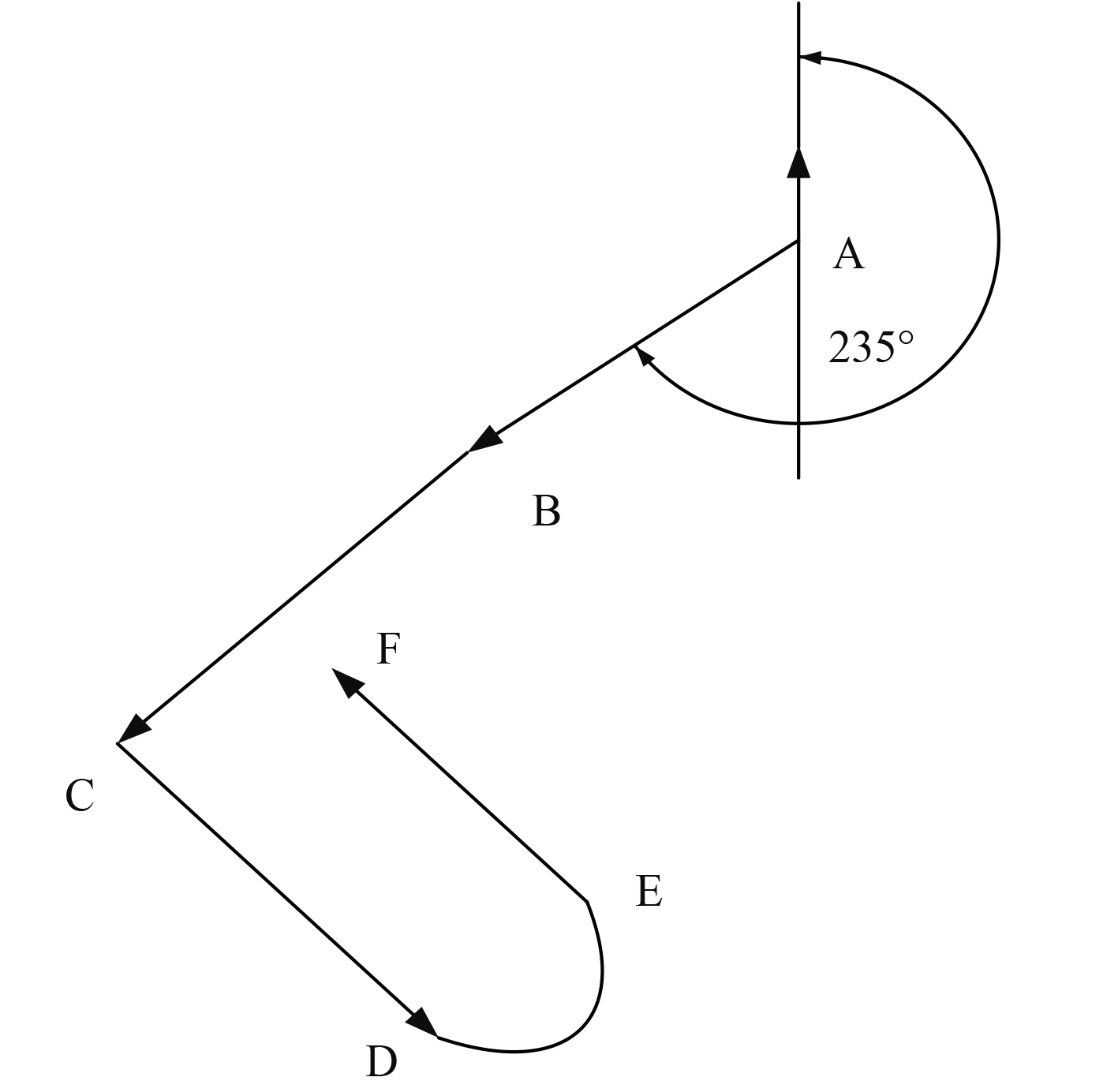
3.2 AUV数字仿真平台仿真AUV数字仿真平台使用AUV控制程序全真模拟实际航行条件对控制算法进行仿真验证,该部分主要对公式(6)尺度变换函数中的参数k进行调整。设定航向PID参数调整量最大取值maxΔkp=20%kp,maxΔki=100%ki,maxΔkd=20%kd。AUV前向速度2节,航行深度5 m,航行规划如图3所示。AUV从A点出发,航向使命依次为:235°,225°,135°和315°,各使命航行时间均为5 min,转向角度依次增大。在相同的航行任务下,分别设定误差尺度变换函数参数ke=0.2,0.4,0.6,误差变化率尺度变换函数参数kec=0.2,0.4,0.6进行仿真测试。对不同条件下的系统动态性能进行统计,结果如表4所示。
|
图 3 航行规划图 Fig. 3 Navigation plan |
|
|
表 4 尺度变换函数参数取不同数值情况下的仿真结果 Tab.4 Simulation results of scale conversion function parameters taking different values |
表中,PID表示航行器中原始算法,FPID表示改进后的模糊PID算法,σ代表超调的度数,t代表调节时间。从结果可以看出,相同航行任务下,ke=kec=0.4时,系统响应的动态性能较好。此时为了进一步提高控制效果,在ke=kec=0.4的条件下,改变maxΔkp数值大小继续仿真,将maxΔkp=20%kp改为maxΔkp=30%kp,航行速度和深度不变,航行使命变为航向220°航行转到240°,随后再转到60°,各使命航行时间5 min,仿真结果如表5所示。
|
|
表 5 改变比例项参数幅值后的仿真结果 Tab.5 Simulation result after changing the amplitude of the proportional term parameter |
从结果可以看出,适当的调整模糊PID参数调整量的幅值对控制效果有较大的改善。模糊PID控制器比例项参数调整量的幅值增大到0.3倍后,AUV进行大角度转向时,系统动态性能具有较大的改善,小角度转向时系统超调减小,但调节时间有所增加。结合表1可以得出,在控制器参数调整时,很难获得最优的控制器参数使得各种工况下都能获得最好的控制效果,但可以根据需求获得整体较优的参数,并可以根据不同的任务需求对参数进行适当的调整来得到重点关注的控制效果。
4 航行试验2018年12月在浙江省千岛湖进行了湖上试验,试验用载体为鱼雷外形重型AUV,长度8.4 m左右,直径534 mm,最大下潜深度200 m,空气中重量1.6 t。该AUV为十字形尾舵,并配有垂直槽道推进器用于低速时的深度控制。
根据惯性组合导航单元记录的数据绘制AUV航行轨迹如图4所示。该次航行规划的航行使命如下:AUV从图中A点出发,航行控制器使用原始PID控制器,航行深度5 m,前向速度2 kn,初始航向220°,航行时间5 min,使命结束到达B点后目标航向调整到240°,继续航行5 min,5 min后到达C点,AUV执行航行到D点这一使命,到达D点后目标航向调整到340°航行1 min,然后再次将目标航向调整到60°,航行时间5 min,使命结束后航行到A1点,切换到模糊PID控制器重复以上航行使命。试验时ke=kec=0.4,比例项最大调整量maxΔkp=30%kp,积分项参数的最大调整量maxΔki=100%ki,微分项参数的最大调整量maxΔkd=20%kd。

|
图 4 AUV 航迹图 Fig. 4 AUV Navigation path recorder chart |
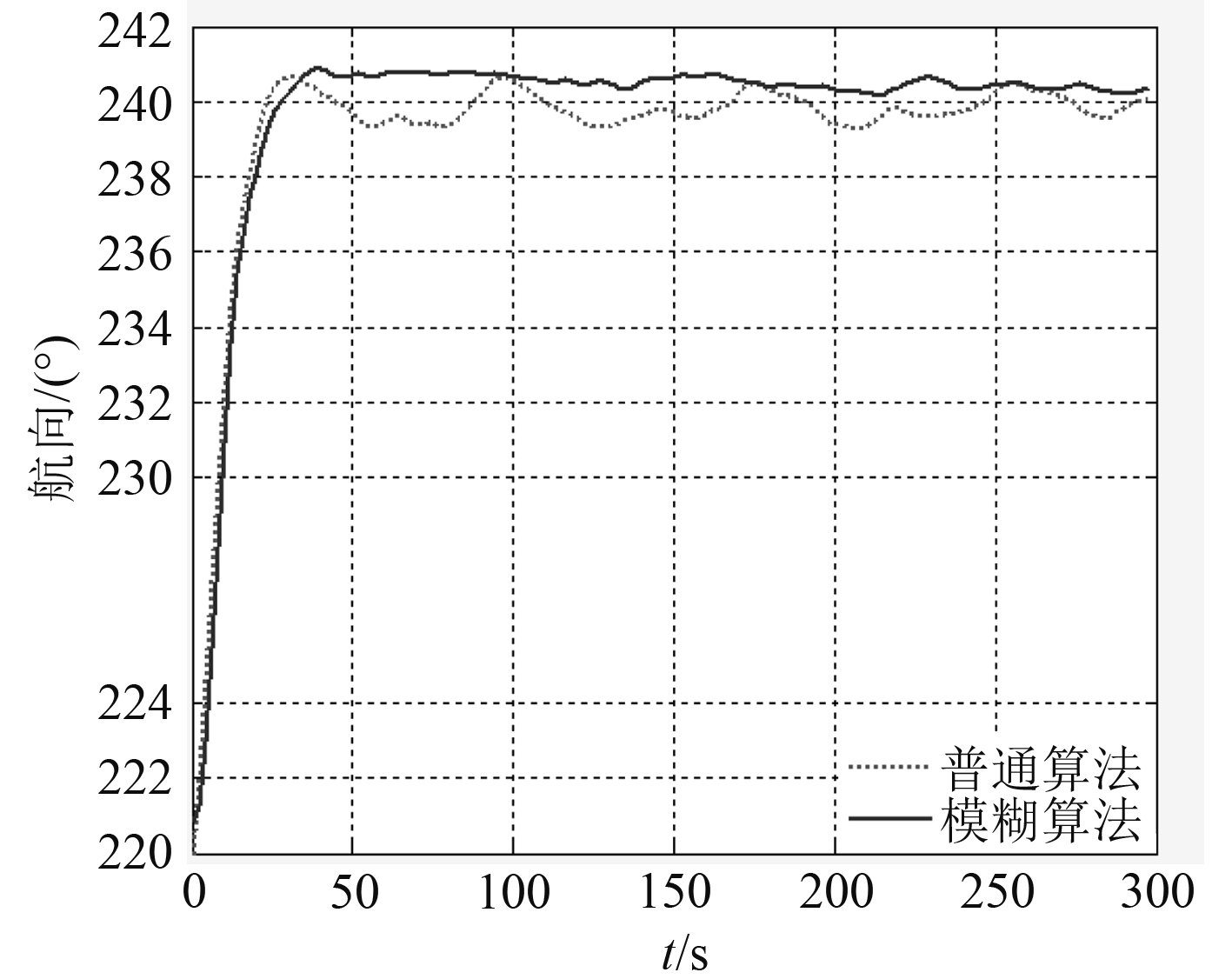
使命规划的初衷是研究相同条件下,AUV小角度转向(航向220°转到240°)和大角度转向(340°转到60°)时,不同航向控制器的控制效果。下面对各段航行数据分别进行对比分析。图5为航向220°转到240°过程中,AUV的航向变化曲线。能够比较明显的看出,在稳态航行阶段使用模糊PID控制算法AUV航向保持更加稳定,航向误差均方差0.18°,优于原始PID算法的0.38°。超调量方面,模糊PID算法最大超过目标值0.87°,略大于原始PID控制的0.67°。
|
图 5 小角度转向AUV航向变化曲线 Fig. 5 Small angle steering AUV course change curve |
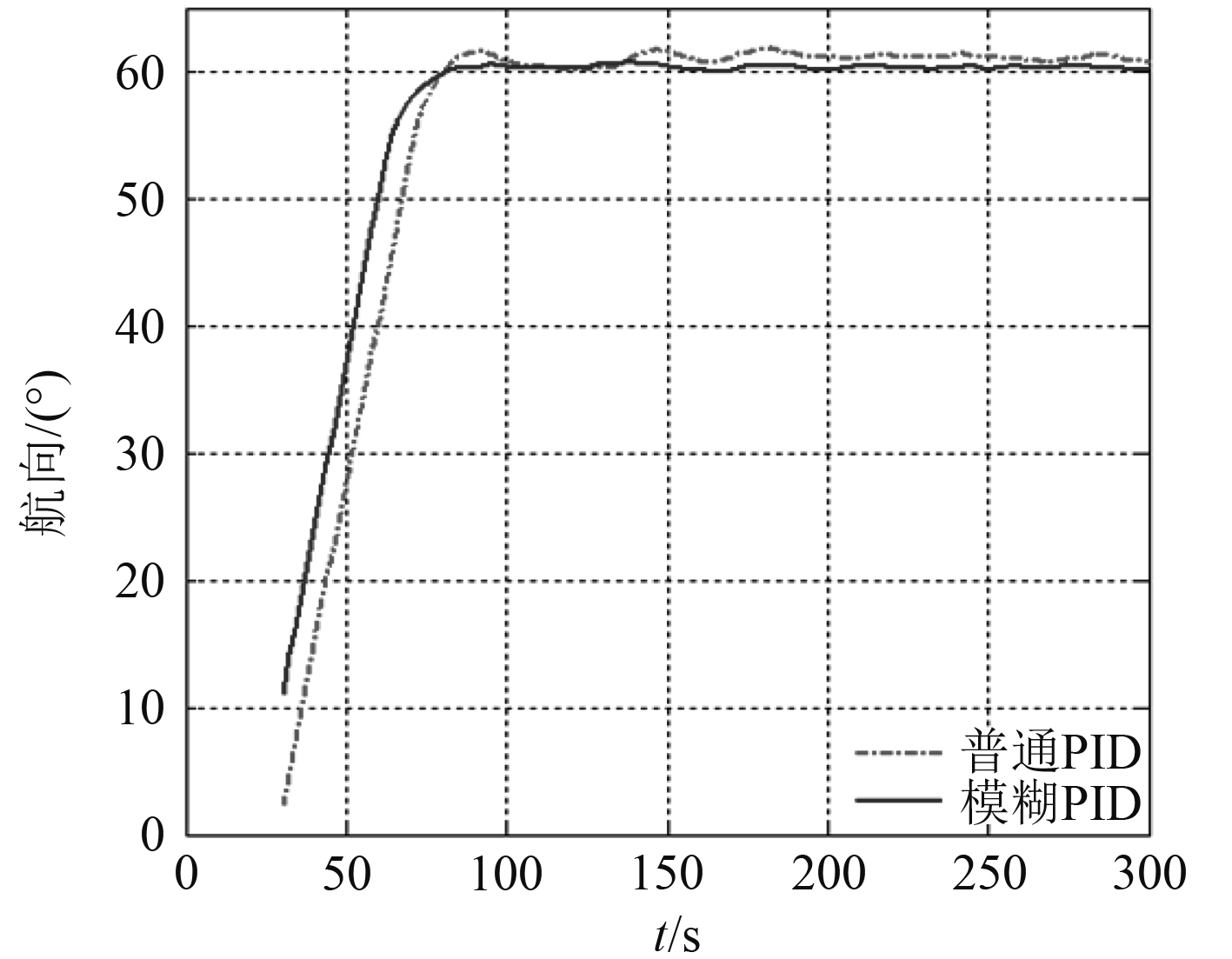
图6为AUV从航向340°转到60°过程中的航向变化曲线。可以明显看出,在大角度转向时,使用模糊PID控制算法进行航向控制所获得的控制效果整体优于原PID算法,具体数据如表6所示。
|
图 6 大角度转向AUV航向变化曲线 Fig. 6 Large angle steering AUV course change curve |
|
|
表 6 大角度转向时系统响应数据对比 Tab.6 Comparison of system response during large angle steering |
表中,s2代表航向误差均方差,
模糊PID控制算法具有一定的自适应特性,而模糊控制规则的设计对控制效果具有重要的影响。在Matlab仿真部分,通过系统响应与输入曲线间的关系对模糊规则进行改进可以改变系统的响应特性,获得预期的控制效果。模糊PID控制器输入变量的尺度变换函数的参数要根据实际工况进行选取,该参数的选取直接影响到控制的品质,从算法原理的角度来说,选择该参数的过程就是选择将控制规则表作用在不同的偏差区域的过程。湖上试验中,在相同的水域和使命条件下对2种控制算法进行了对比试验。结果表明所设计的模糊PID控制器能够满足工作需求,小角度转向时,航向稳态精度高;大角度转向时,该算法控制性能整体优于PID算法,效果明显。
本研究目前对2 kn航速下的控制特性进行了研究,后续工作将考虑变速条件下的控制问题,此外该方法在深度控制和速度控制中的应用也是今后研究的方向。
| [1] |
Y. SATO, Ma ki, Toshihiro, Ku me, et al. Path replanning method foran AUV in natural hydrothermal vent fields: toward 3D imaging of a hydrothermal chimney[J]. Marine Technology Society, 2014, 48(3): 104-114. DOI:10.4031/MTSJ.48.3.5 |
| [2] |
CHOYEKH M K, NaOMI S, et al. Vertical water column survey in the gulf of mexico using autonomous underwater vehicle SOTAB-I[J]. Marine Technology Society Journal, 2015, 49(3): 88-101. DOI:10.4031/MTSJ.49.3.8 |
| [3] |
严浙平, 周佳加. 水下无人航行器控制技术[M]. 北京: 国防工业出版社, 2015: 153-154.
|
| [4] |
贾鹤鸣. 基于反步法的欠驱动UUV空间目标跟踪非线性控制方法研究[D]. 哈尔滨: 哈尔滨工程大学. 2012. JIA H M. Study of spatial tracking nonlinear control of underactuated UUV based on backstepping[D]. Harbin: Harbin Engineering University. 2012. |
| [5] |
LEKKAS A, FOSSEN T I. A Quaternion-based LOS guidance scheme for path following of AUVs[J]. Ifac Proceedings Volumes, 2013, 46(33): 245-250. DOI:10.3182/20130918-4-JP-3022.00070 |
| [6] |
AGUIAR A P, PASCOAL A M. Dynamic positioning and way-point tracking of underactuated AUVs in the presence of ocean currents[C]// IEEE Conference on Decision & Control. IEEE, 2002.
|
| [7] |
YANG R, CLEMENT B, et al. Robust heading control and its application to ciscrea underwater vehicle[C]// Oceans. IEEE, 2015.
|
| [8] |
MASHHAD A M, MASHHADI S K M. H infinity robust controller comparison with PD like fuzzy logic controller for an AUV control[C]// Fuzzy & Intelligent Systems. IEEE, 2016.
|
| [9] |
姜春萌. 自主水下机器人智能控制与参数优化技术研究[D]. 哈尔滨: 哈尔滨工程大学. 2018. JIANG C M. Research on AUV Intelligent Control and Parameter Optimization Technology[D]. Harbin Engineering University. 2018. |
| [10] |
HEALEY A J. Multivariable sliding mode control for autonomous diving and steering of unmanned underwater vehicles[J]. IEEE J. Oceanic Eng, 1993, 18(3): 327-339. DOI:10.1109/JOE.1993.236372 |
| [11] |
MARCO D B, HEALEY A J. Command, control, and navigation experimental results with the NPS ARIES AUV[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 466-476. DOI:10.1109/48.972079 |
| [12] |
孙增圻, 邓志东, 张再兴. 智能控制理论与技术[M]. 北京: 清华大学出版社, 2011: 17.
|
| [13] |
从爽. 智能控制系统及其应用[M]. 合肥: 中国科学技术大学出版社, 2013: 138-143.
|
| [14] |
徐德民, 严卫生. 鱼雷控制系统计算机辅助分析设计与仿真[M]. 西安: 西北工业大学出版社, 2000: 79-80.
|
 2020, Vol. 42
2020, Vol. 42
