2. 江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003
2. School of Naval Architecture and Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China
随着人类社会的发展,陆地上的资源将消耗殆尽,世界上各国对海洋资源的开发与利用逐渐重视起来,而进行海洋资源的开发与利用离不开先进的海洋监测技术与设备。水下滑翔机(autonomous underwater glider,AUG)[1-4]作为一种新型的水下航行器,对能源的需求量小,可以高效率、长时间地在海洋中航行,又因其成本和维护费用较低,可以重复使用和大量投放,已在大范围海洋探索和监测中发挥出越来越重要的作用。
相较于由回转体、水翼和操纵面组成的传统布局水下滑翔机,翼身融合(blended-wing-body,BWB)水下滑翔机具有扁平翼型剖面形状的机身,且水翼平滑地与机身融合在一起,可大幅提高升阻比。但翼身融合水下滑翔机的外形曲面复杂,机身与机翼连接处运用了大量的曲线、曲面平滑过渡,很难用简单的外形参数描述,因此,如何进行精细化的参数化建模是对其进行水动力性能分析和设计的先决条件。
谷海涛等[5]将描述水下滑翔机机翼的形状尺寸参数定义为状态变量,直接驱动CATIA参数化程序完成了滑翔机外形的几何参数化建模;孙春亚等[6]选择UG作为开发平台,针对翼身融合水下滑翔机的平面形状和翼型相对厚度分布进行了基于CAD的参数化研究,完成了翼身融合水下滑翔机外形的参数化建模。此外,Li等[7]也使用CST(class function-shape function transformation)方法对翼身融合水下滑翔机的翼型截面进行了参数化,进而实现翼身融合水下滑翔机外形的建模。上述学者对水下滑翔机的基本外形特征进行了参数化,提取了一些关键的几何参数化变量。本文在以上成果的基础上,对翼身融合滑翔机平面外形以及各翼型截面这类复杂曲线曲面进行精细的参数化,从而实现翼身融合滑翔机外形的精细化建模,更充分挖掘翼身融合构型的高升阻比潜力。
本文基于非均匀有理B样条(non-uniform rational b-spline,NURBS)方法,依次从翼型剖面曲线和几何外形曲面的NURBS参数化入手,提出一种精细化的参数化建模方法,可通过操纵局部或全局参数化变量实现翼身融合水下滑翔机外形的局部或整体变形。
1 翼身融合水下滑翔机外形特征理论上讲,水下滑翔机的升力越大,阻力越小,其滑翔效率越高。借鉴于航空飞机新一代翼身融合布局[8]的高升阻比优势,翼身融合水下滑翔机的机身采用扁平椭球形状,并与机翼进行平滑地连接(见图1),以大幅提高升力,进而提高升阻比。

|
图 1 翼身融合水下滑翔机外形 Fig. 1 Shape of BWB underwater glider |
此外,为了获得更高的升阻比,翼身融合水下滑翔机外形有一个显著特性:每一个横截面都是由翼型剖面组成,如图1中曲线剖面所示。
2 基于NURBS的外形参数化 2.1 NURBS建模基础理论NURBS曲线、曲面建模技术[9-10]是现代工业几何建模中最为广泛流行的技术。相较于B样条方法,其能精确表示圆锥截线及初等解析曲面,克服了B样条曲线在进行产品几何定义时的不确定性,使曲线曲面具有统一的数学描述形式。目前,基于NURBS曲面建模技术成为最为广泛流行的技术,并被广泛应用于汽车、飞机、船舶等工业设计及制造领域以及其他高新科技领域。
| $ C(u) = \frac{{\displaystyle\sum\nolimits_{i = 0}^n {{N_{i,p}}(u){w_i}{P_i}} }}{{\displaystyle\sum\nolimits_{i = 0}^n {{N_{i,p}}(u){w_i}} }}, \;\;a \leqslant u \leqslant b {\text{。}} $ | (1) |
其中:
| $ \begin{split} & {N_{i,p}}(u) = \dfrac{{u - {u_i}}}{{{u_{i + p}} - {u_i}}}{N_{i,p - 1}}(u) + \\ & \;\;\;\;\;\;\;\;\;\dfrac{{{u_{i + p + 1}} - u}}{{{u_{i + p + 1}} - {u_{i + 1}}}}{N_{i + 1,p - 1}}(u) {\text{,}} \end{split} $ | (2) |
节点矢量
| $ { U} = \left\{ {\underbrace {{\rm{0}},...{\rm{0}}}_{p + 1},{u_{p + 1}},...,{u_{m - p - 1}},\underbrace {{\rm{1}},...,{\rm{1}}}_{p + 1}} \right\} {\text{,}} $ | (3) |
对于在
| $ \begin{split} &S(u,v) = \frac{{\displaystyle\sum\nolimits_{i = 0}^n {\displaystyle\sum\nolimits_{j = 0}^m {{N_{i,p}}(u){N_{j,p}}(v){w_{i,j}}{P_{i,j}}} } }}{{\displaystyle\sum\nolimits_{i = 0}^n {\displaystyle\sum\nolimits_{j = 0}^m {{N_{i,p}}(u){N_{j,p}}(v){w_{i,j}}} } }} {\text{,}} \\ & \;\;\;\;\;\;\;\;\;{\rm{ }} 0 \leqslant u,v \leqslant 1 {\text{。}} \end{split} $ | (4) |
其中:
| $ { U} = \left\{ {\underbrace {0,...0}_{p + 1},{u_{p + 1}},...,{u_{r - p - 1}},\underbrace {1,...,1}_{p + 1}} \right\} {\text{,}} $ | (5) |
| $ { V} = \left\{ {\underbrace {0,...0}_{q + 1},{u_{q + 1}},...,{u_{s - q - 1}},\underbrace {1,...,1}_{q + 1}} \right\} {\text{。}} $ | (6) |
NURBS可以通过控制网格点
设
|
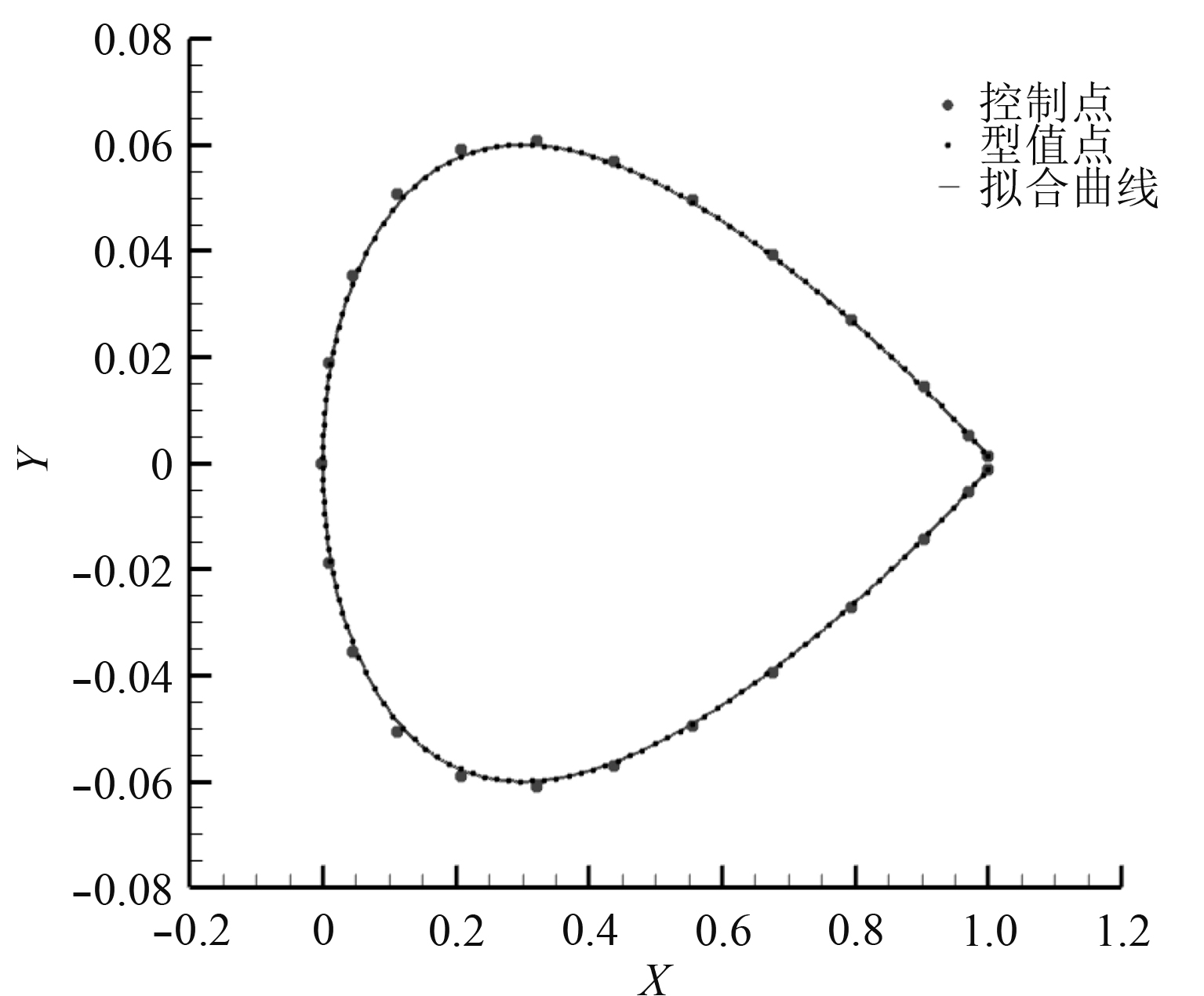
图 2 翼型剖面型值点与NURBS拟合曲线 Fig. 2 Data points of airfoil section and NURBS curve |
试图寻找一条如下的
| $ C(u) = \sum\limits_{i = 0}^n {{N_{i,p}}} (u){P_i}, \;\;{\rm{0}} \leqslant u \leqslant {\rm{1}} {\text{。}} $ | (7) |
在满足条件:
| $ {\sum\limits_{k = 1}^{l - 1} {\left| {{Q_k} - C(\overline {{u_k}} )} \right|} ^2} {\text{。}} $ | (8) |
其中,
具体的翼型剖面曲线拟合过程如下:
1)需要给出每一个型值点
| $ d = \sum\limits_{k = 1}^l {\sqrt {\left| {{Q_k} - {Q_{k - 1}}} \right|} } ,\;\;\overline {{u_0}} = 0,\overline {{u_l}} = 1 {\text{,}} $ | (9) |
| $ \overline {{u_k}} = \overline {{u_{k - 1}}} + \frac{{\sqrt {\left| {{Q_k} - {Q_{k - 1}}} \right|} }}{d}, k = 1,2, \cdots ,l - 1 {\text{。}} $ | (10) |
2)按如下方法选定节点矢量U,保证每一个节点区间内至少包含一个
| $ d = \frac{{l + 1}}{{n - p + 1}}, i = {\rm{int}} (jd), a = jd - i {\text{,}} $ | (11) |
| $ {u_{p + j}} = (1 - a)\overline {{u_{i - 1}}} + a\overline {{u_i}} , j = 1,2, \cdots ,n - p {\text{。}} $ | (12) |
3)建立一个含
| $ ({{ N}^{\rm T}}N)P = R {\text{。}} $ | (13) |
其中,
| $ { N} = \left[ {\begin{array}{*{20}{c}} {{N_{1,p}}(\overline {{u_1}} )}& \cdots &{{N_{n - 1,p}}(\overline {{u_1}} )} \\ \vdots & \ddots & \vdots \\ {{N_{1,p}}(\overline {{u_{l - 1}}} )}& \cdots &{{N_{n - 1,p}}(\overline {{u_{l - 1}}} )} \end{array}} \right]{\text{;}} $ | (14) |
| $ R = \left[ {\begin{array}{*{20}{c}} {{N_{1,p}}(\overline {{u_1}} ){R_1} + \cdots + {N_{1,p}}(\overline {{u_{l - 1}}} ){R_{l - 1}}} \\ \vdots \\ {{N_{n - 1,p}}(\overline {{u_1}} ){R_1} + \cdots + {N_{n - 1,p}}(\overline {{u_{l - 1}}} ){R_{l - 1}}} \end{array}} \right]{\text{,}} $ | (15) |
| $ {R_k} = {Q_k} - {N_{0,p}}(\overline {{u_k}} ){Q_0} - {N_{n,p}}(\overline {{u_k}} ){Q_l} {\text{,}} $ | (16) |
| $ P = {[\begin{array}{*{20}{c}} {{P_1}}& \cdots &{{P_{n - 1}}} \end{array}]^{\rm T}} {\text{。}} $ | (17) |
求解式(13)即可得到拟合的NURBS翼型曲线,如图2所示。本文选择对应的控制点为翼型剖面曲线的NURBS参数化变量。
2.3 几何外形曲面的NURBS参数化对于翼身融合水下滑翔机外形,基于上节翼型剖面的参数化方法,进一步实现几何外形曲面的NURBS参数化,详细过程如下:
1)分别使用
2)在
| $ {B_{ij}} = {s_i}({A_{ij}} - {\delta _i}) {\text{。}} $ | (18) |
3)使用
| $ \begin{split} {C_{ij}} = \,& \left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos {\beta _i}}&{ - \sin {\beta _i}} \\ 0&{\sin {\beta _i}}&{\cos {\beta _i}} \end{array}} \right) \times \\ &\left( {\begin{array}{*{20}{c}} {\cos {\alpha _i}}&0&{\sin {\alpha _i}} \\ 0&1&0 \\ { - \sin {\alpha _i}}&0&{\cos {\alpha _i}} \end{array}} \right) \times \\ &\left( {\begin{array}{*{20}{c}} {\cos {\gamma _i}}&{ - \sin {\gamma _i}}&0 \\ {\sin {\gamma _i}}&{\cos {\gamma _i}}&0 \\ 0&0&1 \end{array}} \right){B_{ij}} {\text{。}} \end{split} $ | (19) |
4)使用
| $ {D_{ij}} = {C_{ij}} + {T_i} {\text{。}} $ | (20) |
5)基于NURBS的曲面方程,翼身融合水下滑翔机外形的数学表述式为:
| $ S(u,v) = \sum\limits_{i = 0}^n {\sum\limits_{j = 0}^m {{R_{i,j}}(u,v){D_{ij}}} } {\text{。}} $ | (21) |
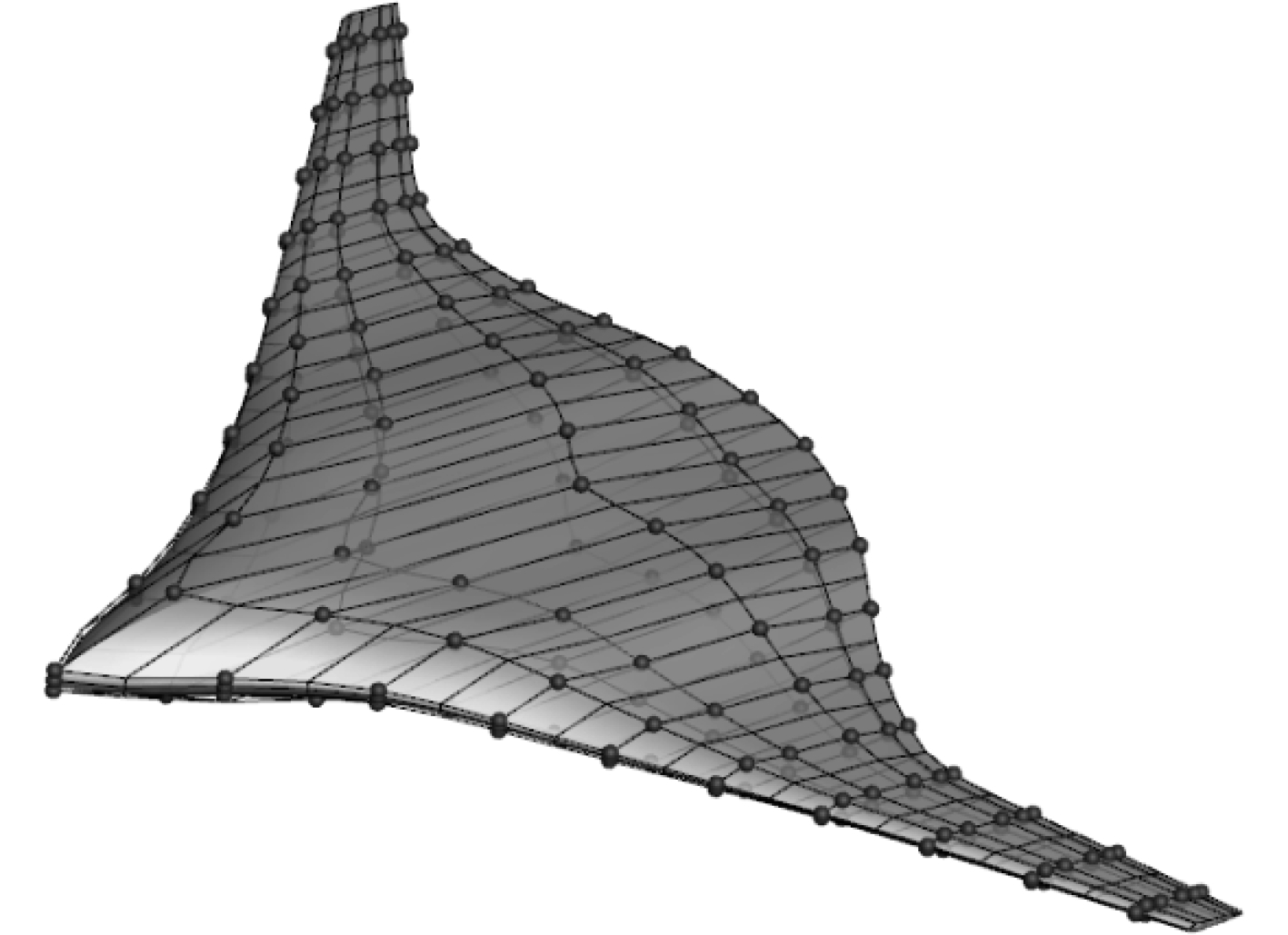
相应的NURBS参数化示意图如图3所示。
|
图 3 基于NURBS的水下滑翔机参数化外形 Fig. 3 Parametric shape of BWB based on NURBS |
综上,翼身融合水下滑翔机外形的参数化建模过程主要通过局部和全局参数化变量对各个翼型剖面的控制点进行操控实现,详细介绍见表1。
|
|
表 1 翼身融合水下滑翔机外形的参数化变量 Tab.1 Parametric variables of BWB shape |
通过改变表1中的局部和全局参数化变量,可实现翼身融合水下滑翔机外形的几何变形。
3 实例分析为了分析所提参数化方法的可行性,以一型翼身融合水下滑翔机外形进行实例分析,其具体的外形参数化为:1)外形左右对称,共由11个翼型剖面组成,且每个剖面的型值点为NACA0012的型值点;2)各个翼型剖面的弦长从左至右依次为[0.10 m,0.18 m,0.28 m,0.57 m,0.96 m,1.45 m,0.96 m,0.57 m,0.28 m,0.18 m,0.11 m],展长为3 m;3)各个翼型剖面的前缘位置坐标从左至右依次为:[(1.38,0.04,–1.50),(1.16,0.02,–1.20),(0.93,0.01,–0.90),(0.71,0.01,–0.60),(0.44,–0.01,–0.30),(0,0,0),(0.44,–0.01,0.30),(0.71,0.01,0.60),(0.93,0.01,0.90),(1.16,0.02,1.20),(1.38,0.04,1.50)]。
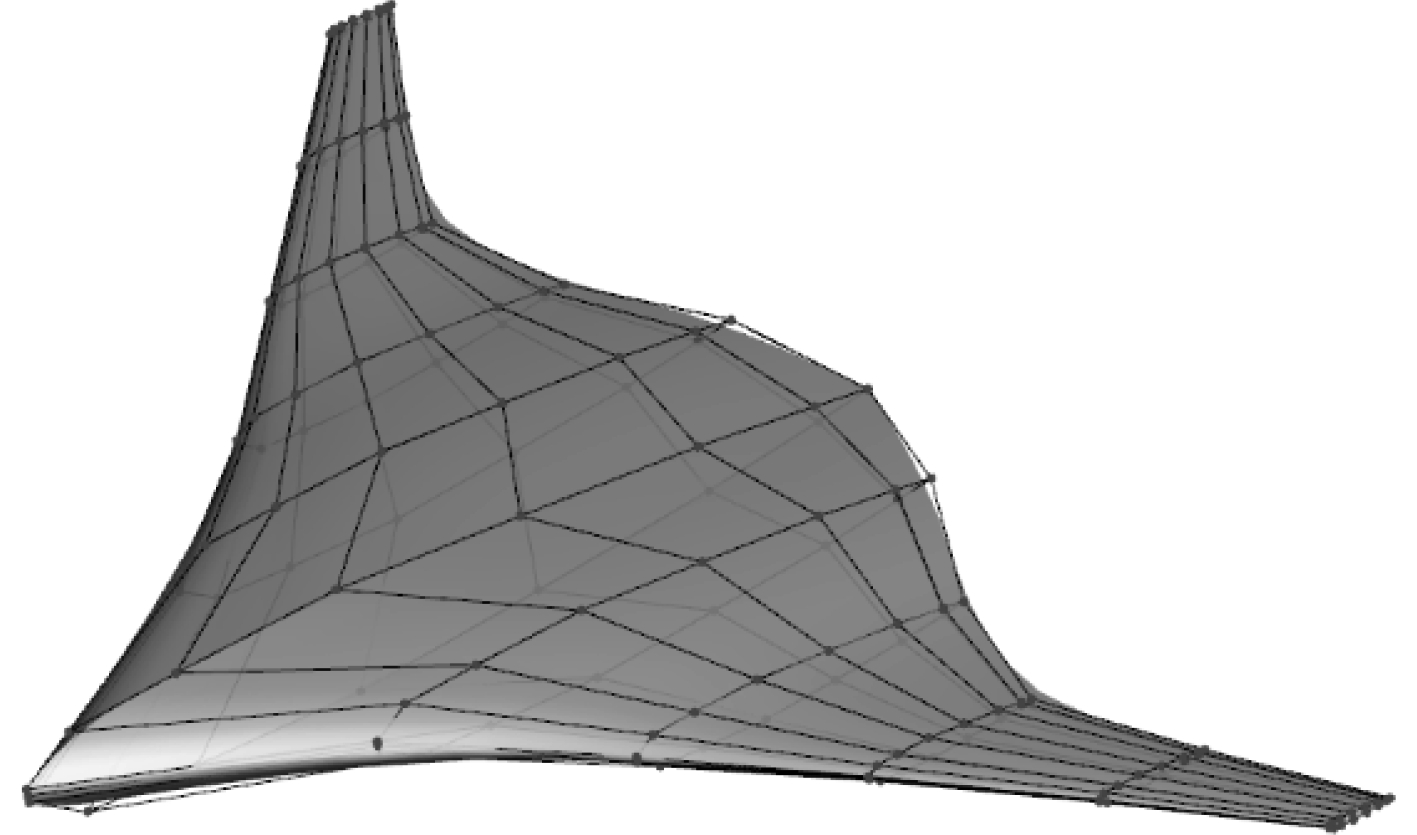
利用本文提出的精细参数化建模方法,设置各翼型剖面曲线通过15个控制点进行参数化,共165个控制点,可得到如图4所示的几何模型。
|
图 4 翼身融合水下滑翔机建模实例 Fig. 4 Modeling of BWB underwater glider shape |
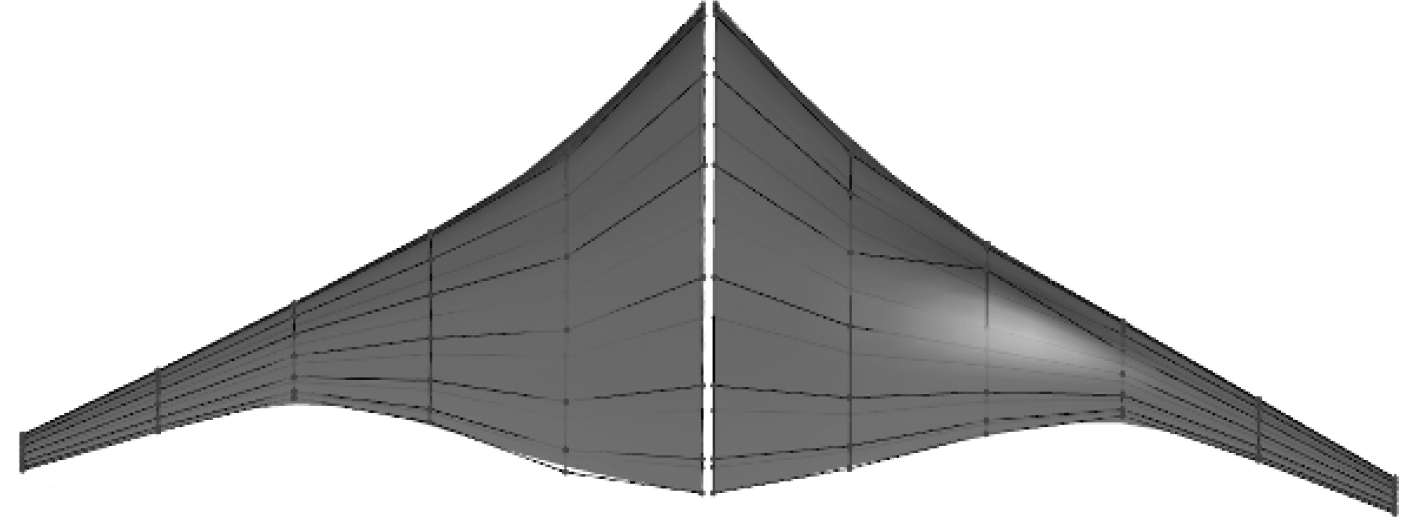
将第8个翼型剖面的第4个控制点的纵坐标增加0.03 m,可得到如图5所示的几何模型。因外形左右对称,为了突出对比效果,图5中左边为初始外形,右边为改变后的外形。
|
图 5 改变翼型剖面控制点后的外形对比 Fig. 5 Shape comparison after control points of an airfoil section changed |
分别改变第4、第8个翼型剖面(左右对称)的弦长为0.90 m,可得到如图6所示的几何模型。同样,图6左边为初始外形,右边为改变弦长后的外形。

|
图 6 改变弦长参数化变量后的外形对比 Fig. 6 Shape comparison after chord length parametric variables changed |
分析图5和图6可以发现,通过改变局部参数化变量和全局参数化变量可实现外形的局部和全局几何控制,进而实现翼身融合水下滑翔机外形的精细参数化建模和几何控制。
4 结 语翼身融合水下滑翔机具有高升阻比特性,但如何实现精细化的外形参数化建模是充分挖掘其高升阻比潜力的先决条件。针对这一现状,本文提出了一种基于NURBS方法的翼身融合水下滑翔机外形参数化建模方法,该方法具有以下特性:
1)对各个翼型剖面的型值点,采用最小二乘法进行拟合,并将各个翼型剖面的控制点作为局部参数化变量,实现各个翼型剖面的局部几何控制。
2)利用偏移因子、比例因子、旋转角度、放置坐标等参数化变量对各个翼型剖面的控制点进行操控,并基于NURBS曲面方程进行参数化建模,实现翼身融合水下滑翔机外形的精细参数化建模及几何控制。
| [1] |
WOOD S, ALLEN T, KUHN S, et al. The Development of an Autonomous Underwater Powered Glider for Deep-sea Biological, Chemical and Physical Oceanography[C]. Oceans, IEEE. 2007: 1-6.
|
| [2] |
BACHMAYER R, LEONARD N E, BHATTA P, et al. Dynamics, control and coordination of underwater gliders[M]. Advances in Unmanned Marine Vehicles. 2006.
|
| [3] |
沈新蕊, 王延辉, 杨绍琼, 等. 水下滑翔机技术发展现状与展望[J]. 水下无人系统学报, 2018, 26(2): 89-105. |
| [4] |
LEONARD N E, PALEY D A, LEKIEN F, et al. Collective motion, sensor networks, and ocean sampling[J]. Proceeding of the IEEE, 2007, 95(1): 48-74. DOI:10.1109/JPROC.2006.887295 |
| [5] |
谷海涛, 林扬, 胡志强, 等. 基于代理模型的水下滑翔机机翼设计优化方法[J]. 机械工程学报, 2009, 45(12): 7-14. |
| [6] |
孙春亚, 宋保维, 王鹏. 翼身融合水下滑翔机外形设计与水动力特性分析[J]. 舰船科学技术, 2016, 38(19): 78-83. |
| [7] |
CHENGSHAN L, PENG W, HUACHAO D, et al. A simplified shape optimization strategy for blended-wing-body underwater gliders[J]. Structural and Multidisciplinary Optimization, 2018, 2018(58): 2189-2202. |
| [8] |
QIN N, VAVALLE A, MOIGNE A L, et al. Aerodynamic considerations of blended wing body aircraft[J]. Progress in Aerospace Sciences, 2004, 40(6): 321-343. DOI:10.1016/j.paerosci.2004.08.001 |
| [9] |
PIEGL L A, TILLER W. The NURBS book. [M]. Springer Berlin Heidelberg, 1997.
|
| [10] |
施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 北京: 高等教育出版社, 2001.
|
 2020, Vol. 42
2020, Vol. 42
