在最近的几十年中,大量的海洋探索工具被开发出来,扩展了人类的研究范围,获得了关于海洋的更多知识,使得深海的矿藏能够得到有效利用[1-2]。其中,AUV(Autonomous underwater vehicle)是一种广泛使用的潜水器,它有高速和活动范围大的优势[3-4]。大部分AUV在水中是中性浮力的,为了维持中性浮力,AUV需要安装很多浮力材料,增加了AUV的体积及AUV在水中航行时的阻力。
本文针对一种负浮力四倾转推进器AUV(negative-buoyancy quad tilt-rotor autonomous underwater vehicle, NQTAUV),进行了抗干扰姿态跟踪控制设计。NQTAUV没有安装浮力材料,因此在水中有剩余重量。NQTAUV质量为
NQTAUV有独特的机身倾转悬停(body-tilt-hover, BTH)功能,即在机身实现大幅度俯仰角机动的时候,能够悬停在水中一个位置点,而不产生水平的分力,不会引起水平的位移。对于普通AUV来说,一般是在艇体尾部有一个推进器,部分在艇体上还有垂向和横向的推进器,实现垂向和水平机动。不过,这些推进器一般固定在艇体上,只能提供固定方向的力或力矩,不能提供矢量推力,所以不能做机身倾转悬停。然而,NQTAUV可以借助自身的矢量推力进行机身倾转悬停[7-8]。BTH是一项有用的功能。比如,AUV前部一般安装有摄像机,用以提供视频信息。通常来讲,为了更大的视角,摄像机安装在一个二自由度云台上。然而,当云台损坏后,相机的视角被限制,此时,可以采用BTH功能,操作手可以重新获得原来的视角。不过,当工作在BTH模式时,因为舵机会随着俯仰角而转动,引起转动惯量的变化,同时产生一定的干扰力矩,且不能计算或测量得到干扰量幅值。因此,需要更鲁棒的姿态控制器,实现姿态的跟踪。此外,在BTH模式下,水动力矩也会随着机身的旋转运动而改变。因此,研究干扰的估计和补偿策略,以及在干扰下的姿态跟踪,是符合实际应用需要的。
为了进行干扰下的控制,学者们进行了大量研究。Li[9]设计了四自由度非线性滑动状态观测器,建立了ROV的洋流模型和简化的脐带干扰力模型,基于简化的索力模型表征电缆的干扰力,并实时估计缆的干扰力,提高了观测精度,减少了抖振。Yuan[10]设计了一种非线性自抗扰控制方案控制气动肌肉执行器,采用连续离散扩展状态观测器估计总扰动,然后使用非线性复合控制器,在气动平台上进行了实验,验证了整个系统的可控性。Cui[11]对路径跟踪问题,设计了自适应神经网络控制器,考虑了外部干扰、控制输入非线性和模型不确定性等因素。Liu[12]用非线性干扰观测器估算了作用在飞行器上的风效应,然后将风信息与控制器结合,设计了一种抗干扰导航算法,实现风干扰下的实时路径跟踪,并理论分析了复合控制器的全局渐近稳定性,进行了软件在环的仿真。对小型飞机进行的飞行仿真试验,验证了其性能。可以看出,在以往的研究中,对于干扰观测的研究取得了大量进展,部分控制器的稳定性得到了证明。不过,这些算法在实际应用中存在调参数量多的问题,不利于控制器实际的部署和调整。
姿态跟踪控制是NQTAUV的重要功能,一般作为路径跟踪等更高一级控制的内环,它的性能决定了上层控制的精度[13]。干扰力矩对姿态控制精度影响很大,为了补偿干扰对姿态跟踪控制的影响,设计调试简单,易于部署的抗干扰控制器,本文提出了基于干扰观测器的姿态跟踪控制器设计框架,并进行了姿态跟踪实验。
首先,基于修正的罗德里格斯参数(modified Rodrigues parameters, MRPs)姿态表示法建立NQTAUV的运动学和动力学模型,并进一步推导出姿态跟踪误差模型。其次,设计干扰观测器,估计作用在姿态上的干扰;设计姿态跟踪控制系统,并证明控制系统的稳定性。最后,进行实时姿态跟踪实验,验证了所提方法的控制性能。
1 NQTAUV数学模型 1.1 运动学和动力学在姿态跟踪控制中用到了3个坐标系:地球坐标系
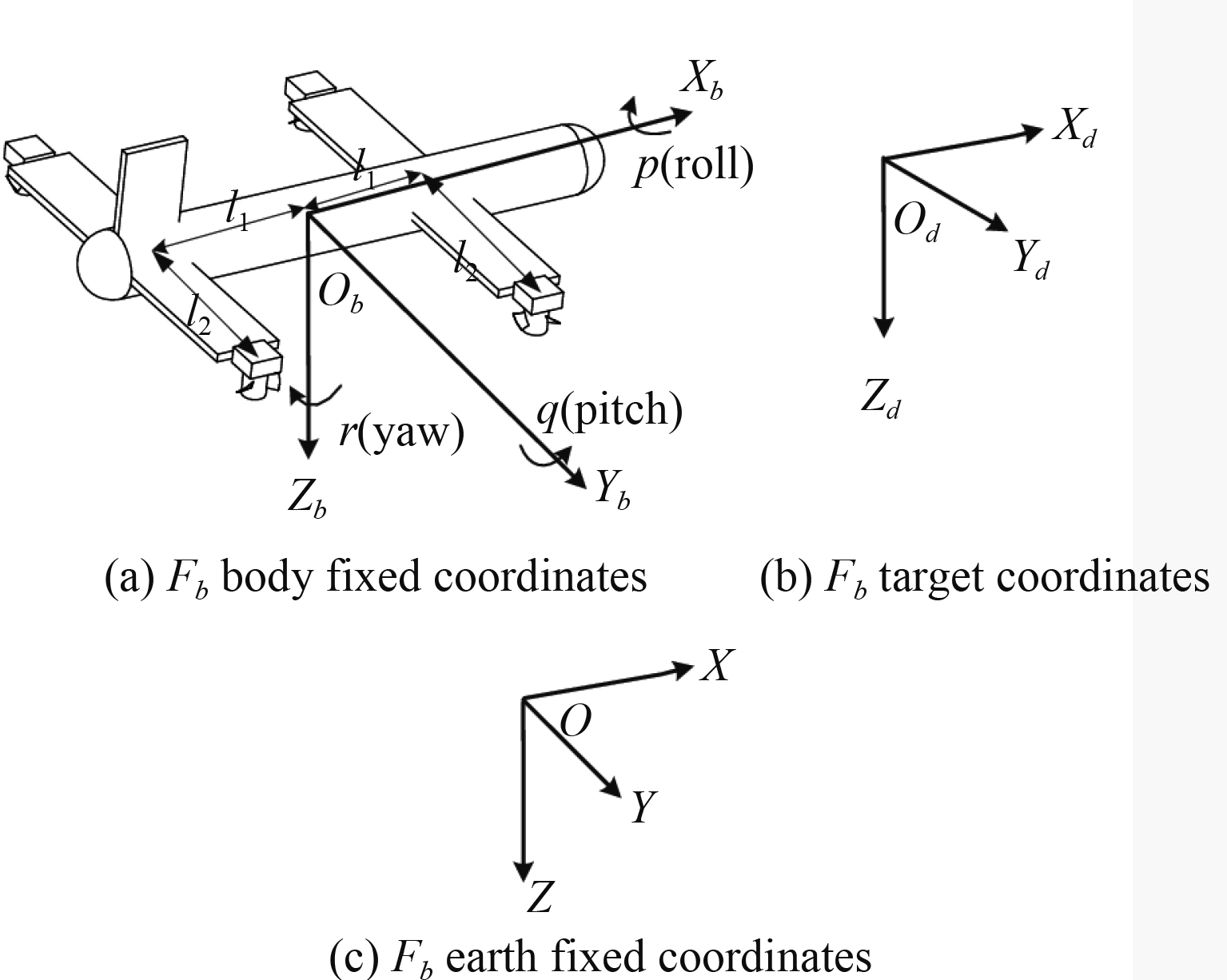
|
图 1 坐标系 Fig. 1 Coordinates |
BTH模式示意图如图2所示。
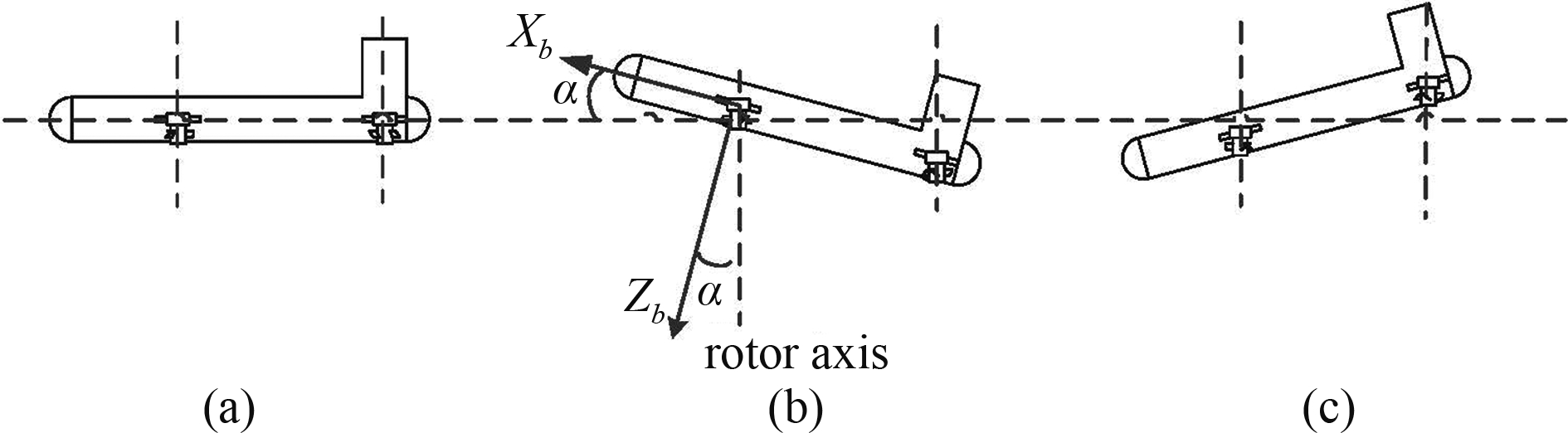
|
图 2 机身倾转悬停模式 Fig. 2 Body-tilt-hover mode |
表示刚体姿态的方法有多种,其中欧拉角是三参数姿态表示法,因为简单、直观,被广泛应用。然而,欧拉角在
NQTAUV的运动学和动力学方程为:
| $\dot \sigma = G(\sigma )\omega $ | (1) |
| $ J\dot \omega {\rm{ }} = - S(\omega )J\omega - {{ I}_A}\dot \omega - { C}(\omega )\omega - D(\omega ) + \tau $ | (2) |
其中:
| $ S(\lambda ) = \left[ {\begin{array}{*{20}{c}} 0&{ - {\lambda _3}}&{{\lambda _2}} \\ {{\lambda _3}}&0&{ - {\lambda _1}} \\ { - {\lambda _2}}&{{\lambda _1}}&0 \end{array}} \right] {\text{,}} $ | (3) |
其中:
| $ G(\sigma ) = \frac{1}{4}[(1 - {\sigma ^T}\sigma )I + 2S(\sigma ) + 2\sigma {\sigma ^{\rm T}}] {\text{,}} $ | (4) |
| $ \sigma G(\sigma ) = \frac{1}{4}(1 + {\sigma ^T}\sigma )\sigma {\text{。}} $ | (5) |
在姿态跟踪问题中,定义目标姿态
| $ \tilde \sigma = \sigma \otimes \sigma _d^{ - 1} = \frac{{{\sigma _d}({\sigma ^{\rm T}}\sigma - 1) + \sigma (1 - \sigma _d^{\rm T}{\sigma _d}) - 2S({\sigma _d})\sigma }}{{1 + \sigma _d^{\rm T}{\sigma _d}{\sigma ^{\rm T}}\sigma + 2\sigma _d^{\rm T}\sigma }} {\text{,}} $ | (6) |
相对角速度为:
| $ \tilde \omega = \omega - \tilde { R}{\omega _d} {\text{,}} $ | (7) |
其中,
| $ \tilde { R} = \frac{{(1 - 6{{\tilde \sigma }^{\rm T}}\tilde \sigma + {{({{\tilde \sigma }^{\rm T}}\tilde \sigma )}^2})I + 8\tilde \sigma {{\tilde \sigma }^{\rm T}} - 4(1 - {{\tilde \sigma }^{\rm T}}\tilde \sigma )S(\tilde \sigma )}}{{{{(1 + {{\tilde \sigma }^{\rm T}}\tilde \sigma )}^2}}}{\text{,}} $ | (8) |
| $ \dot {\tilde { R}} = - S(\tilde \omega )\tilde { R} {\text{,}} $ | (9) |
| $ \dot {\tilde \omega} = \dot \omega - (\dot{ \tilde { R}}{\omega _d} + \tilde { R}{{\dot {\tilde \omega}} _d}) = \dot \omega - [ - S(\tilde \omega )\tilde { R}{\omega _d} + \tilde{ R}{{\dot{ \tilde \omega}} _d}] {\text{,}} $ | (10) |
因此,姿态跟踪误差模型为:
| $ \dot {\tilde \sigma} = G(\tilde \sigma )\tilde \omega {\text{,}} $ | (11) |
| $ \begin{split} \dot {\tilde \omega} = & {J^{ - 1}}[ - S(\omega )J\omega - {{ I}_A}\dot \omega - { C}(\omega )\omega - { D}(\omega ) + \tau ] - \\ &( - S(\tilde \omega )\tilde R{\omega _d} + \tilde R{{\dot {\tilde \omega}} _d}){\text{,}} \end{split} $ | (12) |
其中,
用反馈线性化消去系统动态中的非线性项:
| $ \begin{split} \tau = & \nu + [S(\omega )J\omega + {I_A}\dot \omega + C(\omega )\omega + { D}(\omega )] +\\ & J( - S(\tilde \omega )\tilde R{\omega _d} + \tilde R{{\dot {\tilde \omega}} _d}) {\text{,}} \end{split} $ | (13) |
其中,
| $ \dot {\tilde \omega} = {J^{ - 1}}(\nu + d) {\text{。}} $ | (14) |
其中:
| $ \dot {\tilde \omega} = {J^{ - 1}}\nu + d' {\text{。}} $ | (15) |
基于干扰观测器的控制框架如图3所示。
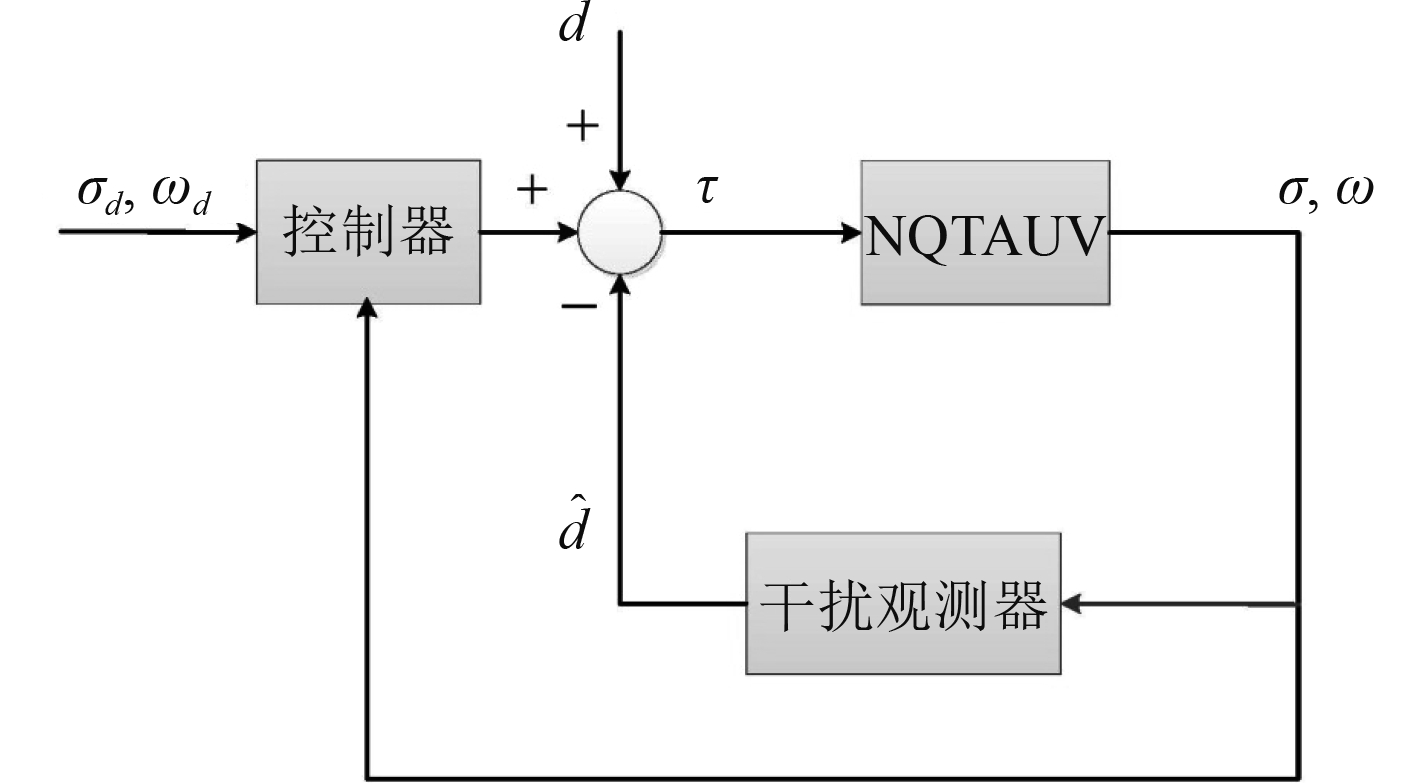
|
图 3 控制框架 Fig. 3 Control scheme |
作用在NQTAUV上的干扰不能被直接测量,因此需要引入干扰观测器估计这个干扰。假设干扰是常值,记
| $ \dot z{\rm{ }} = - l(\tilde \omega )[z + p(\tilde \omega ) + {J^{ - 1}}\nu ] {\text{,}} $ | (16) |
| $ \hat d'{\rm{ }} = z + p(\tilde \omega ) {\text{,}} $ | (17) |
其中,
| $ l(\tilde \omega ) = \frac{{\partial p(\tilde \omega )}}{{\partial \tilde \omega }} {\text{。}} $ | (18) |
干扰观测误差的导数为:
| $ \begin{split} & \dot {\tilde d'} = \dot d' - \dot {\hat d'} = 0 - [\dot z + \frac{{\partial p(\tilde \omega )}}{{\partial \tilde \omega }}\dot {\tilde \omega} ]= \\ & l(\tilde \omega )[z + p(\tilde \omega ) + {J^{ - 1}}\nu ] + l(\tilde \omega )\dot {\tilde \omega} = \\ & l(\tilde \omega )[\hat d' + {J^{ - 1}}\nu ] - l(\tilde \omega )({J^{ - 1}}\nu + d') =\\ & - l(\tilde \omega )[d' - \hat d']= \\ & - l(\tilde \omega )\tilde d' {\text{。}} \end{split} $ | (19) |
同时,因为
| $ \dot {\tilde d }= - l(\tilde \omega )\tilde d {\text{。}} $ | (20) |
选取
| $ l(\tilde \omega ) = {k_3},{k_3} > 0 {\text{,}} $ | (21) |
故得到:
| $ p(\tilde \omega ) = \int l (\tilde \omega ){\rm d}\tilde \omega = {k_3}\tilde \omega {\text{。}} $ | (22) |
选取李雅普诺夫函数:
| $ {V_1}{\rm{ }} = 2{k_1}\ln (1 + {\tilde \sigma ^{\rm T}}\tilde \sigma ) + \frac{1}{2}{\tilde \omega ^{\rm T}}J\tilde \omega {\text{,}} $ | (23) |
其中
| $ \begin{split} {{\dot V}_1} =& 4{k_1}\frac{{{{\tilde \sigma }^{\rm T}}\dot {\tilde \sigma} }}{{1 + {{\tilde \sigma }^T}\tilde \sigma }} + {{\tilde \omega }^{\rm T}}J\dot {\tilde \omega} = \\ & {k_1}{{\tilde \omega }^{\rm T}}\tilde \sigma + {{\tilde \omega }^{\rm T}}(\nu + d) = {{\tilde \omega }^{\rm T}}({k_1}\tilde \sigma + \nu + d) {\text{,}} \end{split} $ | (24) |
假设干扰
| $ \nu = - {k_1}\tilde \sigma - {k_2}\tilde \omega - \hat d {\text{,}} $ | (25) |
其中
| $ {{\dot V}_1}{\rm{ }} = - {k_2}{{\tilde \omega }^{\rm T}}\tilde \omega + {{\tilde \omega }^{\rm T}}\tilde d \leqslant - {k_2}||\tilde \omega |{|^2} + ||\tilde \omega ||||\tilde d|| {\text{。}} $ | (26) |
用李雅普诺夫稳定性理论分析整个系统的稳定性。选取李雅普诺夫函数:
| $ {V_2} = \frac{1}{2}{\tilde d^2} {\text{,}} $ | (27) |
| $ {{\dot V}_2} = \tilde d\dot {\tilde d} = - {k_3}{{\tilde d}^2} {\text{,}} $ | (28) |
又选取李雅普诺夫函数
| $ {\dot V_3} = {\dot V_1} + {\dot V_2} \le - {k_2}||\tilde \omega |{|^2} + ||\tilde \omega ||||\tilde d|| - {k_3}{\tilde d^{'2}} {\text{。}} $ | (29) |
选取
实验采用浸入水中的三自由度测试平台进行。NQTAUV本体通过一个球铰连接在固定的基座上,使得本体能够实现俯仰和横摇各
|
|
表 1 NQTAUV机械参数 Tab.1 Mechanical parameters of the NQTAUV |
控制器和观测器参数选取为
| $ {\sigma _d} = \left[ {\begin{array}{*{20}{c}} 0 \\ {\tan\left(\dfrac{{\text{π}} }{{72}}\right)\sin\left(\frac{{\text{π}}}{{10}}t\right)} \\ 0 \end{array}} \right]{\text{。}} $ | (30) |
在
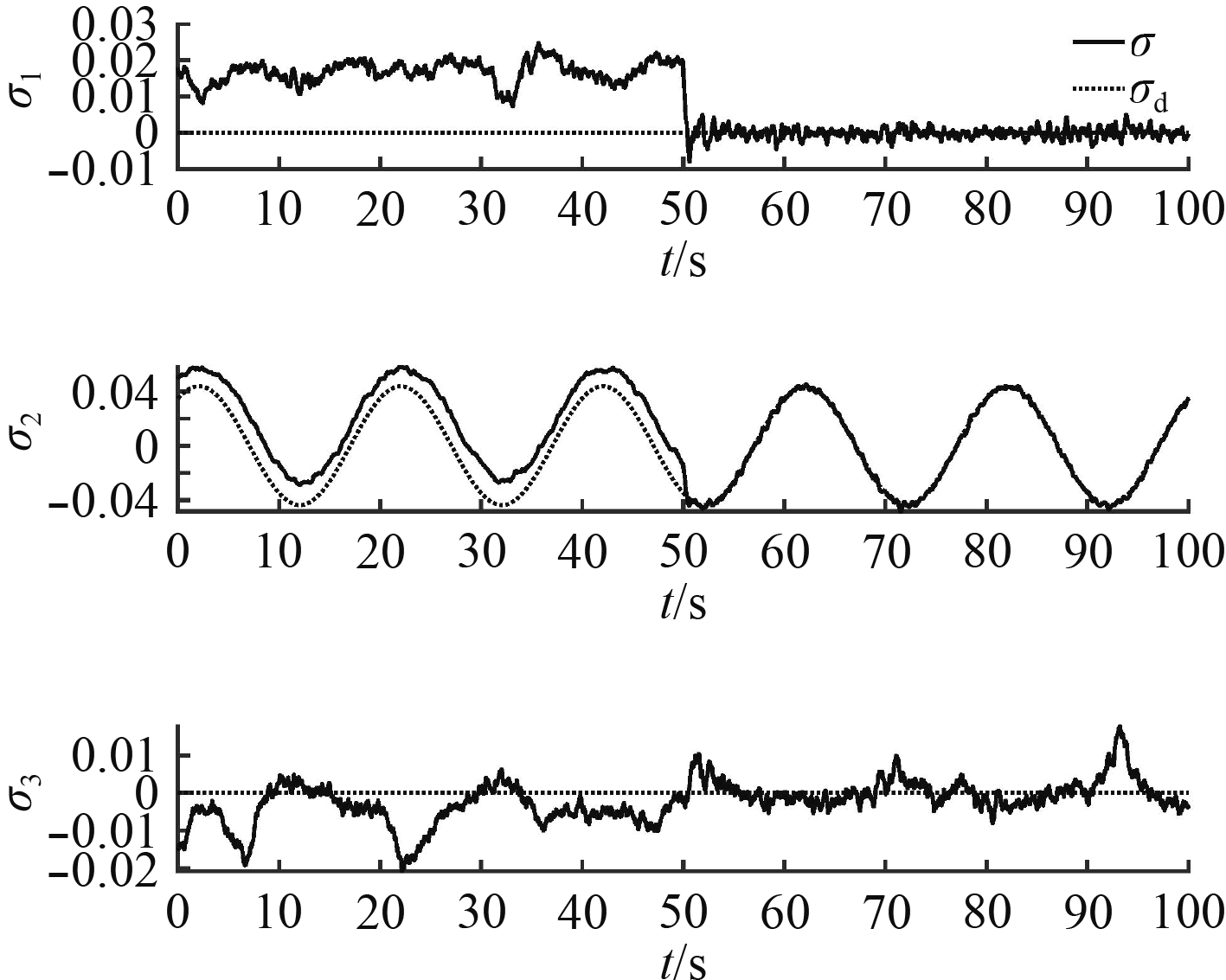
|
图 4 正弦信号姿态跟踪结果 Fig. 4 Sinusoidal attitude tracking performance |

|
图 5 控制输入 Fig. 5 Control input |
|
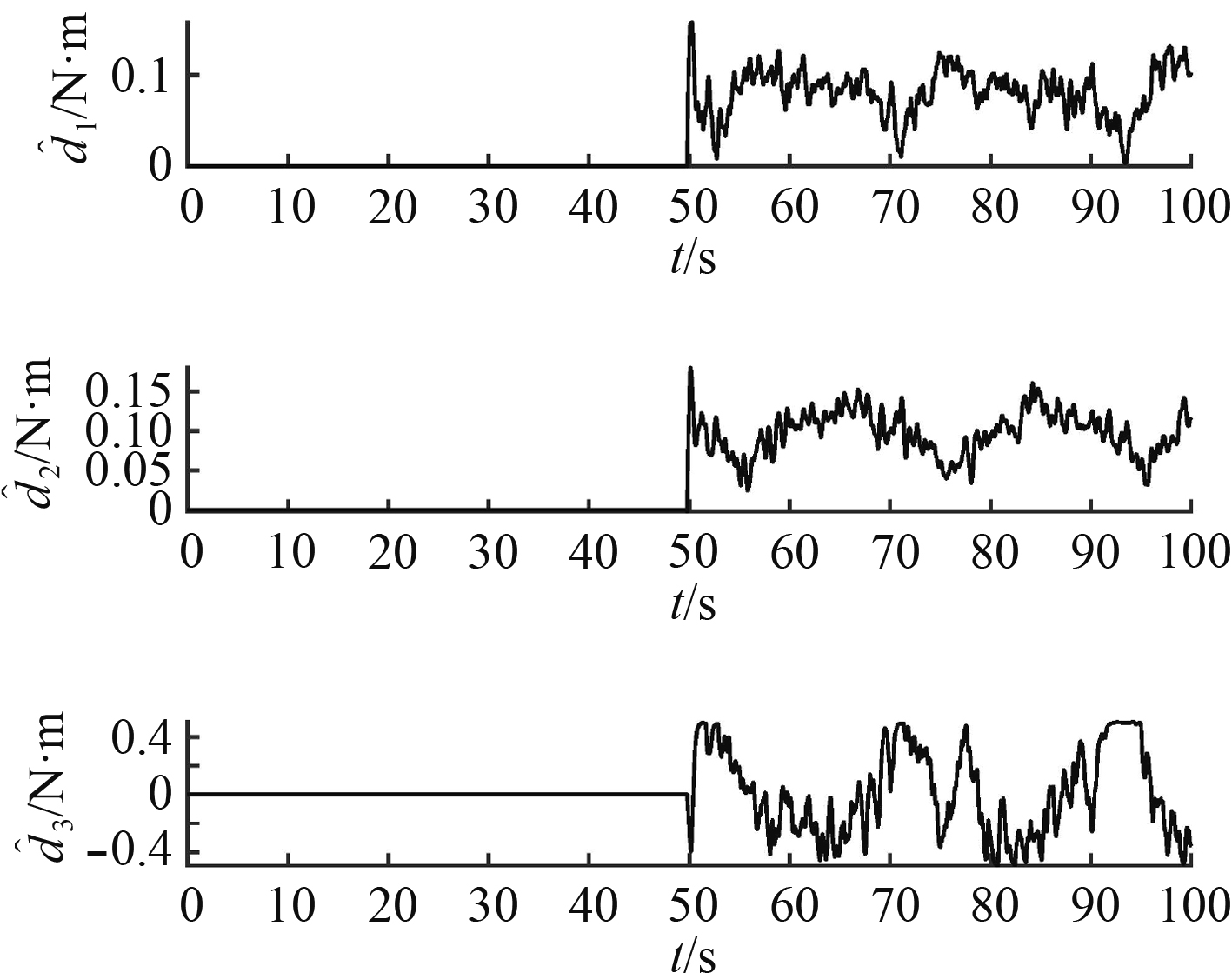
图 6 干扰观测值 Fig. 6 Disturbance estimation |
从图4可以看出,当干扰观测器关闭时,能跟踪正弦跟踪信号,但是会产生大约0.02的姿态偏移量,且有大约1 s的相位滞后。同时可以看出,姿态波动幅值很大,说明受干扰影响很大。当干扰观测器激活后,姿态偏移量为0,相位滞后也被消除,姿态波动非常小,说明干扰被补偿掉,实际姿态能够精确跟踪目标姿态。
从图5可以看出,在激活干扰观测器后,控制输出有一个整体的增加,说明对常值干扰力矩进行了补偿。
从图6可以看出,当干扰观测器激活后,干扰估计值呈现波动,与正弦信号相位相吻合。在正弦姿态跟踪时,NQTAUV受到周期性的水动力,其周期和相位与本体运动相同,由于目标姿态信号周期为20 s,因此这是缓慢变化的干扰。这也说明干扰观测器不但可以估计常值干扰,还可以估计缓慢变化的干扰。
综上,干扰观测器能够准确估计常值干扰,对缓慢变化的干扰也有准确的估计。所提的姿态跟踪控制器能够准确跟踪目标姿态。
4 结 语本文针对负浮力四倾转推进器水下机器人,设计了抗干扰控制框架。基于修正的罗德里格斯参数,导出了负浮力四倾转推进器水下机器人姿态跟踪的数学模型。然后设计了干扰观测器来估计干扰,并基于此干扰观测器设计了姿态跟踪控制器。控制框架的稳定性得到了证明。最后,通过实时姿态跟踪实验,比较干扰观测器激活和关闭2种不同情况下的姿态跟踪表现,验证了控制框架的性能。所提出的基于干扰观测器的控制框架,抗干扰能力强,参数数量少,调节简单,易于实际部署。
| [1] |
FOSSEN, T. Guidance and control of ocean vehicles[M]. John Willey & Sons: 1994.
|
| [2] |
BROWN, C. L. In Deep sea mining and robotics: Assessing legal, societal and ethical implications[C]// 2017 IEEE Workshop on Advanced Robotics and its Social Impacts (ARSO), Austin, TX, USA, 2017: 1-2.
|
| [3] |
LI Y, PAN D, ZHAO Q, et al. Hydrodynamic performance of an autonomous underwater glider with a pair of bioinspired hydro wings–a numerical investigation[J]. Ocean Engineering, 2018, 163: 51-57. DOI:10.1016/j.oceaneng.2018.05.052 |
| [4] |
WYNN R B, HUVENNE V A I, LE BAS T P, et al. Autonomous underwater vehicles (auvs): Their past, present and future contributions to the advancement of marine geoscience[J]. Marine Geology, 2014, 352: 451-468. DOI:10.1016/j.margeo.2014.03.012 |
| [5] |
WANG T, WU C, WANG J, et al. Modeling and control of negative-buoyancy tri-tilt-rotor autonomous underwater vehicles based on immersion and invariance methodology[J]. Applied Sciences, 2018, 8. |
| [6] |
HUI Y, TONG G, JIA-WANG L, et al. In Prediction of mode and static stability of negative buoyancy vehicle[C]// 2011 Chinese Control and Decision Conference (CCDC), 2011: 1903-1909.
|
| [7] |
WU N, WU C, GE, T, et al. Pitch channel control of a remus auv with input saturation and coupling disturbances[J]. Applied Sciences, 2018, 8. |
| [8] |
XIANG X, LAPIERRE L, JOUVENCEL B. Smooth transition of auv motion control: From fully-actuated to under-actuated configuration[J]. Robotics and Autonomous Systems, 2015, 67: 14-22. DOI:10.1016/j.robot.2014.09.024 |
| [9] |
LI X, ZHAO M, GE T. A nonlinear observer for remotely operated vehicles with cable effect in ocean currents[J]. Applied Sciences, 2018, 8. |
| [10] |
YUAN Y, YU Y, GUO L. Nonlinear active disturbance rejection control for the pneumatic muscle actuators with discrete-time measurements[J]. Ieee Transactions on Industrial Electronics, 2019, 66: 2044-2053. |
| [11] |
CUI R, YANG C, LI Y, SHARMA S. Adaptive neural network control of auvs with control input nonlinearities using reinforcement learning[J]. Ieee Transactions on Systems Man Cybernetics-Systems, 2017, 47: 1019-1029. DOI:10.1109/TSMC.2016.2645699 |
| [12] |
LIU C, MCAREE O, CHEN W H. Path following for small uavs in the presence of wind disturbance, Control [C]// (Control), 2012 UKACC International Conference on, Cardiff, UK, 2012: 613-618.
|
| [13] |
PALOMERAS N, VALLICROSA G, MALLIOS A, et al. Auv homing and docking for remote operations[J]. Ocean Engineering, 2018, 154: 106-120. DOI:10.1016/j.oceaneng.2018.01.114 |
| [14] |
XING G Q, SHABBIR A P. Alternate forms of relative attitude kinematics and dynamics equations[C]// 2001 Flight Mechanics Symposium, Greenbelt, MD, USA, 2001: 83-97.
|
 2020, Vol. 42
2020, Vol. 42
