2. 中船重工七〇五研究所昆明分部,云南 昆明 650102
2. The 705 Research Institute Kunming Branch, Kunming 605118, China
针对洋流对AUV航行轨迹的影响,研究人员已经进行了大量的分析和研究。高富东[1]建立了一种AUV在洋流和波浪扰动作用下的数学模型。范双双[2]探讨了洋流影响下的水下滑翔机多体动力学模型,为洋流中滑翔机的运动预测及控制器和观测器设计提供参考。房萍萍[3]研究了侧向流对AUV运动姿态的影响,并得出了洋流影响下的航行器水动力特征。这些研究成果为研究洋流对AUV的影响机理提供了较好的参考依据。
另一方面,研究人员也针对洋流环境中的AUV航路规划和控制问题进行了大量研究。姚鹏[5]针对复杂海洋环境下AUV三维避障问题,提出了一种高效的修正导航向量场方法,但是该算法的研究对象是AUV的避障问题,与减小洋流影响的方法存在差异性。苗润龙等[6]提出了遗漏海湾和重复海湾及其进入点、退出点和门户的路径规划环境表达概念,并将其应用在基于行为的锯齿形完全遍历路径规划改进算法中,有效地减少了海洋自主航行器全覆盖地形测绘的重复区域和遗漏区域,但是该路径规划算法并未考虑洋流的影响。鲁燕[7]针对定向洋流干扰下的AUV航路规划问题,提出了一种基于改进模糊控制理论的运动规划方法,但是该方法需要经历状态感知、动作、效果比较和监控、再规划等步骤,算法过于复杂、实施难度大。文献[8]分析了水下运载器在存在复杂干扰、运动模型未知的情况下的轨迹跟踪控制问题,并提出了滑模控制算法。为了减弱抖振现象对系统带来的影响,Levant等[9-10]设计了一种新型的2阶滑模控制方法,T.Salgado[11]和Imran[12]等成功地将此方法应用到了AUV的航迹跟踪控制上,并取得了良好的控制效果,但是这类算法考虑的环境条件与本文考虑的洋流影响条件存在一定差异,适用性不足。为此,需要设计一种简单有效的减小洋流影响的方法。
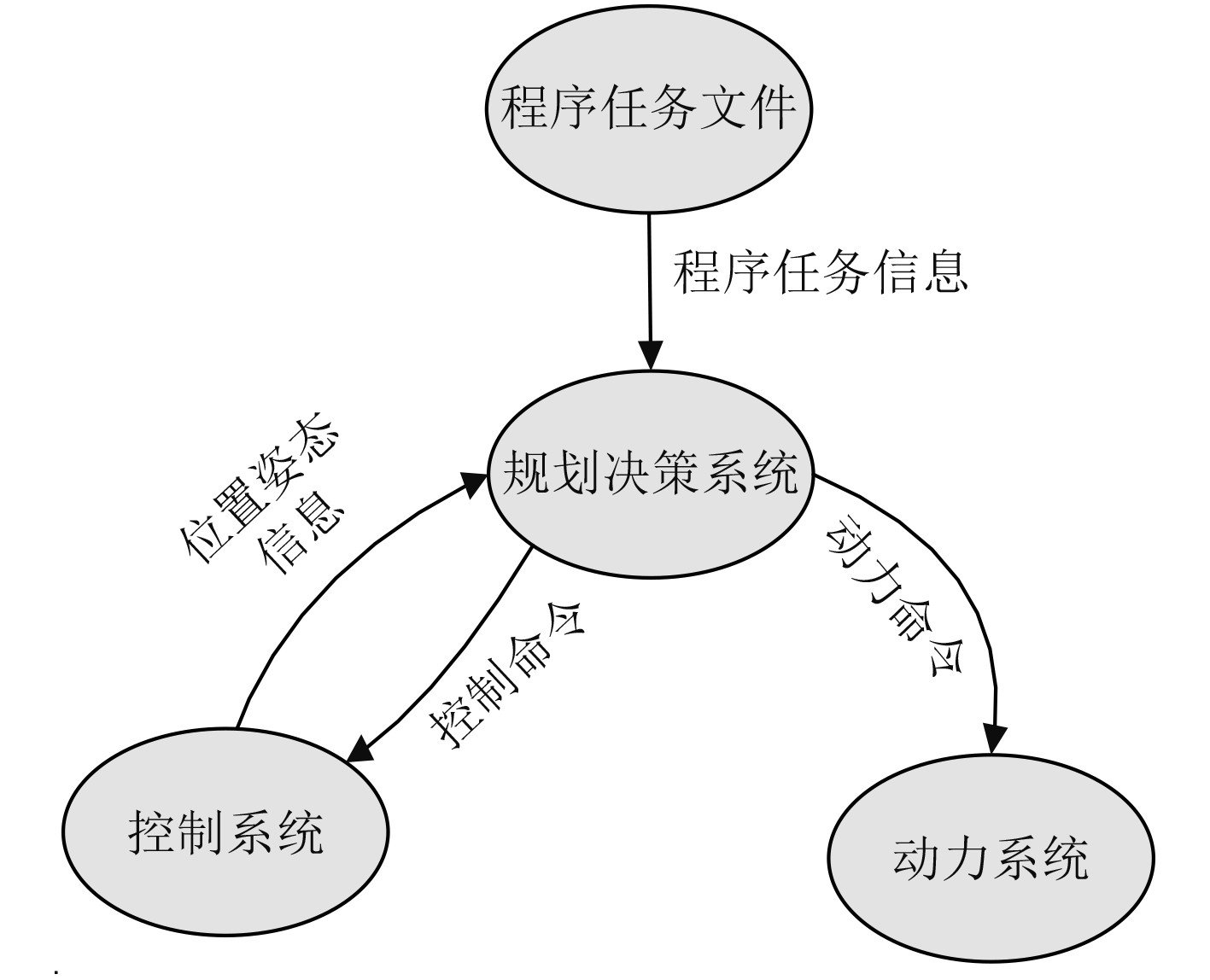
1 洋流对低速AUV的影响 1.1 低速AUV的特点低速AUV除了航速低航程远,还具备非固定航向的特点。低速AUV工作模式分为水面遥控航行模式和程序任务航行模式,本文只考虑程序任务航行模式。在程序任务航行模式下,低速AUV启动前通过读取程序任务文件,设置程序任务航行信息,同时控制系统将当前位置、姿态等信息发送给规划决策系统,然后规划决策系统开始规划航行路线(即一系列航路控制点)。启动后,控制系统在每个航行周期内,将当前位置、姿态等信息发送给规划决策系统,然后规划决策系统开始规划航行路线,并且分别向控制系统和动力系统发送控制命令和动力命令,控制系统和动力系统再分别操作舵机和电机进行航速和航向控制,到达控制点后,再采用同样的方式控制AUV向下一个航路控制点航行,直至到达目标点。AUV的信息流向如图1所示。在每个周期内,控制系统向规划决策系统反馈当前的位置和姿态信息,随后规划决策系统根据设定的程序任务信息和当前的位置和姿态信息,解算出相应的航速和航向信息,分别发送给动力系统和控制系统完成姿态控制。可以看出,在程序任务航行模式下,低速AUV的航向不固定。
|
图 1 AUV信息流向图 Fig. 1 Information flow direction figure of AUV |
根据经验分析,洋流对低速AUV的影响主要分为2个方面:一是垂直于AUV航行方向的洋流,会使低速AUV偏离航线,使其无法沿既定的轨迹直线航行;二是平行于AUV航行方向的洋流,会降低低速AUV的航行速度。
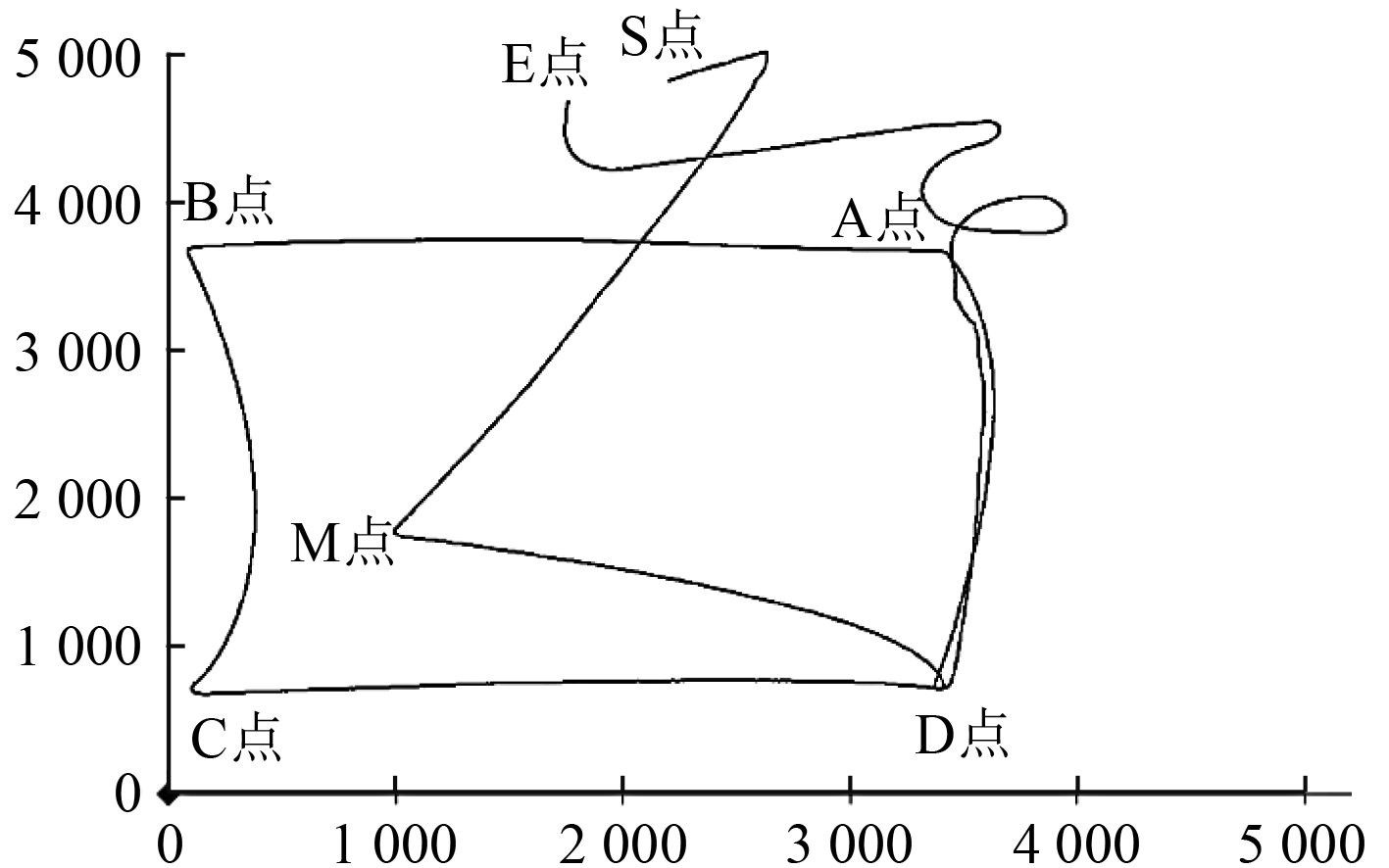
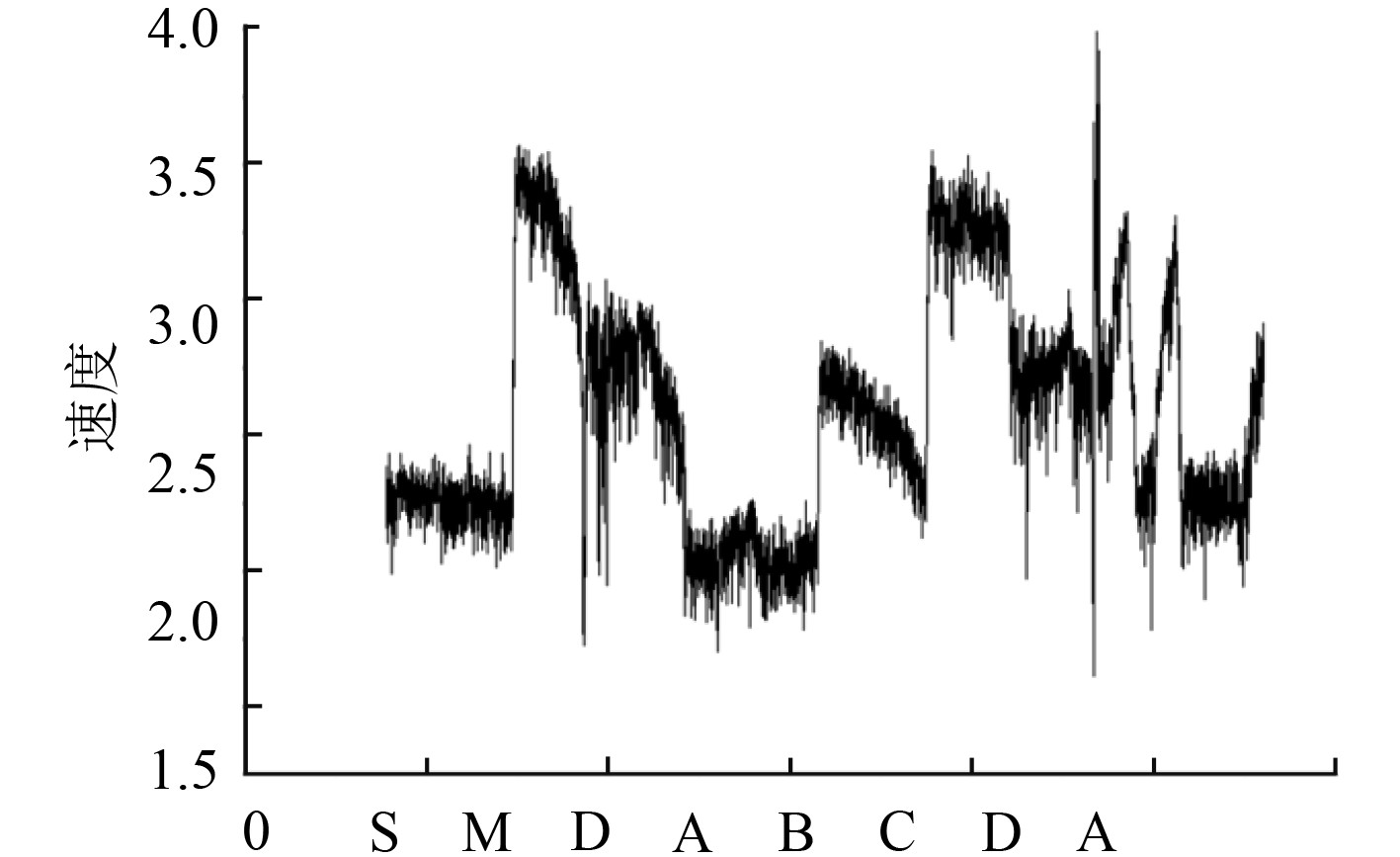
1.3 实航影响分析事实上,上述影响已经在某型AUV实航过程中有所体现,在某次实航过程中,经测量当地流速约2 kn,流向279.7°(正北为0°,北偏西为正,即流向大约为正东)AUV的设定航速为6 kn(约3 m/s),如图2所示。AUV自S点启动向M点航行时,由于顶流的原因航速大约为2.25 m/s,而在M点向D点航行时,由于顺流航速大约为3.3 m/s,航速差大约为1 m/s,这与流速2 kn是吻合的。特别是在图中由B点向正南方3 km外的C点航行过程中,设定速度为6 kn(约3 m/s),AUV的实际航行轨迹并未像预先设计的直线航行,而是形成一段向东有弧线突出的“半枣核型”轨迹,速度也受到影响不断下降,平均航速约为2.5 m/s。航行轨迹如图2所示,航速的变化如图3所示。
|
图 2 低速AUV航行轨迹图 Fig. 2 Low-speed sailing tracks figure of AUV |
|
图 3 AUV航速变化图 Fig. 3 Sailing speed change figure of AUV |
可见,AUV的航行速度较低,受到的洋流影响是比较大的,但是由于AUV的控制模型是“向目标点”航行,而不是“固定航向”航行,所以AUV在航行过程中不断调整航向,最终还是可以到达目标点,但是会偏离实际的轨迹,并且速度和航程也会下降。
2 潮流的特点及对低速AUV的影响机理分析 2.1 潮流的特点在引潮力的作用下,海水做周期性的水平运动,称为潮流。潮流和潮汐是潮波运动过程的2个方面,潮流的一些特征(如日周期、半日周期、大潮流、小潮流等)与潮汐现象相似,但是潮流更多受地形、海底摩擦及地球自转的影响。
2.2 潮流的运动及简化由于潮流主要是水平运动,
| $ \left\{ \begin{aligned} & \frac{{\partial \delta }}{{\partial t}} + \frac{{\partial (hu)}}{{\partial x}} + \frac{{\partial (hv)}}{{\partial x}} = 0 {\text{,}} \\ & \frac{{\partial u}}{{\partial t}} - 2\omega \sin \lambda \cdot v = - \frac{\partial }{{\partial x}}(\varOmega + g\delta ) {\text{,}} \\ & \frac{{\partial v}}{{\partial t}} + 2\omega \sin \lambda \cdot u = - \frac{\partial }{{\partial y}}(\varOmega + g\delta ) {\text{。}} \end{aligned} \right. $ | (1) |
式中:
对于一元推进潮波,地球偏向力和摩擦力的作用可以略去,并认为潮波已经转为不计潮力的自由潮波运动,在这种情况下的运动方程和连续方程为:
| $ \left\{ \begin{aligned} & \frac{{\partial u}}{{\partial t}} + g\frac{{\partial \delta }}{{\partial x}} = 0 {\text{,}} \\ & \frac{{\partial \delta }}{{\partial t}} + h\frac{{\partial u}}{{\partial x}} = 0 {\text{。}} \end{aligned} \right. $ | (2) |
在海面上的垂向运动可视为一简谐函数,即
| $ \delta = a\sin (\omega t - kx) {\text{。}} $ | (3) |
式中:
| $ u = C\frac{a}{h}\sin (\omega t - kx) = \frac{C}{h}\delta = \sqrt g \frac{\delta }{{\sqrt h }} {\text{。}} $ | (4) |
式中:
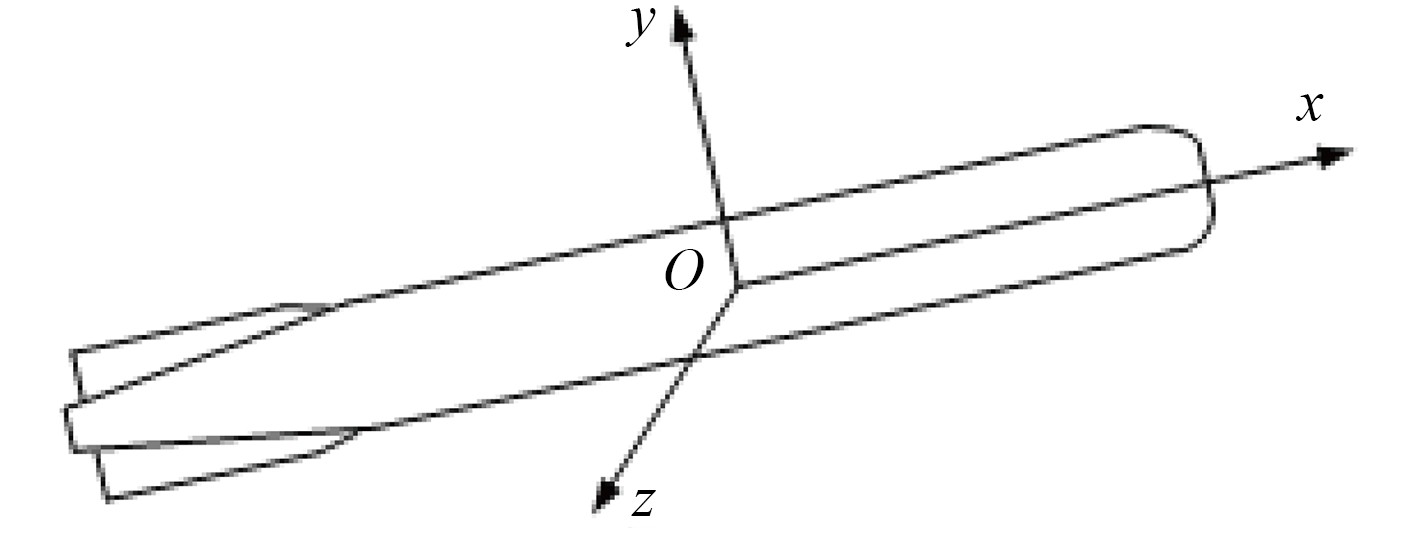
潮流对低速AUV的影响主要是作用在低速AUV上的流体动力,以低速AUV为研究对象,无论洋流的流向如何,总能被分解为沿低速AUV纵轴(
|
图 4 低速AUV坐标分解图 Fig. 4 Coordinate decomposition figure of 低速AUV |
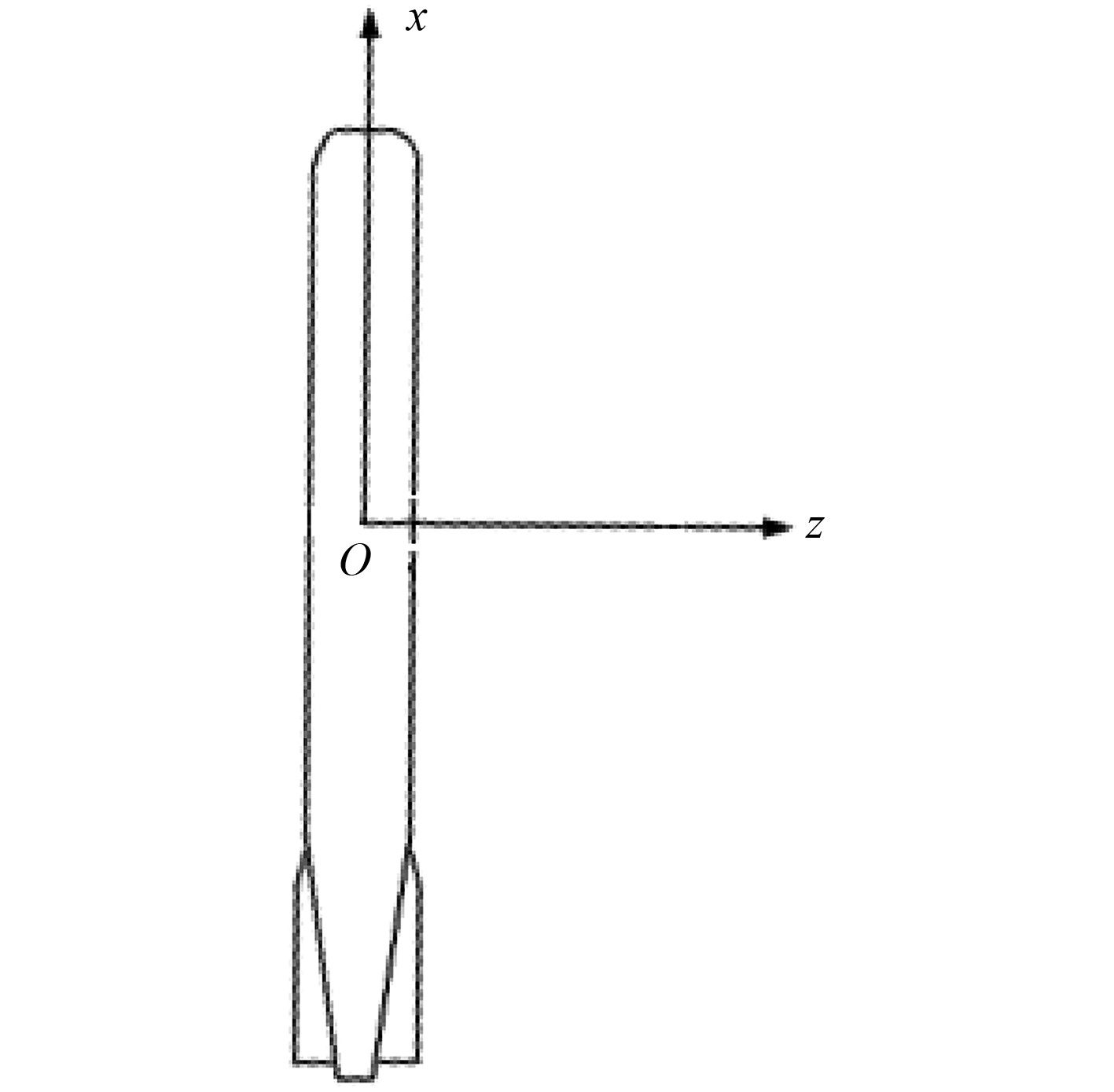
|
图 5 受洋流影响示意图 Fig. 5 Effects on ocean current schematic diagram |
洋流作用在低速AUV上的流体动力,可以等效为在低速AUV的纵轴(
设低速AUV航向为
沿航路的速度分量
| $ {v_x} = {v_0} + {v_1} \cdot \cos (\theta - \varphi ) {\text{,}} $ | (5) |
垂直航路的速度分量
| $ {v_z} = {v_1} \cdot \sin (\theta - \varphi ) {\text{,}} $ | (6) |
航迹向(低速AUV的实际航向)
| $ \eta = \theta + {{{v_z}} / {{v_x}}} {\text{,}} $ | (7) |
低速AUV的实际航速
| $ v = \sqrt {{v_x}^2 + {v_z}^2} {\text{。}} $ | (8) |
通过对上式分析,当
洋流对高速AUV影响不大,是因为高速AUV航速较大,一般为几十节,以流速2 kn,流向与高速AUV航向垂直,航行器航速50 kn为例,
潮流对低速AUV航渡的影响主要是通过沿航路方向的分量影响低速AUV的实际航速,通过垂直航路方向的分量影响低速AUV的实际航向。因此,要减小潮流对低速AUV航渡的影响也是从这2个方面入手。
1)减小洋流对低速AUV航速的影响。可采用速度闭环控制的方式来实现,即动力系统的控制目标不再是螺旋桨转速,而是低速AUV的航行速度。
2)减小洋流对低速AUV航迹偏移量的影响。从式(8)中分析应该是使
针对第2类方案进行研究,即减小洋流对低速AUV航迹偏移的影响,使航迹接近于直线。为了实现上述目标,提出3种决策方法。
3.1 加装水平推进器在低速AUV中心位置加装水平方向的推进器,抵消洋流在这个方向的速度。该方法的优点是低速AUV的航迹始终沿预设航路方向,可以最大限度地发挥主推进器效能,缺点是在小型或微型AUV因空间限制实现比较困难。
3.2 航路纠正航路纠正是在不考虑加装水平方向推进器的情况下,使低速AUV的航向不沿预设航路方向,在垂直预设航路方向产生一个速度分量,抵消洋流在这个方向的速度。航路纠正又分为主动预防偏离航路和被动纠正偏离航路2种方法。
主动预防偏离航路是根据洋流的流速、流向计算洋流在垂直预设航路方向的速度分量,调整低速AUV航向、航速,使低速AUV在垂直预设航路方向的速度分量与洋流在垂直预设航路方向的速度分量大小相等方向相反。该方法的优点是低速AUV始终在航路上,没有航程损失,缺点是在每个航渡周期内需要获取(存储或测量)当地洋流的流速、流向信息,难度较大,特别是在非我方控制的陌生海域。
被动纠正偏离航路的方法是在航渡时期内将航向始终拽指向目标点,在偏离航路的情况下,被动返回航路,该方法的优点是不需要获取洋流的流速、流向信息,缺点也是存在航程损失。
3.3 增加航路控制点通过仿真发现,低速AUV偏离预设航路的偏移量与距离目标点的距离有关,距离目标点越远,到达目标点的时间越长。
以图6中由B点向正南方3 km外的C点的航渡过程为例,设定初始速度为6 kn(约3 m/s),做以下3种情况的对比实验:

|
图 6 不同航路控制点下的航迹图 Fig. 6 Tracks figure of different sailing control points |
1)不插入航路控制点时,此时只有一个航路控制点,即点C,低速AUV到达目标点的时间较长,洋流对低速AUV影响效果较明显,航迹最大偏差约为750 m。
2)在中间每1 km处插入2个航路控制点时,此时有3个航路控制点(包括点C),洋流对低速AUV影响效果就减弱,航迹最大偏差约为500 m。
3)在中间每500 m处插入5个航路控制点时,此时共有6个航路控制点(包括点C),洋流对低速AUV影响效果就明显减弱,约为50 m,航迹最大偏差约为350 m。
这3种情况下的计划航程、航迹最大偏差、航迹最大偏差率(航迹最大偏差/计划航程)如表1所示。可以发现,采用在预设航路上多设一些航路控制点,减小每2个航路控制点之间的距离,可以减小洋流对低速AUV航迹偏移的影响,使航迹接近于直线。这种决策方法相对于安装水平方向的推进器的方法和航路纠正的方法,约束条件更少,更加灵活和便捷性更强。
|
|
表 1 仿真实验不同航路控制点下的偏差统计 Tab.1 Deviation statistics of simulative experiment on different sailing control points condition |
实航实验的条件如表2所示。
|
|
表 2 实航实验条件 Tab.2 Real experiment condition |
在所提的3个决策方法中,前2个方法可以用逻辑分析得出,不需实验验证,因此仅对第3种方法进行验证。为了验证方法的正确性,对实航数据进行统计分析。
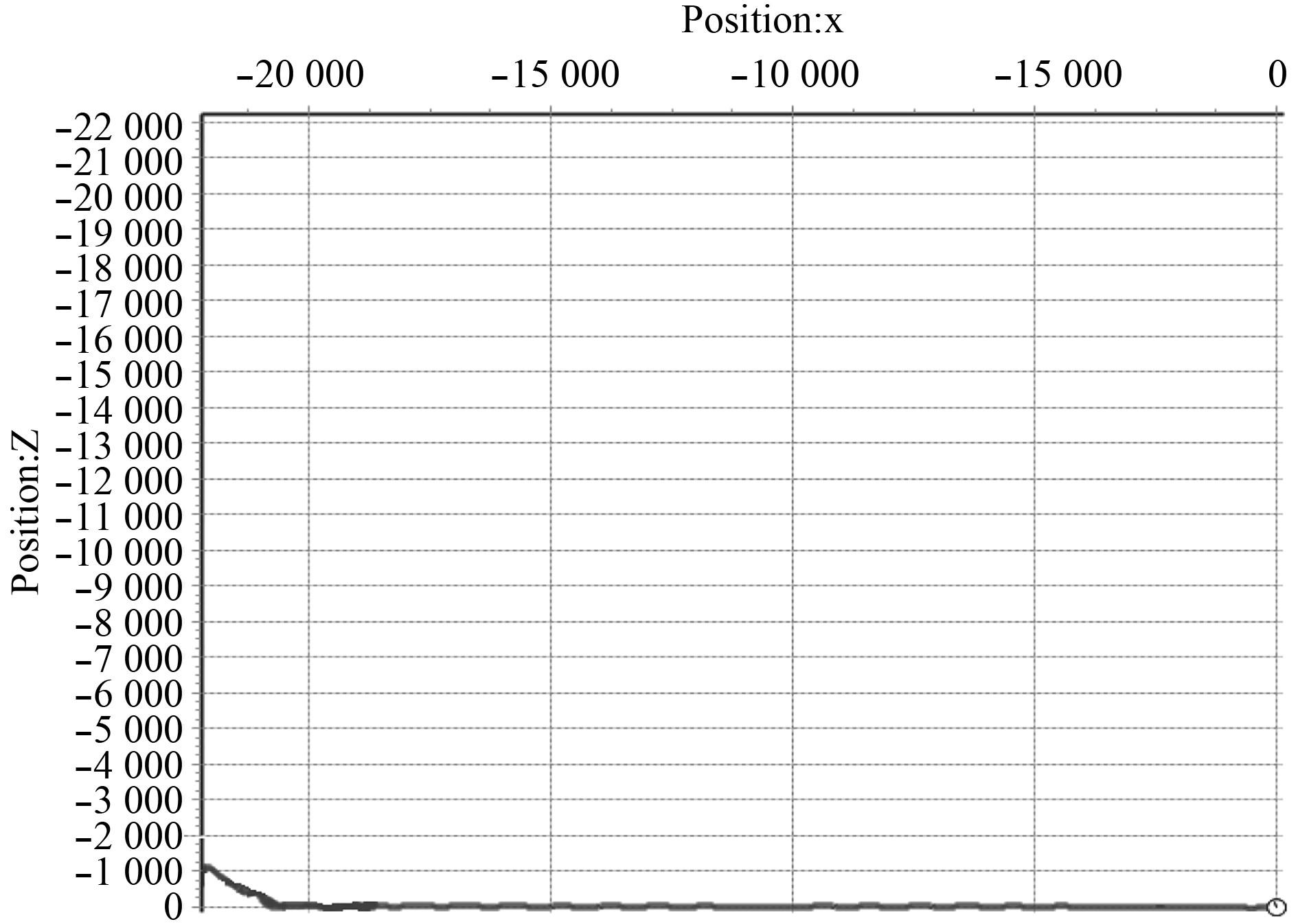
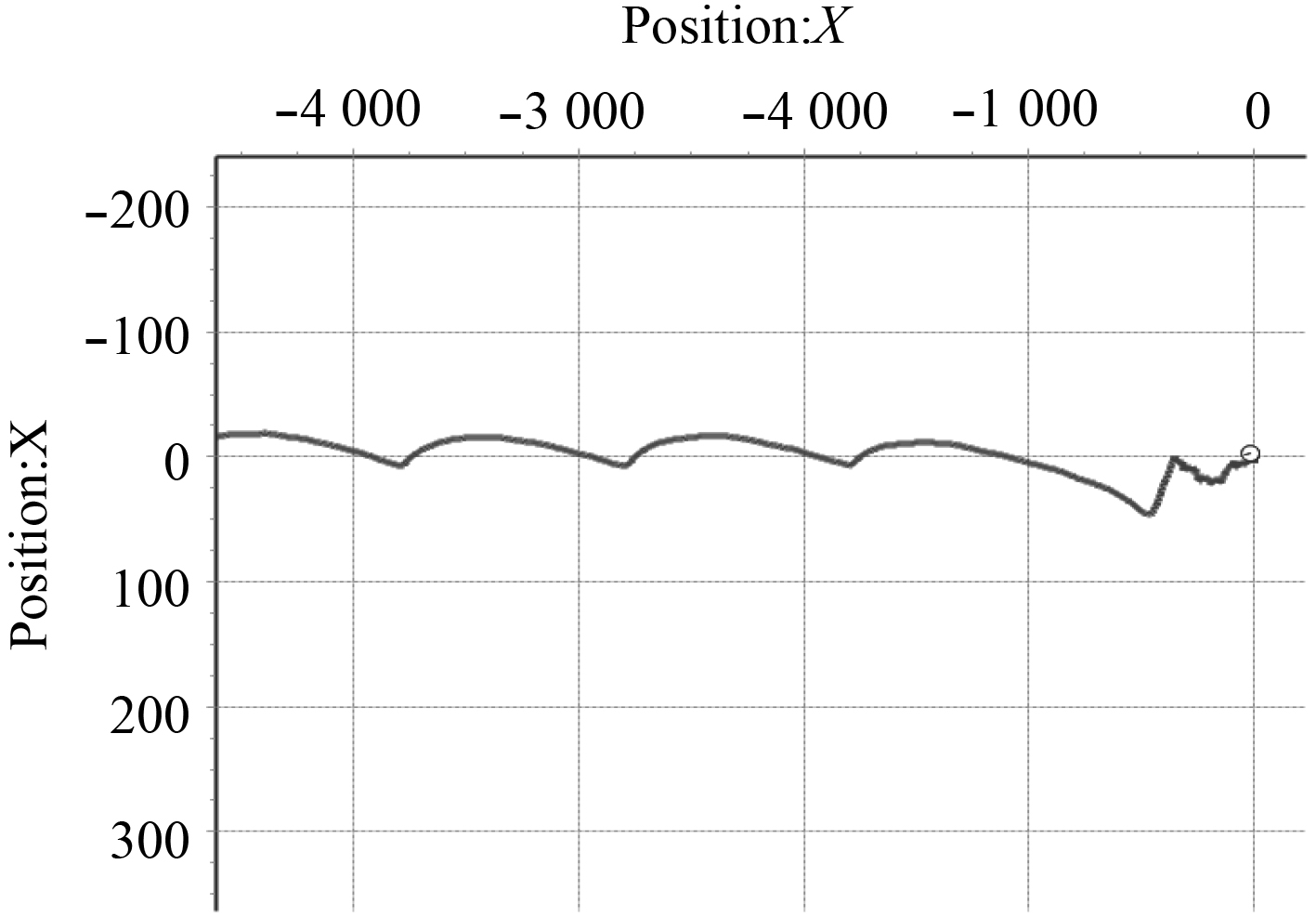
AUV从原点出发沿正西方向航行约22 km,每隔1 km插入一个航程控制点。实航实验的轨迹如图7所示。图8为实航实验的0~4.5 km部分轨迹图。由于实航实验成本较高,未进行实航对比实验,因此采用仿真的办法进行验证。
|
图 7 AUV实航轨迹图 Fig. 7 Real experiment tracks figure of AUV |
|
图 8 AUV实航实验的0~4.5 km部分轨迹图 Fig. 8 0~4 km part of real experiment tracks figure of AUV |
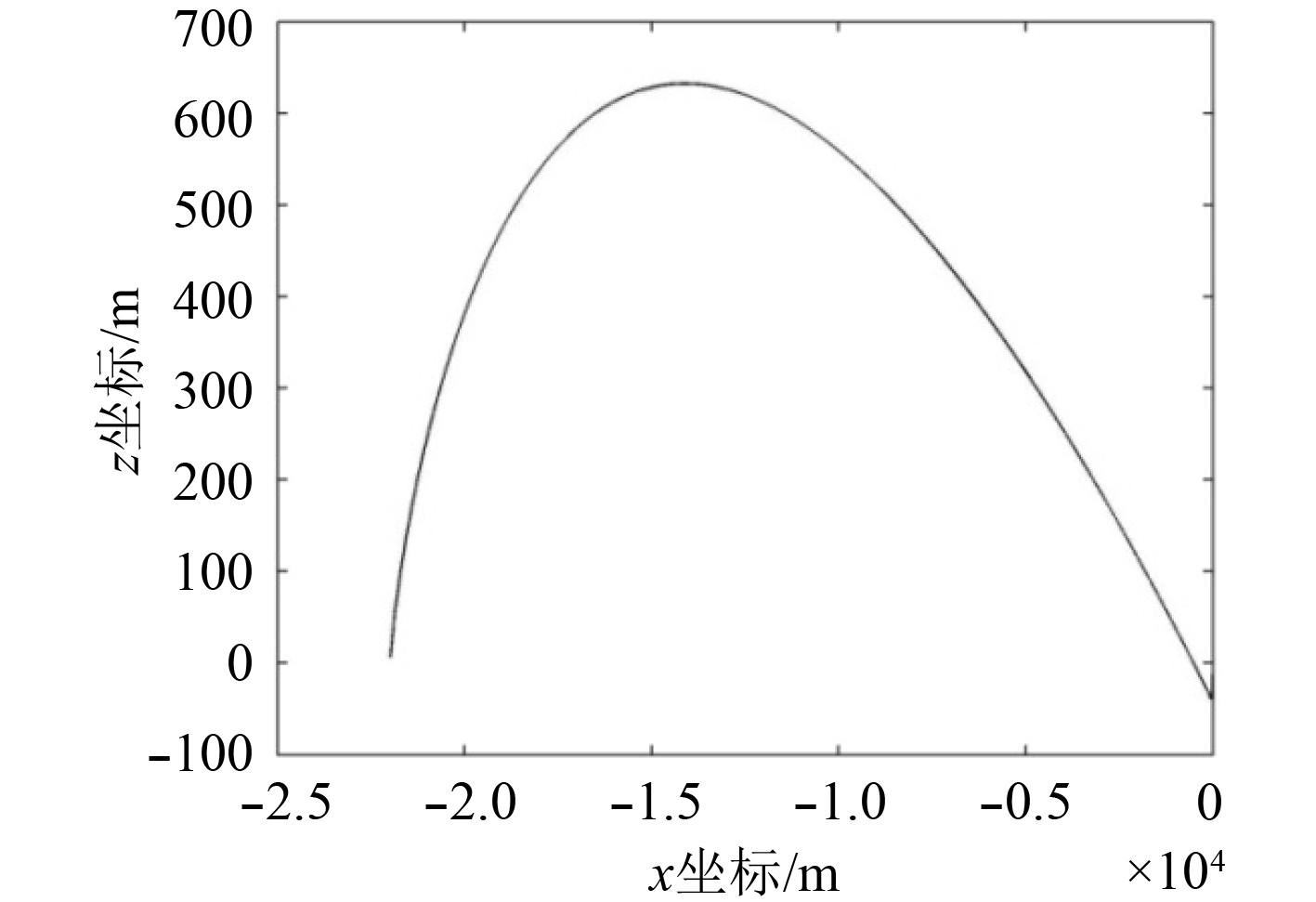
仿真实验的实验条件与实航实验条件完全相同,轨迹如图9所示。图10为仿真实验的0~4.5 km部分轨迹图。
|
图 9 AUV仿真实验轨迹图 Fig. 9 Simulative experiment tracks figure of AUV |
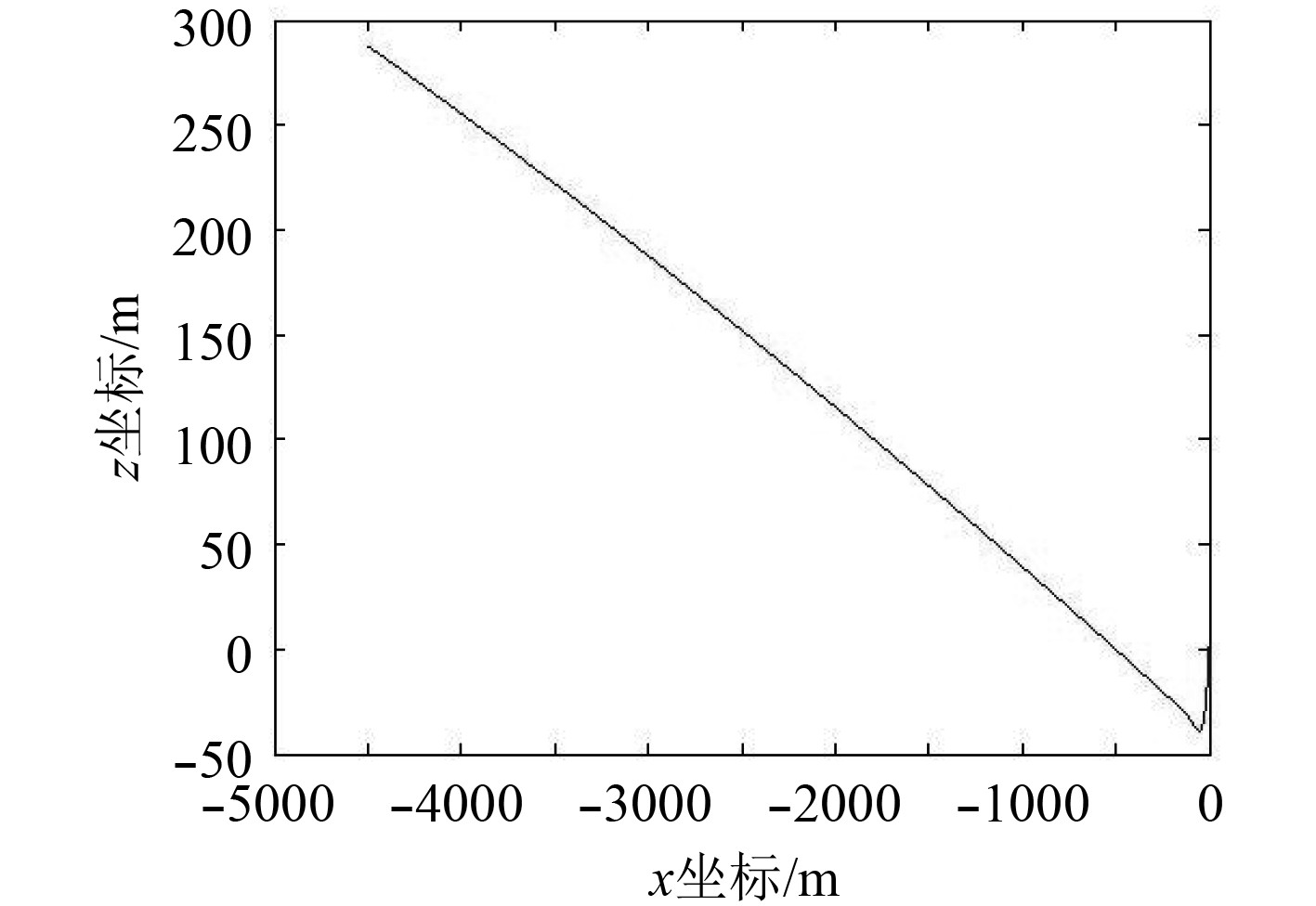
|
图 10 AUV仿真实验0~4.5 km部分轨迹图 Fig. 10 Simulative experiment 0~4 km tracks figure of AUV |
实航实验和仿真实验的实验结果对比如表3所示。插入控制点的方法航迹偏差率为0.2%,不插入控制点的方法航迹偏差率为2.87%,二者相差10倍。实验结果表明,插入航路控制点的方法可以有效减小洋流对低速AUV航迹偏移量的影响,降低航迹偏差率,使航迹更接近于直线。
|
|
表 3 实航实验与仿真的对比 Tab.3 Comparation between real experiment result and simulative experiment result |
本文通过分析AUV在航行阶段受到洋流影响现象,探究了洋流对AUV的影响机理,有针对性地提出几种减小洋流影响的方案,并对预设航路增加控制点的方案进行仿真验证。仿真结果证明预设航路控制点的方法能有效减小洋流对低速AUV航迹偏移量的影响,降低航迹偏差率,使航迹更接近于直线。该方法在实航试验中也得到了验证,并已得到实际工程应用。
| [1] |
高富东. 复杂海况下新型AUV设计与关键技术研究[D]. 长沙: 国防科技大学, 2012
|
| [2] |
范双双. 洋流影响下的水下滑翔机动力学建模、运动分析与控制器研究[D]. 杭州: 浙江大学, 2013.
|
| [3] |
房萍萍. 计及侧向流影响的自治AUV6_DOF运动仿真[D]. 天津: 天津大学, 2014.
|
| [4] |
陈玉. 复杂海洋环境下行形体的水动力特性研究[D]. 哈尔滨: 哈尔滨工程大学硕, 2012
|
| [5] |
姚鹏, 解则晓. 基于修正导航向量场的AUV自主避障方法[J/OL]. 自动化学报, 1-11[2019-03-19]. https://doi-org-443.e.buaa.edu.cn/10.16383/j.aas.c180219
|
| [6] |
苗润龙, 庞硕, 姜大鹏, 等. 海洋自主航行器多海湾区域完全遍历路径规划[J]. 测绘学报, 2019(2): 256-264. |
| [7] |
鲁燕. 海流环境中水下机器人实时运动规划方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2006.
|
| [8] |
YOERGER D, SLOTINE J. Robust trajectory control of underwater vehicles[J]. IEEE J ocean eng, 1985, 10(4): 462-470. DOI:10.1109/JOE.1985.1145131 |
| [9] |
LEVANT, ARIE. Sliding order and sliding accuracy in sliding mode control. International journal of control[J]. 1993, 58(6): 1247-1263.
|
| [10] |
LEVANT, ARIE. Higher-orderslidingmodes, differentiationandoutput-feedbackcontrol[J]. International journal of control, 2003, 76(9-10): 924-941. DOI:10.1080/0020717031000099029 |
| [11] |
SALGADO-JIMENEZ T, SPIEWAK J M, FRAISSE P, et al. Arobust control algorithm for AUV: based on a high order sliding mode[J]. IEEEtechno-ocean’04, 2004, 276-281. |
| [12] |
KHAN I, BHATTI AI, KHAN Q, et al. Sliding mode control of lateral dynamics of an AUV[C]// Proceedings of 2012 9th International Bhurban Conference on Applied Sciences Technology, 2012: 27-31.
|
 2020, Vol. 42
2020, Vol. 42
