无人水下航行器(UUV)是执行海底探测、开发、搜寻任务的重要工具[1]。本文以UUV总重量作为主优化目标进行多学科优化设计,UUV总重量的降低不仅会降低研发成本,还能大大提升UUV的续航能力和最高航速,对于高性能UUV研发具有十分重要的意义[2]。
将UUV分为阻力学科、结构学科、能源学科、推进学科4个分学科,各学科间变量参数互相存在着影响与协调的耦合关系。一般的无人水下航行器设计流程为传统的串行设计流程[3],根据设计要求,按部就班完成所有各系统设计,没有考虑各个子系统之间耦合关系,也没有考虑子系统间的统一和耦合,不仅研发成本高,也很难得到最优UUV设计方案[4]。目前国内已经开展了一些UUV多学科设计优化的技术研究,也得到了一些不错的效果,但是大部分研究都是基于常规MDO算法的局部应用性研究,目前尚没有被普遍认可的适用于UUV总体多学科设计优化的理论和方法[4]。针对单一优化方法解集覆盖率低的问题,本文基于协同MDO优化方法策略,通过组合优化的方法进行多学科优化设计以得到UUV的全局最优解。
1 UUV分学科设计 1.1 阻力学科UUV壳体分为首部、中段和尾部3个部分,其中首部和尾部分别通过进流段和去流段各自连接一部分平行中体组成,中段部分的壳体为标准圆柱形回转体,进流段和去流段均由国际通用的Myring曲线回转生成,如图1所示。

|
图 1 无人水下航行器侧视图 Fig. 1 Side view of UUV |
UUV首、尾段线型公式如下:
| $ {{r}}\left( {{x}} \right) = \frac{1}{2}{{d}}{\left[ {1 - {{\left( {\frac{{{{x}} - {{a}}}}{{{a}}}} \right)}^2}} \right]^{\frac{1}{2}}} {\text{,}} $ | (1) |
| $ \begin{split} {r} \left( x \right) =\,& \frac{1}{2}d - \left( {\frac{{3d}}{{2{c^2}}} - \frac{{\tan q}}{c}} \right){\left( {x - a - b} \right)^2} + \\ &\left( {\frac{d}{{{c^3}}} - \frac{{\tan q}}{c}} \right){\left( {x - a - b} \right)^3} {\text{。}} \end{split} $ | (2) |
式中:a为首部长度,b为中段长度,c为尾部长度,d为直径,θ为尾椎角,n为首部锐度。
UUV作业过程中如果下潜深度超过了自身长度,就能够忽略兴波阻力的影响,那么巡航速度下总阻力为:
| $ \begin{split} & {R} = {R_f} + {R_{PV}} + {R_{AP}}{\text{,}} \\ & {R} = \frac{1}{2}rV_{el}^2S\left( {{C_f} + V{C_f} + {C_{PV}} + {C_{AP}}} \right) {\text{。}} \end{split} $ | (3) |
式中:R为总阻力,Rf为摩擦阻力,Rpv为形状阻力,Rap为外加阻力,Cf为摩擦阻力系数,Cpv为形状阻力系数,Cap为
本文拟优化的UUV航行深度为100 m,根据《潜水器系统和潜水器入级与建造规范》完成强度校核。耐压舱包括变频舱和电池舱,全部选择铝合金材料,UUV强度校核方法如下:
1)确定计算压力
| ${{P} _j} = 1.5 \times rgh = 1.5{\rm MPa}$ | (4) |
2)公式里的代表符号与辅助函数
| $ {u} = \frac{{\sqrt[4]{{3\left( {1 - {m^2}} \right)}}}}{2}\frac{l}{{\sqrt {Rt} }};{y} = \frac{{\sqrt {3\left( {1 - {m^2}} \right)} }}{2}\frac{{{P_j}{R^2}}}{{E{t^2}}}{\text{,}} $ | (5) |
| $ \beta = \frac{{lt}}{F};{{u} _1} = u\sqrt {1 - y};{{u} _2} = u\sqrt {1 + y}{\text{,}} $ | (6) |
| $ {{\mathop{ F}\nolimits} _1}\left( {{u_1},{u_2}} \right) = \frac{{\sqrt {1 - {y^2}} \left( {ch2{u_1} - \cos 2{u_2}} \right)}}{{{F_5}\left( {{u_1},{u_2}} \right)}} {\text{,}} $ | (7) |
| $ {{\mathop{ F}\nolimits} _2}\left( {{u_1},{u_2}} \right) = \frac{{3\left( {1 - 0.5m} \right)\left( {{u_2}sh2{u_1} - {u_1}\sin2{u_2}} \right)}}{{\sqrt {3\left( {1 - {m^2}} \right)} {F_5}\left( {{u_1},{u_2}} \right)}}{\text{,}} $ | (8) |
| $ \begin{split} &{{\mathop{ F}\nolimits} _3}\left( {{u_1},{u_2}} \right) =\\ &\frac{{6\left( {1 - 0.5m} \right)\left( {{u_1}ch{u_1}\sin {u_2} - {u_2}sh{u_1}\cos {u_2}} \right)}}{{\sqrt {3\left( {1 - {m^2}} \right)} {F_5}\left( {{u_1},{u_2}} \right)}}{\text{,}} \end{split} $ | (9) |
| $ \begin{split} & {{\mathop{ F}\nolimits} _4}\left( {{u_1},{u_2}} \right) =\\ & \frac{{2\left( {1 - 0.5m} \right)\left( {{u_1}ch{u_1}\sin {u_2} + {u_2}sh{u_1}\cos {u_2}} \right)}}{{{F_5}\left( {{u_1},{u_2}} \right)}}{\text{,}} \end{split} $ | (10) |
| $ {{\mathop{ F}\nolimits} _5}\left( {{u_1},{u_2}} \right) = {u_2}sh2{u_1} + {u_1}\sin 2{u_2} {\text{。}} $ | (11) |
式中:Pj为计算压力,u为象征外形几何形状的数据,t为壳体厚度,R为UUV的半径,μ为泊松比,l为肋板间距,F为肋板截面积,E为材料弹性模量。
3)应力计算与校验
本文中选取的UUV结构形式为等间距的环形肋板结构。环形肋板结构周围包覆的壳体同时受到均匀的深水静压力作用产生的侧向压力以及轴向压力的作用,导致结构的变形,甚至最后发生破坏。对结构强度的计算采用下面的公式:
1)工字梁中点处的水平均应力
| $ \sigma _2^0 = - K_2^0\frac{{{P_j}R}}{t}{\text{。}} $ | (12) |
式中:R为UUV中部半径;h为UUV在水中的航行的深度,Pj为在该深度下的深水静压。
2)肋板处结构的纵向相当应力
| $ {\left( {{\sigma _l}} \right)_{x = \frac{1}{2}}} = - \left( {0.91{K_1} - 0.3{K_r}} \right)\frac{{{P_j}R}}{t} {\text{。}} $ | (13) |
3)肋板上的应力
| $ {\sigma _r} = - {K_r}\frac{{{P_j}R}}{t} {\text{。}} $ | (14) |
UUV的能源系统氛围控制用电和动力用电两类,根据搭载试验设备的要求,选用500 AH/300 V的电池。装载电池组模块的电池箱尺寸为840 mm×1 180 mm×720 mm,电池组模块的重量约为820 kg。UUV最高设计航速15 kn,以最高航速航行的最远航程需花费10 h。螺旋桨的有效功率为:
| $ {{P} _E} = {V_{\rm Max}}{R_{\rm Max}} {\text{。}} $ | (15) |
式中:Vmax为最大航速;Rmax为最大航速航行时的阻力,能够经由阻力系统中的阻力估算公式得到。
航行器主机功率为:
| $ {{P} _S} = \frac{{{P_E}}}{{{\eta _1}{\eta _2}}} {\text{。}} $ | (16) |
式中:η1为螺旋桨的效率,选择起始值0.53;η2为电机效率,按经验值取0.75。电池放电按90%计算,电源需要的总能量为:
| $ {W} = {P_{\max}}h/90\% {\text{,}} $ | (17) |
电池的重量为:
| $ {M} = r\left( {{V_d} + {V_c}} \right) {\text{。}} $ | (18) |
螺旋桨推力和效率设计要求如下:
1)螺旋桨的推力大于航行器的最大阻力
| $ {Cons} = \rho {K_t}{M^2}D_p^4 - {R_{\max}} > 0 {\text{。}} $ | (19) |
式中:Kt为推进力系数,M为螺旋桨的转速,Dp为螺旋桨的直径。
2)螺旋桨的功率小于主机功率
| $ {ConsP} = {P_s} - 2{\text{π}} {M} Q > 0 {\text{。}} $ | (20) |
式中Q为螺旋桨转矩。
3)螺旋桨的直径超过航行器直径的0.8倍
| $ {ConsD} = 0.8d - {D_p} > 0 {\text{。}} $ | (21) |
本文选择协同优化方法(CO),对UUV进行多学科优化设计。协同优化方法将把整体分作两级:系统级与子系统级。各个子系统分别进行优化,信息在系统内不进行传递。所有子系统解出的解集合输入系统级完成优化,最后解出一组达到所有子系统和总体性能要求前提下优化结果。UUV在协同优化方法下的多学科优化设计流程如图2所示。

|
图 2 协同优化方法示意图 Fig. 2 Diagram of CO |
以UUV总重量最低为优化目标,结构壳体与搭载的设备占据质量绝大部分,UUV多学科优化设计的系统级变量如表1所示。
|
|
表 1 无人水下航行器系统级参数 Tab.1 System data of UUV |
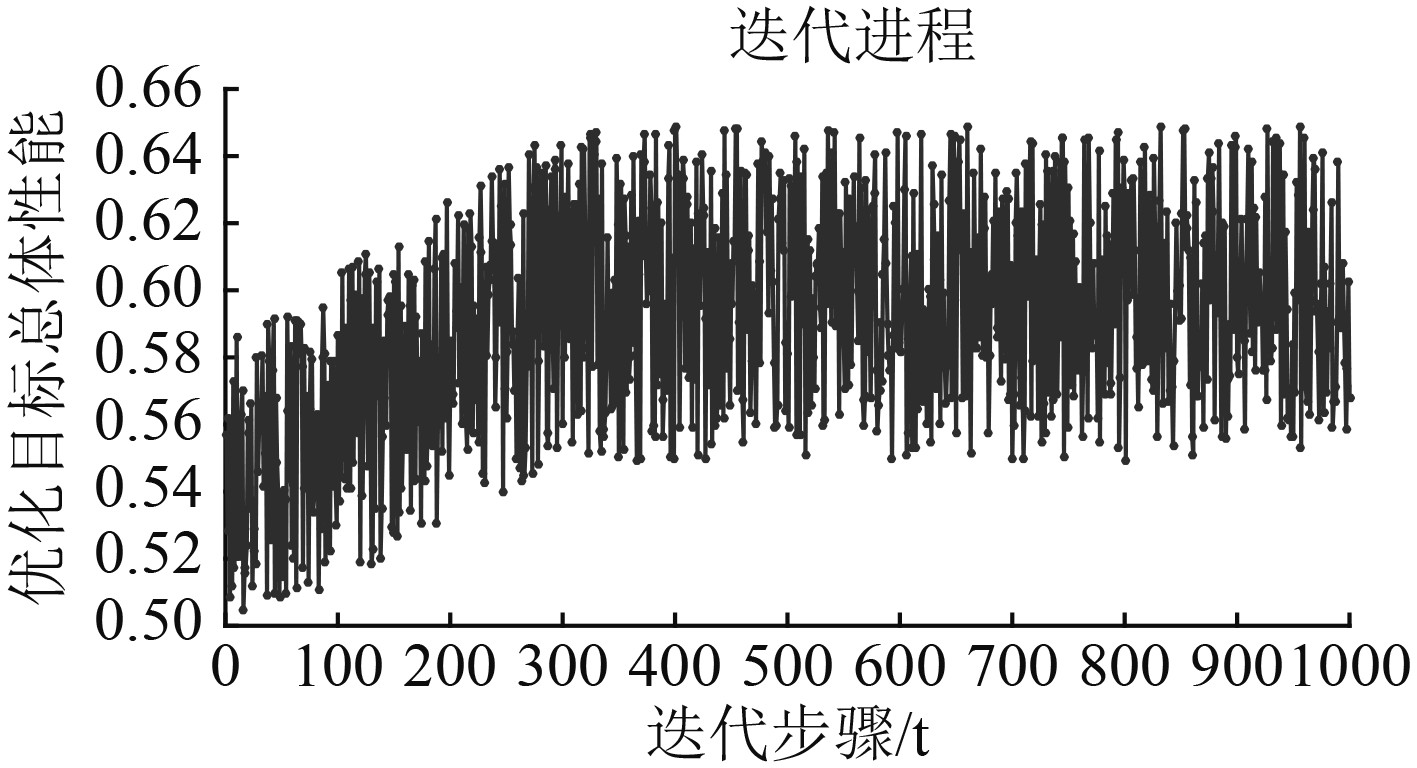
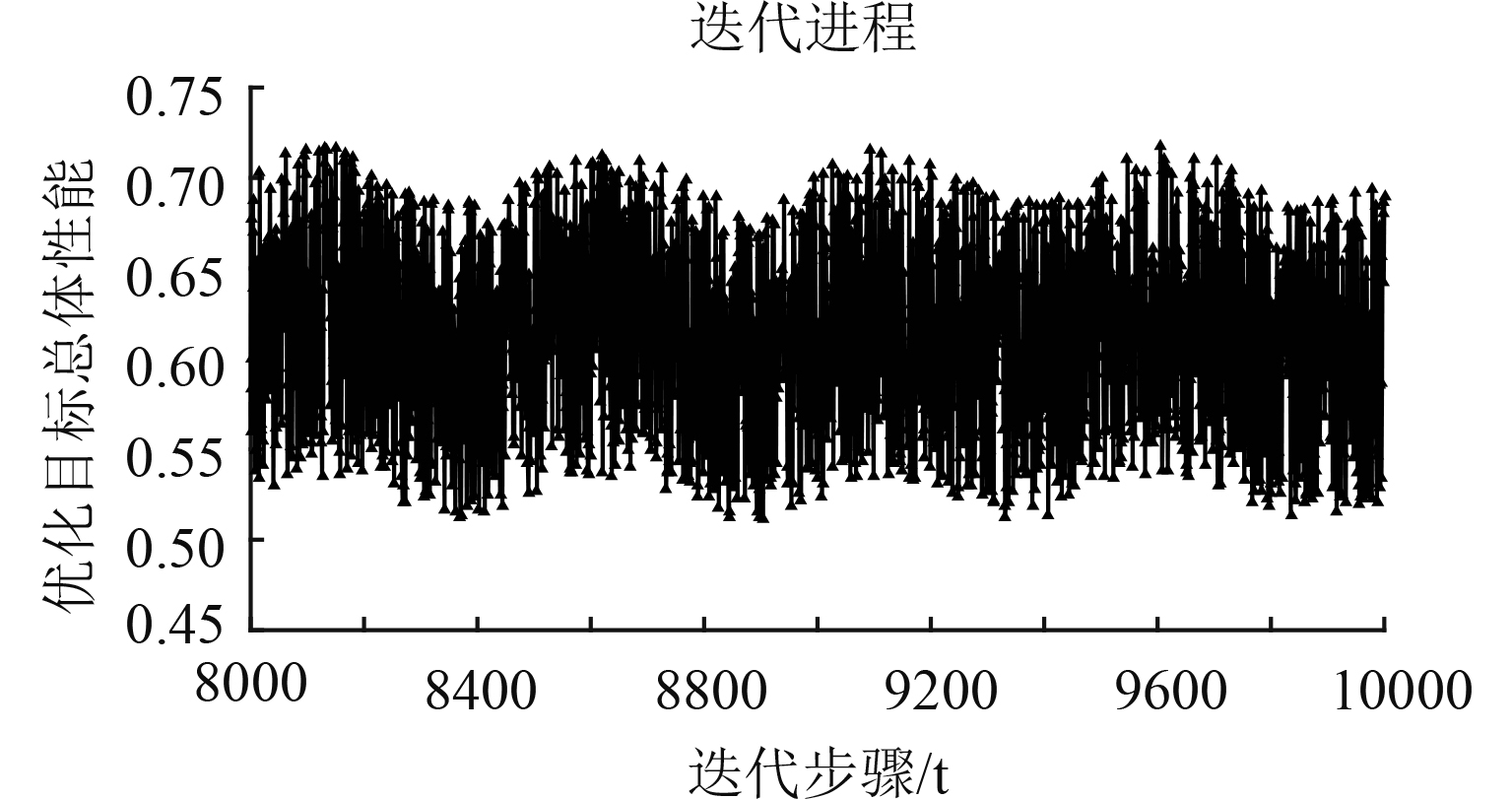
系统级优化选择序列二次规划法加多岛遗传算法组合以及序列二次规划法加自适应模拟退火法。2种组合优化方法迭代历程如图3和图4所示。
|
图 3 NLPQL+MIGA算法目标函数迭代历程(0~1 000步) Fig. 3 Iteration of NLPQL combined with MIGA |
|
图 4 NLPQL+ASA算法目标函数迭代历程(8 000~10 000步) Fig. 4 Iteration of NLPQL combined with ASA |
子系统先分别完成优化,接下来将所得解集输入至系统级。子系统级的模型的建立以及优化分析,包括所有的设计参数、约束条件、输出参数、构造模型与选取的优化算法完全一致。
3 结果分析与仿真校验 3.1 结果分析基于协同多学科优化策略的UUV优化结果如表2所示。
|
|
表 2 无人水下航行器优化结果 Tab.2 Optimization result of UUV |
由表3可以看出,UUV采用协同优化方法进行组合优化时,通过对目标总体质量以及设计变量首部、中段、尾部长度、中段直径、壳体厚度、主机功率、最大阻力、螺旋桨效率的优化,使总体质量最多降低23.07%。对比2种方法可以知道在协同优化方法下序列二次规划法结合自适应模拟退火法的结果更优。
|
|
表 3 水下无人航行器模态分析振动频率 Tab.3 Modality analysis vibration frequency of UUV |
根据无人水下航行器双点起吊方式以及海上起吊环境,对整个船体及其内部结构在36 t(3倍自重载荷)静载荷作用下的力学强度及稳定性进行分析,用Ansys进行静力学分析,由于复合材料是各向异性材料,出于可靠性考虑选用所有计算均采用小数值进行模拟计算。考虑连接加强效果,所有连接处均做一体化处理,计算结果如图5所示。

|
图 5 UUV静力学分析云图 Fig. 5 UUV static analysis cloud image |
图5(a)~图5(c)所示为UUV整体结构在36 t静载荷下空间X,Y,Z三个方向的变形量,变形量都小于1 mm。竖直Y方向的变形量最小,变形量较大部分主要集中在UUV中间吊点附近。纵向Z轴方向变形量最大约为0.546 mm,变形量符合无人水下航行器的设计要求,最大变形位置主要集中在无人水下航行器头部位置。图5中(d)~图5(f)为无UUV整体结构在空间X,Y,Z三个方向的应力分布。X方向最大应力约为4.975 9E+6 Pa,应力分布较为均匀,在X方向应力集中不明显。Y方向最大应力为6.97E+6 Pa,Z方向最大应力为7.33E+6 Pa,应力主要集中在吊点附近,所以吊点处需要用钛合金局部加强。
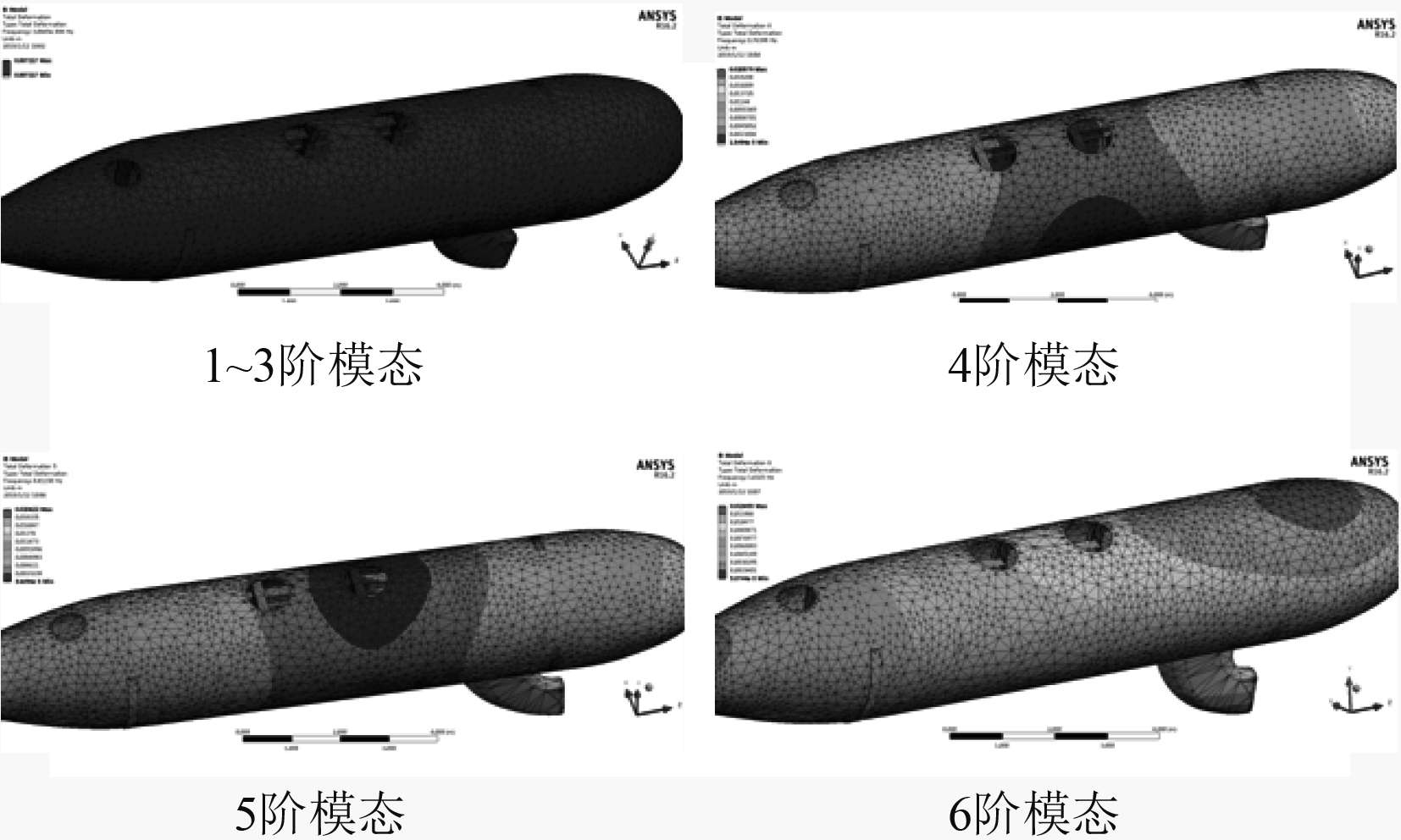
3.2.2 稳定性分析在UUV实际作业过程中,当外界激励的频率接近航行器的固有频率时,无人水下航行器自身振动对其测量精度产生了不可忽略的影响。因此,对UUV进行模态分析,确保UUV自身的固有频率远离外界干扰的频率,以保证UUV的稳定性。为方便计算,在进行UUV模态分析时,假设UUV内部质量均匀分布。对UUV进行各阶模态分析后得到其各阶的频率,如表3所示。
根据表3能够看出UUV前3阶模态下本体结构没有出现变形,前3阶频率基本为0。以第4阶为起点,UUV振动频率迅速增大,此时UUV并不相当于刚体,会发生较大程度的变形。也就是说现实情况下应该重点关注第四阶开始的情况,UUV如果出现共振会对它的可靠性和传感器的测量精度产生严重干扰。UUV前6阶模态下的整体变形量云图如图6所示。
|
图 6 UUV的1~6阶模态 Fig. 6 UUV 1~6 modes |
UUV在水下进行运动时螺旋桨持续进行工作,螺旋桨的动力来自于舵机,最高转速是700 r/min,此转速下频率是11.67 Hz,与6阶的共振频率相差巨大,因此主推达到设计要求。
UUV在水下进行运动时的方向改变和方向维持,通过转向舵完成,转向舵机转速是1 000 r/min,此转速下频率是16.67 Hz,由于并未达到UUV的共振频率,转向舵机符合要求。UUV在水中进行运动时下潜、上浮和维持指定深度运动通过航行器的俯仰舵机来进行,俯仰舵机转速是2 400 r/min,此转速下频率是40 Hz,同样并未达到UUC的共振频率,所以俯仰舵机符合要求。
4 结 语本文基于协同多学科设计优化方法,在满足UUV各个子系统约束要求的前提下,使优化的目标重量明显减小,实现了对UUV的整体优化。本文的多学科优化设计问题中,将无人水下航行器分为4个子系统,为了得到真正的最优解,本文选择以序列二次规划算法(NLPQL)结合自适应模拟退火算法(ASA)和序列二次规划算法(NLPQL)结合多岛遗传算法(MIGA)的组合优化。最后对UUV本体进行结构静力学分析与稳定性分析,验证了本文优化结果的准确性。根据优化结果,UUV总重量降低23.07%,在一定程度上降低了UUV制造成本,使得单位航程能耗降低,同时提高了航速。
| [1] |
MAHMOUDZADEH S, POWERS D M W, ATYABI A. UUV's Hierarchical DE-Based Motion Planning in a Semi Dynamic Underwater Wireless Sensor Network[J]. IEEE Transactions on Cybernetics, 2018, 99: 1-14. |
| [2] |
潘光, 宋保维, 黄桥高, 等. 水下无人系统发展现状及其关键技术[J]. 水下无人系统学报, 2017, 25(2): 44-51. |
| [3] |
齐翔, 唐晓, 齐欢. 基于改进Jackson船型的潜艇外形多学科设计优化[J]. 舰船科学技术, 2018, 40(21): 35-38. |
| [4] |
ZHANG D, SONG B, WANG P, CHEN X. Multidisciplinary optimization design of a new underwater vehicle with highly efficient gradient calculation[J]. Structural & Multidisciplinary Optimization, 2017, 55(4): 1483-1502. |
| [5] |
张礼华, 刘芳华, 楼飞, 等. 单体式无人航行器的设计、实验及优化[J]. 中国造船, 2016, 57(4): 131-138. DOI:10.3969/j.issn.1000-4882.2016.04.015 |
 2020, Vol. 42
2020, Vol. 42
