2. 中国舰船研究设计中心上海分部,上海 201108;
3. 上海交通大学 海洋智能装备与系统教育部重点实验室,海洋工程国家重点实验室,上海 200240
2. China Ship Development and Design Center Shanghai Branch, Shanghai 201108, China;
3. MOE Key Laboratory of Marine Intelligent Equipment and System, State Key Laboratory of Marine Engineering, Shanghai Jiaotong University, Shanghai 200240, China
滑行艇在军事和民用领域的应用非常广泛,其相关研究工作也在大量进行。传统上,滑行艇的设计和优化工作基于经验公式和模型试验。随着CFD技术的发展,模型试验结合CFD成为滑行艇设计优化和性能分析的主流手段之一。CFD技术在滑行艇水动力性能分析中扮演了愈来愈重要的角色。相比潜艇和排水型船,高速滑行艇的数值仿真难度更大。Brizzolara等[1]和王硕等[2]分别进行了滑行艇数值仿真计算精度的研究,均使用了NACA公布的滑行楔形体模型。Brizzolara等在数值仿真计算中使用了六面体网格,王硕等在数值仿真计算中使用了六面体网格和切割体网格。他们的研究工作表明基于CFD的滑行艇数值仿真精度很高,误差在实验测量误差之内,表明基于CFD的滑行艇数值仿真计算可以应用于实际工程中。
网格是CFD分析的基础。现实中的滑行艇通常具有复杂几何形状的船体表面,经典的六面体网格很难对其进行网格划分。因此,采用非结构性网格成为解决此类网格贴面问题的重要手段。传统上,四面体网格被用来适配一些滑行艇的复杂几何表面,但近年来切割体网格(trimmed mesh或cut cell)开始得到比较广泛的应用。除了非结构性的四面体网格和切割体网格外,多面体网格也逐渐得到广泛应用。多面体网格已经在空气动力学相关领域有了广泛的应用并赢得良好的口碑[3]。但是多面体网格在海洋工程领域中的应用十分有限。多面体网格是一种非结构网格。二维多面体网格主要由六边形网格构成,其几何形式广泛存在于自然界中;三维多面体网格单元为任意多面体形状。多面体网格在引入可靠的基于面的有限体积法和相关的多面体网格生成器后才逐渐可用,并在近几年得到了商业解算器的推广。相较于同为非结构网格的四面体网格,多面体网格有更多的临近单元,能够更加精确地计算梯度及局部的流动状况,并且对几何变形没有四面体网格敏感。对于一种新兴的并具有良好特性的网格,有必要验证其在海洋工程领域中的适用性。
研究人员在对滑行艇进行数值计算时经常会遇到伪扩散的问题。一层薄空气层会附在船体,与实际船体表面水气分布不符合。若使用VOF法[4]捕捉自由面,伪扩散意味着船体浸没表面部分或全部的水组分不等于1。这个空气层会直接影响船体表面的切应力。伪扩散解方程欧拉型模式所特有的,其大小与所用的有限差分格式有关。为了克服伪扩散,须采取特殊的技术措施和各种不同的差分格式。在网格设置方面,克服伪扩散的方法有增加网格密度,沿流线方向布置网格。王志刚等[5]指出,网格加密10倍伪扩散效应就减小1个量级。每个方向按10 倍进行加密,那么3个方向的网格数将是原网格数的1 000 倍,需要付出极大的计算代价。故采用网格加密不能有效减小伪扩散效应,而沿流线方向布置网格总体上仅对静态仿真有效,当网格发生改变时原有优化布置的网格很可能不再与流线方向相符合。此外,FRISK[6]在研究中通过添加源汇,强制性将船体湿表面处水组分小于0.7的地方设置为1。Spiegel等[7]对比分析了四面体网格和多面体网格在脑血管动力学仿真计算中的应用效果,认为多面体网格收敛性更好,且对WSS(wall shear stress)的计算更准确,这对计算滑行艇的摩擦阻力是有益的。参考文献[7]并考虑到多面体网格有更多的临近单元,能够更加精确地计算梯度及局部的流动状况,本文尝试通过使用多面体网格处理滑行艇数值仿真中遇到的伪发散问题。
研究证实,基于多面体网格滑行艇的水动力预报具有相当高的精度,完全满足工程需要,多面体对控制滑行艇仿真计算中出现的伪扩散问题有很大改善。
1 多面体网格计算精度分析使用NACA公开的滑行楔形体几何模型及相关的实验设置和实验数据[8]。滑行楔形体的几何尺寸参见文献[8],几何模型如图1所示。选择底部斜升角为20°的模型。仿真计算采用固定模式,即模型初始状态设置为水池实验中测量到的状态。选择其中几个典型的工况进行仿真计算,如表1所示。实验中测得的升力平均相对误差为3%,最大相对误差为8%;测得的阻力平均相对误差为20%,最大相对误差为50%;速度平均相对误差为0.70%,最大相对误差为1.30%;吃水平均相对误差为5%,最大相对误差为10%;纵倾角平均相对误差为2%,最大相对误差为5%。
|
图 1 NACA滑行楔形体几何轮廓 Fig. 1 NACA planing wedge |
|
|
表 1 基于NACA滑行楔形体的数值计算工况统计 Tab.1 Statistics on simulations of NACA planing wedge |
数值仿真计算使用重叠网格,背景网格使用切割体网格控制网格密度,减小网格数量和提高网格的分层性和正交性。随体网格通过合理布置获得良好分层性和正交性的多面体网格。合理布置网格密度及改善网格的正交性和分层性对自由面锯齿现象的消除及兴波与飞溅的捕捉非常关键。计算域和网格设置如图2所示。由于使用重叠网格,网格数量在260万左右。
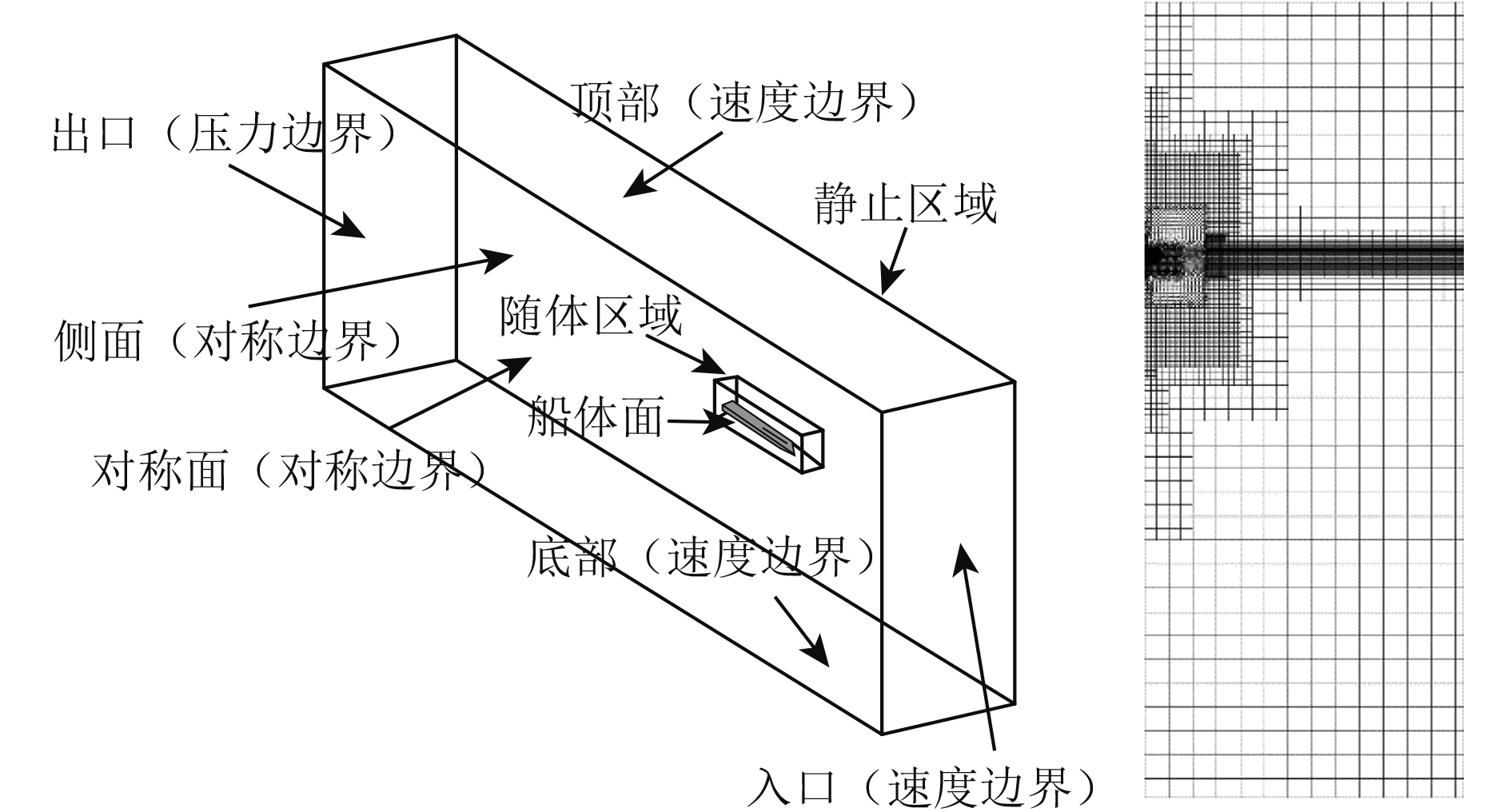
|
图 2 基于NACA滑行楔形体的计算域设置及网格 Fig. 2 Computational domain settings and mesh |
计算选用STAR CCM作为求解器来求解非稳态RANS方程。数值计算选用SST k-ω[9]湍流模型。为了对自由面的捕捉,使用VOF(volume of fluid)模型。为了减小计算代价并参考文献[10],使用高yplus(又称y+)壁面函数和较为粗糙的近壁面网格在一定程度上减少网格数量来提高计算速度。
数值仿真计算给出了光顺的兴波图,在传统非结构网格在波形描绘中出现的等高线锯齿现象有很大改善,如图3所示。将本文的计算结果同水池实验结果及文献[1]和文献[2]中的阻力和升力结果进行汇总(见表2和表3)。表4和表5进一步汇总了本文及文献[1]和文献[2]中的计算误差。文献[1]基于六面体网格的计算结果标记为HEX-1;基于六面体网格的计算结果标记为HEX-2,文献[2]基于切割体网格的计算结果标记为TRIMMED;本文的计算结果标记为POLY。对比文献[8]中NACA给出的水池一般性固有误差可见,基于多面体网格的数值仿真计算的升力误差与其3%固有平均误差相比稍微偏大,但误差均小于最大相对误差,而阻力计算误差远小于其20%的参考值。同其他计算结果对比表明,基于多面体网格的阻力预报的精度稍高,而升力的预报的误差稍微偏大。对比每一个工况下不同网格的阻力和升力预报可知,基于多面体网格的预报结果误差值和分布具有一定的相似性。

|
图 3 NACA滑行楔形体兴波(case2) Fig. 3 Wave making of NACA planing wedge (case2) |
|
|
表 2 不同网格的NACA滑行楔形体阻力计算结果 Tab.2 Numerical results of drag of NACA planing wedge based on different meshes |
|
|
表 3 不同网格的NACA滑行楔形体升力计算结果 Tab.3 Numerical results of lift of NACA planing wedge based on different meshes |
|
|
表 4 不同网格的NACA滑行楔形体阻力计算结果误差 Tab.4 Drag error of NACA planing wedge based on different meshes |
|
|
表 5 不同网格的NACA滑行楔形体升力计算结果误差 Tab.5 Lift error of NACA planing wedge based on different meshes |
通过以上对比可见,基于多面体网格的滑行艇水动力预报具有相当高的精度,完全满足工程需要。
2 多面体网格对伪扩散的改善在基于切割体网格、尝试使用STAR CCM作为求解器对某一细长尖肶滑行艇进行数值仿真计算时遇到了伪扩散问题,表现为船体湿表面处的水组分值应为1的地方却小于1。但在使用多面体网格(填充随体区域)和六面体网格(填充静止区域)构成的混合网格并利用FLuent求解时未遇到伪扩散问题,船底湿表面处水组分值为1,如图4所示。在研究过程中发现,通过合理设置第一层网格的高度和选择合适的壁面函数可以改善基于切割体网格的伪扩散问题,但不能完全解决。为了验证多面体网格改善伪扩散的能力,对比不同yplus下,Fn=1.63时分别基于切割体网格和多面体网格的船体表面水组分分布及阻力预报结果。网格采用上一节中的设置,区别在于随体区域分别由切割体网格填充和由多面体网格填充。船体固定,姿态设置为基于四面体网格给出的预报值。计算基于求解非稳态RANS方程。
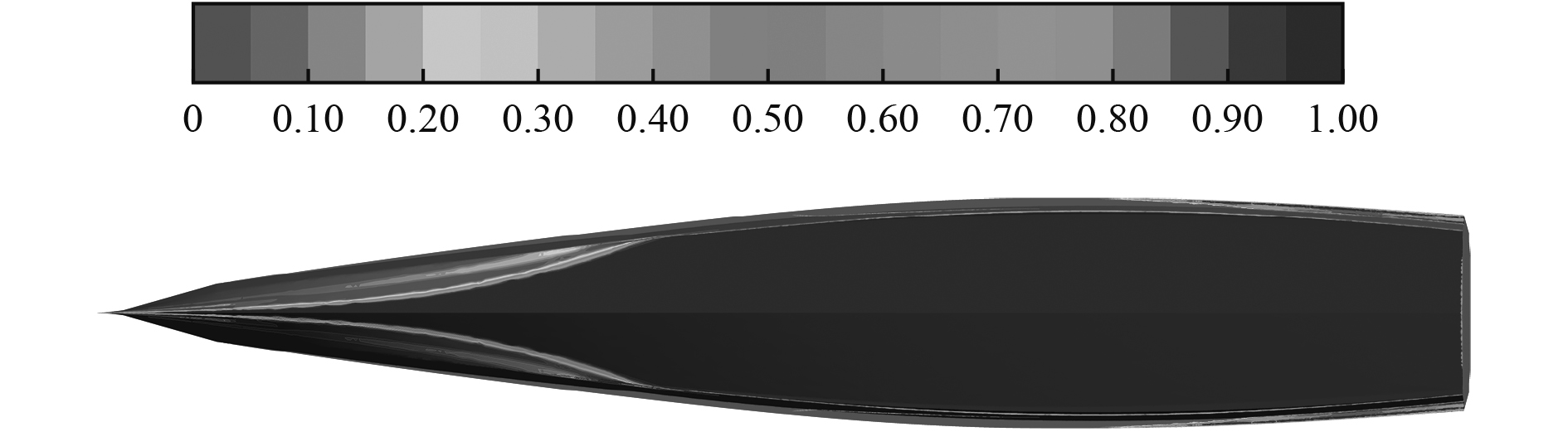
|
图 4 基于多面体网格的船体表面水组分分布 Fig. 4 Volume fraction of water on the hull bottom predicted by polyhedral mesh |
由图5可知,不同yplus下切割体网格对伪扩散的敏感性要明显高于多面体网格。对比工况a和工况b,可见在壁面函数选择和yplus值分布区间不合理时,基于多面体网格的数值仿真计算仍然给出了合理的船底水组分分布,而基于切割体网格的数值仿真计算则出现了严重的伪扩散。水组分分布直接影响了摩擦阻力的预报。由表6可知,工况a所得的摩擦阻力系数远小于其他工况所得的摩擦阻力系数。当选合理选择壁面函数和yplus值分布区间时,基于切割体网格的数值仿真计算遇到的伪扩散问题有很大改善,但是没有彻底消除。而基于多面体网格的数值仿真计算未遇到伪扩散的问题,对伪扩散不敏感。因此在不能很好确定流场状况及第一层网格高度的情况下,使用多面体网格可以减小预报误差。此外,本文研究结果也同文献[7]中提到的多面体网格对WSS(wall shear stress)的计算更准确形成呼应。

|
图 5 不同yplus下的基于多面体网格和切割体网格船底面水组分分布 Fig. 5 Volume fraction of water on the hull bottom predicted by polyhedral and trimmed meshes under different yplus |
|
|
表 6 不同工况下网格参数及阻力系数 Tab.6 Mesh information and drag coefficient of different cases |
本文研究得到以下结论:
1)基于多面体网格的滑行艇数值仿真计算具有相当高的精度,完全满足工程需要;
2)多面体可以改善滑行艇仿真计算中遇到的伪扩散问题。通过对比切割体网格可知,基于多面网格的滑行艇的数值计算对伪扩散问题不敏感。对于一些具有复杂外形设计、难以使用六面体网格计算域填充的滑行艇仿真案例,若使用切割网格遇到伪扩散问题时则可以考虑使用多面体网格,或者直接使用多面体网格填充随体区域来尝试解决遇到的伪扩散问题。
| [1] |
BRIZZOLARA S, SERRA F. Accuracy of CFD codes in the prediction of planing surfaces hydrodynamic characteristics[C]//2nd International Conference on Marine Research and Transportation. 2007: 147-159.
|
| [2] |
王硕, 苏玉民, 庞永杰, 等. 高速滑行艇CFD精度研究[J]. 船舶力学, 2013, 17(10): 1107-1114. DOI:10.3969/j.issn.1007-7294.2013.10.002 |
| [3] |
DIEDRICHS B. Aerodynamic calculations of crosswind stability of a high-speed train using control volumes of arbitrary polyhedral shape[J]. Bluff Bodies Aerodynamics & Applications, 2008(6): 20-24. |
| [4] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of computational physics, 1981, 39(1): 201-225. DOI:10.1016/0021-9991(81)90145-5 |
| [5] |
王志刚, 禚玉群, 陈昌和, 等. 四角切圆锅炉流场伪扩散效应网格的研究[J]. 中国电机工程学报, 2007, 27(5): 22-28. DOI:10.3321/j.issn:0258-8013.2007.05.005 |
| [6] |
FRISK D, TEGEHALL L. Prediction of high-speed planing hull resistance and running attitude[D]. Chalmers University of Technology, 2015
|
| [7] |
SPIEGEL M, REDEL T, ZHANG Y J, et al. Tetrahedral vs. polyhedral mesh size evaluation on flow velocity and wall shear stress for cerebral hemodynamic simulation[J]. Computer Methods in Biomechanics and Biomedical Engineering, 2011, 14(1): 9-22. DOI:10.1080/10255842.2010.518565 |
| [8] |
CHAMBLISS D B, BOYD G M. The planing characteristics of two V-shaped prismatic surfaces having angles of deadrise of 20° and 40°[R]. Langley Aeronautical Laboratory, NACA. Tech. Note 2876. Washington, 1953.
|
| [9] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
| [10] |
孙华伟, 马伟佳, 朱江波. 影响滑行艇阻力数值计算的网格因素研究[J]. 中国造船, 2015, 56(2): 170-178. DOI:10.3969/j.issn.1000-4882.2015.02.020 |
 2020, Vol. 42
2020, Vol. 42
